Effect of Temperatures on Drying Kinetics, Extraction Yield, Phenolics, Flavonoids, and Antioxidant Activity of Phaleria macrocarpa (Scheff.) Boerl. (Mahkota Dewa) Fruits
Abstract
:1. Introduction
2. Materials and Methods
2.1. Chemicals, Reagents, and Equipment
2.2. Collection of Raw Materials
2.3. Sample Preparation
2.4. Drying Kinetics
2.4.1. Determination of Thin-Layer Mathematical Modelling
2.4.2. Determination of Effective Moisture Diffusivity
2.4.3. Determination of Activation Energy
2.5. Estimation of Extraction Yield
2.6. Estimation of Phenolics and Flavonoids
2.6.1. Total Phenolic Content
2.6.2. Total Flavonoid Content
2.7. Estimation of Antioxidant Activity
2.8. Statistical Analysis
3. Results and Discussion
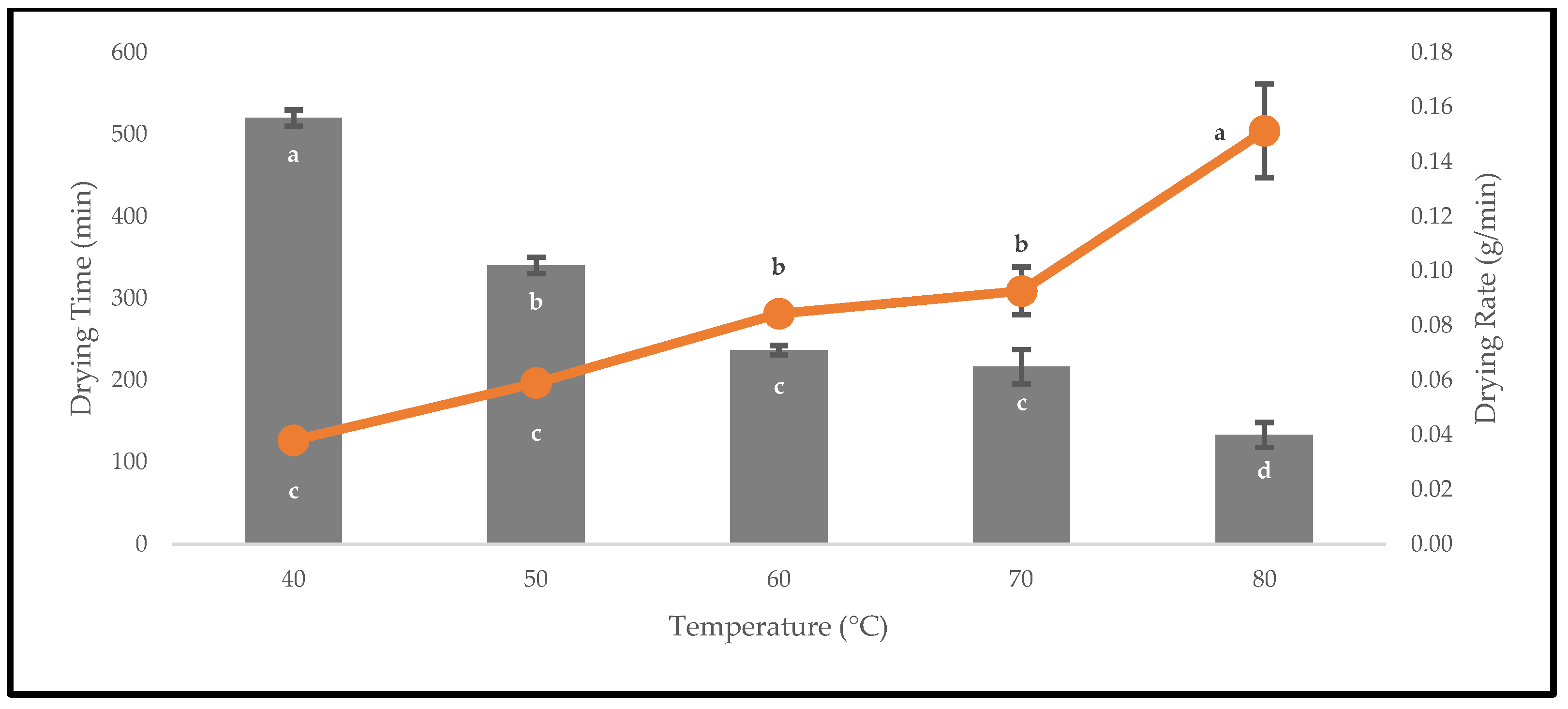
3.1. Effect of Drying Temperatures on Drying Times and Drying Rates
3.2. Effect of Drying Temperatures on Moisture Removal Rates
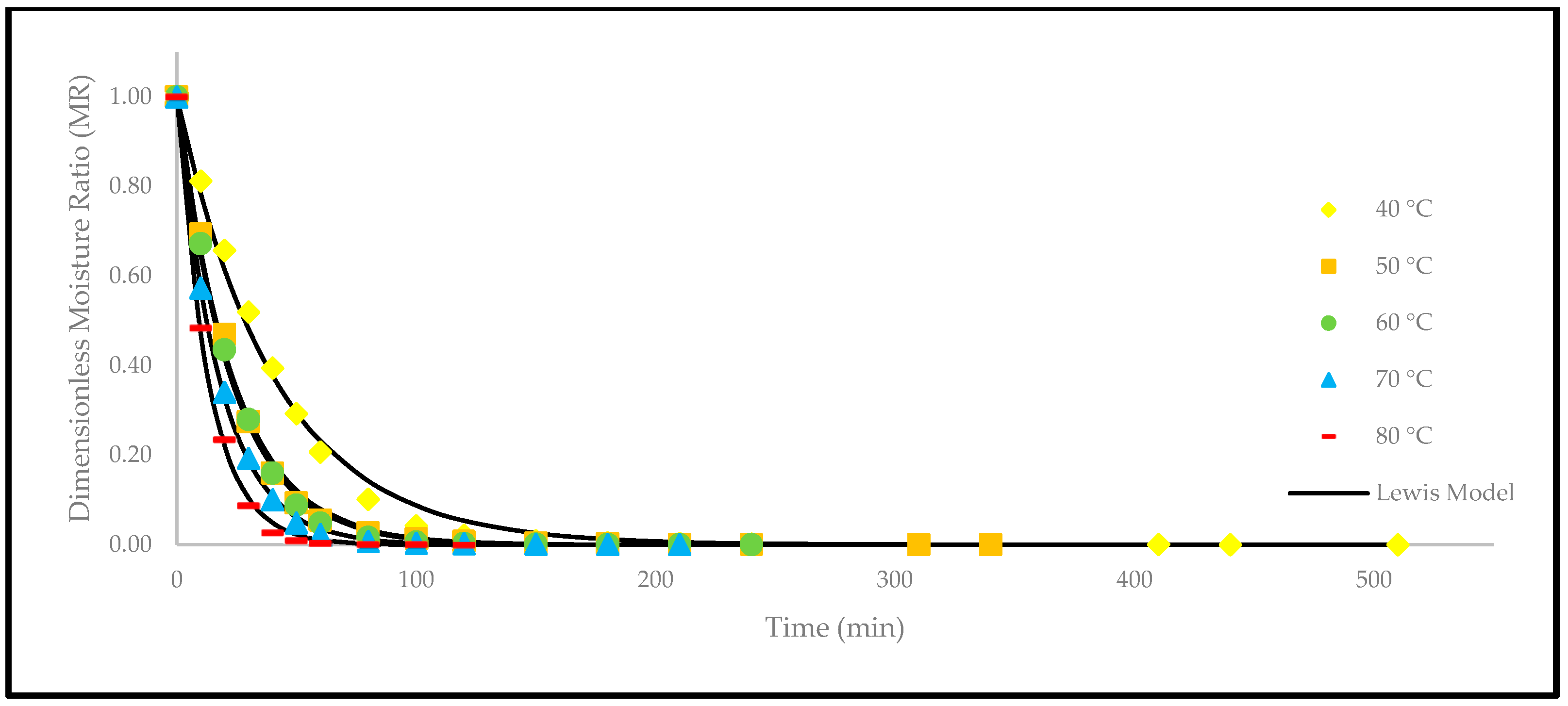
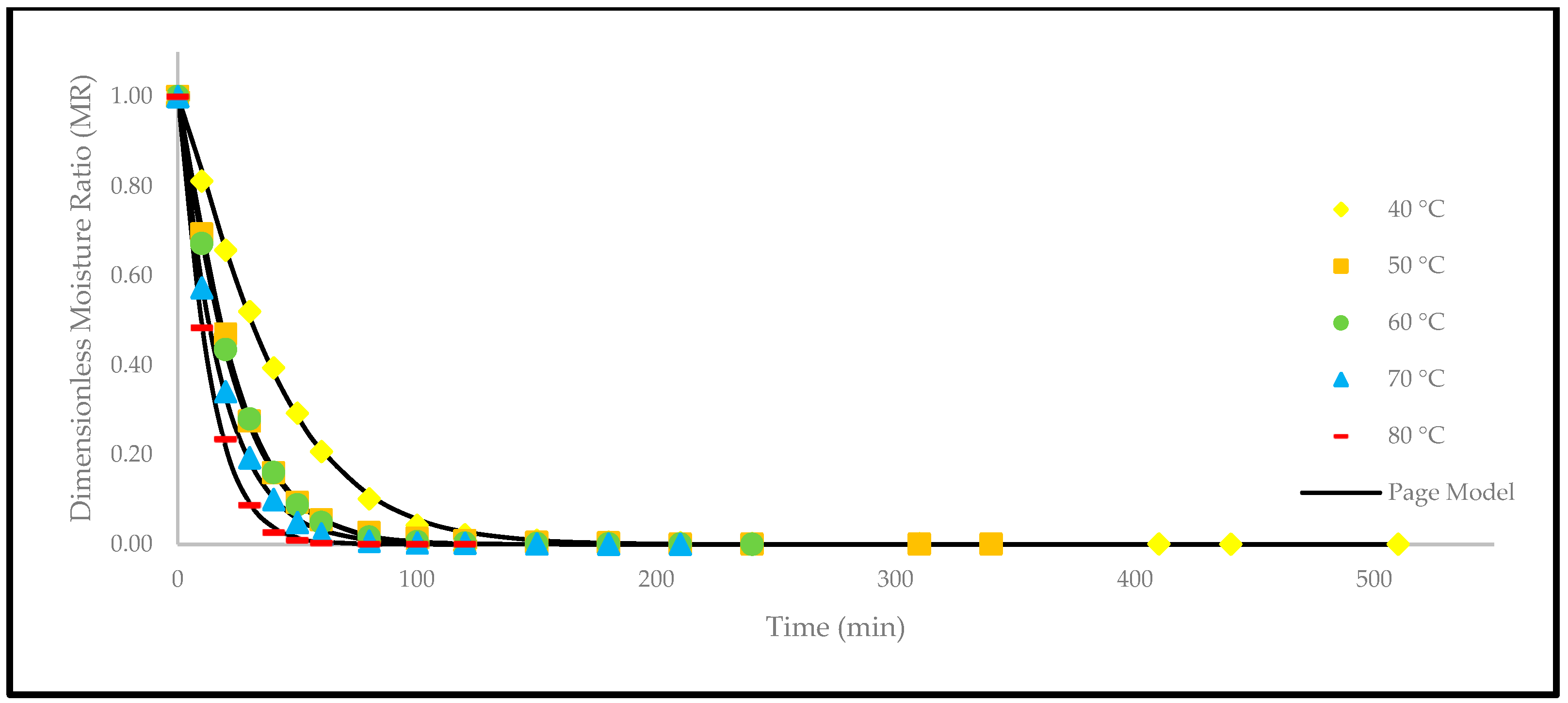
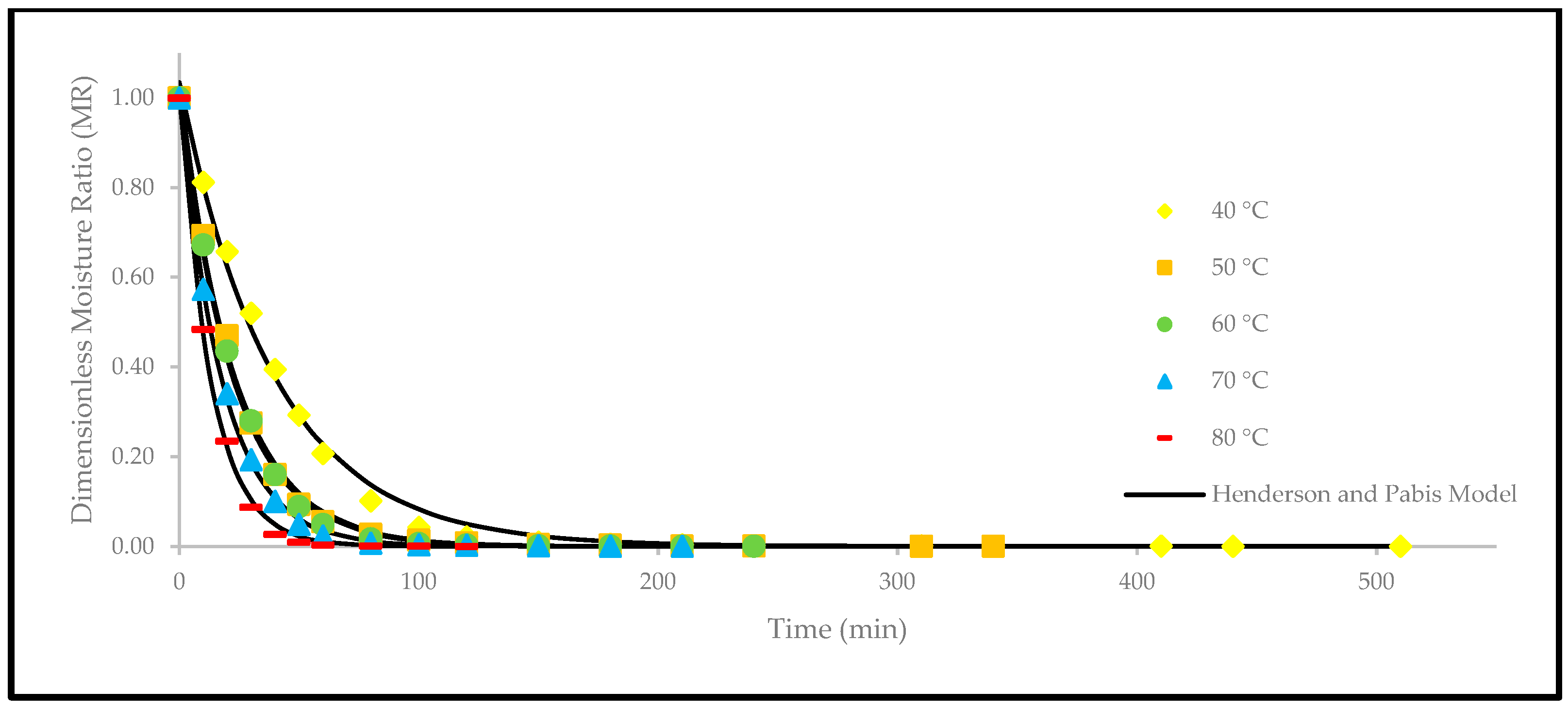
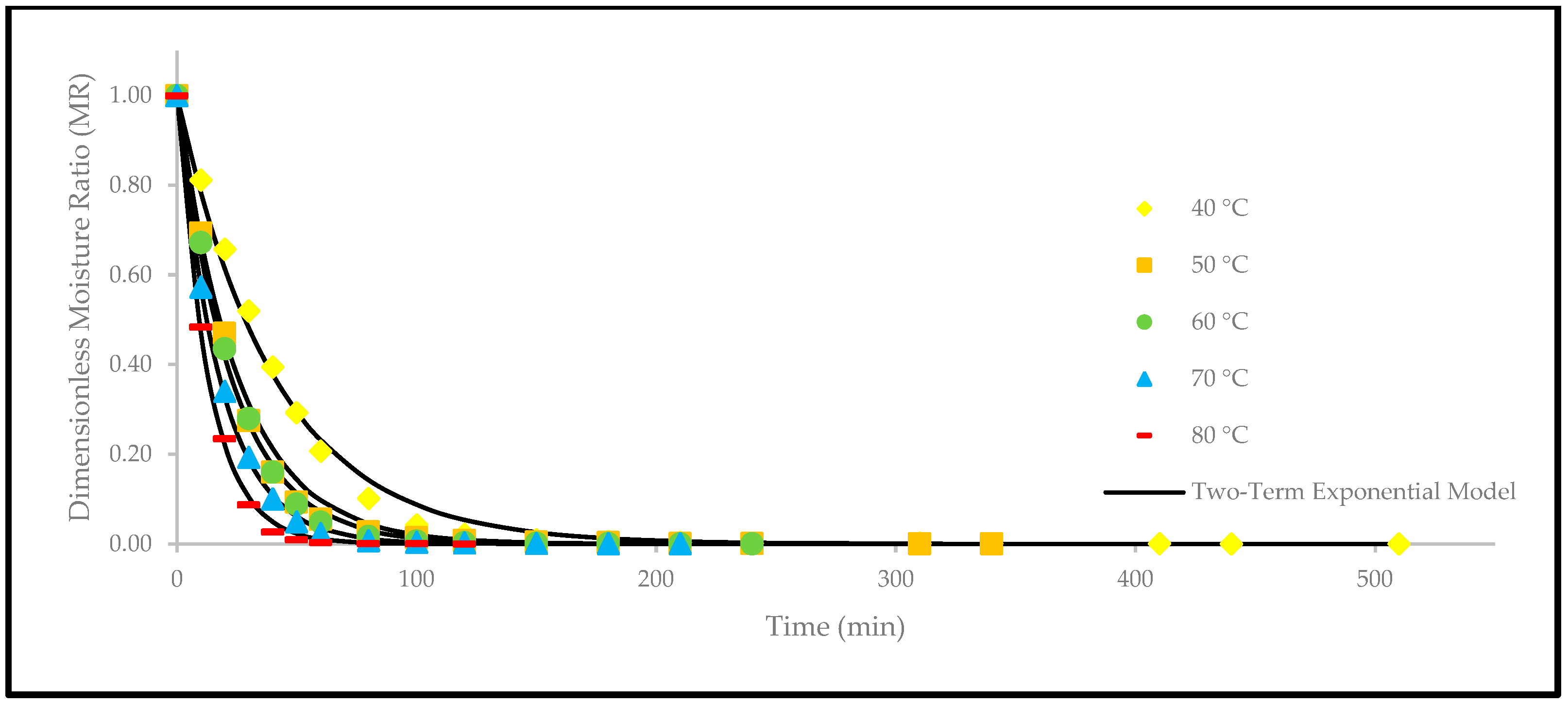
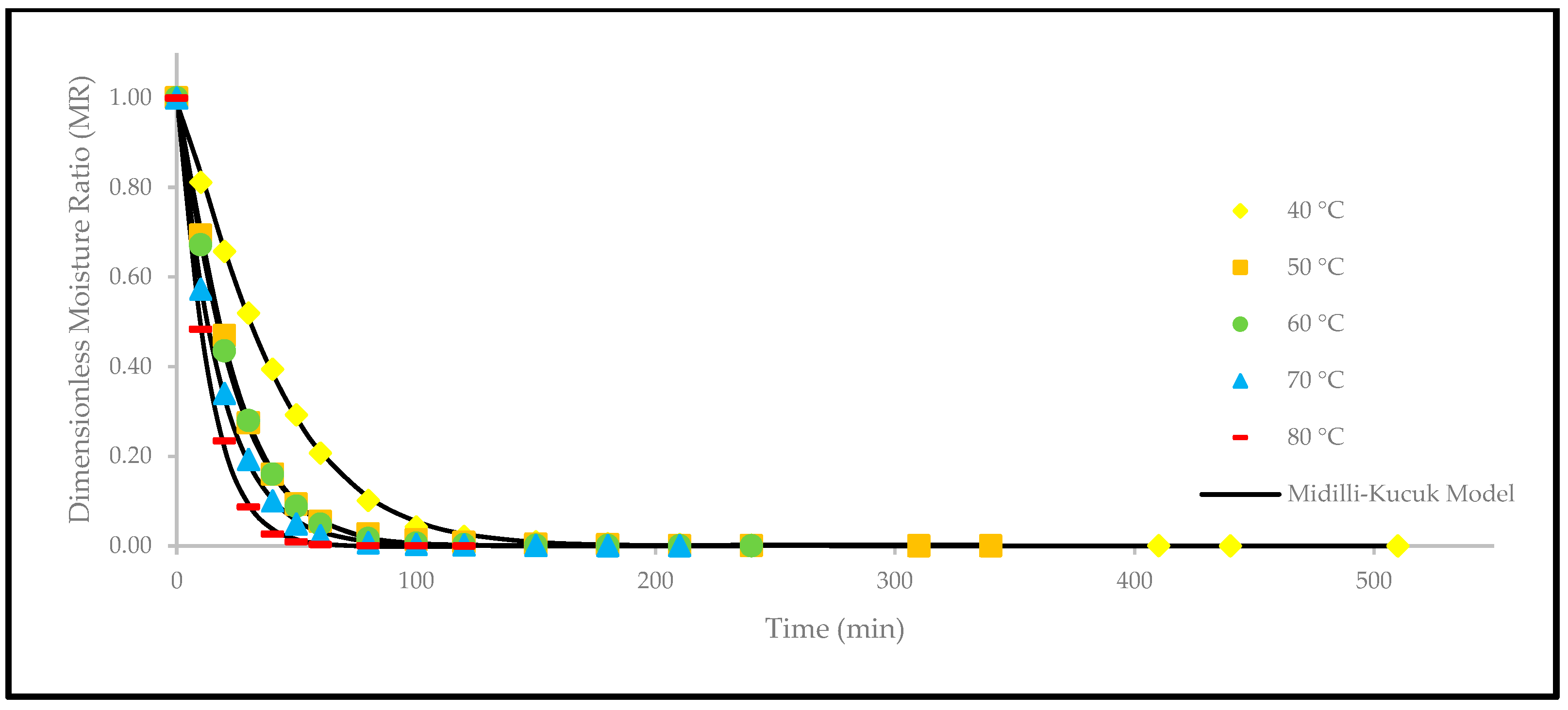
3.3. Effect of Drying Temperatures on Thin-Layer Drying Models
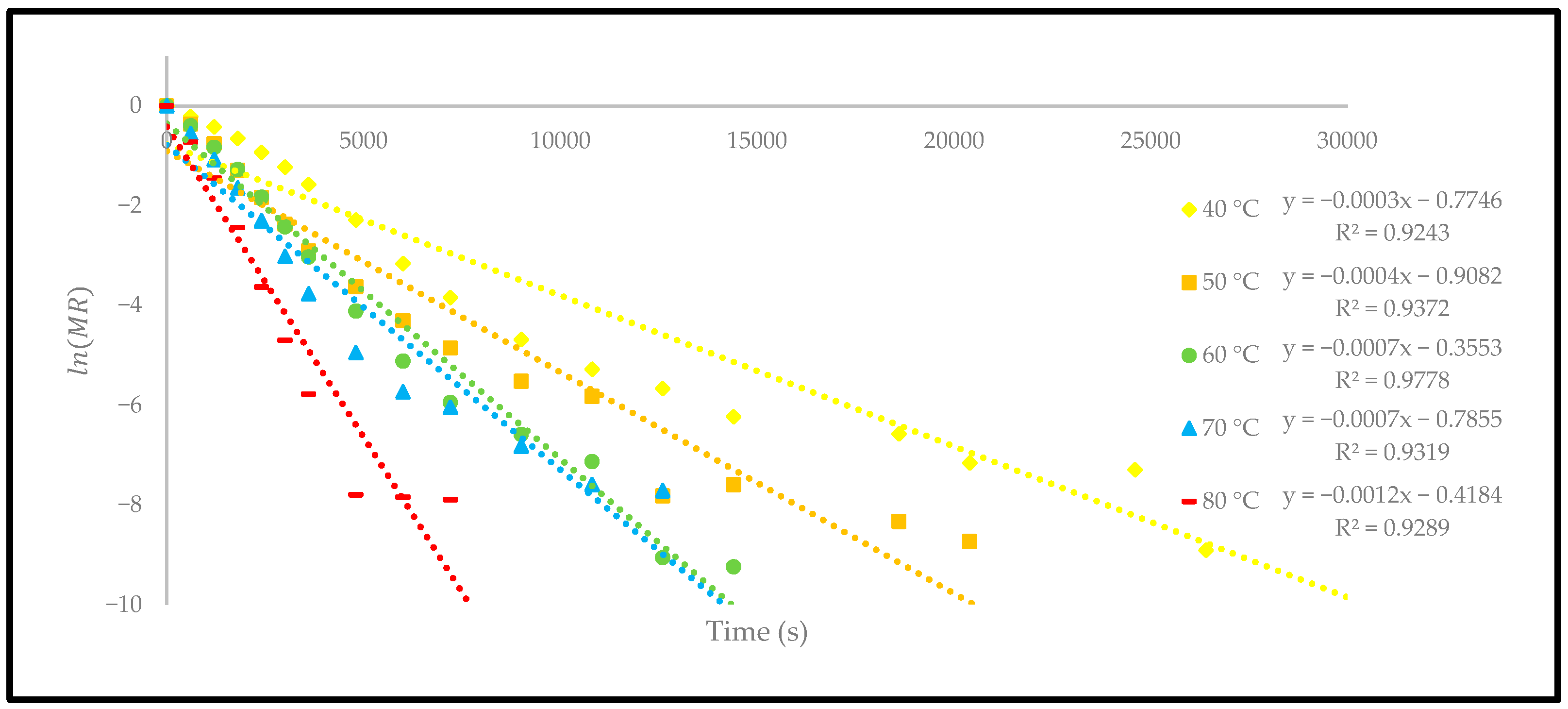
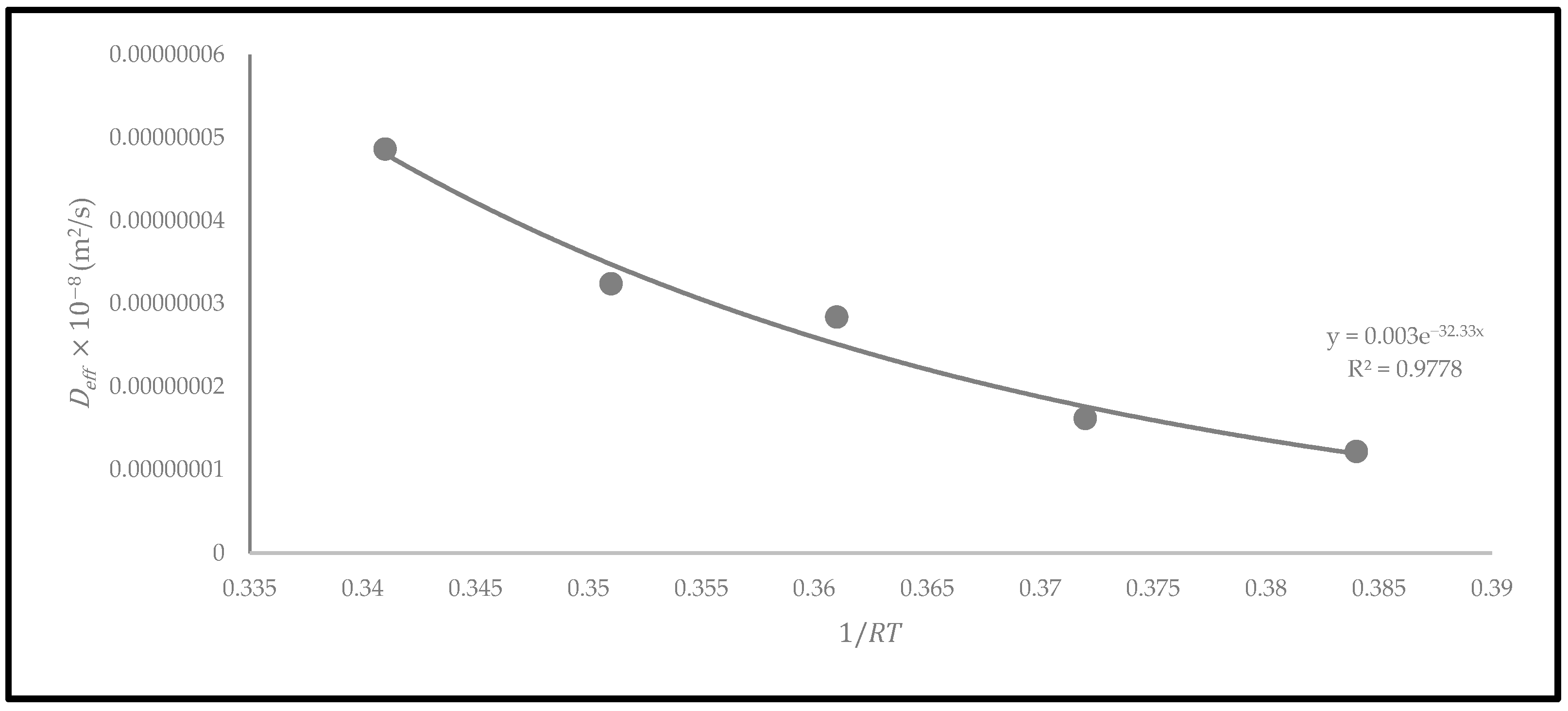
3.4. Effect of Drying Temperatures on Effective Moisture Diffusivity and Activation Energy
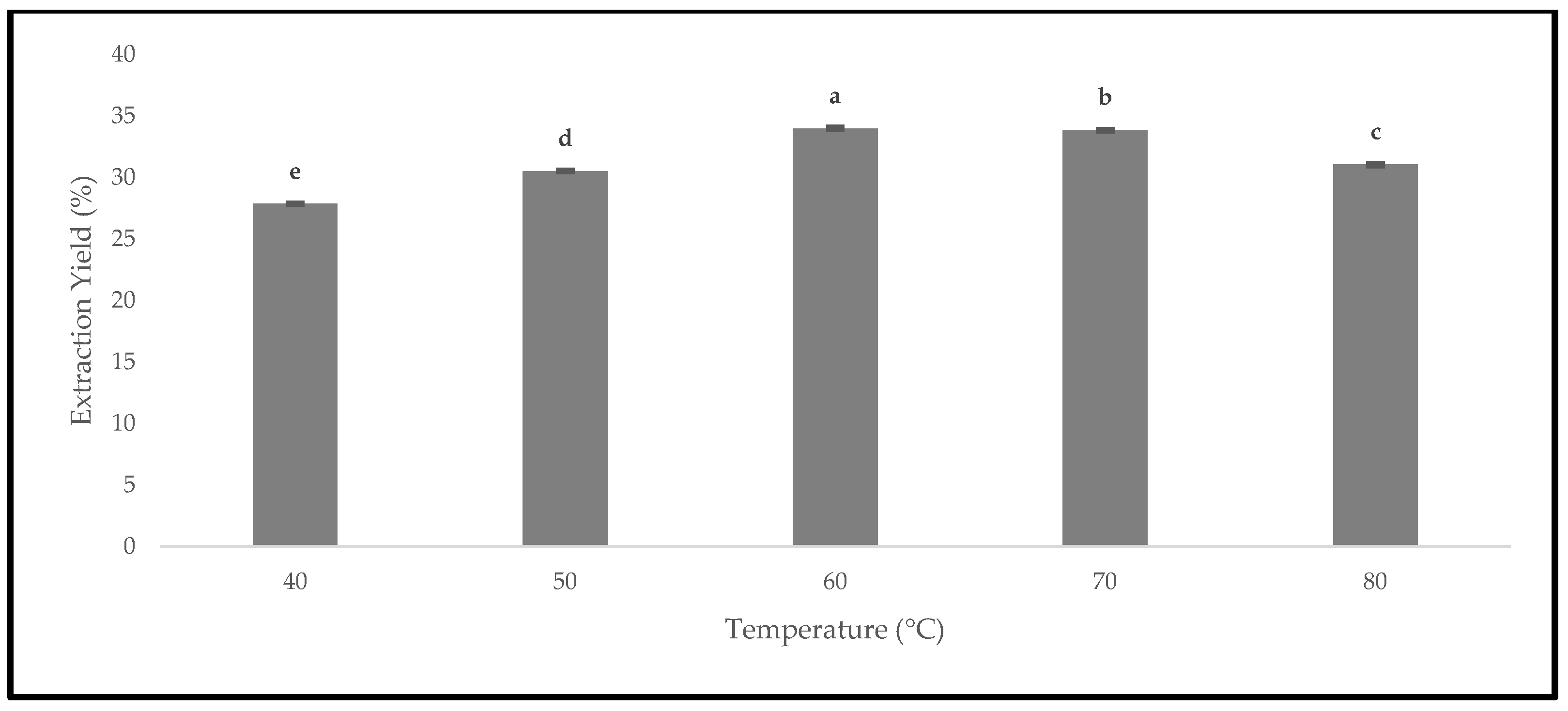
3.5. Effect of Drying Temperatures on Extraction Yield
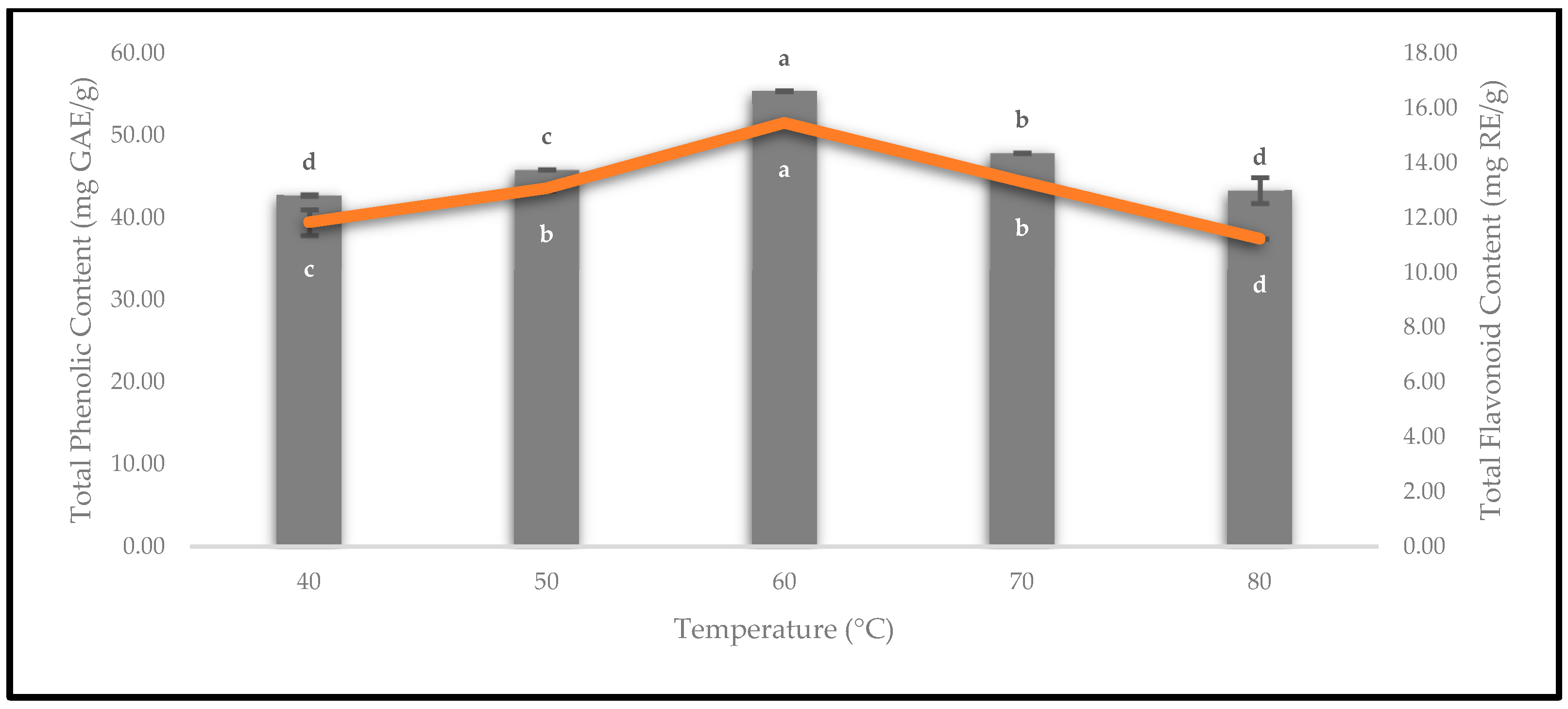
3.6. Effect of Drying Temperatures on Phenolics and Flavonoids
3.7. Effect of Drying Temperatures on Antioxidant Activity
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Atanasov, A.G.; Waltenberger, B.; Pferschy-Wenzig, E.M.; Linder, T.; Wawrosch, C.; Uhrin, P.; Temml, V.; Wang, L.; Schwaiger, S.; Heiss, E.H.; et al. Discovery and resupply of pharmacologically active plant-derived natural products: A review. Biotechnol. Adv. 2015, 33, 1582–1614. [Google Scholar] [CrossRef] [Green Version]
- Othman, S.N.A.M.; Sarker, S.D.; Nahar, L.; Basar, N. The ethnomedicinal, phytochemical and pharmacological properties of Phaleria macrocarpa (Scheff). Boerl. TANG–Humanitas Trait. Med. 2014, 4, e22. [Google Scholar] [CrossRef] [Green Version]
- Kurnia, D.; Akiyama, K.; Hayashi, H. 29-Norcucurbitacin derivatives isolated from the Indonesian medicinal plant, Phaleria macrocarpa (Scheff.) Boerl. Biosci. Biotechnol. Biochem. 2008, 72, 618–620. [Google Scholar] [CrossRef] [Green Version]
- Andrean, D.; Prasetyo, S.; Kristijarti, A.P.; Hudaya, T. The extraction and activity test of bioactive compounds in Phaleria macrocarpa as antioxidants. Procedia Chem. 2014, 9, 94–101. [Google Scholar] [CrossRef] [Green Version]
- Nurhaslina, C.R.; Andi Bacho, S.; Mustapa, A.N. Review on drying methods for herbal plants. Mater. Today Proc. 2022, 63, S122–S139. [Google Scholar] [CrossRef]
- Mediani, A.; Abas, F.; Khatib, A.; Tan, C.P. Cosmos caudatus as a potential source of polyphenolic compounds: Optimisation of oven drying conditions and characterisation of its functional properties. Molecules 2013, 18, 10452–10464. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Inyang, U.E.; Oboh, I.O.; Etuk, B.R. Kinetic models for drying techniques—Food materials. Adv. Chem. Eng. Sci. 2018, 08, 27–48. [Google Scholar] [CrossRef] [Green Version]
- Ronoh, E.K.; Kanali, C.L.; Mailutha, J.T.; Shitanda, D. Thin layer drying kinetics of amaranth (Amaranthus cruentus) grains in a natural convection solar tent dryer. African J. Food Agric. Nutr. Dev. 2010, 10, 2218–2233. [Google Scholar] [CrossRef] [Green Version]
- Amiri Chayjan, R. Modeling some drying characteristics of high moisture potato slices in fixed, semi fluidized and fluidized bed conditions. J. Agric. Sci. Technol. 2012, 14, 1229–1241. [Google Scholar]
- Lewis, W.K. The rate of drying of solid materials. J. Ind. Eng. Chem. 1921, 13, 427–432. [Google Scholar] [CrossRef]
- Page, G.E. Factors Influencing the Maximum Rates of Air Drying Shelled Corn in Thin Layers. Master’s Thesis, Purdue University, West Lafayette, IN, USA, 1949. [Google Scholar]
- Henderson, S.M.; Pabis, S. Grain drying theory. I. Temperature effect on drying coefficients. J. Agric. Eng. Res. 1961, 6, 169–174. [Google Scholar]
- Sharaf-Eldeen, Y.; Blaisdell, J.; Hamdy, M. A model for ear corn drying. Trans. ASAE 1980, 23, 1261–1265. [Google Scholar] [CrossRef]
- Midilli, A.; Kucuk, H. Mathematical modeling of thin layer drying of pistachio by using solar energy. Energy Convers. Manag. 2003, 44, 1111–1122. [Google Scholar] [CrossRef]
- Fakhrulddin, I.M.; Ramaiya, S.D.; Muta Harah, Z.; Nur Leena Wong, W.S.; Awang, M.A.; Ismail, N.I.M. Effects of temperature on drying kinetics and biochemical composition of Caulerpa lentillifera. Food Res. 2022, 6, 168–173. [Google Scholar] [CrossRef] [PubMed]
- Chandra, P.K.; Singh, R.P. Applied Numerical Methods for Food and Agricultural Engineers, 1st ed.; CRC Press: Boca Raton, FL, USA, 1994; pp. 163–167. [Google Scholar]
- Awang, M.A.; Chua, L.S.; Abdullah, L.C.; Pin, K.Y. Drying kinetics and optimization of quercetrin extraction from Melastoma malabathricum leaves. Chem. Eng. Technol. 2021, 44, 1214–1220. [Google Scholar] [CrossRef]
- Erbay, Z.; Icier, F. A review of thin layer drying of foods: Theory, modeling, and experimental results. Crit. Rev. Food Sci. Nutr. 2010, 50, 441–464. [Google Scholar] [CrossRef] [PubMed]
- Ainsworth, E.A.; Gillespie, K.M. Estimation of total phenolic content and other oxidation substrates in plant tissues using Folin-Ciocalteu reagent. Nat. Protoc. 2007, 2, 875–877. [Google Scholar] [CrossRef]
- Awang, M.A.; Daud, N.N.N.N.M.; Ismail, N.I.M.; Cheng, P.G.; Ismail, M.F.; Ramaiya, S.D. Antioxidant and cytotoxicity activity of Cordyceps militaris extracts against human colorectal cancer cell line. J. Appl. Pharm. Sci. 2021, 11, 105–109. [Google Scholar] [CrossRef]
- Nithianantham, K.; Shyamala, M.; Chen, Y.; Latha, L.Y.; Jothy, S.L.; Sasidharan, S. Hepatoprotective potential of Clitoria ternatea leaf extract against paracetamol induced damage in mice. Molecules 2011, 16, 10134–10145. [Google Scholar] [CrossRef] [Green Version]
- Babu, A.K.; Kumaresan, G.; Raj, V.A.A.; Velraj, R. Review of leaf drying: Mechanism and influencing parameters, drying methods, nutrient preservation, and mathematical models. Renew. Sustain. Energy Rev. 2018, 90, 536–556. [Google Scholar] [CrossRef]
- Nguyen, T.V.L.; Nguyen, M.D.; Nguyen, D.C.; Bach, L.G.; Lam, T.D. Model for thin layer drying of lemongrass (Cymbopogon citratus) by hot air. Processes 2019, 7, 21. [Google Scholar] [CrossRef] [Green Version]
- Raaf, A.; Putra, T.W.; Mulana, F.; Syamsuddin, Y.; Supardan, M.D. Investigation of kinetics of amla (Emblica officinalis) fruit drying process. South African J. Chem. Eng. 2022, 41, 10–16. [Google Scholar] [CrossRef]
- Chikpah, S.K.; Korese, J.K.; Sturm, B.; Hensel, O. Colour change kinetics of pumpkin (Cucurbita moschata) slices during convective air drying and bioactive compounds of the dried products. J. Agric. Food Res. 2022, 10, 100409. [Google Scholar] [CrossRef]
- Joseph Bassey, E.; Cheng, J.-H.; Sun, D.-W. Improving drying kinetics, physicochemical properties and bioactive compounds of red dragon fruit (Hylocereus species) by novel infrared drying. Food Chem. 2022, 375, 131886. [Google Scholar] [CrossRef] [PubMed]
- Krzykowski, A.; Dziki, D.; Rudy, S.; Gawlik-Dziki, U.; Janiszewska-Turak, E.; Biernacka, B. Wild strawberry Fragaria vesca L.: Kinetics of fruit drying and quality characteristics of the dried fruits. Processes 2020, 8, 1265. [Google Scholar] [CrossRef]
- Mphahlele, R.R.; Pathare, P.B.; Opara, U.L. Drying kinetics of pomegranate fruit peel (cv. Wonderful). Sci. African 2019, 5, e00145. [Google Scholar] [CrossRef]
- Onwude, D.I.; Hashim, N.; Janius, R.B.; Nawi, N.M.; Abdan, K. Modeling the thin-layer drying of fruits and vegetables: A review. Compr. Rev. Food Sci. Food Saf. 2016, 15, 599–618. [Google Scholar] [CrossRef]
- Jalal, F.E.; Xu, Y.; Iqbal, M.; Javed, M.F.; Jamhiri, B. Predictive modeling of swell-strength of expansive soils using artificial intelligence approaches: ANN, ANFIS and GEP. J. Environ. Manage. 2021, 289, 112420. [Google Scholar] [CrossRef]
- Bajoub, A.; Ennahli, N.; Ouaabou, R.; Chaji, S.; Hafida, H.; Soulaymani, A.; Idlimam, A.; Merah, O.; Lahlali, R.; Ennahli, S. Investigation into solar drying of Moroccan strawberry tree (Arbutus unedo L.) fruit: Effects on drying kinetics and phenolic composition. Appl. Sci. 2023, 13, 769. [Google Scholar] [CrossRef]
- Vega-Gálvez, A.; Poblete, J.; Rojas-Carmona, R.; Uribe, E.; Pastén, A.; Goñi, M.G. Vacuum drying of Chilean papaya (Vasconcellea pubescens) fruit pulp: Effect of drying temperature on kinetics and quality parameters. J. Food Sci. Technol. 2021, 58, 3482–3492. [Google Scholar] [CrossRef]
- Puente-Díaz, L.; Spolmann, O.; Nocetti, D.; Zura-Bravo, L.; Lemus-Mondaca, R. Effects of infrared-assisted refractance windowTM drying on the drying kinetics, microstructure, and color of Physalis fruit purée. Foods 2020, 9, 343. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rocha, R.P.; Melo, E.C.; Radünz, L.L. Influence of drying process on the quality of medicinal plants: A review. J. Med. Plant Res. 2011, 5, 7076–7084. [Google Scholar] [CrossRef]
- Karakaplan, N.; Goz, E.; Tosun, E.; Yuceer, M. Kinetic and artificial neural network modeling techniques to predict the drying kinetics of Mentha spicata L. J. Food Process. Preserv. 2019, 43, e14142. [Google Scholar] [CrossRef]
- Doymaz, I. Evaluation of mathematical models for prediction of thin-layer drying of banana slices. Int. J. Food Prop. 2010, 13, 486–497. [Google Scholar] [CrossRef] [Green Version]
- Sacilik, K. Effect of drying methods on thin-layer drying characteristics of hull-less seed pumpkin (Cucurbita pepo L.). J. Food Eng. 2007, 79, 23–30. [Google Scholar] [CrossRef]
- Freixo, R.; Brandão, T.M.R.S.; Silva, J.; Gomes, A.; Pintado, M.; Silva, C.L.M.; Morais, A.M.M.B.; Teixeira, P. Prebiotics as drying aids for spray drying fruit juices. Sci. Study Res. Chem. Chem. Eng. Biotechnol. Food Ind. 2016, 17, 309–313. [Google Scholar]
- Che Sulaiman, I.S.; Basri, M.; Fard Masoumi, H.R.; Chee, W.J.; Ashari, S.E.; Ismail, M. Effects of temperature, time, and solvent ratio on the extraction of phenolic compounds and the anti-radical activity of Clinacanthus nutans Lindau leaves by response surface methodology. Chem. Cent. J. 2017, 11, 54. [Google Scholar] [CrossRef] [Green Version]
- Mishra, A.; Kavita, K.; Jha, B. Characterization of extracellular polymeric substances produced by micro-algae Dunaliella salina. Carbohydr. Polym. 2011, 83, 852–857. [Google Scholar] [CrossRef]
- Fikselová, M.; Šilhár, S.; Mareček, J.; Frančáková, H. Extraction of carrot (Daucus carota L.) carotenes under different conditions. Czech J. Food Sci. 2008, 26, 268–274. [Google Scholar] [CrossRef] [Green Version]
- Cheng, X.F.; Zhang, M.; Adhikari, B. The inactivation kinetics of polyphenol oxidase in mushroom (Agaricus bisporus) during thermal and thermosonic treatments. Ultrason. Sonochem. 2013, 20, 674–679. [Google Scholar] [CrossRef]
- Muthukumar, P.; Lakshmi, D.V.N.; Koch, P.; Gupta, M.; Srinivasan, G. Effect of drying air temperature on the drying characteristics and quality aspects of black ginger. J. Stored Prod. Res. 2022, 97, 101966. [Google Scholar] [CrossRef]
- Izli, G.; Izli, N.; Taskin, O.; Yildiz, G. Convective drying of kumquat slices: Comparison of different drying temperatures on drying kinetics, colour, total phenolic content and antioxidant capacity. Lat. Am. Appl. Res. 2018, 48, 37–42. [Google Scholar] [CrossRef]
- Kessy, H.N.E.; Hu, Z.; Zhao, L.; Zhou, M. Effect of steam blanching and drying on phenolic compounds of litchi pericarp. Molecules 2016, 21, 729. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sharma, K.; Ko, E.Y.; Assefa, A.D.; Ha, S.; Nile, S.H.; Lee, E.T.; Park, S.W. Temperature-dependent studies on the total phenolics, flavonoids, antioxidant activities, and sugar content in six onion varieties. J. Food Drug Anal. 2015, 23, 243–252. [Google Scholar] [CrossRef] [PubMed]
- Moon, J.-K.; Shibamoto, T. Antioxidant assays for plant and food components. J. Agric. Food Chem. 2009, 57, 1655–1666. [Google Scholar] [CrossRef]
- Krishnan, K.R.; Rayaguru, K.; Nayak, P.K. Ultra-sonicated vacuum drying’s effect on antioxidant activity, TPC, TFC and color of elephant apple slices. Food Biosci. 2020, 36, 100629. [Google Scholar] [CrossRef]
- Kaur, R.; Kaur, K.; Ahluwalia, P. Effect of drying temperatures and storage on chemical and bioactive attributes of dried tomato and sweet pepper. LWT—Food Sci. Technol. 2020, 117, 108604. [Google Scholar] [CrossRef]
- Aryal, S.; Baniya, M.K.; Danekhu, K.; Kunwar, P.; Gurung, R.; Koirala, N. Total phenolic content, flavonoid content and antioxidant potential of wild vegetables from western Nepal. Plants 2019, 8, 96. [Google Scholar] [CrossRef] [Green Version]





| Model | Model Expression | References |
|---|---|---|
| Lewis | [10] | |
| Page | [11] | |
| Henderson and Pabis | [12] | |
| Two-term exponential | [13,14] | |
| Logarithmic | [15,16] | |
| Midilli and Kucuk | [14,17] |
| Model | Temperature (°C) | Constant | |||
|---|---|---|---|---|---|
| Lewis | 40 | = 0.024 | 0.994 | 2.797 | 1.258 |
| 50 | = 0.042 | 0.996 | 1.697 | 0.248 | |
| 60 | = 0.044 | 0.998 | 1.041 | 1.503 | |
| 70 | = 0.056 | 0.999 | 0.240 | 0.671 | |
| 80 | = 0.075 | 0.999 | 0.782 | 3.910 | |
| Page | 40 | = 0.011 | 1.000 | 0.324 | 0.228 |
| = 1.202 | |||||
| 50 | = 0.024 | 0.999 | 0.234 | 0.637 | |
| = 1.173 | |||||
| 60 | = 0.029 | 1.000 | 0.145 | 0.103 | |
| = 1.122 | |||||
| 70 | = 0.05 | 1.000 | 0.174 | 0.210 | |
| = 1.035 | |||||
| 80 | = 0.056 | 0.999 | 0.307 | 0.721 | |
| = 1.102 | |||||
| Henderson and Pabis | 40 | = 1.034 | 0.995 | 2.284 | 4.320 |
| = 0.025 | |||||
| 50 | = 1.023 | 0.997 | 1.486 | 1.569 | |
| = 0.043 | |||||
| 60 | = 1.015 | 0.998 | 0.929 | 3.034 | |
| = 0.044 | |||||
| 70 | = 1.002 | 0.999 | 0.237 | 0.818 | |
| = 0.056 | |||||
| 80 | = 1.005 | 0.999 | 0.765 | 4.959 | |
| = 0.076 | |||||
| Two-term exponential | 40 | = 1.000 | 0.994 | 2.797 | 1.258 |
| = 0.024 | |||||
| 50 | = 1.000 | 0.993 | 3.092 | 38.081 | |
| = 0.039 | |||||
| 60 | = 1.000 | 0.998 | 1.041 | 1.503 | |
| = 0.044 | |||||
| 70 | = 1.000 | 0.999 | 0.240 | 0.671 | |
| = 0.056 | |||||
| 80 | = 1.000 | 0.999 | 0.782 | 3.910 | |
| = 0.075 | |||||
| Logarithmic | 40 | = 1.041 | 0.996 | 2.057 | 0.000 |
| = 0.025 | |||||
| = −0.009 | |||||
| 50 | = 1.026 | 0.997 | 1.437 | 0.088 | |
| = 0.043 | |||||
| = −0.004 | |||||
| 60 | = 1.021 | 0.998 | 0.795 | 0.000 | |
| = 0.043 | |||||
| = −0.007 | |||||
| 70 | = 1.005 | 1.000 | 0.209 | 0.000 | |
| = 0.055 | |||||
| = −0.003 | |||||
| 80 | = 1.013 | 0.999 | 0.560 | 0.000 | |
| = 0.074 | |||||
| = −0.009 | |||||
| Midilli and Kucuk | 40 | = 0.989 | 0.999 | 0.290 | 0.030 |
| = 0.010 | |||||
| = 1.222 | |||||
| = 0.000 | |||||
| 50 | = 0.998 | 0.999 | 0.224 | 0.138 | |
| = 0.023 | |||||
| = 1.178 | |||||
| = 0.000 | |||||
| 60 | = 0.998 | 1.000 | 0.143 | 0.028 | |
| = 0.029 | |||||
| = 1.125 | |||||
| = −0.000 | |||||
| 70 | = 0.998 | 1.000 | 0.172 | 0.075 | |
| = 0.050 | |||||
| = 1.036 | |||||
| = −0.000 | |||||
| 80 | = 0.999 | 0.999 | 0.297 | 0.120 | |
| = 0.056 | |||||
| = 1.099 | |||||
| = −0.000 |
| Temperature (°C) | |||
|---|---|---|---|
| 40 | −0.0003 | 1.22 | 0.9243 |
| 50 | −0.0004 | 1.62 | 0.9372 |
| 60 | −0.0007 | 2.84 | 0.9778 |
| 70 | −0.0008 | 3.24 | 0.9319 |
| 80 | −0.0012 | 4.86 | 0.9289 |
| Antioxidant Activity | TPC | TFC | ||
|---|---|---|---|---|
| R | p-Value | R | p-Value | |
| DPPH | 0.97 ** | 0.00 | 0.90 ** | 0.00 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stephenus, F.N.; Benjamin, M.A.Z.; Anuar, A.; Awang, M.A. Effect of Temperatures on Drying Kinetics, Extraction Yield, Phenolics, Flavonoids, and Antioxidant Activity of Phaleria macrocarpa (Scheff.) Boerl. (Mahkota Dewa) Fruits. Foods 2023, 12, 2859. https://doi.org/10.3390/foods12152859
Stephenus FN, Benjamin MAZ, Anuar A, Awang MA. Effect of Temperatures on Drying Kinetics, Extraction Yield, Phenolics, Flavonoids, and Antioxidant Activity of Phaleria macrocarpa (Scheff.) Boerl. (Mahkota Dewa) Fruits. Foods. 2023; 12(15):2859. https://doi.org/10.3390/foods12152859
Chicago/Turabian StyleStephenus, Fatin Nurain, Mohammad Amil Zulhilmi Benjamin, Adilah Anuar, and Mohd Azrie Awang. 2023. "Effect of Temperatures on Drying Kinetics, Extraction Yield, Phenolics, Flavonoids, and Antioxidant Activity of Phaleria macrocarpa (Scheff.) Boerl. (Mahkota Dewa) Fruits" Foods 12, no. 15: 2859. https://doi.org/10.3390/foods12152859
APA StyleStephenus, F. N., Benjamin, M. A. Z., Anuar, A., & Awang, M. A. (2023). Effect of Temperatures on Drying Kinetics, Extraction Yield, Phenolics, Flavonoids, and Antioxidant Activity of Phaleria macrocarpa (Scheff.) Boerl. (Mahkota Dewa) Fruits. Foods, 12(15), 2859. https://doi.org/10.3390/foods12152859







