Effects of Morphology on the Bulk Density of Instant Whole Milk Powder
Abstract
:1. Introduction
2. Experiment
2.1. Experimental Procedure
2.1.1. Powder Preparation
2.1.2. Sieving
2.1.3. Image Processing
2.1.4. Tap Testing
2.1.5. Simplex-Centroid Design (SCD)
2.2. Morphology Analysis
2.2.1. Shape Factors
2.2.2. Statistical Analysis and Mathematical Modelling
Principal Component Analysis (PCA)
Partial Least Squares (PLS) Regression
Artificial Neural Networks (ANNs)
3. Results and Discussion
3.1. Univariate Analysis
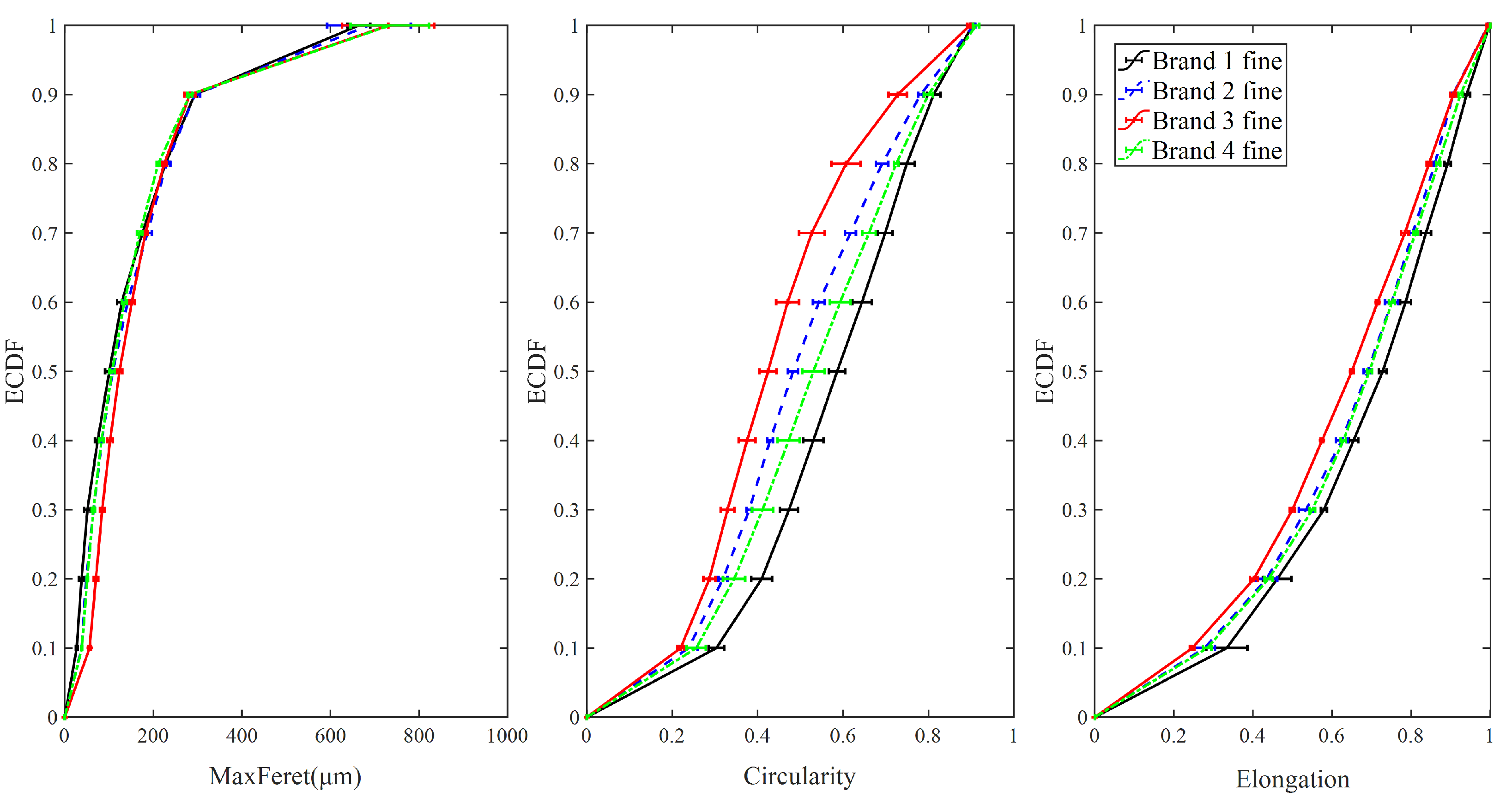
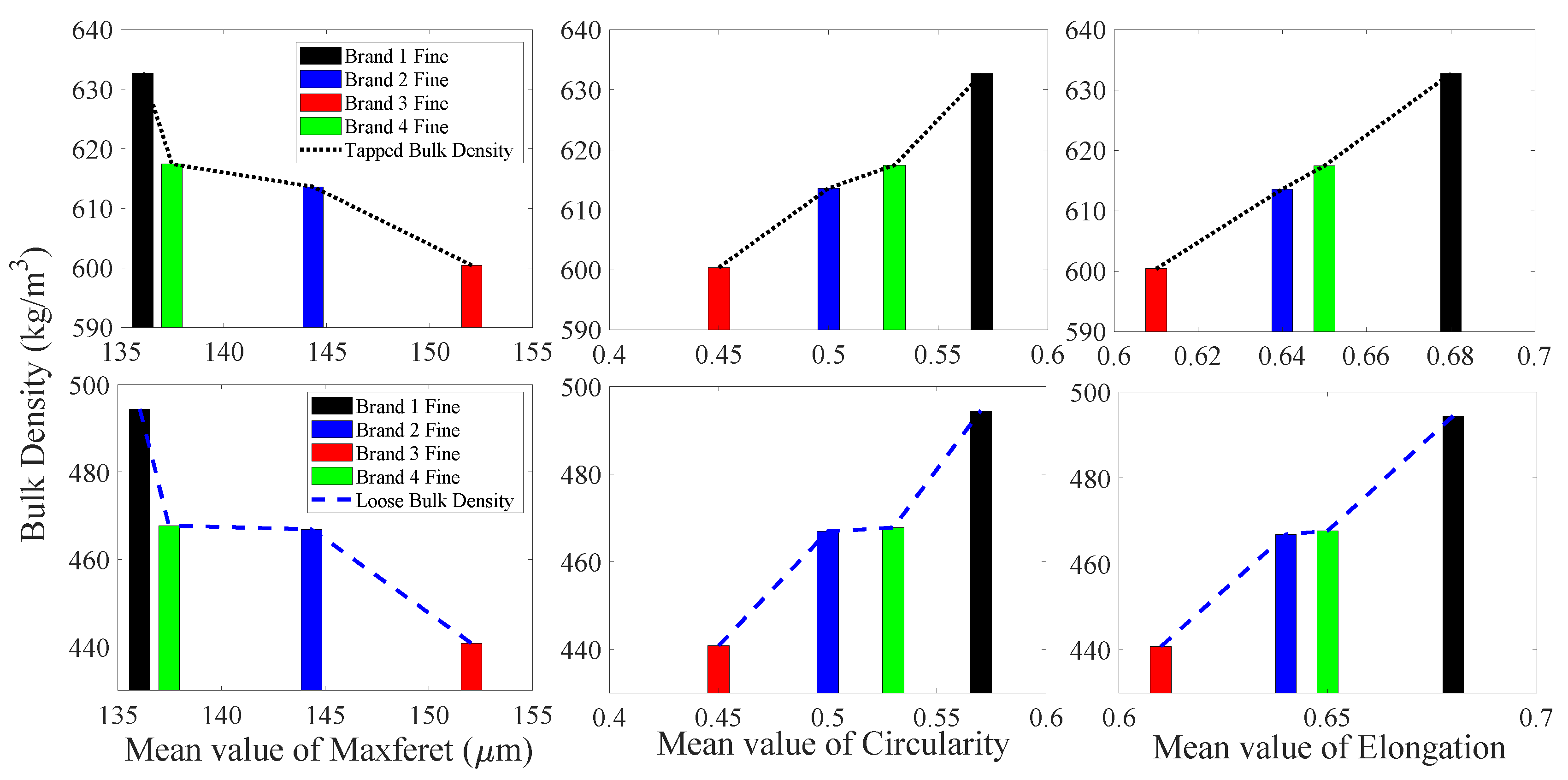
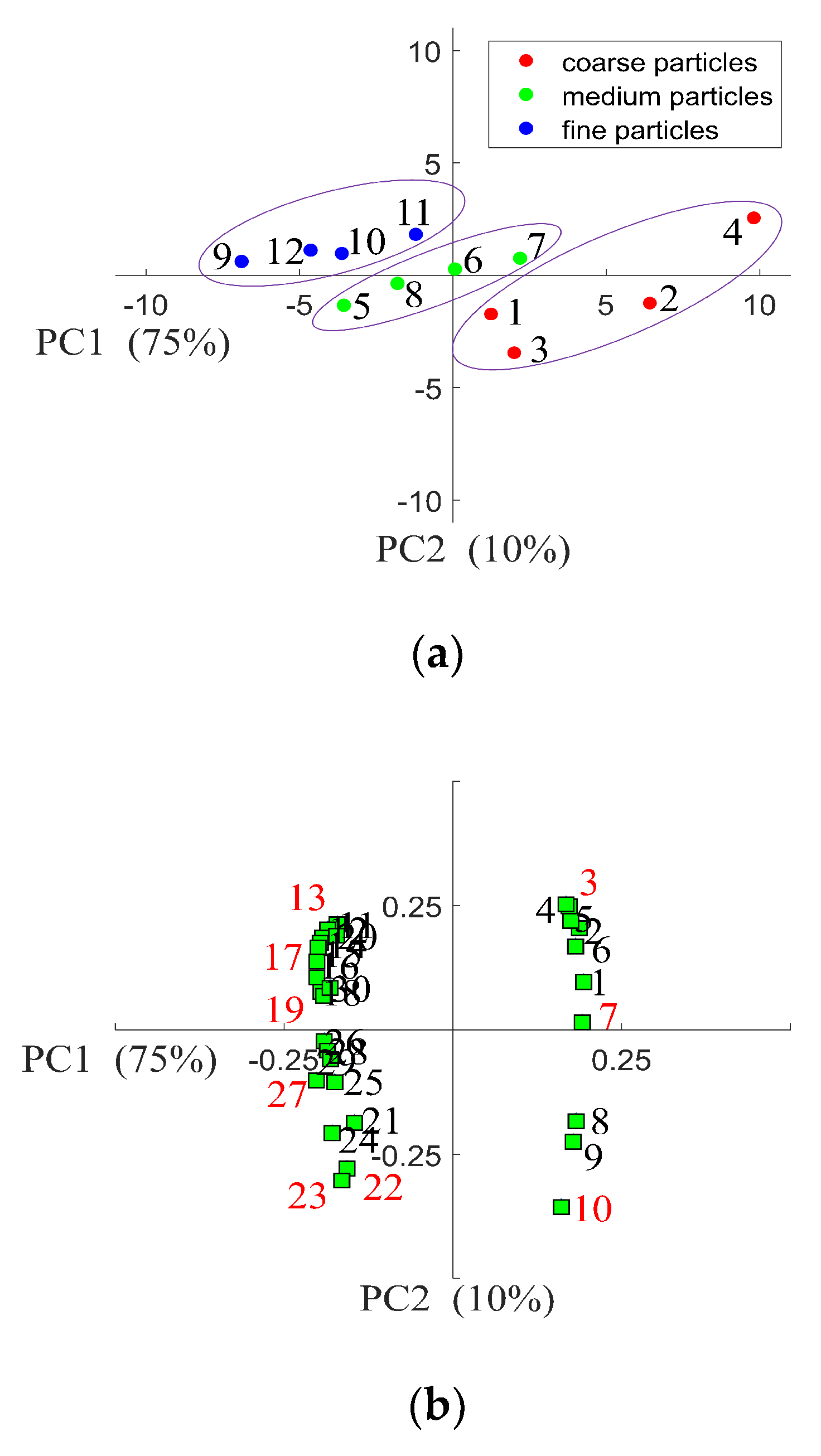
3.1.1. Fine Particles
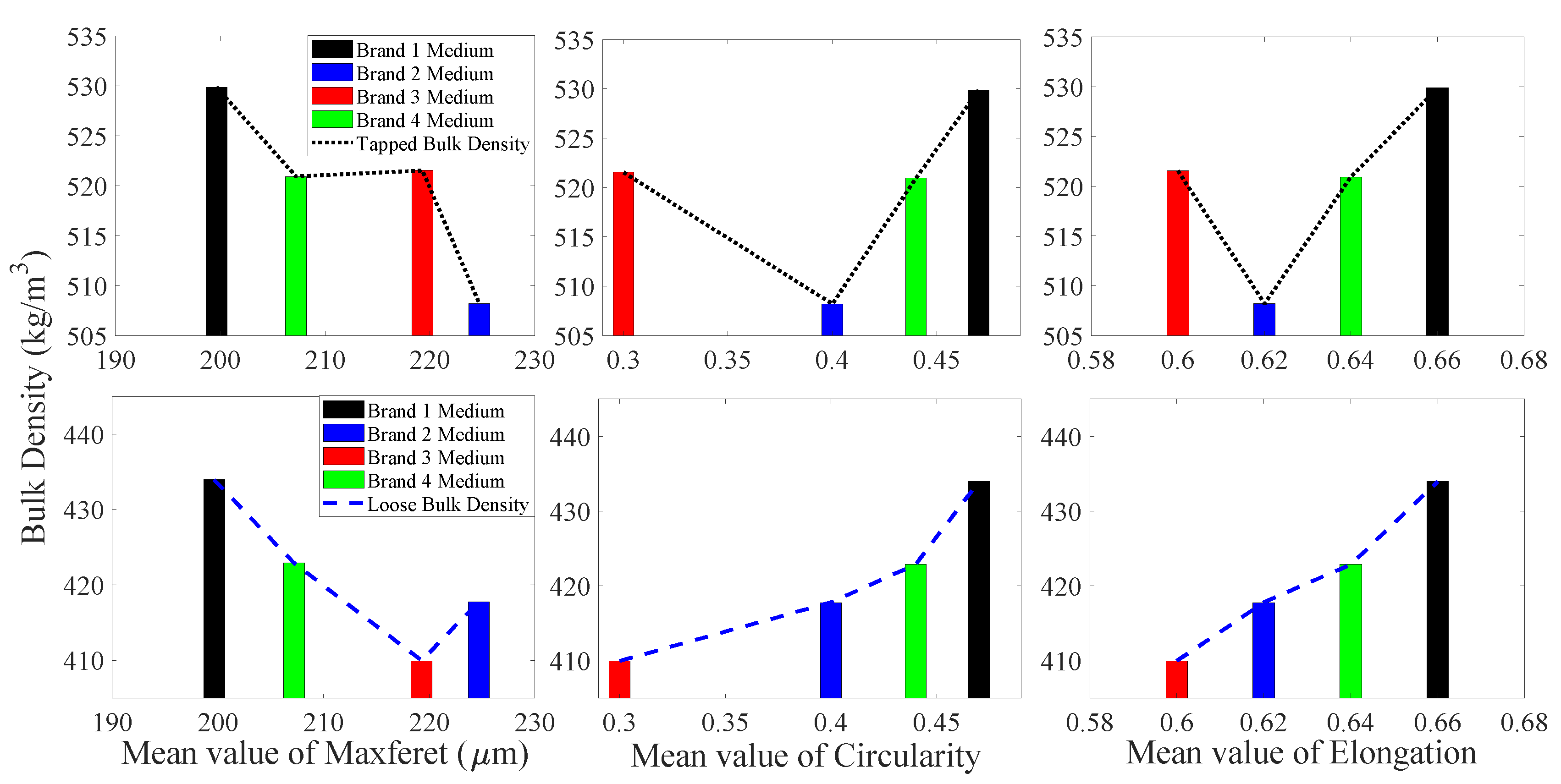
3.1.2. Medium Particles
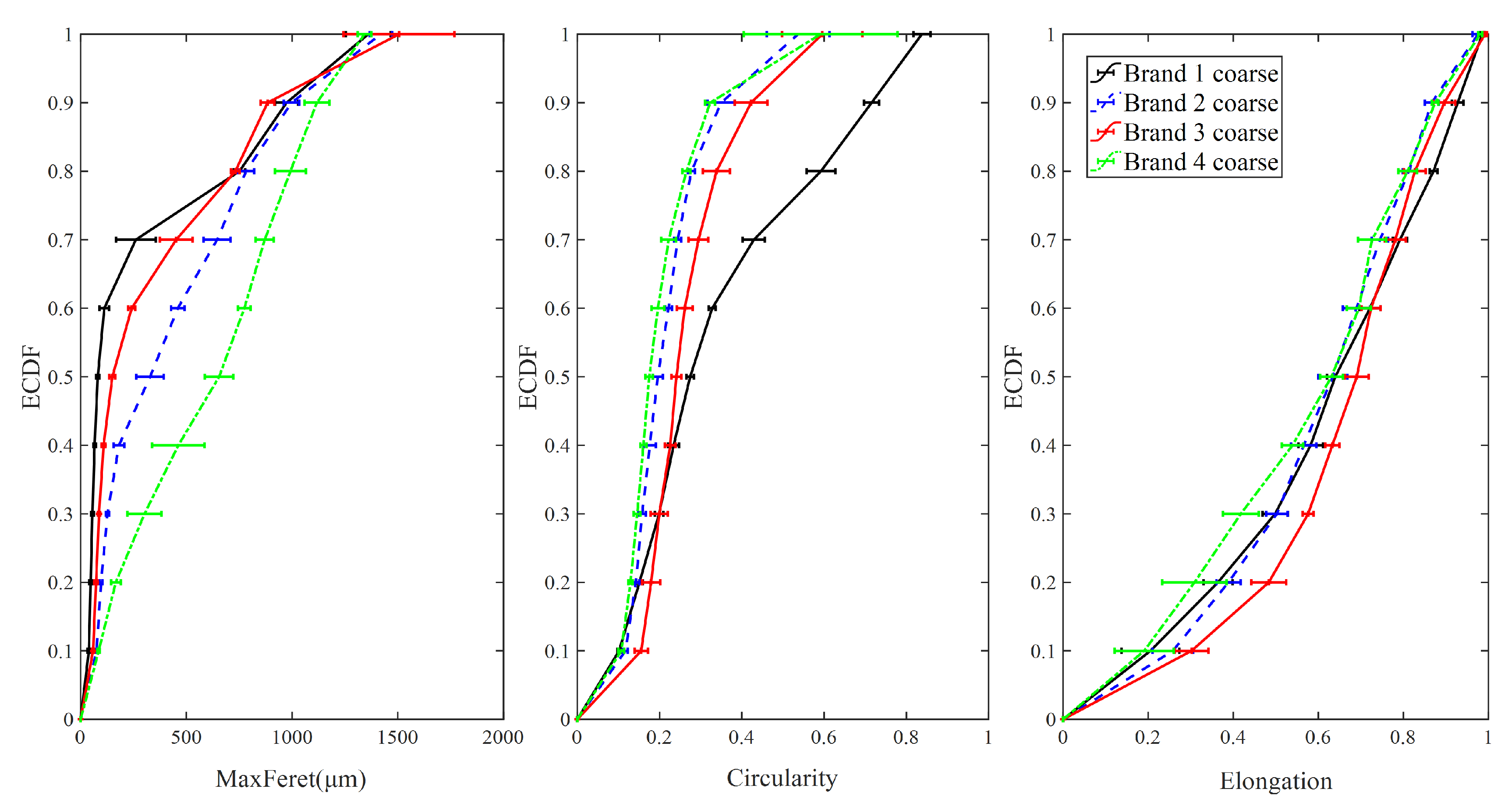
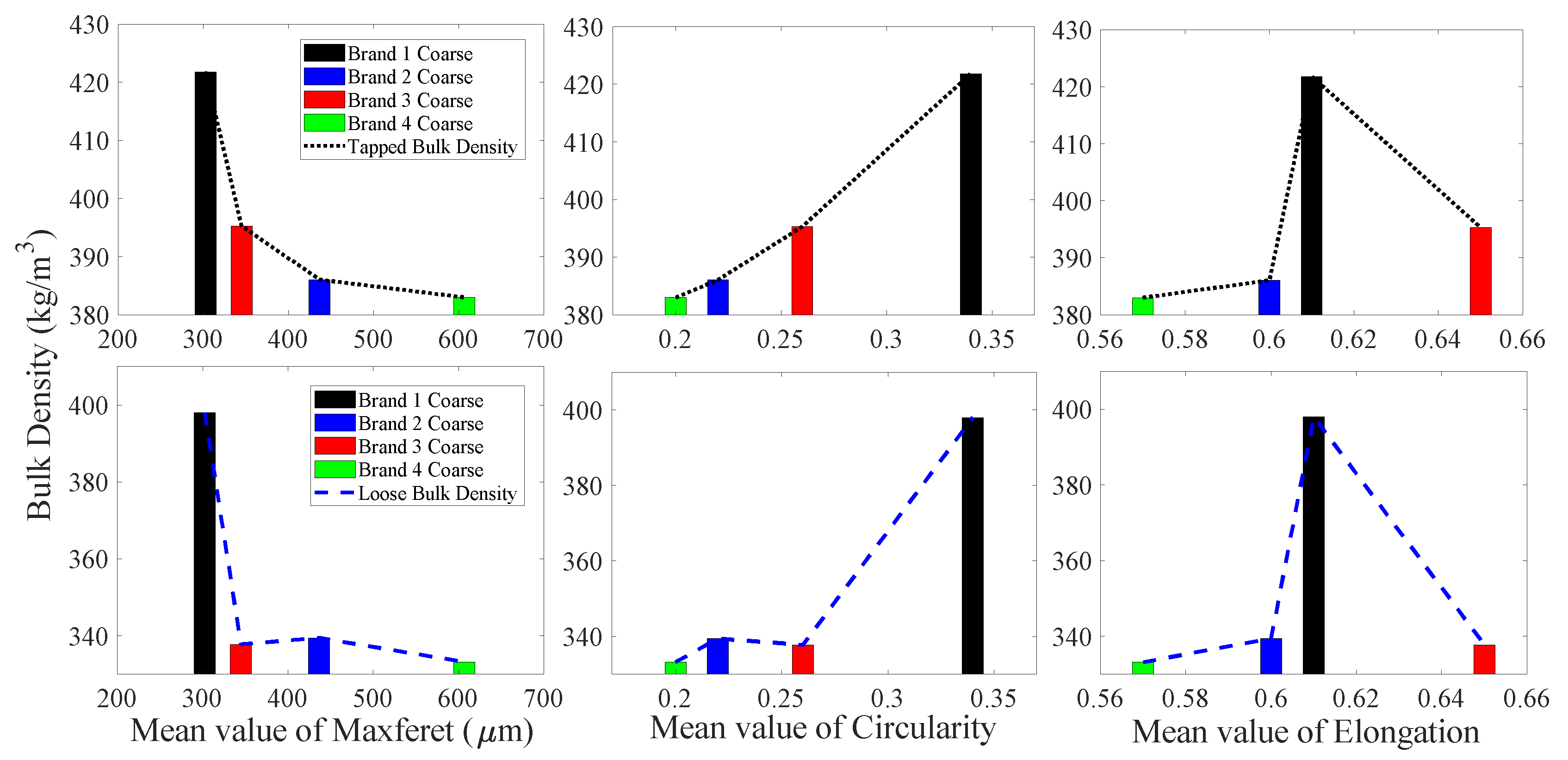
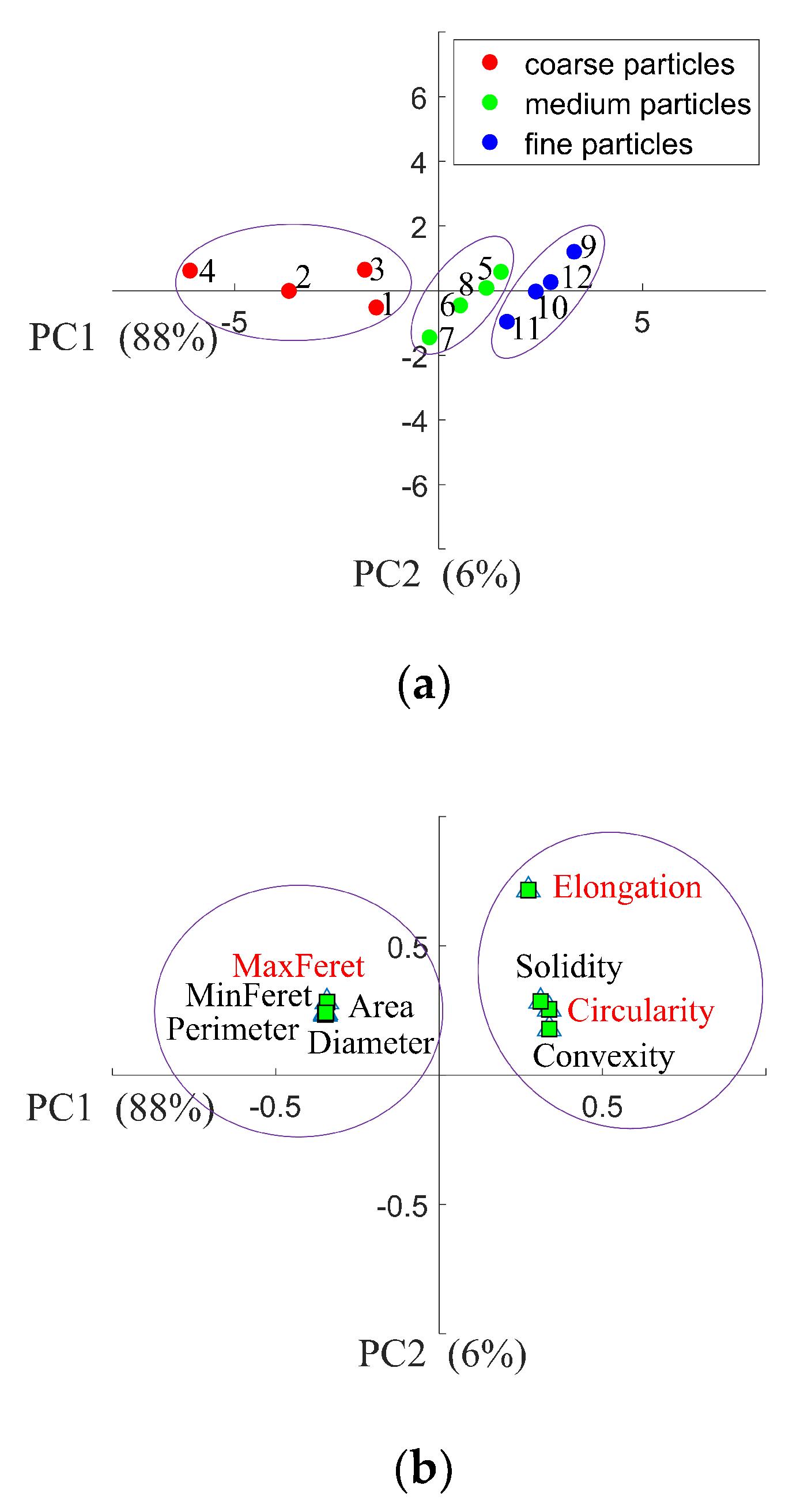
3.1.3. Coarse Particles
3.2. Principal Component Analysis
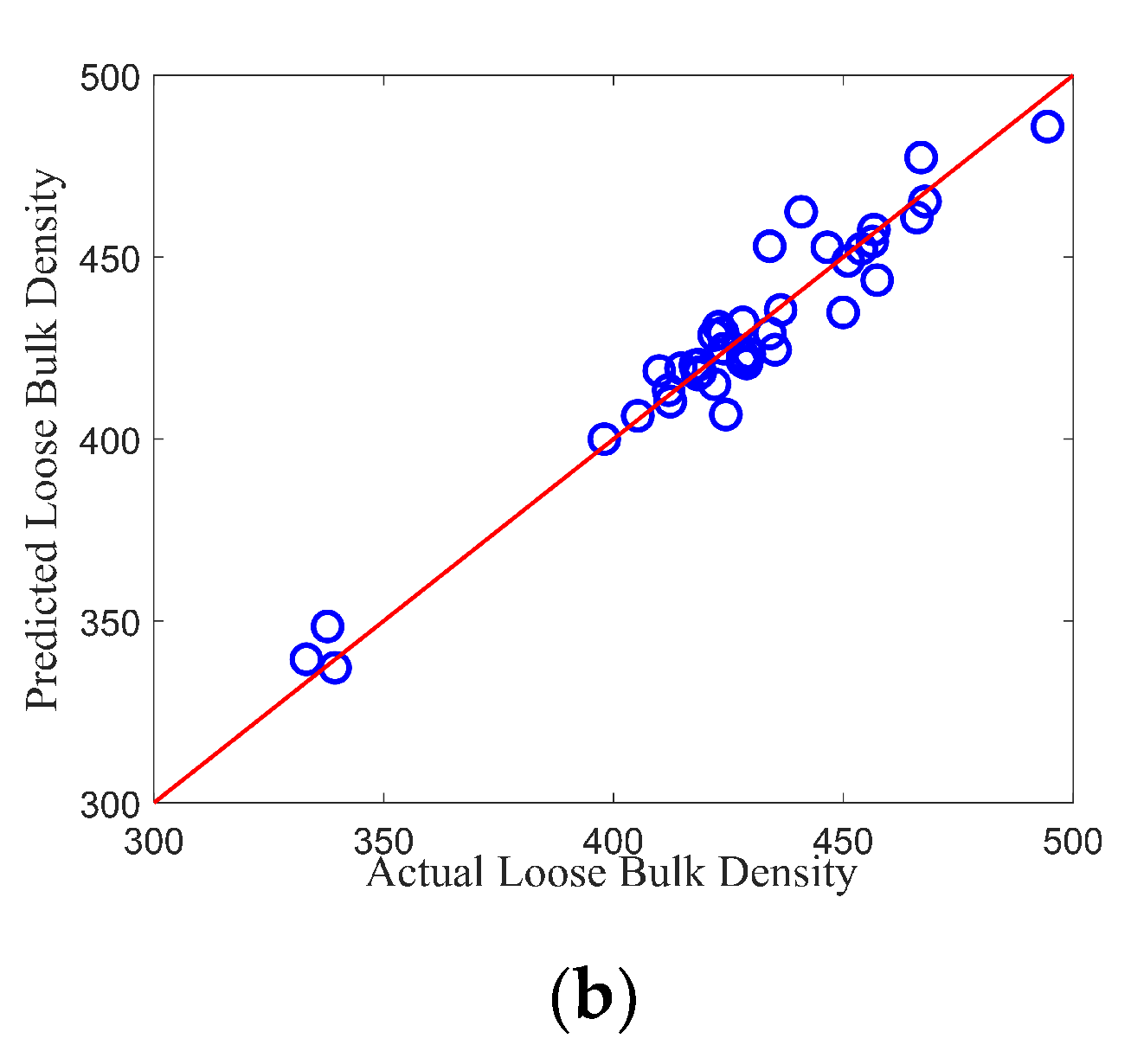
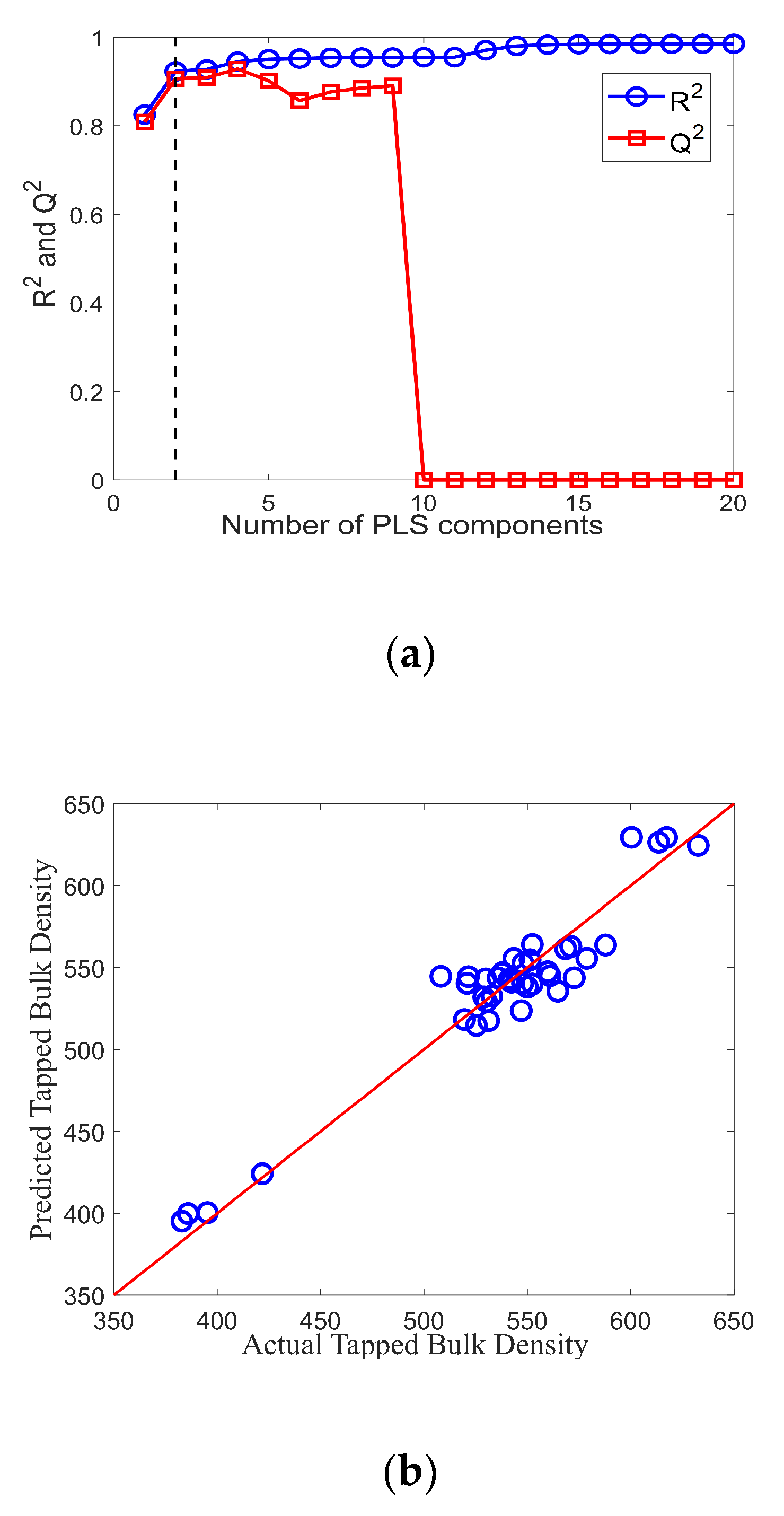
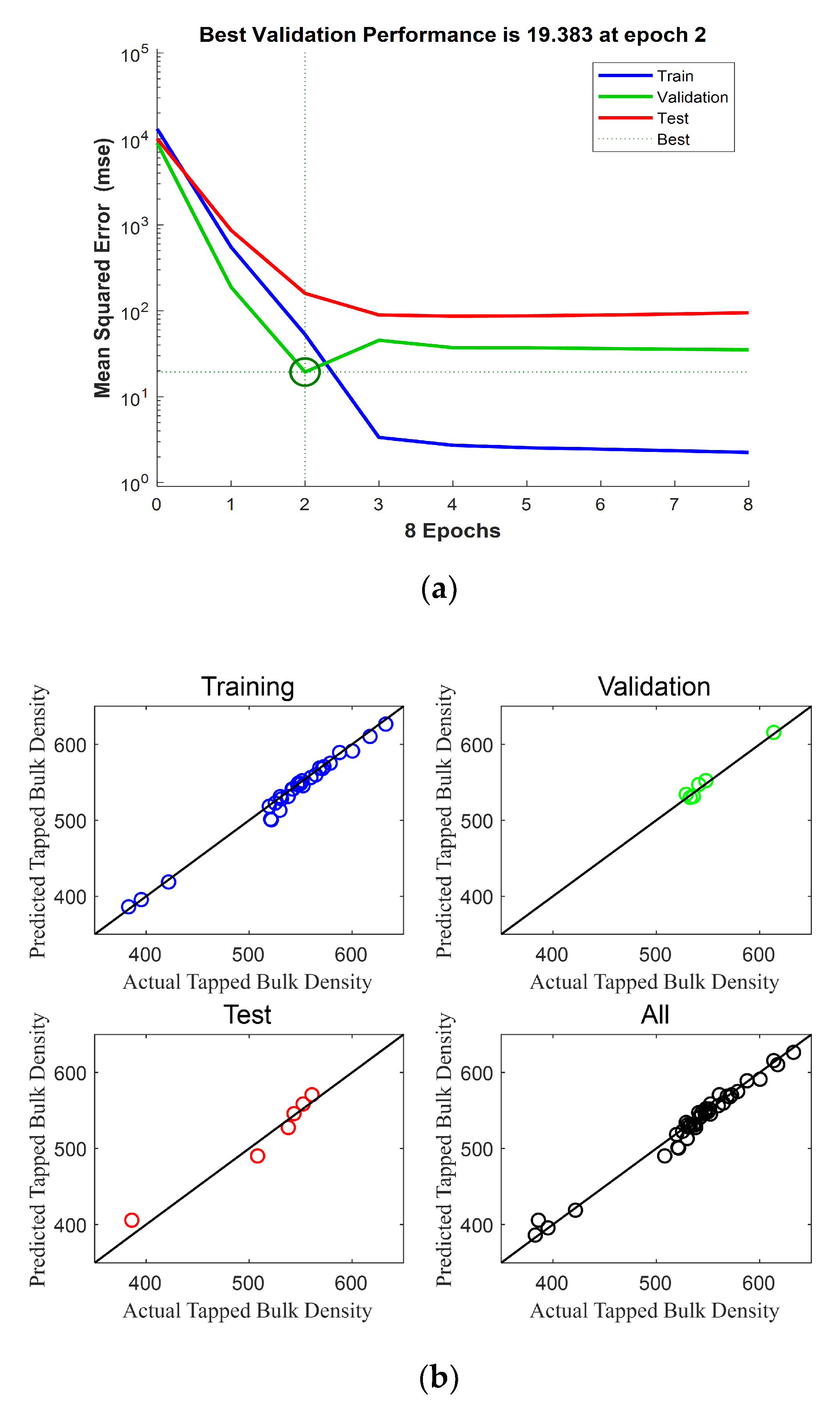
3.3. Prediction of the Bulk Density
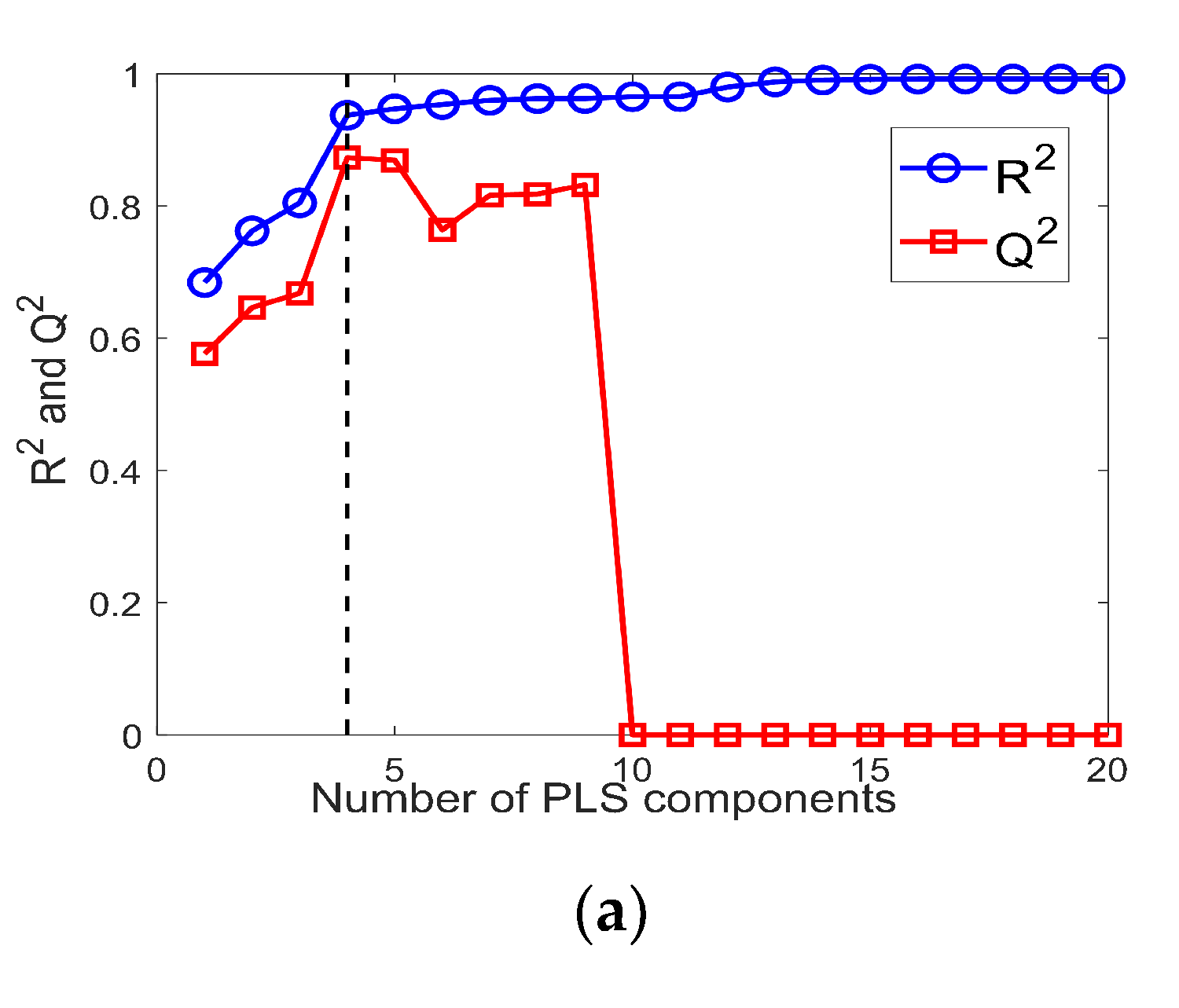
3.3.1. Partial Least Squares Models
3.3.2. Artificial Neural Network models
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Pugliese, A.; Cabassi, G.; Chiavaro, E.; Paciulli, M.; Carini, E.; Mucchetti, G. Physical characterization of whole and skim dried milk powders. J. Food Sci. Technol. 2017, 54, 3433–3442. [Google Scholar] [CrossRef] [PubMed]
- Pisecky, J. Handbook of Milk Powder Manufacture; GEA Process Engineering A/S: Soeborg, Denmark, 2012. [Google Scholar]
- Sharma, A.; Jana, A.; Chavan, R.S. Functionality of Milk Powders and Milk Based Powders for End Use Applications—A Review. Compr. Rev. Food Sci. Food Saf. 2012, 11, 518–528. [Google Scholar] [CrossRef]
- Juliano, P.; Muhunthan, B.; Barbosa-Cánovas, G.V. Flow and shear descriptors of preconsolidated food powders. J. Food Eng. 2006, 72, 157–166. [Google Scholar] [CrossRef]
- Bhandari, B. Spray drying and powder properties. In Food Drying Science and Technology: Microbiology, Chemistry, Applications; DEStech Publications, Inc.: Lancaster, PA, USA, 2008; pp. 215–249. [Google Scholar]
- Abdullah, E.C.; Geldart, D. The use of bulk density measurements as flowability indicators. Powder Technol. 1999, 102, 151–165. [Google Scholar] [CrossRef]
- Tuohy, J.J. Some physical properties of milk powders. Ir. J. Food Sci. Technol. 1989, 13, 141–152. [Google Scholar]
- Nijdam, J.J.; Langrish, T. An Investigation of Milk Powders Produced by a Laboratory-Scale Spray Dryer. Dry. Technol. 2005, 23, 1043–1056. [Google Scholar] [CrossRef]
- Jallo, L.J.; Ghoroi, C.; Gurumurthy, L.; Patel, U.; Davé, R.N. Improvement of flow and bulk density of pharmaceutical powders using surface modification. Int. J. Pharm. 2012, 423, 213–225. [Google Scholar] [CrossRef]
- Martín, M.Á.; Reyes, M.; Taguas, F.J. Estimating soil bulk density with information metrics of soil texture. Geoderma 2017, 287, 66–70. [Google Scholar] [CrossRef] [Green Version]
- Ding, H.; Yu, W.; Boiarkina, I.; DePree, N.; Young, B.R. Effects of morphology on the dispersibility of instant whole milk powder. J. Food Eng. 2020, 276, 109841. [Google Scholar] [CrossRef]
- Gaiani, C.; Ehrhardt, J.; Scher, J.; Hardy, J.; Desobry, S.; Banon, S. Surface composition of dairy powders observed by X-ray photoelectron spectroscopy and effects on their rehydration properties. Colloids Surf. B Biointerfaces 2006, 49, 71–78. [Google Scholar] [CrossRef]
- Murrieta-Pazos, I.; Gaiani, C.; Galet, L.; Scher, J. Composition gradient from surface to core in dairy powders: Agglomeration effect. Food Hydrocoll. 2012, 26, 149–158. [Google Scholar] [CrossRef] [Green Version]
- Boiarkina, I.; Ye, J.; Prince-Pike, A.; Yu, W.; Young, B.R.; Wilson, D.I. The morphology of instant whole milk powder from different industrial plants. In Proceedings of the Chemeca 2016: Chemical Engineering-Regeneration, Recovery and Reinvention, Engineers Australia, Melbourne, Victoria, Australia, 25 September 2016; pp. 945–953. [Google Scholar]
- Boiarkina, I.; Sang, C.; DePree, N.; Prince-Pike, A.; Yu, W.; Wilson, D.; Young, B. The significance of powder breakdown during conveying within industrial milk powder plants. Adv. Powder Technol. 2016, 27, 2363–2369. [Google Scholar] [CrossRef] [Green Version]
- Guerin, E.; Tchoreloff, P.; Leclerc, B.; Tanguy, D.; Deleuil, M.; Couarraze, G. Rheological characterization of pharmaceutical powders using tap testing, shear cell and mercury porosimeter. Int. J. Pharm. 1999, 189, 91–103. [Google Scholar] [CrossRef]
- Handa, C.L.; De Lima, F.S.; Guelfi, M.F.G.; Georgetti, S.R.; Ida, E.I. Multi-response optimisation of the extraction solvent system for phenolics and antioxidant activities from fermented soy flour using a simplex-centroid design. Food Chem. 2016, 197, 175–184. [Google Scholar] [CrossRef]
- Jiao, D.; Shi, C.; Yuan, Q.; An, X.; Liu, Y. Mixture design of concrete using simplex centroid design method. Cem. Concr. Compos. 2018, 89, 76–88. [Google Scholar] [CrossRef]
- Eriksson, L.; Johansson, E.; Wikström, C. Mixture design—Design generation, PLS analysis, and model usage. Chemom. Intell. Lab. Syst. 1998, 43, 1–24. [Google Scholar] [CrossRef]
- Rosin, P.L. Shape partitioning by convexity. IEEE Trans. Syst. Man Cybern. Part A Syst. Hum. 2000, 30, 202–210. [Google Scholar] [CrossRef]
- Bouwman, A.M.; Bosma, J.C.; Vonk, P.; Wesselingh, J.A.; Frijlink, H.W. Which shape factor(s) best describe granules? Powder Technol. 2004, 146, 66–72. [Google Scholar] [CrossRef]
- Abdi, H.; Williams, L.J. Principal component analysis. Wiley Interdiscip. Rev. Comput. Stat. 2010, 2, 433–459. [Google Scholar] [CrossRef]
- Chen, X.; Samson, E.; Tocqueville, A.; Aubin, J. Environmental assessment of trout farming in France by life cycle assessment: Using bootstrapped principal component analysis to better define system classification. J. Clean. Prod. 2015, 87, 87–95. [Google Scholar] [CrossRef]
- Pan, A.; Bosch, D.J.; Ma, H. Assessing Water Poverty in China Using Holistic and Dynamic Principal Component Analysis. Soc. Indic. Res. 2015, 130, 537–561. [Google Scholar] [CrossRef]
- Wold, S.; Esbensen, K.; Geladi, P. Principal component analysis. Chemom. Intell. Lab. Syst. 1987, 2, 37–52. [Google Scholar] [CrossRef]
- David, C.C.; Jacobs, N.J. Principal Component Analysis: A Method for Determining the Essential Dynamics of Proteins. Adv. Struct. Saf. Stud. 2013, 1084, 193–226. [Google Scholar] [CrossRef] [Green Version]
- Gaiani, C.; Boyanova, P.; Hussain, R.; Pazos, I.M.; Karam, M.; Burgain, J.; Scher, J. Morphological descriptors and colour as a tool to better understand rehydration properties of dairy powders. Int. Dairy J. 2011, 21, 462–469. [Google Scholar] [CrossRef]
- Munir, M.; Wilson, D.; Yu, W.; Young, B. An evaluation of hyperspectral imaging for characterising milk powders. J. Food Eng. 2018, 221, 1–10. [Google Scholar] [CrossRef]
- Zhang, H.; Miao, Y.; Takahashi, H.; Chen, J.Y. Amylose Analysis of Rice Flour Using Near-Infrared Spectroscopy with Particle Size Compensation. Food Sci. Technol. Res. 2011, 17, 361–367. [Google Scholar] [CrossRef] [Green Version]
- Chin, W.W. The partial least squares approach to structural equation modeling. Mod. Methods Bus. Res. 1998, 295, 295–336. [Google Scholar]
- Wold, S.; Sjöström, M.; Eriksson, L. PLS-regression: A basic tool of chemometrics. Chemom. Intell. Lab. Syst. 2001, 58, 109–130. [Google Scholar] [CrossRef]
- Jain, A.; Mao, J.; Mohiuddin, K. Artificial neural networks: A tutorial. Computer 1996, 29, 31–44. [Google Scholar] [CrossRef] [Green Version]
- Svozil, D.; Kvasnička, V.; Pospíchal, J. Introduction to multi-layer feed-forward neural networks. Chemom. Intell. Lab. Syst. 1997, 39, 43–62. [Google Scholar] [CrossRef]
- Guo, Z.; Zhao, W.; Lu, H.; Wang, J. Multi-step forecasting for wind speed using a modified EMD-based artificial neural network model. Renew. Energy 2012, 37, 241–249. [Google Scholar] [CrossRef]
- Piotrowski, A.P.; Napiorkowski, J.J. Optimizing neural networks for river flow forecasting–Evolutionary Computation methods versus the Levenberg–Marquardt approach. J. Hydrol. 2011, 407, 12–27. [Google Scholar] [CrossRef]
- DePree, N.; Prince-Pike, A.; Young, B.; Wilson, D. Predictive modelling of instant whole milk powder functional performance across three industrial plants. J. Food Eng. 2019, 252, 1–9. [Google Scholar] [CrossRef]






| Brand 1 | Brand 2 | Brand 3 | Brand 4 | ||
|---|---|---|---|---|---|
| Loose bulk density (kg/m3) | Coarse | 397.99 ± 3.67 | 339.40 ± 0.43 | 337.76 ± 1.11 | 333.17 ± 1.05 |
| Medium | 433.97 ± 8.17 | 417.79 ± 6.84 | 409.95 ± 4.22 | 422.88 ± 2.83 | |
| Fine | 494.41 ± 2.23 | 466.90 ± 5.36 | 440.84 ± 5.82 | 467.74 ± 7.62 | |
| Tapped bulk density (kg/m3) | Coarse | 421.81 ± 4.76 | 386.03 ± 1.48 | 395.28 ± 0.95 | 382.98 ± 0.39 |
| Medium | 529.88 ± 3.75 | 508.21 ± 2.01 | 521.54 ± 1.31 | 520.94 ± 0.40 | |
| Fine | 632.73 ± 3.12 | 613.60 ± 1.36 | 600.41 ± 3.20 | 617.45 ± 0.95 |
| Sample Class | Brand 1 | Brand 2 | Brand 3 | Brand 4 | |
|---|---|---|---|---|---|
| Loose bulk density (kg/m3) | 4 | 457.35 ± 8.25 | 424.42 ± 0.91 | 405.29 ± 3.53 | 412.36 ± 2.50 |
| 5 | 466.00 ± 6.66 | 449.95 ± 1.74 | 423.75 ± 2.09 | 436.35 ± 1.86 | |
| 6 | 456.31 ± 6.82 | 429.58 ± 2.18 | 418.49 ± 1.38 | 421.91 ± 1.23 | |
| 7 | 453.90 ± 2.71 | 428.94 ± 1.26 | 418.29 ± 6.68 | 428.17 ± 2.33 | |
| 8 | 456.65 ± 5.33 | 434.00 ± 3.51 | 424.02 ± 1.36 | 428.14 ± 2.73 | |
| 9 | 451.02 ± 2.76 | 421.98 ± 5.31 | 411.96 ± 1.68 | 414.67 ± 1.68 | |
| 10 | 446.50 ± 1.84 | 428.07 ± 1.89 | 418.89 ± 3.10 | 435.14 ± 2.55 | |
| Tapped bulk density (kg/m3) | 4 | 547.10 ± 1.58 | 531.36 ± 0.81 | 519.63 ± 1.51 | 525.39 ± 0.71 |
| 5 | 587.91 ± 3.58 | 571.09 ± 1.97 | 552.46 ± 1.53 | 568.58 ± 0.74 | |
| 6 | 559.97 ± 2.96 | 537.92 ± 1.89 | 538.09 ± 1.24 | 535.88 ± 0.30 | |
| 7 | 572.73 ± 1.23 | 547.81 ± 2.18 | 542.48 ± 0.42 | 550.08 ± 1.18 | |
| 8 | 578.76 ± 1.11 | 551.39 ± 1.01 | 543.58 ± 0.55 | 547.97 ± 1.01 | |
| 9 | 564.82 ± 0.79 | 528.94 ± 0.81 | 532.86 ± 0.51 | 530.32 ± 0.41 | |
| 10 | 561.04 ± 1.05 | 541.04 ± 1.28 | 541.78 ± 2.26 | 552.40 ± 0.17 |
| Samples | MSE | R2 | |
|---|---|---|---|
| Training | 28 | 10.80 | 0.98 |
| Validation | 6 | 34.26 | 0.98 |
| Test | 6 | 62.13 | 0.97 |
| All | 40 | 22.02 | 0.98 |
| Samples | MSE | R2 | |
|---|---|---|---|
| Training | 28 | 53.04 | 0.98 |
| Validation | 6 | 19.38 | 0.98 |
| Test | 6 | 159.71 | 0.96 |
| All | 40 | 63.99 | 0.98 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ding, H.; Li, B.; Boiarkina, I.; Wilson, D.I.; Yu, W.; Young, B.R. Effects of Morphology on the Bulk Density of Instant Whole Milk Powder. Foods 2020, 9, 1024. https://doi.org/10.3390/foods9081024
Ding H, Li B, Boiarkina I, Wilson DI, Yu W, Young BR. Effects of Morphology on the Bulk Density of Instant Whole Milk Powder. Foods. 2020; 9(8):1024. https://doi.org/10.3390/foods9081024
Chicago/Turabian StyleDing, Haohan, Bing Li, Irina Boiarkina, David I. Wilson, Wei Yu, and Brent R. Young. 2020. "Effects of Morphology on the Bulk Density of Instant Whole Milk Powder" Foods 9, no. 8: 1024. https://doi.org/10.3390/foods9081024




