A Deep Learning Algorithm for Multi-Source Data Fusion to Predict Effluent Quality of Wastewater Treatment Plant
Abstract
:1. Introduction
2. Materials and Methods
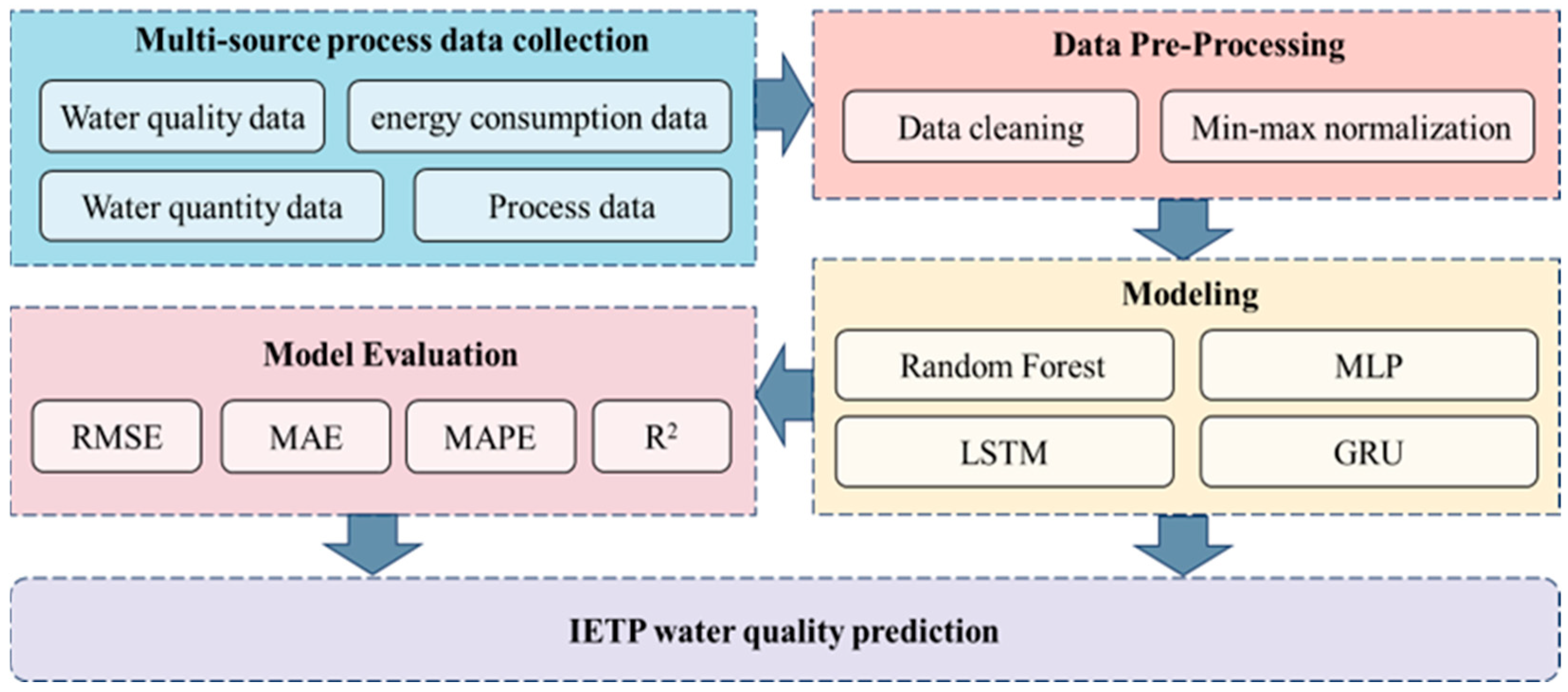
2.1. The Research Framework
2.2. Data Pre-Processing
2.3. Predictive Model
2.3.1. Random Forest (RF)
2.3.2. Multilayer Perceptron (MLP)
2.3.3. Long Short-Term Memory (LSTM)
2.3.4. Gated Recurrent Unit (GRU)
2.4. Strategies for Multi-Source Feature Fusion (RReliefF)
2.5. Evaluation of Model Performance
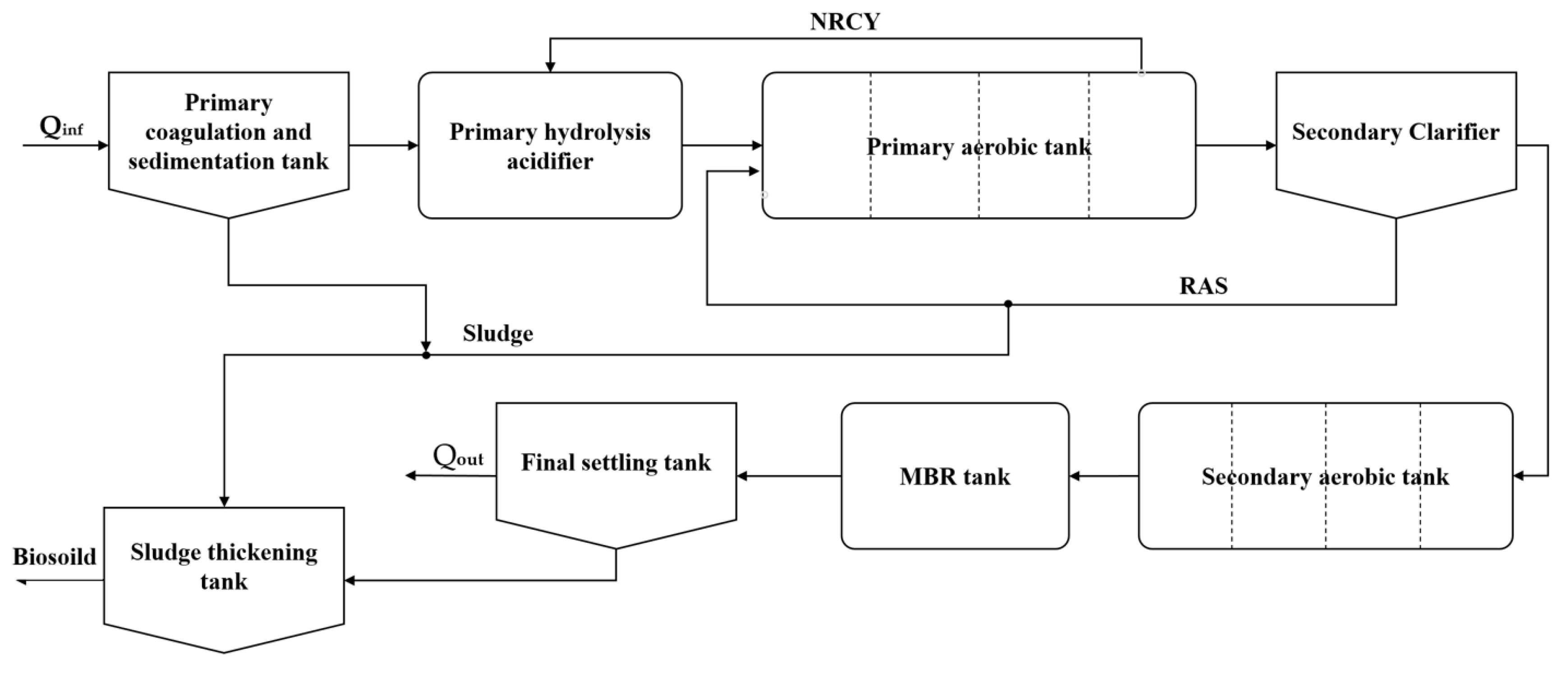
2.6. IETP
2.7. Statistical Information on Data
2.8. Model Development
3. Results and Discussion
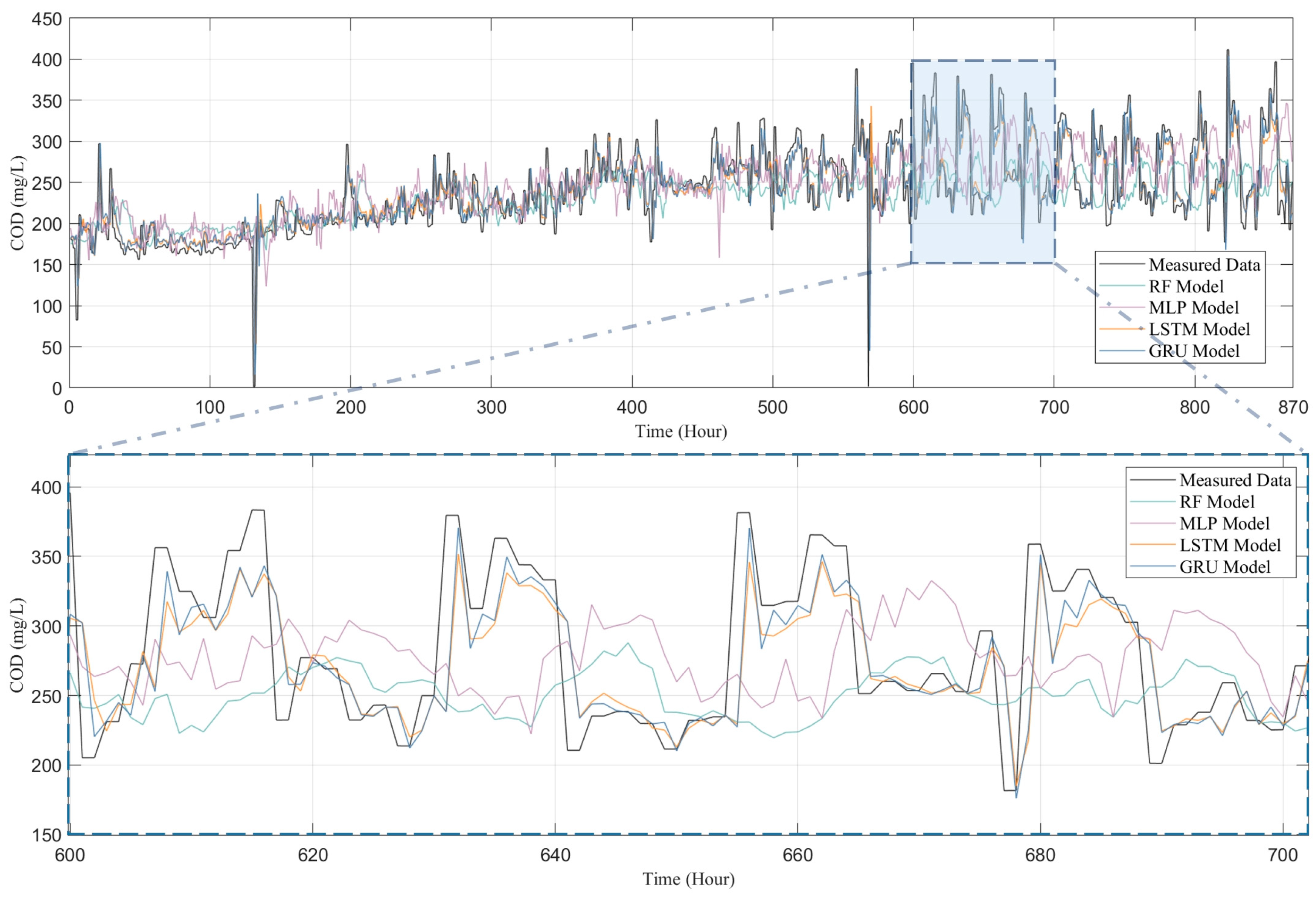
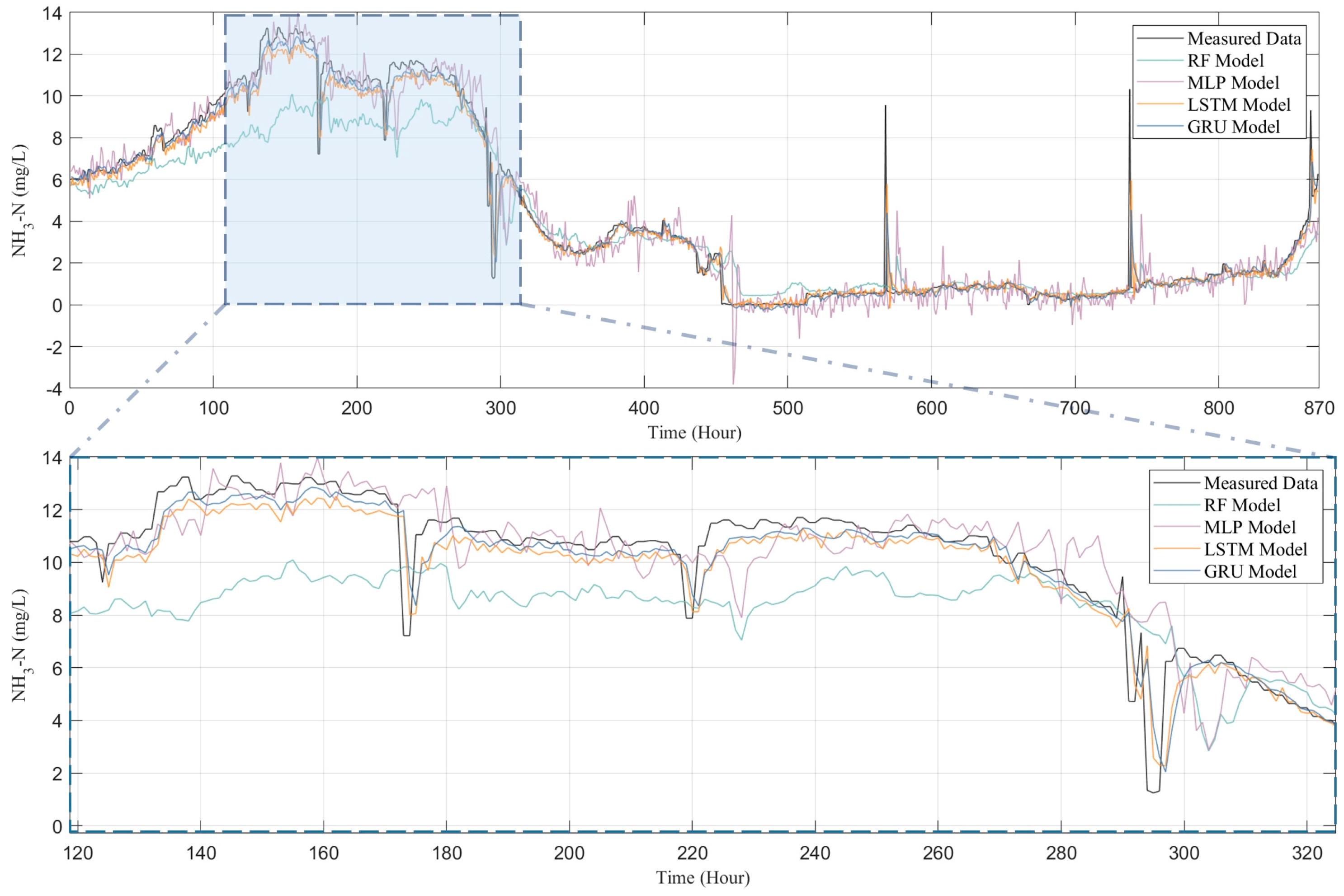
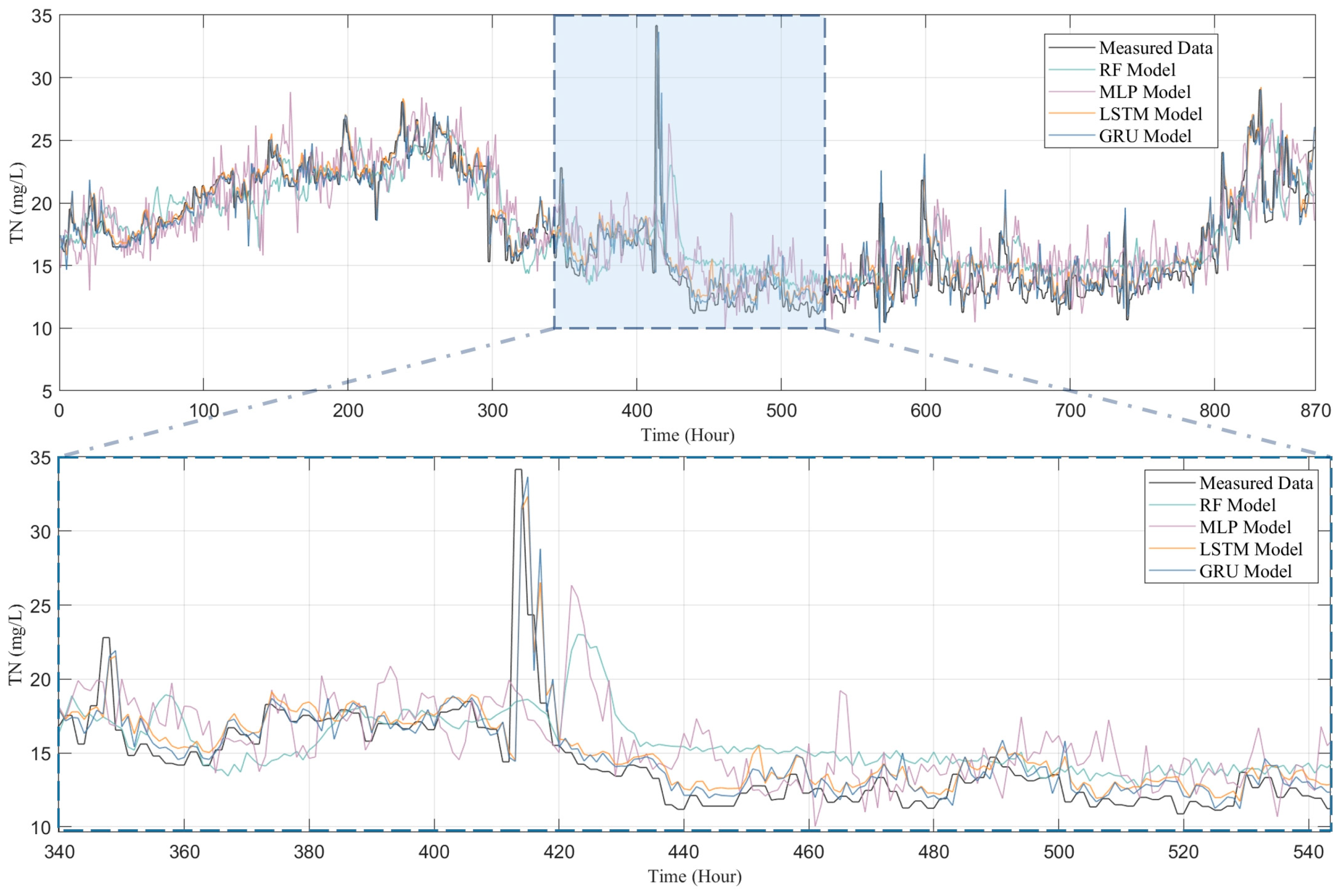
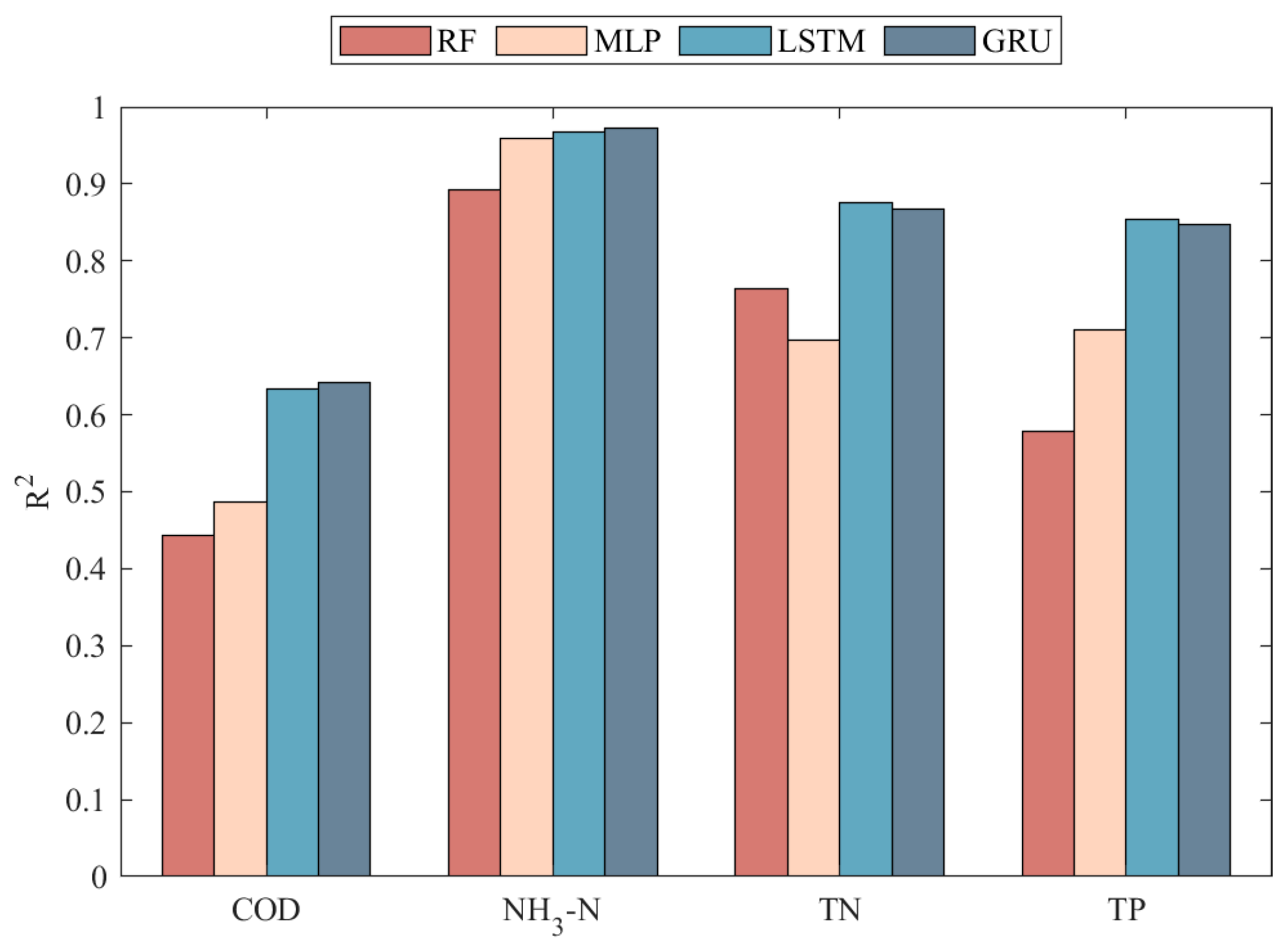
3.1. Evaluation of Prediction Results and Model Performance
3.2. Comparison of the Models
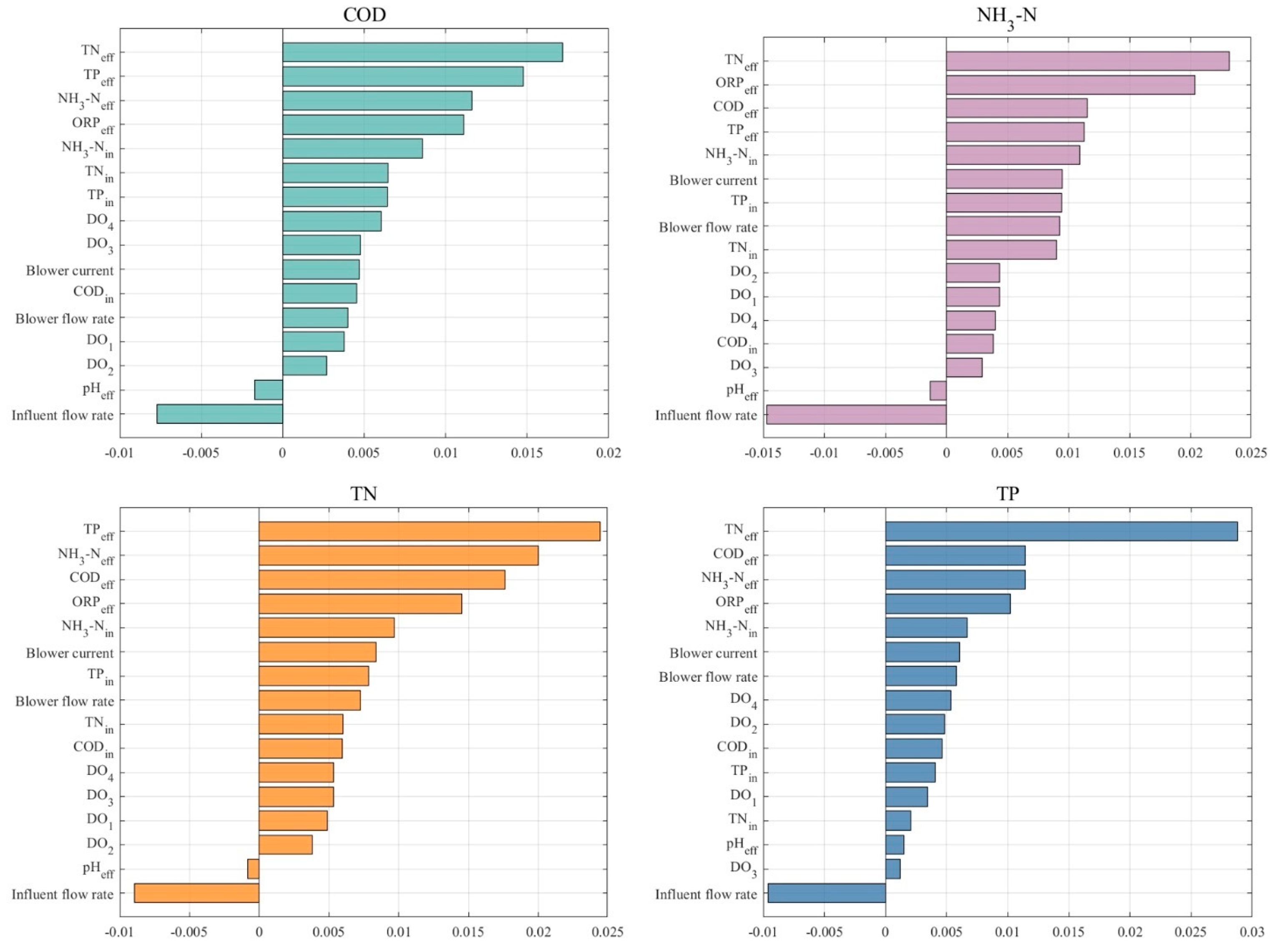
3.3. Further Understanding Changes in Effluent Quality Through RreliefF
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Akinnawo, S.O. Eutrophication: Causes, consequences, physical, chemical and biological techniques for mitigation strategies. Environ. Chall. 2023, 12, 100733. [Google Scholar] [CrossRef]
- Eriksen, T.E.; Jacobsen, D.; Demars, B.O.; Brittain, J.E.; Søli, G.; Friberg, N. Effects of pollution-induced changes in oxygen conditions scaling up from individuals to ecosystems in a tropical river network. Sci. Total Environ. 2022, 814, 151958. [Google Scholar] [CrossRef]
- Panhota, R.S.; da Cunha Santino, M.B.; Bianchini, I., Jr. Oxygen consumption and formation of recalcitrant organic carbon from the decomposition of free-floating macrophyte leachates. Environ. Sci. Pollut. Res. 2023, 30, 101379–101391. [Google Scholar] [CrossRef]
- Wurtsbaugh, W.A.; Paerl, H.W.; Dodds, W.K. Nutrients, eutrophication and harmful algal blooms along the freshwater to marine continuum. Wiley Interdiscip. Rev. Water 2019, 6, e1373. [Google Scholar] [CrossRef]
- Guo, W.; Pan, B.; Sakkiah, S.; Yavas, G.; Ge, W.; Zou, W.; Tong, W.; Hong, H. Persistent organic pollutants in food: Contamination sources, health effects and detection methods. Int. J. Environ. Res. Public Health 2019, 16, 4361. [Google Scholar] [CrossRef]
- Fan, Y.; Xu, Z.; Huang, Y.; Wang, T.; Zheng, S.; DePasquale, A.; Brüeckner, C.; Lei, Y.; Li, B. Long-term continuous and real-time in situ monitoring of Pb (II) toxic contaminants in wastewater using solid-state ion selective membrane (S-ISM) Pb and pH auto-correction assembly. J. Hazard. Mater. 2020, 400, 123299. [Google Scholar] [CrossRef]
- Haimi, H.; Mulas, M.; Corona, F.; Vahala, R. Data-derived soft-sensors for biological wastewater treatment plants: An overview. Environ. Model. Softw. 2013, 47, 88–107. [Google Scholar] [CrossRef]
- Therrien, J.-D.; Nicolaï, N.; Vanrolleghem, P.A. A critical review of the data pipeline: How wastewater system operation flows from data to intelligence. Water Sci. Technol. 2020, 82, 2613–2634. [Google Scholar] [CrossRef] [PubMed]
- Wang, T.; Xu, Z.; Huang, Y.; Dai, Z.; Wang, X.; Lee, M.; Bagtzoglou, C.; Brückner, C.; Lei, Y.; Li, B. Real-time in situ auto-correction of K+ interference for continuous and long-term NH4+ monitoring in wastewater using solid-state ion selective membrane (S-ISM) sensor assembly. Environ. Res. 2020, 189, 109891. [Google Scholar] [CrossRef]
- Abba, S.I.; Hadi, S.J.; Sammen, S.S.; Salih, S.Q.; Abdulkadir, R.A.; Pham, Q.B.; Yaseen, Z.M. Evolutionary computational intelligence algorithm coupled with self-tuning predictive model for water quality index determination. J. Hydrol. 2020, 587, 124974. [Google Scholar] [CrossRef]
- Lv, Z.; Ran, X.; Liu, J.; Feng, Y.; Zhong, X.; Jiao, N. Effectiveness of chemical oxygen demand as an indicator of organic pollution in aquatic environments. Ocean-Land-Atmos. Res. 2024, 3, 0050. [Google Scholar] [CrossRef]
- Liu, X.; Yang, C.; Zhou, L.; Ding, Z.; Jiang, D.; Fei, J. Study on Eutrophication, Phosphorus Pollution and Morphological Analysis of Separated Lakes. J. Phys. Conf. Ser. 2025, 2941, 012078. [Google Scholar] [CrossRef]
- Brdjanovic, D.; Meijer, S.C.; Lopez-Vazquez, C.M.; Hooijmans, C.M.; van Loosdrecht, M.C. Applications of Activated Sludge Models; IWA Publishing: London, UK, 2015. [Google Scholar]
- Gujer, W.; Henze, M.; Mino, T.; Matsuo, T.; Wentzel, M.C.; Marais, G. The activated sludge model No. 2: Biological phosphorus removal. Water Sci. Technol. 1995, 31, 1–11. [Google Scholar] [CrossRef]
- Gujer, W.; Henze, M.; Mino, T.; Van Loosdrecht, M. Activated sludge model No. 3. Water Sci. Technol. 1999, 39, 183–193. [Google Scholar] [CrossRef]
- Wang, D.; Thunéll, S.; Lindberg, U.; Jiang, L.; Trygg, J.; Tysklind, M.; Souihi, N. A machine learning framework to improve effluent quality control in wastewater treatment plants. Sci. Total Environ. 2021, 784, 147138. [Google Scholar] [CrossRef]
- Cao, W.; Yang, Q. Online sequential extreme learning machine based adaptive control for wastewater treatment plant. Neurocomputing 2020, 408, 169–175. [Google Scholar] [CrossRef]
- Guo, H.; Jeong, K.; Lim, J.; Jo, J.; Kim, Y.M.; Park, J.-P.; Kim, J.H.; Cho, K.H. Prediction of effluent concentration in a wastewater treatment plant using machine learning models. J. Environ. Sci. 2015, 32, 90–101. [Google Scholar] [CrossRef]
- Chen, J.; N’Doye, I.; Myshkevych, Y.; Aljehani, F.; Monjed, M.K.; Laleg-Kirati, T.-M.; Hong, P.-Y. Viral particle prediction in wastewater treatment plants using nonlinear lifelong learning models. NPJ Clean Water 2025, 8, 28. [Google Scholar] [CrossRef]
- Liu, H.; Yang, C.; Carlsson, B.; Qin, S.J.; Yoo, C. Dynamic nonlinear partial least squares modeling using Gaussian process regression. Ind. Eng. Chem. Res. 2019, 58, 16676–16686. [Google Scholar] [CrossRef]
- Lu, H.; Ma, X. Hybrid decision tree-based machine learning models for short-term water quality prediction. Chemosphere 2020, 249, 126169. [Google Scholar] [CrossRef]
- Abouzari, M.; Pahlavani, P.; Izaditame, F.; Bigdeli, B. Estimating the chemical oxygen demand of petrochemical wastewater treatment plants using linear and nonlinear statistical models–A case study. Chemosphere 2021, 270, 129465. [Google Scholar] [CrossRef]
- Yang, C.; Zhang, Y.; Huang, M.; Liu, H. Adaptive dynamic prediction of effluent quality in wastewater treatment processes using partial least squares embedded with relevance vector machine. J. Clean. Prod. 2021, 314, 128076. [Google Scholar] [CrossRef]
- Prucha, B.; Graham, D.; Watson, M.; Avenant, M.; Esterhuyse, S.; Joubert, A.; Kemp, M.; King, J.; Le Roux, P.; Redelinghuys, N. MIKE-SHE integrated groundwater and surface water model used to simulate scenario hydrology for input to DRIFT-ARID: The Mokolo River case study. Water SA 2016, 42, 384–398. [Google Scholar] [CrossRef]
- Kim, J.; Lee, T.; Seo, D. Algal bloom prediction of the lower Han River, Korea using the EFDC hydrodynamic and water quality model. Ecol. Model. 2017, 366, 27–36. [Google Scholar] [CrossRef]
- He, M.; Qian, Q.; Liu, X.; Zhang, J.; Curry, J. Recent Progress on Surface Water Quality Models Utilizing Machine Learning Techniques. Water 2024, 16, 3616. [Google Scholar] [CrossRef]
- Dargan, S.; Kumar, M.; Ayyagari, M.R.; Kumar, G. A survey of deep learning and its applications: A new paradigm to machine learning. Arch. Comput. Methods Eng. 2020, 27, 1071–1092. [Google Scholar] [CrossRef]
- Mjalli, F.S.; Al-Asheh, S.; Alfadala, H. Use of artificial neural network black-box modeling for the prediction of wastewater treatment plants performance. J. Environ. Manag. 2007, 83, 329–338. [Google Scholar] [CrossRef] [PubMed]
- Choi, D.-J.; Park, H. A hybrid artificial neural network as a software sensor for optimal control of a wastewater treatment process. Water Res. 2001, 35, 3959–3967. [Google Scholar] [CrossRef] [PubMed]
- Asami, H.; Golabi, M.; Albaji, M. Simulation of the biochemical and chemical oxygen demand and total suspended solids in wastewater treatment plants: Data-mining approach. J. Clean. Prod. 2021, 296, 126533. [Google Scholar] [CrossRef]
- Qiao, J.; Quan, L.; Yang, C. Design of modeling error PDF based fuzzy neural network for effluent ammonia nitrogen prediction. Appl. Soft Comput. 2020, 91, 106239. [Google Scholar] [CrossRef]
- Zhao, L.; Yuan, D.; Chai, T.; Tang, J. KPCA and ELM ensemble modeling of wastewater effluent quality indices. Procedia Eng. 2011, 15, 5558–5562. [Google Scholar] [CrossRef]
- Wang, G.; Jia, Q.-S.; Zhou, M.; Bi, J.; Qiao, J. Soft-sensing of wastewater treatment process via deep belief network with event-triggered learning. Neurocomputing 2021, 436, 103–113. [Google Scholar] [CrossRef]
- Bekkari, N.; Zeddouri, A. Using artificial neural network for predicting and controlling the effluent chemical oxygen demand in wastewater treatment plant. Manag. Environ. Qual. Int. J. 2019, 30, 593–608. [Google Scholar] [CrossRef]
- Farhi, N.; Kohen, E.; Mamane, H.; Shavitt, Y. Prediction of wastewater treatment quality using LSTM neural network. Environ. Technol. Innov. 2021, 23, 101632. [Google Scholar] [CrossRef]
- Cheng, T.; Harrou, F.; Kadri, F.; Sun, Y.; Leiknes, T. Forecasting of wastewater treatment plant key features using deep learning-based models: A case study. IEEE Access 2020, 8, 184475–184485. [Google Scholar] [CrossRef]
- Zhu, S.; Han, H.; Guo, M.; Qiao, J. A data-derived soft-sensor method for monitoring effluent total phosphorus. Chin. J. Chem. Eng. 2017, 25, 1791–1797. [Google Scholar] [CrossRef]
- Zhang, H.; Yang, C.; Shi, X.; Liu, H. Effluent quality prediction in papermaking wastewater treatment processes using dynamic Bayesian networks. J. Clean. Prod. 2021, 282, 125396. [Google Scholar] [CrossRef]
- Cao, J.; Xue, A.; Yang, Y.; Cao, W.; Hu, X.; Cao, G.; Gu, J.; Zhang, L.; Geng, X. Deep learning based soft sensor for microbial wastewater treatment efficiency prediction. J. Water Process Eng. 2023, 56, 104259. [Google Scholar] [CrossRef]
- Chang, P.; Li, Z. Over-complete deep recurrent neutral network based on wastewater treatment process soft sensor application. Appl. Soft Comput. 2021, 105, 107227. [Google Scholar] [CrossRef]
- Wang, G.; Jia, Q.-S.; Zhou, M.; Bi, J.; Qiao, J.; Abusorrah, A. Artificial neural networks for water quality soft-sensing in wastewater treatment: A review. Artif. Intell. Rev. 2022, 55, 565–587. [Google Scholar] [CrossRef]
- Alnowaiser, K.; Alarfaj, A.A.; Alabdulqader, E.A.; Umer, M.; Cascone, L.; Alankar, B. IoT based smart framework to predict air quality in congested traffic areas using SV-CNN ensemble and KNN imputation model. Comput. Electr. Eng. 2024, 118, 109311. [Google Scholar] [CrossRef]
- Qambar, A.S.; Al Khalidy, M.M.M. Development of local and global wastewater biochemical oxygen demand real-time prediction models using supervised machine learning algorithms. Eng. Appl. Artif. Intell. 2023, 118, 105709. [Google Scholar] [CrossRef]
- Ren, T.; Liu, X.; Niu, J.; Lei, X.; Zhang, Z. Real-time water level prediction of cascaded channels based on multilayer perception and recurrent neural network. J. Hydrol. 2020, 585, 124783. [Google Scholar] [CrossRef]
- Graves, A.; Graves, A. Long short-term memory. In Supervised Sequence Labelling with Recurrent Neural Networks; Springer Nature: Dordrecht, The Netherlands, 2012; pp. 37–45. [Google Scholar]
- Cho, K.; Van Merriënboer, B.; Gulcehre, C.; Bahdanau, D.; Bougares, F.; Schwenk, H.; Bengio, Y. Learning phrase representations using RNN encoder-decoder for statistical machine translation. In Proceedings of the 2014 Conference on Empirical Methods in Natural Language Processing (EMNLP), Doha, Qatar, 25–29 October 2014; pp. 1724–1734. [Google Scholar]
- Subbiah, S.S.; Chinnappan, J. Deep learning based short term load forecasting with hybrid feature selection. Electr. Power Syst. Res. 2022, 210, 108065. [Google Scholar] [CrossRef]
- Zhao, M.; Liu, T.; Jiang, H. Quantitative detection of moisture content of corn by olfactory visualization technology. Microchem. J. 2024, 199, 109937. [Google Scholar] [CrossRef]
- Li, Z.; Xu, R.; Luo, X.; Cao, X.; Sun, H. Short-term wind power prediction based on modal reconstruction and CNN-BiLSTM. Energy Rep. 2023, 9, 6449–6460. [Google Scholar] [CrossRef]
- Bergstra, J.; Bengio, Y. Random search for hyper-parameter optimization. J. Mach. Learn. Res. 2012, 13, 281–305. [Google Scholar]





| Measurement | Mean | Median | STD | CV | Comments |
|---|---|---|---|---|---|
| Influent flow rate | 153.33 | 128 | 112.009 | 0.88 | Instantaneous influent flow |
| CODin | 1169.24 | 1240.2 | 656.726 | 0.53 | Influent chemical oxygen demand-—mg/L |
| NH3-Nin | 7.8 | 1.89 | 15.021 | 7.95 | Influent ammonia nitrogen—mg/L |
| TPin | 0.87 | 0.66 | 0.61 | 0.92 | Influent total phosphorus—mg/L |
| TNin | 23.99 | 19.22 | 17.278 | 0.90 | Influent total nitrogen—mg/L |
| pHeff | 7.8 | 7.84 | 0.321 | 0.04 | Effluent potential of hydrogen—mg/L |
| ORPeff | 22.53 | 22.8 | 3.768 | 0.17 | Effluent oxidation-reduction potential—mg/L |
| DO1 | 3.27 | 3.27 | 0.307 | 0.09 | Dissolved oxygen in the primary aerobic tank—mg/L |
| DO2 | 3.27 | 3.27 | 0.35 | 0.11 | Dissolved oxygen in the primary aerobic tank—mg/L |
| DO3 | 1.18 | 0.57 | 1.382 | 2.42 | Dissolved oxygen in the secondary aerobic tank—mg/L |
| DO4 | 1.43 | 0.6 | 1.753 | 2.92 | Dissolved oxygen in the secondary aerobic tank—mg/L |
| Blower flow rate | 109.1 | 109.7 | 16.096 | 0.15 | Air blower flow rate—m3/h |
| Blower current | 254.88 | 261.7 | 44.311 | 0.17 | Blower current—A |
| CODeff | 234.45 | 234.8 | 41.541 | 0.18 | Effluent chemical oxygen demand—mg/L |
| NH3-Neff | 4.75 | 2.86 | 4.89 | 1.71 | Effluent ammonia nitrogen—mg/L |
| TPeff | 0.25 | 0.2 | 0.172 | 0.86 | Effluent total phosphorus—mg/L |
| TNeff | 22.48 | 21.69 | 7.8 | 0.36 | Effluent total nitrogen—mg/L |
| Model | Parameters | Value |
|---|---|---|
| RF | Min samples leaf | 16 |
| Min samples split | 2 | |
| Max depth | 5 | |
| Estimators | 100 | |
| MLP | Number of layers | 3 |
| Number of neurons | 50, 10 | |
| Activation | Identity | |
| Batch size | 512 | |
| Optimiser | adam | |
| LSTM | Number of layers | 2 |
| Number of neurons | 128, 128 | |
| Activation | Relu | |
| Batch size | 512 | |
| Optimiser | adam | |
| GRU | Number of layers | 2 |
| Number of neurons | 128, 128 | |
| Activation | Relu | |
| Batch size | 512 | |
| Optimiser | adam |
| Water Quality Indicators | Model | Evaluation Index | |||
|---|---|---|---|---|---|
| RMSE | MAE | MAPE | R2 | ||
| COD | RF | 41.349 | 28.913 | 62.450% | 0.444 |
| MLP | 39.715 | 28.688 | 62.681% | 0.487 | |
| LSTM | 33.385 | 19.825 | 52.255% | 0.634 | |
| GRU | 33.045 | 18.653 | 49.551% | 0.642 | |
| NH3-N | RF | 1.398 | 0.881 | / | 0.892 |
| MLP | 0.861 | 0.508 | / | 0.959 | |
| LSTM | 0.768 | 0.364 | / | 0.967 | |
| GRU | 0.714 | 0.290 | / | 0.972 | |
| TN | RF | 2.134 | 1.588 | 10.205% | 0.764 |
| MLP | 2.418 | 1.829 | 11.487% | 0.697 | |
| LSTM | 1.562 | 0.994 | 6.301% | 0.876 | |
| GRU | 1.614 | 0.938 | 5.811% | 0.867 | |
| TP | RF | 0.046 | 0.036 | 13.716% | 0.578 |
| MLP | 0.038 | 0.028 | 11.472% | 0.710 | |
| LSTM | 0.027 | 0.016 | 6.832% | 0.854 | |
| GRU | 0.027 | 0.017 | 6.805% | 0.848 | |
| Water Quality Indicators | Modelling Scenario | Feature Quantity | Evaluation Index | ||
|---|---|---|---|---|---|
| RMSE | MAE | R2 | |||
| COD | A | 16 | 33.045 | 18.653 | 0.642 |
| B | 14 | 32.883 | 18.528 | 0.649 | |
| C | 8 | 35.234 | 20.193 | 0.550 | |
| D | 8 | 43.283 | 26.366 | 0.163 | |
| NH3-N | A | 16 | 0.714 | 0.290 | 0.972 |
| B | 14 | 0.695 | 0.259 | 0.981 | |
| C | 9 | 0.710 | 0.284 | 0.974 | |
| D | 7 | 1.418 | 0.618 | 0.454 | |
| TN | A | 16 | 1.614 | 0.938 | 0.867 |
| B | 14 | 1.597 | 0.927 | 0.874 | |
| C | 12 | 1.623 | 0.942 | 0.862 | |
| D | 4 | 3.051 | 2.101 | 0.108 | |
| TP | A | 16 | 0.0270 | 0.0170 | 0.848 |
| B | 15 | 0.0269 | 0.0168 | 0.851 | |
| C | 8 | 0.0269 | 0.0184 | 0.850 | |
| D | 8 | 0.0416 | 0.0301 | 0.392 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, S.; Cao, J.; Gao, Y.; Sun, F.; Yang, Y. A Deep Learning Algorithm for Multi-Source Data Fusion to Predict Effluent Quality of Wastewater Treatment Plant. Toxics 2025, 13, 349. https://doi.org/10.3390/toxics13050349
Zhang S, Cao J, Gao Y, Sun F, Yang Y. A Deep Learning Algorithm for Multi-Source Data Fusion to Predict Effluent Quality of Wastewater Treatment Plant. Toxics. 2025; 13(5):349. https://doi.org/10.3390/toxics13050349
Chicago/Turabian StyleZhang, Shitao, Jiafei Cao, Yang Gao, Fangfang Sun, and Yong Yang. 2025. "A Deep Learning Algorithm for Multi-Source Data Fusion to Predict Effluent Quality of Wastewater Treatment Plant" Toxics 13, no. 5: 349. https://doi.org/10.3390/toxics13050349
APA StyleZhang, S., Cao, J., Gao, Y., Sun, F., & Yang, Y. (2025). A Deep Learning Algorithm for Multi-Source Data Fusion to Predict Effluent Quality of Wastewater Treatment Plant. Toxics, 13(5), 349. https://doi.org/10.3390/toxics13050349






