Experimental Methods for Measuring the Breakup Frequency in Turbulent Emulsification: A Critical Review
Abstract
:1. Introduction
2. Breakup Frequency
2.1. Definition
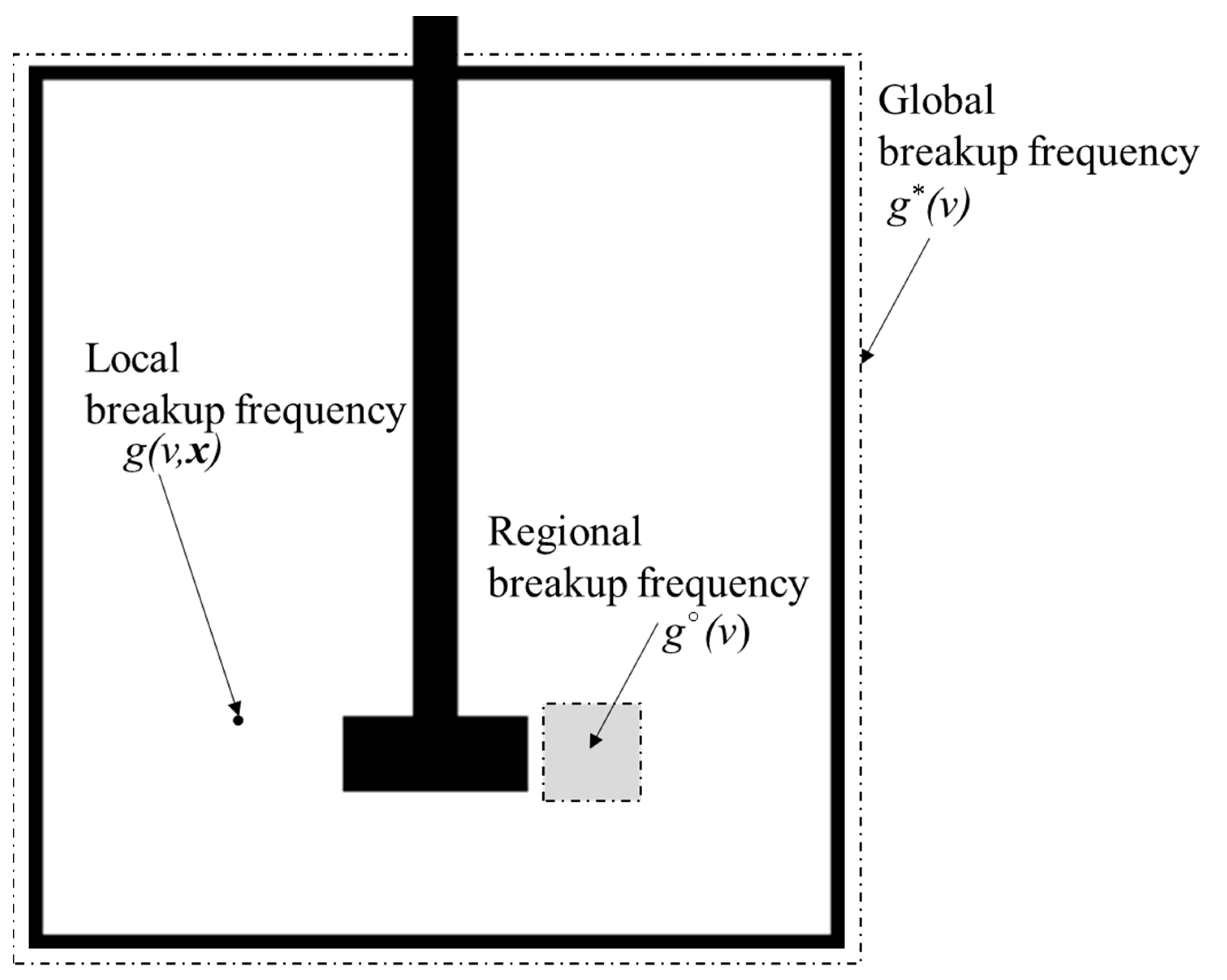
2.2. Local, Regional, and Global Breakup Frequency
- A sufficiently low volume fraction of the disperse phase, hence, fragmentation is the only source term for the PBE;
- A statistically stationary flow, hence, the fragmentation kernels do not depend on time;
- The batch tank is ideally well-mixed, hence, all points in space have the same DSD.
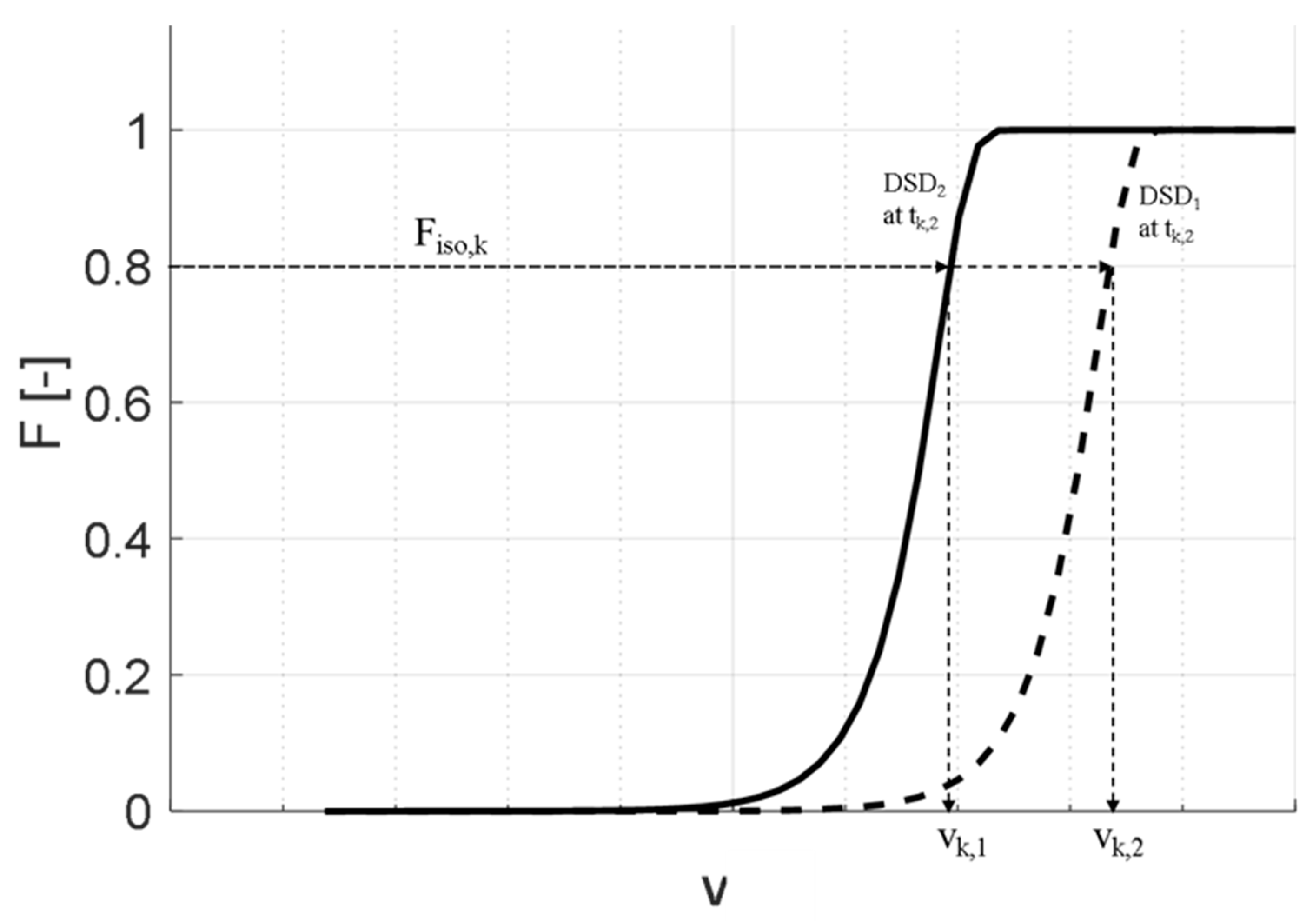
2.3. The Cumulative Formulation of the PBE
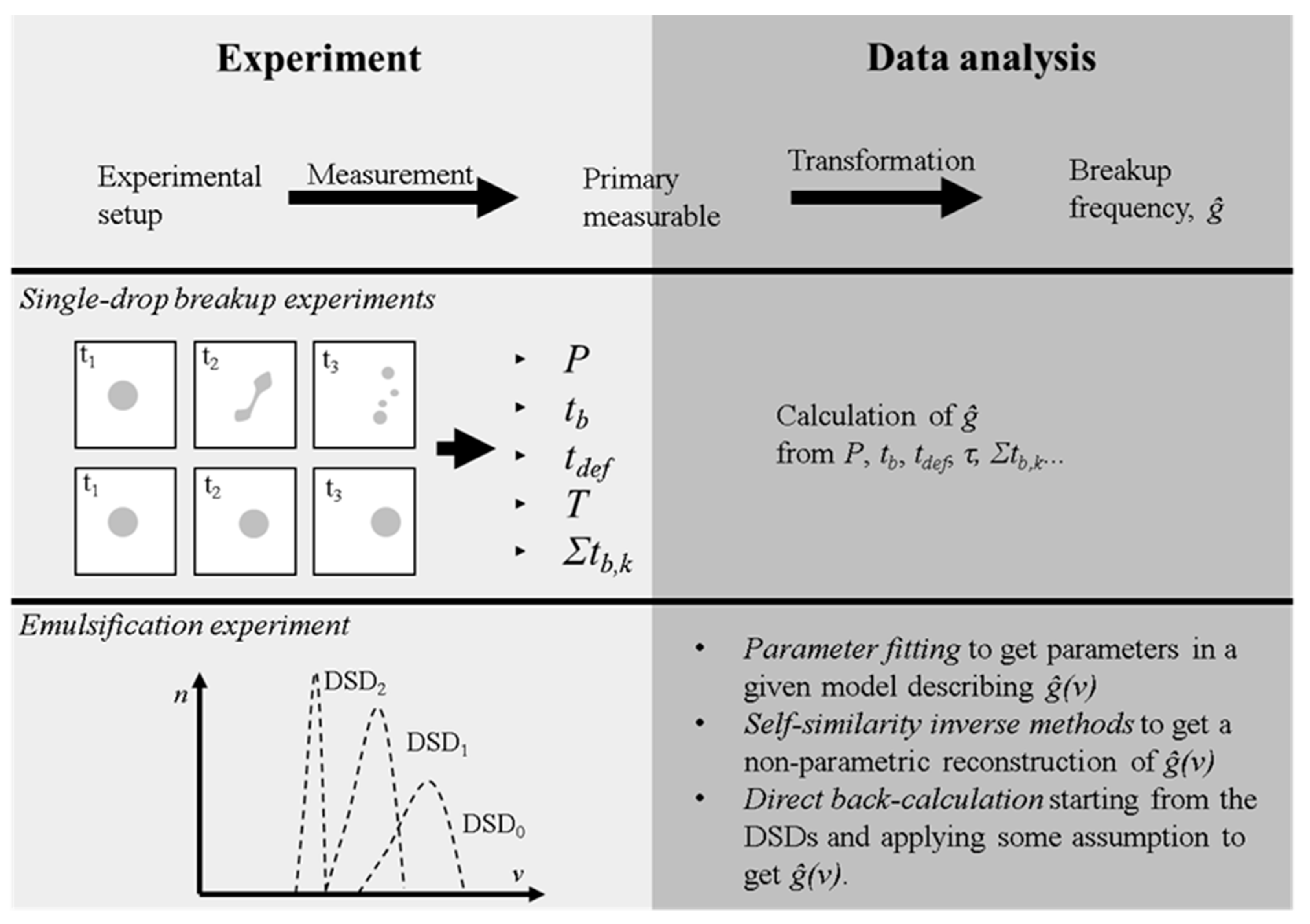
3. Classification of Methods
4. Single Drop Breakup Experiments
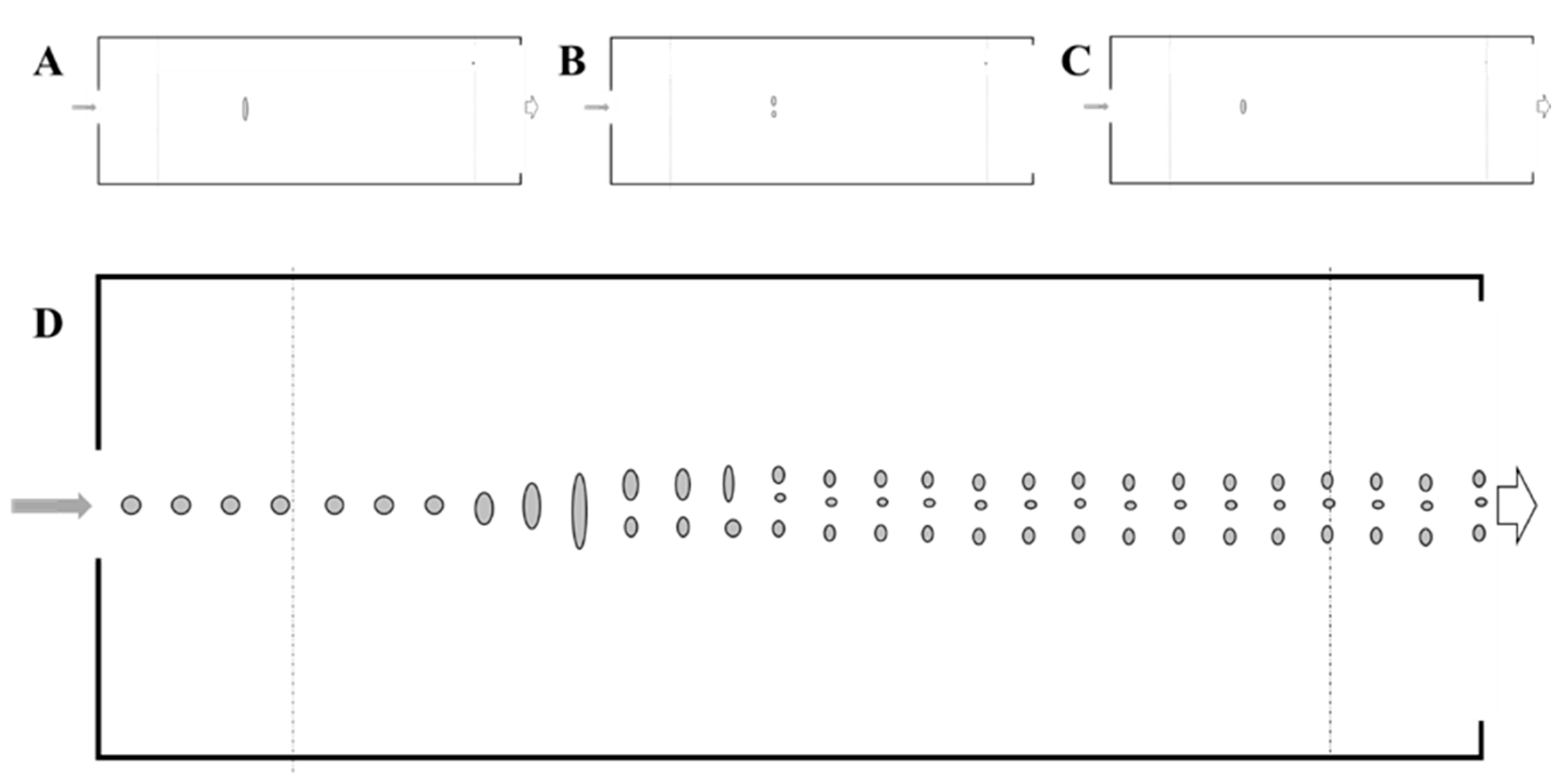
4.1. The Typical Experimental Setup
- The number of drops fragmented before exiting the zone;
- The percentage of drops fragmented upon passing the zone;
- The number of daughter drops formed per breakup;
- The size distributions of the daughter drops.
4.2. Methods for Estimating the Breakup Frequency
4.3. Individual Studies—Experimental Setup
4.4. Experimental Considerations
- Sufficient resolution of the drops to accurately measure the size of fragments;
- Sufficiently large depth of field (DOF) to make sure the drop does not become blurry;
- Sufficiently high contrast between the drop and continuous phase;
- Sufficiently fast camera.
4.4.1. Image Resolution
4.4.2. Depth of Field (DOF)
4.4.3. Contrast
4.4.4. Camera Speed
5. Parametric Determination
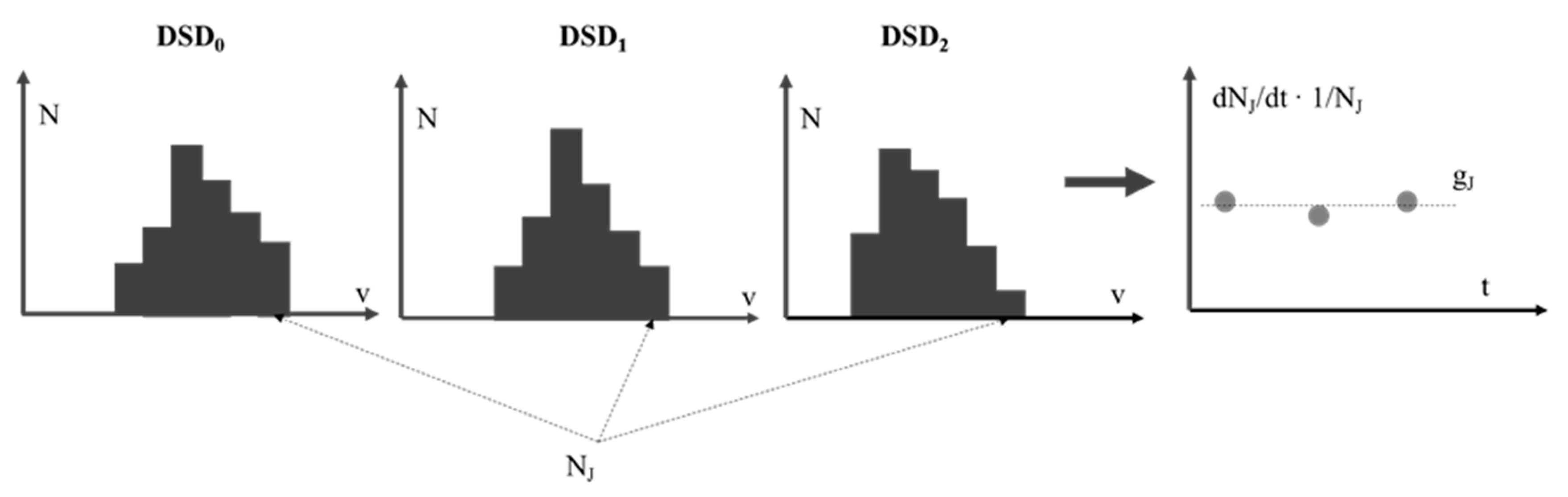
5.1. The General Approach
5.2. Individual Studies
5.3. Critique
6. Self-Similarity-Based Inverse Methods
6.1. General Approach
6.2. Self-Similarity
6.3. The Three Steps Employed for Calculating the Breakup Frequency
- Testing if the fragmentation process is self-similar;
- Calculating the shape of the scaled breakup frequency through a direct integration of experimental data;
- Determining the scaling and cumulative fragment size distribution through a non-linear regression on the self-similar PBE solution expanded in terms of basis functions.
6.4. Individual Studies
6.5. Critique
7. Direct Back-Calculation
7.1. General Approach
7.2. Individual Studies
8. Experimental Considerations for Emulsification Experiment-Based Methods
9. Discussion, Comparisons, and Summary
9.1. Comparing the Single Drop Breakup and Emulsification Approach
9.2. Comparisons of Single Drop Breakup Techniques
- Valid identification of breakup from the single drop experiment. Without a well-resolved drop, clearly distinguishable from its background, and a sufficient number of frames captured during the breakup, the quality of the primary measurables will be poor, and hence, the quality of the estimated breakup frequency will also be poor. Section 4.4 gives some suggestions on guidelines of how to achieve the conditions allowing for valid identifications of breakup events;
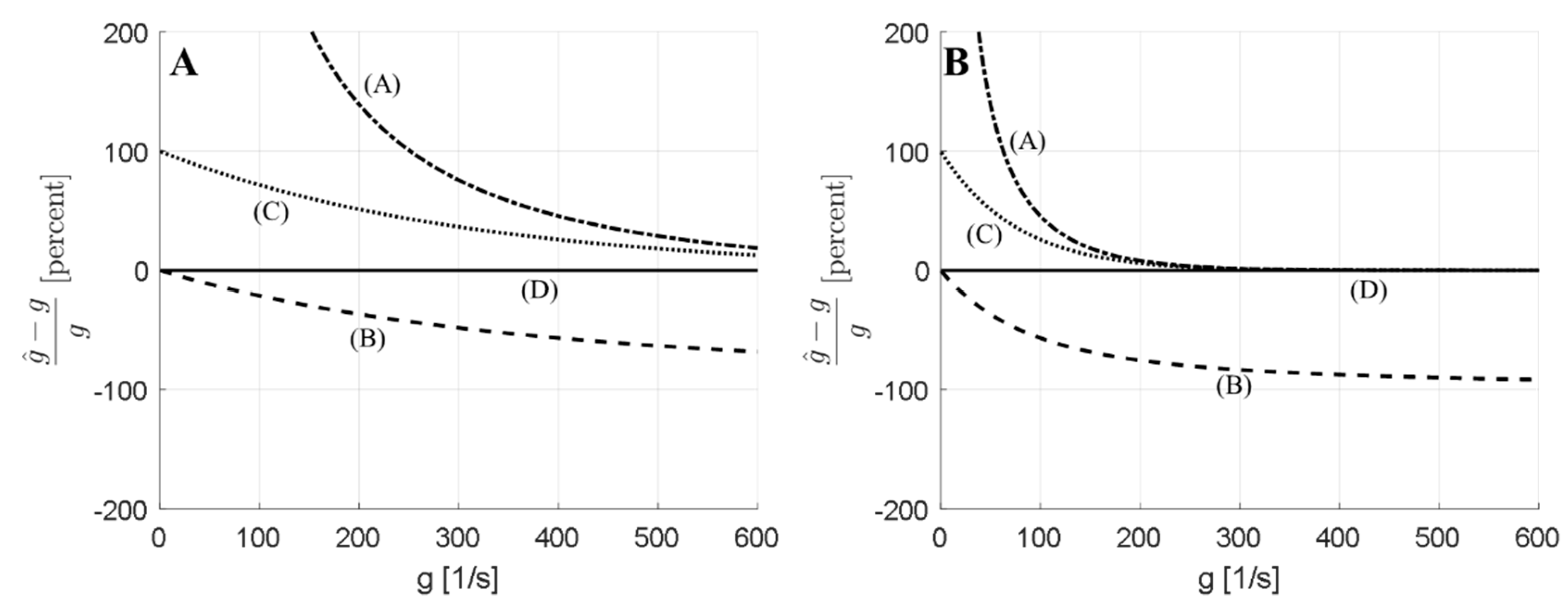
- Valid estimates of the breakup frequency. Since the ultimate objective of all breakup frequency determination is a PBE analysis, the method used when translating the primary measurables, such as the breakup probability, breakup time-scales, etc., into the breakup frequency must be valid in terms of the PBE. Of the 4–5 different suggestions (see Table 1) used in previous studies, several are invalid in this sense [52]; only one (method D, Equation (17)) has been shown to be valid [12,52]. This should be the preferred method for evaluating single drop breakup experiments until more comprehensive investigations of the validity of the other methods have been presented;
- Reliable estimates of the breakup frequency. There will always be some degree of measurement uncertainty in the primary measurables, even in directly observable quantities such as the breakup probability. It is reasonable to assume that some methods are more sensitive to measurement uncertainty than others. Systematic investigations comparing how reliably the breakup frequency can be calculated from different single drop breakup setups are not yet available, but would be a valuable addition to the field. The general uncertainty measurement methodology [85] could provide a framework for these investigations;
- Quick to converge. When comparing methods that are both valid and reliable in measuring the breakup frequency from a single drop breakup experiment, one should also consider their convergence behavior, i.e., how many breakup events must be observed in order for them to give valid and reliable estimates of the breakup frequency.
9.3. Comparison of Emulsification-Based Techniques
9.4. Suggestions for Further Investigations
- Between-method comparisons. Most studies on the experimental determination of the breakup frequency suggest a new method, apply it to turbulent flow under a few different conditions (stirrer speed, drop diameter, drop viscosity, etc.), and report the results. However, as seen in this review, each new method suggested to measure the breakup frequency makes different assumptions about the breakup process, and many of these assumptions are difficult to test. A deeper understanding on the validity of the method, as well as a better understanding of the fragmentation process itself, could be obtained by comparing several methods to the same experimental setup. To the best of the author’s knowledge, there is of yet only a few comparisons of methods; one comparison of parametric determination and single drop breakup visualizations [14] and one comparison of two types of inverse self-similarity methods [66]. Of special interest would be studies comparing single drop breakup visualizations with one of the most promising emulsification data-based methods [33,63,69] for the same setup, or studies comparing the three emulsification data-based methods;
- Single drop breakup experiments. Single drop breakup investigations are often seen as the ‘golden standard’ when determining the breakup frequency. This may have partly resulted from the misconception that it is possible to obtain a direct observation of the breakup frequency. Whereas this is not the case (as seen in Section 4.2, some transformation is needed, and not all of the transformations used are valid), single drop breakup experiment methods remain promising, since the estimations are still more direct than the alternative techniques. Moreover, provided that the right method is used to transform the primary observations (method D, Equation (17)), they can provide a valid estimation of the breakup frequency. Further investigations along these lines are expected to continue contributing to the field;
- Standard implementation. Two of the three most promising techniques for measuring the breakup frequency from emulsification data [33,63] are difficult to implement. The mathematical and numerical complexities are likely to have contributed to the fact that other, theoretically less valid methods, have often been used instead, especially in the applied emulsification research community. Consequently, the community would greatly benefit from standard implementations of these methods, available in a format that is easy to use in applied emulsification research.
9.5. Summary
Funding
Acknowledgments
Conflicts of Interest
References
- McClements, D.J. Food Emulsions: Principles, Practices, and Techniques, 3rd ed.; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]
- Rayner, M.; Dejmek, P. Engineering Aspects of Food Emulsification and Homogenization; CRC Press: Boca Raton, FL, USA, 2015. [Google Scholar]
- Håkansson, A.; Fuchs, L.; Innings, F.; Revstedt, J.; Trägårdh, C.; Bergenståhl, B. High resolution experimental measurement of turbulent flow field in a high pressure homogenizer model its implication on turbulent drop fragmentation. Chem. Eng. Sci. 2011, 66, 1790–1801. [Google Scholar] [CrossRef]
- Kelemen, K.; Crowther, F.E.; Cierpka, C.; Hecht, L.L.; Kähler, C.J.; Schuchmann, H.P. Investigations on the characterization of laminar and transitional flow conditions after high pressure homogenization orifices. Microfluid Nanofluid 2015, 18, 599–612. [Google Scholar] [CrossRef]
- Mortensen, H.H.; Calabrese, R.V.; Innings, F.; Rosendahl, L. Characteristics of a batch rotor-stator mixer performance elucidated by shaft torque and angle resolved PIV measurements. Can. J. Chem. Eng. 2011, 89, 1076–1095. [Google Scholar] [CrossRef]
- Ashar, M.; Arlov, D.; Carlsson, F.; Innings, F.; Andersson, R. Single droplet breakup in a rotor-stator mixer. Chem. Eng. Sci. 2018, 181, 186–198. [Google Scholar] [CrossRef]
- Innings, F.; Trägårdh, C. Visualization of the drop deformation and break-up process in a high-pressure homogenizer. Chem. Eng. Technol. 2005, 28, 882–891. [Google Scholar] [CrossRef]
- Kelemen, K.; Gepperth, S.; Koch, R.; Bauer, H.-J.; Schuchmann, H.P. On the visualization of droplet deformation and breakup during high-pressure homogenization. Microfluid. Nanofluid. 2015, 19, 1139–1158. [Google Scholar] [CrossRef]
- Galinat, S.; Masbernat, O.; Guiraud, P.; Dalmazzone, C.; Noïk, C. Drop break-up in turbulent pipe flow downstream of a restriction. Chem. Eng. Sci. 2005, 60, 6511–6528. [Google Scholar] [CrossRef]
- Galinat, S.; Garrido Torres, L.; Masbernat, O. Breakup of a drop in a liquid-liquid pipe flow through an orifice. AIChE J. 2007, 53, 56–68. [Google Scholar] [CrossRef]
- Eastwood, C.D.; Armi, L.; Lasheras, J.C. The breakup of immiscible fluids in turbulent flows. J. Fluid Mech. 2004, 502, 309. [Google Scholar] [CrossRef] [Green Version]
- Vejražka, J.; Zedníková, M.; Stranovský, P. Experiments on breakup of bubbles in a turbulent flow. AIChE J. 2018, 64, 740–757. [Google Scholar] [CrossRef]
- Solsvik, J.; Jakobsen, H.A. Single drop breakup experiments in stirred liquid-liquid tank. Chem. Eng. Sci. 2015, 131, 219–234. [Google Scholar] [CrossRef]
- Maaß, S.; Kraume, M. Determination of breakage rates using single drop experiments. Chem. Eng. Sci. 2012, 70, 146–164. [Google Scholar] [CrossRef]
- Boxall, J.A.; Koh, C.A.; Sloan, E.D.; Sum, A.K.; Wu, D.T. Droplet size scaling of water-in-oil emulsions under turbulent flow. Langmuir 2012, 28, 104–110. [Google Scholar] [CrossRef]
- Vankova, N.; Tcholakova, S.; Denkov, N.D.; Ivanov, I.; Vulchev, V.D.; Danner, T. Emulsification in turbulent flow 1. Mean and maximum drop diameters in inertial and viscous regimes. J. Colloid Interface Sci. 2007, 312, 363–380. [Google Scholar] [CrossRef] [PubMed]
- Håkansson, A. Emulsion formation by homogenization: Current understanding and future perspectives. Annu. Rev. Food Sci. Technol. 2019, 10, 239–258. [Google Scholar] [CrossRef] [PubMed]
- Rayner, M. Scales and forces in emulsification. In Engineering Aspects of Food Emulsification and Homogenization; Rayner, M., Dejmek, P., Eds.; CRC Press: Boca Raton, FL, USA, 2015; pp. 3–32. [Google Scholar]
- Janssen, J.; Hoogland, H. Modelling strategies for emulsification in industrial practice. Can. J. Chem. Eng. 2014, 92, 198–202. [Google Scholar] [CrossRef]
- Ramkrishna, D. Population Balances–Theory and Applications to Particulate Systems in Engineering; Academic Press: San Diego, CA, USA, 2000. [Google Scholar]
- Ramkrishna, D.; Singh, M.R. Population balance modeling: Current status and future prospects. Annu. Rev. Chem. Biomol. Eng. 2014, 5, 123–146. [Google Scholar] [CrossRef] [Green Version]
- Håkansson, A.; Trägårdh, C.; Bergenståhl, B. Dynamic simulation of emulsion formation in a high pressure homogenizer. Chem. Eng. Sci. 2009, 64, 2915–2925. [Google Scholar] [CrossRef]
- Raikar, N.B.; Bhatia, S.R.; Malone, M.F.; McClements, D.J.; Henson, M.A. Predicting the effect of the homogenization pressure on emulsion drop-size distributions. Ind. Eng. Chem. Res. 2011, 50, 6089–6100. [Google Scholar] [CrossRef]
- Maindarkar, S.N.; Hoogland, H.; Hansen, M.A. Predicting the combined effects of oil and surfactant concentrations on the drop size distributions of homogenized emulsions. Colloids Surf. A Physicochem. Eng. Asp. 2015, 467, 18–30. [Google Scholar] [CrossRef]
- Silva, L.F.L.R.; Damian, R.B.; Lage, P.L.C. Implementation and analysis of numerical solution of the population balance equation in CFD packages. Comput. Chem. Eng. 2008, 32, 2933–2945. [Google Scholar] [CrossRef]
- Liao, Y.; Lucas, D. A literature review of theoretical models for drop and bubble breakup in turbulent dispersions. Chem. Eng. Sci. 2009, 64, 3389–3406. [Google Scholar] [CrossRef]
- Lasheras, J.C.; Eastwood, C.; Martínez-Bazán, C.; Montañés, J.L. A review of statistical models for the break-up of an immiscible fluid immersed into a fully developed turbulent flow. Int. J. Multiph. Flow 2002, 28, 247–278. [Google Scholar] [CrossRef] [Green Version]
- Sajjadi, B.; Raman, A.A.A.; Shah, R.S.S.R.E.; Ibrahim, S. Review on applicable breakup/coalescence models in turbulent liquid-liquid flows. Rev. Chem. Eng. 2013, 29, 131–158. [Google Scholar] [CrossRef]
- Karimi, M.; Andersson, R. Dual mechanism model for fluid particle breakup in the entire turbulent spectrum. AIChE J. 2019, 65, e16600. [Google Scholar] [CrossRef] [Green Version]
- Håkansson, A. An experimental investigation of the probability distribution of turbulent fragmenting stresses in a high-pressure homogenizer. Chem. Eng. Sci. 2018, 177, 139–150. [Google Scholar] [CrossRef]
- Sathyagal, A.N.; Ramkrishna, D. Droplet breakage in stirred dispersions. Breakage functions from experimental drop-size distributions. Chem. Eng. Sci. 1996, 51, 1377–1391. [Google Scholar] [CrossRef]
- Azizi, F.; Al Taweel, A.M. Turbulently flowing liquid-liquid dispersions. Part I: Drop breakage and coalescence. Chem. Eng. Sci. 2011, 166, 715–725. [Google Scholar] [CrossRef]
- Vankova, N.; Tcholakova, S.; Denkov, N.D.; Vulchev, V.D.; Danner, T. Emulsification in turbulent flow 2. Breakage rate constants. J. Colloid Interface Sci. 2007, 313, 612–629. [Google Scholar] [CrossRef]
- Håkansson, A.; Askaner, M.; Innings, F. Extent and mechanism of coalescence in rotor-stator mixer food emulsion emulsification. J. Food Eng. 2016, 175, 127–135. [Google Scholar] [CrossRef]
- Håkansson, A. Experimental methods for measuring coalescence during emulsification—A critical review. J. Food Eng. 2016, 178, 47–59. [Google Scholar] [CrossRef]
- Jafari, S.M.; Assadpoor, E.; He, Y.; Bhandari, B. Re-coalescence of emulsion droplets during high-energy emulsification. Food Hydrocoll. 2008, 22, 1191–1202. [Google Scholar] [CrossRef]
- Henry, J.V.L.; Fryer, P.J.; Frith, W.J.; Norton, I.T. Emulsification mechanism and storage instabilities of hydrocarbon in-water sub-micron emulsions stabilized with Tweens (20 and 80), Brij 96v and sucrose monoesters. J. Colloid Interface Sci. 2009, 338, 201–206. [Google Scholar] [CrossRef] [PubMed]
- Lobo, L.; Svereika, A.; Nair, M. Coalescence during emulsification: 1. Method development. J. Colloid Interface Sci. 2002, 253, 409–418. [Google Scholar] [CrossRef] [PubMed]
- Mohan, S.; Narsimhan, G. Coalescence of protein-stabilized emulsions in a high-pressure homogenizer. J. Colloid Interface Sci. 1997, 192, 1–15. [Google Scholar] [CrossRef]
- Taisne, L.; Walstra, P.; Cabane, B. Transfer of oil between emulsion droplets. J. Colloid Interface Sci. 1996, 184, 378–390. [Google Scholar] [CrossRef]
- Coulaloglou, C.A.; Tavlarides, L.L. Description of interaction processes in agitated liquid-liquid dispersions. Chem. Eng. Sci. 1977, 32, 1289–1297. [Google Scholar] [CrossRef]
- Kumar, S.; Ramkrishna, D. On the solution of population balance equations by discretization—I. A fixed pivot technique. Chem. Eng. Sci. 1996, 51, 1311–1332. [Google Scholar] [CrossRef]
- Kumar, J.; Warnecke, G.; Peglow, M.; Heinrich, S. Comparison of numerical methods for solving populations balance equations incorporating aggregation and breakage. Powder Technol. 2009, 189, 218–229. [Google Scholar] [CrossRef]
- Håkansson, A.; Hounslow, M.J. Simultaneous determination of fragmentation and coalescence rates during pilot-scale high-pressure homogenization. J. Food Eng. 2013, 116, 7–13. [Google Scholar] [CrossRef]
- Bisten, A.; Schuchmann, H.P. Optical measuring methods for the investigation of high-pressure homogenisation. Processes 2016, 4, 41. [Google Scholar] [CrossRef] [Green Version]
- Solsvik, J.; Maaß, S.; Jakobsen, H.A. Definition of the single drop breakup event. Ind. Eng. Chem. Res. 2016, 55, 2872–2882. [Google Scholar] [CrossRef]
- Hančil, V.; Rod, V. Break-up of a drop in a stirred tank. Chem. Eng. Process. 1988, 23, 189–193. [Google Scholar] [CrossRef]
- Schmidt, S.A.; Simon, M.; Attarakih, M.M.; Lagar, L.; Bart, H.-J. Droplet population balance modelling—hydrodynamics and mass transfer. Chem. Eng. Sci. 2006, 61, 246–256. [Google Scholar] [CrossRef]
- Gourdon, C.; Casamatta, G. Influence of mass transfer direction on the operation of a pulsed sieve-plate pilot column. Chem. Eng. Sci. 1991, 46, 2799–2808. [Google Scholar] [CrossRef]
- Andersson, R.; Andersson, B. Modeling the breakup of fluid particles in turbulent flows. AIChE J. 2006, 52, 2031–2038. [Google Scholar] [CrossRef]
- Andersson, R.; Andersson, B. On the breakup of fluid particles in turbulent flows. AIChE J. 2006, 52, 2020–2030. [Google Scholar] [CrossRef]
- Håkansson, A. On the validity of different methods to estimate breakup frequency from single drop experiments. Chem. Eng. Sci. 2020, 227, 115908. [Google Scholar] [CrossRef]
- Bouaifi, M.; Mortensen, M.; Andersson, R.; Orciuch, W.; Andersson, B.; Chopard, F.; Norén, T. Experimental and numerical investigations of a jet mixing in a multifunctional channel reactor. Passive and Reactive Systems. Chem. Eng. Res. Des. 2004, 82, 274–283. [Google Scholar] [CrossRef]
- Thoroddsen, S.T.; Etoh, T.G.; Takehara, K. High-speed imaging of drops and bubbles. Ann. Rev. Fluid Mech. 2008, 40, 257–285. [Google Scholar] [CrossRef]
- Tsouris, C.; Tavlarides, L.L. Breakage and coalescence models for drops in turbulent dispersions. AIChE J. 1994, 40, 395–406. [Google Scholar] [CrossRef]
- Konno, M.; Aoki, M.; Saito, S. Scale effect on breakup process in liquid-liquid agitated tanks. J. Chem. Eng. Jpn. 1983, 16, 312–319. [Google Scholar] [CrossRef] [Green Version]
- Ribeiro, M.M.; Regueiras, P.F.; Guimaraes, M.M.L.; Madureira, C.M.N.; Cruz-Pinto, J.J.C. Optimization of breakage and coalescence model parameters in a steady-state batch agitated dispersion. Ind. Eng. Chem. Res. 2011, 50, 2182–2191. [Google Scholar] [CrossRef]
- Lever, J.; Krzywinski, M.; Altman, N. Model selection and overfitting. Nat. Methods 2016, 13, 703–704. [Google Scholar] [CrossRef]
- Hawkins, D.M. The Problem of Overfitting. J. Chem. Inf. Model. 2004, 44, 1–12. [Google Scholar]
- Mayer, J.; Khairy, K.; Howard, J. Drawing an elephant with four complex parameters. Am. J. Phys. 2010, 78, 648–649. [Google Scholar] [CrossRef]
- Sovová, H. Breakage and coalescence of drops in a batch stirred vessel–II. Comparison of model and experiments. Chem. Eng. Sci. 1981, 36, 1567–1573. [Google Scholar] [CrossRef]
- Narsimhan, G.; Ramkrishna, D.; Gupta, J.P. Analysis of drop size distributions in lean liquid-liquid dispersions. AIChE J. 1980, 26, 991–999. [Google Scholar] [CrossRef]
- Sathyagal, A.N.; Ramkrishna, D.; Narsimhan, G. Solution of inverse problems in population balances—II. Particle break-up. Comput. Chem. Eng. 1995, 19, 437–451. [Google Scholar] [CrossRef]
- Kostoglou, M.; Karabelas, A.J. A contribution towards predicting the evolution of droplet size distribution in flowing dilute liquid/liquid dispersions. Chem. Eng. Sci. 2001, 56, 4283–4292. [Google Scholar] [CrossRef]
- Raikar, N.B.; Bhatia, S.R.; Malone, M.F.; Henson, M.A. Self-similar inverse population balance modeling for turbulently prepared batch emulsions: Sensitivity to measurement errors. Chem. Eng. Sci. 2006, 61, 7421–7435. [Google Scholar] [CrossRef]
- O’Rourke, A.M.; MacLoughlin, P.F. A study of drop breakup in lean dispersions using the inverse-problem method. Chem. Eng. Sci. 2010, 65, 3681–3694. [Google Scholar] [CrossRef]
- Niknafs, N.; Spyropopoulos, F.; Norton, I.T. Development of a new reflectance technique to investigate the mechanism of emulsification. J. Food Eng. 2011, 104, 603–611. [Google Scholar] [CrossRef]
- Hounslow, M.J.; Ni, X. Population balance modelling of droplet coalescence and break-up in an oscillatory baffled reactor. Chem. Eng. Sci. 2004, 59, 819–828. [Google Scholar] [CrossRef]
- Martínez-Bazán, C.; Montañés, J.L.; Lasheras, J.C. On the breakup of an air bubble injected into a fully developed turbulent flow. Part 1. Breakup frequency. J. Fluid Mech. 1999, 401, 157–182. [Google Scholar] [CrossRef] [Green Version]
- Tcholakova, S.; Vanova, N.; Denkov, N.D.; Danner, T. Emulsification in turbulent flow: 3. Daughter drop-size distribution. J. Colloid Interface Sci. 2007, 310, 570–589. [Google Scholar] [CrossRef]
- Jokela, P.; Flether, P.D.I.; Aveyard, R.; Lu, J.-R. The use of computerized microscopy image analysis to determine emulsion droplet size distributions. J. Colloid Interface Sci. 1990, 134, 417–426. [Google Scholar] [CrossRef]
- Maaß, S.; Wollny, S.; Voigt, A.; Kraume, M. Experimental comparison of measurement techniques for drop size distributions in liquid/liquid dispersions. Exp. Fluids 2011, 50, 259–269. [Google Scholar] [CrossRef]
- Walstra, P. Estimating globule-size distributions of oil-in-water emulsions by spectroturbidimetry. J. Colloid Interface Sci. 1968, 27, 493–500. [Google Scholar] [CrossRef]
- Attermann Abildgaard, O.H.; Revall Frisvad, J.; Falster, V.; Parker, A.; Christensen, N.J.; Bjorholm Dal, A.; Larsen, R. Noninvasive particle sizing using camera-based diffuse reflectance spectroscopy. Appl. Opt. 2016, 44, 3840–3846. [Google Scholar] [CrossRef] [Green Version]
- Ransmark, E.; Svensson, B.; Svedberg, I.; Göransson, A.; Skoglund, T. Measurement of homogenisation efficiency of milk by laser diffraction and centrifugation. Int. Dairy J. 2019, 96, 93–97. [Google Scholar] [CrossRef]
- Lien, T.R.; Phillips, C.R. Determination of particle size distributions of oil-in-water emulsions by electronic counting. Environ. Sci. Technol. 1974, 8, 558–561. [Google Scholar] [CrossRef]
- Denkova, P.S.; Tcholakova, S.; Denkov, N.D.; Danov, K.D.; Campbell, B.; Shawl, C.; Kim, D. Evaluation of the precision of drop-size determination in oil/water emulsions by low-resolution NMR spectroscopy. Langmuir 2004, 20, 11402–11413. [Google Scholar] [CrossRef] [PubMed]
- Van der Tuuk Opedal, N.; Sorland, G.; Sjöblom, J. Methods for droplet size distribution determination of water-in-oil emulsions using low-field NMR. Diffus. Fundam. 2009, 9, 1–29. [Google Scholar]
- Filipe, V.; Hawe, A.; Jiskoot, W. Critical evaluation of nanoparticle tracking analysis (NTA) by NanoSight for the measurement of nanoparticles and protein aggregates. Pharm. Res. 2010, 27, 796–810. [Google Scholar] [CrossRef] [Green Version]
- Kenta, S.; Raikos, V.; Koliadima, A.; Karaiskakis, G. Sedimentation field-flow fractionation as a tool for the study of milk protein-stabilized model oil-in-water emulsions: Effect of protein concentration and homogenization pressure. J. Liq. Chromatogr. Relat. Technol. 2012, 36, 288–303. [Google Scholar] [CrossRef]
- Nilsson, L. Separation and characterization of food macromolecules using field-flow fractionation: A review. Food Hydrocoll. 2013, 30, 1–11. [Google Scholar] [CrossRef]
- Li, M.; Wilkinson, D.; Patchigolla, K. Comparison of particle size distributions measured using different techniques. Part. Sci. Technol. 2007, 23, 265–284. [Google Scholar] [CrossRef]
- Abidin, M.I.I.Z.; Raman, A.A.A.; Nor, M.I.M. Review on measurement techniques for drop size distribution in a stirred vessel. Ind. Eng. Chem. Res. 2013, 52, 16085–16094. [Google Scholar] [CrossRef]
- Keck, C.M.; Müller, R.H. Size analysis of submicron particles by laser diffractometry—90% of the published measurements are false. Int. J. Pharm. 2008, 355, 150–163. [Google Scholar] [CrossRef]
- Evaluation of Measurement Data—Guide to the Expression of Uncertainty in Measurements. Joint Committee for Guides in Metrology. Available online: https://www.bipm.org/en/publications/guides/gum.html (accessed on 2 April 2020).

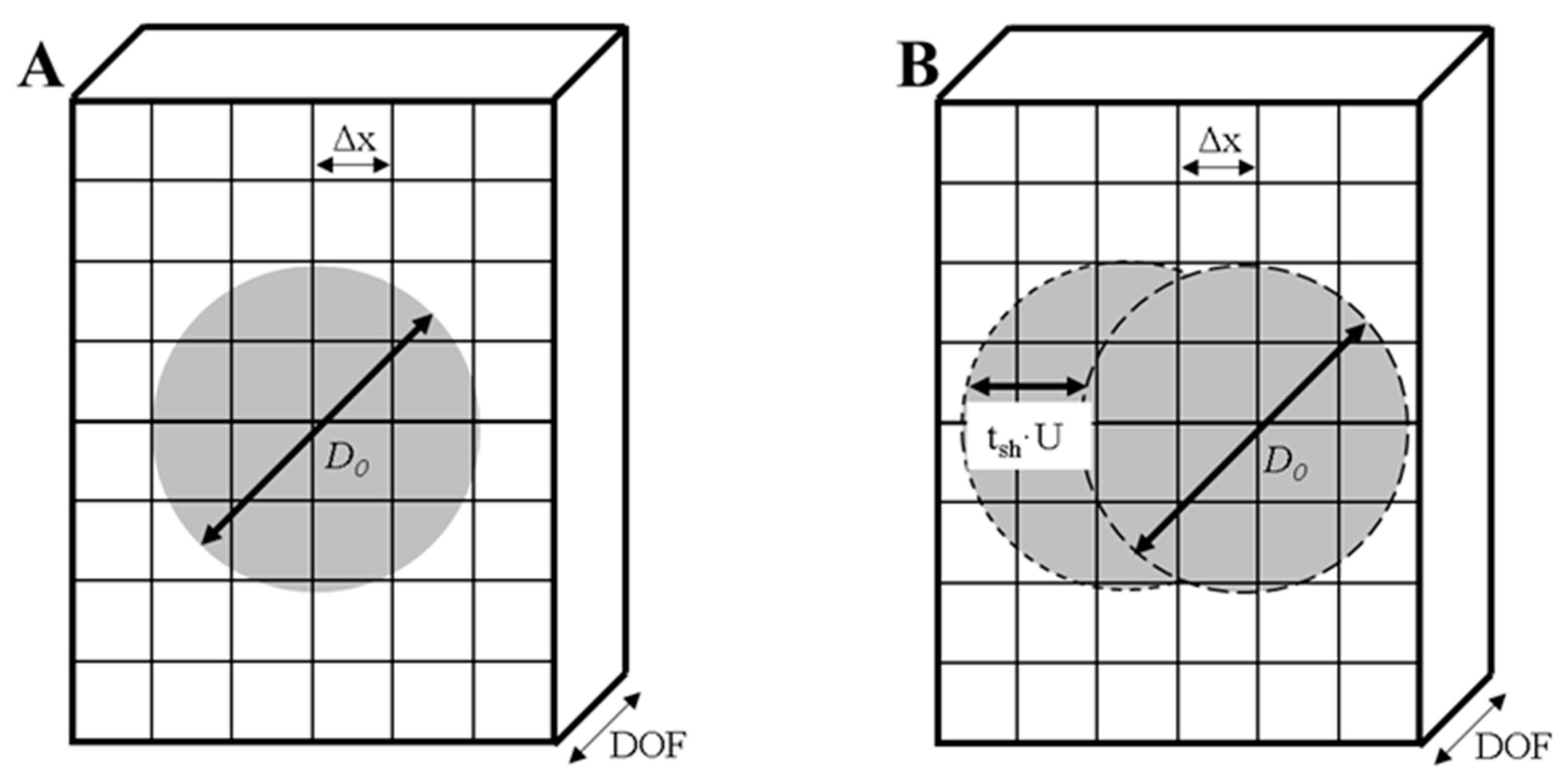

| Ref. | Application | Flow | Re (103) | D0 [µm] | N0 [-] | N1 [-] | tdef? | tb? | P? | Nbr. frag. ? | Frag PDF? | Trans-Formation |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| [47] | Stirred tank | Flow near the impeller | 5 | 1000–4000 | 543 | ? | YES | YES | A | |||
| [48] | Rotating disc contractor | ? | 2000–5000 | ? | ? | YES | B | |||||
| [49] | Pulsed sieve-plate column | ? | ? | ? | ? | YES | B | |||||
| [14] | Stirred tank | Wake of impeller blade | 20–40 | 500–3500 | ~4 500 | ~3 000 | YES | YES | C | |||
| [50,51] | Static mixer | Near uniform intensity | 7 | 1000 | 300 | ? | YES | YES | YES | YES | C | |
| [13] | Stirred tank | Flow near the impeller | 21–29 | 2500–3400 | 457 | ? | YES | YES | YES | YES | C | |
| [6,29] | Rotor-stator mixer | Jet from a stator slot | 20 | 70–550 | 285 | 56 | YES | YES | YES | C’ | ||
| [12] | Nozzle jet | Jet | 6–26 | 2000–5000 | ? | 1089 | YES | YES | D | |||
| Ref. | Studied Conditions | Contrast | Camera | Calculated Properties | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| U [m/s] | tb [ms] | D0 [µm] | Contrast-Enhancer | Lighting | Shutter Time tsh [µs] | FPS | Δx [µm/pixel] | Pixels Per Drop.diam (D0/Δx) [-] | Movement Per Shutter Time in % of a D0 (tsh·U)/D0 [-] | Movement Per Shutter Time in Pixels (tsh·U)/Δx [-] | Images Per Breakup (FPS·tb) [-] | |
| [47] | 0.4 | >3000 | 1000–4000 | None | ? | ? | ? | ? | ? | ? | ? | ? |
| [14] | 1–3 | ~12–34 | 500–3500 | ‘Black dye’ | ? | ? | ? | ? | ? | ? | ? | ? |
| [50,51] | 7 * | ~3–11 | 1000 | None | Front light + reflector behind | 10–100 | 4000 | 18 | 60 | 7–70% | 4–40 | 10–40 |
| [13] | 2 | 15–25 | 2500–3400 | None | Halogen lights + light diffuser | ? | 1000 | 10 ** | 100 | ? | ? | 40–90 |
| [6,29] | 4 | ~1.5–3.0 | 70–550 | None | Halogen light 5 × 50 W | 5 | 2800–3000 | 25 | 3–20 | 3–30% | 0.8 | 4–9 |
| [12] | 0.3 | ? | 2000–5000 | None | ? | 170–250 | 2000 | 92.5 | 20–50 | 1–3% | 0.6–0.8 | ? |
| Reference | System under Investigation | D [µm] | DSD Determination | Method for Determining g* |
|---|---|---|---|---|
| [41] | Impeller turbine batch tank | 100–600 | Photo-micrographic probe | Param.det. (K = 4) |
| [55] | Rushton impeller turbine batch tank | 100–600 | Laser capillary technique | Param.det. (K = 2) |
| [56] | Impeller turbine batch tank | 100–900 | Photo-micrographic probe | Param.det. (K = 4) |
| [23] | High-pressure homogenizer | 0.1–100 | Laser diffraction analysis | Param.det. (K = 4–5) |
| [32] | Reactor /contractor | 10–1000 | Photo-micrographic probe | Param.det. (K = 4) |
| [57] | Impeller turbine batch tank | 100–1000 | Photo-micrographic probe | Param.det. (K = 4) |
| [62] | Impeller turbine batch tank | 50–400 | Electronic size analysis (Coulter counter) | Inverse SS |
| [31] | Impeller turbine batch tank | 10–500 | Microscopic analysis | Inverse SS |
| [66] | Impeller turbine batch tank | 10–400 | Microscopic analysis | Inverse SS |
| [67] | Impeller turbine batch tank | 20–200 | Light reflectance | Back-calc. |
| [68] | Oscillatory reactor | 5–50 | Microscopic analysis | Back-calc. |
| [44] | High-pressure homogenizer | 0.2–100 | Laser diffraction analysis | Back-calc. |
| [34] | Rotor-stator mixer | 0.2–100 | Laser diffraction analysis | Back-calc. |
| [11] | Turbulent jet | 1000–2000 | High-speed camera | Back-calc. |
| [33] | Jet homogenizer | 1–50 | Microscope | Back-calc. |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Håkansson, A. Experimental Methods for Measuring the Breakup Frequency in Turbulent Emulsification: A Critical Review. ChemEngineering 2020, 4, 52. https://doi.org/10.3390/chemengineering4030052
Håkansson A. Experimental Methods for Measuring the Breakup Frequency in Turbulent Emulsification: A Critical Review. ChemEngineering. 2020; 4(3):52. https://doi.org/10.3390/chemengineering4030052
Chicago/Turabian StyleHåkansson, Andreas. 2020. "Experimental Methods for Measuring the Breakup Frequency in Turbulent Emulsification: A Critical Review" ChemEngineering 4, no. 3: 52. https://doi.org/10.3390/chemengineering4030052
APA StyleHåkansson, A. (2020). Experimental Methods for Measuring the Breakup Frequency in Turbulent Emulsification: A Critical Review. ChemEngineering, 4(3), 52. https://doi.org/10.3390/chemengineering4030052




