A Machine Learning-Based Study of Li+ and Na+ Metal Complexation with Phosphoryl-Containing Ligands for the Selective Extraction of Li+ from Brine
Abstract
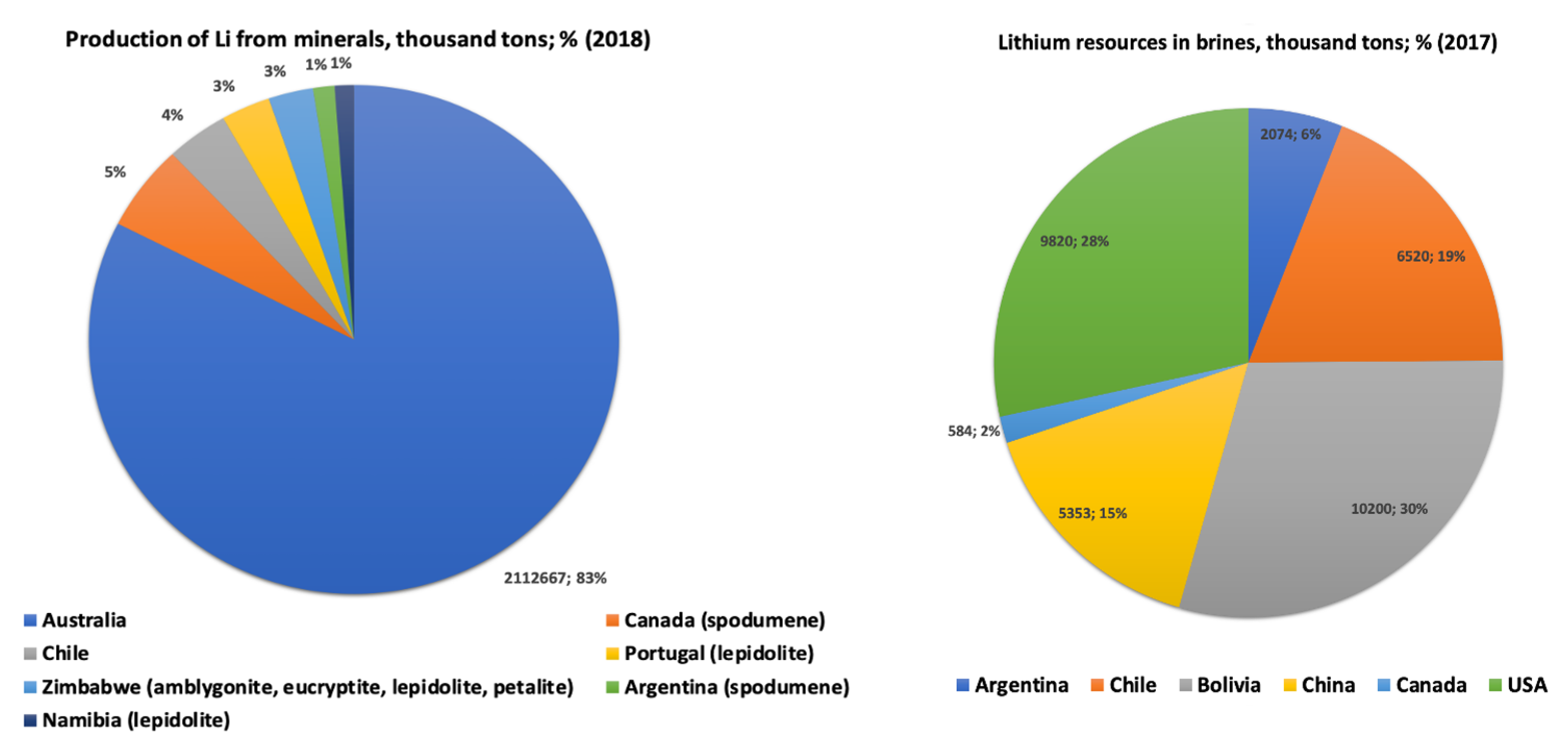
:1. Introduction
2. Materials and Methods
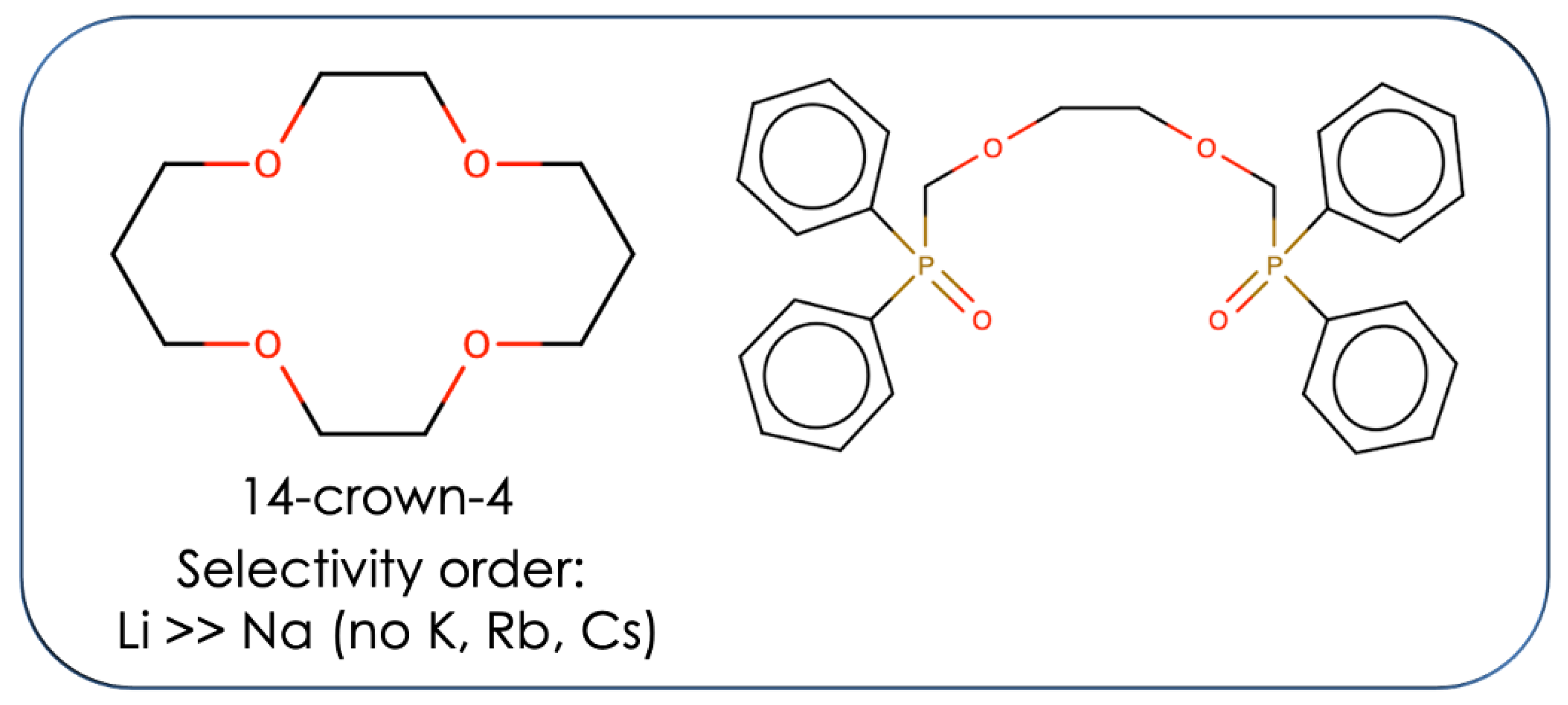
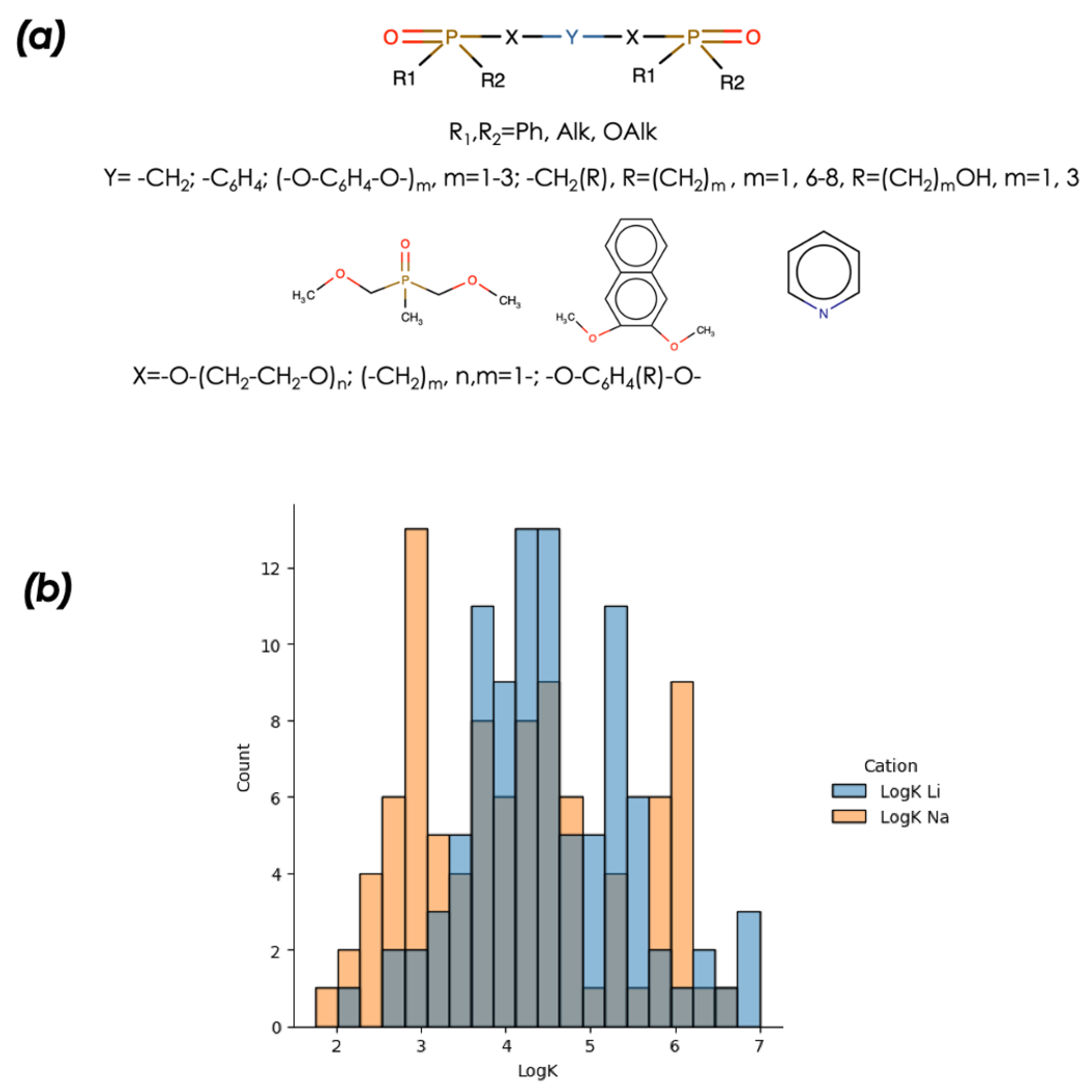
2.1. ExperimentalData
2.2. Methodology
3. Results and Discussion
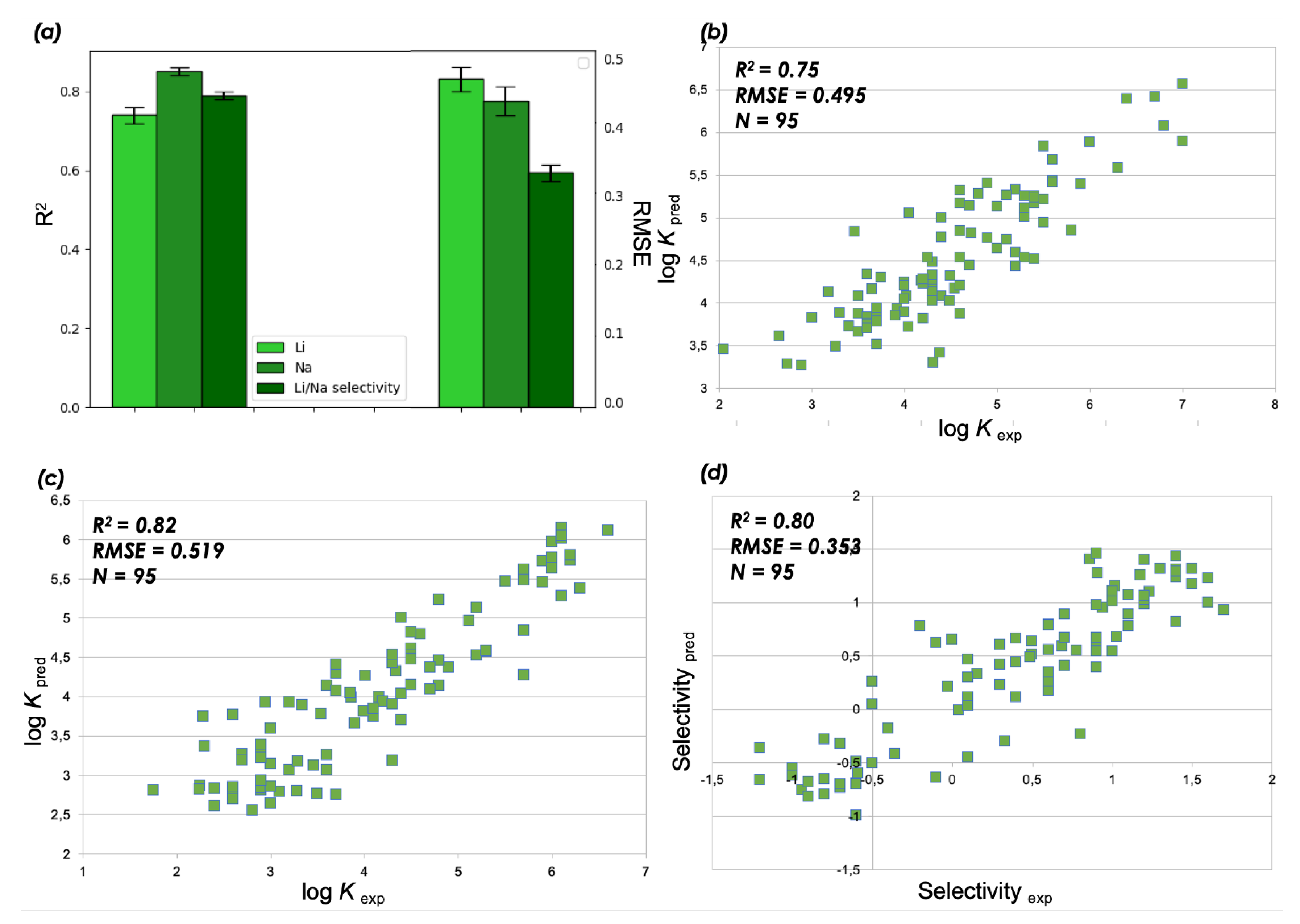
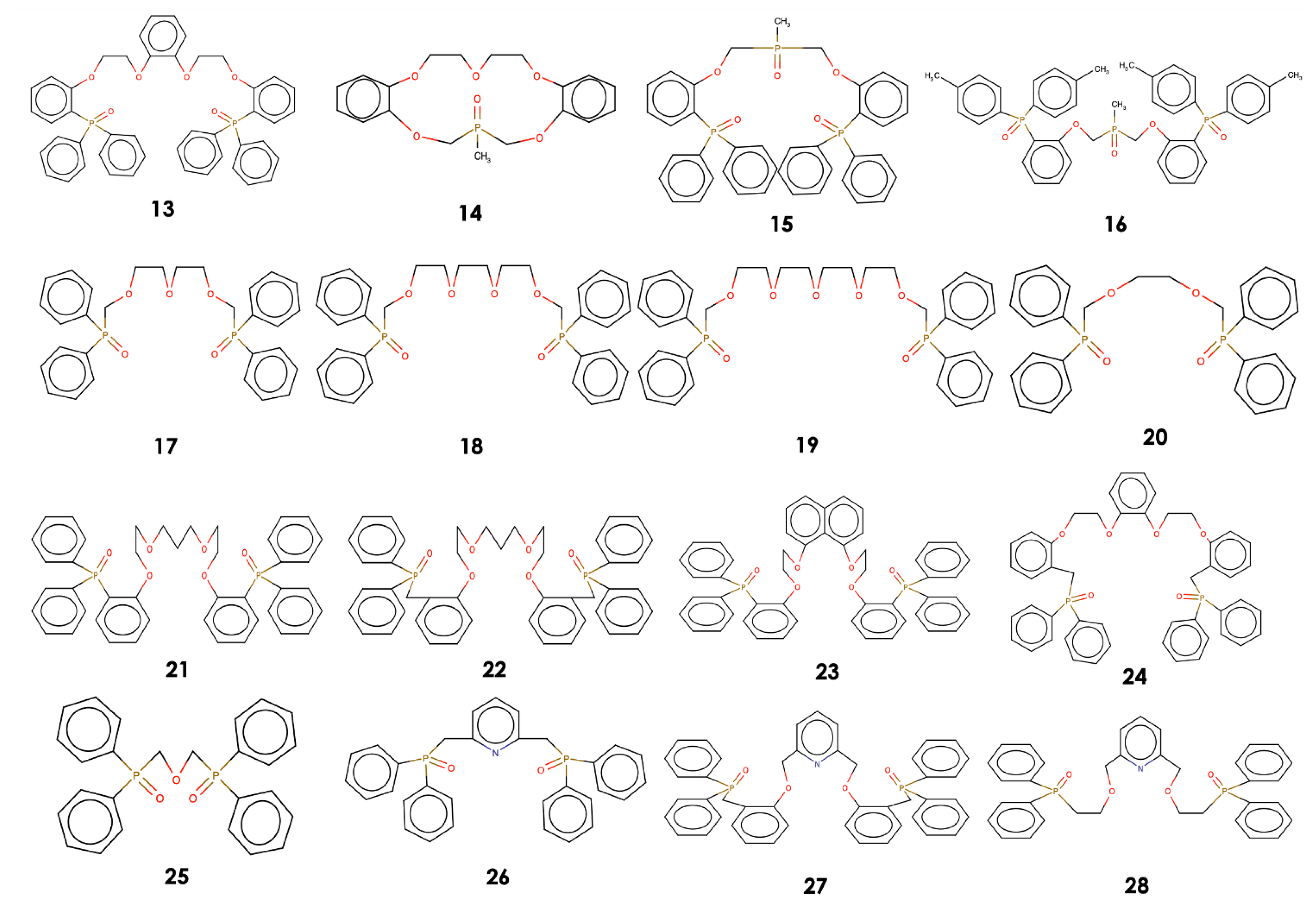
3.1. Results of QSPR Modelling and Stability Constant Value Prediction for Selective Li Podandic Ligand Complex Formation
| Ligand | logK Li (pred) | logK Na (pred) | Sel. (pred) | Ligand | logK Li (exp) | logK Li (pred) | logK Na (exp) | logK Na (pred) | Sel. (exp) | Sel. (pred) |
|---|---|---|---|---|---|---|---|---|---|---|
| Ligand 1 | 5.54 | 4.38 | 1.24 | Ligand 13 | 7.0 | 6.56 | 6.1 | 6.04 | 0.9 | 0.54 |
| Ligand 2 | 5.56 | 4.62 | 1.24 | Ligand 14 | 3.26 | 3.69 | 3.29 | 3.69 | −0.03 | 0.40 |
| Ligand 3 | 4.65 | 3.68 | 1.05 | Ligand 15 | 6.0 | 5.17 | 5.0 | 4.26 | 1.0 | 0.55 |
| Ligand 4 | 5.03 | 4.46 | 0.84 | Ligand 16 | 6.1 | 5.22 | 5.1 | 4.27 | 1.0 | 0.55 |
| Ligand 5 | 4.57 | 3.59 | 1.04 | Ligand 17 | 5.2 | 4.08 | 4.2 | 3.68 | 1 | 0.15 |
| Ligand 6 | 3.65 | 3.61 | 0.57 | Ligand 18 | 4.8 | 4.02 | 4.5 | 4.2 | 0.3 | −0.18 |
| Ligand 7 | 4.44 | 3.47 | 0.81 | Ligand 19 | 4.6 | 3.85 | 5.2 | 4.79 | −0.6 | −0.62 |
| Ligand 8 | 4.24 | 3.28 | 1.12 | Ligand 20 | 5.7 | 4.2 | 3.6 | 3.54 | 2.1 | 0.97 |
| Ligand 9 | 4.91 | 4.33 | 0.79 | Ligand 21 | 5.4 | 5.83 | 5.1 | 5.98 | 0.3 | 0.6 |
| Ligand 10 | 4.83 | 3.80 | 0.54 | Ligand 22 | 5.2 | 5.55 | 4.9 | 5.72 | 0.3 | 0.72 |
| Ligand 11 | 4.04 | 3.64 | 0.21 | Ligand 23 | 4.1 | 5.3 | 4.5 | 6.1 | −0.4 | 0.64 |
| Ligand 12 | 4.4 | 3.21 | 1.12 | Ligand 24 | 6.7 | 6.32 | 6.0 | 5.75 | 0.7 | 0.83 |
| Ligand 25 | 4.2 | 4.5 | 3.2 | 2.95 | 1.0 | 1.11 | ||||
| Ligand 26 | 6.0 | 4.77 | 5.0 | 3.96 | 1.0 | 1.13 | ||||
| Ligand 27 | 4.6 | 5.15 | 3.8 | 4.34 | 0.8 | 0.89 | ||||
| Ligand 28 | 4.1 | 5.1 | 3.9 | 4.57 | 0.2 | 0.86 |
3.2. Evaluation of the Complementarity of the Host Structures of the Candidate Ligands with the Li Cation Guest
3.3. The Novelty of the Results and the Perspectives
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Swain, B. Separation and purification of lithium by solvent extraction and supported liquid membrane, analysis of their mechanism: A review. J. Chem. Technol. Biotechnol. 2016, 91, 2549–2562. [Google Scholar] [CrossRef]
- US Geological Survey: Lithium Statistics and Information; National Minerals Information Center: Reston, VA, USA, 2018.
- Brown, T. British Geological Survey: World Mineral Production 2012–2016. 2018. Available online: https://www2.bgs.ac.uk/mineralsuk/download/world_statistics/2010s/WMP_2012_2016.pdf (accessed on 16 February 2023).
- Weil, M.; Ziemann, S. 22—Recycling of Traction Batteries as a Challenge and Chance for Future Lithium Availability. In Lithium-Ion Batteries; Pistoia, G., Ed.; Elsevier: Amsterdam, The Netherlands, 2014; pp. 509–528. [Google Scholar] [CrossRef]
- Harper, G.; Sommerville, R.; Kendrick, E.; Driscoll, L.; Slater, P.; Stolkin, R.; Walton, A.; Christensen, P.; Heidrich, O.; Lambert, S.; et al. Recycling lithium-ion batteries from electric vehicles. Nature 2019, 575, 75–86. [Google Scholar] [CrossRef] [PubMed]
- Ji, Z.Y.; Yang, F.J.; Zhao, Y.Y.; Liu, J.; Wang, N.; Yuan, J.S. Preparation of titanium-base lithium ionic sieve with sodium persulfate as eluent and its performance. Chem. Eng. J. 2017, 328, 768–775. [Google Scholar] [CrossRef]
- Liu, G.; Zhao, Z.; Ghahreman, A. Novel approaches for lithium extraction from salt-lake brines: A review. Hydrometallurgy 2019, 187, 81–100. [Google Scholar] [CrossRef]
- Baulin, V.E. Phosphorylcontaining Podands. Synthesis, Properties and Application. Doctoral Thesis Work. Ph.D. Thesis, Chernogolovka, Russia, 2012. Unpublished. [Google Scholar]
- Izatt, R.M.; Pawlak, K.; Bradshaw, J.S.; Bruening, R.L. Thermodynamic and Kinetic Data for Macrocycle Interaction with Cations, Anions, and Neutral Molecules. Chem. Rev. 1995, 95, 2529–2586. [Google Scholar] [CrossRef]
- Kostelnik, T.I.; Scheiber, H.; Cappai, R.; Choudhary, N.; Lindheimer, F.; Guadalupe Jaraquemada-Peláez, M.d.; Orvig, C. Phosphonate Chelators for Medicinal Metal Ions. Inorg. Chem. 2021, 60, 5343–5361. [Google Scholar] [CrossRef] [PubMed]
- Kodina, G.E.; Maruk, A.Y.; Klementyeva, O.E.; Mitrofanov, Y.A.; Malysheva, A.O.; Lunev, A.S.; Luneva, K.A.; Tsebrikova, G.S.; Baulin, V.E.; Ragulin, V.V. Comparative Evaluation of the Properties of Aminopolyphosphonates as Chemical Precursors of Samarium-153 Radiopharmaceuticals. Russ. J. Gen. Chem. 2022, 92, 878–890. [Google Scholar] [CrossRef]
- Maruk, A.Y.; Ragulin, V.V.; Mitrofanov, I.A.; Tsebrikova, G.S.; Solov’ev, V.P.; Lunev, A.S.; Lunyova, K.A.; Klementyeva, O.E.; Baulin, V.E.; Kodina, G.E.; et al. Synthesis, Complexation Properties, and Evaluation of New Aminodiphosphonic Acids as Vector Molecules for 68Ga Radiopharmaceuticals. Molecules 2021, 26, 2357. [Google Scholar] [CrossRef]
- Alyapyshev, M.Y.; Babain, V.A.; Ustynyuk, Y.A. Recovery of minor actinides from high-level wastes: Modern trends. Russ. Chem. Rev. 2016, 85, 943–961. [Google Scholar] [CrossRef]
- Safiulina, A.M.; Lizunov, A.V.; Semenov, A.A.; Baulin, D.V.; Baulin, V.E.; Tsivadze, A.Y.; Aksenov, S.M.; Tananaev, I.G. Recovery of Uranium, Thorium, and Other Rare Metals from Eudialyte Concentrate by a Binary Extractant Based on 1,5-bis[2-(hydroxyethoxyphosphoryl)-4-ethylphenoxy]-3-oxapentane and Methyl Trioctylammonium Nitrate. Minerals 2022, 12, 1469. [Google Scholar] [CrossRef]
- Turanov, A.N.; Karandashev, V.K.; Khvostikov, V.A.; Baulin, V.E.; Tsivadze, A.Y. Extraction of REE(III), U(VI), and Th(IV) from Perchloric Acid Solutions with 2,6-Bis(diphenylphosphorylmethyl)pyridine N-Oxide. Radiochemistry 2021, 63, 28–34. [Google Scholar] [CrossRef]
- Solov’ev, V.P.; Varnek, A.; Wipff, G. Modeling of Ion Complexation and Extraction Using Substructural Molecular Fragments. J. Chem. Inf. Comput. Sci. 2000, 40, 847–858. [Google Scholar] [CrossRef] [PubMed]
- Varnek, A.; Fourches, D.; Kireeva, N.; Klimchuk, O.; Marcou, G.; Tsivadze, A.; Solov’ev, V. Computer-aided design of new metal binders. Radiochim. Acta 2008, 96, 505–511. [Google Scholar] [CrossRef]
- Varnek, A.A.; Morosi, G.; Gamba, A. Molecular modelling of organophosphorus podands and their complexes with alkali metal cations. J. Phys. Org. Chem. 1992, 5, 109–118. [Google Scholar] [CrossRef]
- Varnek, A.; Volkova, T.; Petrukhin, O.M.; Wipff, G. Switching Ca2+/Ba2+ to Ba2+/Ca2+ Potentiometric Selectivities of Podands with Phosphoryl-containing Terminal Groups: A Molecular Modelling Study. J. Incl. Phenom. Macrocycl. Chem. 2000, 37, 407–421. [Google Scholar] [CrossRef]
- Varnek, A.; Ten Elshof, J.; Glebov, A.; Solov’ev, V.; Baulin, V.; Tsvetkov, E. Complexation of lithium and sodium cations with beta-phosphorylate ethers, modelling terminal groups of organophosphorus podands. An experimental and theoretical study. J. Mol. Struct. 1992, 271, 311–325. [Google Scholar] [CrossRef]
- Solov’ev, V.; Baulin, D.; Tsivadze, A. Design of phosphoryl containing podands with Li+/Na+ selectivity using machine learning. SAR QSAR Environ. Res. 2021, 32, 521–539. [Google Scholar] [CrossRef]
- Solov’ev, V.P.; Kireeva, N.V.; Tsivadze, A.Y.; Varnek, A.A. Structure-property modelling of complex formation of strontium with organic ligands in water. J. Struct. Chem. 2006, 47, 298–311. [Google Scholar] [CrossRef]
- Solov’ev, V.P.; Tsivadze, A.Y.; Varnek, A. New Approach for Accurate QSPR Modeling of Metal Complexation: Application to Stability Constants of Complexes of Lanthanide Ions Ln3+, Ag+, Zn2+, Cd2+ and Hg2+ with Organic Ligands in Water. Macroheterocycles 2012, 5, 404–410. [Google Scholar] [CrossRef]
- Solov’ev, V.; Varnek, A.; Tsivadze, A. QSPR ensemble modelling of the 1:1 and 1:2 complexation of Co2+, Ni2+, and Cu2+ with organic ligands: Relationships between stability constants. J. Comput.-Aided Mol. Des. 2014, 28, 549–564. [Google Scholar] [CrossRef]
- Solov’ev, V.; Kireeva, N.; Ovchinnikova, S.; Tsivadze, A. The complexation of metal ions with various organic ligands in water: Prediction of stability constants by QSPR ensemble modelling. J. Incl. Phenom. Macrocycl. Chem. 2015, 83, 89–101. [Google Scholar] [CrossRef]
- Solov’ev, V.; Tsivadze, A.; Marcou, G.; Varnek, A. Classification of Metal Binders by Naïve Bayes Classifier on the Base of Molecular Fragment Descriptors and Ensemble Modeling. Mol. Inform. 2019, 38, 1900002. [Google Scholar] [CrossRef] [PubMed]
- Chaube, S.; Goverapet Srinivasan, S.; Rai, B. Applied machine learning for predicting the lanthanide-ligand binding affinities. Sci. Rep. 2020, 10, 14322. [Google Scholar] [CrossRef] [PubMed]
- Kanahashi, K.; Urushihara, M.; Yamaguchi, K. Machine learning-based analysis of overall stability constants of metal–ligand complexes. Sci. Rep. 2022, 12, 11159. [Google Scholar] [CrossRef] [PubMed]
- Tetko, I.V.; Solov’ev, V.P.; Antonov, A.V.; Yao, X.; Doucet, J.P.; Fan, B.; Hoonakker, F.; Fourches, D.; Jost, P.; Lachiche, N.; et al. Benchmarking of Linear and Nonlinear Approaches for Quantitative Structure-Property Relationship Studies of Metal Complexation with Ionophores. J. Chem. Inf. Model. 2006, 46, 808–819. [Google Scholar] [CrossRef]
- Shi, Z.G.; McCullough, E.A. A computer simulation —Statistical procedure for predicting complexation equilibrium constants. J. Incl. Phenom. Mol. Recognit. Chem. 1994, 18, 9–26. [Google Scholar] [CrossRef]
- Solovev, V.P.; Varnek, A.A. Structure—Property modeling of metal binders using molecular fragments. Russ. Chem. Bull. 2004, 53, 1434–1445. [Google Scholar] [CrossRef]
- Solov’ev, V.P.; Kireeva, N.; Tsivadze, A.Y.; Varnek, A. QSPR ensemble modelling of alkaline-earth metal complexation. J. Incl. Phenom. Macrocycl. Chem. 2013, 76, 159–171. [Google Scholar] [CrossRef]
- Ghasemi, J.; Saaidpour, S. QSPR modeling of stability constants of diverse 15-crown-5 ethers complexes using best multiple linear regression. J. Incl. Phenom. Macrocycl. Chem. 2008, 60, 339–351. [Google Scholar] [CrossRef]
- Li, Y.; Su, L.; Zhang, X.; Huang, X.; Zhai, H. Prediction of association constants of cesium chelates based on Uniform Design Optimized Support Vector Machine. Chemom. Intell. Lab. Syst. 2011, 105, 106–113. [Google Scholar] [CrossRef]
- Varnek, A.; Wipff, G.; Solov’e, V.P.; Solotnov, A.F. Assessment of the Macrocyclic Effect for the Complexation of Crown-Ethers with Alkali Cations Using the Substructural Molecular Fragments Method. J. Chem. Inf. Comput. Sci. 2002, 42, 812–829. [Google Scholar] [CrossRef] [PubMed]
- Hay, B.P.; Firman, T.K. HostDesigner: A Program for the de Novo Structure-Based Design of Molecular Receptors with Binding Sites that Complement Metal Ion Guests. Inorg. Chem. 2002, 41, 5502–5512. [Google Scholar] [CrossRef] [PubMed]
- Hay, B.P.; Firman, T.K.; Lumetta, G.J.; Rapko, B.M.; Garza, P.A.; Sinkov, S.I.; Hutchison, J.E.; Parks, B.W.; Gilbertson, R.D.; Weakley, T.J. Toward the computer-aided design of metal ion sequestering agents. J. Alloys Compd. 2004, 374, 416–419. [Google Scholar] [CrossRef]
- Hay, B.P.; Oliferenko, A.A.; Uddin, J.; Zhang, C.; Firman, T.K. Search for Improved Host Architectures: Application of de Novo Structure-Based Design and High-Throughput Screening Methods To Identify Optimal Building Blocks for Multidentate Ethers. J. Am. Chem. Soc. 2005, 127, 17043–17053. [Google Scholar] [CrossRef] [PubMed]
- Ishimori, K.; Imura, H. The Synergistic selective extraction of lithium(I) with 2-thenoyiltrifluoroacetone and 1,10-phenanthroline derivatives. Solvent Extr. Res Dev. Jpn. 2002, 9, 13–25. [Google Scholar]
- Mauri, A.; Consonni, V.; Pavan, M.; Todeschini, R. Dragon software: An easy approach to molecular descriptor calculations. Match. 2006, 56, 237–248. [Google Scholar]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016. [Google Scholar]
- Frye, C.; Mijolla, D.; Begley, T.; Cowton, L.; Stanley, M.; Feige, I. Shapley Explainability on the Data Manifold. arXiv 2020, arXiv:2006.01272. [Google Scholar]
- Shapley, L. A Value for n-Person Game; Princeton University Press: Princeton, NJ, USA, 1956. [Google Scholar]
- O’Boyle, N.M.; Banck, M.; James, C.A.; Morley, C.; Vandermeersch, T.; Hutchison, G.R. Open Babel: An open chemical toolbox. J. Cheminform. 2011, 3, 33. [Google Scholar] [CrossRef]
- Rey, J.; Dourdain, S.; Dufrêche, J.F.; Berthon, L.; Muller, J.M.; Pellet-Rostaing, S.; Zemb, T. Thermodynamic Description of Synergy in Solvent Extraction: I. Enthalpy of Mixing at the Origin of Synergistic Aggregation. Langmuir 2016, 32, 13095–13105. [Google Scholar] [CrossRef]
- Rey, J.; Bley, M.; Dufrêche, J.F.; Gourdin, S.; Pellet-Rostaing, S.; Zemb, T.; Dourdain, S. Thermodynamic Description of Synergy in Solvent Extraction: II Thermodynamic Balance of Driving Forces Implied in Synergistic Extraction. Langmuir 2017, 33, 13168–13179. [Google Scholar] [CrossRef]
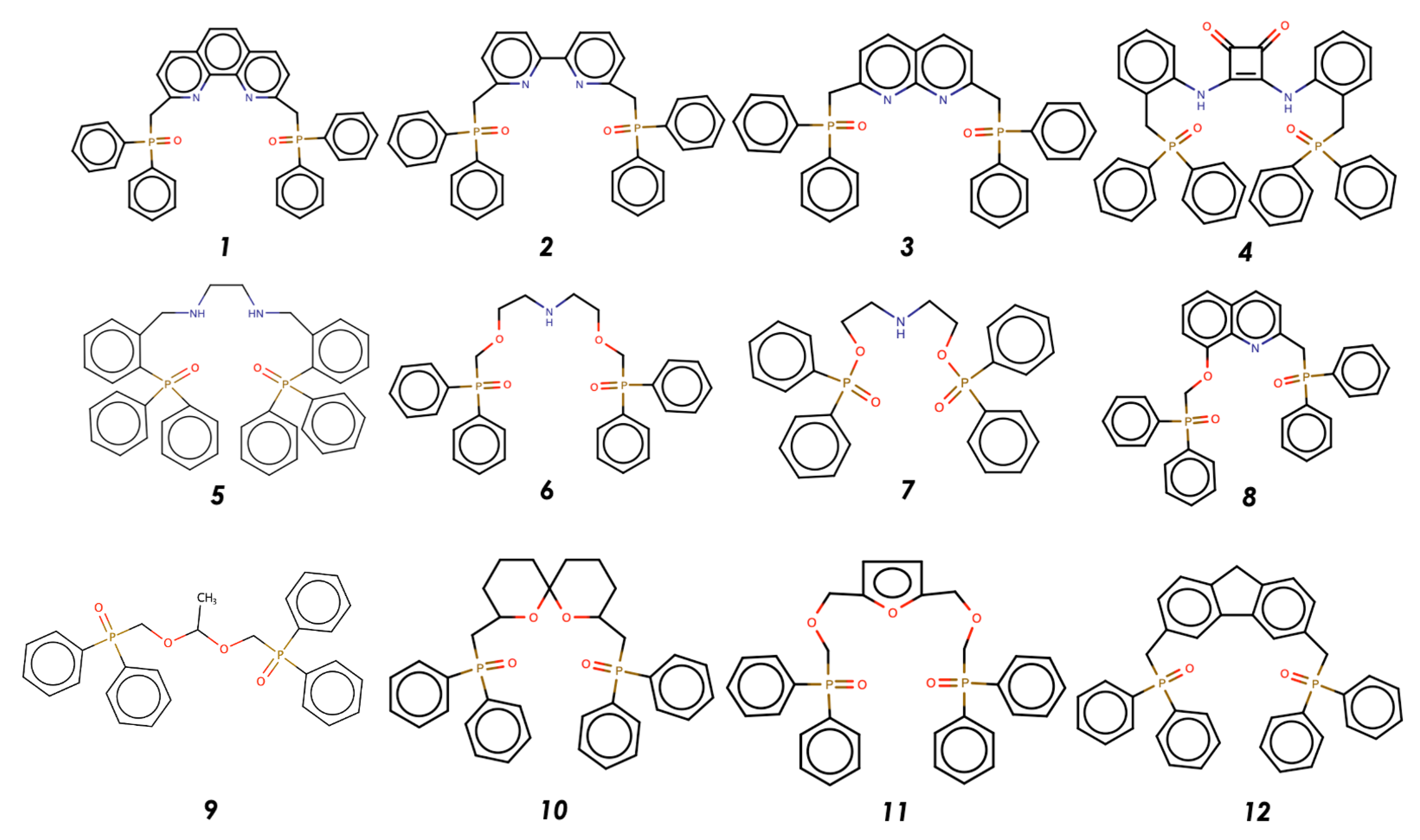

| Ligand | RMSD | E, kcal/mol | logK Li (pred) |
|---|---|---|---|
| Ligand 1 | 2.507 | 1.240 | 5.54 |
| Ligand 2 | 1.405 | 1.550 | 5.56 |
| Ligand 3 | 2.783 | 1.240 | 4.65 |
| Ligand 7 | 2.339 | 2.480 | 4.44 |
| Ligand 6 | 3.938 | 3.938 | 3.65 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kireeva, N.; Baulin, V.E.; Tsivadze, A.Y. A Machine Learning-Based Study of Li+ and Na+ Metal Complexation with Phosphoryl-Containing Ligands for the Selective Extraction of Li+ from Brine. ChemEngineering 2023, 7, 41. https://doi.org/10.3390/chemengineering7030041
Kireeva N, Baulin VE, Tsivadze AY. A Machine Learning-Based Study of Li+ and Na+ Metal Complexation with Phosphoryl-Containing Ligands for the Selective Extraction of Li+ from Brine. ChemEngineering. 2023; 7(3):41. https://doi.org/10.3390/chemengineering7030041
Chicago/Turabian StyleKireeva, Natalia, Vladimir E. Baulin, and Aslan Yu. Tsivadze. 2023. "A Machine Learning-Based Study of Li+ and Na+ Metal Complexation with Phosphoryl-Containing Ligands for the Selective Extraction of Li+ from Brine" ChemEngineering 7, no. 3: 41. https://doi.org/10.3390/chemengineering7030041
APA StyleKireeva, N., Baulin, V. E., & Tsivadze, A. Y. (2023). A Machine Learning-Based Study of Li+ and Na+ Metal Complexation with Phosphoryl-Containing Ligands for the Selective Extraction of Li+ from Brine. ChemEngineering, 7(3), 41. https://doi.org/10.3390/chemengineering7030041






