Modeling the Mechanical Properties of a Polymer-Based Mixed-Matrix Membrane Using Deep Learning Neural Networks
Abstract
:1. Introduction
- (i)
- Underestimation of model overfitting, which is significant for NN models trained with small datasets [24];
- (ii)
- Inadequate evaluation of the model accuracy, with the experimental data distributed over a wide range.
- Stress;
- Stain;
- Elastic modulus;
- Toughness.
| Ref. | Material | NN Type | Hidden Layer Architecture | # of Predicted Parameters | Technique to Optimize Model Overfitting | Dataset Size | Were Experimental Data Points Used to Test the Model? (# of Data Points) | Model Performance Evaluation (Using Experimental Data) | Model Evaluation Performance (Using Non-Experimental Data) |
|---|---|---|---|---|---|---|---|---|---|
| [19] | PC and PMMA (polymers) | DLNN | (133-200) | 4 | NM $ | 200 simulated data points + 4 EDPL * | Yes (2) | NM $ | Correlation coefficient = 0.99 |
| [20] | Aluminum alloys | DLNN | (100-100-10) | 2 | ES regularization | 713 data points extracted from commercial material datasheet + 1 EDPL * | Yes (1) | Confidence level > 95% | Pearson correlation coefficient = 0.86–0.88 |
| [21] | Cotton fiber/ polypropylene composite | DLNN | (200-200-200-200) | 1 | Dropout regularization | 6 EDPL * + ±10% deviation of EDPLs * | Yes (NM $) | NM $ | NM |
| [18] | Steels | SNN | Model 1: (5) Model 2: (12) Model 3: (14) | 4 | NM $ | Only experimental datasets were used, but the size was not mentioned | Yes (NM $) | Combined training (known data) and testing (unknown data) performances reported as RMSE = 6.38j, 11.69; HV, 7.79%; 8.68 MPA | NA # |
| Current study | PLA (polymers) | DLNN | (16-12-8-4) | 4 | Dropout regularization + ES regularization | 1214 interpolated data points + 26 EDPL * | Yes (26) | R2 = 0.78–0.88 | R2 = 0.93–0.95 |
2. Data Generation
2.1. Manufacturing Methodology
2.2. Mechanical Properties
3. Computational Methodology
3.1. Background
3.1.1. DLNN Modeling
3.1.2. Dropout
3.1.3. Early Stopping
3.1.4. Stratified K-Fold Cross Validation
3.1.5. Data Interpolation
3.1.6. ReLU
3.1.7. Model Evaluation
3.1.8. Computational Framework
3.2. Model Development
3.2.1. Data Preprocessing
3.2.2. Tuning Hyperparameters and Model Selection
3.2.3. Training the Models
3.2.4. Testing and Performance Analysis of the Trained Models
4. Results and Discussion
4.1. Dataset Analysis
4.2. Model Generalization
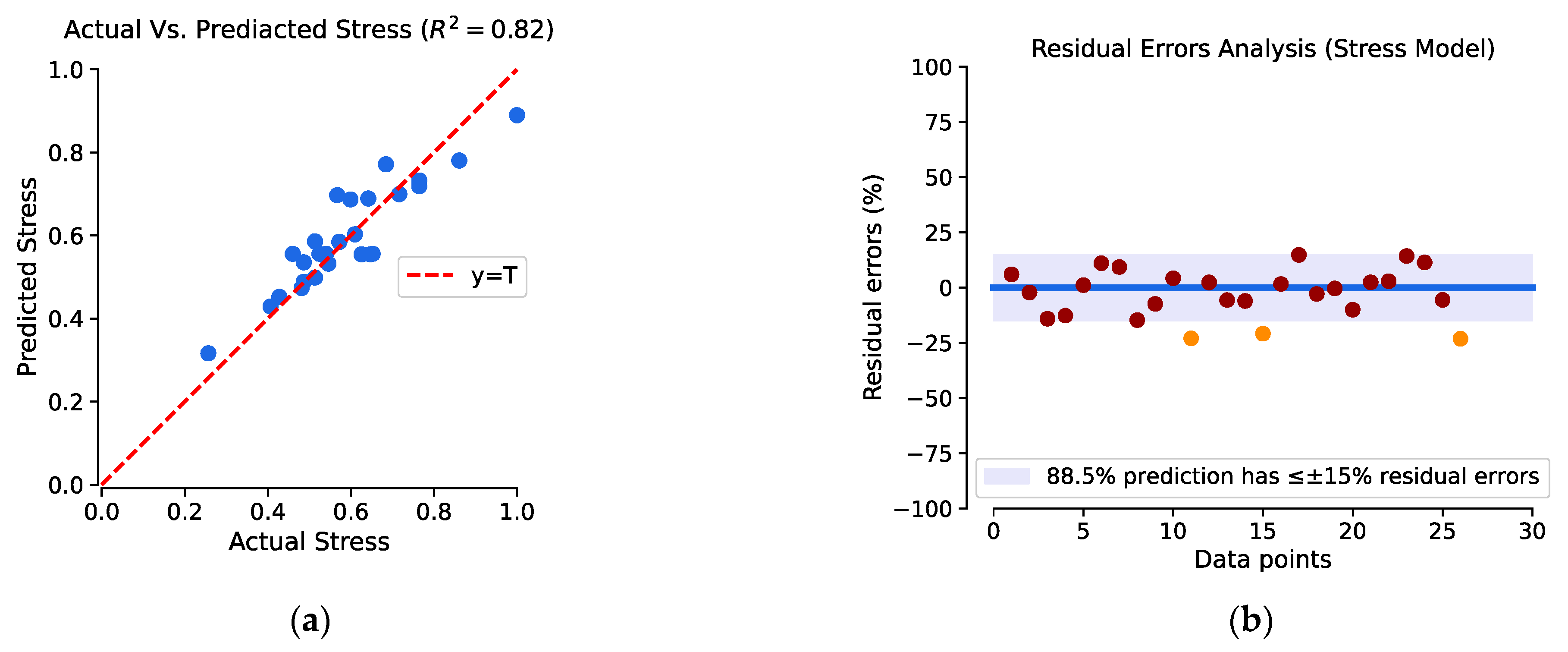
4.3. Performance Evaluation
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Tuned Hyperparameters
| Hyperparameter | Tuning Option |
|---|---|
| Hidden layers | 4 |
| Neurons | 40 |
| Kernel initializer | GlorotNormal |
| Activation function | ReLU (for hidden layers) Linear (for output layers) |
| Model optimizer | Adam |
| Learning rate | 10−4 (for NN model without dropout) 10−3 (for NN model with dropout) |
| Loss function | MSE |
| Epochs | 1000–1500 |
| Dropout rate | Stress modeling: 7–8% Strain modeling: 4–5% E modeling: 12–15% Toughness modeling: 10–13% |
References
- La Rosa, D. Life cycle assessment of biopolymers. In Biopolymers and Biotech Admixtures for Eco-Efficient Construction Materials; Pacheco-Torgal, F., Ivanov, V., Karak, N., Jonkers, H., Eds.; Woodhead Publishing: Sawston, UK, 2016; pp. 57–78. [Google Scholar] [CrossRef]
- Sternberg, J.; Sequerth, O.; Pilla, S. Green chemistry design in polymers derived from lignin: Review and perspective. Prog. Polym. Sci. 2021, 113, 101344. [Google Scholar] [CrossRef]
- Muneer, F.; Nadeem, H.; Arif, A.; Zaheer, W. Bioplastics from Biopolymers: An Eco-Friendly and Sustainable Solution of Plastic Pollution. Polym. Sci. Ser. C 2021, 63, 47–63. [Google Scholar] [CrossRef]
- Kumari, S.V.G.; Pakshirajan, K.; Pugazhenthi, G. Recent advances and future prospects of cellulose, starch, chitosan, polylactic acid and polyhydroxyalkanoates for sustainable food packaging applications. Int. J. Biol. Macromol. 2022, 221, 163–182. [Google Scholar] [CrossRef] [PubMed]
- Ilyas, R.A.; Sapuan, S.M.; Harussani, M.M.; Hakimi, M.Y.A.Y.; Haziq, M.Z.M.; Atikah, M.S.N.; Asyraf, M.R.M.; Ishak, M.R.; Razman, M.R.; Nurazzi, N.M.; et al. Polylactic Acid (PLA) Biocomposite: Processing, Additive Manufacturing and Advanced Applications. Polymers 2021, 13, 1326. [Google Scholar] [CrossRef] [PubMed]
- Bioplastics Market Development Update 2019. Available online: https://www.european-bioplastics.org/wp-content/uploads/2019/11/Report_Bioplastics-Market-Data_2019_short_version.pdf (accessed on 10 June 2023).
- Chung, T.-S.; Jiang, L.Y.; Li, Y.; Kulprathipanja, S. Mixed matrix membranes (MMMs) comprising organic polymers with dispersed inorganic fillers for gas separation. Prog. Polym. Sci. 2007, 32, 483–507. [Google Scholar] [CrossRef]
- Shah, M.; McCarthy, M.C.; Sachdeva, S.; Lee, A.K.; Jeong, H.-K. Current Status of Metal–Organic Framework Membranes for Gas Separations: Promises and Challenges. Ind. Eng. Chem. Res. 2012, 51, 2179–2199. [Google Scholar] [CrossRef]
- Li, Y.; Fu, Z.; Xu, G. Metal-organic framework nanosheets: Preparation and applications. Coord. Chem. Rev. 2019, 388, 79–106. [Google Scholar] [CrossRef]
- Knebel, A.A.; Caro, J. Metal–organic frameworks and covalent organic frameworks as disruptive membrane materials for energy-efficient gas separation. Nat. Nanotechnol. 2022, 17, 911–923. [Google Scholar] [CrossRef]
- Richardson, N. Investigating Mechano-Chemical Encapsulation of Anti-cancer Drugs on Aluminum Metal-Organic Framework Basolite A100—ProQuest. Master’s Thesis, Morgan State University, Baltimore, MD, USA, 2021. Available online: https://www.proquest.com/openview/9adc81f41808abbc2bf9a503d2095a45 (accessed on 10 June 2023).
- Lin, R. MOFs-Based Mixed Matrix Membranes for Gas Separation. Ph.D. Thesis, The University of Queensland, Saint Lucia, Australia, 2016. Available online: https://core.ac.uk/reader/83964620 (accessed on 10 June 2023).
- Alhulaybi, Z.A. Fabrication of Porous Biopolymer/Metal-Organic Framework Composite Membranes for Filtration Applications. Ph.D. Thesis, University of Nottingham, Nottingham, UK, 2020. Available online: https://eprints.nottingham.ac.uk/63048/ (accessed on 10 June 2023).
- Stănescu, M.M.; Bolcu, A. A Study of the Mechanical Properties in Composite Materials with a Dammar Based Hybrid Matrix and Reinforcement from Crushed Shells of Sunflower Seeds. Polymers 2022, 14, 392. [Google Scholar] [CrossRef]
- Soltane, H.B.; Roizard, D.; Favre, E. Effect of pressure on the swelling and fluxes of dense PDMS membranes in nanofiltration: An experimental study. J. Membr. Sci. 2013, 435, 110–119. [Google Scholar] [CrossRef]
- Miao, Z.; Ji, X.; Wu, M.; Gao, X. Deep learning-based evaluation for mechanical property degradation of seismically damaged RC columns. Earthq. Eng. Struct. Dyn. 2023, 52, 2498–2519. [Google Scholar] [CrossRef]
- Gyurova, L.A. Sliding Friction and Wear of Polyphenylene Sulfide Matrix Composites: Experimental and Artificial Neural Network Approach. Ph.D. Thesis, Technische Universität Kaiserslautern, Kaiserslautern, Germany, 2010. Available online: https://kluedo.ub.rptu.de/frontdoor/index/index/docId/4717 (accessed on 10 June 2023).
- Sterjovski, Z.; Nolan, D.; Carpenter, K.R.; Dunne, D.P.; Norrish, J. Artificial neural networks for modelling the mechanical properties of steels in various applications. J. Mater. Process. Technol. 2005, 170, 536–544. [Google Scholar] [CrossRef]
- Park, S.; Marimuthu, K.P.; Han, G.; Lee, H. Deep learning based nanoindentation method for evaluating mechanical properties of polymers. Int. J. Mech. Sci. 2023, 246, 108162. [Google Scholar] [CrossRef]
- Merayo, D.; Rodríguez-Prieto, A.; Camacho, A.M. Prediction of Mechanical Properties by Artificial Neural Networks to Characterize the Plastic Behavior of Aluminum Alloys. Materials 2020, 13, 5227. [Google Scholar] [CrossRef]
- Kazi, M.-K.; Eljack, F.; Mahdi, E. Optimal filler content for cotton fiber/PP composite based on mechanical properties using artificial neural network. Compos. Struct. 2020, 251, 112654. [Google Scholar] [CrossRef]
- Charilaou, P.; Battat, R. Machine learning models and over-fitting considerations. World J. Gastroenterol. 2022, 28, 605–607. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Ling, C. A strategy to apply machine learning to small datasets in materials science. npj Comput. Mater. 2018, 4, 25. [Google Scholar] [CrossRef]
- Marin, A.; Skelin, K.; Grujic, T. Empirical Evaluation of the Effect of Optimization and Regularization Techniques on the Generalization Performance of Deep Convolutional Neural Network. Appl. Sci. 2020, 10, 7817. [Google Scholar] [CrossRef]
- Feng, S.; Zhou, H.; Dong, H. Using deep neural network with small dataset to predict material defects. Mater. Des. 2019, 162, 300–310. [Google Scholar] [CrossRef]
- Song, H.; Ahmad, A.; Farooq, F.; Ostrowski, K.A.; Maślak, M.; Czarnecki, S.; Aslam, F. Predicting the compressive strength of concrete with fly ash admixture using machine learning algorithms. Constr. Build. Mater. 2021, 308, 125021. [Google Scholar] [CrossRef]
- Long, X.; Mao, M.; Lu, C.; Li, R.; Jia, F. Modeling of heterogeneous materials at high strain rates with machine learning algorithms trained by finite element simulations. J. Micromech. Mol. Phys. 2021, 6, 2150001. [Google Scholar] [CrossRef]
- Jha, K.; Jha, R.; Jha, A.K.; Hassan, M.A.M.; Yadav, S.K.; Mahesh, T. A Brief Comparison On Machine Learning Algorithms Based On Various Applications: A Comprehensive Survey. In Proceedings of the 2021 IEEE International Conference on Computation System and Information Technology for Sustainable Solutions (CSITSS), Bangalore, India, 16–18 December 2021; pp. 1–5. [Google Scholar] [CrossRef]
- Liu, G.; Bao, H.; Han, B. A Stacked Autoencoder-Based Deep Neural Network for Achieving Gearbox Fault Diagnosis. Math. Probl. Eng. 2018, 2018, e5105709. [Google Scholar] [CrossRef]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A simple way to prevent neural networks from overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- Wang, S.; Manning, C. Fast dropout training. In Proceedings of the 30th International Conference on Machine Learning, Atlanta, GA, USA, 16–21 June 2013; pp. 118–126. Available online: https://proceedings.mlr.press/v28/wang13a.html (accessed on 10 June 2023).
- Prechelt, L. Early Stopping—But When? In Neural Networks: Tricks of the Trade; Orr, G.B., Müller, K.-R., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 1998; pp. 55–69. [Google Scholar] [CrossRef]
- Ji, Z.; Li, J.; Telgarsky, M. Early-stopped neural networks are consistent. In Proceedings of the 35th Conference on Neural Information Processing Systems, Virtual, 6–14 December 2021. [Google Scholar]
- Bhagat, M.; Bakariya, B. Implementation of Logistic Regression on Diabetic Dataset using Train-Test-Split, K-Fold and Stratified K-Fold Approach. Natl. Acad. Sci. Lett. 2022, 45, 401–404. [Google Scholar] [CrossRef]
- Shaikhina, T.; Lowe, D.; Daga, S.; Briggs, D.; Higgins, R.; Khovanova, N. Machine Learning for Predictive Modelling based on Small Data in Biomedical Engineering. IFAC-PapersOnLine 2015, 48, 469–474. [Google Scholar] [CrossRef]
- Hafsa, N.; Rushd, S.; Al-Yaari, M.; Rahman, M. A Generalized Method for Modeling the Adsorption of Heavy Metals with Machine Learning Algorithms. Water 2020, 12, 3490. [Google Scholar] [CrossRef]
- Podder, S.; Majumder, C.B. The use of artificial neural network for modelling of phycoremediation of toxic elements As(III) and As(V) from wastewater using Botryococcus braunii. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2016, 155, 130–145. [Google Scholar] [CrossRef]
- Biran, A. (Ed.) Chapter 7—Cubic Splines. In Geometry for Naval Architects; Butterworth-Heinemann: Oxford, UK, 2019; pp. 305–324. [Google Scholar] [CrossRef]
- Artley, B. Cubic Splines: The Ultimate Regression Model. Medium. 4 August 2022. Available online: https://towardsdatascience.com/cubic-splines-the-ultimate-regression-model-bd51a9cf396d (accessed on 20 April 2023).
- Won, W.; Lee, K.S. Adaptive predictive collocation with a cubic spline interpolation function for convection-dominant fixed-bed processes: Application to a fixed-bed adsorption process. Chem. Eng. J. 2011, 166, 240–248. [Google Scholar] [CrossRef]
- Ding, B.; Qian, H.; Zhou, J. Activation functions and their characteristics in deep neural networks. In Proceedings of the 2018 Chinese Control and Decision Conference (CCDC), Shenyang, China, 9–11 June 2018; pp. 1836–1841. [Google Scholar] [CrossRef]
- Scikit-Learn: Machine Learning in Python—Scikit-Learn 1.2.2 Documentation. Available online: https://scikit-learn.org/stable/index.html (accessed on 20 April 2023).
- Google Colaboratory. Available online: https://colab.research.google.com/ (accessed on 22 April 2023).
- Keras: Deep Learning for Humans. Available online: https://keras.io/ (accessed on 22 April 2023).
- Artley, B. Regressio. Available online: https://github.com/brendanartley/Regressio (accessed on 11 June 2023).
- Hagan, M.T.; Demuth, H.B.; Beale, M.H.; Jesús, O.D. Neural Network Design, 2nd ed.; Martin Hagan: San Francisco, CA, USA, 2014. [Google Scholar]
- Moore, D.S.; Notz, W.I.; Fligner, M.A. The Basic Practice of Statistics, 6th ed.; W. H. Freeman: New York, NY, USA, 2011. [Google Scholar]
- Cheng, C.-L.; Shalabh; Garg, G. Coefficient of determination for multiple measurement error models. J. Multivar. Anal. 2014, 126, 137–152. [Google Scholar] [CrossRef]
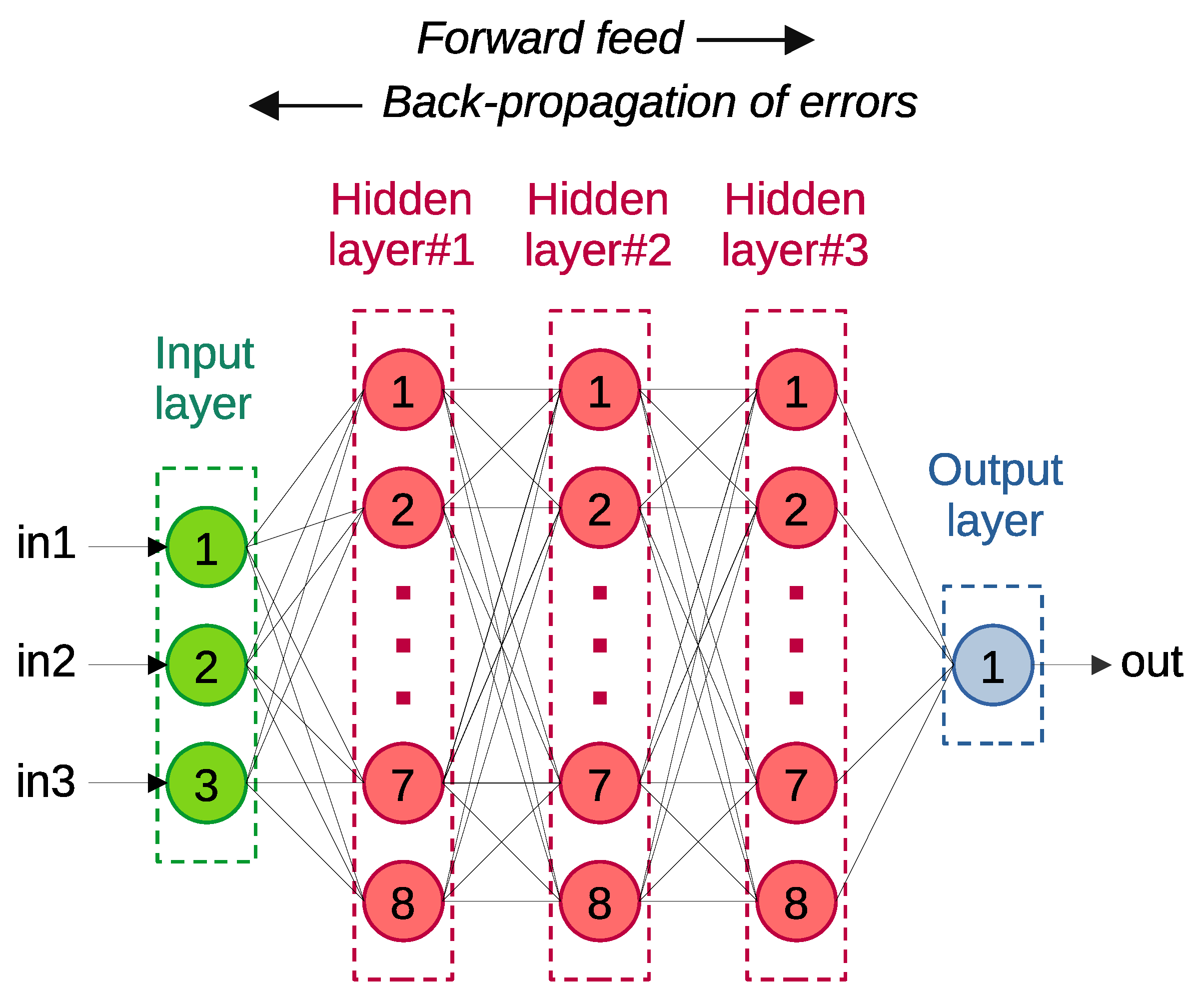

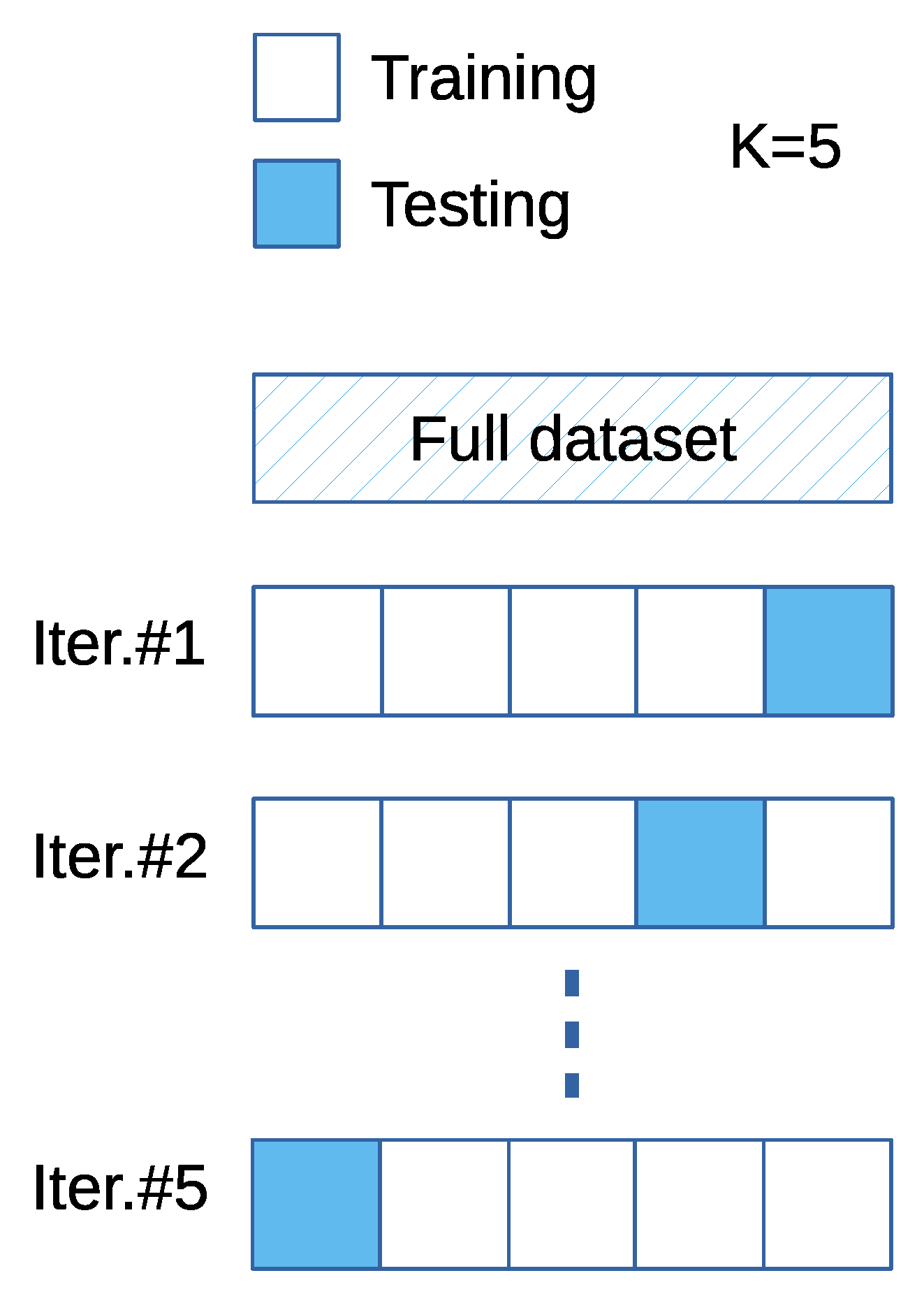



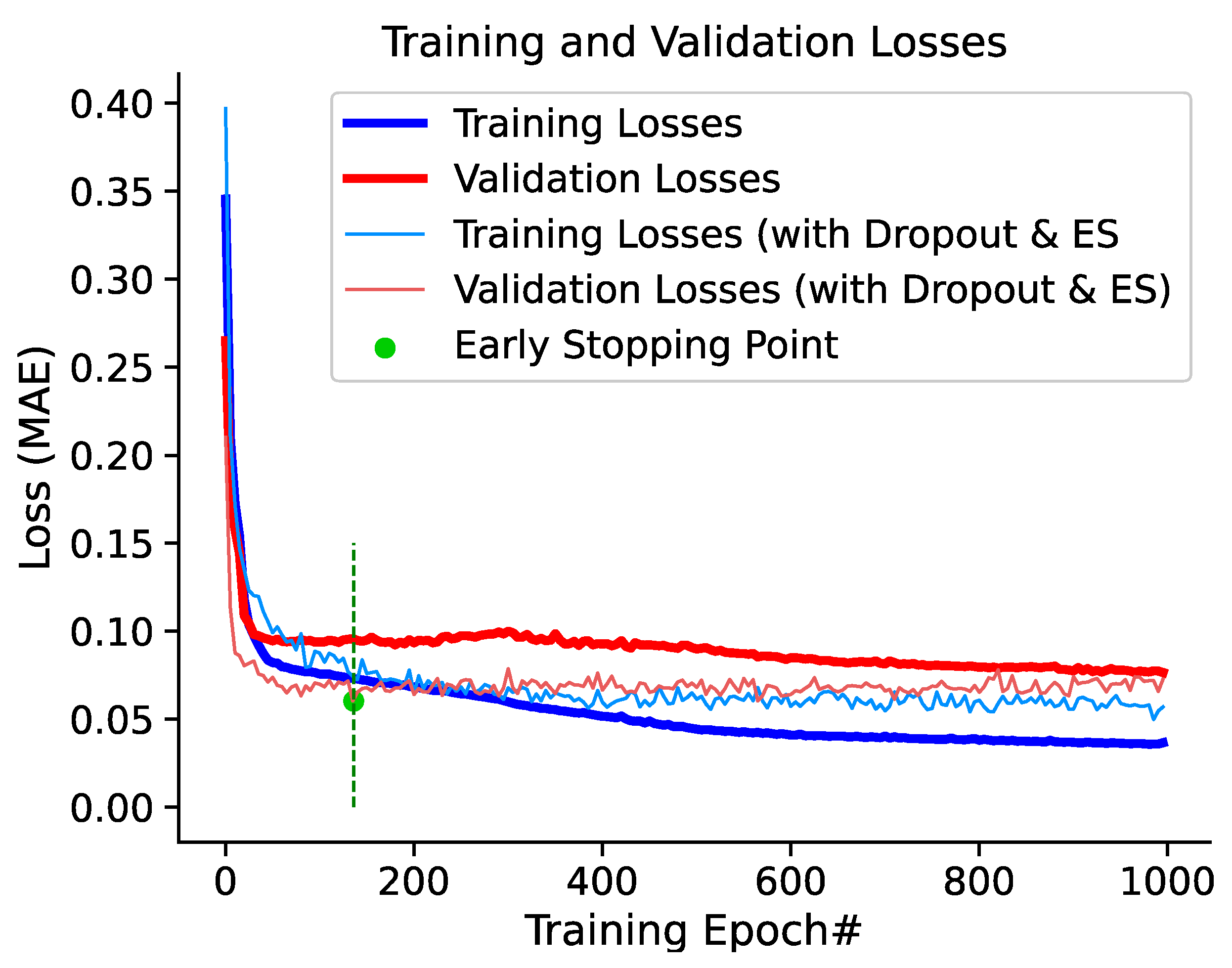

| Input 1 | Input 2 | Input 3 | Input 4 | Output 1 | Output 2 | Output 3 | Output 4 |
|---|---|---|---|---|---|---|---|
| PLA wt% | HKUST-1 wt% | Casting Thickness (µm) | Immersion Time (min) | Stress (MPa) | Strain | E (MPa) | Toughness (KJ/m3) |
| 100 | 0 | 150 | 1440 | 1.43 | 0.11 | 39.30 | 10.26 |
| 100 | 0 | 150 | 90 | 1.07 | 0.13 | 27 | 9.94 |
| 100 | 0 | 150 | 10 | 0.96 | 0.08 | 30.40 | 4.48 |
| 100 | 0 | 100 | 1440 | 1.28 | 0.16 | 32.30 | 15.61 |
| 100 | 0 | 100 | 90 | 1.14 | 0.16 | 23.90 | 11.96 |
| 100 | 0 | 100 | 10 | 1.87 | 0.18 | 42.50 | 21.90 |
| 100 | 0 | 50 | 1440 | 1.61 | 0.08 | 60.80 | 12.07 |
| 100 | 0 | 50 | 90 | 1.12 | 0.06 | 52.50 | 7.53 |
| 100 | 0 | 50 | 10 | 1.2 | 0.08 | 46.70 | 7.68 |
| 100 | 0 | 25 | 1440 | 1.43 | 0.07 | 65.20 | 7.32 |
| 100 | 0 | 25 | 90 | 1.06 | 0.04 | 48.50 | 3.25 |
| 100 | 0 | 25 | 10 | 1.34 | 0.08 | 43.50 | 6.85 |
| 95 | 5 | 150 | 1440 | 0.80 | 0.10 | 26.60 | 6.98 |
| 95 | 5 | 150 | 90 | 0.98 | 0.09 | 30.10 | 4.80 |
| 95 | 5 | 150 | 10 | 0.86 | 0.08 | 30.70 | 4.37 |
| 95 | 5 | 100 | 1440 | 0.90 | 0.12 | 25.70 | 8.65 |
| 95 | 5 | 100 | 90 | 1.22 | 0.08 | 37 | 9.72 |
| 95 | 5 | 100 | 10 | 1.01 | 0.06 | 27.60 | 3.65 |
| 95 | 5 | 50 | 1440 | 0.91 | 0.13 | 18.60 | 9.80 |
| 95 | 5 | 50 | 90 | 0.91 | 0.05 | 39.50 | 3.64 |
| 95 | 5 | 50 | 10 | 1.02 | 0.04 | 41.60 | 3.68 |
| 95 | 5 | 25 | 1440 | 0.96 | 0.04 | 45.70 | 2.57 |
| 95 | 5 | 25 | 90 | 1.21 | 0.04 | 49 | 4.78 |
| 95 | 5 | 25 | 10 | 1.17 | 0.05 | 44.70 | 4.72 |
| 90 | 10 | 50 | 90 | 0.76 | 0.05 | 39.54 | 3.64 |
| 80 | 20 | 50 | 90 | 0.48 | 0.05 | 18.68 | 1.78 |
| Statistical Properties | Original Dataset | Interpolated Dataset | ||||||
|---|---|---|---|---|---|---|---|---|
| Stress (MPa) | Strain | Elastic Modulus (MPa) | Toughness (Kj/m3) | Stress (MPa) | Strain | Elastic Modulus (MPa) | Toughness (Kj/m3) | |
| Data Points | 26 | 26 | 26 | 26 | 286 | 288 | 338 | 302 |
| Min. | 0.48 | 0.04 | 18.60 | 1.78 | 0.46 | 0.04 | 16.60 | 1.28 |
| Max. | 1.87 | 0.18 | 65.2 | 21.9 | 1.89 | 0.18 | 67.15 | 22.35 |
| Mean | 1.10 | 0.09 | 37.99 | 7.37 | 1.17 | 0.11 | 41.88 | 11.82 |
| Std. Deviation | 0.29 | 0.04 | 12.03 | 4.54 | 0.41 | 0.04 | 14.66 | 6.11 |
| # | Modeling Output | Dropout Rate | Model Performance Evaluation | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Using Type-1 Dataset (Known Interpolated Data Points) | Using Type-2 Dataset (Unknown Interpolated Data Points) | Using Type-3 Dataset (Unknown Original Data Points) | |||||||||
| MAE | RMSE | R2 | MAE | RMSE | R2 | MAE | RMSE | R2 | |||
| 1 | Stress | 7.5% | 0.04 | 0.05 | 0.95 | 0.04 | 0.05 | 0.95 | 0.05 | 0.06 | 0.82 |
| 2 | Strain | 4.5% | 0.03 | 0.05 | 0.97 | 0.03 | 0.05 | 0.97 | 0.05 | 0.08 | 0.88 |
| 3 | Elastic modulus | 12.5% | 0.04 | 0.05 | 0.96 | 0.04 | 0.05 | 0.96 | 0.05 | 0.07 | 0.82 |
| 4 | Toughness | 11.5% | 0.06 | 0.07 | 0.93 | 0.06 | 0.07 | 0.93 | 0.06 | 0.10 | 0.78 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alhulaybi, Z.A.; Martuza, M.A.; Rushd, S. Modeling the Mechanical Properties of a Polymer-Based Mixed-Matrix Membrane Using Deep Learning Neural Networks. ChemEngineering 2023, 7, 80. https://doi.org/10.3390/chemengineering7050080
Alhulaybi ZA, Martuza MA, Rushd S. Modeling the Mechanical Properties of a Polymer-Based Mixed-Matrix Membrane Using Deep Learning Neural Networks. ChemEngineering. 2023; 7(5):80. https://doi.org/10.3390/chemengineering7050080
Chicago/Turabian StyleAlhulaybi, Zaid Abdulhamid, Muhammad Ali Martuza, and Sayeed Rushd. 2023. "Modeling the Mechanical Properties of a Polymer-Based Mixed-Matrix Membrane Using Deep Learning Neural Networks" ChemEngineering 7, no. 5: 80. https://doi.org/10.3390/chemengineering7050080
APA StyleAlhulaybi, Z. A., Martuza, M. A., & Rushd, S. (2023). Modeling the Mechanical Properties of a Polymer-Based Mixed-Matrix Membrane Using Deep Learning Neural Networks. ChemEngineering, 7(5), 80. https://doi.org/10.3390/chemengineering7050080







