Using Excel Solver’s Parameter Function in Predicting and Interpretation for Kinetic Adsorption Model via Batch Sorption: Selection and Statistical Analysis for Basic Dye Removal onto a Novel Magnetic Nanosorbent
Abstract
1. Introduction
2. Materials and Methods
2.1. Experimental Dataset
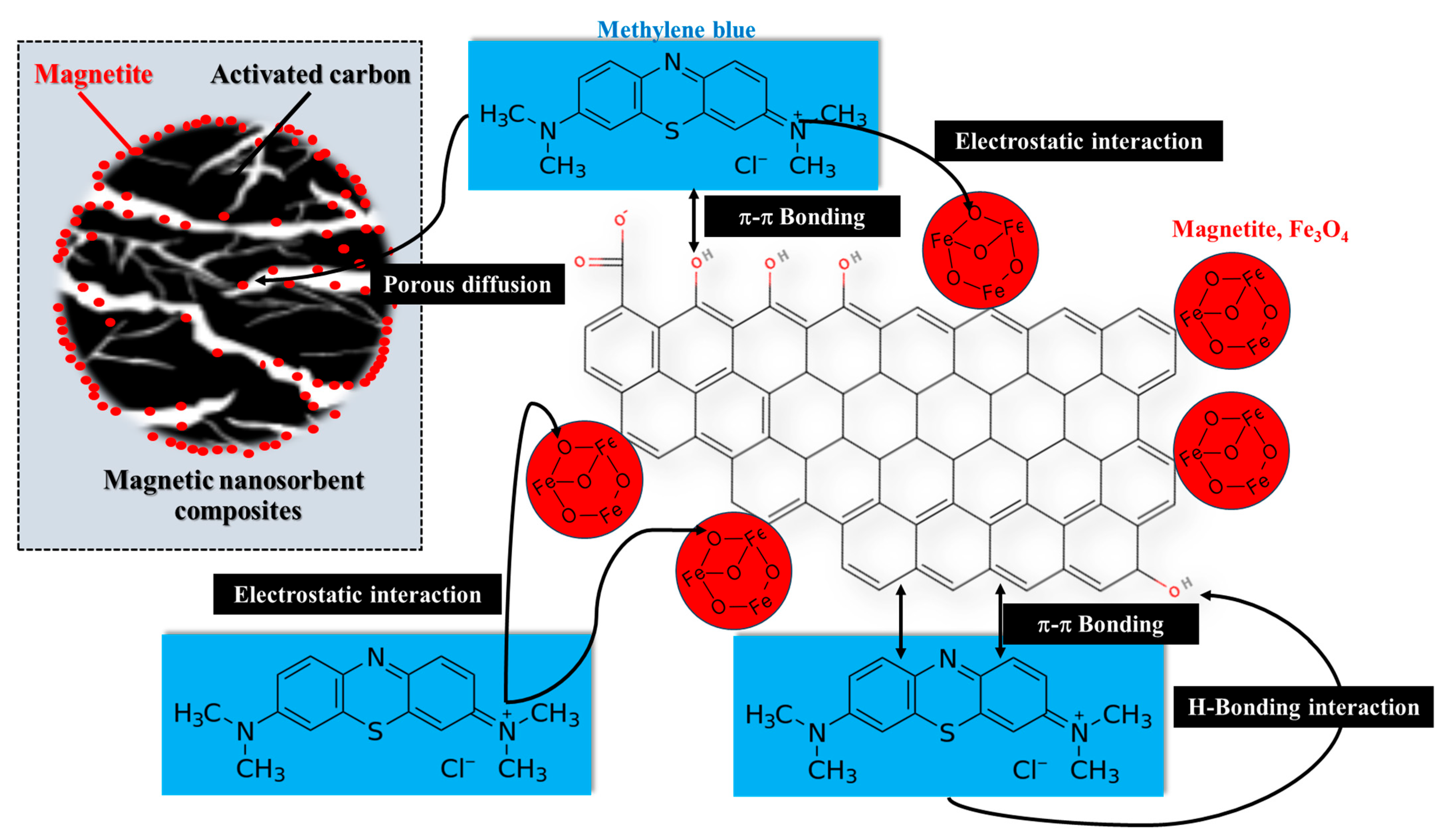
2.2. Kinetic Adsorption Models
2.3. Error Function Statistic Tools for Kinetic Adsorption Model
2.4. Microsoft Excel Minimized Solver Error Functions and Kinetic Adsorption Models
2.4.1. Experimental Dataset
2.4.2. Microsoft Excel Solver’s Parameter Function
2.4.3. Evaluating the Statistical Results
3. Results and Discussion
3.1. Substantiation of Kinetic Adsorption Model Data via Microsoft Excel Solver Function
3.1.1. Two-Parameter Kinetic Adsorption Models
3.1.2. Three-Parameter Kinetic Adsorption Models
3.2. Comparison of Kinetic Adsorption Model Parameters and Error Functions with Advanced Program Tools
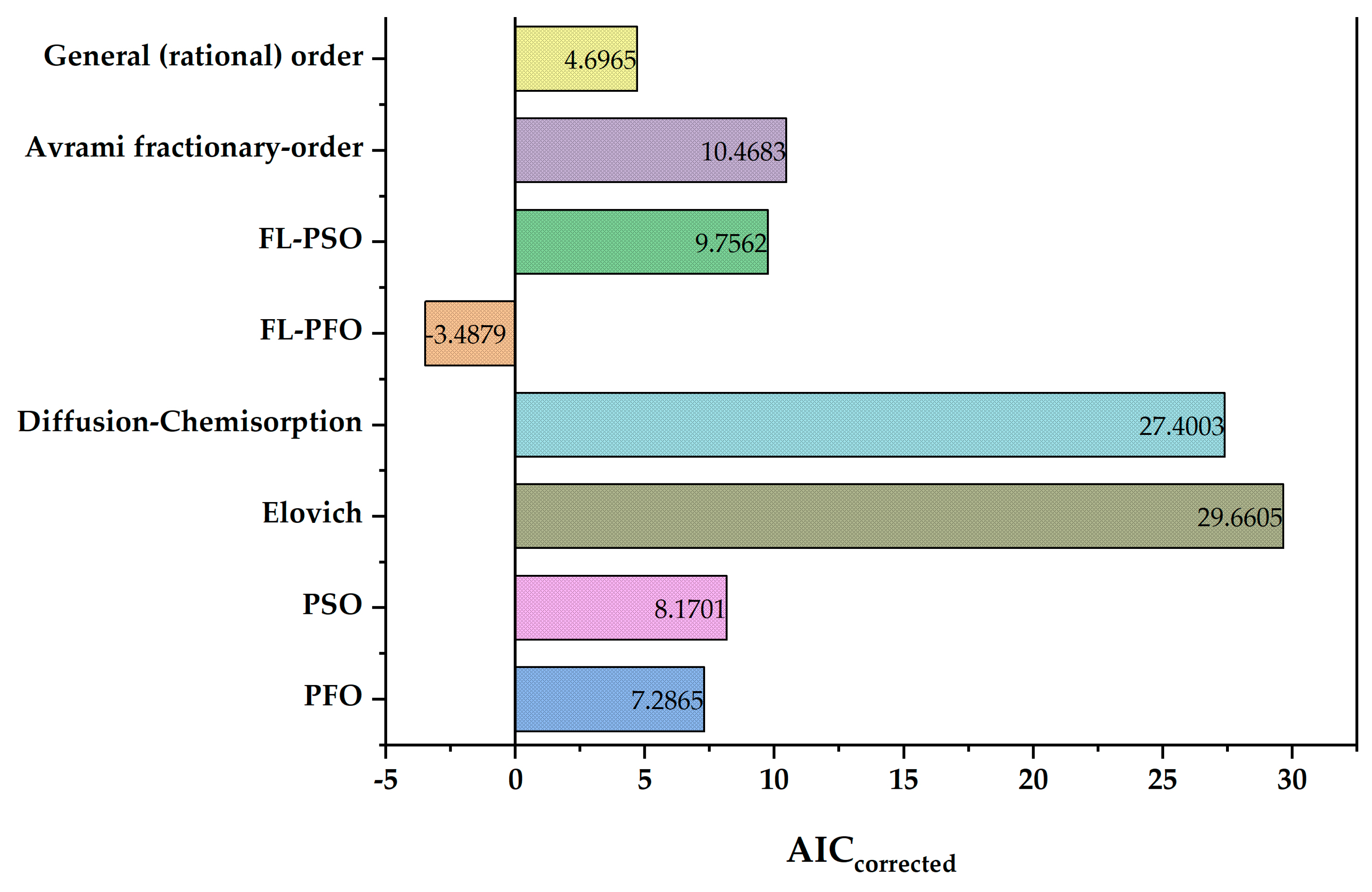
3.3. Application of Akaike’s Information Criterion for the Selected Kinetic Adsorption Model
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Adj R-square | Adjusted nonlinear coefficient of determination |
| C0 | Initial concentration of basic dyes (mg L−1) |
| Ce | Concentration of basic dyes at equilibrium (mg L−1) |
| k1,FL-PFO | FL-PFO rate constant (min−1) |
| k1,PFO | PFO rate constant (min−1) |
| k2,FL-PSO | FL-PSO rate constant (g mg−1 min−1) |
| k2,PSO | PSO rate constant (g mg−1 min−1) |
| kav | Avrami kinetic constant (min−1) |
| kDC | Diffusion-Chemisorption constant (mg g−1 min−n) |
| kGen | General order rate constant for the order r |
| m | Mass of nanosorbent (g) |
| n | Order of reaction |
| nav | Avrami model exponent |
| qe | Predicted mass of adsorbed basic dyes at equilibrium (mg g−1) |
| qm | Maximum adsorption capacity (mg g−1) |
| qt | Mass of adsorbed basic dyes at t time (mg g−1) |
| qt,ex | Mass of adsorbed basic dyes at t time (experimental) (mg g−1) |
| R | Universal gas constant (8.314 J mol−1 K−1) |
| R-square | Coefficient of determination |
| t | Adsorption contact time (min) |
| V | Volume of solution (mL) |
| αe | Initial adsorption rate of Elovich model (mg g−1 min−1) |
| βe | Elovich desorption constant (g mg−1) |
| χ2 | Chi-square test |
| Abbreviations | |
| AIC | Akaike’s information criterion |
| ARE | Average Relative Error |
| EABS | Sum of Absolute Errors |
| HYBRID | Hybrid Fractional Error Function |
| MPSD | Marquard’s Percent Standard Deviation |
| NSD | Normalized Standard Deviation |
| RMSE | Root Mean Square Error |
| SSE | Sum of Square Error |
References
- Thirunavukkarasu, A.; Nithya, R.; Sivashankar, R. A review on the role of nanomaterials in the removal of organic pollutants from wastewater. Rev. Environ. Sci. Bio/Technol. 2020, 19, 751–778. [Google Scholar] [CrossRef]
- Wongcharee, S.; Aravinthan, V.; Erdei, L.; Sanongraj, W. Use of macadamia nut shell residues as magnetic nanosorbents. Int. Biodeterior. Biodegrad. 2017, 124, 276–287. [Google Scholar] [CrossRef]
- Dobe, N.; Abia, D.; Tcheka, C.; Tejeogue, J.P.N.; Harouna, M. Removal of amaranth dye by modified Ngassa clay: Linear and non-linear equilibrium, kinetics and statistical study. Chem. Phys. Lett. 2022, 801, 139707. [Google Scholar] [CrossRef]
- Malhotra, N.; Lee, J.S.; Liman, R.A.D.; Ruallo, J.M.S.; Villaflores, O.B.; Ger, T.R.; Hsiao, C.D. Potential Toxicity of Iron Oxide Magnetic Nanoparticles: A Review. Molecules 2020, 25, 3159. [Google Scholar] [CrossRef] [PubMed]
- Ma, Z.; Mohapatra, J.; Wei, K.; Liu, J.P.; Sun, S. Magnetic Nanoparticles: Synthesis, Anisotropy, and Applications. Chem. Rev. 2023, 123, 3904–3943. [Google Scholar] [CrossRef]
- Chaidez, C.; Gerba, C.P. Comparison of the microbiologic quality of point-of-use (POU)-treated water and tap water. Int. J. Environ. Health Res. 2004, 14, 253–260. [Google Scholar] [CrossRef] [PubMed]
- Peralta, M.E.; Ocampo, S.; Funes, I.G.; Onaga Medina, F.; Parolo, M.E.; Carlos, L. Nanomaterials with Tailored Magnetic Properties as Adsorbents of Organic Pollutants from Wastewaters. Inorganics 2020, 8, 24. [Google Scholar] [CrossRef]
- Perwez, M.; Fatima, H.; Arshad, M.; Meena, V.K.; Ahmad, B. Magnetic iron oxide nanosorbents effective in dye removal. Int. J. Environ. Sci. Technol. 2023, 20, 5697–5714. [Google Scholar] [CrossRef]
- Jaishankar, M.; Tseten, T.; Anbalagan, N.; Mathew, B.B.; Beeregowda, K.N. Toxicity, mechanism and health effects of some heavy metals. Interdiscip. Toxicol. 2014, 7, 60–72. [Google Scholar] [CrossRef]
- Ihaddaden, S.; Aberkane, D.; Boukerroui, A.; Robert, D. Removal of methylene blue (basic dye) by coagulation-flocculation with biomaterials (bentonite and Opuntia ficus indica). J. Water Process Eng. 2022, 49, 102952. [Google Scholar] [CrossRef]
- Amesimeku, J.; Fan, L.; Jakpa, W.; Wang, C. Dyeing properties of meta-aramid fabric dyed with basic dye using ultrasonic-microwave irradiation. J. Clean. Prod. 2021, 285, 124844. [Google Scholar] [CrossRef]
- Rosario, A.; Howell, A.; Bhattacharya, S.K. A revisit to staining reagents for neuronal tissues. Ann. Eye Sci. 2022, 7, 6. [Google Scholar] [CrossRef] [PubMed]
- Hamel, P.; Tan, L. Blue–green infrastructure for flood and water quality management in Southeast Asia: Evidence and knowledge gaps. Environ. Manag. 2022, 69, 699–718. [Google Scholar] [CrossRef] [PubMed]
- Suwannahong, K.; Sirilamduan, C.; Deepatana, A.; Kreetachat, T.; Wongcharee, S. Characterization and Optimization of Polymeric Bispicolamine Chelating Resin: Performance Evaluation via RSM Using Copper in Acid Liquors as a Model Substrate through Ion Exchange Method. Molecules 2022, 27, 7210. [Google Scholar] [CrossRef]
- Suwannahong, K.; Wongcharee, S.; Rioyo, J.; Sirilamduan, C.; Kreetachart, T. Insight into molecular weight cut off characteristics and reduction of melanoidin using microporous and mesoporous adsorbent. Eng. Appl. Sci. Res. 2021, 49, 47–57. [Google Scholar]
- Wongcharee, S.; Aravinthan, V.; Erdei, L.; Sanongraj, W. Mesoporous activated carbon prepared from macadamia nut shell waste by carbon dioxide activation: Comparative characterisation and study of methylene blue removal from aqueous solution. Asia-Pac. J. Chem. Eng. 2018, 13, e2179. [Google Scholar] [CrossRef]
- Neogi, S.; Sharma, V.; Khan, N.; Chaurasia, D.; Ahmad, A.; Chauhan, S.; Singh, A.; You, S.; Pandey, A.; Bhargava, P.C. Sustainable biochar: A facile strategy for soil and environmental restoration, energy generation, mitigation of global climate change and circular bioeconomy. Chemosphere 2022, 293, 133474. [Google Scholar] [CrossRef] [PubMed]
- Shi, K.; Zhang, H.; Xu, H.; Liu, Z.; Kan, G.; Yu, K.; Jiang, J. Adsorption behaviors of triclosan by non-biodegradable and biodegradable microplastics: Kinetics and mechanism. Sci. Total Environ. 2022, 842, 156832. [Google Scholar] [CrossRef] [PubMed]
- Tan, K.; Hameed, B. Insight into the adsorption kinetics models for the removal of contaminants from aqueous solutions. J. Taiwan Inst. Chem. Eng. 2017, 74, 25–48. [Google Scholar] [CrossRef]
- Dassanayake, R.S.; Acharya, S.; Abidi, N. Biopolymer-based materials from polysaccharides: Properties, processing, characterization and sorption applications. In Advanced Sorption Process Applications; IntechOpen: London, UK, 2018. [Google Scholar]
- Rodrigues, A.E.; Silva, C.M. What’s wrong with Lagergreen pseudo first order model for adsorption kinetics? Chem. Eng. J. 2016, 306, 1138–1142. [Google Scholar] [CrossRef]
- Moussout, H.; Ahlafi, H.; Aazza, M.; Maghat, H. Critical of linear and nonlinear equations of pseudo-first order and pseudo-second order kinetic models. Karbala Int. J. Mod. Sci. 2018, 4, 244–254. [Google Scholar] [CrossRef]
- Bujdák, J. Adsorption kinetics models in clay systems. The critical analysis of pseudo-second order mechanism. Appl. Clay Sci. 2020, 191, 105630. [Google Scholar]
- Ncibi, M.C. Applicability of some statistical tools to predict optimum adsorption isotherm after linear and non-linear regression analysis. J. Hazard. Mater. 2008, 153, 207–212. [Google Scholar] [CrossRef] [PubMed]
- Revellame, E.D.; Fortela, D.L.; Sharp, W.; Hernandez, R.; Zappi, M.E. Adsorption kinetic modeling using pseudo-first order and pseudo-second order rate laws: A review. Clean. Eng. Technol. 2020, 1, 100032. [Google Scholar] [CrossRef]
- Vilardi, G.; Di Palma, L.; Verdone, N. Heavy metals adsorption by banana peels micro-powder: Equilibrium modeling by non-linear models. Chin. J. Chem. Eng. 2018, 26, 455–464. [Google Scholar] [CrossRef]
- Dadou, S.; Berrama, T.; Doufene, N.; Zekkaoui, C.; Beriber, A. Evaluating untreated clay’s adsorptive capacity to remove an anionic dye from aqueous solution. Arab. J. Sci. Eng. 2019, 44, 9889–9903. [Google Scholar] [CrossRef]
- Rashidi, N.A.; Bokhari, A.; Yusup, S. Evaluation of kinetics and mechanism properties of CO2 adsorption onto the palm kernel shell activated carbon. Environ. Sci. Pollut. Res. 2021, 28, 33967–33979. [Google Scholar] [CrossRef] [PubMed]
- Mahmoud, M.E.; El-Said, G.F.; Ibrahim, G.A.; Elnashar, A.A. Effective removal of hexavalent chromium from water by sustainable nano-scaled waste avocado seeds: Adsorption isotherm, thermodynamics, kinetics, and error function. Biomass Convers. Biorefinery 2022, 12, 1–19. [Google Scholar] [CrossRef]
- Akdemir, M.; Isik, B.; Cakar, F.; Cankurtaran, O. Comparison of the adsorption efficiency of cationic (Crystal Violet) and anionic (Congo Red) dyes on Valeriana officinalis roots: Isotherms, kinetics, thermodynamic studies, and error functions. Mater. Chem. Phys. 2022, 291, 126763. [Google Scholar] [CrossRef]
- Vareda, J.P. On validity, physical meaning, mechanism insights and regression of adsorption kinetic models. J. Mol. Liq. 2023, 376, 121416. [Google Scholar] [CrossRef]
- Kumar, K.V. Linear and non-linear regression analysis for the sorption kinetics of methylene blue onto activated carbon. J. Hazard. Mater. 2006, 137, 1538–1544. [Google Scholar] [CrossRef] [PubMed]
- Azizian, S.; Fallah, R.N. A new empirical rate equation for adsorption kinetics at solid/solution interface. Appl. Surf. Sci. 2010, 256, 5153–5156. [Google Scholar] [CrossRef]
- Bergmann, C.P.; Machado, F.M. Carbon Nanomaterials as Adsorbents for Environmental and Biological Applications; Springer: New York, NY, USA, 2015; pp. 1–105. [Google Scholar]
- Azizian, S.; Bagheri, M. Enhanced adsorption of Cu2+ from aqueous solution by Ag doped nano-structured ZnO. J. Mol. Liq. 2014, 196, 198–203. [Google Scholar] [CrossRef]
- Sutherland, C.; Venkobachar, C. A diffusion-chemisorption kinetic model for simulating biosorption using forest macro-fungus, fomes fasciatus. Int. Res. J. Plant Sci. 2010, 1, 107–117. [Google Scholar]
- Cardoso, N.F.; Lima, E.C.; Pinto, I.S.; Amavisca, C.V.; Royer, B.; Pinto, R.B.; Alencar, W.S.; Pereira, S.F. Application of cupuassu shell as biosorbent for the removal of textile dyes from aqueous solution. J. Environ. Manag. 2011, 92, 1237–1247. [Google Scholar] [CrossRef] [PubMed]
- Rahman, M.M.; Pal, A.; Uddin, K.; Thu, K.; Saha, B.B. Statistical Analysis of Optimized Isotherm Model for Maxsorb III/Ethanol and Silica Gel/Water Pairs. EVERGREEN Jt. J. Nov. Carbon Resour. Sci. Green Asia Strategy 2018, 5, 1–12. [Google Scholar] [CrossRef]
- Jasper, E.E.; Ajibola, V.O.; Onwuka, J.C. Nonlinear regression analysis of the sorption of crystal violet and methylene blue from aqueous solutions onto an agro-waste derived activated carbon. Appl. Water Sci. 2020, 10, 132. [Google Scholar] [CrossRef]
- Kapoor, A.; Yang, R. Correlation of equilibrium adsorption data of condensible vapours on porous adsorbents. Gas Sep. Purif. 1989, 3, 187–192. [Google Scholar] [CrossRef]
- Bruce, P.; Bruce, A.; Gedeck, P. Practical Statistics for Data Scientists: 50+ Essential Concepts using R and Python; O’Reilly Media: Sebastopol, CA, USA, 2020. [Google Scholar]
- Azqhandi, M.H.A.; Foroughi, M.; Yazdankish, E. A highly effective, recyclable, and novel host-guest nanocomposite for Triclosan removal: A comprehensive modeling and optimization-based adsorption study. J. Colloid Interface Sci. 2019, 551, 195–207. [Google Scholar] [CrossRef]
- Shah, K.J.; Gandhi, V. Advances in Wastewater Treatment II; Materials Research Forum LLC: Millersville, PA, USA, 2021. [Google Scholar]
- Foo, K.Y.; Hameed, B.H. Insights into the modeling of adsorption isotherm systems. Chem. Eng. J. 2010, 156, 2–10. [Google Scholar] [CrossRef]
- Chan, L.; Cheung, W.; Allen, S.; McKay, G. Error analysis of adsorption isotherm models for acid dyes onto bamboo derived activated carbon. Chin. J. Chem. Eng. 2012, 20, 535–542. [Google Scholar] [CrossRef]
- López-Luna, J.; Ramírez-Montes, L.E.; Martinez-Vargas, S.; Martínez, A.I.; Mijangos-Ricardez, O.F.; González-Chávez, M.d.C.A.; Carrillo-González, R.; Solís-Domínguez, F.A.; Cuevas-Díaz, M.d.C.; Vázquez-Hipólito, V. Linear and nonlinear kinetic and isotherm adsorption models for arsenic removal by manganese ferrite nanoparticles. SN Appl. Sci. 2019, 1, 950. [Google Scholar] [CrossRef]
- Bapat, S.; Jaspal, D.; Malviya, A. Efficacy of parthenium hysterophorus waste biomass compared with activated charcoal for the removal of CI Reactive Red 239 textile dye from wastewater. Color. Technol. 2021, 137, 234–250. [Google Scholar] [CrossRef]
- Deb, H.; Hasan, K.; Islam, M.Z.; Kai, L.; Yang, S.; Zhang, Y.; Yao, J. The Statistical Error Optimization of Dye Sorption Equilibria for the Precise Prediction of Adsorption Isotherms on Activated Graphene. Appl. Sci. 2023, 13, 8106. [Google Scholar] [CrossRef]
- Suwannahong, K.; Wongcharee, S.; Kreetachart, T.; Sirilamduan, C.; Rioyo, J.; Wongphat, A. Evaluation of the Microsoft Excel Solver Spreadsheet-Based Program for Nonlinear Expressions of Adsorption Isotherm Models onto Magnetic Nanosorbent. Appl. Sci. 2021, 11, 7432. [Google Scholar] [CrossRef]
- George William, K.; Serkan, E.; Atakan, Ö.; Özcan, H.K.; Serdar, A. Modelling of Adsorption Kinetic Processes—Errors, Theory and Application. In Advanced Sorption Process Applications; Serpil, E., Ed.; IntechOpen: Rijeka, Croatia, 2018. [Google Scholar]
- Plazinski, W.; Rudzinski, W.; Plazinska, A. Theoretical models of sorption kinetics including a surface reaction mechanism: A review. Adv. Colloid Interface Sci. 2009, 152, 2–13. [Google Scholar] [CrossRef] [PubMed]
- Pourebrahimi, S.; Pirooz, M. Reversible iodine vapor capture using bipyridine-based covalent triazine framework: Experimental and computational investigations. Chem. Eng. J. Adv. 2021, 8, 100150. [Google Scholar] [CrossRef]
- Kulkarni, P.S.; Watwe, V.S.; Kulkarni, S.D. Dynamic studies of copper adsorption on mesoporous alginate beads using an integrated approach of fractal-like kinetic reaction and diffusion modeling. Int. J. Chem. Kinet. 2022, 54, 726–736. [Google Scholar] [CrossRef]
- Gautam, R.K.; Chattopadhyaya, M.C. Advanced Nanomaterials for Wastewater Remediation; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]
- Pandikumar, A.; Rameshkumar, P.; Veerakumar, P. Biomass-Derived Carbon Materials: Production and Applications; Wiley: Hoboken, NJ, USA, 2022. [Google Scholar]
- Rajahmundry, G.K.; Garlapati, C.; Kumar, P.S.; Alwi, R.S.; Vo, D.-V.N. Statistical analysis of adsorption isotherm models and its appropriate selection. Chemosphere 2021, 276, 130176. [Google Scholar] [CrossRef]
- Sodeifian, G.; Garlapati, C.; Hazaveie, S.M.; Sodeifian, F. Solubility of 2,4,7-Triamino-6-phenylpteridine (Triamterene, Diuretic Drug) in Supercritical Carbon Dioxide: Experimental Data and Modeling. J. Chem. Eng. Data 2020, 65, 4406–4416. [Google Scholar] [CrossRef]
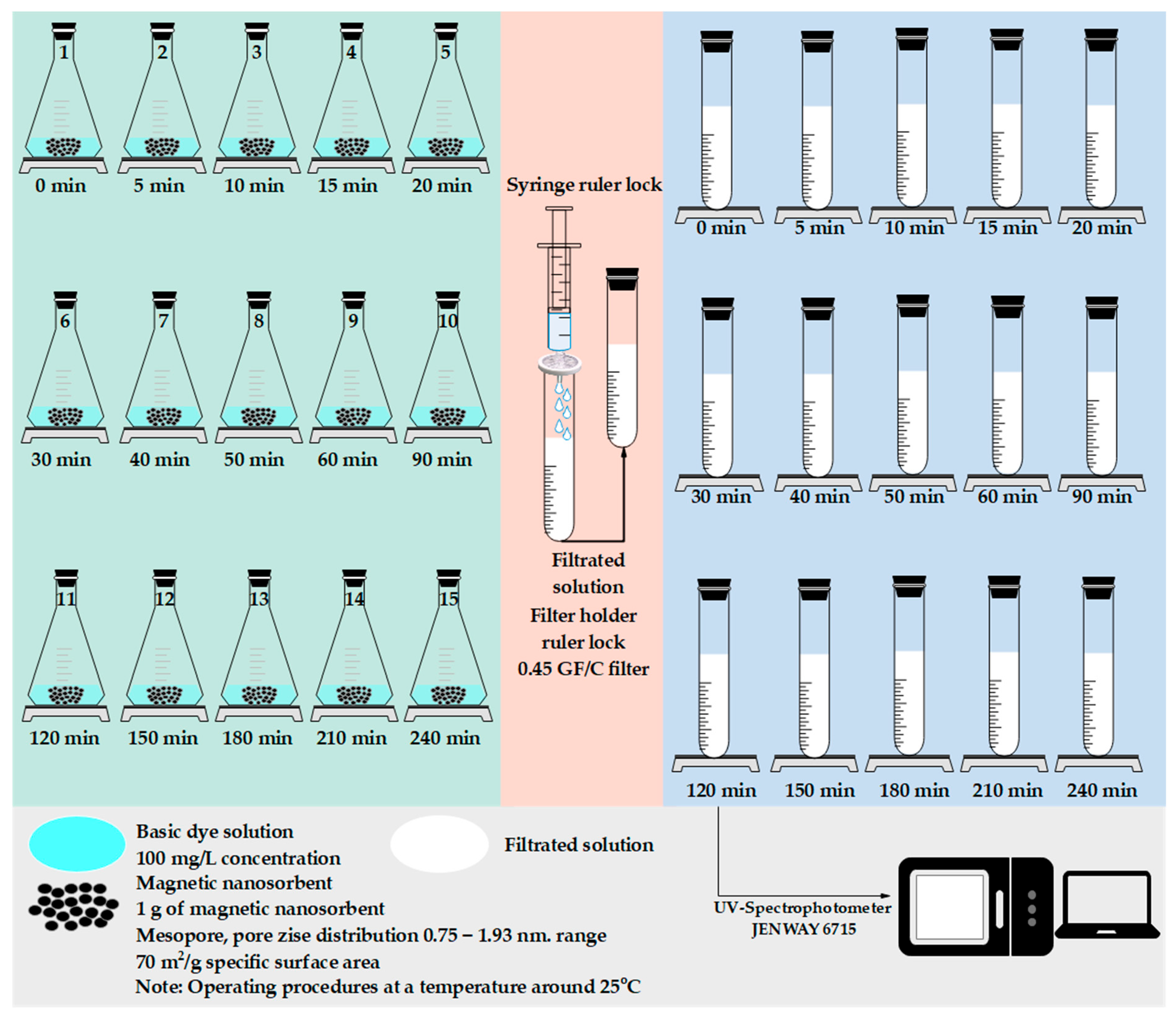

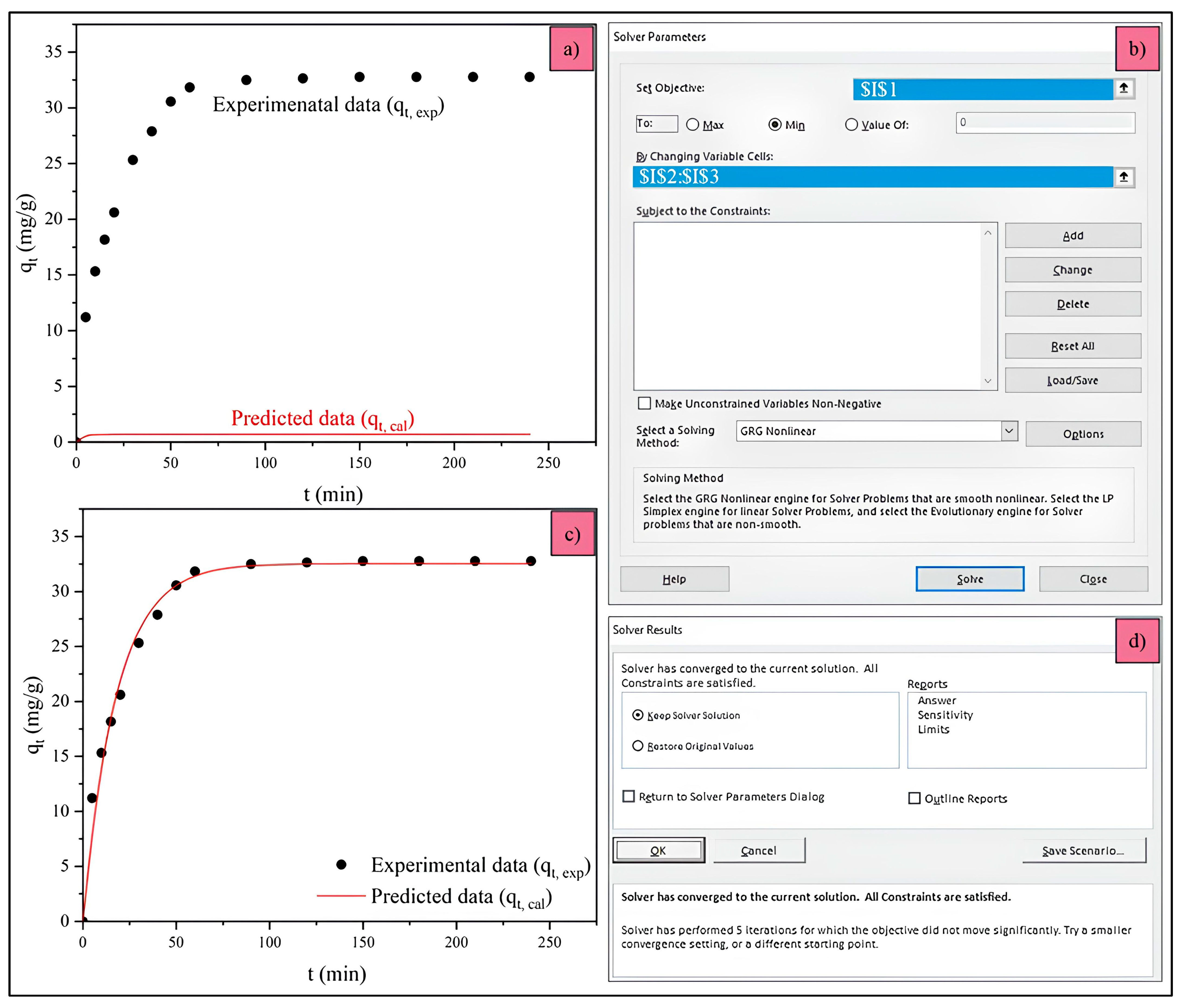
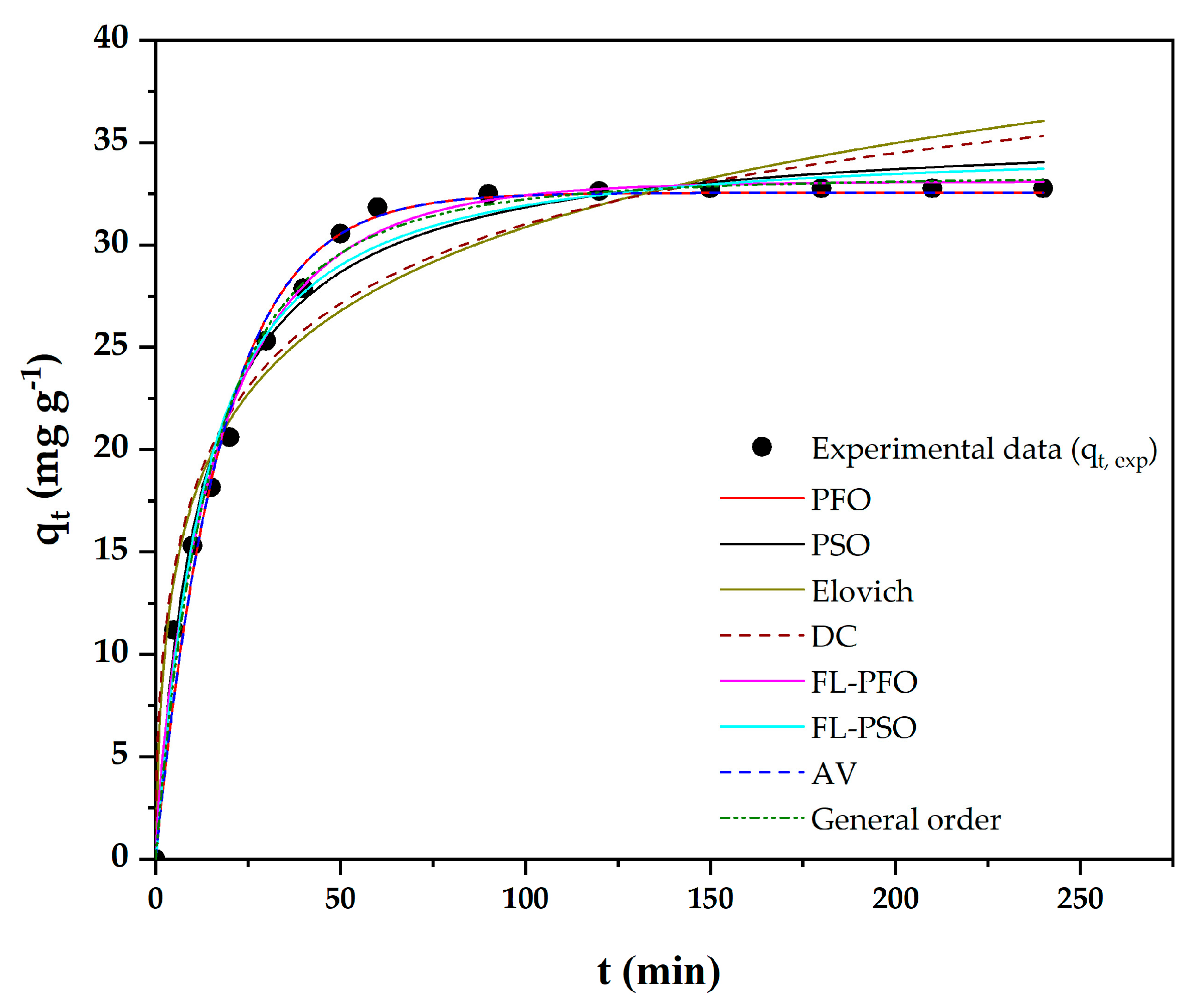
| t, t at the Equilibrium Adsorption (min) | qt,exp at Time t (mg g−1) |
|---|---|
| 0 | 0.00 |
| 5 | 11.20 |
| 10 | 15.31 |
| 15 | 18.16 |
| 20 | 20.60 |
| 30 | 25.32 |
| 40 | 27.88 |
| 50 | 30.55 |
| 60 | 31.84 |
| 90 | 32.50 |
| 120 | 32.63 |
| 150 | 32.76 |
| 180 | 32.76 |
| 210 | 32.76 |
| 240 | 32.76 |
| Row/ Column | Time, t | qt,exp | qt,cal | Residual | Residual2 | Upper, CI | Lower, CI | Abbreviation | Factor Result | Abbreviation | Statistical Result |
|---|---|---|---|---|---|---|---|---|---|---|---|
| A | B | C | D | E | F | G | H | I | J | K | |
| 1 | 0 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.7006 | −0.70 | SSR | 17.465 | SSE | 17.465 |
| 2 | 5 | 11.1995 | 7.9189 | −3.2805 | 10.7619 | 8.6196 | 7.22 | k1 | 0.056 | Chi-sq | 1.284 |
| 3 | 10 | 15.3123 | 13.9111 | −1.4013 | 1.9636 | 14.6117 | 13.21 | qe,PFO | 32.546 | ARE | 1.928 |
| 4 | 15 | 18.1638 | 18.4452 | 0.2814 | 0.0792 | 19.1459 | 17.74 | Mean of qt,exp | 25.135 | RMSE | 1.159 |
| 5 | 20 | 20.6035 | 21.8762 | 1.2727 | 1.6198 | 22.5768 | 21.18 | df | 13.000 | HYBRID | 2.249 |
| 6 | 30 | 25.3165 | 26.4368 | 1.1204 | 1.2552 | 27.1375 | 25.74 | SE of qt,exp | 0.324 | MPSD | 19.087 |
| 7 | 40 | 27.8788 | 29.0481 | 1.1693 | 1.3674 | 29.7488 | 28.35 | R-square | 0.9877 | NSD | 111.692 |
| 8 | 50 | 30.5507 | 30.5433 | −0.0073 | 0.0001 | 31.2440 | 29.84 | Critical t | 2.160 | EABS | 10.114 |
| 9 | 60 | 31.8384 | 31.3994 | −0.4390 | 0.1927 | 32.1001 | 30.70 | CI | 0.701 | ||
| 10 | 90 | 32.4954 | 32.3310 | −0.1644 | 0.0270 | 33.0316 | 31.63 | Adjust R-square | 0.9867 | ||
| 11 | 120 | 32.6268 | 32.5058 | −0.1210 | 0.0146 | 33.2065 | 31.81 | ||||
| 12 | 150 | 32.7582 | 32.5387 | −0.2196 | 0.0482 | 33.2393 | 31.84 | ||||
| 13 | 180 | 32.7582 | 32.5448 | −0.2134 | 0.0455 | 33.2455 | 31.84 | ||||
| 14 | 210 | 32.7582 | 32.5460 | −0.2122 | 0.0450 | 33.2466 | 31.85 | ||||
| 15 | 240 | 32.7582 | 32.5462 | −0.2120 | 0.0450 | 33.2468 | 31.85 | ||||
| Row/ Column | Time, t | qt,exp | qt,cal | PFO Model (Equation (2)) | Residual | Residual2 | Abbreviation | Factor Results | Abbreviation | Statistic Results |
|---|---|---|---|---|---|---|---|---|---|---|
| A | B | C | D | E | H | I | J | K | ||
| 1 | 0 | 0.0000 | 0.0000 | $I$3*(1 − EXP(−$I$2*A1)) | 0.0000 | 0.0000 | SSR | 10,376.070 | SSE | 10,376.070 |
| 2 | 5 | 11.1995 | 0.2754 | $I$3*(1 − EXP(−$I$2*A2)) | −10.6556 | 113.5427 | k1 | 0.300 | Chi-sq | 358.083 |
| 3 | 10 | 15.3123 | 0.4425 | $I$3*(1 − EXP(−$I$2*A3)) | −14.6472 | 214.5405 | qe,PFO | 0.700 | ARE | 97.213 |
| 4 | 15 | 18.1638 | 0.5438 | $I$3*(1 − EXP(−$I$2*A4)) | −17.4716 | 305.2554 | Mean of qt,exp | 25.135 | RMSE | 5.044 |
| 5 | 20 | 20.6035 | 0.6053 | $I$3*(1 − EXP(−$I$2*A5)) | −19.9052 | 396.2180 | df | 13.000 | HYBRID | 113.416 |
| 6 | 30 | 25.3165 | 0.6651 | $I$3*(1 − EXP(−$I$2*A6)) | −24.6165 | 605.9744 | SE of qt,exp | 7.538 | MPSD | 962.364 |
| 7 | 40 | 27.8788 | 0.6872 | $I$3*(1 − EXP(−$I$2*A7)) | −27.1788 | 738.6879 | R-square | −6.3269 | NSD | 2722.403 |
| 8 | 50 | 30.5507 | 0.6953 | $I$3*(1 − EXP(−$I$2*A8)) | −29.8507 | 891.0619 | Critical t | 2.160 | EABS | 367.419 |
| 9 | 60 | 31.8384 | 0.6983 | $I$3*(1 − EXP(−$I$2*A9)) | −31.1384 | 969.6002 | CI | 16.285 | ||
| 10 | 90 | 32.4954 | 0.6999 | $I$3*(1 − EXP(−$I$2*A10)) | −31.7954 | 1010.9485 | Adjust R-square | −6.8905 | ||
| 11 | 120 | 32.6268 | 0.7000 | $I$3*(1 − EXP(−$I$2*A11)) | −31.9268 | 1019.3218 | ||||
| 12 | 150 | 32.7582 | 0.7000 | $I$3*(1 − EXP(−$I$2*A12)) | −32.0582 | 1027.7296 | ||||
| 13 | 180 | 32.7582 | 0.7000 | $I$3*(1 − EXP(−$I$2*A13)) | −32.0582 | 1027.7296 | ||||
| 14 | 210 | 32.7582 | 0.7000 | $I$3*(1 − EXP(−$I$2*A14)) | −32.0582 | 1027.7296 | ||||
| 15 | 240 | 32.7582 | 0.7000 | $I$3*(1 − EXP(−$I$2*A15)) | −32.0582 | 1027.7296 | ||||
| Row/ Column | Time, t | qt,exp | qt,cal | Residual | Residual2 | Upper, CI | Lower, CI | Abbreviation | Factor Result | Abbreviation | Statistical Result |
|---|---|---|---|---|---|---|---|---|---|---|---|
| A | B | C | D | E | F | G | H | I | J | K | |
| 1 | 0 | 0 | 0.0000 | 0.0000 | 0.0000 | 2.5791 | −2.5791 | SSR | 18.528 | SSE | 18.528 |
| 2 | 5 | 11.1995 | 10.2650 | −0.9344 | 0.8731 | 12.8441 | 7.6859 | k2,PSO | 0.002 | Chi-sq | 0.733 |
| 3 | 10 | 15.3123 | 15.9556 | 0.6432 | 0.4137 | 18.5347 | 13.3765 | qe,pso | 35.804 | ARE | −0.154 |
| 4 | 15 | 18.1638 | 19.5723 | 1.4085 | 1.9838 | 22.1514 | 16.9932 | Mean of qt,exp | 25.135 | RMSE | 1.194 |
| 5 | 20 | 20.6035 | 22.0741 | 1.4706 | 2.1626 | 24.6532 | 19.4950 | df | 13.000 | HYBRID | −0.180 |
| 6 | 30 | 25.3165 | 25.3092 | −0.0073 | 0.0001 | 27.8883 | 22.7301 | SE of qt,exp | 1.194 | MPSD | 1.527 |
| 7 | 40 | 27.8788 | 27.3105 | −0.5683 | 0.3230 | 29.8896 | 24.7314 | R-square | 0.9869 | NSD | 115.040 |
| 8 | 50 | 30.5507 | 28.6707 | −1.8799 | 3.5341 | 31.2498 | 26.0916 | Critical t | 2.160 | EABS | 13.680 |
| 9 | 60 | 31.8384 | 29.6554 | −2.1830 | 4.7654 | 32.2345 | 27.0763 | CI | 2.579 | ||
| 10 | 90 | 32.4954 | 31.4560 | −1.0394 | 1.0803 | 34.0351 | 28.8769 | Adjust R-square | 0.9859 | ||
| 11 | 120 | 32.6268 | 32.4409 | −0.1859 | 0.0346 | 35.0200 | 29.8618 | ||||
| 12 | 150 | 32.7582 | 33.0620 | 0.3038 | 0.0923 | 35.6411 | 30.4829 | ||||
| 13 | 180 | 32.7582 | 33.4894 | 0.7312 | 0.5346 | 36.0685 | 30.9103 | ||||
| 14 | 210 | 32.7582 | 33.8016 | 1.0433 | 1.0885 | 36.3807 | 31.2224 | ||||
| 15 | 240 | 32.7582 | 34.0395 | 1.2813 | 1.6417 | 36.6186 | 31.4604 | ||||
| Row/ Column | Time, t | qt,exp | qt,cal | Residual | Residual2 | Upper, CI | Lower, CI | Abbreviation | Factor Result | Abbreviation | Statistical Result |
|---|---|---|---|---|---|---|---|---|---|---|---|
| A | B | C | D | E | F | G | H | I | J | K | |
| 1 | 0 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 5.2795 | −5.2795 | SSR | 77.637 | SSE | 77.637 |
| 2 | 5 | 11.1995 | 13.6427 | 2.4432 | 5.9693 | 18.9221 | 8.3632 | αe | 10.592 | Chi-sq | 3.055 |
| 3 | 10 | 15.3123 | 17.4592 | 2.1469 | 4.6091 | 22.7387 | 12.1798 | βe | 0.168 | ARE | −1.732 |
| 4 | 15 | 18.1638 | 19.7657 | 1.6020 | 2.5663 | 25.0452 | 14.4863 | Mean of qt,exp | 25.135 | RMSE | 2.444 |
| 5 | 20 | 20.6035 | 21.4238 | 0.8203 | 0.6730 | 26.7033 | 16.1444 | df | 13.000 | HYBRID | −2.021 |
| 6 | 30 | 25.3165 | 23.7824 | −1.5341 | 2.3535 | 29.0618 | 18.5029 | SE of qt,exp | 2.444 | MPSD | 17.146 |
| 7 | 40 | 27.8788 | 25.4670 | −2.4118 | 5.8169 | 30.7464 | 20.1875 | R-square | 0.9452 | NSD | 235.488 |
| 8 | 50 | 30.5507 | 26.7784 | −3.7722 | 14.2297 | 32.0579 | 21.4990 | Critical t | 2.160 | EABS | 29.564 |
| 9 | 60 | 31.8384 | 27.8524 | −3.9860 | 15.8880 | 33.1319 | 22.5730 | CI | 5.279 | ||
| 10 | 90 | 32.4954 | 30.2470 | −2.2484 | 5.0555 | 35.5264 | 24.9675 | Adjust R-square | 0.9410 | ||
| 11 | 120 | 32.6268 | 31.9498 | −0.6770 | 0.4584 | 37.2292 | 26.6703 | ||||
| 12 | 150 | 32.7582 | 33.2722 | 0.5140 | 0.2642 | 38.5517 | 27.9927 | ||||
| 13 | 180 | 32.7582 | 34.3535 | 1.5953 | 2.5449 | 39.6330 | 29.0740 | ||||
| 14 | 210 | 32.7582 | 35.2682 | 2.5100 | 6.3002 | 40.5477 | 29.9888 | ||||
| 15 | 240 | 32.7582 | 36.0609 | 3.3027 | 10.9078 | 41.3404 | 30.7815 | ||||
| Row/ Column | Time, t | qt,exp | qt,cal | Residual | Residual2 | Upper, CI | Lower, CI | Abbreviation | Factor Result | Abbreviation | Statistical Result |
|---|---|---|---|---|---|---|---|---|---|---|---|
| A | B | C | D | E | F | G | H | I | J | K | |
| 1 | 0 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 4.8965 | −4.8965 | SSR | 66.781 | SSE | 66.781 |
| 2 | 5 | 11.1995 | 14.1201 | −2.9206 | 8.5299 | 19.0165 | 9.2236 | kDC | 9.001 | Chi-sq | 2.936 |
| 3 | 10 | 15.3123 | 17.7717 | −2.4593 | 6.0483 | 22.6681 | 12.8752 | qe,DC | 47.309 | ARE | −2.421 |
| 4 | 15 | 18.1638 | 20.0712 | −1.9075 | 3.6384 | 24.9677 | 15.1748 | Mean of qt,exp | 25.135 | RMSE | 2.266 |
| 5 | 20 | 20.6035 | 21.7488 | −1.1453 | 1.3118 | 26.6453 | 16.8524 | df | 13.000 | HYBRID | −2.825 |
| 6 | 30 | 25.3165 | 24.1424 | 1.1741 | 1.3785 | 29.0388 | 19.2459 | SE of qt,exp | 2.266 | MPSD | 23.969 |
| 7 | 40 | 27.8788 | 25.8374 | 2.0414 | 4.1672 | 30.7339 | 20.9410 | R-square | 0.9528 | NSD | 218.404 |
| 8 | 50 | 30.5507 | 27.1377 | 3.4129 | 11.6482 | 32.0342 | 22.2413 | Critical t | 2.160 | EABS | 27.528 |
| 9 | 60 | 31.8384 | 28.1848 | 3.6536 | 13.3491 | 33.0812 | 23.2883 | CI | 4.896 | ||
| 10 | 90 | 32.4954 | 30.4430 | 2.0524 | 4.2125 | 35.3394 | 25.5465 | Adjust R-square | 0.9450 | ||
| 11 | 120 | 32.6268 | 31.9699 | 0.6569 | 0.4315 | 36.8664 | 27.0735 | ||||
| 12 | 150 | 32.7582 | 33.1030 | −0.3448 | 0.1189 | 37.9995 | 28.2066 | ||||
| 13 | 180 | 32.7582 | 33.9924 | −1.2341 | 1.5231 | 38.8888 | 29.0959 | ||||
| 14 | 210 | 32.7582 | 34.7173 | −1.9590 | 3.8378 | 39.6137 | 29.8208 | ||||
| 15 | 240 | 32.7582 | 35.3245 | −2.5663 | 6.5856 | 40.2209 | 30.4280 | ||||
| Row/ Column | Time, t | qt,exp | qt,cal | Residual | Residual2 | Upper, CI | Lower, CI | Abbreviation | Factor Result | Abbreviation | Statistical Result |
|---|---|---|---|---|---|---|---|---|---|---|---|
| A | B | C | D | E | F | G | H | I | J | K | |
| 1 | 0 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 1.6507 | −1.6507 | SSR | 6.887 | SSE | 6.887 |
| 2 | 5 | 11.1995 | 9.8172 | −1.3822 | 1.9105 | 11.4679 | 8.1666 | αFL-PFO | 0.804 | Chi-sq | 0.368 |
| 3 | 10 | 15.3123 | 15.1939 | −0.1185 | 0.0140 | 16.8446 | 13.5432 | k1,FL-PFO | 0.096 | ARE | 0.404 |
| 4 | 15 | 18.1638 | 18.9705 | 0.8067 | 0.6508 | 20.6211 | 17.3198 | qe,FL-PFO | 33.089 | RMSE | 0.758 |
| 5 | 20 | 20.6035 | 21.7786 | 1.1751 | 1.3810 | 23.4293 | 20.1280 | Mean of qt,exp | 25.135 | HYBRID | 0.514 |
| 6 | 30 | 25.3165 | 25.6126 | 0.2961 | 0.0877 | 27.2632 | 23.9619 | df | 12.000 | MPSD | 3.266 |
| 7 | 40 | 27.8788 | 28.0133 | 0.1345 | 0.0181 | 29.6639 | 26.3626 | SE of qt,exp | 0.758 | NSD | 70.139 |
| 8 | 50 | 30.5507 | 29.5780 | −0.9726 | 0.9460 | 31.2287 | 27.9274 | R-square | 0.9951 | EABS | 7.592 |
| 9 | 60 | 31.8384 | 30.6255 | −1.2129 | 1.4710 | 32.2762 | 28.9749 | Critical t | 2.179 | ||
| 10 | 90 | 32.4954 | 32.1841 | −0.3113 | 0.0969 | 33.8347 | 30.5334 | CI | 1.651 | ||
| 11 | 120 | 32.6268 | 32.7343 | 0.1075 | 0.0115 | 34.3849 | 31.0836 | Adjust R-square | 0.9943 | ||
| 12 | 150 | 32.7582 | 32.9433 | 0.1851 | 0.0343 | 34.5940 | 31.2927 | ||||
| 13 | 180 | 32.7582 | 33.0269 | 0.2687 | 0.0722 | 34.6776 | 31.3763 | ||||
| 14 | 210 | 32.7582 | 33.0617 | 0.3035 | 0.0921 | 34.7123 | 31.4110 | ||||
| 15 | 240 | 32.7582 | 33.0765 | 0.3183 | 0.1013 | 34.7272 | 31.4259 | ||||
| Row/ Column | Time, t | qt,exp | qt,cal | Residual | Residual2 | Upper, CI | Lower, CI | Abbreviation | Factor Result | Abbreviation | Statistical Result |
|---|---|---|---|---|---|---|---|---|---|---|---|
| A | B | C | D | E | F | G | H | I | J | K | |
| 1 | 0 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 2.5671 | −2.5671 | SSR | 16.658 | SSE | 16.658 |
| 2 | 5 | 11.1995 | 9.3616 | −1.8379 | 3.3777 | 11.9287 | 6.7945 | αFL-PSO | 1.130 | Chi-sq | 0.810 |
| 3 | 10 | 15.3123 | 15.5317 | 0.2193 | 0.0481 | 18.0987 | 12.9646 | k2,FL-PSO | 0.002 | ARE | 0.409 |
| 4 | 15 | 18.1638 | 19.5089 | 1.3451 | 1.8092 | 22.0759 | 16.9418 | qe,FL-PSO | 34.887 | RMSE | 1.178 |
| 5 | 20 | 20.6035 | 22.2272 | 1.6237 | 2.6364 | 24.7942 | 19.6601 | Mean of qt,exp | 25.135 | HYBRID | 0.520 |
| 6 | 30 | 25.3165 | 25.6471 | 0.3306 | 0.1093 | 28.2141 | 23.0800 | df | 12.000 | MPSD | 3.305 |
| 7 | 40 | 27.8788 | 27.6811 | −0.1977 | 0.0391 | 30.2482 | 25.1141 | SE of qt,exp | 1.178 | NSD | 109.079 |
| 8 | 50 | 30.5507 | 29.0165 | −1.5342 | 2.3538 | 31.5835 | 26.4494 | R-square | 0.9882 | EABS | 12.553 |
| 9 | 60 | 31.8384 | 29.9546 | −1.8838 | 3.5486 | 32.5217 | 27.3876 | Critical t | 2.179 | ||
| 10 | 90 | 32.4954 | 31.5961 | −0.8993 | 0.8087 | 34.1632 | 29.0291 | CI | 2.567 | ||
| 11 | 120 | 32.6268 | 32.4453 | −0.1816 | 0.0330 | 35.0123 | 29.8782 | Adjust R-square | 0.9863 | ||
| 12 | 150 | 32.7582 | 32.9592 | 0.2010 | 0.0404 | 35.5263 | 30.3922 | ||||
| 13 | 180 | 32.7582 | 33.3017 | 0.5435 | 0.2954 | 35.8688 | 30.7347 | ||||
| 14 | 210 | 32.7582 | 33.5453 | 0.7871 | 0.6196 | 36.1124 | 30.9783 | ||||
| 15 | 240 | 32.7582 | 33.7269 | 0.9687 | 0.9384 | 36.2940 | 31.1599 |
| Row/ Column | Time, t | qt,exp | qt,cal | Residual | Residual2 | Upper, CI | Lower, CI | Abbreviation | Factor Result | Abbreviation | Statistical Result |
|---|---|---|---|---|---|---|---|---|---|---|---|
| A | B | C | D | E | F | G | H | I | J | K | |
| 1 | 0 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 2.6286 | −2.6286 | SSR | 17.466 | SSE | 17.466 |
| 2 | 5 | 11.1995 | 7.9144 | 3.2851 | 10.7917 | 10.5430 | 5.2858 | kav | 0.378 | Chi-sq | 1.286 |
| 3 | 10 | 15.3123 | 13.9044 | 1.4079 | 1.9823 | 16.5330 | 11.2758 | qe,av | 32.550 | ARE | 1.937 |
| 4 | 15 | 18.1638 | 18.4380 | −0.2742 | 0.0752 | 21.0666 | 15.8094 | nav | 0.147 | RMSE | 1.206 |
| 5 | 20 | 20.6035 | 21.8692 | −1.2657 | 1.6021 | 24.4978 | 19.2407 | Mean of qt,exp | 25.135 | HYBRID | 2.466 |
| 6 | 30 | 25.3165 | 26.4317 | −1.1152 | 1.2438 | 29.0603 | 23.8031 | df | 12.000 | MPSD | 15.659 |
| 7 | 40 | 27.8788 | 29.0452 | −1.1664 | 1.3605 | 31.6738 | 26.4166 | SE of qt,exp | 1.206 | NSD | 111.693 |
| 8 | 50 | 30.5507 | 30.5423 | 0.0084 | 0.0001 | 33.1709 | 27.9137 | R-square | 0.9877 | EABS | 10.084 |
| 9 | 60 | 31.8384 | 31.3999 | 0.4386 | 0.1923 | 34.0284 | 28.7713 | Critical t | 2.179 | ||
| 10 | 90 | 32.4954 | 32.3337 | 0.1617 | 0.0262 | 34.9622 | 29.7051 | CI | 2.629 | ||
| 11 | 120 | 32.6268 | 32.5092 | 0.1176 | 0.0138 | 35.1378 | 29.8806 | Adjust R-square | 0.9856 | ||
| 12 | 150 | 32.7582 | 32.5422 | 0.2160 | 0.0467 | 35.1708 | 29.9136 | ||||
| 13 | 180 | 32.7582 | 32.5484 | 0.2098 | 0.0440 | 35.1770 | 29.9198 | ||||
| 14 | 210 | 32.7582 | 32.5496 | 0.2087 | 0.0435 | 35.1781 | 29.9210 | ||||
| 15 | 240 | 32.7582 | 32.5498 | 0.2084 | 0.0434 | 35.1783 | 29.9212 | ||||
| Row/ Column | Time, t | qt,exp | qt,cal | Residual | Residual2 | Upper, CI | Lower, CI | Abbreviation | Factor Result | Abbreviation | Statistical Result |
|---|---|---|---|---|---|---|---|---|---|---|---|
| A | B | C | D | E | F | G | H | I | J | K | |
| 1 | 0 | 0.00000 | 0.00000 | 0.00000 | 0.0000 | 2.1692 | −2.1692 | SSR | 11.894 | SSE | 11.894 |
| 2 | 5 | 11.19945 | 8.93986 | 2.25959 | 5.1058 | 11.1091 | 6.7706 | kGen | 0.019 | Chi-sq | 0.736 |
| 3 | 10 | 15.31235 | 14.92560 | 0.38675 | 0.1496 | 17.0948 | 12.7564 | qe,Gen | 33.312 | ARE | 0.888 |
| 4 | 15 | 18.16378 | 19.08772 | −0.92394 | 0.8537 | 21.2569 | 16.9185 | nGen | 1.348 | RMSE | 0.996 |
| 5 | 20 | 20.60349 | 22.07370 | −1.47021 | 2.1615 | 24.2429 | 19.9045 | Mean of qt,exp | 25.135 | HYBRID | 1.130 |
| 6 | 30 | 25.31646 | 25.92949 | −0.61303 | 0.3758 | 28.0987 | 23.7603 | df | 12.000 | MPSD | 7.175 |
| 7 | 40 | 27.87881 | 28.19517 | −0.31637 | 0.1001 | 30.3644 | 26.0260 | SE of qt,exp | 0.995 | NSD | 92.174 |
| 8 | 50 | 30.55066 | 29.61534 | 0.93532 | 0.8748 | 31.7846 | 27.4461 | R-square | 0.9916 | EABS | 9.855 |
| 9 | 60 | 31.83840 | 30.55165 | 1.28676 | 1.6557 | 32.7209 | 28.3824 | Critical t | 2.179 | ||
| 10 | 90 | 32.49542 | 31.98413 | 0.51129 | 0.2614 | 34.1533 | 29.8149 | CI | 2.169 | ||
| 11 | 120 | 32.62682 | 32.57076 | 0.05606 | 0.0031 | 34.7400 | 30.4015 | Adjust R-square | 0.9902 | ||
| 12 | 150 | 32.75822 | 32.85548 | −0.09726 | 0.0095 | 35.0247 | 30.6863 | ||||
| 13 | 180 | 32.75822 | 33.01052 | −0.25230 | 0.0637 | 35.1797 | 30.8413 | ||||
| 14 | 210 | 32.75822 | 33.10226 | −0.34403 | 0.1184 | 35.2715 | 30.9330 | ||||
| 15 | 240 | 32.75822 | 33.16007 | −0.40184 | 0.1615 | 35.3293 | 30.9909 | ||||
| Model Parameter | Parameter Values for the Kinetic Adsorption Models | ||
|---|---|---|---|
| Microsoft Excel | MATLAB | OriginPro | |
| PFO | |||
| qe,PFO | 32.55 | 32.55 | 32.55 |
| k1,PFO | 0.056 | 0.056 | 0.056 |
| R-sq. | 0.9877 | 0.9877 | 0.9877 |
| Adj R-sq. | 0.9867 | 0.9867 | 0.9867 |
| SSE | 17.47 | 17.47 | 17.47 |
| Chi-sq. | 1.284 | - | 1.284 |
| ARE | 1.928 | - | - |
| RMSE | 1.159 | 1.159 | - |
| HYBRID | 2.249 | - | - |
| MPSD | 19.087 | - | - |
| NSD | 111.692 | - | - |
| EABS | 10.114 | - | - |
| PSO | |||
| qe,PSO | 35.80 | 35.80 | 35.80 |
| k2,PSO | 0.002 | 0.002 | 0.002 |
| R-sq. | 0.9869 | 0.9869 | 0.9869 |
| Adj R-sq. | 0.9859 | 0.9859 | 0.9859 |
| SSE | 18.53 | 18.53 | 18.53 |
| Chi-sq. | 0.733 | - | 0.733 |
| ARE | −0.154 | - | - |
| RMSE | 1.194 | 1.194 | - |
| HYBRID | −0.180 | - | - |
| MPSD | 1.527 | - | - |
| NSD | 115.040 | - | - |
| EABS | 13.680 | - | - |
| Elovich | |||
| αe | 10.59 | 10.59 | 10.59 |
| βe | 0.168 | 0.168 | 0.168 |
| R-sq. | 0.9452 | 0.9452 | 0.9452 |
| Adj R-sq. | 0.9410 | 0.9410 | 0.9410 |
| SSE | 77.64 | 77.64 | 77.64 |
| Chi-sq. | 3.055 | - | 3.055 |
| ARE | −1.732 | - | - |
| RMSE | 2.444 | 2.444 | - |
| HYBRID | −2.021 | - | - |
| MPSD | 17.146 | - | - |
| NSD | 235.488 | - | - |
| EABS | 29.564 | - | - |
| Diffusion-Chemisorption | |||
| qe,DC | 47.31 | 47.31 | 47.31 |
| kDC | 9.001 | 9.002 | 9.001 |
| R-sq. | 0.9528 | 0.9528 | 0.9528 |
| Adj R-sq. | 0.9450 | 0.9450 | 0.9450 |
| SSE | 66.78 | 66.78 | 66.78 |
| Chi-sq. | 2.936 | - | 2.936 |
| ARE | −2.421 | - | - |
| RMSE | 2.267 | 2.267 | - |
| HYBRID | −2.825 | - | - |
| MPSD | 23.969 | - | - |
| NSD | 218.404 | - | - |
| EABS | 27.528 | - | - |
| FL-PFO | |||
| αFL-PFO | 0.804 | 0.804 | 0.803 |
| k1,FL-PFO | 0.096 | 0.096 | 0.097 |
| qe,FL-PFO | 33.09 | 33.09 | 33.09 |
| R-sq. | 0.9951 | 0.9951 | 0.9951 |
| Adj R-sq. | 0.9943 | 0.9943 | 0.9943 |
| SSE | 6.89 | 6.89 | 6.89 |
| Chi-sq. | 0.368 | - | 0.368 |
| ARE | 0.404 | - | - |
| RMSE | 0.758 | 0.758 | - |
| HYBRID | 0.514 | - | - |
| MPSD | 3.266 | - | - |
| NSD | 70.139 | - | - |
| EABS | 7.592 | - | - |
| FL-PSO | |||
| αFL-PSO | 1.13 | 1.13 | 1.13 |
| k2,FL-PSO | 0.002 | 0.002 | 0.002 |
| qe,FL-PSO | 34.88 | 34.88 | 34.88 |
| R-sq. | 0.9883 | 0.9883 | 0.9882 |
| Adj R-sq. | 0.9863 | 0.9863 | 0.9863 |
| SSE | 16.66 | 16.66 | 16.66 |
| Chi-sq. | 0.810 | - | 0.810 |
| ARE | 0.409 | - | - |
| RMSE | 1.178 | 1.178 | - |
| HYBRID | 0.520 | - | - |
| MPSD | 3.305 | - | - |
| NSD | 109.079 | - | - |
| EABS | 12.553 | - | - |
| Avrami Fractionary-Order | |||
| qe,av | 32.55 | 32.55 | 32.55 |
| kav | 0.378 | 0.378 | 0.236 |
| nav | 0.147 | 0.147 | 0.236 |
| R-sq. | 0.9877 | 0.9877 | 0.9877 |
| Adj R-sq. | 0.9856 | 0.9856 | 0.9856 |
| SSE | 17.47 | 17.47 | 17.47 |
| Chi-sq. | 1.286 | - | 1.286 |
| ARE | 1.937 | - | - |
| RMSE | 1.206 | 1.206 | - |
| HYBRID | 2.466 | - | - |
| MPSD | 15.585 | - | - |
| NSD | 111.693 | - | - |
| EABS | 10.084 | - | - |
| General (rational) Order | |||
| qe,Gen | 33.34 | 33.31 | 33.34 |
| kGen | 0.019 | 0.019 | 0.019 |
| nGen | 1.348 | 1.348 | 1.348 |
| R-sq. | 0.9916 | 0.9916 | 0.9916 |
| Adj R-sq. | 0.9902 | 0.9902 | 0.9902 |
| SSE | 11.89 | 11.89 | 11.89 |
| Chi-sq. | 0.736 | - | 0.736 |
| ARE | 0.888 | - | - |
| RMSE | 0.9956 | 0.9956 | - |
| HYBRID | 1.430 | - | - |
| MPSD | 7.175 | - | - |
| NSD | 92.174 | - | - |
| EABS | 9.855 | - | - |
| Kinetic Adsorption Models | N | K | SSE | AIC | AICcorrected |
|---|---|---|---|---|---|
| PFO | 15 | 2 | 17.47 | 6.2865 | 7.2865 |
| PSO | 15 | 2 | 18.53 | 7.1701 | 8.1701 |
| Elovich | 15 | 2 | 77.64 | 28.6605 | 29.6605 |
| Diffusion-Chemisorption | 15 | 2 | 66.78 | 26.4003 | 27.4003 |
| FL-PFO | 15 | 3 | 6.89 | −5.6697 | −3.4879 |
| FL-PSO | 15 | 3 | 16.66 | 7.5744 | 9.7562 |
| Avrami Fractionary-Order | 15 | 3 | 17.47 | 8.2865 | 10.4683 |
| General (rational) Order | 15 | 3 | 11.89 | 2.5147 | 4.6965 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wongphat, A.; Wongcharee, S.; Chaiduangsri, N.; Suwannahong, K.; Kreetachat, T.; Imman, S.; Suriyachai, N.; Hongthong, S.; Phadee, P.; Thanarat, P.; et al. Using Excel Solver’s Parameter Function in Predicting and Interpretation for Kinetic Adsorption Model via Batch Sorption: Selection and Statistical Analysis for Basic Dye Removal onto a Novel Magnetic Nanosorbent. ChemEngineering 2024, 8, 58. https://doi.org/10.3390/chemengineering8030058
Wongphat A, Wongcharee S, Chaiduangsri N, Suwannahong K, Kreetachat T, Imman S, Suriyachai N, Hongthong S, Phadee P, Thanarat P, et al. Using Excel Solver’s Parameter Function in Predicting and Interpretation for Kinetic Adsorption Model via Batch Sorption: Selection and Statistical Analysis for Basic Dye Removal onto a Novel Magnetic Nanosorbent. ChemEngineering. 2024; 8(3):58. https://doi.org/10.3390/chemengineering8030058
Chicago/Turabian StyleWongphat, Akkharaphong, Surachai Wongcharee, Nuttapon Chaiduangsri, Kowit Suwannahong, Torpong Kreetachat, Saksit Imman, Nopparat Suriyachai, Sukanya Hongthong, Panarat Phadee, Preut Thanarat, and et al. 2024. "Using Excel Solver’s Parameter Function in Predicting and Interpretation for Kinetic Adsorption Model via Batch Sorption: Selection and Statistical Analysis for Basic Dye Removal onto a Novel Magnetic Nanosorbent" ChemEngineering 8, no. 3: 58. https://doi.org/10.3390/chemengineering8030058
APA StyleWongphat, A., Wongcharee, S., Chaiduangsri, N., Suwannahong, K., Kreetachat, T., Imman, S., Suriyachai, N., Hongthong, S., Phadee, P., Thanarat, P., & Rioyo, J. (2024). Using Excel Solver’s Parameter Function in Predicting and Interpretation for Kinetic Adsorption Model via Batch Sorption: Selection and Statistical Analysis for Basic Dye Removal onto a Novel Magnetic Nanosorbent. ChemEngineering, 8(3), 58. https://doi.org/10.3390/chemengineering8030058







