Abstract
We present a mesoscale model and the simulation results of a system composed of polyacrylonitrile (PAN), carbon nanotubes (CNTs), and a mixed solvent of dimethylsulfoxide (DMSO) and water. The model describes a fragment of a nascent PAN/CNT composite fiber during coagulation. This process represents one of the stages in the production of PAN composite fibers, which are considered as precursors for carbon fibers with improved properties. All calculations are based on dynamic density functional theory. The results obtained show that the greatest structural heterogeneity of the system is observed when water dominates in the composition of the mixed solvent, which is identified with the conditions of a non-solvent coagulation bath. The model also predicts that the introduction of CNTs can lead to an increase in structural heterogeneity in the polymer matrix with increasing water content in the system. In addition, it is shown that the presence of a surface modifier on the CNT surface, which increases the affinity of the filler to the polymer, can sufficiently reduce the inhomogeneity of the nascent fiber structure.
1. Introduction
Carbon fibers (CFs) are high-tech nanomaterials that combine many different properties, such as high Young’s modulus (up to 960 GPa), low density (1.75–2.18 g/cm3), thermal conductivity, high thermal stability, electrical conductivity, chemical resistance, environmental friendliness, and biocompatibility [1,2,3,4]. As a consequence, they are widely used as reinforcing components in composite materials for aerospace, machinery, shipbuilding, nuclear and wind energy, medicine, sports equipment, and many other applications [2,3,4,5,6].
CFs typically consist of turbostratic carbon planes with a spacing of ≈0.34 nm (larger than the ideal spacing of 0.335 nm between graphite planes) and have a core–shell structure [2]. It is believed that high-modulus carbon fibers should have small interlayer spacing, low defect density, and a high degree of crystallinity, with crystallites having a preferred orientation parallel to the fiber axis [2]. Although cellulose was the first precursor used for carbon fiber, it is now primarily made from polyacrylonitrile (PAN)-based precursors, which occupy ~90% of the CF market [3,7,8]. This is because PAN has a high carbon yield value (50–60%), good mechanical properties, and high temperature resistance [2,6,9]. One of the key properties of PAN is its ability to undergo cyclization reactions at high temperatures [2,8,9,10,11]. These reactions lead to the formation of disordered, layered, polyaromatic, graphene-like structures, which are believed to form CFs [12].
The mechanical properties of PAN-based carbon fibers are still well below their theoretical limit (less than 10% of the carbon–carbon bond strength of 100–150 GPa [3]), which is mainly explained by the presence of a large number of different defects in the polymer matrix. To reduce them, it is necessary to consider the influence of many factors, such as the composition of PAN fibers, the conditions of their formation and various post-treatments [6,13], etc.
The preferred way to produce PAN fibers is dry-jet-wet spinning technology [2,8]. In this method, the spinning solution (a solution of the polymer in a “good” solvent with a concentration of 10–30 wt% [7,13]) is pressed out of the spinneret holes in the form of thin jets into the air, after which the fiber enters a coagulation (precipitation) bath filled with a non-solvent for PAN. The primary structure of PAN fibers is formed in the process of diffusion exchange between the dope jet and the coagulation bath [14]. As-spun fibers typically have a fibrillar network structure (gel-like) with numerous pores, capillaries, and voids [15,16,17]. These structural inhomogeneities can significantly affect the properties of the fiber in subsequent processing steps.
To increase the strength of PAN fibers, various fillers are embedded in the spinning solution. Carbon nanotubes (CNTs) and graphene are considered the most suitable fillers for PAN [6,18,19,20,21,22,23,24,25,26,27,28,29]. The PAN/CNT composite fibers exhibit improved mechanical (Young’s modulus and tensile strength), thermal dimensional stability, and electrical conductivity properties [6,8,9,18,23,27,28]. While traditional fillers help to improve some properties, such as modulus and stiffness at the expense of tensile strength, it is sufficient to introduce only ≤20 wt% of CNTs to improve all mechanical properties, including an increase of ~26–75% in tensile strength [6,9,29] and 16–144% in Young’s modulus [6,9,29]. This ability to tune their properties makes them good candidates as precursors for the production of next-generation carbon fibers [27], electrochemical supercapacitor electrodes [9,29], and smart and functional textiles [28].
The strengthening effect of PAN/CNT fibers is explained by the fact that CNTs, due to their 1D structure and good compatibility with PAN molecules, can act both as a nucleation center during PAN crystallization and as an orientation template for the polymer chains [24]. The orientation of the PAN chains in the composite fiber is generally higher (orientation coefficient ~0.62) than in unfilled PAN samples (orientation coefficient ~0.52). The influence of different types of CNTs has been studied separately [22,27]. It can be concluded that all types of CNTs contribute to the improvement of the properties of the resulting material. The maximum increase in Young’s modulus (by 75%) is observed in composites containing single-walled CNTs (SWCNTs). Composites with MWCNTs show a significant increase in the work of rupture of fibers (by 230% [9]). In addition, according to the data obtained, the size of PAN crystallites in the composite fibers is 35% larger than in the reference PAN fibers, while the overall crystallinity of PAN is slightly lower. Separately, we can mention studies dedicated to the modification of the surface of CNTs with different functional groups [19,29,30,31]. This way, the functionalization makes it possible to obtain a uniform distribution of the filler in the volume of the polymer matrix, which can give structural integrity to the nanocomposites and contribute to the effective redistribution of the load between the matrix and the filler.
Despite the large number of works devoted to PAN, there is currently no rigorous and generally accepted theory relating the properties of fibers with the parameters of their production process [13]. In this case, computer modeling is a powerful method to identify the structure–property relationship at different scale levels of material organization; see, for example, a review [32]. It should be noted that most simulation studies of the fiber nucleation process are based on the solution of diffusion equations, the main parameters of which are usually adjusted on the basis of experimental data [14,33,34,35,36,37,38]. These models have been used to study the main aspects of the kinetics of mass transfer between the nascent fiber and the coagulation bath. At the same time, direct atomistic and coarse-grained simulations have focused on the behavior of a single PAN chain in the solution [39] and on the interaction of PAN with solvents [40] and with SWCNT [41,42,43,44].
Previously [45], we developed a mesoscale model to describe a mixture of polyacrylonitrile with a two-component (mixed) solvent based on dynamic density functional theory (DDFT) [46]. It was used to study structure formation in a mixture of high-concentration polyacrylonitrile with dimethyl sulfoxide (DMSO, the good solvent for PAN) and water (the non-solvent for PAN). We have associated the nascent fiber state of PAN with this system. It was shown that the greatest heterogeneity of the PAN structure occurs with high water content in the system. In this case, a large number of high-density areas are formed in the polymer, which we consider to be nuclei of the crystalline phase. Conversely, when a good solvent dominates over the non-solvent in the system, a homogeneous spatial structure of the polymer matrix is formed.
In this work, we modified our DDFT model [45] to take into account the effect of the carbon filler, namely carbon nanotubes, and studied the influence of their volume fraction on the formation of the structure of the PAN nascent fiber. The influence of CNT surface modification on the system structure is also analyzed. As before, we associate the quality of the mixed solvent in the system with the influence of the coagulation bath composition. Thus, our study aims to investigate the effect of the mixed solvent and the volume fraction of the filler on the structure of the PAN matrix.
The rest of the paper is organized as follows. Section 2 describes the model of the system under study and its parameterization and provides the most important information about the modeling method used. Section 3 presents the methodology used to perform all calculations and characterize the system. The results obtained are further described in Section 4 and discussed in Section 5. Section 6 gives a brief overview of the results and a summary of the work performed. The Supplementary Materials file contains the additional data used to build our model.
2. Model and Simulation Method
The molecular weights of PAN used in the production of precursor fibers are 30,000−250,000 Da (≈570−4700 monomers), and the diameter of multiwalled carbon nanotubes can reach 5−30 nm, with a length of more than 1 μm. The use of such molecular objects is far beyond the capabilities of all atom computer simulations. Based on our previous experience in studying molecular systems [47,48,49], we chose a mesoscale modeling methodology based on the use of dynamic density functional theory as a working tool. This method allows us to model melts and solutions of macromolecules on relatively large scales of ~200 nm and time intervals of ~1 μs.
2.1. Highlights of the DDFT
Let us dwell on some details of DDFT to make clear to the reader the parameters of our model and the peculiarities of the presentation of the results. For more details and examples of the use of the engaged method, see articles [46,47,48,49,50,51]. A distinguishing feature of DDFT from other mesoscale modeling methods is the use of scalar density fields ρα(r,t) to describe the spatial distribution of molecular subsystems with index α in the volume of the simulation box LxLyLz = V (Li is the edge size). Since periodic boundary conditions are imposed on its faces, it is possible to indirectly take into account the continuous nature of the system under study. The selection of subsystems (coarsening) is usually done by analyzing and dividing the initial chemical structures into individual subunits based on their role (sometimes hypothetical) in the formation of supramolecular structures during the evolution of the system under consideration. For convenience, they are represented as structureless coarse particles (further referred to as particles) of the same diameter σ, which determines the characteristic scale length of the model. This way, density fields can be assigned to single molecules and their fragments, as well as to sets of molecules of low molecular weight components.
The Langevin diffusion equations are used to describe the evolution of the system under study [46,47,50]:
where F[ρ,ω] is the free energy functional, D is the average particle diffusion coefficient, and ηα(r,t) is the term describing stochastic noise with a distribution that obeys the fluctuation dissipation theorem [52]. The factor δF[ρ,ω]/δρα(r,t), the functional derivative, gives the partial chemical potential μα(r) of the subsystem α at the point determined by the end of the radius vector r. Thus, the evolution of the density field ρα(r,t) is governed by the gradient of the chemical potential arising due to the peculiarities of the interaction of different molecular subsystems and thermal noise.
∂ρα(r,t)/∂t = D/kBT·∑β ∫Vδαβδ(r − r′)∇rρβ(r)∇r′ δF[ρ,ω]/δρβ(r′,t)dr′ + ηα(r,t),
Since the system described by Equation (1) is non-equilibrium, additional external fields ωα(r) are introduced, acting on each component and chosen so that at any moment, t, the density distribution ρα(r,t) corresponds to an equilibrium state. The relation between ρα(r,t) and ωα(r) (at a fixed time) is determined by the following equation:
where nM is the number of molecules in the system, kB is the Boltzmann constant, T is the absolute temperature (since this method uses dimensionless units, kBT = 1), and ZM is the intramolecular statistical integral. The analytical form of the ZM depends on the model representation of the polymer chain. As before, we used the ZM expression from [50,51].
ρα[ω](r) = −nMkBT·∂lnZM[ω]/∂ωα(r),
To obtain the free energy of the system F[ρ,ω], we used the representation given in Ref. [47]:
where <ρα> is the average density of the α component and κT is the compressibility parameter (κT = 10 kBT) [46]. Equation (3) was written under the approximation that all molecules have a Gaussian coil conformation. The force constants εαβ determine the interaction between the subsystems of the model. They are related to the Flory–Huggins parameters χαβ [53,54] by the following equations [54,55]:
F[ρ,ω] = −kBT·ln∏MZMnM[ω]/∏MnM! − ∑α∫ωα(r)ρα(r)dr + ½∑αβ∫∫εαβ(3/2πa2)3/2exp(−3(r − r′)2/2πa2)ρα(r)ρβ(r′)drdr′ + ½ κTν2∫(∑αρα(r) − ∑α <ρα>)2dr,
χαβ = (εαβ + εβα − εαα − εββ)/2νkBT.
The Flory–Huggins parameters provide a relationship between the chemical properties of the molecular subsystems of the model and the interaction energy of the corresponding coarse particles. The method for their estimation is given below in Section 2.4.
The representation of the modeled system as a set of interacting structureless particles of equal volume in combination with the Flory–Huggins model is a convenient technique to obtain an analytical representation of the free energy functional of the system. The implementation of the computational scheme is described in detail in our publications [47,49].
2.2. Model Description
As in Ref. [45], we selected DMSO as the solvent for PAN and water as the non-solvent. We assume that when a jet of spinning solution (usually, its composition includes 20 vol% of PAN and 80 vol% of the solvent [1,25,56,57,58]) comes into contact with the coagulation bath (containing a mixture of solvent and non-solvent in different ratios), diffusion exchange occurs between the jet of spinning solution and the contents of the bath. During this process, two countercurrent flows occur. Because DMSO and water mix well at different ratios, the excess solvent diffuses out of the jet and is replaced by the non-solvent. As the amount of water increases, PAN, being insoluble in water, first becomes a viscous, easily deformable, filamentous structure. When the water content reaches a threshold, the polymer coagulates to form a separate solid phase. This greatly slows down the mass transfer and creates conditions for a quasi-equilibrium state of a mixture of the solid phase of the polymer with a certain amount of residual solvent, consisting of solvent and non-solvent [14,34,36,59,60,61]. According to the literature, an as-spun fiber, comprising coagulated polymer with the mixed combined solvent, consists of a dense shell (where the non-solvent dominates) and a soft core (where the good solvent is prevalent). The final microstructure of the system depends on the residence time in the coagulation bath, the chemical composition of the spinning solution, the contents of the bath, and its temperature.
Because the diameter of the PAN nascent fibers (~60 μm) and the time of their formation (several seconds) exceeded the spatial and temporal scales available in DDFT, we considered the coagulation as a quasi-equilibrium process taking place inside the simulation cell with a fixed composition. As in Ref. [45], we assumed that the simulation cell could be located at different distances from the fiber surface (see Figure 1). Thus, large values of the volume fraction of solvent in the cell correspond to areas of the fiber closer to its center. The simulation cell was also interpreted differently, as a part of the fiber located at a fixed distance from the surface. In this case, the composition of the system was determined by the time elapsed relative to the onset of mass transfer in the coagulation bath. Thus, by changing the composition of the system, we can indirectly study the state of a given fiber fragment (I) at different times during the coagulation process and (II) at different distances from the surface at the moment the filament leaves the coagulation bath (see Figure 1).
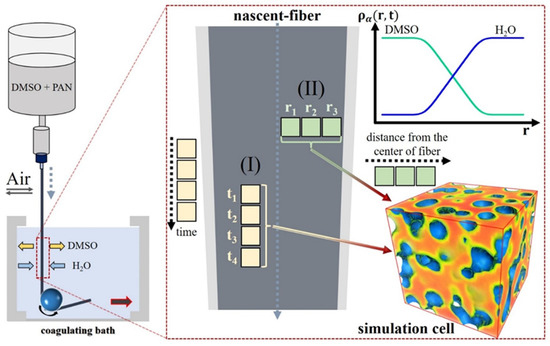
Figure 1.
Sketch of the dry-jet-wet spinning process and the interpretation of the internal states in the simulation cell. It can be assumed that fragments of a nascent fiber are located at different distances from the surface. Thus, the farther the simulation cell is from the surface, the greater the volume fraction of dimethyl sulfoxide (DMSO) it contains. As an alternative, it can be assumed that the simulation cell is located near the fiber surface. Therefore, the change in the DMSO/water ratio can be considered as (I) a quasi-stationary state of the system at different stages of the coagulation process or (II) the effect of the composition of the coagulation bath on the fiber structure at a fixed distance from the center. The cubic box shows an example of the polymer density distribution obtained in the simulations (blue color corresponds to the lowest density, dark red to the highest density).
The main parameters of our model were the volume fraction of the residual solvent, the solvent quality (DMSO/water ratio), and the filler content. To reduce the number of parameters, the temperature was fixed. As the output data of the DDFT model, we calculatedthe density distribution of the main components of the model, which gave us information about the structure of the system, namely the nature of the distribution of the system components, porosity, size of crystalline nuclei, etc.
When mapping real molecular structures onto the DDFT model representation, we used the same coarsening principles as in Ref. [45]. The approach of coarsening polymer chains and small molecules has already been used in our previous studies to investigate the phase separation of molecular systems [47,48,49]. It was assumed that all molecular components consist of identical spherical particles. The chosen scheme for mapping the atomistic structures of PAN, MWCNT, DMSO, and water to the coarse-grained representation is shown schematically in Figure 2. P-type particles correspond to a statistical segment of the polymer chain, and D- and W-type particles correspond to DMSO and water molecules, respectively. In addition, we have introduced in our model C-type particles associated with a carbon nanotube fragment. The particle contents were determined by the Cα parameters, which define the volume fractions of each component.
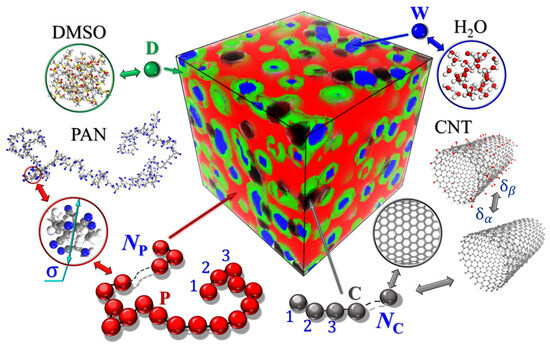
Figure 2.
The principle of mapping the atomistic structure of PAN, DMSO, and water to coarse-grained representations. Particles of type P correspond to a segment of the PAN chain containing the comonomers acrylonitrile and itaconic acid (not explicitly shown), D—DMSO molecules, W—water, and C—a piece of MWCNT. Colors of atoms in atomistic models: carbon—gray; oxygen—red; sulfur—yellow; nitrogen—blue; hydrogen—white. The colors of the coarse-grained particles also correspond to the colors of the density fields ρα in other figures. The parameters NP and NC denote the number of coarse-grained particles in the polymer chain and CNT models, respectively.
2.3. Model Characteristic Scale
As in Ref. [45], we used the polymer chain with a length of NP = 34 coarse-grained particles. The length of the model chain was chosen based on the following considerations. In the DDFT model, real polymer chains are mapped to the equivalent of the freely jointed chains. According to Refs. [62,63], the length of the equivalent chain N is determined by the degree of polymerization and a characteristic ratio C∞ of the polymer molecules (a measure of the stiffness of the polymer chain):
where MP is the molecular weight of the real chain, and Mmon is the molecular weight of the monomer. Thus, assuming an average molecular weight of PAN of ~103,000 Da, and using the average experimental value of 10.1−18.5 [64] for C∞, we obtained the length of an equivalent chain of 136 coarse-grained particles. Since such chains require the use of large simulation cells, we reduced the length of the model chain to 34 particles and rescaled the Flory–Huggins parameters to decrease the computational cost [62]. Thus, in our model, the value of the characteristic scale length σ was related to the degree of coarsening in the polymer chain.
NP = Mp/(MmonC∞),
In addition to the range of C∞ values mentioned above, lower values of 6.2 [65] and 6.49 [66] can be found in the literature. In these studies, the characteristic ratio was calculated for many polymers, including PAN, using the group contribution and all-atom molecular dynamics simulation methods with subsequent comparison with experiment. At the same time, the theoretical estimate of C∞ using the Bicerano method gave us 7.33, which was used in Ref. [67] to model a mixture of PAN with polyglycolide. Since itaconic acid [1,10] is introduced into PAN chains as a comonomer (in particular, to reduce the rigidity of the polymer chains), when estimating σ, we chose the smallest of the range of values found for C∞ = 6.2–10.1. In this case, the characteristic length scale of our model is about 2 nm. The following remark should be made here. The choice of the length scale of molecular objects in any coarse-grained model is usually illustrative for an approximate recalculation of the size of the structures observed in the simulation cell, measured in dimensionless units σ. Therefore, this choice does not affect the calculation results.
In turn, 30 coarse-grained D-type particles were used to build carbon nanotube models. The chosen value of the scale unit allowed us to interpret the model CNTs as multiwalled CNTs with a diameter of 2 nm.
2.4. Interaction Parameters
The intermolecular interaction force constants εαβ (α, β = P, C, D, and W) in Equations (3) and (4) were calculated based on the Hildebrand solubility parameters δα [62], which are related to the Flory–Huggins interaction parameters χαβ by the following expression [51,54,63,68,69]:
where R is the universal gas constant, and υ is the average molecular volume of the original molecular structures associated with the major subsystems of the model. The values of δα and υ can be measured experimentally, obtained from atomistic molecular dynamics simulations [47,68,70], as well as using the Bicerano [62] and Askadskii [71] regression models.
χαβ = υ (δα − δβ)2/RT,
When estimating χαβ by Equation (6), we used υ = 47.8 cm3/mol obtained by averaging the molecular volumes of PAN, DMSO, and water calculated by the Askadskii method [71]. The Hildebrand solubility parameters δα, according to literature data, are in the following value ranges: 25.3−27.43 (J/cm3)1/2 for PAN [68,72,73,74], 22.14−29.0 (J/cm3)1/2 for DMSO [68,70,73,74,75,76], 47.5−48.0 (J/cm3)1/2 for water [51,68,75,77], and 20.35−20.79 (J/cm3)1/2 for CNTs [78,79]. Their averaging gave: δP = 26.6 (J/cm3)1/2 for PAN, δD = 26.1 (J/cm3)1/2 for DMSO, δW = 47.8 (J/cm3)1/2 for water, and δC = 20.6 (J/cm3)1/2 for CNTs. The proximity of δP and δD means that DMSO is a good solvent for PAN, which is a well-known fact [73,76]. The difference between δP and δC is also small, indicating good miscibility of PAN with CNTs, which is also in good agreement with literature data [20,21,22,24,26,28].
The PAN solubility parameter was corrected based on the following considerations. As mentioned above, to obtain carbon fibers, itaconic acid (IA) comonomers are introduced into the PAN from 2 wt% to 15 wt% [1,2,10] to weaken the intermolecular interactions and reduce the viscosity of the spinning solution (PAN contains highly polar nitrile groups, which effectively makes the polymer chain rigid). In addition, IA affects the cyclization process of PAN, lowering the stabilization temperature, reducing the rate of heat release, and accelerating the stabilization reactions [3,7]. The presence of IA can be accounted for by correcting the solubility parameter of PAN using a simple additive equation [77]:
where φ is the comonomer fraction, and δIA is the solubility parameter of IA. To evaluate δP,corr, we assumed that φ = 0.05 (≈5 wt%) and δIA = 22.6 (J/cm3)1/2 [80], which slightly reduced the initial value of δP to 26.4 (J/cm3)1/2.
δP,corr = (1 − φ) δP + φ·δIA,
Thus, using Equation (6) for T = 300 K, we obtained the following estimates for the values of the Flory–Huggins interaction parameters: χP,D = 0.0, χP,W = 8.8, χP,C = 0.6, χD,W = 9.0, χD,C = 0.6, and χC,W = 14.2. The zero value of χP,D from the point of view of the Flory– Huggins and Hildebrand solubility theories [53,54,63,68] for polymers indicates that DMSO is a good solvent for PAN, and the large value of χP,W = 8.8 clearly shows that water is a non-solvent for it. Thus, by changing the DMSO/water ratio, it is possible to change the thermodynamic quality of the solvent mixture for polyacrylonitrile [81]. However, the obtained value χD,W = 9.0 (DMSO/water) contradicts the known experimental fact about the good miscibility of DMSO and water in any ratio. When this value is used in DDFT calculations, DMSO and water are completely separated. The large value of χD,W is explained by the fact that Hildebrand’s theory [72] does not take into account the formation of hydrogen bonds between DMSO and water molecules [82]. Therefore, to account for the good miscibility of DMSO and water, the value of χD,W was adjusted in all further calculations by setting χD,W = 0.
In the introduction, it was noted that the modification of the surface of CNTs can significantly affect the nature of their distribution in the volume of the polymer matrix. In DDFT, the modification of the CNT surface can be taken into account by changing the value of the solubility parameter corresponding to the CNT subsystem δC. Our estimates (made using the MULTICOMP package (ver. 1.1.20) [83] and the PCFF valence force field [84]; see Section S1 in the Supplementary Materials file), showed that there is a certain optimal value of the modifier surface density (<5%) at which the adhesion energy of PAN to the CNT surface increases. Thus, reducing the difference (δP − δC) reduces the value of the Flory–Huggins parameter χPC, which improves the miscibility of CNTs with a polymer matrix and makes it possible to account for the modifier on their surface.
3. Calculation and System Characterization Methodology
According to the literature, pores in nascent fibers that appear during coagulation play the role of defects that reduce the strength properties of carbon fibers [59,85,86,87]. Our previous results [45] indicated that a homogeneous structure of PAN nascent fibers can be formed as a result of slowing down the coagulation by increasing the amount of DMSO in the coagulation bath. In this work, our goal was to determine what additional effect the filler in the form of carbon nanotubes can have on the structure of PAN in the presence and absence of surface modification.
All calculations were performed at a fixed temperature of 300 K. As in our previous study [45], we assumed that in the late stages of coagulation, the nascent fiber consists of 80 vol% PAN + CNTs and 20 vol% mixed solvent DMSO + water, since the non-solvent does not completely replace the solvent [37,58,73,88]. The fraction of water in the mixed solvent composition was determined using the parameter fW = CW/(CW + CD). The amount of CNTs, CC, in the system was varied from 0 to 5 vol% (correspondingly, the amount of PAN, CP, was varied from 80 to 75 vol%), and the amount of water, fW, in the mixed solvent was varied from 0 to 1.
Equation (1) was solved on a regular cubic grid with a step of 1σ and a total number of nodes Ntotal equal to 32 × 32 × 32. Note that the polymer chain model used had the following geometric properties: The end-to-end distance was 5.8 σ, and the radius of gyration was 2.4 σ, which was much less than half of the edge length of the simulation cell. Since the characteristic length scale of the model was σ ≈ 2 nm, the constructed model allows us to study the structure formation in a cubic cell with an edge length of ≈64 nm. The integration step of Equation (1) over time, Δt, was chosen equal to 0.5 τ (τ is the time scale). To set the coefficients, D, in the system of Equation (1), we used an averaged value of the diffusion coefficients for DMSO and water equal to 3.3 × 10−11 m2/s [89], which gave a time scale τ ≈ 121 ns.
For the initial states, we used random distributions of density fields ρα(r,0) (α = P, C, D, and W) generated in such a way that each ρα(r,0), on average, fills the volume of the simulation cell uniformly. The total calculation time tmax was controlled by the free energy convergence condition (|F(t2) − F(t1)| < ς, where ς is a small value) (see, e.g., Figure 3). Depending on the parameter set, the value of tmax varies from 150 to 10,000 Δt (here and below, the time is given in the integration steps of the calculation scheme Δt), which can be roughly converted to real time in the range of ≈6 μs to ≈600 μs. It should be noted that in the literature, it is possible to find values of D for water and DMSO in the range of 0.22 × 10−11 m2/s to 15 × 10−11 m2/s [34,37,61,89], which allows us to compare the upper simulation time with a range of 1.3 μs to 9091 μs. For each set of parameters, three statistically independent calculations were performed. The data obtained for each series of calculations are used to average the values analyzed.
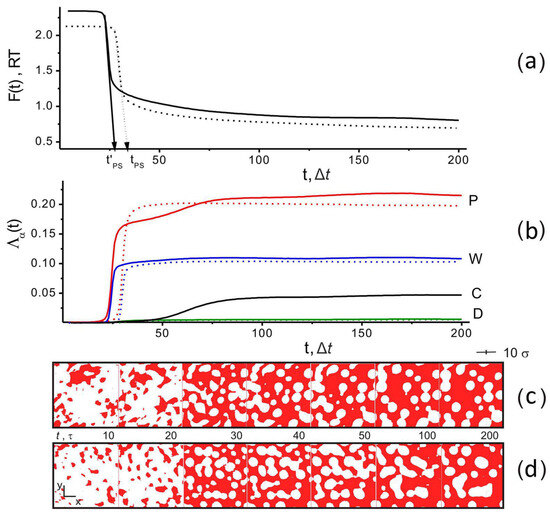
Figure 3.
(a) Free energy density F, (b) order parameters Λα (P—PAN, D—DMSO, W—water, C—CNTs), as a function of time for systems without CNTs (CP = 80 vol%, fW = 0.5, dotted lines), in the presence of CNTs (CP = 75 vol%, CC = 5 vol%, fW = 0.5, solid lines). Instantaneous snapshots show the PAN density field distribution ρP ≥ 0.75 (red color) on the cross-section of the simulation cell: (c) without filler and (d) with filler. The values of the time points, t, when they were obtained are given between snapshots. The completion time of the polymer/water phase separation, tPS, is determined by linear extrapolation of the region of a sharp decrease of F(t) up to the intersection with the time axis (shown by the dotted line), which is schematically shown in part (a) of this figure. T = 300 K.
To control the phase transitions occurring in the PAN/CNT/DMSO/water mixture, the order parameters Λα were calculated. These properties were defined as the volume-averaged difference between the square of the local non-stationary density field ρα(r,t) and the square of the average density ρα of particles of type α, respectively:
Λα(t) = ν/V ∫V[ρα2(r,t) − <ρα>2] dr.
When all values of Λα were close to zero, all components of the system formed a homogeneous mixture. If Λα > 0, the component α tends to form a separate phase. Figure 3a,b show the typical time dependencies of the free energy, F, and order parameters for the two systems: without filler CP = 80 vol%, fW = 0.5 (dotted lines) and with filler CP = 75 vol%, CC = 5 wf%, fW = 0.5 (solid lines). Their shape indicates that the non-solvent induced phase separation. At t ~ 25, it is accompanied by a sharp decrease in the free energy and a rapid increase in the order parameter for water and polymer.
Figure 3c,d also show a visualization of the structural changes in the system at the cross-section of a simulation box with the plane (xOy) in the form of color maps of the PAN density distribution when ρP(r,t) > 0.75 (PAN) at different times in the absence and presence of filler in the system. Intense structural changes occur as the simulation time approaches tPS, which we defined as the time of phase separation (coagulation) of PAN and water; see Figure 3a (and snapshots for t = 20 Δt, 30 Δt in Figure 3c,d). The phase separation time, tPS, was estimated by linear extrapolation of the region of rapid change in the free energy of the system along the time axis (see Figure 3a). As can be seen from the snapshots, regions of low density are formed in the polymer matrix, which are occupied by other components of the system (CNTs and water).
When t > 50 Δt and there is no filler in the system, the values of Λα (α = P, W) quickly reach saturation, and the structure of the system (according to the visualization in Figure 3c) remains practically unchanged. With the introduction of CNTs into the system, the separation of the PAN/water phases is faster due to the CNTs acting as nuclei of the polymer phase. This can be seen in Figure 3a, which shows tPS (no filler) and t’PS (filler present).
If the filler is present in the system, ΛW reaches saturation after the water has formed a separate phase. At the same time, the PAN order parameter, ΛP, continues to increase slowly as the filler tends to form its phase. The latter occurs over a long time, starting from t > 40 Δt to t ≈ 75 Δt. This process is accompanied by a slow increase of ΛC, and up to t > 40 Δt, it is difficult to observe it visually. In the time interval 40 Δt < t < 75 Δt, a feature in the form of a small bend appears in the ΛP(t) behavior. An additional increase in ΛP is accompanied by an increase in the number of high-density areas in the polymer matrix. This is discussed below. The delay in the separation of the PAN/CNT phases is due to the proximity of their solubility parameters δP and δC. As mentioned above, the value of the Flory–Huggins interaction parameter for these subsystems is χP,C = 0.6, which is close to the threshold value of 0.5, at which the system is on the border of phase separation. Therefore, a significant diffusion time is required for the phase separation of PAN and CNT. In the case of DMSO, the value of ΛD (according to Figure 3b) does not exceed 0.01, indicating the absence of order in this subsystem, since DMSO mixes well with PAN (χP,D = 0.0) and water (χW,D = 0.0).
Additionally in Figure 3a,b, in the behavior of F(t) and the order parameter ΛP(t), one can observe the presence of weak long-period oscillations (in the case of ΛW and ΛC, they are of the nature of small perturbations) at large simulation times t > 120 Δt. This behavior is associated with slow relaxation processes as a result of the ongoing redistribution of density fields since PAN, DMSO, and CNT have similar solubility parameters. This is accompanied by slight changes in the structure of the polymer matrix, which can be observed in Figure 3c,d by the change in shape of the regions where ρP(r,t) > 0.75. Although the structure of the system continues to evolve at t > 120 Δt, its main motifs remain stable. This is confirmed by the data in Figure 4, which shows the distribution of a fraction of PAN regions, NP(ρP,t)/Ntotal, with density ρP in a simulation cell at different simulation times. It can be seen from the figure that when t > 100 Δt for ρ < 1.3, the NP(ρP,t)/Ntotal profiles practically do not change. In particular, the position of the maxima at ρP ≈ 1.19 remains unchanged. It can be concluded that in the matrix structure, the number of regions with high-density ρP > 1.3 continues to increase, but their content does not exceed 1%, while the free energy changes by a value <0.1 RT. Thus, although the structure of the system tended to evolve, this did not lead to significant changes in the distribution of ρP(r,t). Therefore, we stopped our simulation when (|F(tmax − 50Δt) − F(tmax)|) < 0.1 RT.
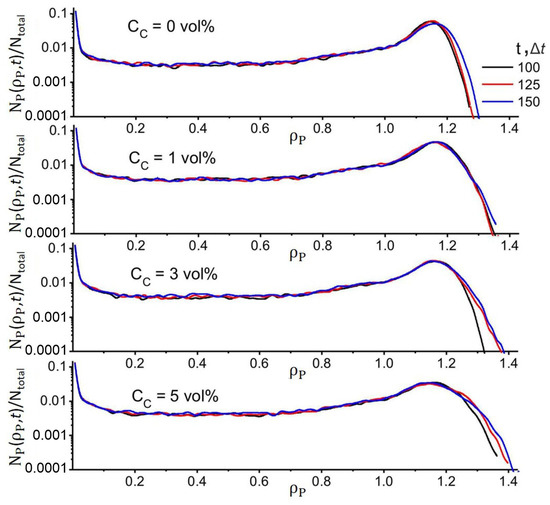
Figure 4.
Distribution profiles of the fraction of PAN domains, NP(ρP,t)/Ntotal, in the simulation cell with density ρP at different simulation times and filler contents. NP(ρP,t) is the number of nodes with density equal to ρP, and Ntotal is the total number of grid nodes in the simulation cell). CP = (80 − CC) vol%; fW = 0.5. Ntotal is the total number of grid points in the modeling cell.
In the final state t = tmax, when fW > 0.3, the PAN matrix looks like a porous structure (like a gel network). An example of such a state for CP = 75 vol%, CC = 5 vol%, fW = 0.5, and t = 200 Δt is shown in Figure 5 (the evolution of this system was shown earlier in Figure 3b,d). In this case, the average pore size is ≈6 ± 1σ. The pores are filled with a mixture of DMSO and water, which is visible in a combined plot of all density fields (Figure 5d). The PAN density field distribution with ρP(r, tmax) > 0.75 shows that high-density areas form an unoriented fibrillary three-dimensional network structure (Figure 5a) whose pores are filled with water (Figure 5b) and interspersed with areas formed by filler (Figure 5c). In this case, DMSO has a uniform distribution in the system volume, see Figure 5b, where the water (blue color) and DMSO (green color) density fields are given. Thus, with the developed model, we could observe structural changes in the PAN/CNT/DMSO/water mixture at different simulation times.
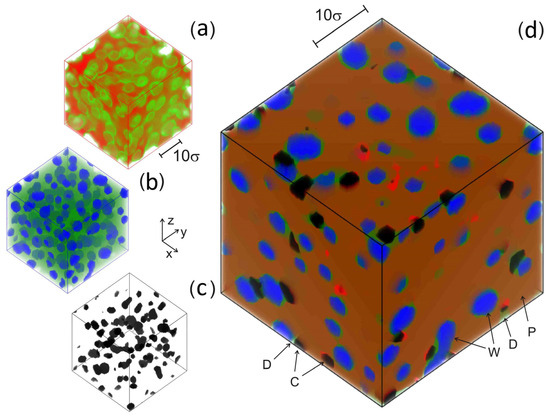
Figure 5.
Density field distribution ρα(r,tmax) for (a) PAN (red, ρP > 0.75; green color shows the surface of pores in a polymer matrix); (b) DMSO (green, ρD > 0.02) and water (blue, ρW > 0.8); (c) CNT (black, ρC > 0.8); and (d) combined plot (PAN—dark and bright red [bright red—regions with high-density ρP > 1.3], DMSO—green, water—blue, CNT—black). CP = 75 vol%, CC = 5 vol%, fW = 0.5, T = 300 K, tmax = 200 Δt. Letters correspond to model component designations shown in Figure 1.
4. Results
4.1. Effect of Filler and Mixed Solvent Quality on PAN Structure
To evaluate the effect of the filler content and mixed solvent quality on the structure of the PAN/DMSO/water/CNT system, a series of calculations were performed with different CNT contents in the system and DMSO/water ratios. The last one was controlled by the fW parameter. Thus, the more water present in the system, the greater the difference between the Hildebrand solubility parameter of the DMSO/water mixture and the solubility parameters of PAN and CNT (see Section S2), making the DMSO/water mixture a non-solvent for the polymer and filler.
First, the polymer/water phase separation time, tPS (which can be considered as the coagulation time), was calculated as a function of the filler volume fraction, CC. The results shown in Figure 6 indicate that the introduction of filler has the greatest effect on the coagulation time at low water content, where tPS decreases significantly with the increase of the filler volume fraction.
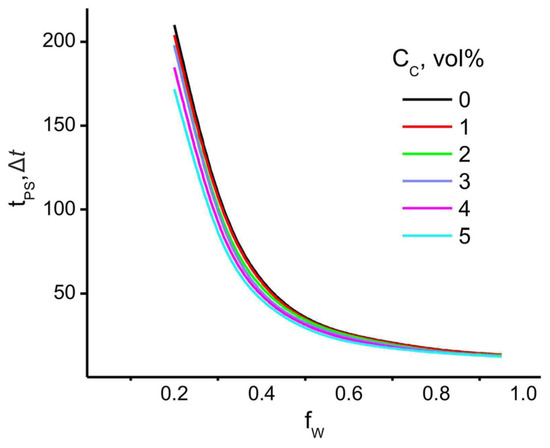
Figure 6.
PAN/water phase separation time as a function of the CNT content and the mixed solvent composition in the system. CP = 80−75 vol%, CC = 0−5 vol%, T = 300 K.
The visualization of the distribution of density fields for PAN + CNT and water (Figure 7) allowed us to get a clear idea of the structural changes occurring in the system. At low water content fW < 0.15, the system remains homogeneous, which is in agreement with our previous results [45]. When 0.15 < fW ≤ 0.2 (Figure 7, region I) and there is no filler, PAN also forms a homogeneous structure, although the water starts to form small spherical domains with an uneven distribution in the volume of the simulation cell. At the same water content (fW = 0.2), the introduction of filler (CC = 3 vol%) first causes the formation of PAN regions with high-density ρP > 1.3, then at CC > 3 vol%, the filler also begins to form high-density areas. We associated the formation of such regions with the formation of crystalline nuclei in the case of PAN and with the formation of aggregates in the case of filler. The region 0.2 < fW < 0.5 (Figure 7, region II) is characterized by a gradual increase in the number of spherical water domains in the system. In this case, a significant number of high-density areas are formed in the volume of the polymer matrix, even in the absence of filler. Their number increases significantly with increasing CC.
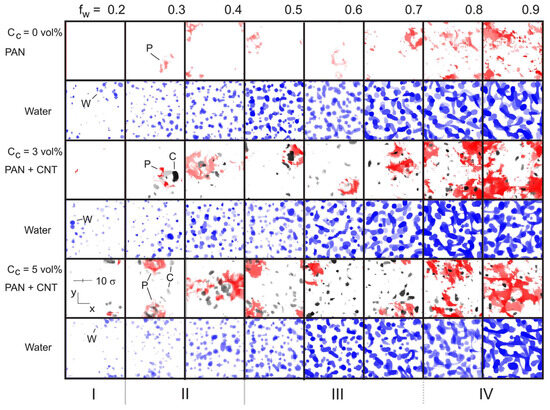
Figure 7.
Visualization of the density field distribution: PAN + CNT (ρP > 1.3, ρC > 0.8) and water (ρW > 0.8) at different values of fW and volume fraction of filler in the system. The following ranges of fW are conventionally denoted by Roman numerals: (I) PAN forms a homogeneous structure in the absence of filler, (II) water forms discrete spherical domains, (III) water forms elongated domains, and (IV) water domains form a percolating network of pores. Letters correspond to model component designations shown in Figure 1.
When fW reaches a value of 0.5, the water domains begin to merge and form elongated dumbbell-shaped structures (Figure 7, region III). Finally, when a threshold value is reached (fW ≈ 0.8), the water domains form a 3D network structure that fills the entire volume of the simulation cell (Figure 7, region IV). In the latter case, the strongest perturbation of the polymer structure is observed in the form of the appearance of regions of high density. Thus, an increase in the water content leads to the formation of regions with high water content, which provokes the development of regions of high density in the polymer with uneven distribution in the volume. It can also be concluded that, as in our previous study [45], the strongest perturbation of the polymer density distribution is observed above the percolation threshold of the water domains. At the same time, the introduction of filler leads to a significant increase in the number of inhomogeneities in the system; see Figure 7.
Quantitative information about the influence of water and filler on the formation of regions with different densities is given in Figure 8, where the distributions of the values of the fraction of domains Nα(ρ,tmax)/Ntotal (α = P, C, and W) with density ρ are plotted. In the case of α = P, the most significant fluctuations in the maximum density values become most pronounced with increasing filler volume fraction at average values of fW (see Figure 8a). It can be seen from the figure that at large fW, the maximum value of the PAN density increases quite smoothly. Figure 8b also shows that increasing the volume fraction of the filler leads to a gradual widening of the range of the density values of the corresponding domains. This can be interpreted as an indication of possible nanotube aggregation during CC growth. According to Figure 8c, the filler has virtually no effect on the nature of the water distribution in the cell volume. The most noticeable effect appears only at high fW values. It is also clear from Figure 8 that the NP(ρ)/Ntotal distribution for PAN has a clear maximum at ρP ≈ 1.03. Its position is weakly dependent on the filler content and shifts to higher values with increasing fW.
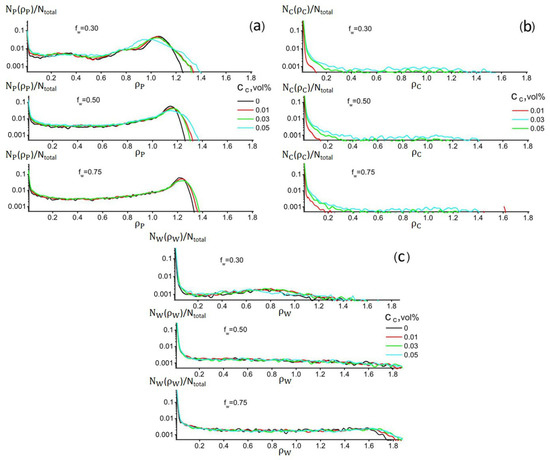
Figure 8.
Distribution profiles of the fraction of domains, Nα(ρ)/Ntotal ≡ Nα(ρ,tmax)/Ntotal (α = P, C, W), in the simulation cell with density ρ at different filler contents and fw for: (a) PAN, (b) CNT, and (c) water. CP = (80 − CC) vol%. Ntotal is the total number of grid points in the simulation cell.
As mentioned above, solvent-filled pores in the polymer matrix are considered defects because they reduce the integrity of the fiber structure. Since the presence of voids prevents the uniform distribution of the applied external load, they can contribute to the destruction of the fiber at high degrees of deformation during the drawing stages of precursor fibers [59,85,86,87]. At the same time, the regions with the highest density of PAN can act as nuclei for the growth of the crystalline phase in the subsequent stages of the fiber drawing and heat treatment process. Since the strengthening of carbon fibers is often associated with an increase in the crystallinity of PAN, we paid special attention to studying the influence of fW and CC on the formation of crystalline nuclei in the system under study. As before [45], we considered all areas in the simulation cell where the PAN density ρP > 1.3 as nuclei of the crystalline phase. As a generalized geometric property of such regions, we evaluated their radius, which was calculated as (3 V/4π)1/3, where V is the average volume of domains with density ρP > 1.3. This feature is conditional, since according to Figure 7, the high-density areas have a very irregular shape; it nevertheless allows us to follow the main trends of changes in the structure of the system with changes in CC and fW.
Figure 9 shows the distribution of the average number of high-density areas, <NP>, which we associated with the PAN crystalline phase, and their conditional radius, <RP>. The maximum average value <RP> = 6.5σ ± 1σ, which, considering the characteristic scale σ ≈ 2 nm, is in good agreement with the values of experimentally recorded crystalline regions in PAN 7−10 nm [90,91]. Figure 9a shows that the dependence <NP>(fW,CC) has a small maximum in the region of fW ≈ 0.3. Its amplitude increases with increasing filler volume fraction. At this water content, the radius of high-density areas has a large scatter of values, which led to a large error in the results. At the same time, in agreement with our previous results [45], a rapid increase in <RP> occurs at fW values corresponding to the final state, in which an interconnected network of water-filled pores is formed in the cell volume; see Figure 7 (region IV). The formation of such a morphology introduces a strong perturbation in the distribution of the PAN density field, which causes the simultaneous growth of <NP> and <RP>.
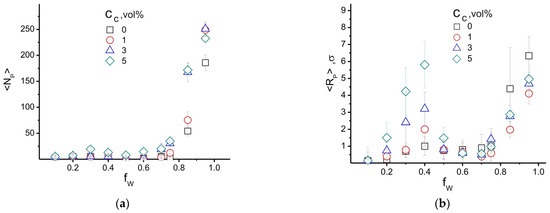
Figure 9.
The average number of (a) high-density (ρP > 1.3) areas in the PAN matrix <NP> and (b) their average radius <RP> as a function of the water content fW and the volume fraction of filler in the system. CP = 80−75 vol%, CC = 0−5 vol%, fW = 0−1, T = 300 K.
The reason for the increase in the size of high-density PAN areas in the range of 0.2 < fW < 0.5 can be explained by the behavior of the average number of CNT high-density areas, <NC>, and their average radius, <RC>, shown in Figure 10. According to this figure, the deterioration of the quality of the mixed solvent (increase in fW) caused by the difference in the Hildebrand solubility parameters (δC and δW) results in a rapid increase in the number of high-density areas formed by the filler (see Figure 7, region II). These areas can be interpreted as CNT aggregates. In this case, the value of fW ≈ 0.3–0.4, where <RC> (according to Figure 10b) has a maximum and the largest spread of values corresponds to a similar water content in the system, where the largest spread in the size of high-density areas is observed for PAN.
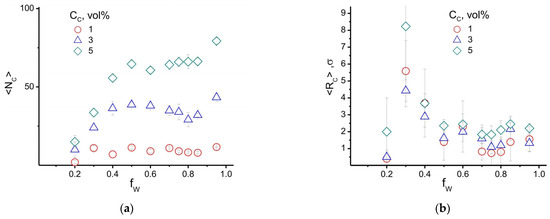
Figure 10.
The average number of (a) ρC > 0.8 areas formed by the filler and (b) their average radius <RC> as a function of the water content fW and the volume fraction of the filler in the system. CP = 80−75 vol%, CC = 0−5 vol%, fW = 0−1, T = 300 K.
The instability of the behavior of <RP> and <RC> at fW ≈ 0.3–0.4 can be explained by the fact that in this case, the largest number of spherical water domains are formed in the cell volume. With a further increase in the amount of water fW from 0.4 to 0.75 (as can be seen in Figure 7), the domains formed by water gradually expand and begin to play the role of obstacles that interfere with the diffusion and merging of high-density areas in the PAN and CNT subsystems. This leads to a stabilization of the <NC> and <RC> values. This conclusion is partially confirmed by the decrease of <RP> with increasing CC at fW > 0.75. At the same water content, the <NP> value continues to increase with increasing CC. Thus, we can conclude that the average size and number of aggregates formed by CNTs are related to the quality of the mixed solvent, which controls the release of CNTs into the separate phase, and the rate of their diffusion, which determines the possibility of the coalescence of CNT aggregates. In turn, the formation of CNT aggregates provokes an increase in the number of high-density areas in the PAN subsystem, which can be associated with an increase in the crystallinity of the polymer matrix.
4.2. Effect of Filler Surface Functionalization on the Structure of the Polymer Matrix
As discussed in Section 2.4, the surface modifier of the CNTs in our model can be accounted for by modifying the Hildebrand solubility parameter δC. Recall that the following values were chosen for the calculations: δP = 26.6 (J/cm3)1/2 for PAN and δC = 20.6 (J/cm3)1/2 for CNTs (see Section 2.4). Thus, an increase in δC reduces the Flory–Huggins parameter χPS, which improves the miscibility of the CNT with the polymer matrix.
To study the effect of the surface functionalization of CNTs, we simulated a system with a fixed composition of CP = 77 vol%, CC = 3 vol%, and fW = 0.8. The water content was chosen based on the consideration that near this value, the heterogeneity of the polymer matrix begins to grow rapidly as the water content in the system increases. Four values of the CNT solubility parameter were used, namely δC = 18, 20, 22, and 24 (J/cm3)1/2. Thus, the first value was chosen lower than the original (assuming poor compatibility of the modifier and PAN), the second one close to the original, and two values close to PAN, reflecting the case of increased adhesion of PAN to the filler surface.
Figure 11 shows the obtained results for the average number of high-density areas and their radii as a function of the δC value. When δC = 20 (J/cm3)1/2, the values of the calculated characteristics are close to the results in Figure 9 and Figure 10. At the same time, decreasing the value to δC = 18 (J/cm3)1/2 leads to a significant increase in the number of areas of high density in PAN and CNT distributions, as well as in their effective radii. Thus, the deterioration of the compatibility of PAN and CNTs leads to a significant increase in the number of inhomogeneities in the polymer matrix. On the other hand, increasing the affinity between the matrix and the filler (namely δC = 22 and 24 [J/cm3]1/2) leads to a simultaneous decrease in the average number of high-density areas of PAN and CNTs, as well as their dimensions (see Figure 11). This is due to the fact that in the case of embedding an unmodified filler, the resulting aggregates provoke the growth of nuclei in the PAN crystalline phase (see Figure 9a). Therefore, by increasing the compatibility of the filler and the polymer, which leads to their better miscibility, it is possible to achieve a uniform distribution of CNTs in the volume of the polymer and to reduce the degree of heterogeneity of the polymer matrix to values without filler. Thus, our model illustrates that by selecting the right type of filler surface modifier, it is possible to significantly influence the properties of the polymer matrix, as well as reduce the filler aggregation.
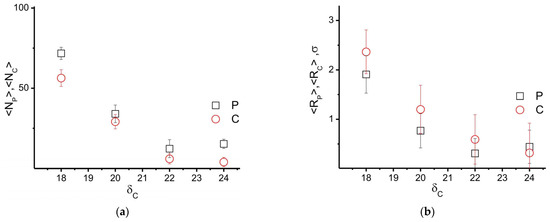
Figure 11.
(a) Average number <N> and (b) average radius <R> of the nuclei of the crystalline phase (ρP > 1.3), and high-density area formed by the filler (ρC > 0.8) as a function of CNT solubility parameter. CP = 77 vol%, CC = 3 vol%, fW = 0.8.
5. Discussion
Since our model is mesoscale, i.e., it takes into account only the general motives of the structure of the main components of the system and the features of their interaction with each other, the results obtained can be interpreted in several ways. Let us look at this in more detail.
One of the possible interpretations of our model could be the following. The position of the simulation cell can be considered as fixed within the fiber volume. For example, its position can be associated with the near-surface layer (see Figure 1). Then, the water fraction in the mixed solvent composition (determined by the fW parameter) can be perceived as determined by the DMSO/water ratio in the coagulation bath composition. Thus, the examples of snapshots of the simulation cell shown in Figure 7 illustrate how different coagulation bath compositions affect the structure of the near-surface layer of the PAN nascent fiber. Looking at Figure 7 vertically, we can conclude that the softer the coagulation bath (DMSO dominates in relation to water), the more homogeneous the structure of the surface layer becomes. At the same time, the formation of a large number of high-density areas (Figure 7, region IV) can be interpreted as the development of a dense layer on the surface of the nascent fibers. The presence of such a layer can significantly slow down the mass transfer between the inner regions of the fiber and the coagulation bath and cause the formation of a core–shell type fiber structure (loose core and dense surface).
Let us consider another way to interpret our results. The horizontal sequences of the system snapshots shown in Figure 7 can be identified with the position of the simulation cell at different distances from the center of the fiber (see Figure 1). Then, the horizontal rows in Figure 7 can be interpreted as a visual representation of how the fiber structure changes from the center to the surface.
Based on the data obtained, we can say that our model clearly shows that the formation of precursor fibers with homogeneous structure is achieved when the coagulation bath contains a high amount of DMSO. This is consistent with the conclusions of experimental studies, which indicate that increasing the solvent content in the coagulation bath reduces the rate of diffusion of the solvent from the fibers and of the non-solvent (water) into the fibers, which slows down the coagulation [13] and prevents the formation of a hard shell (cuticle) on the surface of the fibers of PAN precursors [7]. It should be noted that the presence of such a hard shell leads to a deviation of the fiber cross-section from the round [13]. Thus, the results obtained confirm that one of the possible ways to reduce the porosity of the precursor fibers and obtain a homogeneous structure is to increase the amount of the good solvent in the nascent fiber (soft coagulation bath) [7,10,13,86,92,93,94,95,96,97,98,99,100,101,102]. The model also shows that carbon nanotubes can increase the number of nuclei of crystalline PAN domains. At the same time, an increase in the affinity between PAN and CNTs helps to increase the homogeneity of the system.
When discussing our results, we wrote that the formation of the high-porosity structure at the high non-solvent ratio (Figure 7) is usually considered a defect that weakens the mechanical properties of fibers [7,13]. We believe that there is another way to look at this problem. The high porosity of the structure may be advantageous for applications that require the deposition of a stable layer of colored pigment on the fiber surface, as well as for the production of filters and sorbents for air/water purification [9,103,104]. In addition, based on the chemistry of the thermal stabilization and carbonization process of [10], it can be cautiously assumed that high porosity may be beneficial for better oxygen penetration and removal of off-gassing from the fiber during the final stages of carbon fiber production. In this case, a large number of crystalline regions of PAN can serve as physical cross-links for polymer chains, increasing the stability of the fiber, when the PAN cyclization reaction is not yet complete.
6. Conclusions
The paper presents the DDFT model to study the coagulation of PAN in DMSO spinning solution containing carbon nanotubes. The system under study is a fragment of a PAN/CNT composite fiber. Such fibers are considered as precursors for the production of next-generation carbon fibers due to their improved mechanical properties and smart and functional textiles.
The model allowed us to consider the processes of structure formation of a mixture of PAN, CNTs, DMSO, and water depending on changes in the ratios of all components. We also examined a possible way to take into account the surface modifier on the filler within the framework of DDFT. The obtained results showed that by varying the composition of the coagulation bath, it is possible to control the internal structure of PAN fibers. Our model predicted that when the mixed solvent remaining in the bulk of the fiber during late exposure in the coagulation bath is good for polyacrylonitrile, a uniform spatial fiber structure is formed. This may be a favorable factor for achieving a high degree of orientational order of polymer chains during multistage fiber drawing. On the other hand, the greatest spatial heterogeneity of the as-spun fiber was observed at the high-water content in the coagulation bath. In this case, a large number of regions of high polymer density are formed, which can be considered as nuclei of the crystalline phase. The introduction of carbon nanotubes can also contribute to the development of the heterogeneous fiber structure. At the same time, the use of surface modifiers that increase the affinity between the filler and the polymer matrix significantly contributes to the reduction of the number of aggregates formed by the filler and leads to a more uniform distribution throughout the volume of the material. This can also reduce the crystallinity of the polymer matrix.
Since our model does not operate on specific chemical structures, but on the density distributions of their coarse-grained equivalent representations, its predictive results are also applicable to other composite chemical fibers where the Hildebrand solubility parameters of the polymer/mixed solvent are close to the values chosen in this work. In addition, when this model is combined with continuum methods that predict the composition of the system, for example, based on the solution of diffusion equations, it is possible to visualize the possible structure of the material as a function of changes in the composition of the system in different areas of the fiber at different stages of coagulation. This can be useful for visualizing the kinetics of processes occurring in the fiber during the mass transfer process. Such results can be used to select technological conditions for the formation of chemical fibers with a given structure.
Supplementary Materials
The following supporting information can be downloaded at https://www.mdpi.com/article/10.3390/chemengineering8050097/s1, Section S1: Interaction of polyacrylonitrile oligomer chains with carbon fillers; Figure S1: The adhesion energy of PAN to the surface of three-layer graphene NP as a function of the number of units of the oligomer chain L. The dashed line is an approximation of the results; Figure S2: The adhesion energy of PAN (L = 10) to the graphene NP surface is a function of the number of layers n in the NP. The dashed line is an approximation of the results; Figure S3: The adhesion energy of PAN oligomers with L = 10 to the three-walled CNT as a function of its diameter d. The rightmost points correspond to the adhesion energy of PAN to the surface of three-layer graphene. This system was used as a reference (d→∞). The dashed line is an approximation of the results; Figure S4: The adhesion energy of PAN (L = 10) to the surface of three-layer modified graphene NPs with different surface modifiers (N-(2-aminoethyl)carbamoyl, nitro cyclohexane, benzamide, and dinitrobiphenyl) as a function of their grafting density. The dashed line is an approximation of the results; Section S2: Solubility of PAN in combined DMSO: water solvent; Figure S5: The value of the difference RS − DP,S as a function of water content (fW) in the composition of the DMSO-water combined solvent.
Author Contributions
Conceptualization P.K.; methodology P.K.; software, P.K.; validation, M.M. and P.B.; formal analysis, D.G.; investigation, M.M. and P.B.; writing—original draft preparation, P.K.; writing—review and editing, D.G. and P.K.; visualization, M.M. and P.B.; project administration P.K. All authors have read and agreed to the published version of the manuscript.
Funding
The study was funded by Russian Science Foundation Grant No. 23-23-00065, https://rscf.ru/project/23-23-00065/ (accessed on 30 July 2024).
Data Availability Statement
The original contributions presented in the study are included in the article/Supplementary Materials, further inquiries can be directed to the corresponding author/s.
Acknowledgments
The authors are grateful to V.A. Ivanov and Y.-T. Chiu for the former discussions of the results presented in this paper. The research was carried out using the equipment of the shared research facilities of HPC computing resources at Lomonosov Moscow State University [105], and part of the data processing was performed at the Interlaboratory Computing Center of the Institute of Organoelement Compounds, A. N. Nesmeyanov RAS, supported by the Ministry of Science and Higher Education of the Russian Federation.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Chung, D.D.L. Carbon Fiber Composites; Butterworth-Heinemann: Newton, MA, USA, 1994. [Google Scholar]
- MInus, M.; Kumar, S. The Processing, Properties, and Structure of Carbon Fibers. JOM 2005, 57, 52–58. [Google Scholar] [CrossRef]
- Liu, Y.; Kumar, S. Recent Progress in Fabrication, Structure, and Properties of Carbon Fibers. Polym. Rev. 2012, 52, 234–258. [Google Scholar] [CrossRef]
- Ogale, A.A.; Zhang, M.; Jin, J. Recent Advances in Carbon Fibers Derived from Biobased Precursors. J. Appl. Polym. Sci. 2016, 133, 1–15. [Google Scholar] [CrossRef]
- Liu, H.C.; Chien, A.-T.; Newcomb, B.A.; Liu, Y.; Kumar, S. Processing, Structure, and Properties of Lignin- and CNT-Incorporated Polyacrylonitrile-Based Carbon Fibers. ACS Sustain. Chem. Eng. 2015, 3, 1943–1954. [Google Scholar] [CrossRef]
- Ahn, H.; Yeo, S.Y.; Lee, B.-S. Designing Materials and Processes for Strong Polyacrylonitrile Precursor Fibers. Polymers 2021, 13, 2863. [Google Scholar] [CrossRef]
- Frank, E.; Hermanutz, F.; Buchmeiser, M.R. Carbon Fibers: Precursors, Manufacturing, and Properties. Macromol. Mater. Eng. 2012, 297, 493–501. [Google Scholar] [CrossRef]
- Newcomb, B.A. Processing, Structure, and Properties of Carbon Fibers. Compos. Part A Appl. Sci. Manuf. 2016, 91, 262–282. [Google Scholar] [CrossRef]
- Nataraj, S.K.; Yang, K.S.; Aminabhavi, T.M. Polyacrylonitrile-Based nanofibers—A State-of-the-Art Review. Prog. Polym. Sci. 2012, 37, 487–513. [Google Scholar] [CrossRef]
- Gupta, A.K.; Paliwal, D.K.; Bajaj, P. Acrylic Precursors for Carbon Fibers. Polym. Rev. 1991, 31, 1–89. [Google Scholar] [CrossRef]
- Rahaman, M.S.A.; Ismail, A.F.; Mustafa, A. A Review of Heat Treatment on Polyacrylonitrile Fiber. Polym. Degrad. Stab. 2007, 92, 1421–1432. [Google Scholar] [CrossRef]
- Hoffman, W.P.; Hurley, W.C.; Liu, P.M.; Owens, T.W. The Surface Topography of Non-Shear Treated Pitch and PAN Carbon Fibers as Viewed by the STM. J. Mater. Res. 1991, 6, 1685–1694. [Google Scholar] [CrossRef]
- Frank, E.; Steudle, L.M.; Ingildeev, D.; Spörl, J.M.; Buchmeiser, M.R. Carbon Fibers: Precursor Systems, Processing, Structure, and Properties. Angew. Chem. Int. Ed. Engl. 2014, 53, 5262–5298. [Google Scholar] [CrossRef] [PubMed]
- Paul, D.R. Diffusion during the Coagulation Step of Wet-Spinning. J. Appl. Polym. Sci. 1968, 12, 383–402. [Google Scholar] [CrossRef]
- Takahashi, M.; Watanabe, M. Studies on Acrylic Fiber. Sen Gakkaishi 1959, 15, 951–959. [Google Scholar] [CrossRef][Green Version]
- Craig, J.P.; Knudsen, J.P.; Holland, V.F. Characterization of Acrylic Fiber Structure. Text. Res. J. 1962, 32, 435–448. [Google Scholar] [CrossRef]
- Bell, J.P.; Dumbleton, J.H. Changes in the Structure of Wet-Spun Acrylic Fibers during Processing. Text. Res. J. 1971, 41, 196–203. [Google Scholar] [CrossRef]
- Wang, W.; Murthy, N.S.; Chae, H.G.; Kumar, S. Structural Changes during Deformation in Carbon Nanotube-Reinforced Polyacrylonitrile Fibers. Polymer 2008, 49, 2133–2145. [Google Scholar] [CrossRef]
- Sreekumar, T.V.; Liu, T.; Min, B.G.; Guo, H.; Kumar, S.; Hauge, R.H.; Smalley, R.E. Polyacrylonitrile Single-walled Carbon Nanotube Composite Fibers. Adv. Mater. 2004, 16, 58–61. [Google Scholar] [CrossRef]
- Koganemaru, A.; Bin, Y.; Agari, Y.; Matsuo, M. Composites of Polyacrylonitrile and Multiwalled Carbon Nanotubes Prepared by Gelation/crystallization from Solution. Adv. Funct. Mater. 2004, 14, 842–850. [Google Scholar] [CrossRef]
- Ye, H.; Lam, H.; Titchenal, N.; Gogotsi, Y.; Ko, F. Reinforcement and Rupture Behavior of Carbon Nanotubes–polymer Nanofibers. Appl. Phys. Lett. 2004, 85, 1775–1777. [Google Scholar] [CrossRef]
- Chae, H.G.; Sreekumar, T.V.; Uchida, T.; Kumar, S. A Comparison of Reinforcement Efficiency of Various Types of Carbon Nanotubes in Polyacrylonitrile Fiber. Polymer 2005, 46, 10925–10935. [Google Scholar] [CrossRef]
- Guo, H.; Sreekumar, T.V.; Liu, T.; Minus, M.; Kumar, S. Structure and Properties of Polyacrylonitrile/Single Wall Carbon Nanotube Composite Films. Polymer 2005, 46, 3001–3005. [Google Scholar] [CrossRef]
- Chae, H.G.; Minus, M.L.; Kumar, S. Oriented and Exfoliated Single Wall Carbon Nanotubes in Polyacrylonitrile. Polymer 2006, 47, 3494–3504. [Google Scholar] [CrossRef]
- Chae, H.G.; Kumar, S. Materials Science. Making Strong Fibers. Science 2008, 319, 908–909. [Google Scholar] [CrossRef]
- Chae, H.G.; Choi, Y.H.; Minus, M.L.; Kumar, S. Carbon Nanotube Reinforced Small Diameter Polyacrylonitrile Based Carbon Fiber. Compos. Sci. Technol. 2009, 69, 406–413. [Google Scholar] [CrossRef]
- Guo, H.; Minus, M.L.; Jagannathan, S.; Kumar, S. Polyacrylonitrile/Carbon Nanotube Composite Films. ACS Appl. Mater. Interfaces 2010, 2, 1331–1342. [Google Scholar] [CrossRef] [PubMed]
- Jain, R.; Minus, M.L.; Chae, H.G.; Kumar, S. Processing, Structure, and Properties of PAN/MWNT Composite Fibers. Macromol. Mater. Eng. 2010, 295, 742–749. [Google Scholar] [CrossRef]
- Min, B.G.; Sreekumar, T.V.; Uchida, T.; Kumar, S. Oxidative Stabilization of PAN/SWNT Composite Fiber. Carbon N. Y. 2005, 43, 599–604. [Google Scholar] [CrossRef]
- Zhang, Q.; Chang, Z.; Zhu, M.; Mo, X.; Chen, D. Electrospun Carbon Nanotube Composite Nanofibres with Uniaxially Aligned Arrays. Nanotechnology 2007, 18, 115611. [Google Scholar] [CrossRef]
- Karpushkin, E.A.; Berkovich, A.K.; Artemov, M.V.; Sergeev, V.G. Rheological Properties of Polyacrylonitrile Solutions Containing Highly Dispersed Carbon Nanotubes. Polym. Sci. Ser. A 2014, 56, 681–686. [Google Scholar] [CrossRef]
- Khalatur, P.G. Molecular Dynamics Simulations in Polymer Science. Polym. Sci. A Compr. Ref. 2012, 1, 417–460. [Google Scholar] [CrossRef]
- Oh, S.C.; Wang, Y.S.; Yeo, Y.-K. Modeling and Simulation of the Coagulation Process of Poly(acrylonitrile) Wet-Spinning. Ind. Eng. Chem. Res. 1996, 35, 4796–4800. [Google Scholar] [CrossRef]
- Chen, J.; Wang, C.-G.; Dong, X.-G.; Liu, H.-Z. Study on the Coagulation Mechanism of Wet-Spinning PAN Fibers. J. Polym. Res. 2006, 13, 515–519. [Google Scholar] [CrossRef]
- Zeng, X.; Zhang, G.; Zhang, Y.; Zhao, J.; Pan, D. Diffusion Mechanism of As-spun Polyacrylonitrile Fiber in a Dimethyl Sulfoxide-water Coagulation Bath. J. Macromol. Sci. Part A Pure Appl. Chem. 2006, 43, 1711–1720. [Google Scholar] [CrossRef]
- Chen, J.; Ge, H.; Liu, H.; Li, G.; Wang, C. The Coagulation Process of Nascent Fibers in PAN Wet-Spinning. J. Wuhan Univ. Technol. 2010, 25, 200–205. [Google Scholar] [CrossRef]
- Zhou, P.; Lu, C.; Shi, J.; Li, K.; He, F.; Zhang, S.; Li, Y. Effect of Bath Concentration on Coagulation Kinetics at the Early Stage during Wet Spinning of PAN Copolymer Nascent Fibers. J. Macromol. Sci. Phys. 2011, 50, 1215–1225. [Google Scholar] [CrossRef]
- Xu, N.; Ding, Y.; Schiesser, W.E.; Kothare, M.V. Mathematical Simulation of Wet Spinning Coagulation Process: Dynamic Modeling and Numerical Results. AIChE J. 2016, 62, 3432–3440. [Google Scholar] [CrossRef]
- Pires, J.M.; de Oliveira, O.V.; Freitas, L.C.G.; Filho, E.A.d.S.; Prado, A.R. Molecular Dynamic Simulations of Polyacrylonitrile in Ethanol and Water Solvents. Comput. Theor. Chem. 2012, 995, 75–78. [Google Scholar] [CrossRef]
- Wu, Q.-Y.; Chen, X.-N.; Wan, L.-S.; Xu, Z.-K. Interactions between Polyacrylonitrile and Solvents: Density Functional Theory Study and Two-Dimensional Infrared Correlation Analysis. J. Phys. Chem. B 2012, 116, 8321–8330. [Google Scholar] [CrossRef]
- Pramanik, C.; Jamil, T.; Gissinger, J.R.; Guittet, D.; Arias-Monje, P.J.; Kumar, S.; Heinz, H. Polyacrylonitrile Interactions with Carbon Nanotubes in Solution: Conformations and Binding as a Function of Solvent, Temperature, and Concentration. Adv. Funct. Mater. 2019, 29, 1905247. [Google Scholar] [CrossRef]
- Tallury, S.S.; Pasquinelli, M.A. Molecular Dynamics Simulations of Flexible Polymer Chains Wrapping Single-Walled Carbon Nanotubes. J. Phys. Chem. B 2010, 114, 4122–4129. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.; Choi, J.I.; Cho, A.E.; Kumar, S.; Jang, S.S.; Kim, Y.-H. Origin and Control of Polyacrylonitrile Alignments on Carbon Nanotubes and Graphene Nanoribbons. Adv. Funct. Mater. 2018, 28, 1706970. [Google Scholar] [CrossRef]
- Heo, S.J.; Kim, K.H.; Han, B.; Chae, H.G.; Lee, S.G. Defect Structure Evolution of Polyacrylonitrile and Single Wall Carbon Nanotube Nanocomposites: A Molecular Dynamics Simulation Approach. Sci. Rep. 2020, 10, 11816. [Google Scholar] [CrossRef]
- Komarov, P.; Malyshev, M.; Baburkin, P.; Guseva, D. Mesoscale Simulations of Structure Formation in Polyacrylonitrile Nascent Fibers Induced by Binary Solvent Mixture. Int. J. Mol. Sci. 2023, 24, 9312. [Google Scholar] [CrossRef]
- Fraaije, J.G.E.M.; van Vlimmeren, B.A.C.; Maurits, N.M.; Postma, M.; Evers, O.A.; Hoffmann, C.; Altevogt, P.; Goldbeck-Wood, G. The Dynamic Mean-Field Density Functional Method and Its Application to the Mesoscopic Dynamics of Quenched Block Copolymer Melts. J. Chem. Phys. 1997, 106, 4260–4269. [Google Scholar] [CrossRef]
- Komarov, P.V.; Veselov, I.N.; Khalatur, P.G. Nanoscale morphology in sulfonated poly(ether ether ketone)-based ionomeric membranes: Mesoscale simulations. Polym. Sci. Ser. A 2010, 52, 191–208. [Google Scholar] [CrossRef]
- Komarov, P.V.; Veselov, I.N.; Chu, P.P.; Khalatur, P.G.; Khokhlov, A.R. Atomistic and Mesoscale Simulation of Polymer Electrolyte Membranes Based on Sulfonated Poly(ether Ether Ketone). Chem. Phys. Lett. 2010, 487, 291–296. [Google Scholar] [CrossRef]
- Komarov, P.V.; Veselov, I.N.; Chu, P.P.; Khalatur, P.G. Mesoscale simulation of polymer electrolyte membranes based on sulfonated poly(ether ether ketone) and Nafion. Soft Matter. 2010, 6, 3939–3956. [Google Scholar] [CrossRef]
- Altevogt, P. The MesoDyn Project: Software for Mesoscale Chemical Engineering. Theochem 1999, 463, 139–143. [Google Scholar] [CrossRef]
- Wescott, J.T.; Qi, Y.; Subramanian, L.; Capehart, T.W. Mesoscale Simulation of Morphology in Hydrated Perfluorosulfonic Acid Membranes. J. Chem. Phys. 2006, 124, 134702. [Google Scholar] [CrossRef]
- Doi, M.; Edwards, S.F. The Theory of Polymer Dynamics; Oxford University Press: Oxford, UK, 1988. [Google Scholar]
- Huggins, M.L. Solutions of Long Chain Compounds. J. Chem. Phys. 1941, 9, 440. [Google Scholar] [CrossRef]
- Flory, P.J. Fifteenth Spiers Memorial Lecture. Thermodynamics of Polymer Solutions. Discuss. Faraday Soc. 1970, 49, 7–29. [Google Scholar] [CrossRef]
- Müller-Plathe, F. Scale-Hopping in Computer Simulations of Polymers. Soft Mater. 2002, 1, 1–31. [Google Scholar] [CrossRef]
- Tan, L.; Chen, H.; Pan, D.; Pan, N. Investigating the Spinnability in the Dry-Jet Wet Spinning of PAN Precursor Fiber. J. Appl. Polym. Sci. 2008, 110, 1997–2000. [Google Scholar] [CrossRef]
- Huang, X. Fabrication and Properties of Carbon Fibers. Materials 2009, 2, 2369–2403. [Google Scholar] [CrossRef]
- Tan, L.; Chen, H.; Pan, D.; Pan, N. Investigation into the Gelation and Crystallization of Polyacrylonitrile. Eur. Polym. J. 2009, 45, 1617–1624. [Google Scholar] [CrossRef]
- Chen, J.; Ge, H.-Y.; Dong, X.-G.; Wang, C.-G. The Formation of Polyacrylonitrile Nascent Fibers in Wet-Spinning Process. J. Appl. Polym. Sci. 2007, 106, 692–696. [Google Scholar] [CrossRef]
- Ge, H.; Liu, H.; Chen, J.; Wang, C. The Skin-Core Structure of Poly(acrylonitrile-Itaconic Acid) Precursor Fibers in Wet-Spinning. J. Appl. Polym. Sci. 2008, 108, 947–952. [Google Scholar] [CrossRef]
- Peng, G.-Q.; Zhang, X.-H.; Wen, Y.-F.; Yang, Y.-G.; Liu, L. Effect of Coagulation Bath DMSO Concentration on the Structure and Properties of Polyacrylonitrile (PAN) Nascent Fibers during Wet-Spinning. J. Macromol. Sci. Phys. 2008, 47, 1130–1141. [Google Scholar] [CrossRef]
- Bicerano, J. Prediction of Polymer Properties, 3rd ed.; CRC Press: Boca Raton, FL, USA, 2002. [Google Scholar]
- Rubinstein, M.; Colby, R.H. Polymer Physics; Oxford University Press: Oxford, UK, 2003. [Google Scholar]
- Kamide, K.; Miyazaki, Y.; Kobayashi, H. Light Scattering and Viscometric Study on Polyacrylonitrile in Dimethylformamide, Ethylene Carbonate/water Mixture, and Aqueous Nitric Acid. Polym. J. 1985, 17, 607–619. [Google Scholar] [CrossRef][Green Version]
- Wu, S. Predicting Chain Conformation and Entanglement of Polymers from Chemical Structure. Polym. Eng. Sci. 1992, 32, 823–830. [Google Scholar] [CrossRef]
- Choi, Y.K.; Park, S.-J.; Park, S.; Kim, S.; Kern, N.R.; Lee, J.; Im, W. CHARMM-GUI Polymer Builder for Modeling and Simulation of Synthetic Polymers. J. Chem. Theory Comput. 2021, 17, 2431–2443. [Google Scholar] [CrossRef] [PubMed]
- Abderaman, M.B.; Talla, K.; Gueye, E.-H.O.; Dione, A.N.; Faye, O.; Beye, A.C. A molecular dynamics simulation study on the miscibility of polyglycolide with polyacrylonitrile. J. Polym. Biopolym. Phys. Chem. 2018, 6, 31–38. [Google Scholar] [CrossRef]
- Hansen, C.M. Hansen Solubility Parameters: A User’s Handbook, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2007. [Google Scholar]
- Miller-Chou, B.A.; Koenig, J.L. A Review of Polymer Dissolution. Prog. Polym. Sci. 2003, 28, 1223–1270. [Google Scholar] [CrossRef]
- Belmares, M.; Blanco, M.; Goddard, W.A., 3rd; Ross, R.B.; Caldwell, G.; Chou, S.-H.; Pham, J.; Olofson, P.M.; Thomas, C. Hildebrand and Hansen Solubility Parameters from Molecular Dynamics with Applications to Electronic Nose Polymer Sensors. J. Comput. Chem. 2004, 25, 1814–1826. [Google Scholar] [CrossRef]
- Askadskiĭ, A.A. Computational Materials Science of Polymers; Cambridge Int Science Publishing: Cambridge, UK, 2003. [Google Scholar]
- Hildebrand, J.H.; Scott, R.L. The Solubility of Nonelectrolytes, 3rd ed.; Reinhold Publishing Corporation: New York, NY, USA, 1950. [Google Scholar]
- Malkin, A.; Ilyin, S.; Roumyantseva, T.; Kulichikhin, V. Rheological Evidence of Gel Formation in Dilute Poly(acrylonitrile) Solutions. Macromolecules 2013, 46, 257–266. [Google Scholar] [CrossRef]
- Eom, Y.; Kim, B.C. Solubility Parameter-Based Analysis of Polyacrylonitrile Solutions in N,N-Dimethyl Formamide and Dimethyl Sulfoxide. Polymer 2014, 55, 2570–2577. [Google Scholar] [CrossRef]
- Barton, A.F.M. Solubility Parameters. Chem. Rev. 1975, 75, 731–753. [Google Scholar] [CrossRef]
- Alshehri, S.; Hussain, A.; Ahsan, M.N.; Ali, R.; Siddique, M.U.M. Thermodynamic, Computational Solubility Parameters in Organic Solvents and GastroPlus Based Prediction of Ketoconazole. ACS Omega 2021, 6, 5033–5045. [Google Scholar] [CrossRef]
- Wypych, G. Handbook of Solvents; ChemTec Publishing: Toronto, ON, Canada, 2001. [Google Scholar]
- Detriche, S.; Zorzini, G.; Colomer, J.F.; Fonseca, A.; Nagy, J.B. Application of the Hansen Solubility Parameters Theory to Carbon Nanotubes. J. Nanosci. Nanotechnol. 2008, 8, 6082–6092. [Google Scholar] [CrossRef]
- Bergin, S.D.; Sun, Z.; Rickard, D.; Streich, P.V.; Hamilton, J.P.; Coleman, J.N. Multicomponent Solubility Parameters for Single-Walled Carbon Nanotube-Solvent Mixtures. ACS Nano 2009, 3, 2340–2350. [Google Scholar] [CrossRef] [PubMed]
- Çavuş, S.; Çakal, E.; Sevgili, L.M. Solvent Dependent Swelling Behaviour of poly(N-Vinylcaprolactam) and poly(N-Vinylcaprolactam-Co-Itaconic Acid) Gels and Determination of Solubility Parameters. Chem. Pap. 2015, 69, 1367–1377. [Google Scholar] [CrossRef]
- Tan, L.; Liu, S.; Pan, D. Water Effect on the Gelation Behavior of Polyacrylonitrile/dimethyl Sulfoxide Solution. Colloids Surf. A Physicochem. Eng. Asp. 2009, 340, 168–173. [Google Scholar] [CrossRef]
- Catalán, J.; Díaz, C.; García-Blanco, F. Characterization of Binary Solvent Mixtures of DMSO with Water and Other Cosolvents. J. Org. Chem. 2001, 66, 5846–5852. [Google Scholar] [CrossRef]
- Akhukov, M.A.; Chorkov, V.A.; Gavrilov, A.A.; Guseva, D.V.; Khalatur, P.G.; Khokhlov, A.R.; Kniznik, A.A.; Komarov, P.V.; Okun, M.V.; Potapkin, B.V.; et al. MULTICOMP Package for Multilevel Simulation of Polymer Nanocomposites. Comput. Mater. Sci. 2023, 216, 111832. [Google Scholar] [CrossRef]
- Sun, H. Ab Initio Calculations and Force Field Development for Computer Simulation of Polysilanes. Macromolecules 1995, 28, 701–712. [Google Scholar] [CrossRef]
- Morgan, P. Carbon Fibers and Their Composites, 1st ed.; CRC Press: Boca Raton, FL, USA, 2005. [Google Scholar] [CrossRef]
- Hua, Z.; Zhong, Y.J.; Li, D.F. Pores in PAN-based carbon fiber and effects of pore defects on mechanical properties. Mater. Sci. Forum 2007, 546, 1665–1668. [Google Scholar] [CrossRef]
- Arbab, S.; Noorpanah, P.; Mohammadi, N.; Soleimani, M. Designing Index of Void Structure and Tensile Properties in Wet-spun Polyacrylonitrile (PAN) Fiber. I. Effect of Dope Polymer or Nonsolvent Concentration. J. Appl. Polym. Sci. 2008, 109, 3461–3469. [Google Scholar] [CrossRef]
- Han, C.D.; Segal, L. A Study of Fiber Extrusion in Wet Spinning. II. Effects of Spinning Conditions on Fiber Formation. J. Appl. Polym. Sci. 1970, 14, 2999–3019. [Google Scholar] [CrossRef]
- Yi, K.; Li, Q.F.; Zhang, L.; Li, N.; Zhou, Y.; Ryu, S.K.; Jin, R.G. Diffusion Coefficients of Dimethyl Sulphoxide (DMSO) and H2O in PAN Wet Spinning and Its Influence on Morphology of Nascent Polyacrylonitrile (PAN) Fiber. J. Eng. Fiber. Fabr. 2013, 8, 155892501300800. [Google Scholar] [CrossRef]
- Wang, B.; Li, C.; Cao, W. Effect of Polyacrylonitrile Precursor Orientation on the Structures and Properties of Thermally Stabilized Carbon Fiber. Materials 2021, 14, 3237. [Google Scholar] [CrossRef] [PubMed]
- Dang, W.; Liu, J.; Wang, X.; Yan, K.; Zhang, A.; Yang, J.; Chen, L.; Liang, J. Structural Transformation of Polyacrylonitrile (PAN) Fibers during Rapid Thermal Pretreatment in Nitrogen Atmosphere. Polymers 2020, 12, 63. [Google Scholar] [CrossRef] [PubMed]
- Bashir, Z. The Hexagonal Mesophase in Atactic Polyacrylonitrile: A New Interpretation of the Phase Transitions in the Polymer. J. Macromol. Sci. Phys. 2001, 40, 41–67. [Google Scholar] [CrossRef]
- Knudsen, J.P. The Influence of Coagulation Variables on the Structure and Physical Properties of an Acrylic Fiber. Text. Res. J. 1963, 33, 13–20. [Google Scholar] [CrossRef]
- Qin, J. The Enhancement of Microvoids in Acrylic Fibers. J. Appl. Polym. Sci. 1992, 44, 1095–1105. [Google Scholar] [CrossRef]
- Wang, Y.-X.; Wang, C.-G.; Yu, M.-J. Effects of Different Coagulation Conditions on Polyacrylonitrile Fibers Wet Spun in a System of Dimethylsulphoxide and Water. J. Appl. Polym. Sci. 2007, 104, 3723–3729. [Google Scholar] [CrossRef]
- Dong, R.; Keuser, M.; Zeng, X.; Zhao, J.; Zhang, Y.; Wu, C.; Pan, D. Viscometric Measurement of the Thermodynamics of PAN terpolymer/DMSO/water System and Effect of Fiber-Forming Conditions on the Morphology of PAN Precursor. J. Polym. Sci. B Polym. Phys. 2008, 46, 1997–2011. [Google Scholar] [CrossRef]
- Dong, R.; Zhao, J.; Zhang, Y.; Pan, D. Morphology Control of Polyacrylonitrile (PAN) Fibers by Phase Separation Technique. J. Polym. Sci. B Polym. Phys. 2009, 47, 261–275. [Google Scholar] [CrossRef]
- Arbab, S.; Zeinolebadi, A.; Noorpanah, P. Exploring the Thermodynamic Aspects of Structure Formation during Wet-Spinning of Polyacrylonitrile Fibres. In Methodologies and Applications for Chemoinformatics and Chemical Engineering; IGI Global: Hershey, PA, USA, 2013; p. 138. [Google Scholar] [CrossRef]
- Ji, B.H. Effect of coagulation bath concentration on the structure and properties of polyacrylonitrile as-spun fibers during wet-spinning. Adv. Mater. Res. 2011, 287, 1832–1836. [Google Scholar] [CrossRef]
- Morris, E.; Weisenberger, M.; Rice, G. Properties of PAN Fibers Solution Spun into a Chilled Coagulation Bath at High Solvent Compositions. Fibers 2015, 3, 560–574. [Google Scholar] [CrossRef]
- Samimi-Sohrforozani, E.; Azimi, S.; Abolhasani, A.; Malekian, S.; Arbab, S.; Zendehdel, M.; Abolhasani, M.M.; Yaghoobi Nia, N. Development of Porous Polyacrylonitrile Composite Fibers: New Precursor Fibers with High Thermal Stability. Electron. Mater. Lett. 2021, 2, 454–465. [Google Scholar] [CrossRef]
- Yushkin, A.; Basko, A.; Balynin, A.; Efimov, M.; Lebedeva, T.; Ilyasova, A.; Pochivalov, K.; Volkov, A. Effect of Acetone as Co-Solvent on Fabrication of Polyacrylonitrile Ultrafiltration Membranes by Non-Solvent Induced Phase Separation. Polymers 2022, 14, 4603. [Google Scholar] [CrossRef] [PubMed]
- Kim, S.C.; Kang, S.; Lee, H.; Kwak, D.-B.; Ou, Q.; Pei, C.; Pui, D.Y.H. Nanofiber Filter Performance Improvement: Nanofiber Layer Uniformity and Branched Nanofiber. Aerosol Air Qual. Res. 2020, 20, 80–88. [Google Scholar] [CrossRef]
- Cheng, X.; Zhao, L.; Zhang, Z.; Deng, C.; Li, C.; Du, Y.; Shi, J.; Zhu, M. Highly Efficient, Low-Resistant, Well-Ordered PAN Nanofiber Membranes for Air Filtration. Colloids Surf. A Physicochem. Eng. Asp. 2022, 655, 130302. [Google Scholar] [CrossRef]
- Voevodin, V.V.; Antonov, A.S.; Nikitenko, D.A.; Shvets, P.A.; Sobolev, S.I.; Sidorov, I.Y.; Stefanov, K.S.; Voevodin, V.V.; Zhumatiy, S.A. Supercomputer Lomonosov-2: Large Scale, Deep Monitoring and Fine Analytics for the User Community. Supercomput. Front. Innov. 2019, 6, 4–11. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).