Determining the Optimal Aquifer Exploitation under Artificial Recharge using the Combination of Numerical Models and Particle Swarm Optimization
Abstract
:1. Introduction
Literature Review
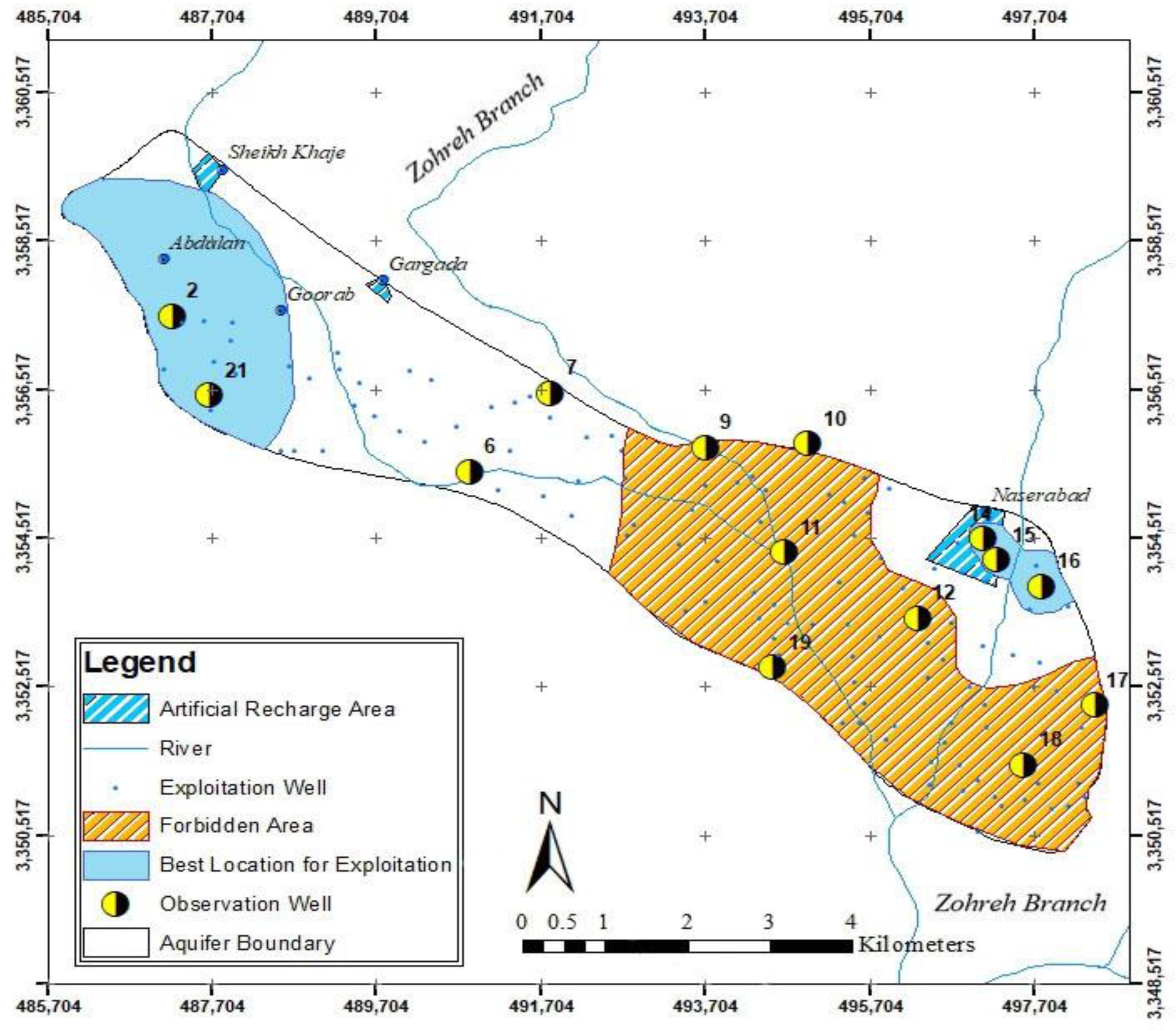
2. Study Area
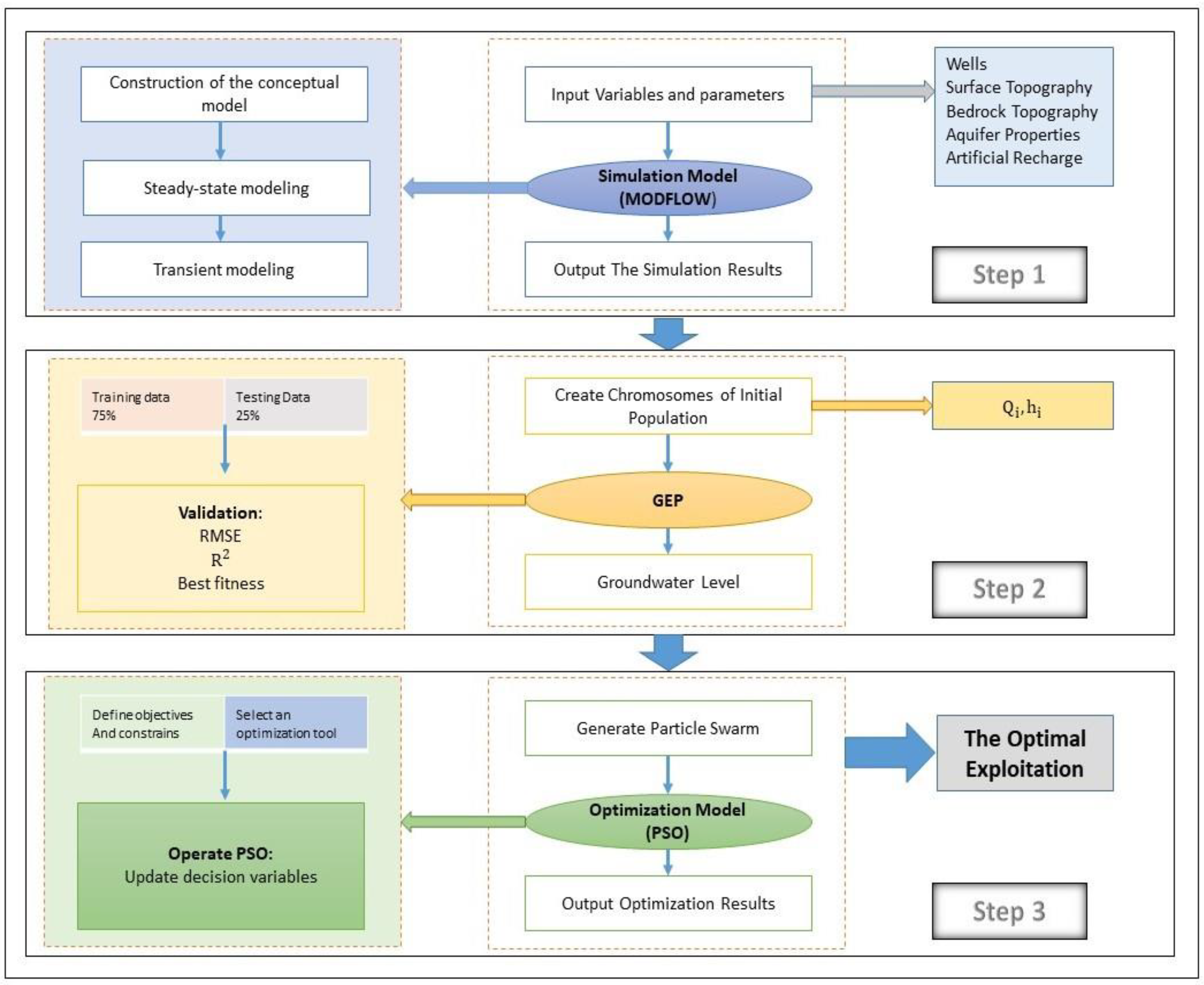
3. Methodology
3.1. Simulation Model of Groundwater
3.2. Estimating the Simulation Model Using Gene Expression Programming
3.3. Particle Swarm Optimization
4. Results and Discussion
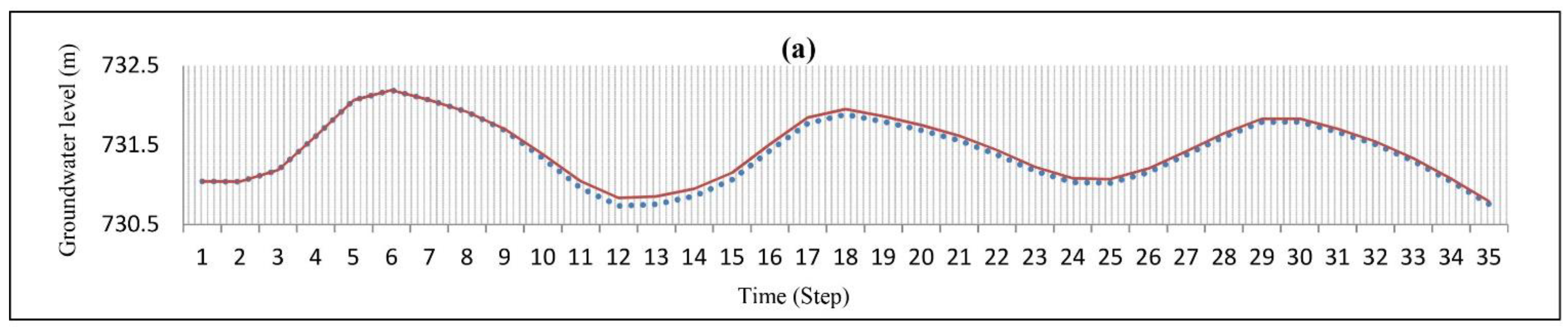
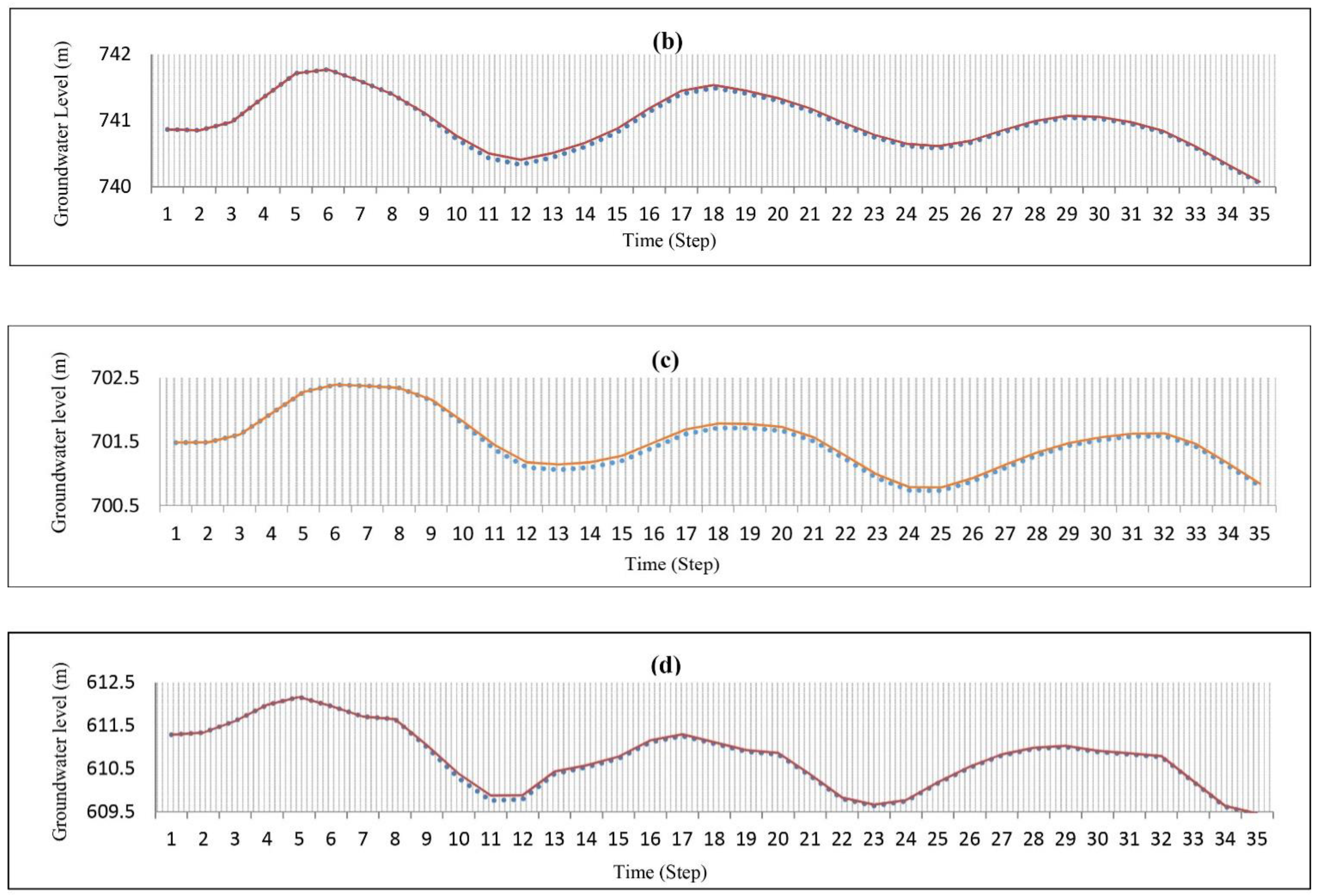
4.1. Simulation of the Yasouj Aquifer
4.2. Result of Gene Expression Programming
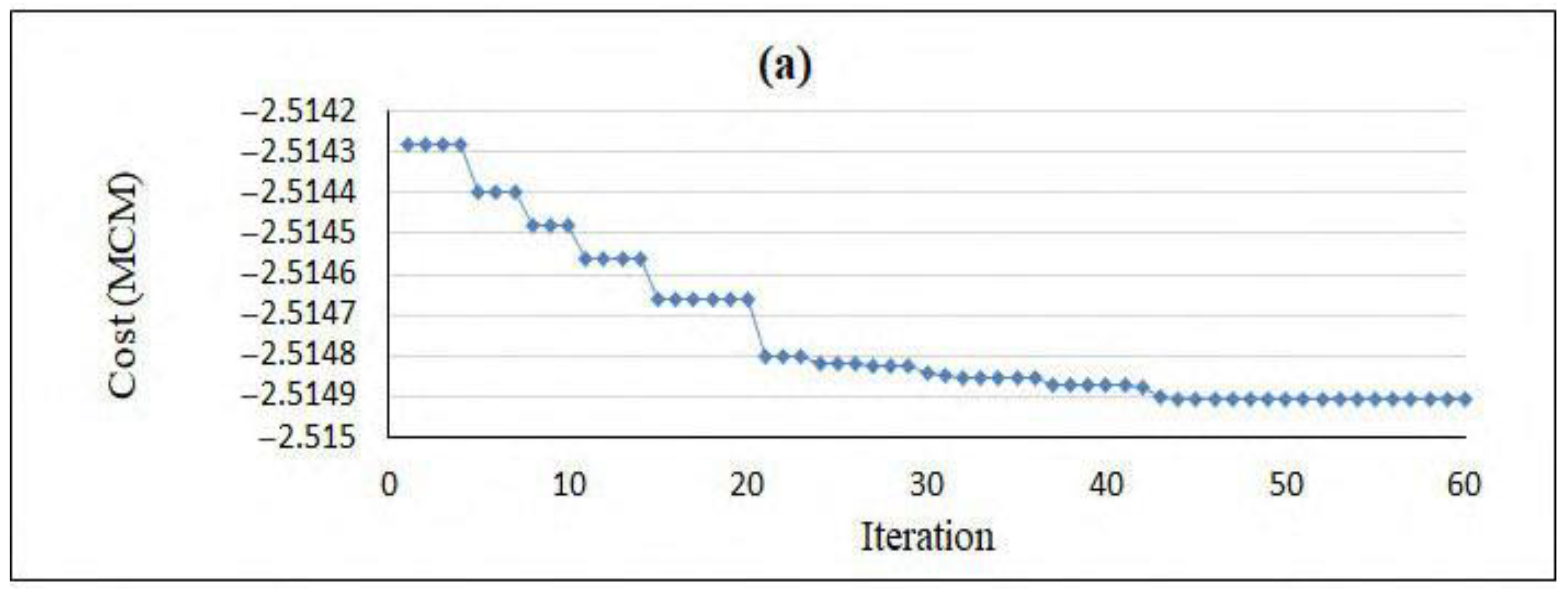
4.3. Result of the Optimization Model
4.4. Sensitivity Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kerebih, M.S.; Keshari, A.K. Distributed Simulation-Optimization Model for Conjunctive Use of Groundwater and Surface Water Under Environmental and Sustainability Restrictions. Water Resour. Manag. 2021, 35, 2305–2323. [Google Scholar] [CrossRef]
- Noori, R.; Maghrebi, M.; Jessen, S.; Bateni, S.M.; Heggy, E.; Javadi, S.; Nouri, M.; Pistre, S.; Abolfathi, S.; AghaKouchak, A. Decline in Iran’s Groundwater Recharge. Res. Sq. 2023. [Google Scholar] [CrossRef]
- Maghrebi, M.; Noori, R.; Mehr, A.D.; Lak, R.; Darougheh, F.; Razmgir, R.; Farnoush, H.; Taherpour, H.; Moghaddam, S.M.R.A.; Araghi, A.; et al. Spatiotemporal Changes in Iranian Rivers’ Discharge. Elem. Sci. Anthr. 2023, 11, 00002. [Google Scholar] [CrossRef]
- Javadi, S.; Mehdy, S.; Shahdany, H.; Neshat, A.; Chambel, A. Multi-Parameter Risk Mapping of Qazvin Aquifer by Classic and Fuzzy Clustering Techniques. Geocarto Int. 2020, 37, 6049. [Google Scholar] [CrossRef]
- Kharanagh, S.G.; Banihabib, M.E.; Javadi, S. An MCDM-Based Social Network Analysis of Water Governance to Determine Actors’ Power in Water-Food-Energy Nexus. J. Hydrol. 2019, 581, 124382. [Google Scholar] [CrossRef]
- Gaur, S.; Chahar, B.R.; Graillot, D. Analytic Elements Method and Particle Swarm Optimization Based Simulation–Optimization Model for Groundwater Management. J. Hydrol. 2011, 402, 217–227. [Google Scholar] [CrossRef]
- Sayit, A.P.; Yazicigil, H. Assessment of Artificial Aquifer Recharge Potential in the Kucuk Menderes River Basin, Turkey. Hydrogeol. J. 2012, 20, 755–766. [Google Scholar] [CrossRef]
- Bremer, L.L.; DeMaagd, N.; Wada, C.A.; Burnett, K.M. Priority Watershed Management Areas for Groundwater Recharge and Drinking Water Protection: A Case Study from Hawai’i Island. J. Environ. Manag. 2021, 286, 111622. [Google Scholar] [CrossRef] [PubMed]
- Narasimhan, L.; Boulet, P.; Kuchta, B.; Schaef, O.; Denoyel, R.; Brunet, P. Molecular Simulations of Water and Paracresol in MFI Zeolite-A Monte Carlo Study. Langmuir 2009, 25, 11598–11607. [Google Scholar] [CrossRef]
- Cao, G.; Han, D.; Moser, J. Groundwater Exploitation Management Under Land Subsidence Constraint: Empirical Evidence from the Hangzhou-Jiaxing-Huzhou Plain, China. Environ. Manag. 2013, 51, 1109–1125. [Google Scholar] [CrossRef] [PubMed]
- Jafari, F.; Javadi, S.; Golmohammadi, G.; Karimi, N. Numerical Simulation of Groundwater Flow and Aquifer-System Compaction Using Simulation and InSAR Technique: Saveh Basin. Environ. Earth Sci. 2016, 75, 833. [Google Scholar] [CrossRef]
- Bierkens, M.; Wada, Y. Non-Renewable Groundwater Use and Groundwater Depletion: A Review. Environ. Res. Lett. 2019, 14, 063002. [Google Scholar] [CrossRef]
- Motevalli, A.; Moradi, H.R.; Javadi, S. A Comprehensive Evaluation of Groundwater Vulnerability to Saltwater Up-Coning and Sea Water Intrusion in a Coastal Aquifer (Case Study: Ghaemshahr-Juybar Aquifer). J. Hydrol. 2018, 557, 753–773. [Google Scholar] [CrossRef]
- Milan, S.G.; Roozbahani, A.; Banihabib, M.E. Fuzzy Optimization Model and Fuzzy Inference System for Conjunctive Use of Surface and Groundwater Resources. J. Hydrol. 2018, 566, 421–434. [Google Scholar] [CrossRef]
- Ghaseminejad, A.; Shourian, M. A Simulation–Optimization Approach for Optimal Design of Groundwater Withdrawal Wells’ Location and Pumping Rate Considering Desalination Constraints. Environ. Earth Sci. 2019, 78, 270. [Google Scholar] [CrossRef]
- Zare, M. Hybrid Signal Processing/Machine Learning and PSO Optimization Model for Conjunctive Management of Surface-Groundwater Resources. Neural Comput. Appl. 2021, 33, 8067–8088. [Google Scholar] [CrossRef]
- Sabale, R.; Jose, M. Optimization of Conjunctive Use of Surface and Groundwater by Using LINGO and PSO in Water Resources Management. Innov. Infrastruct. Solut. 2022, 7, 135. [Google Scholar] [CrossRef]
- Kumar, D.; Prasad, R.K.; Mathur, S. Optimal Design of an In-Situ Bioremediation System Using Support Vector Machine and Particle Swarm Optimization. J. Contam. Hydrol. 2013, 151, 105–116. [Google Scholar]
- Kamali, A.; Niksokhan, M.H. Multi-Objective Optimization for Sustainable Groundwater Management by Developing of Coupled Quantity-Quality Simulation-Optimization Model. J. Hydroinformatics 2017, 19, 973–992. [Google Scholar] [CrossRef]
- Shourian, M.; Davoudi, S.M.J. Optimum Pumping Well Placement and Capacity Design for a Groundwater Lowering System in Urban Areas with the Minimum Cost Objective. Water Resour. Manag. 2017, 31, 4207–4225. [Google Scholar] [CrossRef]
- Alaviani, F.; Sedghi, H.; Moghaddam, A.A.; Babazadeh, H. Adopting Gms–Pso Model to Reduce Groundwater Withdrawal by Integrated Water Resources Management. Int. J. Environ. Res. 2018, 12, 619–629. [Google Scholar] [CrossRef]
- Sabzzadeh, I.; Shourian, M. Maximizing Crops Yield Net Bene Fi t in a Groundwater-Irrigated Plain Constrained to Aquifer Stable Depletion Using a Coupled PSO-SWAT- MODFLOW Hydro-Agronomic Model. J. Clean. Prod. 2020, 262, 121349. [Google Scholar] [CrossRef]
- Dey, S.; Prakash, O. Managing Saltwater Intrusion Using Conjugate Sharp Interface and Density Dependent Models Linked with Pumping Optimization. Groundw. Sustain. Dev. 2020, 11, 100446. [Google Scholar] [CrossRef]
- Fan, Y.; Lu, W.; Miao, T.; Li, J.; Lin, J. Multiobjective Optimization of the Groundwater Exploitation Layout in Coastal Areas Based on Multiple Surrogate Models. Environ. Sci. Pollut. Res. 2020, 27, 19561–19576. [Google Scholar] [CrossRef]
- Safavi, H.R.; Darzi, F.; Mariño, M.A. Simulation-Optimization Modeling of Conjunctive Use of Surface Water and Groundwater. Water Resour. Manag. 2010, 24, 1965–1988. [Google Scholar] [CrossRef]
- Ataie-ashtiani, B.; Ketabchi, H.; Rajabi, M.M. Optimal Management of a Freshwater Lens in a Small Island Using Surrogate Models and Evolutionary Algorithms. Hydrol. Eng. 2014, 19, 339–354. [Google Scholar] [CrossRef]
- Safavi, H.R.; Alijanian, M.A. Optimal Crop Planning and Conjunctive Use of Surface Water and Groundwater Resources Using Fuzzy Dynamic Programming. J. Irrig. Drain. Eng. 2011, 137, 383–397. [Google Scholar] [CrossRef]
- Arya, N.; Zahra, A.; Sami, K.; Milan, G.; Zarif, H. A Hybrid Approach Based on Simulation, Optimization, and Estimation of Conjunctive Use of Surface Water and Groundwater Resources. Environ. Sci. Pollut. Res. 2022, 29, 56828–56844. [Google Scholar] [CrossRef] [PubMed]
- Song, J.; Yang, Y.; Wu, J.; Wu, J.; Sun, X.; Lin, J. Adaptive Surrogate Model Based Multiobjective Optimization for Coastal Aquifer Management. J. Hydrol. 2018, 561, 98–111. [Google Scholar] [CrossRef]
- Lal, A.; Asce, S.M.; Datta, B. Optimal Groundwater-Use Strategy for Saltwater Intrusion Management in a Pacific Island Country. J. Water Resour. Plan. Manag. 2019, 145, 04019032. [Google Scholar] [CrossRef]
- Han, Z.; Lu, W.; Fan, Y.; Xu, J.; Lin, J. Surrogate-Based Stochastic Multiobjective Optimization for Coastal Aquifer Management under Parameter Uncertainty. Water Resour. Manag. 2021, 35, 1479–1497. [Google Scholar] [CrossRef]
- Water Budget Report. The Regional Water Company of Yasouj. 2014. Available online: http://wrs.wrm.ir/amar/login.asp (accessed on 5 March 2023). (In Pesian).
- Harbaugh, A.W.; McDonald, M.G. Programmer’s Documentation for MODFLOW-96, an Update to the US Geological Survey Modular Finite-Difference Ground-Water Flow Model; US Geological Survey, Branch of Information Services: Reston, VI, USA, 1996.
- Luo, Z.; Luo, Z.; Qin, Y.; Wen, L.; Ma, S.; Dai, Z. Developing New Tree Expression Programing and Artificial Bee Colony Technique for Prediction and Optimization of Landslide Movement. Eng. Comput. 2020, 36, 1117–1134. [Google Scholar] [CrossRef]
- Bahmani, R.; Solgi, A.; Ouarda, T.B.M.J. Groundwater Level Simulation Using Gene Expression Programming and M5 Model Tree Combined with Wavelet Transform. Hydrol. Sci. J. 2020, 65, 1430–1442. [Google Scholar] [CrossRef]
- Ebrahimi, H.; Jabbari, E.; Ghasemi, M. Application of the Honey-Bees Mating Programming (HBMP) Algorithm to Sediment Concentration Modelling to Sediment Concentration Modelling. Hydrol. Sci. J. 2015, 60, 1853–1864. [Google Scholar] [CrossRef]
- Ferreira, C. Gene Expression Programming: A New Adaptive Algorithm for Solving Problems. arXiv 2001, arXiv:cs/0102027. [Google Scholar]
- Kenned0y, J.; Eberhart, R. Particle Swarm Optimization. In Proceedings of the ICNN’95—International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995. [Google Scholar]
- Eberhart, R.C.; Shi, Y.; Kennedy, J. Swarm Intelligence; Elsevier Science: Amsterdam, The Netherlands, 2001. [Google Scholar]
- Jarboui, B.; Damak, N.; Siarry, P.; Rebai, A. A Combinatorial Particle Swarm Optimization for Solving Multi-Mode Resource-Constrained Project Scheduling Problems. Appl. Math. Comput. 2008, 195, 299–308. [Google Scholar] [CrossRef]
- Asefpour Vakilian, K. Metaheuristic optimization to improve machine learning in Raman spectroscopic-based detection of foodborne pathogens. In Proceedings of the 2021 7th International Conference on Signal Processing and Intelligent Systems, Tehran, Iran, 29–30 December 2021; pp. 1–5. [Google Scholar] [CrossRef]
- Verardo, E.; Atteia, O.; Rouvreau, L.; Siade, A.; Prommer, H. Identifying Remedial Solutions through Optimal Bioremediation Design under Real-World Field Conditions. J. Contam. Hydrol. 2021, 237, 103751. [Google Scholar] [CrossRef]

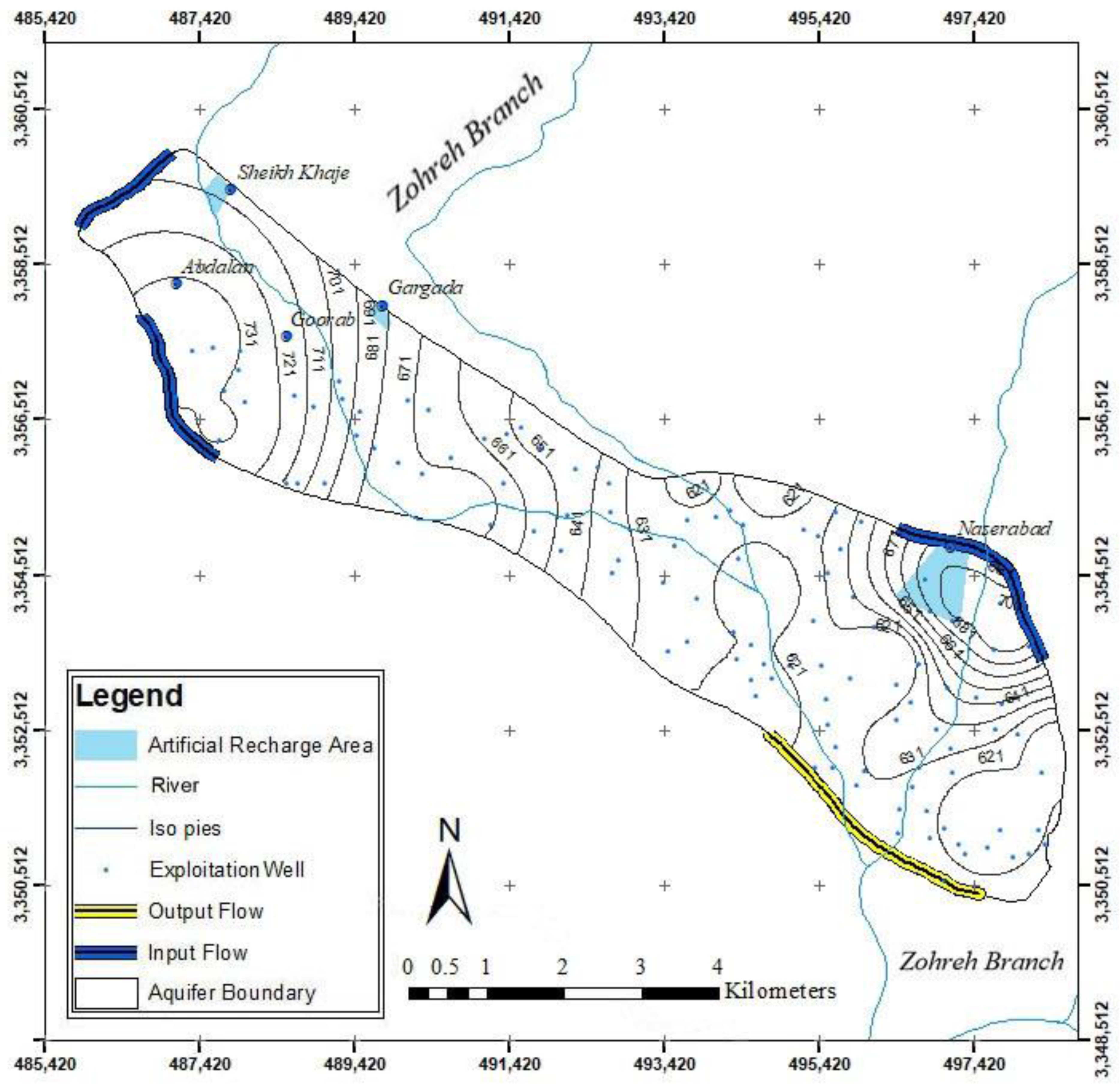
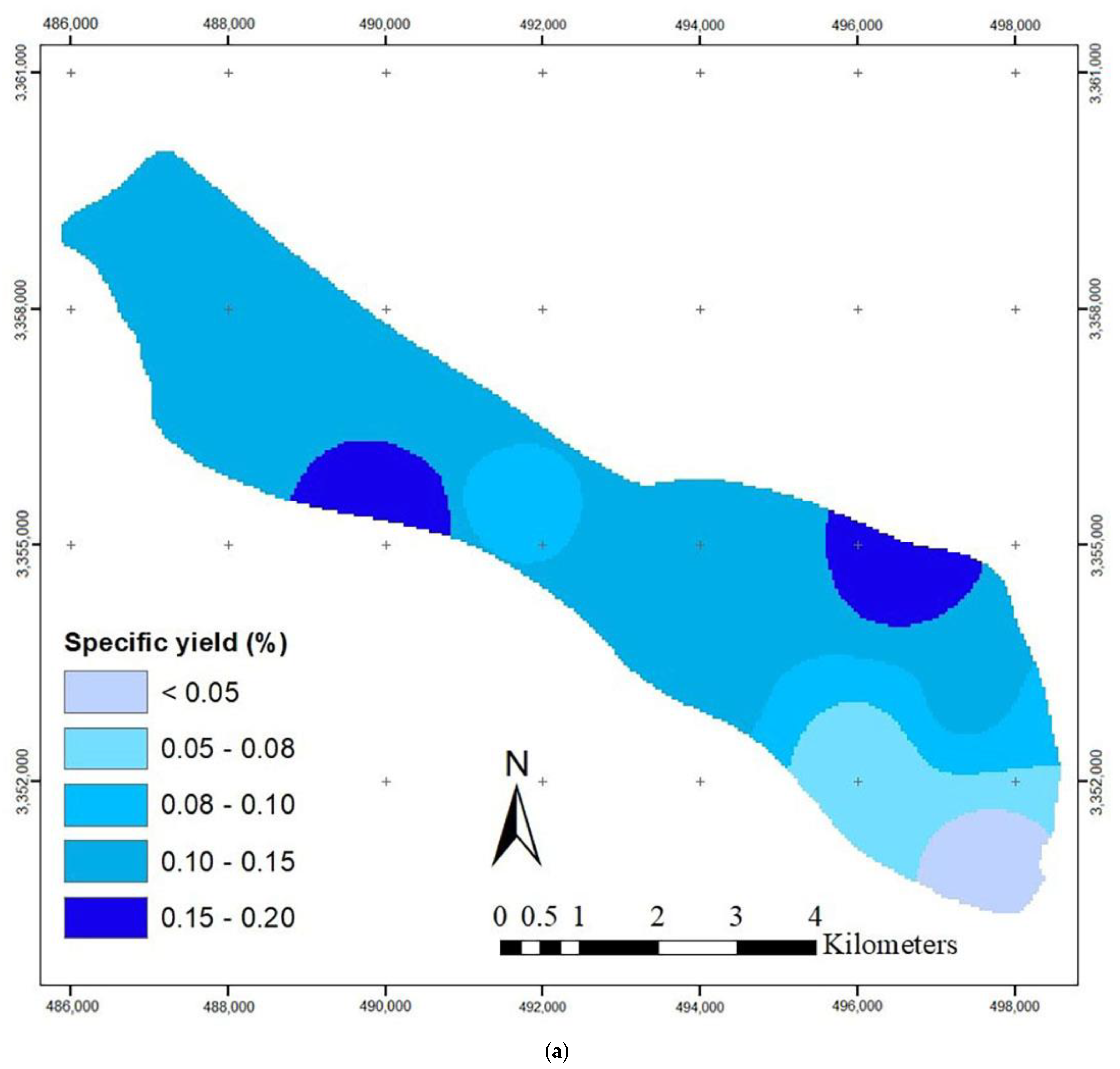
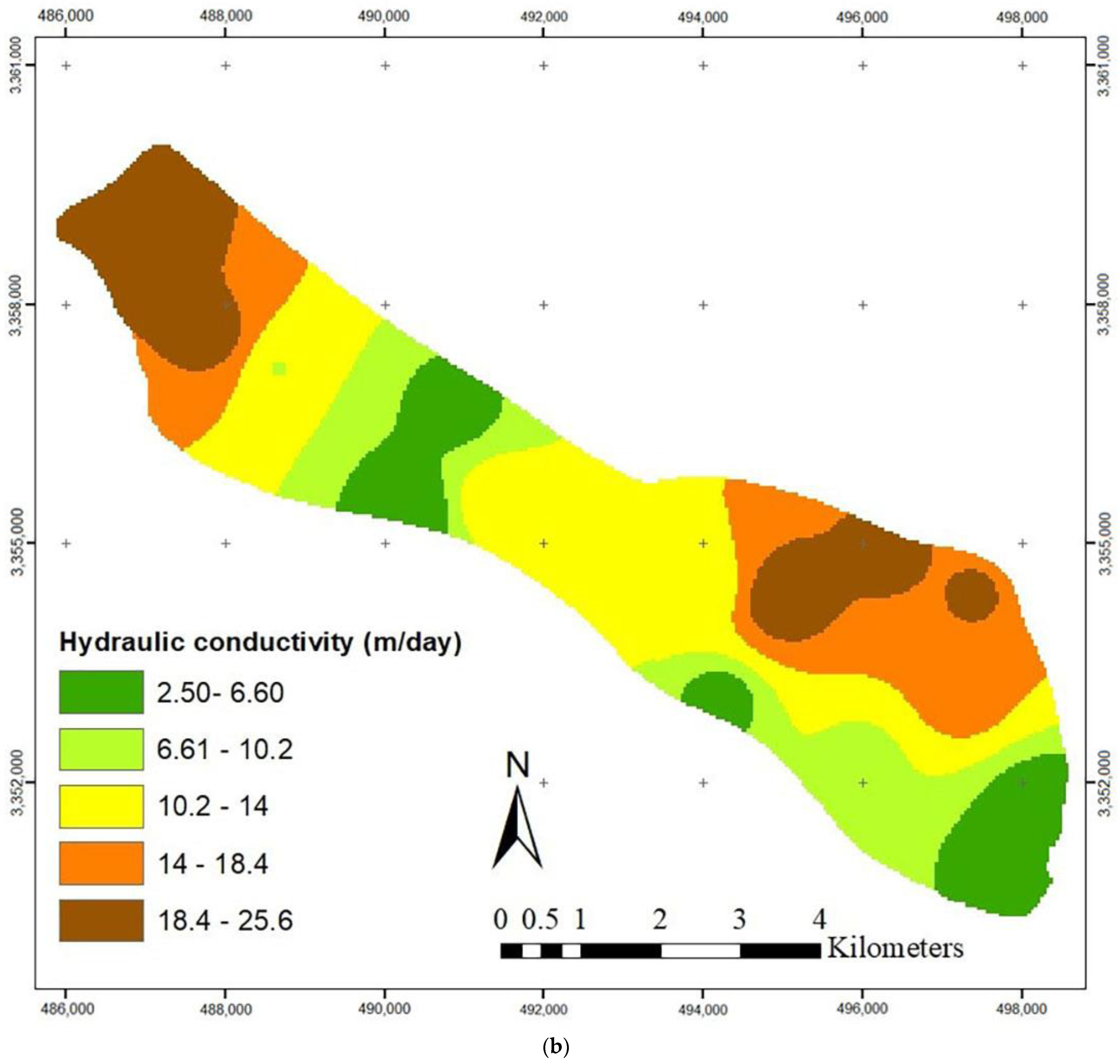
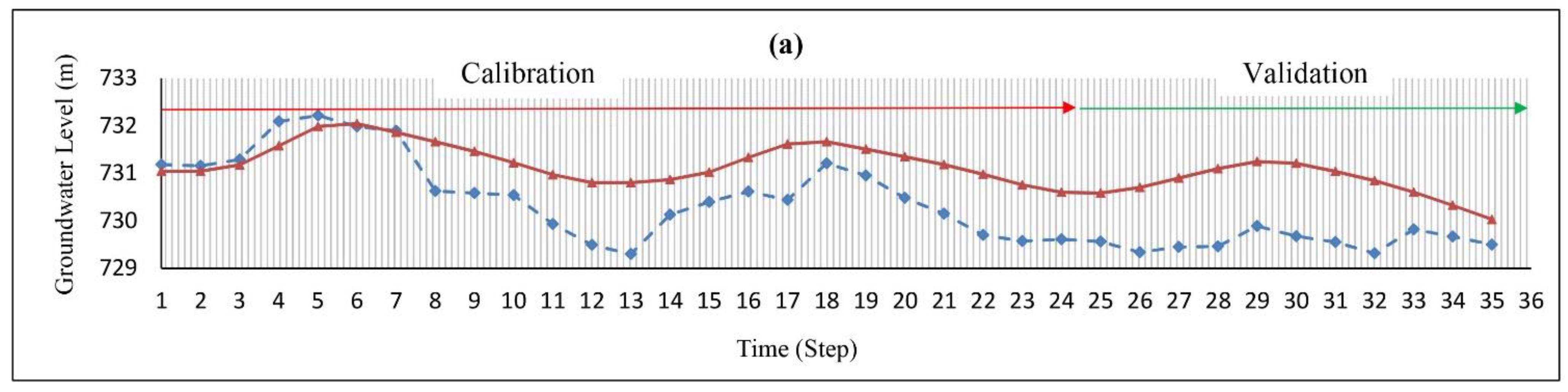
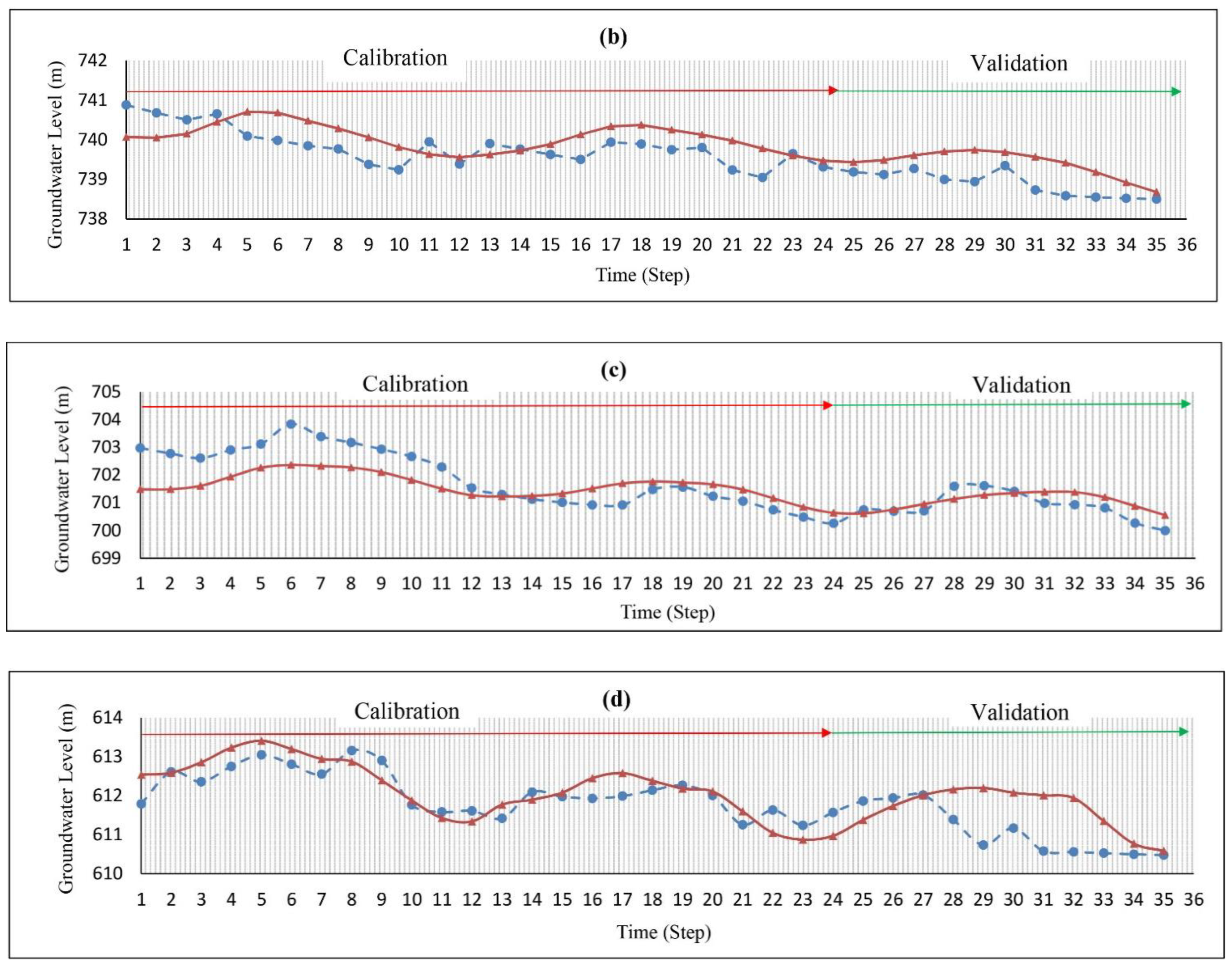
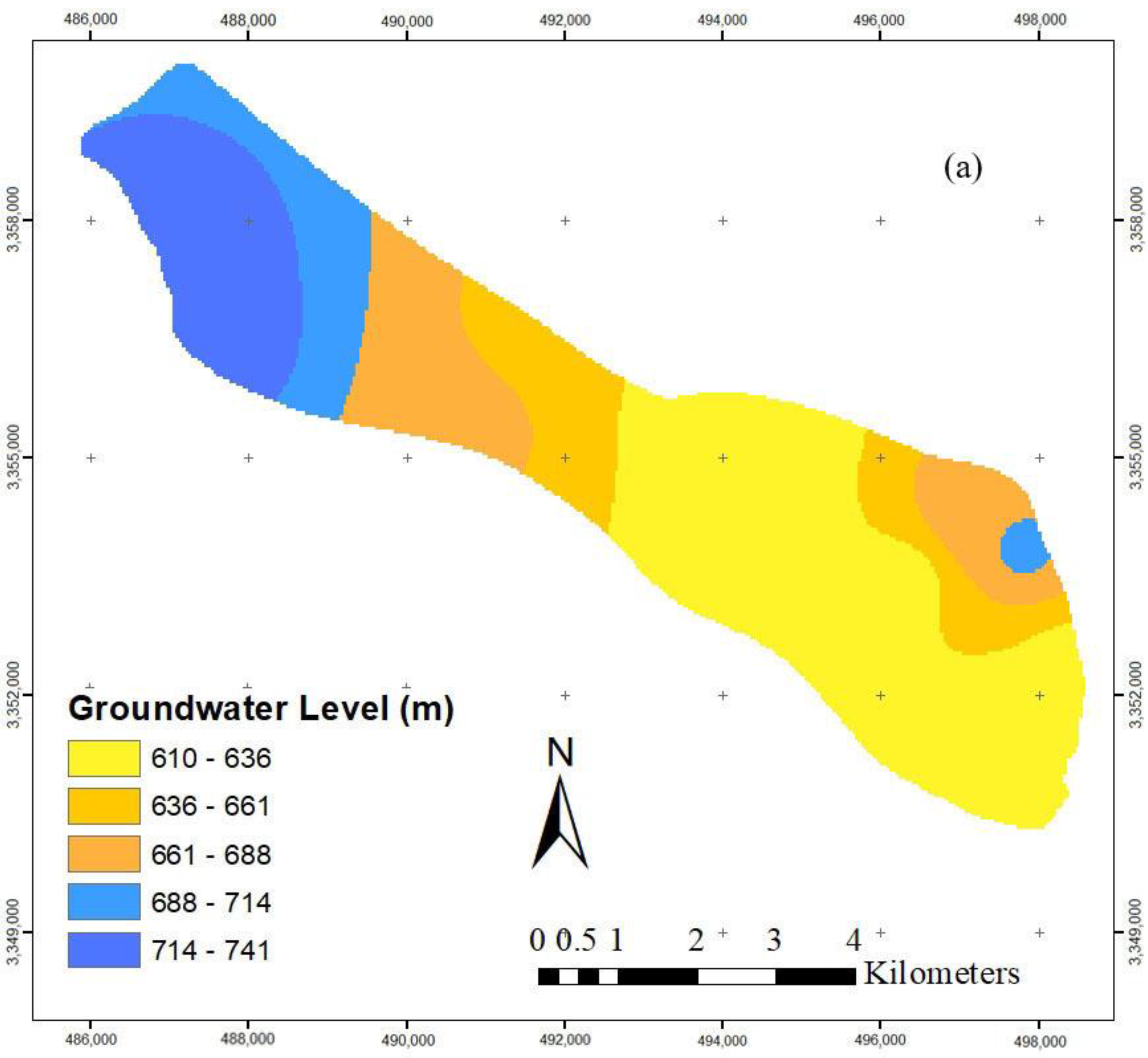
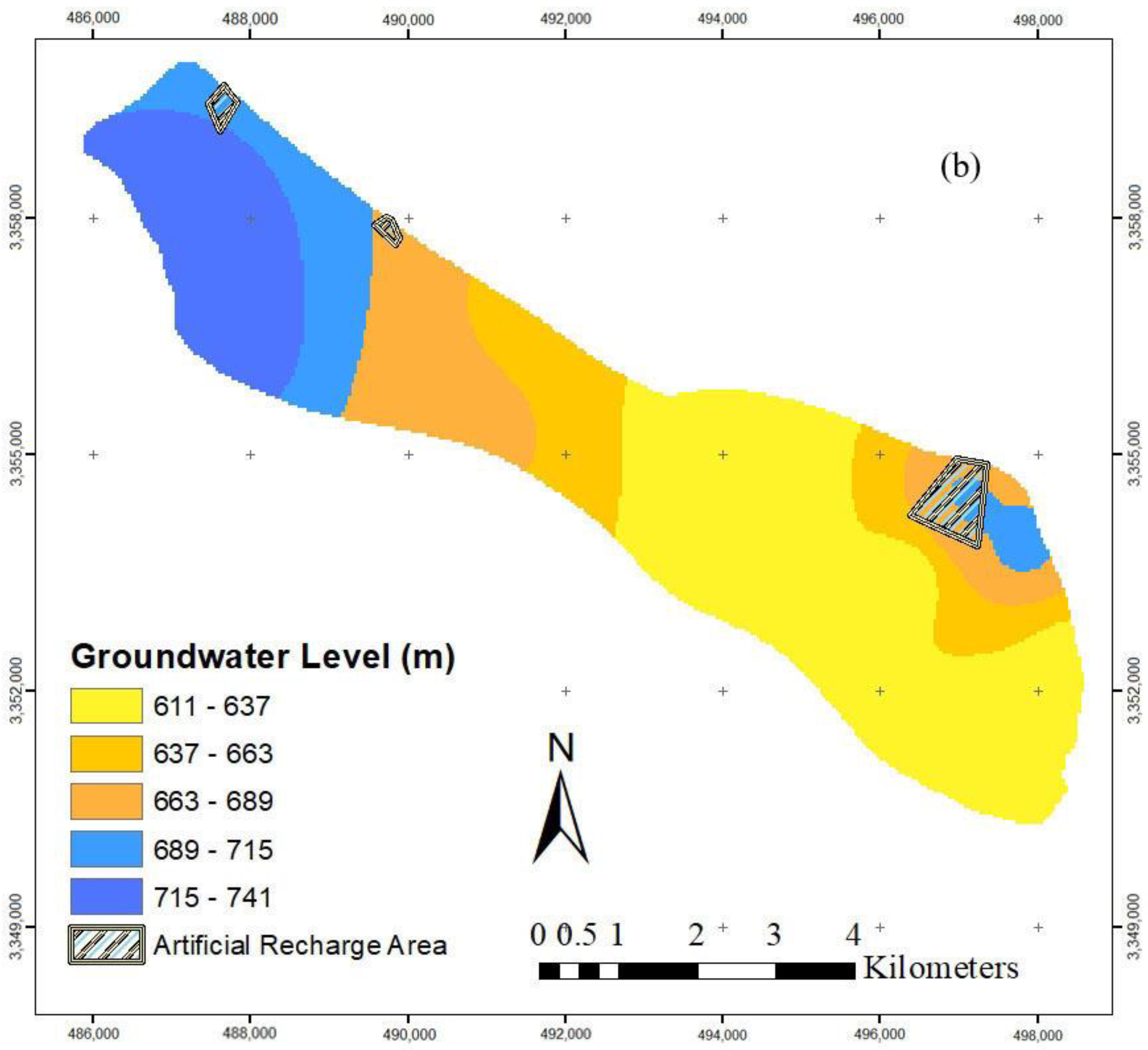


| Name | UTM X (m) | UTM Y (m) | Situation | Area (ha) |
|---|---|---|---|---|
| Naserabad | 497,130 | 3,354,885 | Active | 8500 |
| Sheykh Khaje | 487,831 | 3,359,991 | Active | 3200 |
| Gargada | 489,784 | 3,357,991 | Active | 1000 |
| Goorab | 488,557 | 3,357,590 | Inactive | 200 |
| Abdalan | 487,133 | 3,358,275 | Inactive | 300 |
| Condition | Time (Step) | RMSE (m) | MAE (m) |
|---|---|---|---|
| Steady-state | 1 | 0.7 | 0.64 |
| Transient | 24 | 0.87 | 0.74 |
| Date | Groundwater Level without Artificial Recharge (m) | Groundwater Level without Artificial Recharge and with Maximum Exploitation (m) | Groundwater Level Drop (m) |
|---|---|---|---|
| September 2018–November 2018 | 655 | 648.57 | 6.42 |
| March 2019–May 2019 | 655.37 | 648.74 | 6.63 |
| June 2019–August 2019 | 655.13 | 645.66 | 6.47 |
| Date | Groundwater level with Artificial Recharge (m) | Groundwater Level with Artificial Recharge and Maximum Exploitation (M) | Groundwater Level Drop (m) |
|---|---|---|---|
| September 2018–November 2018 | 655.23 | 648.81 | 6.41 |
| March 2019–May 2019 | 655.62 | 648.99 | 6.62 |
| June 2019–August 2019 | 655.37 | 648.9 | 6.46 |
| Parameters | Value | Parameters | Value |
|---|---|---|---|
| Head size | 7 | Gene recombination rate | 0.1 |
| Number of genes | 3 | Insertion sequence transposition rate | 0.1 |
| Chromosomes | 50 | Root insertion sequence transposition rate | 0.1 |
| Mutation rate | 0.044 | Gene transposition rate | 0.1 |
| Inversion rate | 0.1 | Linking function | Addition |
| One-point recombination rate | 0.3 | Fitness function error type | RRSE |
| Two-point recombination rate | 0.3 | Function set | cos, atan, sqrt, exp, ln, , , |
| Date | Modes | RMSE | Best Fitness | RAE | RSE | RRSE | |
|---|---|---|---|---|---|---|---|
| September 2018–November 2018 | Training | 0.999 | 0.00043 | 993.6145 | 0.0021 | 0.00004 | 0.0064 |
| Testing | 0.999 | 0.00011 | 994.8844 | 0.0053 | 0.00002 | 0.0051 | |
| March 2019–May 2019 | Training | 0.999 | 0.00045 | 988.7120 | 0.0093 | 0.00013 | 0.0114 |
| Testing | 0.999 | 0.00205 | 864.1015 | 0.0160 | 0.02473 | 0.1527 | |
| June 2019–August 2019 | Training | 0.999 | 0.00040 | 993.5044 | 0.0021 | 0.00004 | 0.0065 |
| Testing | 0.996 | 0.00120 | 943.7152 | 0.0409 | 0.00355 | 0.0596 |
| Date | * | * | |
|---|---|---|---|
| September 2018–November 2018 | 2.31 | 2.6 | 0.18 |
| March 2019–May 2019 | 2.14 | 2.41 | 0.2 |
| June 2019–August 2019 | 3.62 | 4.07 | 0.2 |
| Parameter | Value |
|---|---|
| Population | 20 |
| Maximum iteration number | 60 |
| d | 1 |
| Weight updating factor (inertia weight) | 1 |
| Cognitive acceleration ( | 1 |
| Social acceleration ( | 1 |
| c1 | 2 |
| c2 | 2 |
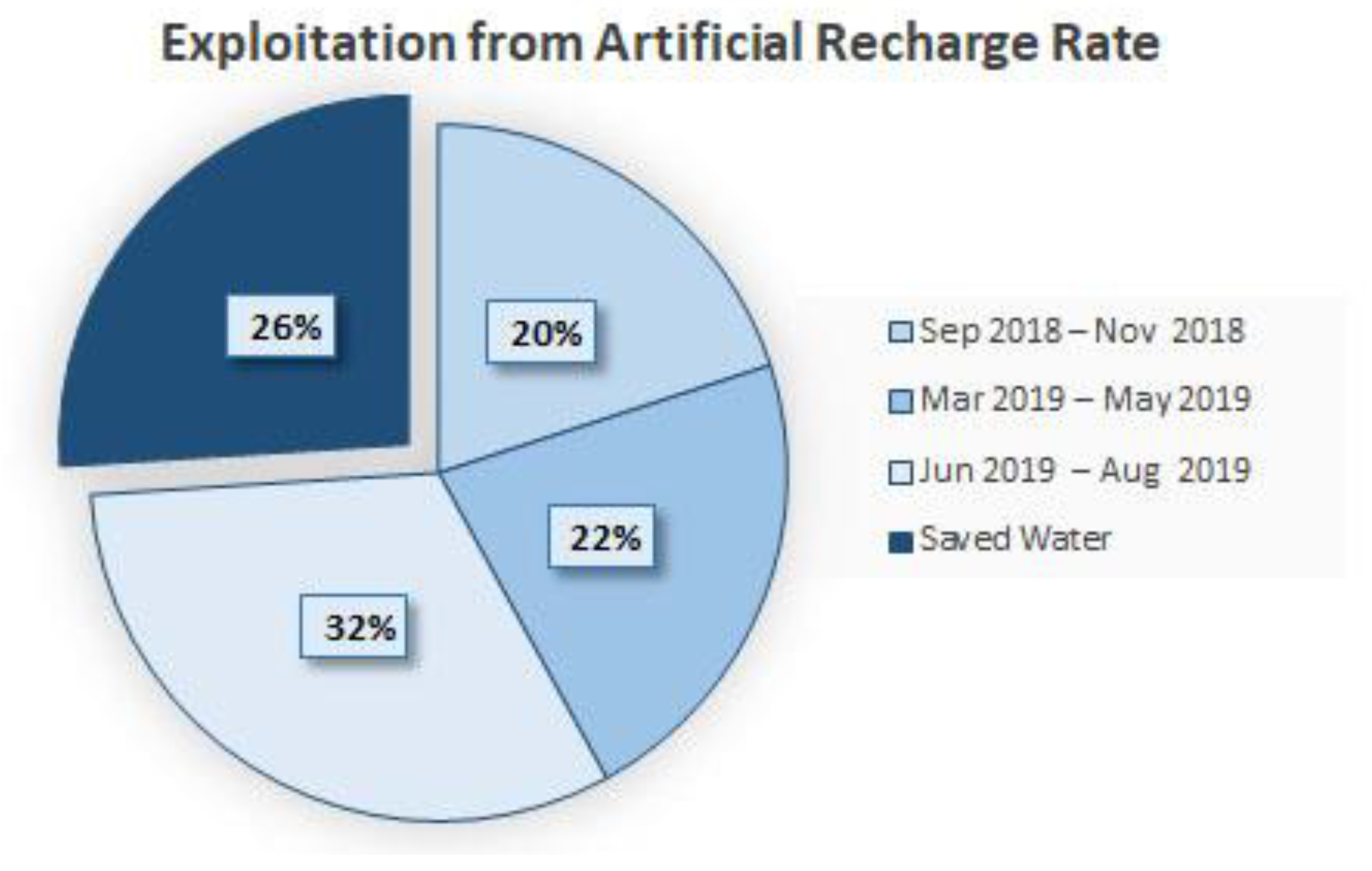
| Date | Minimum Exploitation Rate * | Optimal Exploitation Rate * | Maximum Exploitation Rate * | Exploitation from Artificial Recharge Rate * |
|---|---|---|---|---|
| September 2018–November 2018 | 2.31 | 2.51 | 2.6 | 0.2 |
| March 2019–May 2019 | 2.14 | 2.37 | 2.41 | 0.22 |
| June 2019–August 2019 | 3.62 | 3.94 | 4.07 | 0.32 |
| Total | 8.08 | 8.82 | 9.08 | 0.74 |
| Change in Hydraulic Conductivity | Optimal Exploitation under Artificial Recharge * | Change in Total |
|---|---|---|
| Basic | 0.75 | 0 |
| 50% | 0.6 | −18.9 |
| −50% | 0.72 | −2.7 |
| Change in Maximum Pumping Rate | Optimal Exploitation under Artificial Recharge * | Change in Total |
|---|---|---|
| Basic | 0.74 | 0 |
| Increasing the pumping rate | 0.77 | 4.1 |
| Decreasing the pumping rate | 0.5 | −32.4 |
| Change in Permissible Rate | Optimal Exploitation under Artificial Recharge * | Change in Total |
|---|---|---|
| Basic | 0.74 | 0 |
| 50% | 0.97 | 31.1 |
| −50% | 0.4 | −45.9 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maghsoudi, R.; Javadi, S.; Shourian, M.; Golmohammadi, G. Determining the Optimal Aquifer Exploitation under Artificial Recharge using the Combination of Numerical Models and Particle Swarm Optimization. Hydrology 2023, 10, 100. https://doi.org/10.3390/hydrology10050100
Maghsoudi R, Javadi S, Shourian M, Golmohammadi G. Determining the Optimal Aquifer Exploitation under Artificial Recharge using the Combination of Numerical Models and Particle Swarm Optimization. Hydrology. 2023; 10(5):100. https://doi.org/10.3390/hydrology10050100
Chicago/Turabian StyleMaghsoudi, Rahimeh, Saman Javadi, Mojtaba Shourian, and Golmar Golmohammadi. 2023. "Determining the Optimal Aquifer Exploitation under Artificial Recharge using the Combination of Numerical Models and Particle Swarm Optimization" Hydrology 10, no. 5: 100. https://doi.org/10.3390/hydrology10050100
APA StyleMaghsoudi, R., Javadi, S., Shourian, M., & Golmohammadi, G. (2023). Determining the Optimal Aquifer Exploitation under Artificial Recharge using the Combination of Numerical Models and Particle Swarm Optimization. Hydrology, 10(5), 100. https://doi.org/10.3390/hydrology10050100








