Superconducting Gravimeters: A Novel Tool for Validating Remote Sensing Evapotranspiration Products
Abstract
:1. Introduction
2. Study Site and Methodology
2.1. Study Site
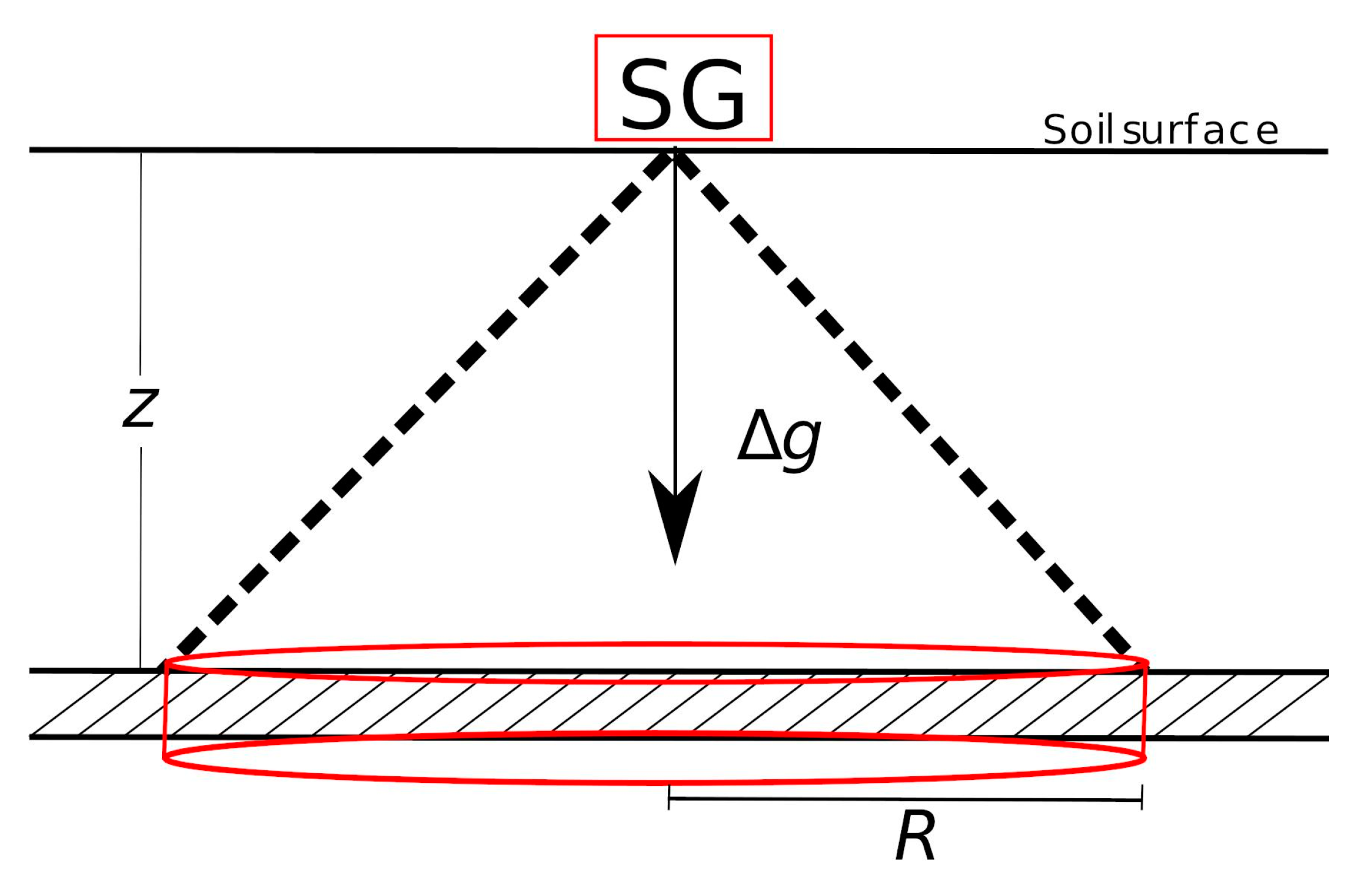
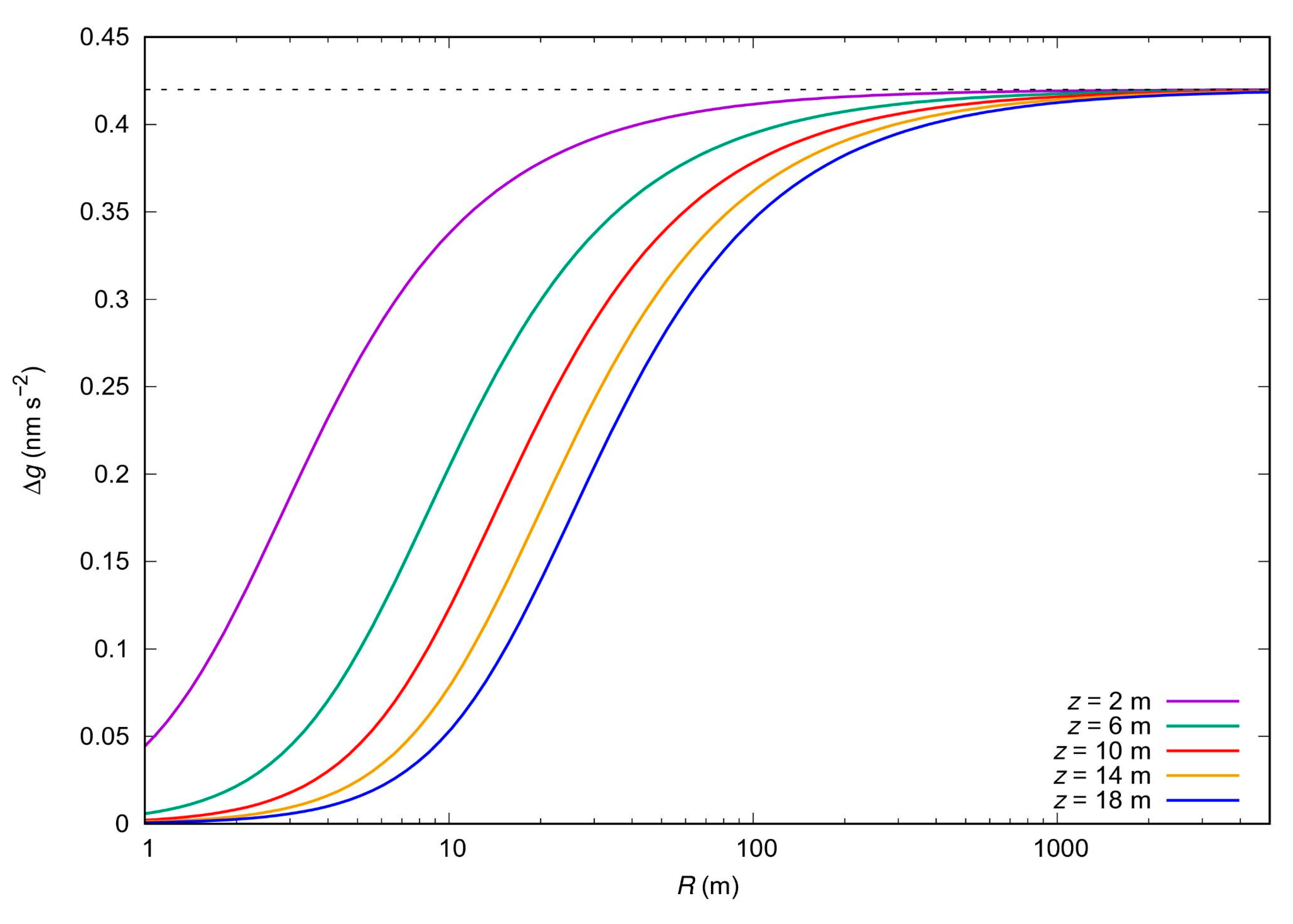
2.2. Superconducting Gravimeter
2.3. Ground-Truth ET Estimates Using SG Data
- Convert the raw SG data to gravity variations using the instrument-specific calibration factor.
- Removal of non-hydrological signals such as Earth tides, atmospheric and oceanic loading, polar motion effects, and instrumental drift using different models.
- The data processing described in the previous steps was performed by the International Geodynamics and Earth Tide Service (IGETS). This product (level 3) can be downloaded from the database of the Information System and Data Centre of the GFZ (GeoForschungsZentrum, Germany) [43].
- Sample precipitation data and gravimetric residuals on the same timescale (e.g., 8 days, one month, etc.).
- Calculate ET using Equation (6).
2.4. Description of the Data Set
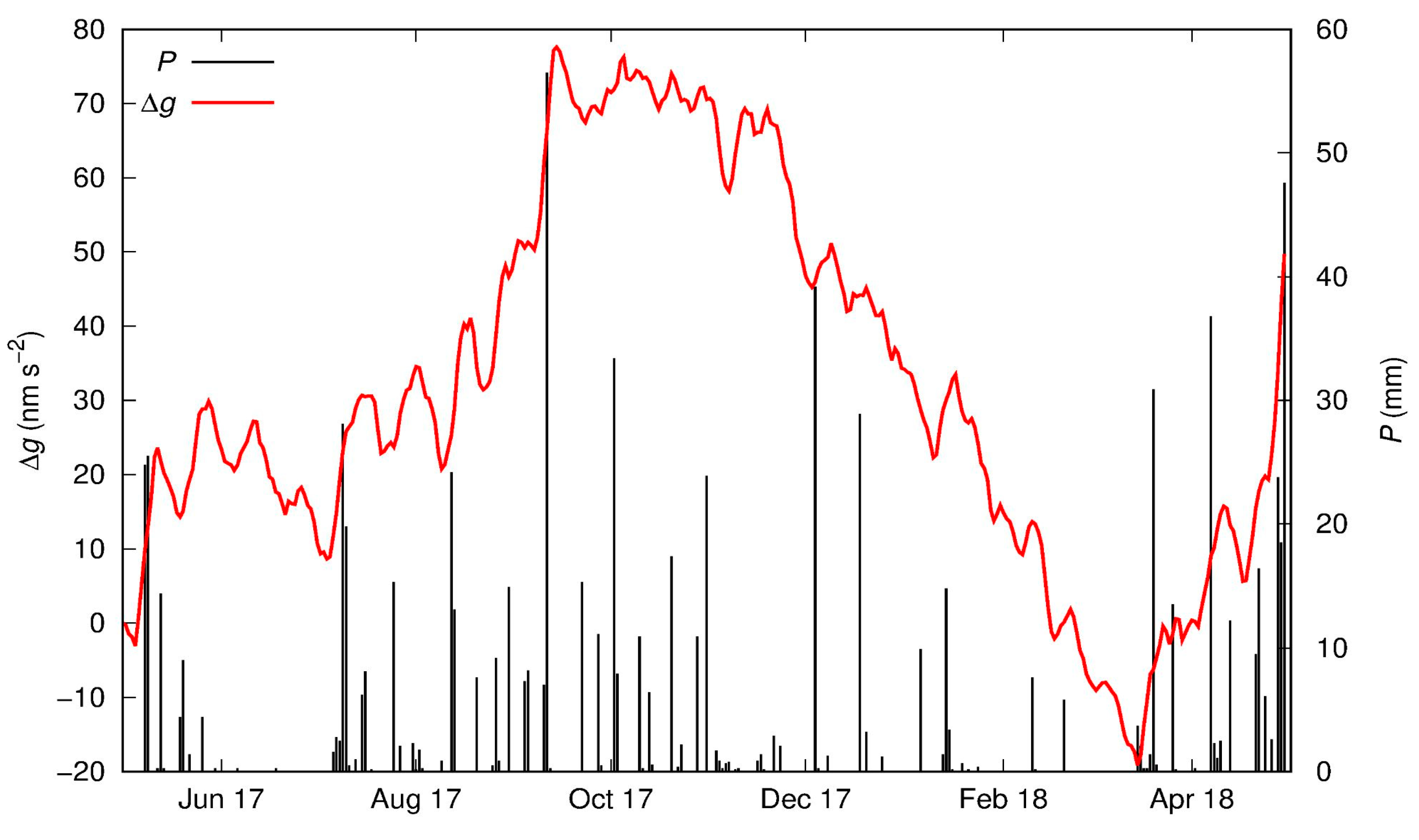
2.4.1. Gravity Residual and Water Storage Change Time Series
2.4.2. Precipitation
2.4.3. Satellite Data (MOD16A2)
2.5. Statistical Performance Metrics
3. Results
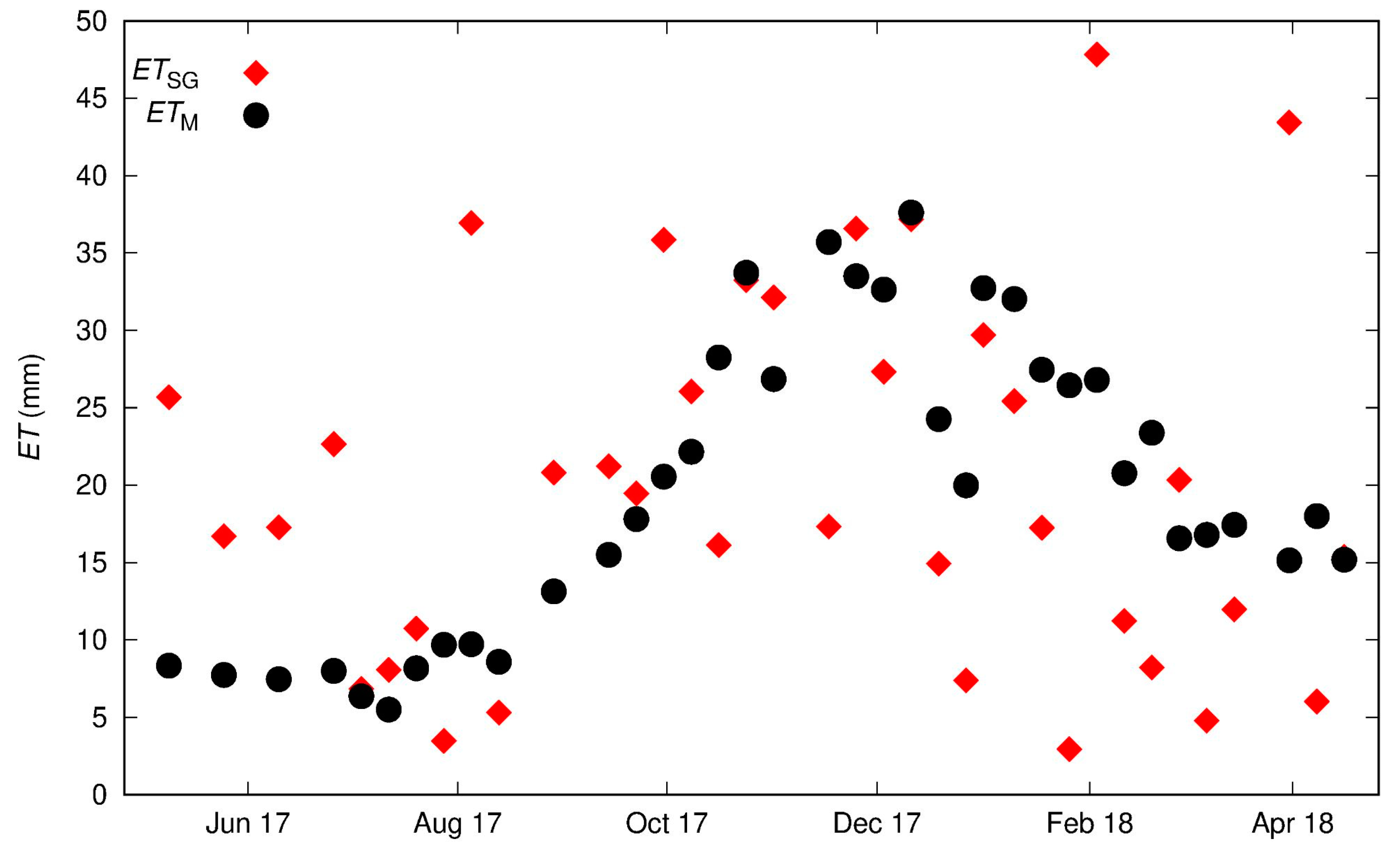
3.1. ET Estimates on an 8-Day Timescale
3.2. Estimation of Monthly ET
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhan, S.; Song, C.; Wang, J.; Sheng, Y.; Quan, J. A global assessment of terrestrial evapotranspiration increase due to surface water area change. Earth’s Future 2019, 7, 266–282. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhao, G.; Li, Y.; Zhou, L.; Gao, H. Evaporative water loss of 1.42 million global lakes. Nat. Commun. 2022, 13, 3686. [Google Scholar] [CrossRef] [PubMed]
- Ekpetere, K.; Abdelkader, M.; Ishaya, S.; Makwe, E.; Ekpetere, P. Integrating Satellite Imagery and Ground-Based Measurements with a Machine Learning Model for Monitoring Lake Dynamics over a Semi-Arid Region. Hydrology 2023, 10, 78. [Google Scholar] [CrossRef]
- Zhang, K.; Kimball, J.S.; Running, S.W. A review of remote sensing based actual evapotranspiration estimation. Wiley Interdisc. Rev. Water 2016, 3, 834–853. [Google Scholar] [CrossRef]
- Abdelkader, M.; Temimi, M.; Colliander, A.; Cosh, M.H.; Kelly, V.R.; Lakhankar, T.; Fares, A. Assessing the Spatiotemporal Variability of SMAP Soil Moisture Accuracy in a Deciduous Forest Region. Remote Sens. 2022, 14, 3329. [Google Scholar] [CrossRef]
- Garousi-Nejad, I.; Tarboton, D.G. A comparison of National Water Model retrospective analysis snow outputs at snow telemetry sites across the Western United States. Hydrol. Process. 2022, 36, e14469. [Google Scholar] [CrossRef]
- Abdelkader, M.; Temimi, M.; Ouarda, T.B. Assessing the National Water Model’s Streamflow Estimates Using a Multi-Decade Retrospective Dataset across the Contiguous United States. Water 2023, 15, 2319. [Google Scholar] [CrossRef]
- Güntner, A.; Reich, M.; Mikolaj, M.; Creutzfeldt, B.; Schroeder, S.; Wziontek, H. Landscape-scale water balance monitoring with an iGrav superconducting gravimeter in a field enclosure. Hydrol. Earth Syst. Sci. 2017, 21, 3167–3182. [Google Scholar] [CrossRef] [Green Version]
- Kandra, B.; Tall, A.; Gomboš, M.; Pavelková, D. Quantification of Evapotranspiration by Calculations and Measurements Using a Lysimeter. Water 2023, 15, 373. [Google Scholar] [CrossRef]
- Schrader, F.; Durner, W.; Fank, J.; Gebler, S.; Pütz, T.; Hannes, M.; Wollschläger, U. Estimating Precipitation and Actual Evapotranspiration from Precision Lysimeter Measurements. Procedia Environ. Sci. 2013, 19, 543–552. [Google Scholar] [CrossRef] [Green Version]
- Rana, G.; Katerji, N. Measurement and estimation of actual evapotranspiration in the field under Mediterranean climate: A review. Eur. J. Agric. 2000, 13, 125–153. [Google Scholar] [CrossRef]
- Creutzfeldt, B.; Güntner, A.; Wziontek, H.; Merz, B. Reducing local hydrology from high precision gravity measurements: A lysimeter-based approach. Geophys. J. Int. 2010, 183, 178–187. [Google Scholar] [CrossRef] [Green Version]
- Huo, S.; Jin, M.; Liang, X.; Hao, H. Estimating impacts of water-table depth on groundwater evaporation and recharge using lysimeter measurement data and bromide tracer. Hydrogeol. J. 2020, 28, 955–971. [Google Scholar] [CrossRef]
- Tapley, B.D.; Watkins, M.M.; Flechtner, F.; Reigber, C.; Bettadpur, S.; Rodell, M.; Sasgen, I.; Famiglietti, J.S.; Landerer, F.W.; Chambers, D.P.; et al. Contributions of GRACE to understanding climate change. Nat. Clim. Chang. 2019, 9, 358–369. [Google Scholar] [CrossRef]
- Long, D.; Longuevergne, L.; Scanlon, B.R. Global analysis ofapproaches for deriving total waterstorage changes from GRACE satellites. Water Resour. Res. 2015, 51, 2574–2594. [Google Scholar] [CrossRef] [Green Version]
- Rodell, M.; Velicogna, I.; Famiglietti, J.S. Satellite-based estimates of groundwater depletion in India. Nature 2009, 460, 999–1002. [Google Scholar] [CrossRef] [Green Version]
- Ciracì, E.; Velicogna, I.; Swenson, S. Continuity of the mass loss of the world's glaciers and ice caps from the GRACE and GRACE Follow-On missions. Geophy. Res. Let. 2020, 47, e2019GL086926. [Google Scholar] [CrossRef]
- Cesanelli, A.; Guarracino, L. Estimation of regional evapotranspiration in the extended Salado Basin (Argentina) from satellite gravity measurements. Hydrogeol. J. 2011, 19, 629–639. [Google Scholar] [CrossRef]
- Swenson, S.; Wahr, J.; Milly, P.C.D. Estimated accuracies of regional water storage variations inferred from the Gravity Recovery and Climate Experiment (GRACE). Water Resour. Res. 2003, 39, 1121–1134. [Google Scholar] [CrossRef]
- Sriwongsitanon, N.; Suwawong, T.; Thianpopirug, S.; Williams, J.; Jia, L.; Bastiaanssen, W. Validation of seven global remotely sensed ET products across Thailand using water balance measurements and land use classifications. J. Hydrol. Reg. Stud. 2020, 30, 100709. [Google Scholar] [CrossRef]
- Dile, Y.; Ayana, E.; Worqlul, A.; Xie, H.; Srinivasan, R.; Lefore, N.; You, L.; Clarke, N. Evaluating satellite-based evapotranspiration estimates for hydrological applications in data-scarce regions: A case in Ethiopia. Sci. Environ. 2020, 743, 140702. [Google Scholar] [CrossRef] [PubMed]
- Luo, Z.; Shao, Q.; Wan, W.; Li, H.; Chen, X.; Zhu, S.; Ding, X. A new method for assessing satellite-based hydrological data products using water budget closure. J. Hydrol. 2021, 594, 125927. [Google Scholar] [CrossRef]
- Creutzfeldt, B.; Güntner, A.; Vorogushyn, S.; Merz, B. The benefits of gravimeter observations for modelling water storage changes at the field scale. Hydrol. Earth Syst. Sci. 2010, 14, 1715–1730. [Google Scholar] [CrossRef] [Green Version]
- Naujoks, M.; Kroner, C.; Weise, A.; Jahr, T.; Krause, P.; Eisner, S. Evaluating local hydrological modelling by temporal gravity observations and a gravimetric three-dimensional model. Geophys. J. Int. 2010, 182, 233–249. [Google Scholar] [CrossRef] [Green Version]
- Kennedy, J.; Ferré, T.P.A.; Creutzfeld, B. Time-lapse gravity data for monitoring and modeling artificial recharge through a thick unsaturated zone. Water Resour. Res. 2016, 52, 7244–7261. [Google Scholar] [CrossRef] [Green Version]
- Pendiuk, J.E.; Guarracino, L.; Reich, M.; Brunini, C.; Güntner, A. Estimating the specific yield of the Pampeano aquifer, Argentina, using superconducting gravimeter data. Hydrogeol. J. 2020, 28, 2303–2313. [Google Scholar] [CrossRef]
- Van Camp, M.; de Viron, O.; Pajot-Métivier, G.; Casenave, F.; Watlet, A.; Dassargues, A.; Vanclooster, M. Direct measurement of evapotranspiration from a forest using a superconducting gravimeter. Geophys. Res. Lett. 2016, 43, 10225–10231. [Google Scholar] [CrossRef] [Green Version]
- Carrière, S.D.; Loiseau, B.; Champollion, C.; Ollivier, C.; Martin-StPaul, N.K.; Lesparre, N.; Olioso, A.; Hinderer, J.; Jougnot, D. The first evidence of correlation between evapotranspiration and gravity at a daily time scale from two vertically spaced superconducting gravimeters. Geophy. Res. Lett. 2021, 48, e2021GL096579. [Google Scholar] [CrossRef]
- Pendiuk, J. Modelado y Análisis de Problemas Hidrogravimétricos. Ph.D. Thesis, National University of La Plata, La Plata, Argentina, 2022. [Google Scholar]
- Bala, A.; Rawat, K.S.; Misra, A.K.; Srivastava, A. Assessment and validation of evapotranspiration using SEBAL algorithm and Lysimeter data of IARI agricultural farm, India. Geocarto Int. 2016, 31, 739–764. [Google Scholar] [CrossRef]
- Kumar, U.; Srivastava, A.; Kumari, N.; Rashmi, S.B.; Chatterjee, C.; Raghuwanshi, N.S. Evaluation of spatio-temporal evapotranspiration using satellite-based approach and lysimeter in the agriculture dominated catchment. J. Indian Soc. Remote Sens. 2021, 49, 1939–1950. [Google Scholar] [CrossRef]
- Sobrino, J.A.; Souza da Rocha, N.; Skoković, D.; Suélen Käfer, P.; López-Urrea, R.; Jiménez-Muñoz, J.C.; Alves Rolim, S.B. Evapotranspiration Estimation with the S-SEBI Method from Landsat 8 Data against Lysimeter Measurements at the Barrax Site, Spain. Remote Sens. 2021, 13, 3686. [Google Scholar] [CrossRef]
- Zoratipour, E.; Mohammadi, A.S.; Zoratipour, A. Evaluation of SEBS and SEBAL algorithms for estimating wheat evapotranspiration (case study: Central areas of Khuzestan province). Appl. Water Sci. 2023, 13, 137. [Google Scholar] [CrossRef]
- Zhao, J.; Chen, X.; Zhang, J.; Zhao, H.; Song, Y. Higher temporal evapotranspiration estimation with improved SEBS model from geostationary meteorological satellite data. Sci. Rep. 2019, 9, 14981. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cui, Y.; Jia, L. Estimation of evapotranspiration of “soil-vegetation” system with a scheme combining a dual-source model and satellite data assimilation. J. Hydrol. 2021, 603, 127145. [Google Scholar] [CrossRef]
- Mokhtari, A.; Sadeghi, M.; Afrasiabian, Y.; Yu, K. OPTRAM-ET: A novel approach to remote sensing of actual evapotranspiration applied to Sentinel-2 and Landsat-8 observations. Remote Sens. Environ. 2023, 286, 113443. [Google Scholar] [CrossRef]
- Pimentel, R.; Arheimer, B.; Crochemore, L.; Andersson, J.C.M.; Pechlivanidis, I.G.; Gustafsson, D. Which potential evapotranspiration formula to use in hydrological modeling world-wide? Water Res. Res. 2023, 59, e2022WR033447. [Google Scholar] [CrossRef]
- Tasumi, M. Estimating evapotranspiration using METRIC model and Landsat data for better understandings of regional hydrology in the western Urmia Lake Basin. Agric. Water Manag. 2019, 226, 105805. [Google Scholar] [CrossRef]
- Xiang, K.; Li, Y.; Horton, R.; Feng, H. Similarity and difference of potential evapotranspiration and reference crop evapotranspiration—A review. Agric. Water Manag. 2020, 232, 106043. [Google Scholar] [CrossRef]
- Degano, M.F.; Carmona, F.; Olivera-Rodríguez, P.; Faramiñán, A.; Rivas, R.; Bayala, M.; Niclòs-Corts, R. Analysis of Priestley-Taylor method in different environments and coverages. In Proceedings of the XIX Workshop on Information Processing and Control (RPIC), San Juan, Argentina, 3–5 November 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Degano, M.F.; Rivas, R.E.; Carmona, F.; Niclòs, R.; Sánchez, J.M. Evaluation of the MOD16A2 evapotranspiration product in an agricultural area of Argentina, the Pampas region. Egypt J. Remote Sens. Space Sci. 2020, 24, 319–328. [Google Scholar] [CrossRef]
- Wziontek, H.; Wolf, P.; Häfner, M.; Hase, H.; Nowak, I.; Rülke, A.; Wilmes, H.; Brunini, C. Superconducting Gravimeter Data from AGGO/La Plata—Level 1. GFZ Data Serv. 2017. [Google Scholar] [CrossRef]
- Mikolaj, M.; Güntner, A.; Brunini, C.; Wziontek, H.; Gende, M.; Schröder, S.; Pasquaré, A.; Cassino, A.M.; Reich, M.; Hartmann, A.; et al. Hydrometeorological and gravity data from the Argentine-German Geodetic Observatory in La Plata. GFZ Data Serv. 2018. [Google Scholar] [CrossRef]
- Nossetto, M.D.; Paez, R.A.; Ballesteros, S.I.; Jobbágy, E.G. Higher water-table and flooding risk under grain vs. livestock production systems in the subhumid plains of the Pampas. Agric. Ecosyst. Environ. 2015, 206, 60–70. [Google Scholar] [CrossRef]
- Hinderer, J.; Crossley, D.; Warburton, R.J. Superconducting Gravimetry. In Treatise on Geophysics, 2nd ed.; 3 Geodesy; Herring, T., Schubert, G., Eds.; Elsevier: Amsterdam, The Netherlands, 2015; pp. 59–115. [Google Scholar] [CrossRef]
- Hector, B.; Hinderer, J.; Séguis, L.; Boy, J.-P.; Calvo, M.; Descloitres, M.; Rosat, S.; Galle, S.; Riccardi, U. Hydro-gravimetry in West-Africa: First results from the Djougou (Benin) superconducting gravimeter. J. Geodyn. 2014, 80, 34–49. [Google Scholar] [CrossRef]
- Telford, W.M.; Geldart, L.P.; Sheriff, R.E. Applied Geophysics, 2nd ed.; Cambridge University Press: New York, NY, USA, 1992. [Google Scholar]
- Van Camp, M.; de Viron, O.; Watlet, A.; Meurers, B.; Francis, O.; Caudron, C. Geophysics from terrestrial time-variable gravity measurements. Rev. Geoph. 2017, 55, 938–992. [Google Scholar] [CrossRef]
- Voigt, C.; Schulz, K.; Koch, F.; Wetzel, K.-F.; Timmen, L.; Rehm, T.; Pflug, H.; Stolarczuk, N.; Förste, C.; and Flechtner, F. Technical note: Introduction of a superconducting gravimeter as novel hydrological sensor for the Alpine research catchment Zugspitze. Hydrol. Earth Syst. Sci. 2021, 25, 5047–5064. [Google Scholar] [CrossRef]
- Reich, M.; Mikolaj, M.; Blume, T.; Güntner, A. Reducing gravity data for the influence of water storage variations beneath observatory buildings. Geophysics 2019, 84, EN15–EN31. [Google Scholar] [CrossRef]
- Mikolaj, M.; Güntner, A.; Brunini, C.; Wziontek, H.; Gende, M.; Schröder, S.; Cassino, A.M.; Pasquaré, A.; Reich, M.; Hartmann, A.; et al. Hydrometerological and gravity signals at the Argentine-German Geodetic Observatory (AGGO) in La Plata. Earth Syst. Sci. Data Discuss. 2019, 11, 1501–1513. [Google Scholar] [CrossRef] [Green Version]
- Mu, Q.Z.; Zhao, M.S.; Running, S.W. Improvements to a MODIS global terrestrial evapotranspiration algorithm. Remote Sens. Environ. 2011, 115, 1781–1800. [Google Scholar] [CrossRef]
- Ruhoff, A.L.; Paz, A.R.; Aragao, L.E.O.C.; Mu, Q.; Malhi, Y.; Collischonn, W. Assessment of the MODIS global evapotranspiration algorithm using eddy covariance measurements and hydrological modelling in the Rio Grande basin. Hydrol. Sci. J. 2013, 58, 1658–1676. [Google Scholar] [CrossRef]
- Hu, G.; Jia, L.; Menenti, M. Comparison of MOD16 and LSA-SAF MSG evapotranspiration products over Europe for 2011. Remote Sens. Environ. 2015, 156, 510–526. [Google Scholar] [CrossRef]
- Kim, H.W.; Hwang, K.; Mu, Q.; Lee, S.O.; Choi, M. Validation of MODIS 16 global terrestrial evapotranspiration products in various climates and land cover types in Asia. KSCE J. Civ. Eng. 2012, 16, 229–238. [Google Scholar] [CrossRef]
- Monteith, J.; Unsworth, M. Principles of Environmental Physics; Edward Arnold: London, UK, 1990; 291p. [Google Scholar]
- Mu, Q.Z.; Heinsch, F.A.; Zhao, M.S.; Running, S.W. Development of a global evapotranspiration algorithm based MODIS and global meteorology data. Remote Sens. Environ. 2007, 111, 519–536. [Google Scholar] [CrossRef]
- Running, S.W.; Mu, Q.Z.; Zhao, M.S. MOD16A2 MODIS/Terra Net Evapotranspiration 8-Day L4 Global 500m SIN Grid V006 [Data Set]. NASA EOSDIS Land Processes DAAC. 2017. Available online: https://lpdaac.usgs.gov/products/mod16a2v006/ (accessed on 27 September 2022).
- Jacovides, C.P.; Kontoyiannis, H. Statistical procedures for the evaluation of evapotranspiration computing models. Agric. Water Manag. 1995, 27, 365–371. [Google Scholar] [CrossRef]
- Hodson, T.O. Root-mean-square error (RMSE) or mean absolute error (MAE): When to use them or not. Geosci. Model Dev. 2022, 15, 5481–5487. [Google Scholar] [CrossRef]
- NOAA. What Is a Perigean Spring Tide? National Ocean Service Website. Available online: https://oceanservice.noaa.gov/facts/perigean-spring-tide.html (accessed on 18 June 2023).
- Fisher, J.B.; Tu, K.P.; Baldocchi, D.D. Global estimates of the land–atmosphere water flux based on monthly AVHRR and ISLSCP-II data, validated at 16 FLUXNET sites. Remote Sens. Environ. 2008, 112, 901–919. [Google Scholar] [CrossRef]
- Brust, C.; Kimball, J.S.; Maneta, M.P.; Jencso, K.; He, M.; Reichle, R.H. Using SMAP Level-4 soil moisture to constrain MOD16 evapotranspiration over the contiguous USA. Remote Sens. Environ. 2021, 255, 112277. [Google Scholar] [CrossRef]

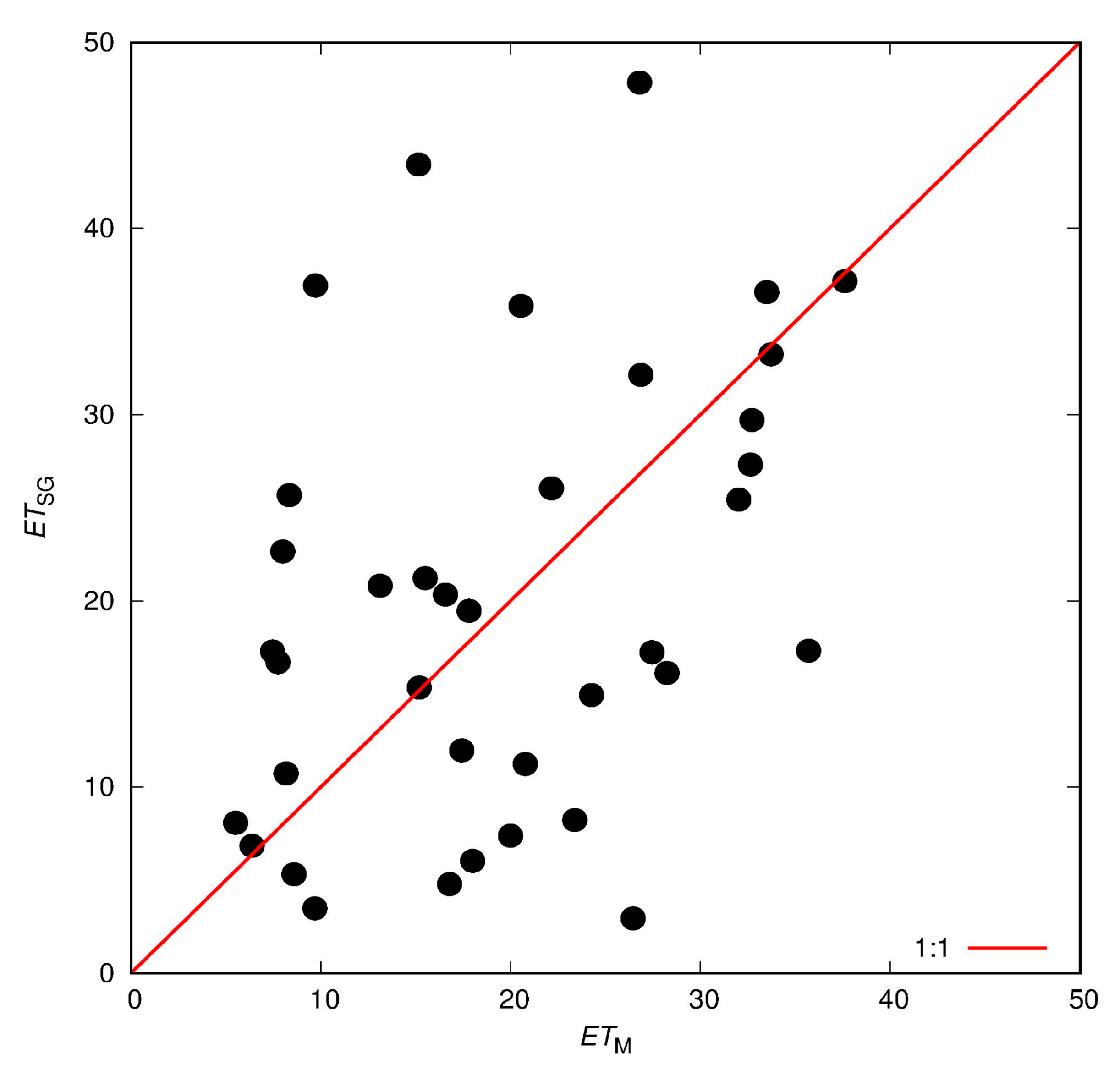
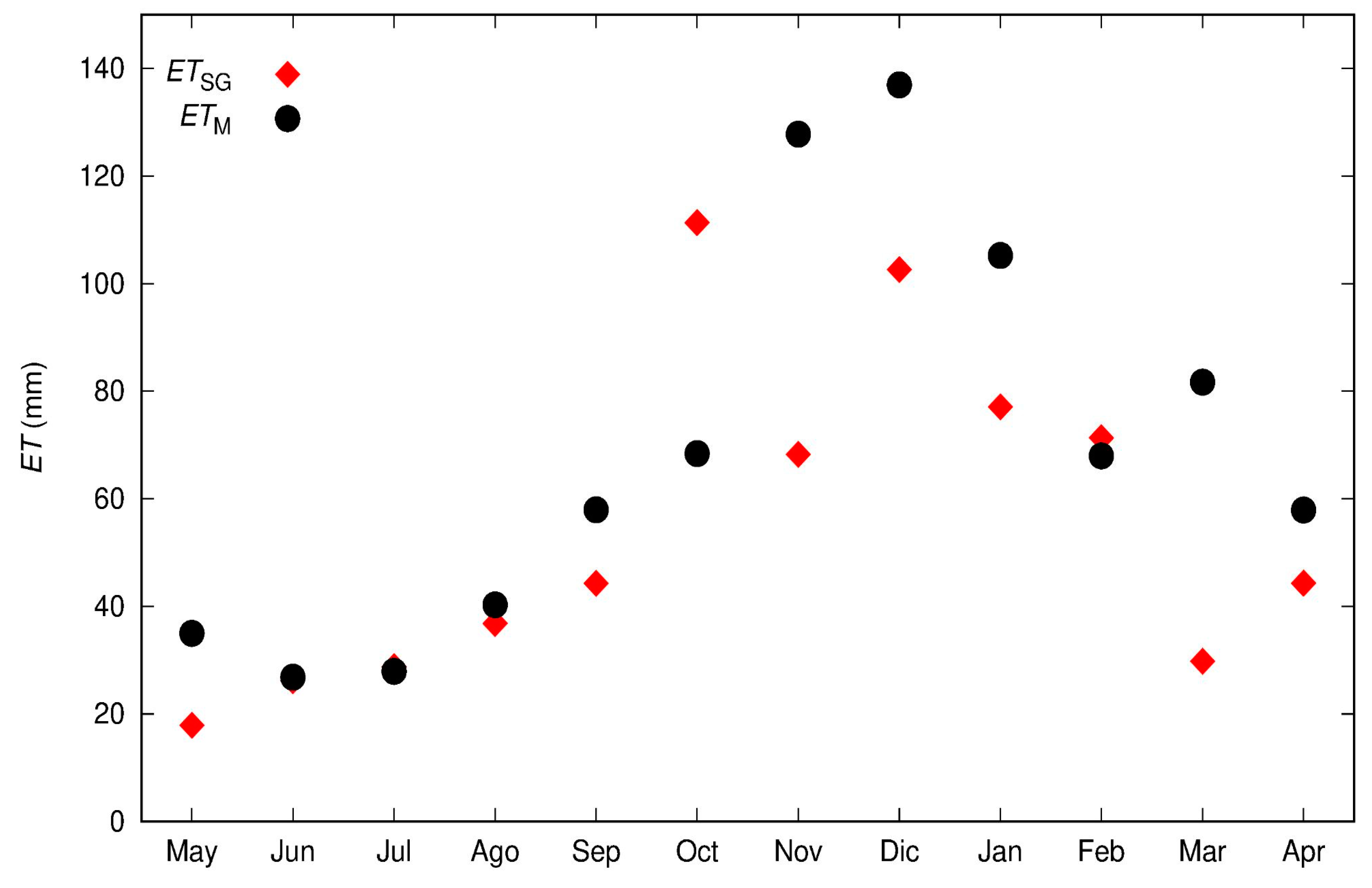
| Coefficient (Units) | Value at 8-Day Scale | Value at Monthly Scale |
|---|---|---|
| MAE (mm) | 9.32 | 24.5 |
| RMSE (mm) | 11.9 | 32.6 |
| r (-) | 0.4 | 0.7 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pendiuk, J.; Degano, M.F.; Guarracino, L.; Rivas, R.E. Superconducting Gravimeters: A Novel Tool for Validating Remote Sensing Evapotranspiration Products. Hydrology 2023, 10, 146. https://doi.org/10.3390/hydrology10070146
Pendiuk J, Degano MF, Guarracino L, Rivas RE. Superconducting Gravimeters: A Novel Tool for Validating Remote Sensing Evapotranspiration Products. Hydrology. 2023; 10(7):146. https://doi.org/10.3390/hydrology10070146
Chicago/Turabian StylePendiuk, Jonatan, María Florencia Degano, Luis Guarracino, and Raúl Eduardo Rivas. 2023. "Superconducting Gravimeters: A Novel Tool for Validating Remote Sensing Evapotranspiration Products" Hydrology 10, no. 7: 146. https://doi.org/10.3390/hydrology10070146
APA StylePendiuk, J., Degano, M. F., Guarracino, L., & Rivas, R. E. (2023). Superconducting Gravimeters: A Novel Tool for Validating Remote Sensing Evapotranspiration Products. Hydrology, 10(7), 146. https://doi.org/10.3390/hydrology10070146






