Long-Term Groundwater Level Prediction Model Based on Hybrid KNN-RF Technique
Abstract
:1. Introduction
2. Related Work
3. Case Study and Data Processing
3.1. Study Area and Data
3.2. Data Preparation
Model Performance and Evaluation Measures
4. Methodology
4.1. K-Nearest Neighbor
- To anticipate the target value, we perform the following steps:
- Use Equation (8) to calculate the distance between a new sample and each of the adjacent points.
- Sort all values calculated in step 1 by increasing order.
- Utilize the greedy search technique to determine the optimal value of K, based on RMSE.
- Enumerate an inverse distance weighted mean using K neighboring examples.
- Return average as the approximated value.
4.2. Artificial Neural Network
4.3. Support Vector Machine
4.4. Random Forest
- Randomly fetch different subsets from a given dataset .
- Use sampled data to create decision trees.
- Enumerate average of the votes from the decision trees.
- Return the average as the final approximated value.
4.5. KNN-RF Ensemble
- Supports using fewer samples to adequately represent data distribution.
- Limits the generalization error.
- Controls variance in a small dataset.
- Relieves the processing burden for model selection.
4.6. Tuning Parameter and Input Selection
4.7. Training and Testing of the Model
4.8. Prediction of Seasonal Changes in Groundwater Depths
5. Experimental Results and Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| MDPI | Multidisciplinary Digital Publishing Institute |
| DOAJ | Directory of open access journals |
| TLA | Three letter acronym |
| LD | linear dichroism |
| RF | Random Forest |
| KNN | K-nearest Neighbor |
| ANN | Artificial Neural Network |
| KNN-RF | K-Nearest Neighbor-Random Forest ensemble model |
| MSE | Mean Squared Error |
| RMSE | Root Mean Squared Error |
| NSE | Nash-Sutcliffe Efficiency |
| MAE | Mean Absolute Error |
| Coefficient of determination | |
| SVM | Support Vector Machine |
| GP | Genetical Programming |
| ELM | Extreme Learning Machine |
| ML | Machine Learning |
| ASCE | American Society of Civil Engineers |
| RWFA | Rwanda Water and Forestry Authority |
| Station ID | Groundwater Station Identification Number |
| MeteoRwanda | Meteorological Agency of Rwanda |
References
- Robins, N.S.; Fergusson, J. Groundwater scarcity and conflict–managing hotspots. Earth Perspect. 2014, 1, 6. [Google Scholar] [CrossRef]
- Khosravi, K.; Pham, B.T.; Chapi, K.; Shirzadi, A.; Dou, J.; Revhaug, I.; Prakash, I.; Bui, D.T. A comparative assessment of decision trees algorithms for flash flood susceptibility modeling at Haraz watershed, northern Iran. Sci. Total. Environ. 2018, 627, 744–755. [Google Scholar] [CrossRef] [PubMed]
- Rulli, M.C.; D’Odorico, P. The water footprint of land grabbing. Geophys. Res. Lett. 2013, 40, 6130–6135. [Google Scholar] [CrossRef]
- Macdonald, A.; Bonsor, H.C.; Dochartaigh, B.É.Ó.; Taylor, R.G. Quantitative maps of groundwater resources in Africa. Environ. Res. Lett. 2012, 7, 024009. [Google Scholar] [CrossRef]
- Döll, P.; Hoffmann-Dobrev, H.; Portmann, F.; Siebert, S.; Eicker, A.; Rodell, M.; Strassberg, G.; Scanlon, B.R. Impact of water withdrawals from groundwater and surface water on continental water storage variations. J. Geodyn. 2012, 59, 143–156. [Google Scholar] [CrossRef]
- Healy, R.W. The future of groundwater in sub-Saharan Africa. Nature 2019, 572, 185–187. [Google Scholar] [CrossRef]
- Castellazzi, P.; Martel, R.; Galloway, D.L.; Longuevergne, L.; Rivera, A. Assessing groundwater depletion and dynamics using GRACE and InSAR: Potential and limitations. Ground Water 2016, 54, 768–780. [Google Scholar] [CrossRef] [Green Version]
- Macdonald, A.; Bonsor, H.C.; Ahmed, K.M.; Burgess, W.; Basharat, M.; Calow, R.C.; Dixit, A.; Foster, S.S.D.; Gopal, K.; Lapworth, D.J.; et al. Groundwater quality and depletion in the Indo-Gangetic Basin mapped from in situ observations. Nat. Geosci. 2016, 9, 762–766. [Google Scholar] [CrossRef]
- Richey, A.S.; Thomas, B.; Lo, M.-H.; Reager, J.T.; Famiglietti, J.; Voss, K.; Swenson, S.; Rodell, M. Quantifying renewable groundwater stress with GRACE. Water Resour. Res. 2015, 51, 5217–5238. [Google Scholar] [CrossRef] [PubMed]
- Makoto, T. Groundwater as a Key of Adaptation to Climate Change. In Groundwater as a Key for Adaptation to Changing Climate and Society; Springer: Tokyo, Japan, 2014; Volume 6, pp. 17–27. [Google Scholar]
- Water, U.N. Wastewater Management—A UN-Water Analytical Brief; UN Water: New York, NY, USA, 2015. [Google Scholar]
- Hass, J.C.; Birk, S. Characterizing the spatiotemporal variability of groundwater levels of alluvial aquifers in different settings using drought indices. Hydrol. Earth Syst. Sci. 2017, 21, 2421–2448. [Google Scholar] [CrossRef] [Green Version]
- De Graaf, I.; Van Beek, R.L.; Gleeson, T.; Moosdorf, N.; Schmitz, O.; Sutanudjaja, E.H.; Bierkens, M.F.P. A global-scale two-layer transient groundwater model: Development and application to groundwater depletion. Adv. Water Resour. 2017, 102, 53–67. [Google Scholar] [CrossRef]
- Rathay, S.; Allen, D.; Kirste, D. Response of a fractured bedrock aquifer to recharge from heavy rainfall events. J. Hydrol. 2018, 561, 1048–1062. [Google Scholar] [CrossRef] [Green Version]
- Stoll, S.; Franssen, H.H.; Butts, M.; Kinzelbach, W. Analysis of the impact of climate change on groundwater related hydrological fluxes: A multimodel approach including different downscaling methods. Hydrol. Earth Syst. Sci. 2011, 15, 21–38. [Google Scholar] [CrossRef] [Green Version]
- Cuthbert, M.O.; Tindimugaya, C. The importance of preferential flow in controlling groundwater recharge in tropical Africa and implications for modelling the impact of climate change on groundwater resources. J. Water Clim. Chang. 2010, 1, 234–245. [Google Scholar] [CrossRef] [Green Version]
- Yu, H.; Feng, Q. Comparative study of hybrid-wavelet artificial intelligence models for monthly groundwater depth forecasting in extreme arid regions, Northwest China. Water Resour. Manag. 2018, 32, 301–323. [Google Scholar] [CrossRef]
- Uhlemann, S.; Smith, A.; Chambers, J.; Dixon, N.; Dijkstra, T.; Haslam, E.; Meldrum, P.; Merritt, A.; Gunn, D.; Mackay, J. Assessment of ground-based monitoring techniques applied to landslide investigations. Geomorphol. 2016, 253, 438–451. [Google Scholar] [CrossRef] [Green Version]
- Yang, W. The Hydroclimate of East Africa: Seasonal Cycle, Decadal Variability, and Human-Induced Climate Change. Ph.D. Thesis, Columbia University, New York, NY, USA, 2015. [Google Scholar]
- Hyland, M.; Russ, J. Water as destiny- The long-term impacts of drought in sub-Saharan Africa. World Dev. 2019, 115, 30–45. [Google Scholar] [CrossRef]
- Xu, Y.; Seward, P.; Gaye, C.; Lin, L.; Olago, D.O. Preface: Groundwater in sub-Saharan Africa. Hydrogeol. J. 2019, 27, 815–822. [Google Scholar] [CrossRef] [Green Version]
- Van Engelenburg, J.; Hueting, R.; Rijpkema, S.; Teuling, A.J.; Uijlenhoet, R.; Ludwig, F. Impact of changes in groundwater extractions and climate change on groundwater-dependent ecosystems in a complex hydrogeological setting. Water Resour. Manag. 2018, 32, 259–272. [Google Scholar] [CrossRef] [Green Version]
- Matengu, B.; Xu, Y.; Tordiffe, E. Hydrogeological characteristics of the Omaruru Delta Aquifer System in Namibia. Hydrogeol. J. 2019, 27, 857–883. [Google Scholar] [CrossRef]
- Aboniyo, J.; Umulisa, D.; Bizimana, A.; Kwisanga, J.M.P.; Mourad, K.A. National Water Resources Management Authority for a Sustainable Water Use in Rwanda. Sustain. Resour. Manag. J. 2017, 2, 1–15. [Google Scholar]
- Abimbola, O.; Wenninger, J.; Venneker, R.; Mittelstet, A. The assessment of water resources in ungauged catchments in Rwanda. J. Hydrol. Reg. Stud. 2017, 13, 274–289. [Google Scholar] [CrossRef]
- Report Strategic Programme for Climate Resilience. 2017. Available online: https://www.climateinvestmentfunds.org/sites/cif_enc/files/knowledge-documents/rwanda_spcr_2017pdf.pdf (accessed on 26 October 2019).
- Ministry of Natural Resources. Water Resources Management Sub-Sector Strategic Plan (2011–2015). 2011. Available online: http://minirena.gov.rw/fileadmin/Land_Subsector/Water/Rwanda-Waterstrategy-04062011-final-1006-corrected1406_01.pdf (accessed on 26 October 2019).
- Gong, H.; Pan, Y.; Zheng, L.; Li, X.; Zhu, L.; Zhang, C.; Huang, Z.; Li, Z.; Wang, H.; Zhou, C. Long-term groundwater storage changes and land subsidence development in the North China Plain (1971–2015). Hydrogeol. J. 2018, 26, 1417–1427. [Google Scholar] [CrossRef] [Green Version]
- Tang, Q.; Oki, T. (Eds.) Terrestrial Water Cycle and Climate Change: Natural and Human-Induced Impacts; John Wiley & Sons: Hoboken, NJ, USA, 2016; Volume 221. [Google Scholar]
- Kenda, K.; Čerin, M.; Bogataj, M.; Senožetnik, M.; Klemen, K.; Pergar, P.; Laspidou, C.; Mladenic, D. Groundwater Modeling with Machine Learning Techniques: Ljubljana polje Aquifer. Multidiscip. Digit. Publ. Inst. Proc. 2018, 2, 697. [Google Scholar] [CrossRef] [Green Version]
- Shortridge, J.E.; Guikema, S.D.; Zaitchik, B.F. Machine learning methods for empirical streamflow simulation: A comparison of model accuracy, interpretability, and uncertainty in seasonal watersheds. Hydrol. Earth Syst. Sci. 2016, 20, 2611–2628. [Google Scholar] [CrossRef] [Green Version]
- Kasiviswanathan, K.S.; Saravanan, S.; Balamurugan, M.; Saravanan, K. Genetic programming based monthly groundwater forecast models with uncertainty quantification. Model. Earth Syst. Environ. 2016, 2, 27. [Google Scholar] [CrossRef] [Green Version]
- Nguyen, D.; Ouala, S.; Drumetz, L.; Fablet, R. EM-like Learning Chaotic Dynamics from Noisy and Partial Observations. arXiv 2019, arXiv:1903.10335. [Google Scholar]
- Brajard, J.; Carrassi, A.; Bocquet, M.; Bertino, L. Combining data assimilation and machine learning to emulate a dynamical model from sparse and noisy observations: A case study with the Lorenz 96 model. arXiv 2020, arXiv:2001.01520. [Google Scholar]
- Sahoo, S.; Russo, T.A.; Elliott, J.; Foster, I. Machine Learning Algorithms for Modeling Groundwater Level Changes in Agricultural Regions of the U.S. Water Resour. Res. 2017, 53, 3878–3895. [Google Scholar] [CrossRef]
- Mohanty, S.; Jha, M.K.; Raul, S.K.; Panda, R.K.; Sudheer, K.P. Using artificial neural network approach for simultaneous forecasting of weekly groundwater levels at multiple sites. Water Resour. Manag. 2008, 29, 5521–5532. [Google Scholar] [CrossRef]
- ASCE Task Committee on Application of Artificial Neural Networks in Hydrology. Artificial Neural Networks in Hydrology. I: Preliminary concepts. J. Hydrol. Eng. 2000, 5, 115–123. [Google Scholar] [CrossRef]
- Peng, T.; Zhou, J.; Zhang, C.; Fu, W. Streamflow forecasting using empirical wavelet transform and artificial neural networks. Water 2017, 9, 406. [Google Scholar] [CrossRef] [Green Version]
- Nourani, V.; Andalib, G. Daily and monthly suspended sediment load predictions using wavelet based artificial intelligence approaches. J. Mt. Sci. 2015, 12, 85–100. [Google Scholar] [CrossRef]
- Izady, A.; Davary, K.; Alizadeh, A.; Nia, A.M.; Ziaei, A.N.; Hasheminia, S.M. Application of NN-ARX model to predict groundwater levels in the Neishaboor Plain, Iran. Water Resour. Manag. 2013, 27, 4773–4794. [Google Scholar] [CrossRef]
- Uddameri, V. Using statistical and artificial neural network models to forecast potentiometric levels at a deep well in South Texas. Environ. Geol. 2007, 51, 885–895. [Google Scholar] [CrossRef]
- Besaw, L.E.; Rizzo, D.M.; Bierman, P.; Hackett, W.R. Hackett. Advances in ungauged streamflow prediction using artificial neural networks. J. Hydrol. 2010, 386, 27–37. [Google Scholar] [CrossRef]
- Graham, F.; Wong, T. System and Method for Using an Artificial Neural Network to Simulate Pipe Hydraulics a Reservoir Simulator. U.S. Patent 10055684, 21 August 2018. [Google Scholar]
- Raghavendra, N.; Deka, P. Support vector machine applications in the field of hydrology: A review. Appl. Soft Comput. 2014, 19, 372–386. [Google Scholar] [CrossRef]
- Huang, S.; Chang, J.; Huang, Q.; Chen, Y. Monthly streamflow prediction using modified EMD-based support vector machine. J. Hydrol. 2014, 511, 764–775. [Google Scholar] [CrossRef]
- Wen, X.; Si, J.; He, Z.; Wu, J.; Shao, H.; Yu, H. Support-vector-machine-based models for modeling daily reference evapotransiration with limited data in extreme arid regions. Water Resour. Manag. 2015, 29, 3195–3209. [Google Scholar] [CrossRef]
- Kisi, O.; Parmar, K.S. Application of least square support vector machine and multivariate adaptive regression spline models in long term prediction of river water pollution. J. Hydrol. 2016, 534, 104–112. [Google Scholar] [CrossRef]
- Sun, W.; Trevor, B. Combining k-nearest-neighbor models for annual peak breakup flow forecasting. Cold Reg. Sci. Technol. 2017, 143, 59–69. [Google Scholar] [CrossRef]
- Lguensat, R.; Tandeo, P.; Ailliot, P.; Pulido, M.; Fablet, R. The analog data assimilation. Mon. Weather Rev. 2017, 145, 4093–4107. [Google Scholar] [CrossRef] [Green Version]
- Zhou, T.; Wang, F.; Yang, Z. Comparative analysis of ANN and SVM models combined with wavelet preprocess for groundwater depth prediction. Water 2018, 9, 781. [Google Scholar] [CrossRef] [Green Version]
- Gong, Y.; Zhang, Y.; Lan, S.; Wang, H. A comparative study of artificial neural networks, support vector machine, and adaptive neuro fuzzy inference system for forecasting groundwater levels near Lake Okeechobee, Florida. Water Resour. Manag. 2016, 30, 375–391. [Google Scholar] [CrossRef]
- Mokhtarzad, M.; Eskandari, F.; Vanjani, N.J.; Arabasadi, A. Drought forecasting by ANN, ANFIS, and SVM and comaprison of the models. Environ. Earth Sci. 2017, 76, 729. [Google Scholar] [CrossRef]
- Natarajan, N.; Sudheer, C. Groundwater levels forecasting using soft computing techniques. Neural Comput. Appl. 2020, 32, 7691–7708. [Google Scholar] [CrossRef]
- Suryanarayana, C.; Sudheer, C.; Mahammood, V.; Panigrahi, B. An integrated wavelet-support vector machine for groundwater level prediction in Visakhapatnam, India. Neurocomputing 2014, 145, 324–335. [Google Scholar] [CrossRef]
- Guzman, S.M.; Paz, J.O.; Tagert, M.L.M.; Mercer, A.E. Artificial neural networks and support vector machines: Contrast study for groundwater level prediction. ASABE Annu. Inter. Natl. Meet. Pap. 2015, 152181983. [Google Scholar] [CrossRef]
- Guzman, S.M.; Paz, J.O.; Tagert, M.L.M.; Mercer, A.E.; Pote, J.W. An integrated SVR and crop model to estimate the impacts of irrigation on daily groundwater levels. Agric. Syst. 2018, 159, 248–259. [Google Scholar] [CrossRef]
- Wunsch, A.; Liesch, T.; Broda, S. Forecasting Groundwater Levels using nonlinear autoregressive networks with exogenous input (NARX). J. Hydrol. 2018, 567, 743–758. [Google Scholar] [CrossRef]
- Guzman, S.M.; Paz, J.O.; Tagert, M.L.M. The use of NARX neural networks to forecast daily groundwater levels. Water Resour. Manag. 2017, 31, 1591–1603. [Google Scholar] [CrossRef]
- Guzman, S.M.; Paz, J.O.; Tagert, M.L.M.; Mercer, A.E. Evaluation of seasonally classified inputs for the prediction of daily groundwater levels: NARX networks vs support vector machines. Environ. Model. Assess. 2019, 24, 223–234. [Google Scholar] [CrossRef]
- Wang, X.; Lui, T.; Zheng, X.; Peng, H.; Xin, J.; Zhang, B. Short-term prediction of groundwater level using improved random forest regression with combination of random features. Appl. Water Sci. 2018, 8, 125. [Google Scholar] [CrossRef] [Green Version]
- Herrera, V.M.; Khoshgoftaar, T.M.; Villanustre, F.; Furht, B. Random forest inplementation and optimization for Big Data analytics on LexisNexis’s high performance computing cluster platform. J. Big Data 2019, 6, 68. [Google Scholar] [CrossRef] [Green Version]
- Naghibi, S.A.; Pourghasemi, H.R.; Barnali, D. GIS-based grounwater potential mapping using boosted regression tree, classification and regression tree, and random forest machine learning models in Iran. Environ. Monit. Assess. 2016, 188, 44. [Google Scholar] [CrossRef] [PubMed]
- Zabihi, M.; Pourghasemi, H.R.; Pourtaghi, Z.S.; Behzadfar, M. GIS-based multivariate adaptive regression spline and random forest models for groundwater potential mapping in Iran. Environ. Earth Sci. 2016, 75, 665. [Google Scholar] [CrossRef]
- Rodriguez-Galiano, V.F.; Mendes, M.P.; Garcia-Soldado, M.J.; Olmo, M.C.; Ribeiro, L. Predictive modeling of groundwater nitrate pollution using Random Forest multisource variables related to intrinsic and specific vulnerability: A case study in an agricultural setting (Southern Spain). Sci. Total. Environ. 2014, 476, 189–206. [Google Scholar] [CrossRef]
- Baudron, P.; Alonso-Sarría, F.; García-Aróstegui, J.-L.; Cánovas-García, F.; Martínez-Vicente, D.; Moreno-Brotóns, J. Identifying the origin of groundwater samples in a multi-layer aquifer system with Random Forest classification. J. Hydrol. 2013, 499, 303–315. [Google Scholar] [CrossRef]
- Tyralis, H.; Papacharalampous, G.; Langousis, A. A brief review of random forest for water scientists and practitioners and their recent history in water resources. Water 2019, 11, 910. [Google Scholar] [CrossRef] [Green Version]
- Ahmed, O.S.; Franklin, S.E.; Wulder, M.A.; White, J.C. Extending airborne lidar-derived estimates of forest canopy cover and height over large areas using knn with landsat time series data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 9, 3489–3496. [Google Scholar] [CrossRef]
- Yu, Y.; Zhang, H.; Singh, V.P. Forward prediction of runoff data in data-scarce basins with an improved ensemble empirical mode decomposition (EEMD) model. Water 2018, 10, 388. [Google Scholar] [CrossRef] [Green Version]
- Maxhuni, A.; Hernandez-Leal, P.; Sucar, L.E.; Osmani, V.; Morales, E.F.; Mayora, O. Stress Modelling and prediction in presence of scarce data. J. Biomed. Inform. 2016, 63, 344–356. [Google Scholar] [CrossRef] [PubMed]
- Biau, G.; Scornet, E.; Welbl, J. Neural random forests. Sankhya A-Springer 2019, 81, 347–386. [Google Scholar] [CrossRef]
- Galelli, S.; Castelletti, A. Assessing the predictive capacity of randomized tree-based ensembles in streamflow modelling. Hydrol. Earth Syst. Sci. 2013, 17, 2669–2684. [Google Scholar] [CrossRef] [Green Version]
- Pisetta, V.; Jouve, P.E.; Zighed, D.A. Learning with ensembles of randomized trees: New insights. In Proceedings of the Joint European Conference on Machine Learning and Knowledge Discovery in Databases, Barcelona, Spain, 19–23 September 2010; Springer: Berlin/Heidelberg, Germany, 2010; pp. 67–82. [Google Scholar]
- Ministry of Disaster Management and Refugee Affairs (MIDMAR). The National Risk Atlas; UNION Publishing Services Section: Nairobi, Kenya, 2015; Volume 2, p. 17. [Google Scholar]
- Rwanda Meteorological Agency. Weather Data; Rwanda Meteorological Agency: Kigali, Rwanda, 2018. [Google Scholar]
- NISR, M. Rwanda Fourth Population and Housing Census 2012; Thematic Report: Population Size, Structure and Distribution; National Institute of Statistics of Rwanda: Kigali, Rwanda, 2014; pp. 10–14. [Google Scholar]
- Niyidufasha, G. Groundwater Potential Eastern Province. In Proceedings of the PowerPoint Presentation at World’s Water Day Conference, Marriott Hotel, Kigali, Rwanda, 19–22 March 2019. [Google Scholar]
- Kamai, T.; Shmuel, A. Assouline. Evaporation from Deep Aquifers in Arid Regions: Analytical Model for Combined Liquid and Vapor Water Fluxes. Water Resour. Res. 2018, 54, 4805–4822. [Google Scholar] [CrossRef]
- Mohammadi, B. Predicting total phosphorus levels as indicators for shallow lake management. Ecol. Indic. 2019, 107, 105664. [Google Scholar] [CrossRef]
- Zhao, J.H.; Dong, Z.; Xu, Z. Effective feature preprocessing for time series forecasting. In Proceedings of the International Conference on Advanced Data Mining and Applications, Xi’an, China, 14–16 August 2006; Springer: Berlin/Heidelberg, Germany, 2006; pp. 769–781. [Google Scholar]
- Python Software Foundation. Python 3.6.6. 2018. Available online: https://www.python.org/downloads/release/python-366/ (accessed on 19 February 2019).
- Scikit-Learn. Sk-Learn 2.20. 2018. Available online: https://www.scikit-learn.org/stable/install.html/ (accessed on 19 February 2019).
- Lindsey, S.D.; Farnsworth, R.K. Sources of solar radiation estimates and their effect on daily evaporation for use in streamflow modelling. J. Hydrol. 1997, 201, 348–366. [Google Scholar] [CrossRef]
- Hocking, M.; Kelly, B.F.J. Groundwater recharge and time lag measurement through Vertosols using impulse response functions. J. Hydrol. 2016, 535, 22–35. [Google Scholar] [CrossRef]
- Pappas, C.; Papalexiou, S.M.; Koutsoyiannis, D. A quick gap filling of missing hydrometeorological data. J. Geophys. Res. Atmos. 2014, 119, 9290–9300. [Google Scholar] [CrossRef]
- Gao, Y.; Merz, C.; Lischeid, G.; Schneider, M. A review on missing hydrological data processing. Environ. Earth Sci. 2018, 77, 47. [Google Scholar] [CrossRef]
- Yoon, H.; Jun, S.C.; Hyun, Y.; Bae, G.O.; Lee, K.K. A comparative study of artificial neural networks and support vector machines for predicting groundwater levels in a coastal aquifer. J. Hydrol. 2011, 396, 128–138. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Gitau, M.W.; Pai, N.; Daggupati, P. Hydrologic and water quality models: Performance measures and evaluation criteria. Trans. ASABE 2015, 58, 1763–1785. [Google Scholar]
- Bennett, N.D.; Croke, B.F.; Guariso, G.; Guillaume, J.H.; Hamilton, S.H.; Jakeman, A.J.; Marssili-Libelli, S.; Newham, L.T.; Norton, J.P.; Perrin, C.; et al. Characterizing performance of environmental models. Environ. Model. Softw. 2013, 40, 1–20. [Google Scholar] [CrossRef]
- Munoz-Carpena, R. Performance evaluation of hydrological models: Statistical significance for reducing subjectivity in goodness-of-fit assessments. J. Hydrol. 2013, 480, 33–45. [Google Scholar]
- Roberts, W.; Williams GJackson, E.; Nelson, E.; Ames, D. Hydrostats: A python package for characterizing Errors between observed and predicted Time Series. Hydrology 2018, 5, 66. [Google Scholar] [CrossRef] [Green Version]
- Amir, N.; Shpigelman, L.; Tishby, N.; Vaadia, E. Nearest neighbor based feature selection for regression and its application to neural activity. In Proceedings of the Advances in Neural Information Processing Systems 18, Vancouver, Canada, 5–8 December 2005; pp. 996–1002. [Google Scholar]
- LaBarr, E. How Good is That Forecast? The Nuances of Prediction Evaluation across Time. In Proceedings of the SAS Global Forum Proceedings; 2018; pp. 1862–2018. Available online: http://sas.com/content/dam/SAS/support/en/sas-global-forum-proceedings/2018/1862-2018.pdf (accessed on 26 March 2019).
- Fukunaga, K.; Hostetler, L. K-nearest-neighbor Bayes-risk estimation. IEEE Trans. Inf. Threory 1975, 21, 285–293. [Google Scholar] [CrossRef]
- Babak, V.; Guan, Y.; Mohammadi, B. Application of hybrid ANN-whale optimization model in evaluation of the field capacity and the permanent wilting point of the soils. Environ. Sci. Pollut. Res. 2020, 1–11. [Google Scholar] [CrossRef]
- Moazenzadeh, R.; Muhammadi, B. Assessment of Bio-Inspired Metaheuristic Optimisation Algorithms for Estimating Soil Temperature. Geoderma 2019, 353, 152–171. [Google Scholar] [CrossRef]
- Njikam, A.N.S.; Zhao, H. A novel activation function for feed-forward neural networks. Appl. Intell. 2016, 45, 75–82. [Google Scholar] [CrossRef]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Aghelpour, P.; Mohammadi, B.; Biazar, S.M. Long-term monthly average temperature forecasting in some climate types of Iran, using the models SARIMA, SVR, and SVR-FA. Theor. Appl. Climatol. 2019, 138, 1471–1480. [Google Scholar] [CrossRef]
- Lin, G.-F.; Chen, G.-R.; Wu, M.-C.; Chou, Y.-C. Effective forecasting of hourly typhoon rainfall using support vector machines. Water Resour. Res. 2009, 45, 8. [Google Scholar] [CrossRef]
- Goyal, M.K.; Bharti, B.; Quilty, J.; Adamowski, J.; Pandey, A. Modeling of daily pan evaporation in sub tropical climates using ANN, LS-SVR, Fuzzy Logic, and ANFIS. Expert Syst. Appl. 2014, 41, 5267–5276. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. IEEE Mach. Learn. 2001, 45, 5–32. [Google Scholar]
- Breiman, L. Bagging predictors. Mach. Learn. 1996, 24, 123–140. [Google Scholar]
- Wang, Y.; Xia, S.-T.; Tang, Q.; Wu, J.; Zhu, X. A novel consistent random forest framework: Bernoulli random forests. IEEE Trans. Neural Networks Learn. Syst. 2017, 29, 3510–3523. [Google Scholar]
- Thomas, G. Ensemble methods in machine learning. In International Workshop on Multiple Classifier Systems; Springer: Berlin/Heidelberg, Germany, 2000; pp. 1–15. [Google Scholar]
- De Amorim, R.C.; Mirkin, B. Minkowski metric, feature weighting and anomalous cluster initializing in K-Means clustering. Pattern Recognit. 2012, 45, 1061–1075. [Google Scholar] [CrossRef]
- Pillai, N.; Schwartz, S.L.; Ho, T.; Dokoumetzidis, A.; Bies, R.; Freedman, I. Estimating parameters of nonlinear dynamic systems in pharmacology using chaos synchronization and grid search. J. Pharmacokinet. Pharmacodyn. 2019, 46, 193–210. [Google Scholar] [CrossRef] [Green Version]
- Sun, Y.; Wendi, D.; Kim, D.; Liong, S.-Y. Technical note: Application of artificial neural networks in groundwater table forecasting—A case study in a Singapore swamp forest. Hydrol. Earth Syst. Sci. 2016, 2, 1405–1412. [Google Scholar] [CrossRef] [Green Version]
- Moosavi, V.; Vafakhah, M.; Shirmohammadi, B.; Behnia, N. A wavelet-ANFIS hybrid model for groundwater level forecasting for different prediction periods. Water Resour. Manag. 2013, 27, 1301–1321. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Fixing weight decay regularization in adam. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Zhang, H.; Weng, T.-W.; Chen, P.-Y.; Hsieh, C.-J.; Daniel, L. Effective neural network robustness certification with general activation functions. In Proceedings of the Advances in Neural Information Processing Systems, Montréal, QC, Canada, 3–8 December 2018; pp. 4939–4948. [Google Scholar]
- Choy, K.; Chan, C. Modelling of river discharges and rainfall using radial basis function networks based on support vector regression. Int. J. Syst. Sci. 2003, 34, 763–773. [Google Scholar] [CrossRef]
- Probst, P.; Wright, M.N.; Boulesteix, A.L. Hyperparameters and tuning strategies for random forest. Wiley Interdiscip. Rev. Data Min. Knowl. Discov. 2019, 9, e1301. [Google Scholar]
- Yoon, H.; Kim, Y.; Ha, K.; Lee, S.H.; Kim, G.P. Comparative evaluation of ANN-and SVM-time series models for predicting freshwater-saltwater interface fluctuations. Water 2016, 9, 323. [Google Scholar] [CrossRef] [Green Version]
- Yoon, H.; Hyun, Y.; Ha, K.; Lee, K.-K.; Kim, G.-B. A method to improve the stability and accuracy of ANN-and SVM-based time series models for long-term groundwater predictions. Comput. Geosci. 2016, 90, 144–155. [Google Scholar] [CrossRef]
- Flach, P. Machine Learning: The Art and Science of Algorithms that Make Sense of Data; Cambridge Press: Cambridge, UK, 2012. [Google Scholar] [CrossRef]
- Rahmati, O.; Choubin, B.; Fathabadi, A.; Coulon, F.; Soltani, E.; Shahabi, H.; Mollaefar, E.; Tiefenbacher, J.; Cipullo, S.; Ahmad, B.B.; et al. Predicting uncertainty of machine learning models for modeling nitrate pollution of groundwater using quantile regression and uneec methods. Sci. Total Environ. 2019, 688, 855–866. [Google Scholar] [CrossRef]
- Naghibi, S.A.; Ahmadi, K.; Daneshi, A. Application of support vector machine, random forest, and genetic algorithm optimized random forest models in groundwater potential mapping. Water Resour. Manag. 2017, 31, 2761–2775. [Google Scholar] [CrossRef]
- Kayzoglu, T.; Mather, P.M. The use of back-propagating artificial neural networks in land cover classification. Int. J. Remote Sens. 2003, 24, 4907–4938. [Google Scholar] [CrossRef]

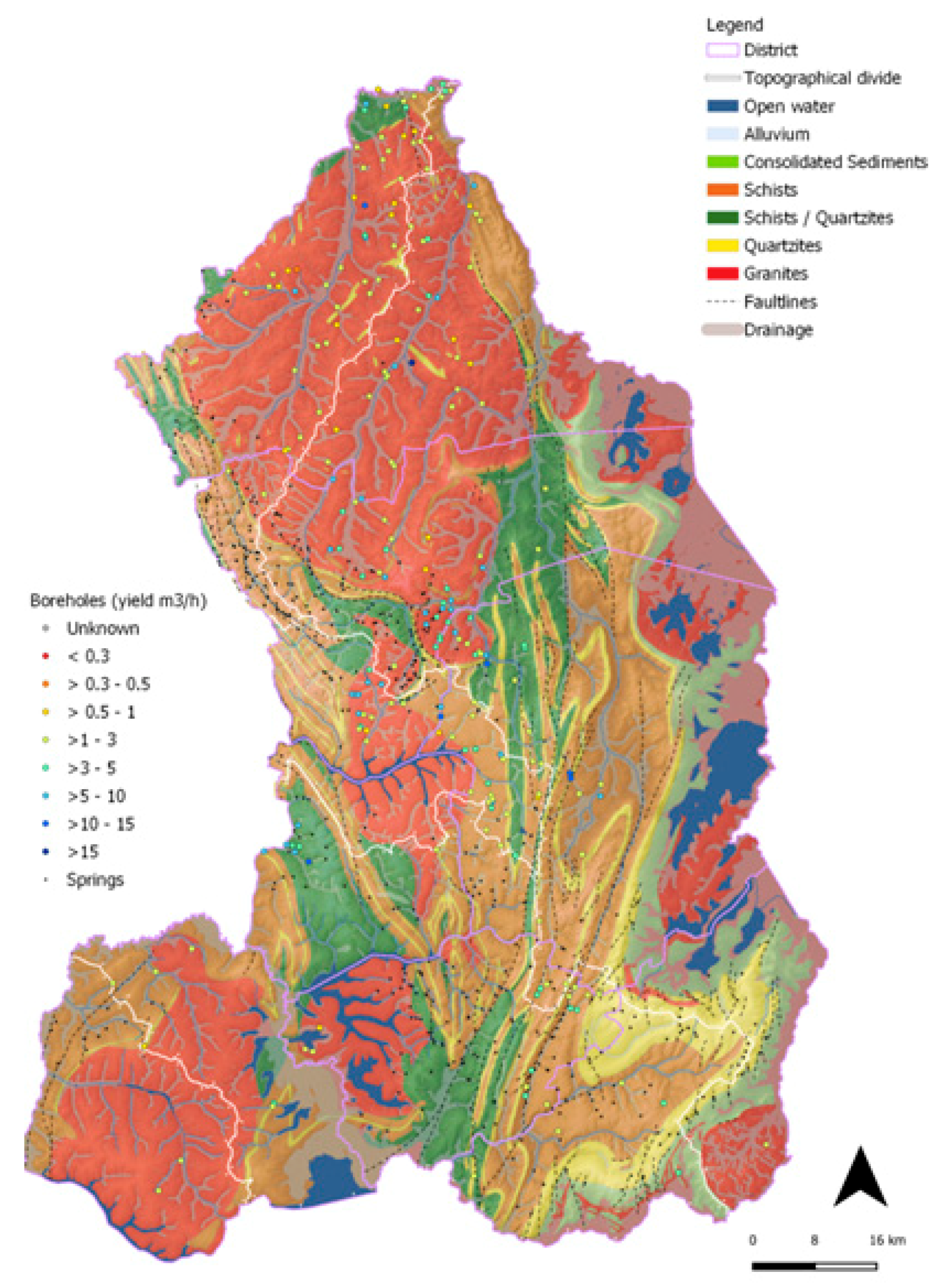








| Station ID | Name | Latitude | Longitude | Aquifer | Availability of Data | Data Time Resolution |
|---|---|---|---|---|---|---|
| F6 | Kayonza-Mukarange | 1.89874154 | 30.5065299 | Permeable Fractured | 3 December 2016–30 December 2018 | Daily |
| L (t + 15) | L (t + 30) | L (t + 60) | L (t + 90) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Input Arrangement | RMSE | MAE | RMSE | MAE | RMSE | MAE | RMSE | MAE | ||||
| P (t−1) S (t) T (t) | 0.0022 | 0.0019 | 0.9791 | 0.0026 | 0.0020 | 0.9619 | 0.0036 | 0.0025 | 0.9185 | 0.0031 | 0.0022 | 0.9387 |
| P (t−2) S (t) T (t) | 0.0061 | 0.0050 | 0.8397 | 0.0069 | 0.0050 | 0.7114 | 0.0068 | 0.0051 | 0.7049 | 0.0065 | 0.0048 | 0.7143 |
| P (t−3) S (t) T (t) | 0.0054 | 0.0043 | 0.8909 | 0.0064 | 0.0047 | 0.7527 | 0.0059 | 0.0044 | 0.7948 | 0.0059 | 0.0044 | 0.7807 |
| P (t−4) S (t) T (t) | 0.0049 | 0.0042 | 0.9179 | 0.0069 | 0.0051 | 0.7739 | 0.0056 | 0.0042 | 0.7989 | 0.0057 | 0.0043 | 0.7882 |
| P (t) S (t−1) T (t) | 0.0060 | 0.0051 | 0.8401 | 0.0067 | 0.0051 | 0.7308 | 0.0064 | 0.0048 | 0.7454 | 0.0061 | 0.0046 | 0.7660 |
| P (t) S (t−2) T (t) | 0.0060 | 0.0051 | 0.8749 | 0.0061 | 0.0048 | 0.7872 | 0.0059 | 0.0047 | 0.7993 | 0.0061 | 0.0046 | 0.7706 |
| P (t) S (t−3) T (t) | 0.0058 | 0.0048 | 0.8639 | 0.0065 | 0.0048 | 0.7438 | 0.0059 | 0.0044 | 0.7948 | 0.0059 | 0.0044 | 0.7783 |
| P (t) S (t−4) T (t) | 0.0058 | 0.0050 | 0.8635 | 0.0062 | 0.0049 | 0.7739 | 0.0061 | 0.0049 | 0.7537 | 0.0057 | 0.0044 | 0.7840 |
| P (t) S (t) T (t−1) | 0.0061 | 0.0050 | 0.8391 | 0.0065 | 0.0049 | 0.7577 | 0.0065 | 0.0049 | 0.7408 | 0.0065 | 0.0048 | 0.7277 |
| P (t) S (t) T (t−2) | 0.0061 | 0.0050 | 0.8411 | 0.0065 | 0.0049 | 0.7601 | 0.0065 | 0.0049 | 0.7518 | 0.0062 | 0.0046 | 0.7553 |
| P (t) S (t) T (t−3) | 0.0058 | 0.0048 | 0.8539 | 0.0064 | 0.0048 | 0.7545 | 0.0062 | 0.0048 | 0.7646 | 0.0059 | 0.0046 | 0.7711 |
| P (t) S (t) T (t−4) | 0.0057 | 0.0047 | 0.8663 | 0.0066 | 0.0049 | 0.7312 | 0.0062 | 0.0048 | 0.7578 | 0.0059 | 0.0045 | 0.7679 |
| L (t + 15) | L (t + 30) | L (t + 60) | L (t + 90) | |
|---|---|---|---|---|
| Input Arrangement | ||||
| P (t−1) S (t) T (t) | 0.9741 | 0.9540 | 0.9130 | 0.9346 |
| P (t−2) S (t) T (t) | 0.7957 | 0.6792 | 0.6657 | 0.6898 |
| P (t−3) S (t) T (t) | 0.8385 | 0.7239 | 0.7532 | 0.7483 |
| P (t−4) S (t) T (t) | 0.8697 | 0.6798 | 0.7720 | 0.7595 |
| P (t) S (t−1) T (t) | 0.7987 | 0.6977 | 0.7083 | 0.7267 |
| P (t) S (t−2) T (t) | 0.8014 | 0.7458 | 0.7488 | 0.7290 |
| P (t) S (t−3) T (t) | 0.8105 | 0.7136 | 0.7532 | 0.7431 |
| P (t) S (t−4) T (t) | 0.8160 | 0.7373 | 0.7339 | 0.7659 |
| P (t) S (t) T (t−1) | 0.7934 | 0.7168 | 0.6968 | 0.6951 |
| P (t) S (t) T (t−2) | 0.7933 | 0.7173 | 0.7023 | 0.7212 |
| P (t) S (t) T (t−3) | 0.8133 | 0.7256 | 0.7274 | 0.7456 |
| P (t) S (t) T (t−4) | 0.8214 | 0.7055 | 0.7260 | 0.7430 |
| SVR | ANN | KNN-RF |
|---|---|---|
| Epsilon: 0.01 | Epsilon: 0.0001 | Epsilon: 0.01 |
| Kernel: RBF | Hidden layer: 1 | Number of trees: 200 |
| Gamma: Scale | Hidden layer neurons: 14 | Maximum depth: 15 |
| Soft-margin(C): 1.0 | Activation function: ReLU | Weights: distance |
| Support vectors: 137 | Learning mode: Adaptive | Metric: Minkowski |
| Degree: 3 | Max-iterations: 500 | Number of estimators: 50 |
| Training algorithm: Adam | Algorithm: Auto |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kombo, O.H.; Kumaran, S.; Sheikh, Y.H.; Bovim, A.; Jayavel, K. Long-Term Groundwater Level Prediction Model Based on Hybrid KNN-RF Technique. Hydrology 2020, 7, 59. https://doi.org/10.3390/hydrology7030059
Kombo OH, Kumaran S, Sheikh YH, Bovim A, Jayavel K. Long-Term Groundwater Level Prediction Model Based on Hybrid KNN-RF Technique. Hydrology. 2020; 7(3):59. https://doi.org/10.3390/hydrology7030059
Chicago/Turabian StyleKombo, Omar Haji, Santhi Kumaran, Yahya H. Sheikh, Alastair Bovim, and Kayalvizhi Jayavel. 2020. "Long-Term Groundwater Level Prediction Model Based on Hybrid KNN-RF Technique" Hydrology 7, no. 3: 59. https://doi.org/10.3390/hydrology7030059
APA StyleKombo, O. H., Kumaran, S., Sheikh, Y. H., Bovim, A., & Jayavel, K. (2020). Long-Term Groundwater Level Prediction Model Based on Hybrid KNN-RF Technique. Hydrology, 7(3), 59. https://doi.org/10.3390/hydrology7030059





