A Fast Data-Driven Tool for Flood Risk Assessment in Urban Areas
Abstract
:1. Introduction
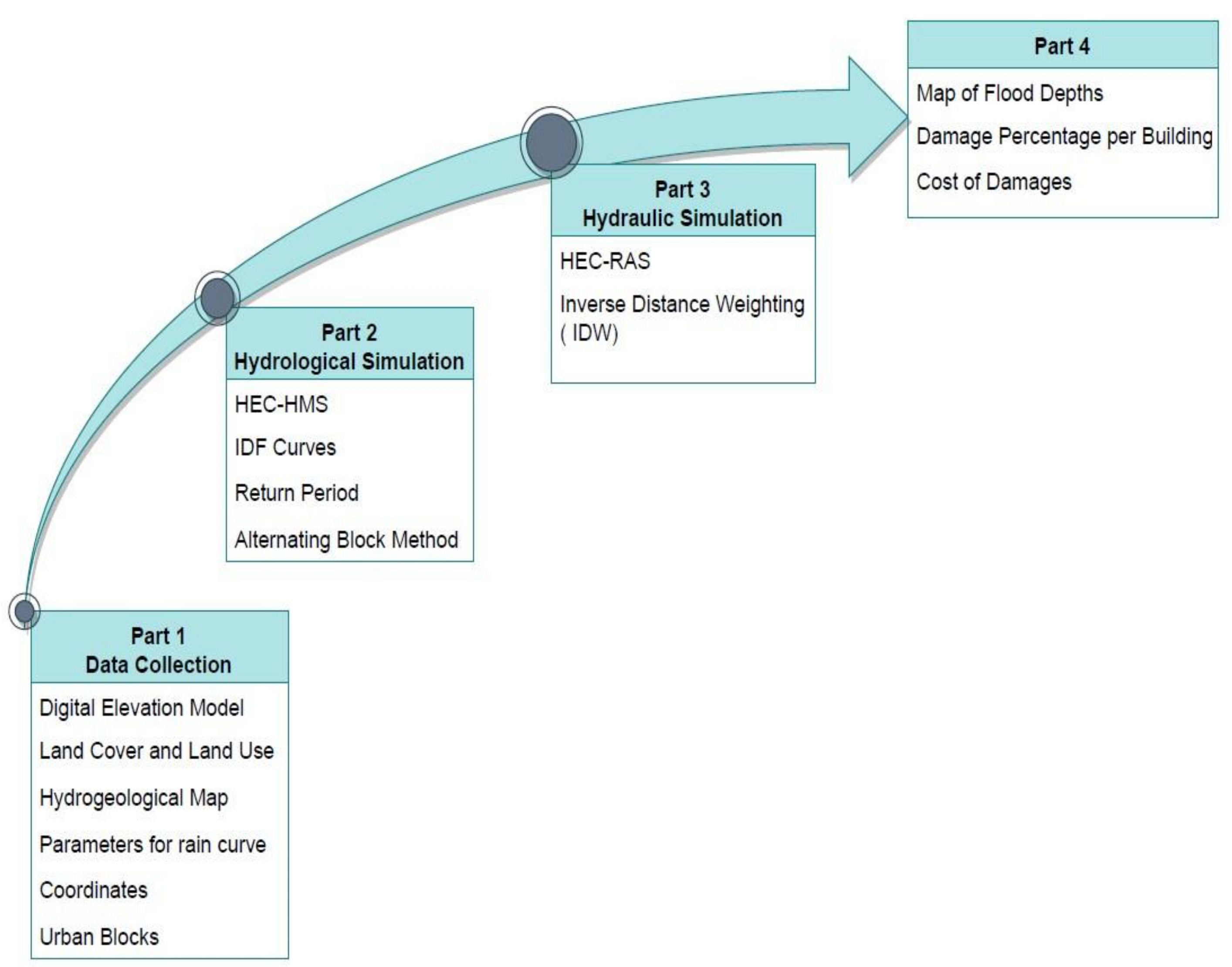
2. Materials and Methods
2.1. Study Area and Data
2.2. Hydrologic Simulations and Flood Hazard
2.3. Flood Risk
3. Results and Discussion
3.1. Hydrologic Simulations
3.2. Flood Hazard
3.3. Flood Risk and Comparison
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Diakakis, M.; Mavroulis, S.D.; Deligiannakis, G. Floods in Greece, a statistical and spatial approach. Nat. Hazards 2012, 62, 485–500. [Google Scholar] [CrossRef]
- Emergency Disaster Database (EM-DAT). Available online: https://apdim.unescap.org/knowledge-hub/emergency-events-database-em-dat (accessed on 5 July 2022).
- Apostolopoulos, K.; Potsiou, C. Consideration on how to introduce gamification tools to enhance citizen engagement in crowdsourced cadastral surveys. Surv. Rev. 2021, 54, 142–152. [Google Scholar] [CrossRef]
- Kourtis, I.M.; Bellos, V.; Kopsiaftis, G.; Psiloglou, B.; Tsihrintzis, V.A. Methodology for holistic assessment of grey-green flood mitigation measures for climate change adaptation in urban basins. J. Hydrol. 2021, 603, 126885. [Google Scholar] [CrossRef]
- Pistrika, A.; Tsakiris, G.; Nalbantis, I. Flood Depth-Damage Functions for Built Environment. Environ. Process. 2014, 1, 553–572. [Google Scholar] [CrossRef]
- Oliveri, E.; Santoro, M. Estimation of urban structural flood damages: The case study of Palermo. Urban Water 2000, 2, 223–234. [Google Scholar] [CrossRef]
- De Moel, H.; Jongman, B.; Kreibich, H.; Merz, B.; Penning-Rowsell, E.; Ward, P. Flood risk assessments at different spatial scales. Mitig. Adapt. Strateg. Glob. Chang. 2015, 20, 865–890. [Google Scholar] [CrossRef]
- Nguyen, V.D.; Metin, A.D.; Alfieri, L.; Vorogushyn, S.; Merz, B. Biases in national and continental flood risk assessments by ignoring spatial dependence. Sci. Rep. 2020, 10, 19387. [Google Scholar] [CrossRef]
- Huizinga, J.; de Moel, H.; Szewczyk, W. Global Flood Depth-Damage Functions: Methodology and the Database with Guidelines; JRC Research Reports; Joint Research Centre: Sevilla, Spain, 2017; Available online: https://ec.europa.eu/jrc10.2760/16510 (accessed on 5 July 2022).
- Tsakiris, G.; Nalbantis, I.; Pistrika, A. Critical Technical Issues on the EU Flood Directive. Eur. Water 2009, 25, 39–51. [Google Scholar]
- European Council. Directive (2007/60/EU) of the European Parliament and of the European Council on the Estimation and Management of Flood Risks. 2007. Available online: http://eur-lex.europa.eu/legal-content/EN/TXT/?uri=CELEX:32007L0060 (accessed on 5 July 2022).
- Nalbantis, I. Use of multiple-time-step information in rainfall-runoff modeling. J. Hydrol. 1995, 65, 135–139. [Google Scholar] [CrossRef]
- Nalbantis, I.; Lymperopoulos, S. Assessment of flood frequency after forest fires in small ungauged basins based on uncertain measurements. Hydrol. Sci. J. 2012, 57, 52–72. [Google Scholar] [CrossRef]
- Batelis, S.C.; Nalbantis, I. Potential effects of forest fires on streamflow in the Enipeas river basin, Thessaly, Greece. Environ. Process. 2014, 1, 73–85. [Google Scholar] [CrossRef]
- Appelbaum, S.J. Determination of urban flood damage. J. Water Resour. Plan. Manag. 1985, 111, 269–283. [Google Scholar] [CrossRef]
- USACE. Generic Depth-Damage Relationships; United States Army Corps of Engineers: New Orleans, LA, USA, 2000.
- Debo, T.N. Urban flood damage estimation curves. J. Hydraul. Div. 1982, 108, 1059–1069. [Google Scholar] [CrossRef]
- FIA. Depth-Percent Damage Curves; Federal Insurance Administration, US Department of Housing and Urban Development: Washington, DC, USA, 1974.
- Kourtis, I.M.; Tsihrintzis, V.A.; Baltas, E. A robust approach for comparing conventional and sustainable flood mitigation measures in urban basins. J. Environ. Manag. 2020, 269, 110822. [Google Scholar] [CrossRef]
- Kourtis, I.M.; Tsihrintzis, V.A. Economic valuation of ecosystem services provided by the restoration of an irrigation canal to a riparian corridor. Environ. Process. 2017, 4, 749–769. [Google Scholar] [CrossRef]
- Bellos, V.; Papageorgaki, I.; Kourtis, I.; Vangelis, H.; Kalogiros, I.; Tsakiris, G. Reconstruction of a flash flood event using a 2D hydrodynamic model under spatial and temporal variability of storm. Nat. Hazards 2020, 101, 711–726. [Google Scholar] [CrossRef]
- Noto, L.V.; La Loggia, G. Use of L-moments approach for regional flood frequency analysis in Sicily, Italy. Water Resour. Manag. 2008, 23, 2207–2229. [Google Scholar] [CrossRef]
- Eregno, F.E.; Nilsen, V.; Seidu, R.; Heistad, A. Evaluating the trend and extreme values of faecal indicator organisms in a raw water source: A potential approach for watershed management and optimizing water treatment practice. Environ. Process. 2014, 1, 287–309. [Google Scholar] [CrossRef]
- Tsakiris, G.; Kordalis, N.; Tsakiris, V. Flood double frequency analysis: 2D-Archimedean copulas vs. bivariate probability distributions. Environ. Process. 2015, 2, 705–716. [Google Scholar] [CrossRef]
- Yannopoulos, S.; Eleftheriadou, E.; Mpouri, S.; Giannopoulou, I. Implementing the requirements of the european flood directive: The case of ungauged and poorly gauged watersheds. Environ. Process. 2015, 2, 191–207. [Google Scholar] [CrossRef]
- Razmi, A.; Golian, S.; Zahmatkesh, Z. Non-stationary frequency analysis of extreme water level: Application of annual maximum series and peak-over threshold approaches. Water Resour. Manag. 2017, 31, 2065–2083. [Google Scholar] [CrossRef]
- Stojkovic, M.; Simonovic, S.P. Mixed General extreme value distribution for estimation of future precipitation quantiles using a weighted ensemble—Case study of the Lim River Basin (Serbia). Water Resour. Manag. 2019, 33, 2885–2906. [Google Scholar] [CrossRef]
- Ullah, H.; Akbar, M. Drought risk analysis for water assessment at gauged and ungauged sites in the low rainfall regions of Pakistan. Environ. Process. 2021, 8, 139–162. [Google Scholar] [CrossRef]
- Razmi, A.; Mardani-Fard, H.A.; Golian, S.; Zahmatkesh, Z. Time-varying univariate and bivariate frequency analysis of nonstationary extreme sea level for New York City. Environ. Process. 2022, 9, 8. [Google Scholar] [CrossRef]
- Tegos, A.; Ziogas, A.; Bellos, V.; Tzimas, A. Forensic hydrology: A complete reconstruction of an extreme flood event in data-scarce area. Hydrology 2022, 9, 93. [Google Scholar] [CrossRef]
- Flood Risk Management Plan for Attica River Basin District (EL06) (2017) IDF Curves. Available online: https://floods.ypeka.gr/egyFloods/gr06/report/I_1_P02_EL06.pdf (accessed on 5 July 2022). (In Greek).
- Zotou, I.; Bellos, V.; Gkouma, A.; Karathanassi, V.; Tsihrintzis, V.A. Using Sentinel-1 imagery to assess predictive performance of a hydraulic model. Water Resour. Manag. 2020, 34, 4415–4430. [Google Scholar] [CrossRef]
- Giandotti, M. Previsione Delle Piene e Delle, Magre dei Corsi D’acqua; Istituto Poligrafico dello Stato: Rome, Italy, 1934; pp. 107–117. [Google Scholar]
- Mimikou, M.A.; Baltas, E.A.; Tsihrintzis, V.A. Hydrology and Water Resource Systems Analysis; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]
- Chow, V.; Maidment, D.; Mays, L. Applied Hydrology; McGraw-Hill Book Company: New York, NY, USA, 1988. [Google Scholar]
- Handrinos, S.; Bellos, V.; Sibetheros, I.A. Simulation of an urban flash flood: The 2017 flood event in Mandra, Attica. In Proceedings of the 17th International Conference on Environmental Science & Technology, Athens, Greece, 1–4 September 2021. [Google Scholar]
- Lu, G.; Wong, D. An adaptive inverse distance weightinh spatial interpolation technique. Comput. Geosci. 2008, 34, 1044–1055. [Google Scholar] [CrossRef]
- Jonkman, N.S.; Bočkarjovab, M.; Kokc, M.; Bernardinid, P. Integrated hydrodynamic and economic modelling of flood damage in the Netherlands. Ecol. Econ. 2008, 66, 77–90. [Google Scholar] [CrossRef]
- Price Zones of Objective Determination of Real Estate Values. Available online: https://www.gov.gr/upourgeia/upourgeio-oikonomikon/oikonomikon/antikeimenikos-prosdiorismos-axion-akineton-apaa (accessed on 5 July 2022).
- Kim, D.; Onof, C. A stochastic rainfall model that can reproduce important rainfall properties across the timescales from several minutes to a decade. J. Hydrol. 2020, 589, 125150. [Google Scholar] [CrossRef]
- Paschalis, A.; Molnar, P.; Fatichi, S.; Burlando, P. On temporal stochastic modeling of precipitation, nesting models across scales. Adv. Water Resour. 2014, 63, 152–166. [Google Scholar] [CrossRef]
- De Luca, D.L.; Petroselli, A. STORAGE (STOchastic RAinfall generator): A user-friendly software for generating long and high-resolution rainfall time series. Hydrology 2021, 8, 76. [Google Scholar] [CrossRef]
- Wheater, H.S.; Chandler, R.E.; Onof, C.J.; Isham, V.S.; Bellone, E.; Yang, C.; Lekkas, D.; Lourmas, G.; Segond, M.L. Spatial-temporal rainfall modelling for flood risk estimation. Stoch. Environ. Res. Risk Assess. 2005, 19, 403–416. [Google Scholar] [CrossRef]
- Cowpertwait, P.S.P. Further developments of the Neyman-Scott clustered point process for modeling rainfall. Water Resour. Res. 1991, 27, 1431–1438. [Google Scholar] [CrossRef]






| Rainfall Depth (mm) for Various Return Periods (Years) | ||||||
|---|---|---|---|---|---|---|
| Duration (h) | 2 | 5 | 10 | 25 | 50 | 100 |
| 1 | 22 | 31 | 37 | 46 | 53 | 62 |
| 2 | 30 | 41 | 50 | 62 | 72 | 83 |
| 3 | 35 | 49 | 59 | 73 | 85 | 98 |
| 6 | 46 | 64 | 77 | 96 | 112 | 129 |
| 12 | 60 | 84 | 101 | 126 | 146 | 168 |
| 24 | 78 | 109 | 132 | 164 | 191 | 219 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Theodosopoulou, Z.; Kourtis, I.M.; Bellos, V.; Apostolopoulos, K.; Potsiou, C.; Tsihrintzis, V.A. A Fast Data-Driven Tool for Flood Risk Assessment in Urban Areas. Hydrology 2022, 9, 147. https://doi.org/10.3390/hydrology9080147
Theodosopoulou Z, Kourtis IM, Bellos V, Apostolopoulos K, Potsiou C, Tsihrintzis VA. A Fast Data-Driven Tool for Flood Risk Assessment in Urban Areas. Hydrology. 2022; 9(8):147. https://doi.org/10.3390/hydrology9080147
Chicago/Turabian StyleTheodosopoulou, Zafeiria, Ioannis M. Kourtis, Vasilis Bellos, Konstantinos Apostolopoulos, Chryssy Potsiou, and Vassilios A. Tsihrintzis. 2022. "A Fast Data-Driven Tool for Flood Risk Assessment in Urban Areas" Hydrology 9, no. 8: 147. https://doi.org/10.3390/hydrology9080147
APA StyleTheodosopoulou, Z., Kourtis, I. M., Bellos, V., Apostolopoulos, K., Potsiou, C., & Tsihrintzis, V. A. (2022). A Fast Data-Driven Tool for Flood Risk Assessment in Urban Areas. Hydrology, 9(8), 147. https://doi.org/10.3390/hydrology9080147









