Interaction of Virus in Cancer Patients: A Theoretical Dynamic Model
Abstract
:1. Introduction
2. Boundedness and Dissipativity
3. The Local Stability of Equilibria Points
4. Lyapunov Stability of Equilibria Points
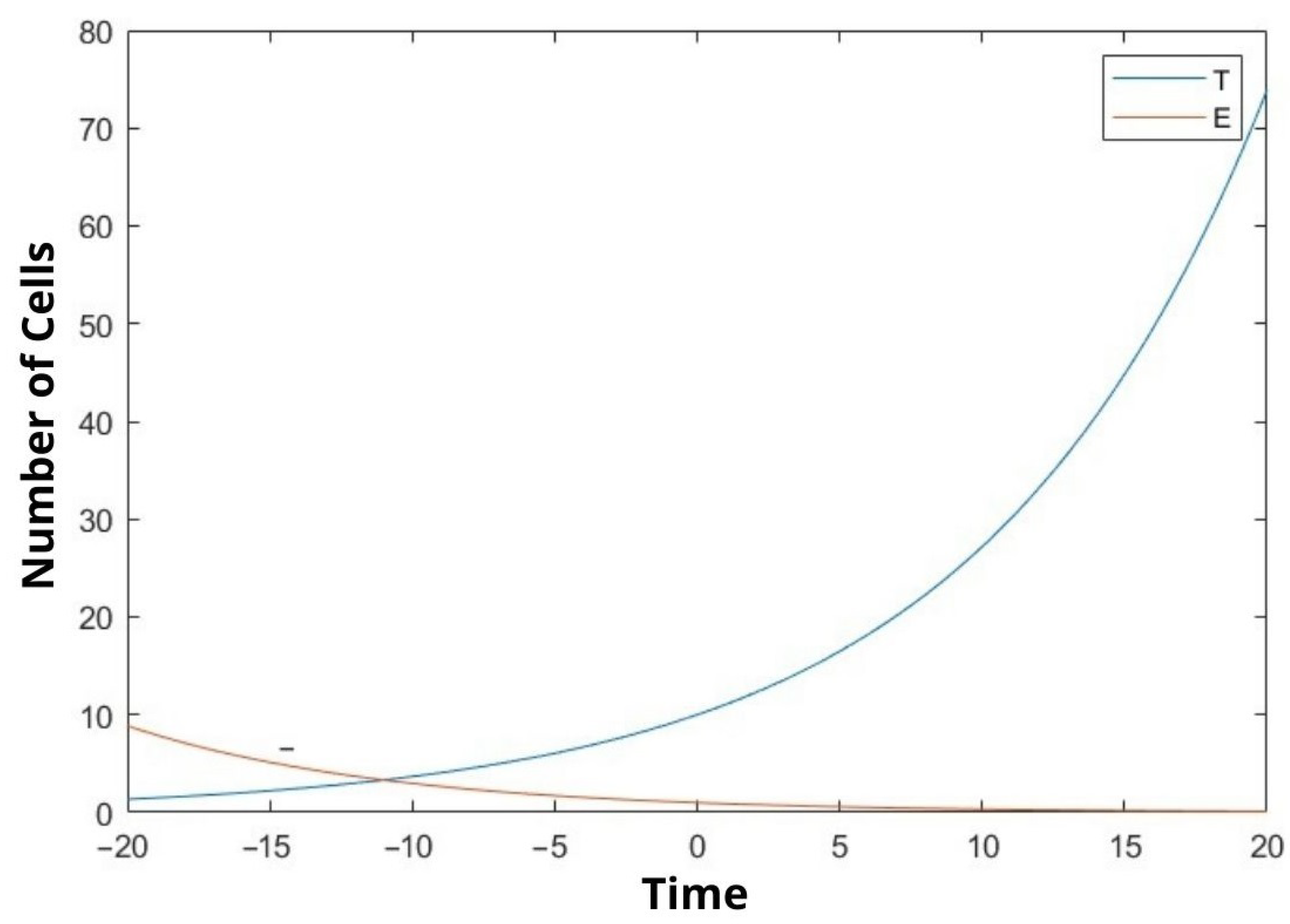
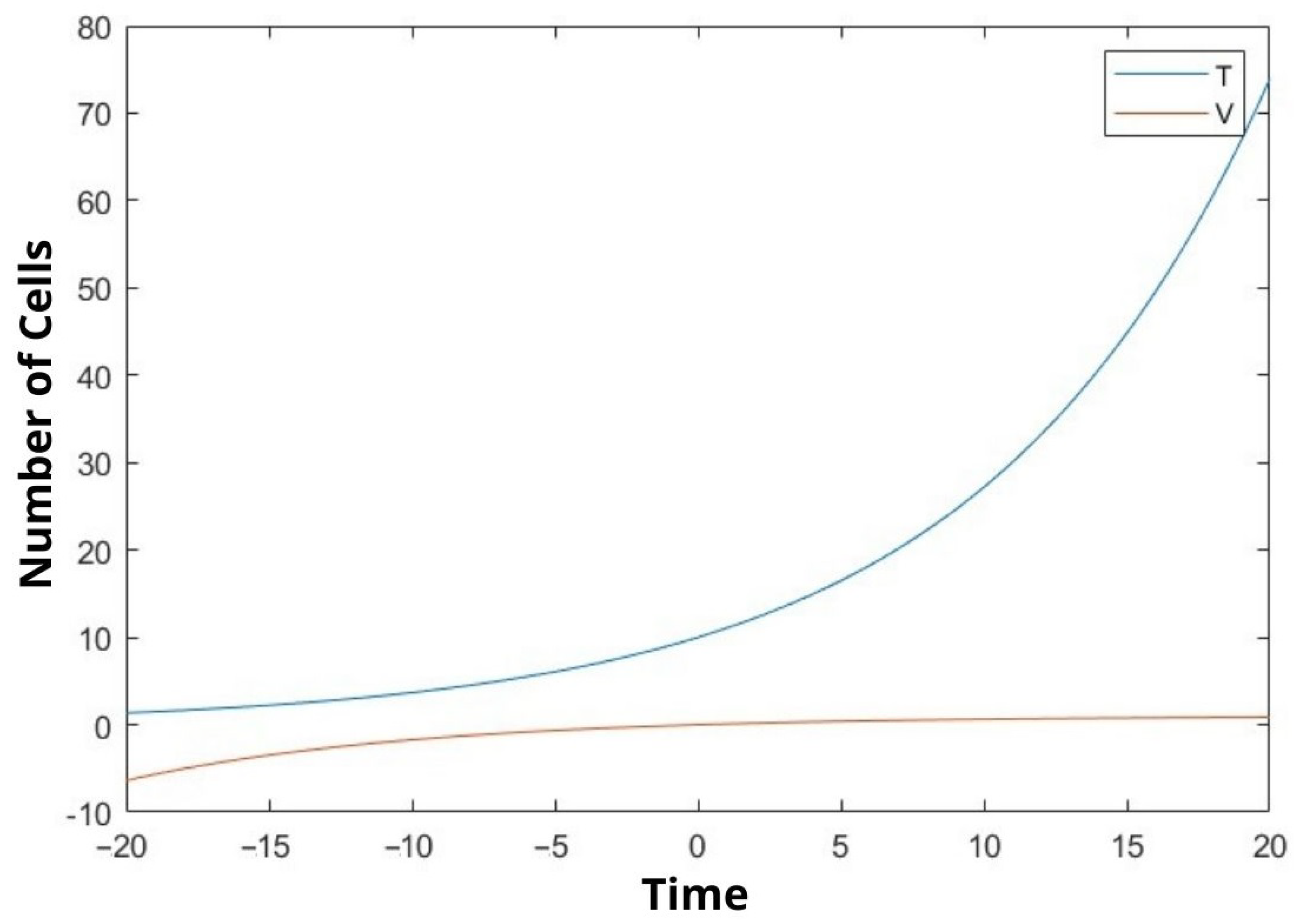
5. Basin of Attractions
6. Discussion
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Adam, J.A.; Bellomo, C. A Survey of Models for Tumor-Immune System Dynamics; Birkhauser: Boston, MA, USA, 1996. [Google Scholar]
- Eftimie, R.; Bramson, J.L.; Earn, D.J.D. Interactions between the immune system and cancer: A brief review of non-spatial mathematical models. Bull. Math. Biol. 2011, 73, 2–32. [Google Scholar] [CrossRef]
- Kirschner, D.; Panetta, J. Modelling immunotherapy of the tumor–immune interaction. J. Math. Biol. 1998, 37, 235–252. [Google Scholar] [CrossRef]
- de Pillis, L.G.; Radunskaya, A. The dynamics of an optimally controlled tumor model: A case study. Math. Comput. Model. 2003, 37, 1221–1244. [Google Scholar] [CrossRef]
- Owen, M.; Sherratt, J. Mathematical modelling macrophage dynamics in tumors. Math. Model. Methods Appl. Sci. 1999, 9, 513–539. [Google Scholar] [CrossRef]
- Chaplain, M.A.J. Special issue on mathematical models for the growth, development and treatment of tumours. Math. Models Meth. Appt. Sci. 1999, 9. [Google Scholar] [CrossRef]
- Starkov, K.E.; Krishchenko, A.P. On the global dynamics of one cancer tumour growth model. Commun. Nonlinear Sci. Numer. Simul. 2014, 19, 1486–1495. [Google Scholar] [CrossRef]
- Itik, I.M.; Banks, S.P. Chaos in a three-dimensional cancer model. Int. J. Bifurc. Chaos 2010, 20, 71–79. [Google Scholar] [CrossRef]
- Jackson, T.; Komarova, N.; Swanson, K. Mathematical oncology: Using mathematics to enable cancer discoveries. Am. Math. Mon. 2014, 121, 840–856. [Google Scholar] [CrossRef]
- Firmani, B.; Guerri, L.; Preziosi, L. Tumor/immune system competition with medically induced activation/deactivation. Math. Model. Methods Appl. Sci. 1999, 4, 491–512. [Google Scholar] [CrossRef]
- Gallas, M.R.; Gallas Marcia, R.; Gallas, J.A.C. Distribution of chaos and periodic spikes in a three-cell population model of cancer. Eur. Phys. J. Spec. Top. 2014, 223, 2131–2144. [Google Scholar] [CrossRef]
- Iarosz, K.C.; Borges, F.S.; Batista, A.M.; Baptista, M.S.; Siqueira, R.A.N.; Viana, R.L.; Lopes, S.R.; Baptista, M.D.S. Mathematical model of brain tumour with glia-neuron interactions and chemotherapy treatment. J. Theor. Biol. 2015, 368, 113–121. [Google Scholar] [CrossRef]
- Sourailidis, D.; Volos, C.; Moysis, L.; Stouboulos, I. Nonlinear phenomena and chaos in a tumor growth model. In Advances in Nonlinear Dynamics: Proceedings of the Second International Non-Linear Dynamics Conference (NODYCON 2021); Springer International Publishing: Cham, Switzerland, 2021; Volume 3, pp. 63–71. [Google Scholar]
- May, R.M. Infectious Diseases of Humans: Dynamics and Control; Oxford University Press: Oxford, UK, 1991. [Google Scholar]
- Nowak, M.A.; Bangham, C.R.M. Population dynamics of immune responses to persistent viruses. Science 1996, 272, 74–79. [Google Scholar] [CrossRef] [PubMed]
- Nowak, M.; May, R.M. Virus Dynamics: Mathematics Principles of Immunology and Virology; Oxford University Press: London, UK, 2000. [Google Scholar]
- Perelson, A.S.; Nelson, P. Mathematical analysis of HIV-1 dynamics in vivo. SIAM Rev. 1999, 41, 3–44. [Google Scholar] [CrossRef]
- Giesl, P. Construction of a global Lyapunov function using radial basis functions with a single operator. IMA J. Appl. Math. 2007, 7, 101–124. [Google Scholar] [CrossRef]
- Yang, C.; Wang, J. A mathematical model for the novel coronavirus epidemic in Wuhan China. Math. Biosci. Eng. 2020, 17, 2708–2724. [Google Scholar] [CrossRef] [PubMed]
- Cucinotta, D.; Vanelli, M. WHO declares COVID-19 a pandemic. Acta Bio Medica Atenei Parm. 2020, 91, 157. [Google Scholar]
- Duradoni, M.; Gursesli, M.C.; Materassi, L.; Serritella, E.; Guazzini, A. The Long-COVID Experience Changed People’s Vaccine Hesitancy but Not Their Vaccination Fear. Int. J. Environ. Res. Public Health 2022, 19, 14550. [Google Scholar] [CrossRef] [PubMed]
- Bekirosa, S.; Kouloumpouc, D. SBDiEM: A new mathematical model of infectious disease dynamics. Chaos Solitons Fractals 2020, 136, 109828. [Google Scholar] [CrossRef]
- Tang, B.; Bragazzi, L.N.; Li, Q.; Tang, S.; Xiao, Y.; Wu, J. An updated estimation of the risk of transmission of the novel coronavirus (2019-nCov). Infect. Dis. Model. 2020, 5, 248–255. [Google Scholar] [CrossRef]
- Khajji, B.; Kada, D.; Balatif, O.; Rachik, M. A multi-region discrete time mathematical modeling of the dynamics of COVID-19 virus propagation using optimal control. J. Appl. Math. Comput. 2020. [Google Scholar] [CrossRef]
- Peirlinck, M.; Linka, K.; Costabal, F.S.; Kuhl, E. Outbreak dynamics of COVID-19 in China and the United States. Biomech. Model. Mechanobiol. 2020. [Google Scholar] [CrossRef] [PubMed]
- Minesh Khatri. Viruses That Can Lead to Cancer; WebMD, July 2020.
- Pham, H. Mathematical Modeling the Time-Delay Interactions between Tumor Viruses and the Immune System with the Effects of Chemotherapy and Autoimmune Diseases. Mathematics 2022, 10, 756. [Google Scholar] [CrossRef]
- Gao, L.; Tan, Y.; Yang, J.; Xiang, C. Dynamic analysis of an age structure model for oncolytic virus therapy. Math. Biosci. Eng. 2022, 20, 3301–3323. [Google Scholar] [CrossRef]
- Qian Lia, Q.; Xiao, Y. Modeling the virus-induced tumor-specific immune response with delay in tumor virotherapy. Commun. Nonlinear Sci. Numer. Simul. 2022, 108, 106196. [Google Scholar]
- Baleanu, D.; Sajjadi, S.S.; Asad, J.H.; Jajarmi, A.; Estiri, E. Hyperchaotic behaviors, optimal control, and ynchronization of a nonautonomous cardiac conduction system. Adv. Differ. Equ. 2021, 2021, 157. [Google Scholar] [CrossRef]
- Baleanu, D.; Abadi, M.H.; Jajarmi, A.; Zarghami, V.K.; Nieto, J.J. A new comparative study on the general fractional model of COVID-19 with isolation and quarantine effects. Alex. Eng. J. 2022, 61, 4779–4791. [Google Scholar] [CrossRef]
- Yasmin, H. Effect of vaccination on non-integer dynamics of pneumococcal pneumonia infection Author links open overlay panel. Chaos Solitons Fractals 2022, 158, 112049. [Google Scholar] [CrossRef]
- Lunn, R.M.; Jahnke, G.D.; Rabkin, C.S. Tumour virus epidemiology. Philos. Trans. R. Soc. Lond. B Biol. Sci. 2017, 372, 1732. [Google Scholar] [CrossRef]
- Shakhmurov, V.; Sahmurova, A. The local and global dynamics model of a cancer tumor growth. Appl. Anal. 2021. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shakhmurov, V.B.; Kurulay, M.; Sahmurova, A.; Gursesli, M.C.; Lanata, A. Interaction of Virus in Cancer Patients: A Theoretical Dynamic Model. Bioengineering 2023, 10, 224. https://doi.org/10.3390/bioengineering10020224
Shakhmurov VB, Kurulay M, Sahmurova A, Gursesli MC, Lanata A. Interaction of Virus in Cancer Patients: A Theoretical Dynamic Model. Bioengineering. 2023; 10(2):224. https://doi.org/10.3390/bioengineering10020224
Chicago/Turabian StyleShakhmurov, Veli B., Muhammet Kurulay, Aida Sahmurova, Mustafa Can Gursesli, and Antonio Lanata. 2023. "Interaction of Virus in Cancer Patients: A Theoretical Dynamic Model" Bioengineering 10, no. 2: 224. https://doi.org/10.3390/bioengineering10020224
APA StyleShakhmurov, V. B., Kurulay, M., Sahmurova, A., Gursesli, M. C., & Lanata, A. (2023). Interaction of Virus in Cancer Patients: A Theoretical Dynamic Model. Bioengineering, 10(2), 224. https://doi.org/10.3390/bioengineering10020224







