Mechanical Characterization of Human Fascia Lata: Uniaxial Tensile Tests from Fresh-Frozen Cadaver Samples and Constitutive Modelling
Abstract
:1. Introduction
2. Materials and Methods
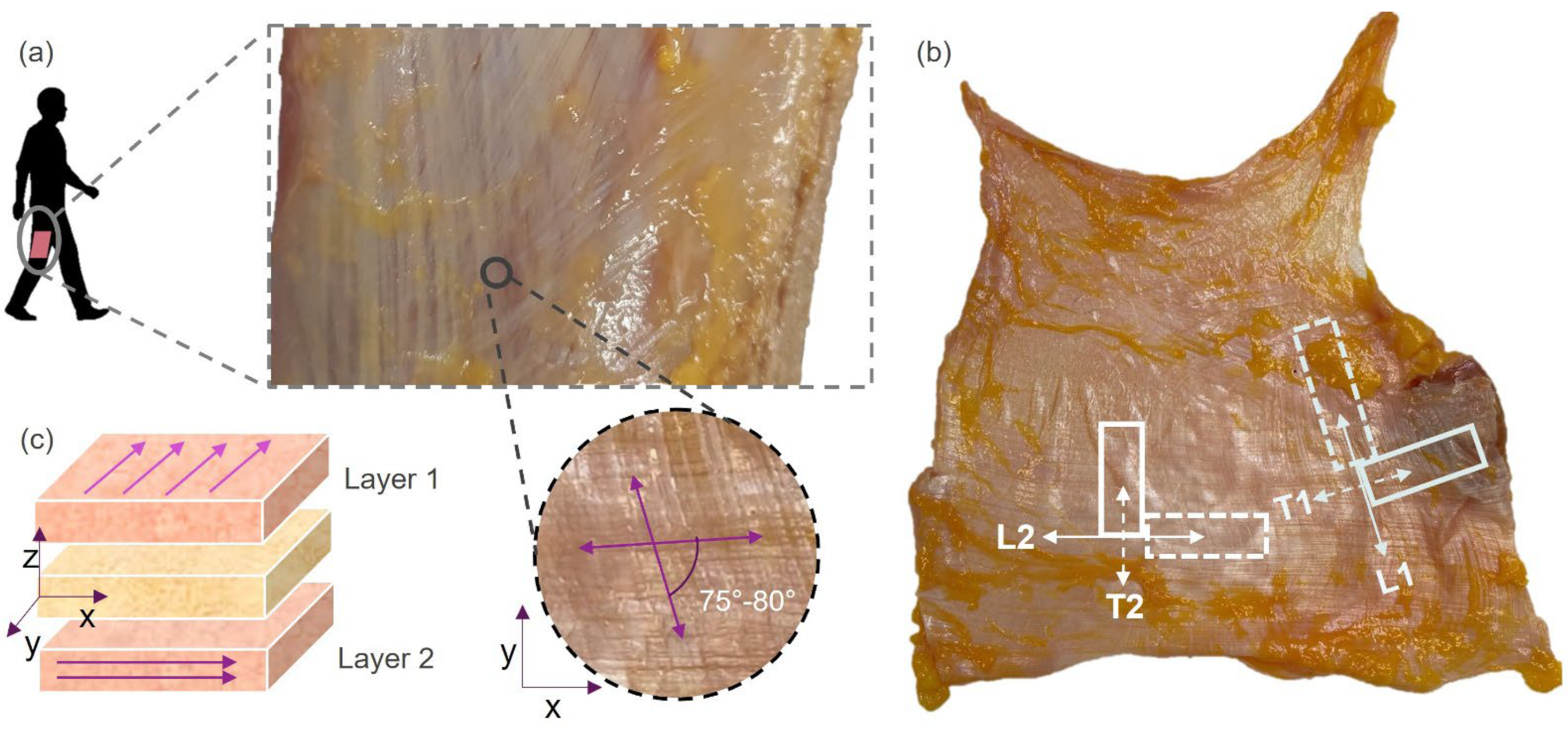
2.1. Human Sample Collection
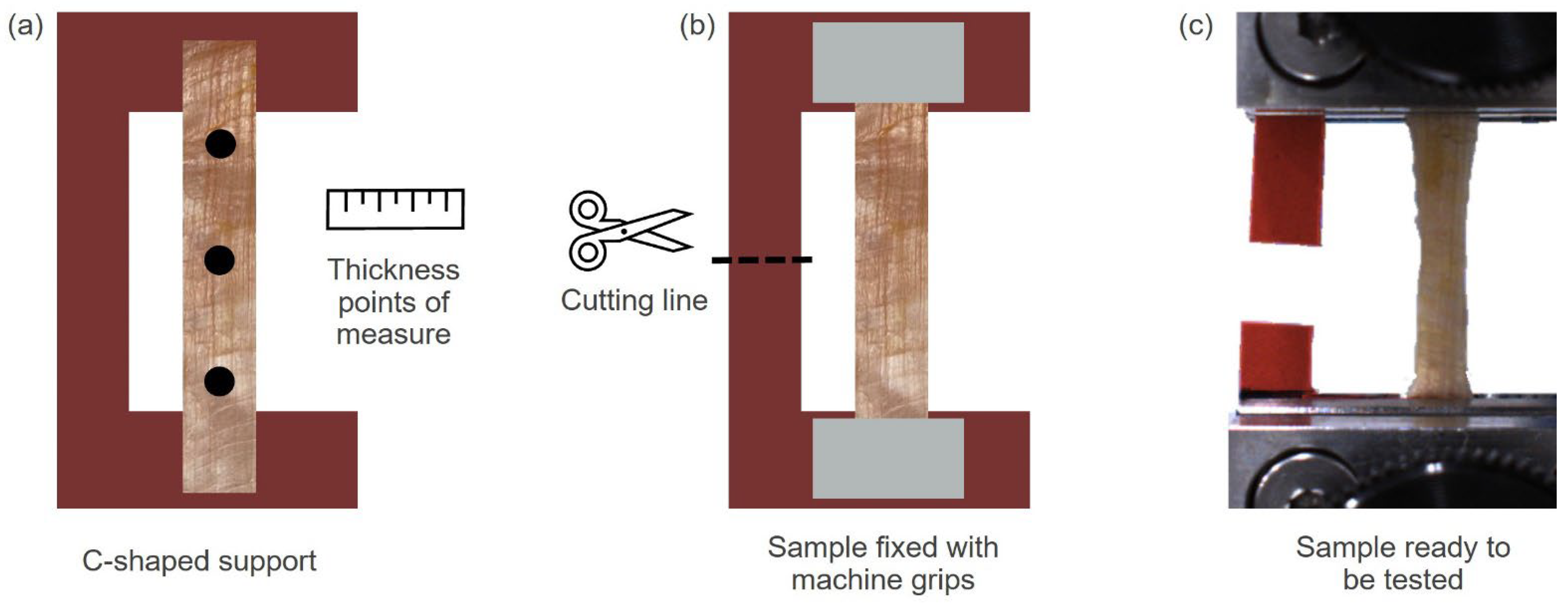
2.2. Experimental Tests on Human Samples
2.3. Constitutive Modelling of Elastic Behavior
2.4. Statistical Analysis
3. Results
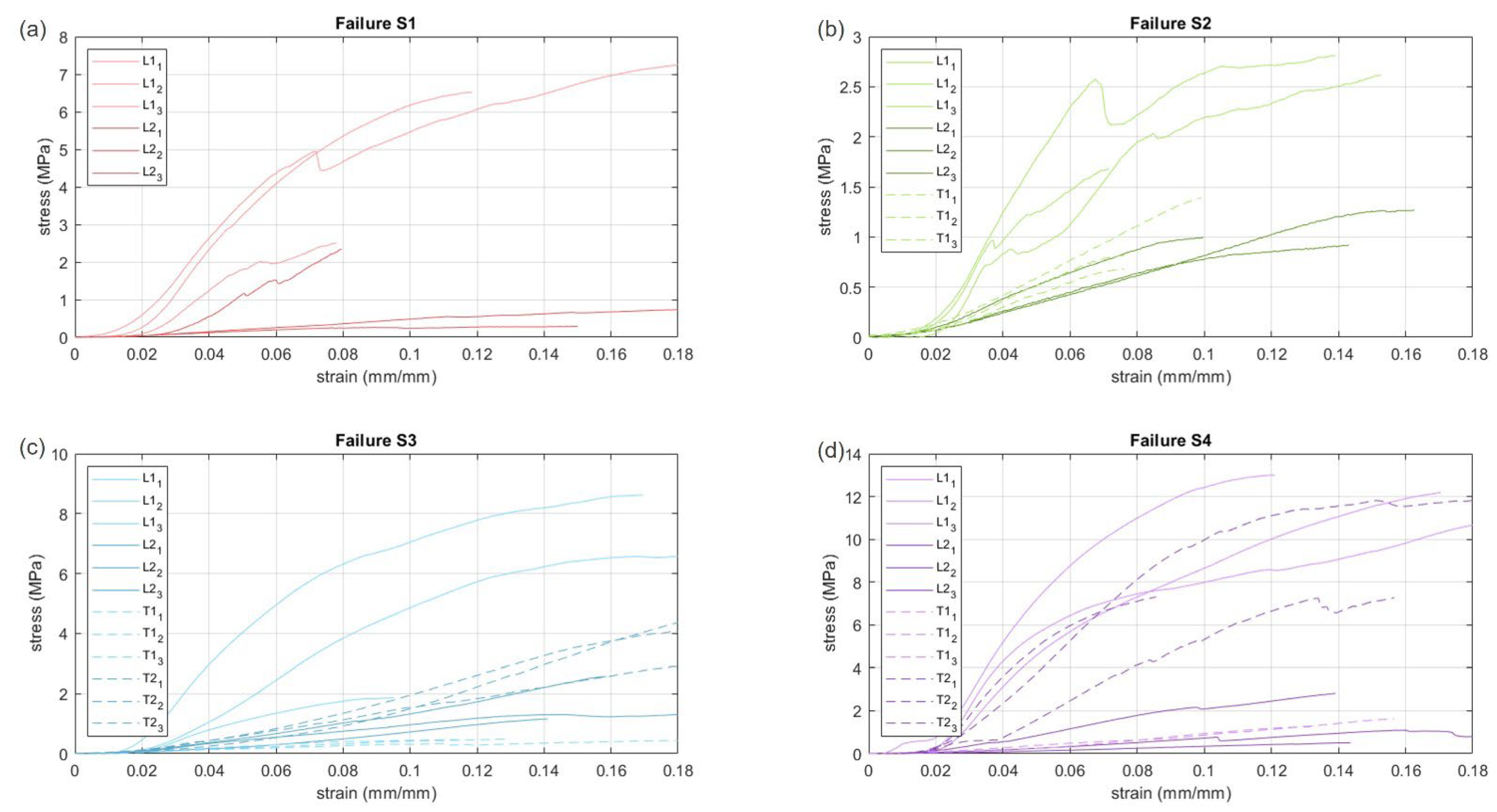
3.1. Failure Tests
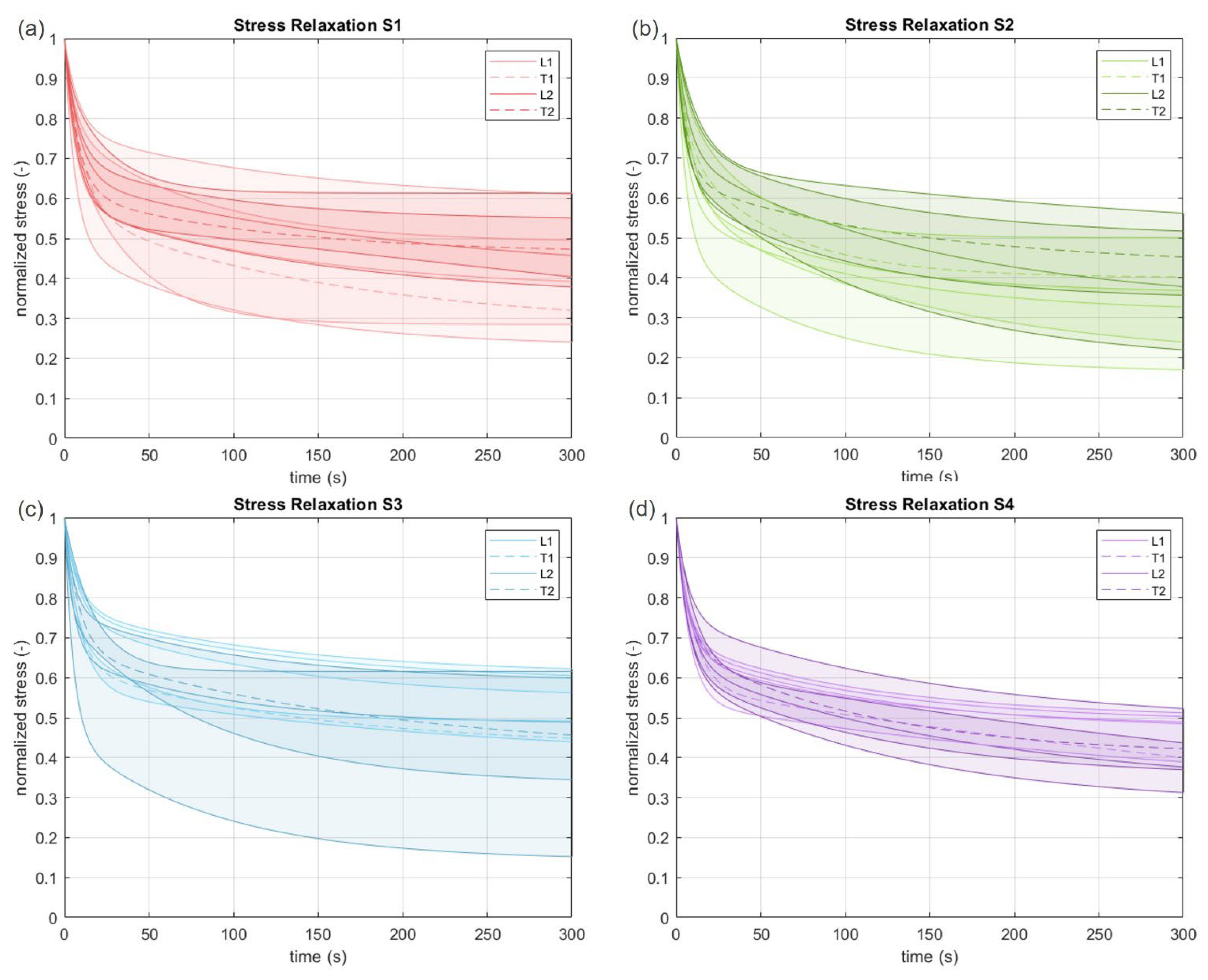
3.2. Viscoelastic Behavior
3.3. Hyper-Elastic Modelling
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Stecco, C. Functional Altas of the Human Fascial System; Churchill Livingstone: London, UK, 2014; ISBN 978-0702044304. [Google Scholar]
- Crawford, J.S. Nature of Fascia Lata and Its Fate after Implantation. Am. J. Ophthalmol. 1969, 67, 900–907. [Google Scholar] [CrossRef] [PubMed]
- Tiengo, C.; Giatsidis, G.; Azzena, B. Fascia Lata Allografts as Biological Mesh in Abdominal Wall Repair: Preliminary Outcomes from a Retrospective Case Series. Plast. Reconstr. Surg. 2013, 132, 631–639. [Google Scholar] [CrossRef] [PubMed]
- Thomas, O.L.; Morrison, C.; Howard, L.; Oni, O.O.A. The Biomechanical Properties of Fascia Lata Grafts: A Preliminary Study. Injury 1998, 29, 227–228. [Google Scholar] [CrossRef] [PubMed]
- Otsuka, S.; Yakura, T.; Ohmichi, Y.; Ohmichi, M.; Naito, M.; Nakano, T.; Kawakami, Y. Site Specificity of Mechanical and Structural Properties of Human Fascia Lata and Their Gender Differences: A Cadaveric Study. J. Biomech. 2018, 77, 69–75. [Google Scholar] [CrossRef] [PubMed]
- Azevedo, C.I.D.C.; Ângelo, A.C.L.P.G.; Quental, C.; Gonçalves, S.; Folgado, J.; Ferreira, N.; Sevivas, N. Proximal and Mid-Thigh Fascia Lata Graft Constructs Used for Arthroscopic Superior Capsule Reconstruction Show Equivalent Biomechanical Properties: An in Vitro Human Cadaver Study. JSES Int. 2021, 5, 439–446. [Google Scholar] [CrossRef] [PubMed]
- Derwin, K.A.; Baker, A.R.; Spragg, R.K.; Leigh, D.R.; Farhat, W.; Iannotti, J.P. Regional Variability, Processing Methods, and Biophysical Properties of Human Fascia Lata Extracellular Matrix. J. Biomed. Mater. Res. Part A 2008, 84A, 500–507. [Google Scholar] [CrossRef] [PubMed]
- Butler, D.L.; Grood, E.S.; Noyes, F.R.; Zernicke, R.F.; Brackett, K. Effects of Structure and Strain Measurement Technique on the Material Properties of Young Human Tendons and Fascia. J. Biomech. 1984, 17, 579–596. [Google Scholar] [CrossRef] [PubMed]
- Erivan, R.; Aubret, S.; Villatte, G.; Cueff, R.; Mulliez, A.; Descamps, S.; Boisgard, S. Irradiation at 11 kGy Conserves the Biomechanical Properties of Fascia Lata Better than Irradiation at 25 kGy. Clin. Biomech. 2018, 60, 100–107. [Google Scholar] [CrossRef] [PubMed]
- Hammer, N.; Lingslebe, U.; Aust, G.; Milani, T.L.; Hädrich, C.; Steinke, H. Ultimate Stress and Age-Dependent Deformation Characteristics of the Iliotibial Tract. J. Mech. Behav. Biomed. Mater. 2012, 16, 81–86. [Google Scholar] [CrossRef] [PubMed]
- Balsly, C.R.; Cotter, A.T.; Williams, L.A.; Gaskins, B.D.; Moore, M.A.; Wolfinbarger, L. Effect of Low Dose and Moderate Dose Gamma Irradiation on the Mechanical Properties of Bone and Soft Tissue Allografts. Cell Tissue Bank. 2008, 9, 289–298. [Google Scholar] [CrossRef] [PubMed]
- Otsuka, S.; Shan, X.; Yoshida, K.; Yakura, T.; Naito, M.; Kawakami, Y. Site Dependent Elastic Property of Human Iliotibial Band and the Effect of Hip and Knee Joint Angle Configuration. J. Biomech. 2020, 109, 109919. [Google Scholar] [CrossRef] [PubMed]
- Zwirner, J.; Babian, C.; Ondruschka, B.; Schleifenbaum, S.; Scholze, M.; Waddell, N.J.; Hammer, N. Tensile Properties of the Human Iliotibial Tract Depend on Height and Weight. Med. Eng. Phys. 2019, 69, 85–91. [Google Scholar] [CrossRef] [PubMed]
- Stecco, C.; Pavan, P.; Pachera, P.; De Caro, R.; Natali, A. Investigation of the Mechanical Properties of the Human Crural Fascia and Their Possible Clinical Implications. Surg. Radiol. Anat. 2014, 36, 25–32. [Google Scholar] [CrossRef] [PubMed]
- Gordon, K.; Brett, A.; Weber, J.F. Uniaxial Biomechanical Testing of Ligaments and Tendons; Elsevier Inc.: Amsterdam, The Netherlands, 2017; ISBN 9780128038550. [Google Scholar]
- Dwyer, N.T.; Kreder, K.J. Fascia Lata Sling, 3rd ed.; Elsevier Inc.: Amsterdam, The Netherlands, 2008; ISBN 9781416023395. [Google Scholar]
- Caplan, N.; Kader, D.F. Biomechanical Analysis of Human Ligament Grafts Used in Knee-Ligament Repairs and Reconstructions. In Classic Papers in Orthopaedics; Springer: London, UK, 2014; pp. 145–147. [Google Scholar]
- Aurora, A.; Mesiha, M.; Tan, C.D.; Walker, E.; Sahoo, S.; Iannotti, J.P.; McCarron, J.A.; Derwin, K.A. Mechanical Characterization and Biocompatibility of a Novel Reinforced Fascia Patch for Rotator Cuff Repair. J. Biomed. Mater. Res. Part A 2011, 99A, 221–230. [Google Scholar] [CrossRef] [PubMed]
- Porzionato, A.; Macchi, V.; Stecco, C.; Mazzi, A.; Rambaldo, A.; Sarasin, G.; Parenti, A.; Scipioni, A.; De Caro, R. Quality Management of Body Donation Program at the University of Padova. Anat. Sci. Educ. 2012, 5, 264–272. [Google Scholar] [CrossRef] [PubMed]
- ImageJ Image Processing and Analysis in Java. Available online: https://imagej.nih.gov/ (accessed on 15 December 2022).
- Cheng, S.; Clarke, E.C.; Bilston, L.E. The Effects of Preconditioning Strain on Measured Tissue Properties. J. Biomech. 2009, 42, 1360–1362. [Google Scholar] [CrossRef] [PubMed]
- Holzapfel, G.A.; Gasser, T.C.; Ogden, R.W. A New Constitutive Framework for Arterial Wall Mechanics and a Comparative Study of Material Models. J. Elast. 2000, 61, 1–48. [Google Scholar] [CrossRef]
- Carniel, E.L.; Gramigna, V.; Fontanella, C.G.; Frigo, A.; Stefanini, C.; Rubini, A.; Natali, A.N. Characterization of the Anisotropic Mechanical Behaviour of Colonic Tissues: Experimental Activity and Constitutive Formulation. Exp. Physiol. 2014, 99, 759–771. [Google Scholar] [CrossRef] [PubMed]
- The MathWorks, Inc. MATLAB and Statistics; The MathWorks, Inc.: Natick, MA, USA, 2020. [Google Scholar]
- Minitab. Minitab Statistical Software; Minitab, Inc.: State College, PA, USA, 2010; Available online: https://www.minitab.com/ (accessed on 15 December 2022).

| Subject | Interlayer Angle (°) | Sample Orientation | UTS (MPa) | Strain at Break (% mm/mm) | Young’s Modulus 1 (MPa) | |||
|---|---|---|---|---|---|---|---|---|
| Mean | SD | Mean | SD | Mean | SD | |||
| S1 | 60 | L1 | 5.4 | 2.7 | 13.2 | 6.0 | 94.3 | 23.1 |
| T1 | N/A | N/A | N/A | N/A | N/A | N/A | ||
| L2 | 0.8 | 0.4 | 22.2 | 12.5 | 18.9 | 24.1 | ||
| T2 | N/A | N/A | N/A | N/A | N/A | N/A | ||
| S2 | 81 | L1 | 2.1 | 0.7 | 12.1 | 4.3 | 55.7 | 7.7 |
| T1 | 1.0 | 0.4 | 8.4 | 8.4 | 12.5 | 1.6 | ||
| L2 | 1.1 | 0.2 | 13.5 | 3.2 | 10.8 | 3.7 | ||
| T2 | N/A | N/A | N/A | N/A | N/A | N/A | ||
| S3 | 77 | L1 | 5.2 | 4.8 | 13.2 | 5.3 | 66.9 | 34.9 |
| T1 | 0.5 | 0.0 | 23.2 | 19.1 | 4.5 | 1.1 | ||
| L2 | 2.0 | 0.7 | 20.0 | 8.8 | 11.0 | 4.3 | ||
| T2 | 4.1 | 1.1 | 19.8 | 1.4 | 13.8 | 3.5 | ||
| S4 | 86 | L1 | 12.0 | 1.0 | 16.3 | 3.8 | 191.9 | 54.5 |
| T1 | 1.4 | 0.2 | 14.9 | 1.5 | 6.9 | 2.0 | ||
| L2 | 1.5 | 1.2 | 18.0 | 6.7 | 10.0 | 9.7 | ||
| T2 | 9.0 | 3.0 | 18.2 | 11.1 | 119.9 | 65.8 | ||
| Subject | Sample Orientation | Residual Stress (%) | Fit Coefficients | ||||
|---|---|---|---|---|---|---|---|
| After 60 s | After 300 s | γ1 | τ1 (s) | γ2 | τ2 (s) | ||
| S1 | L1 | 51 | 39 | 0.41 | 6.37 | 0.22 | 124.38 |
| T1 | 48 | 32 | 0.43 | 10.04 | 0.29 | 158.14 | |
| L2 | 59 | 46 | 0.35 | 8.31 | 0.25 | 199.53 | |
| T2 | 55 | 47 | 0.38 | 7.70 | 0.15 | 112.39 | |
| S2 | L1 | 46 | 33 | 0.43 | 6.27 | 0.25 | 105.29 |
| T1 | 52 | 40 | 0.27 | 6.33 | 0.33 | 57.54 | |
| L2 | 58 | 38 | 0.29 | 7.19 | 0.38 | 150.48 | |
| T2 | 57 | 45 | 0.35 | 6.11 | 0.22 | 134.94 | |
| S3 | L1 | 70 | 61 | 0.24 | 8.06 | 0.18 | 132.55 |
| T1 | 56 | 45 | 0.37 | 7.67 | 0.21 | 140.28 | |
| L2 | 57 | 49 | 0.35 | 5.44 | 0.17 | 94.57 | |
| T2 | 60 | 46 | 0.33 | 8.45 | 0.27 | 182.56 | |
| S4 | L1 | 60 | 50 | 0.32 | 6.65 | 0.19 | 114.18 |
| T1 | 53 | 40 | 0.42 | 9.71 | 0.46 | 615.57 | |
| L2 | 54 | 38 | 0.36 | 7.88 | 0.32 | 178.57 | |
| T2 | 57 | 42 | 0.31 | 7.02 | 0.28 | 108.78 | |
| Subject | (MPa) | (-) | (-) | (-) | (-) | |||
|---|---|---|---|---|---|---|---|---|
| S1 | 0.0754 | 0.6807 | 2.7894 | 55.9368 | 0.0004 | 1.9971 | 578.9087 | 0.1879 |
| S2 | 0.0163 | 0.3597 | 4.3575 | 173.3235 | 0.0767 | 0.7668 | 197.6555 | 0.0392 |
| S3 | 0.0560 | 0.1071 | 5.7467 | 79.3530 | 0.1006 | 1.4018 | 141.6217 | 0.0746 |
| S4 | 0.0431 | 0.4693 | 5.3137 | 42.1639 | 0.0004 | 0.9011 | 115.2489 | 0.0393 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bonaldi, L.; Berardo, A.; Pirri, C.; Stecco, C.; Carniel, E.L.; Fontanella, C.G. Mechanical Characterization of Human Fascia Lata: Uniaxial Tensile Tests from Fresh-Frozen Cadaver Samples and Constitutive Modelling. Bioengineering 2023, 10, 226. https://doi.org/10.3390/bioengineering10020226
Bonaldi L, Berardo A, Pirri C, Stecco C, Carniel EL, Fontanella CG. Mechanical Characterization of Human Fascia Lata: Uniaxial Tensile Tests from Fresh-Frozen Cadaver Samples and Constitutive Modelling. Bioengineering. 2023; 10(2):226. https://doi.org/10.3390/bioengineering10020226
Chicago/Turabian StyleBonaldi, Lorenza, Alice Berardo, Carmelo Pirri, Carla Stecco, Emanuele Luigi Carniel, and Chiara Giulia Fontanella. 2023. "Mechanical Characterization of Human Fascia Lata: Uniaxial Tensile Tests from Fresh-Frozen Cadaver Samples and Constitutive Modelling" Bioengineering 10, no. 2: 226. https://doi.org/10.3390/bioengineering10020226
APA StyleBonaldi, L., Berardo, A., Pirri, C., Stecco, C., Carniel, E. L., & Fontanella, C. G. (2023). Mechanical Characterization of Human Fascia Lata: Uniaxial Tensile Tests from Fresh-Frozen Cadaver Samples and Constitutive Modelling. Bioengineering, 10(2), 226. https://doi.org/10.3390/bioengineering10020226











