Development of a Hip Joint Socket by Finite-Element-Based Analysis for Mechanical Assessment
Abstract
1. Introduction
2. Method
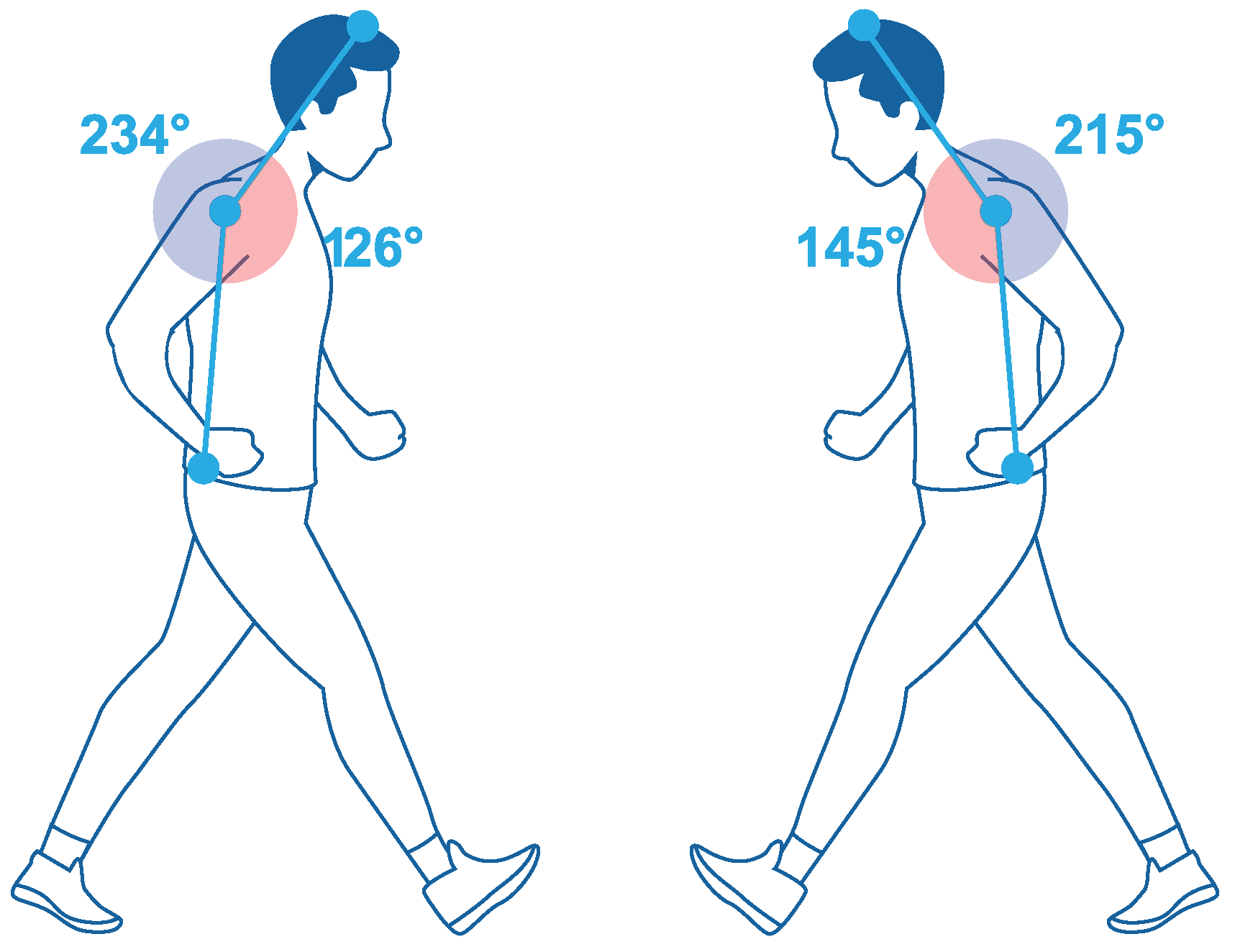
2.1. Data Collection
2.2. Data Analysis
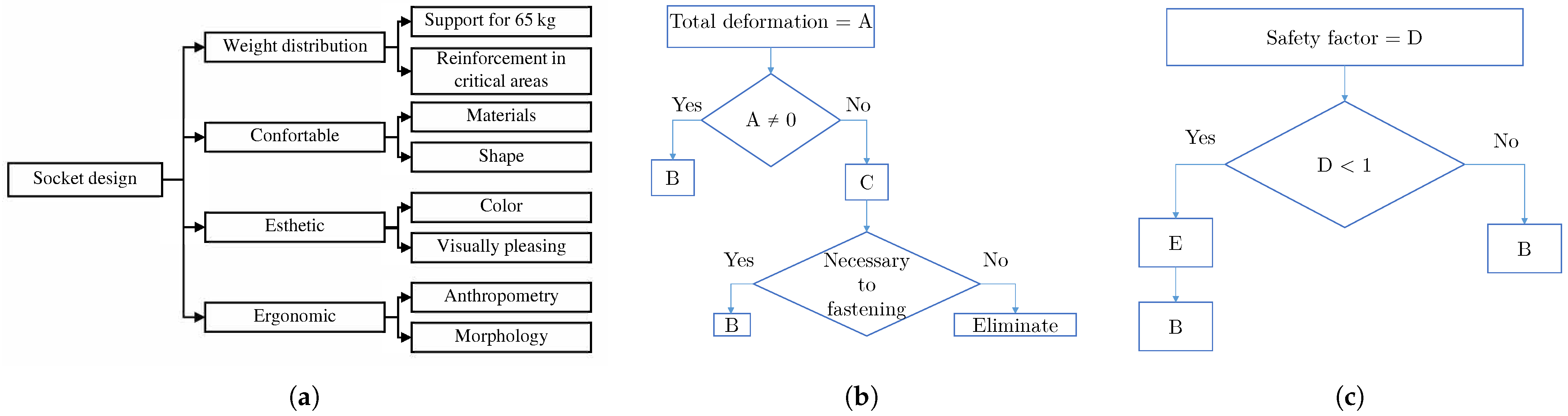
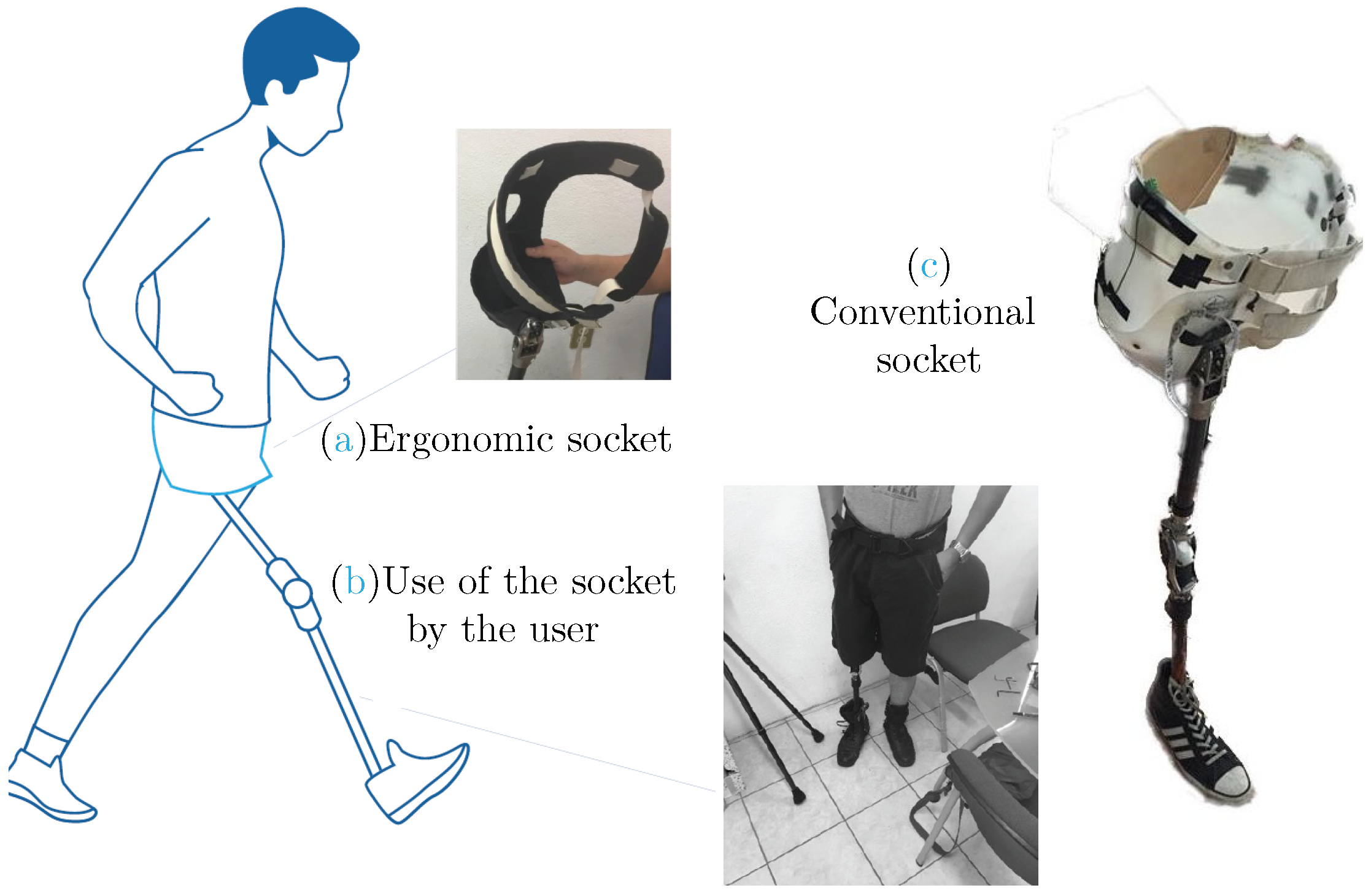
2.3. Socket Design
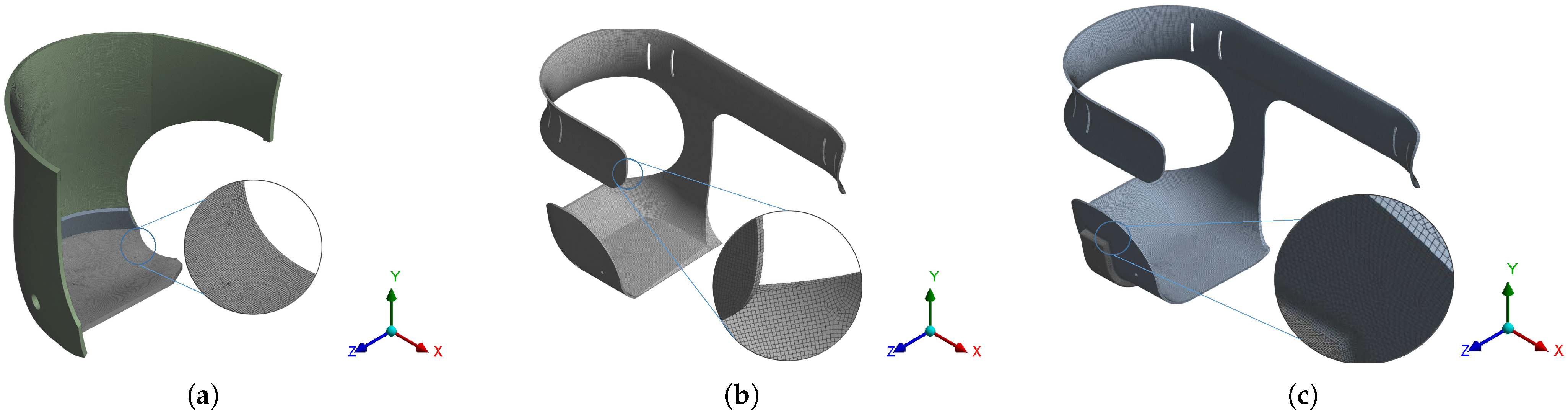
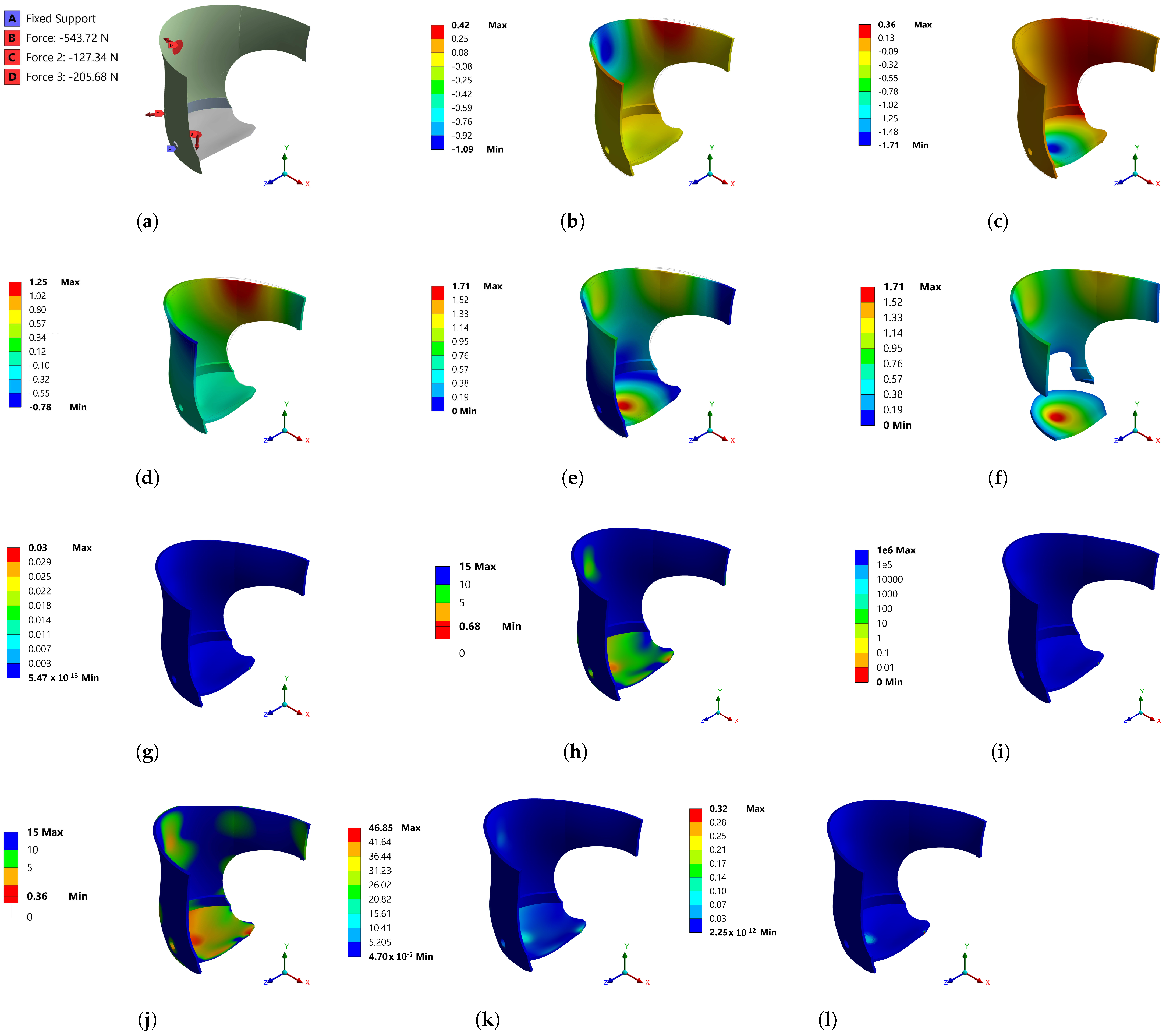
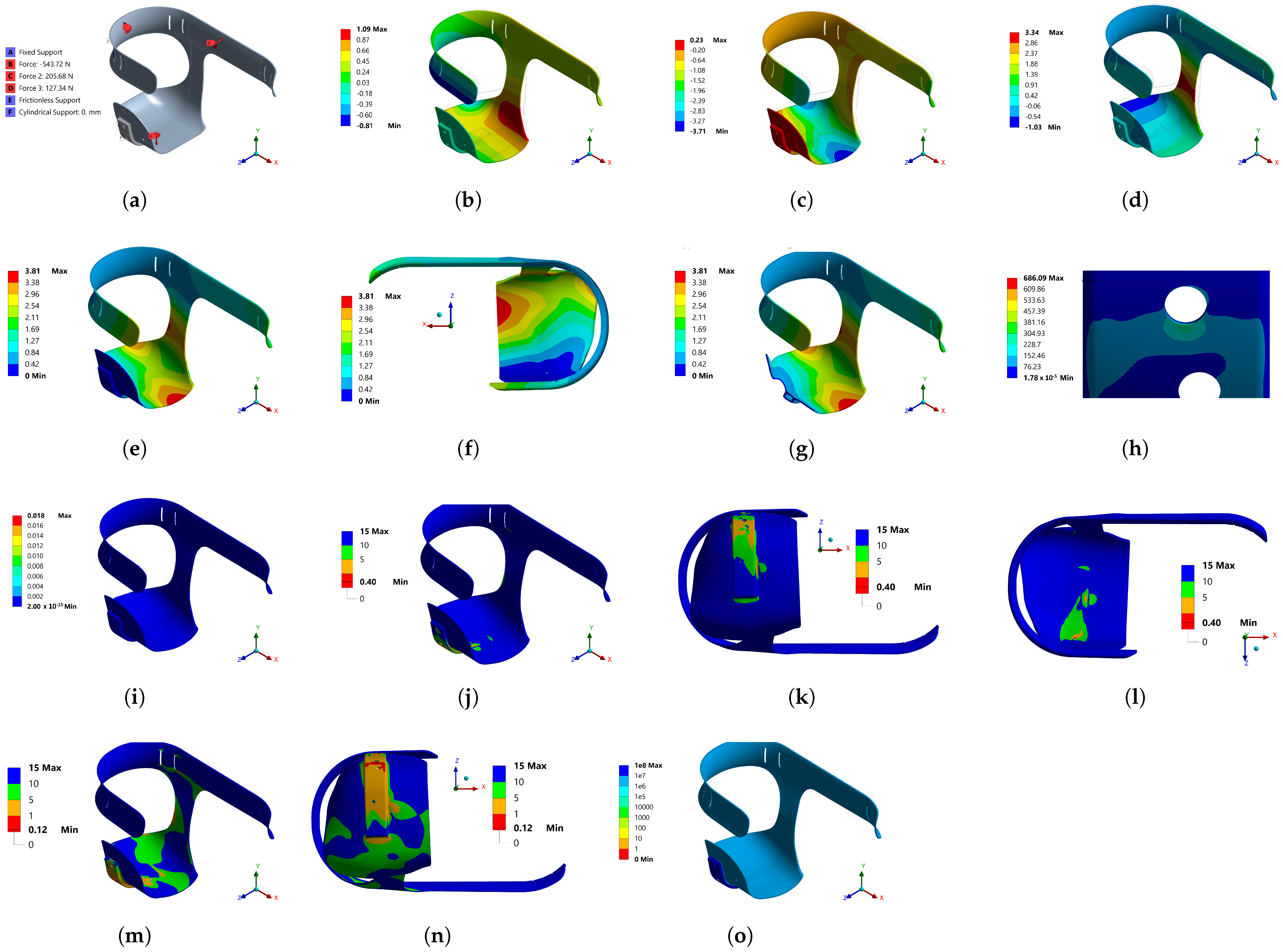
3. Analysis by FEM
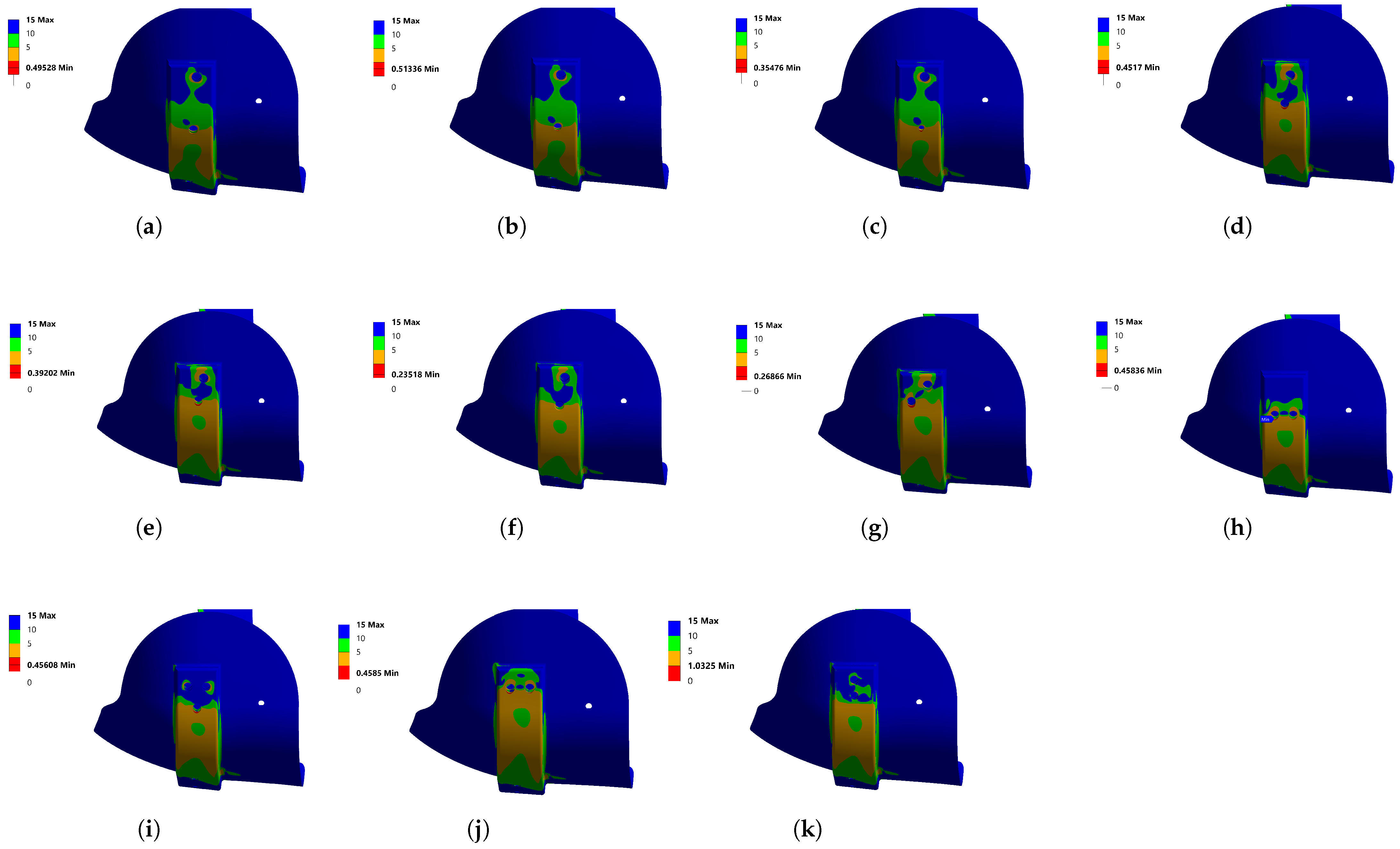
3.1. Stress Concentration Treatment
4. Prototype Manufacture and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Class | Description |
|---|---|
| I | Ambulating with a prosthesis but without other walking aids. |
| II | Independent at home, ambulating with a prosthesis but requiring one walking stick or crutch for outdoor activities. |
| III | Independent indoors, ambulating with a prosthesis and one stick or crutch, but requiring two crutches outdoors and occasionally a wheelchair. |
| IV | Walking indoors with a prosthesis and two crutches or a walker, but requiring a wheelchair for outdoor activities. |
| V | Walking indoors only short distances, ambulating mostly with a wheelchair. |
| VI | Walking with aids but without a prosthesis. |
| VII | Non-ambulatory, except in a wheelchair. |
| Do You Wear Your Prosthesis: | Do You Use Your Prosthesis to Walk: | When Going Outside Wearing Your Prosthesis, Do You: | When Walking with Your Prosthesis Outside, Do You Feel Unstable When: |
|---|---|---|---|
| Less than 25% of walking hours | Just when visiting your doctor or limb-fitting center | Use a wheelchair | Walking on a flat surface |
| Between 25% and 50% of walking hours | At home but do not go outside | Use two crutches, two canes, or walk | Walking on slopes |
| More than 50% of walking hours | Outside the home, on occasion | Use one cane | Walking on rough ground |
| All walking hours | Inside and outside at all times | Use nothing | All of the above |
| 1 Point | 2 Points | 2 Points | 2 Points |
| Activity | No | Yes, with the Help of Someone | Yes, with the Support of an Object | Yes |
|---|---|---|---|---|
| Get up from a chair | X | |||
| Picking up an object from the ground, using a prosthesis | X | |||
| Get up off the ground if you fall | X | |||
| Walk inside the house | X | |||
| Walk outside the house on level ground | X | |||
| Walk outside the house | X | |||
| Walking on uneven ground | X | |||
| Walk outside the house in rain, ice, snow, etc. | X | |||
| Climbing stairs with handrails | X | |||
| Climb a sidewalk | X | |||
| Go down a sidewalk | X | |||
| Climbing stairs without handrails | X |
| Walk | Sit Down | Get Up | Up/Down | ||
|---|---|---|---|---|---|
| Relief | How often has your stump swollen? | 3 | 3 | 3 | 3 |
| How often do you find your socket useful? | 4 | 4 | 3 | 3 | |
| How often have you suffered an injury from the socket? | 4 | 4 | 5 | 5 | |
| How often do you feel your socket gives you benefits? | 2 | 4 | 3 | 3 | |
| Transcendence | How often do you conceive independently using your socket? | 2 | 2 | 2 | 3 |
| How often have you suffered pain from the use of your socket? | 4 | 5 | 4 | 5 | |
| How often should you apply more effort to manipulate your socket? | 4 | 4 | 5 | 5 | |
| How often have you suffered ulcerations from the use of your socket? | 1 | 1 | 1 | 1 | |
| Tranquility | How often is your stump relaxed using your socket? | 5 | 5 | 5 | 5 |
| How often are you confident when using your socket? | 4 | 4 | 4 | 5 | |
| How often would you like to modify some aspect of your socket? | 4 | 5 | 5 | 5 | |
| How often do you feel worried? | 4 | 4 | 4 | 5 |
| Factors | Concept | Indicators |
|---|---|---|
| Relief | 1. How often have you suffered an injury from the socket? | Swelling |
| 2. How often has your stump swollen? | Functionality | |
| 3. How often do you find your socket useful? | Injury | |
| 4. How often have you suffered ulcerations from the use of your socket? | ||
| Transcendence | 5. How often do you conceive independently using your socket? | Independence |
| 6. How often have you suffered pain from using your socket? | Pain | |
| 7. How often should you apply more effort to manipulate your socket? | Effort | |
| 8. How often do you feel that your socket gives you benefits? | ||
| Tranquility | 9. How often is your stump relaxed using your socket? | Relaxation |
| 10. How often do you feel confident using your socket? | Concern | |
| 11. How often would you like to modify some aspect of your socket? | Trust | |
| 12. How often do you feel your socket/socket brings you benefits? |
References
- Dolomisiewicz, E.; Kim, G.; Corcoran, M.; Pasquina, P. A novel suspension system for individuals with proximal transfemoral amputations or hip disarticulations. PM&R 2020, 13, 219–220. [Google Scholar] [CrossRef]
- Ruiz-Diaz, F.D.; Altamirano-Altamirano, A.; Valentino-Orozco, G.A. External knee prosthesis with four bar linkage mechanism. In Proceedings of the 2016 13th International Conference on Electrical Engineering, Computing Science and Automatic Control (CCE), Mexico City, Mexico, 26–30 September 2016. [Google Scholar] [CrossRef]
- Smith, D. Higher challenges: The hip disarticulation and transpelvic amputation levels. InMotion 2005, 15, 38–42. [Google Scholar]
- Solav, D.; Moerman, K.M.; Jaeger, A.M.; Herr, H.M. A framework for measuring the time-varying shape and full-field deformation of residual limbs using 3-D digital image correlation. IEEE Trans. Biomed. Eng. 2019, 66, 2740–2752. [Google Scholar] [CrossRef] [PubMed]
- Hunter, S.W.; Batchelor, F.; Hill, K.D.; Hill, A.M.; Mackintosh, S.; Payne, M. Risk factors for falls in people with a lower limb amputation: A systematic review. PM&R 2016, 9, 170–180. [Google Scholar] [CrossRef]
- Crowe, C.S.; Impastato, K.A.; Donaghy, A.C.; Earl, C.; Friedly, J.L.; Keys, K.A. Prosthetic and orthotic options for lower extremity amputation and reconstruction. Plast. Aesthet. Res. 2019, 2019, 70. [Google Scholar] [CrossRef]
- Olivares Miyares, A.L.; Broche Vázquez, L.; Díaz Novo, C.; Garlobo Castillo, L.; Sagaró Zamora, R. Análisis de la funcionabilidad de prótesis ortopédicas transfemorales. Rev. Cuba. Ortop. Traumatol. 2011, 25, 102–116. [Google Scholar]
- Hawari, N.M.; Jawaid, M.; Tahir, P.M.; Azmeer, R.A. Case study: Survey of patient satisfaction with prosthesis quality and design among below-knee prosthetic leg socket users. Disabil. Rehabil. Assist. Technol. 2017, 12, 868–874. [Google Scholar] [CrossRef]
- Heitzmann, D.W.W.; Leboucher, J.; Block, J.; Günther, M.; Putz, C.; Götze, M.; Wolf, S.I.; Alimusaj, M. The influence of hip muscle strength on gait in individuals with a unilateral transfemoral amputation. PLoS ONE 2020, 15, e0238093. [Google Scholar] [CrossRef]
- Fernández Gay, C. Implicaciones Anatomofuncionales de la Amputación del Miembro Inferior: Cuidados de Muñón y Consecuencias el el sist. Locomotor del uso Prolongado de Prótesis. Bachelor Thesis, Universidad de Valladolid, Valladolid, Spain, 2014. [Google Scholar]
- Sriperumbudur, K.K.; Pau, H.W.; van Rienen, U. Effect of tissue heterogeneity on the transmembrane potential of type-1 spiral ganglion neurons: A simulation study. IEEE Trans. Biomed. Eng. 2018, 65, 658–668. [Google Scholar] [CrossRef]
- Laszczak, P.; McGrath, M.; Tang, J.; Gao, J.; Jiang, L.; Bader, D.L.; Moser, D.; Zahedi, S. A pressure and shear sensor system for stress measurement at lower limb residuum/socket interface. Med. Eng. Phys. 2016, 38, 695–700. [Google Scholar] [CrossRef]
- Ludwigs, E.; Bellmann, M.; Schmalz, T.; Blumentritt, S. Biomechanical differences between two exoprosthetic hip joint systems during level walking. Prosthet. Orthot. Int. 2010, 34, 449–460. [Google Scholar] [CrossRef]
- Pirouzi, G.; Osman, N.A.A.; Eshraghi, A.; Ali, S.; Gholizadeh, H.; Abas, W.A.B.W. Review of the socket design and interface pressure measurement for transtibial prosthesis. Sci. World J. 2014, 2014, 1–9. [Google Scholar] [CrossRef]
- Colombo, G.; Filippi, S.; Rizzi, C.; Rotini, F. A new design paradigm for the development of custom-fit soft sockets for lower limb prostheses. Comput. Ind. 2010, 61, 513–523. [Google Scholar] [CrossRef]
- Weathersby, E.J.; Garbini, J.L.; Larsen, B.G.; McLean, J.B.; Vamos, A.C.; Sanders, J.E. Automatic control of prosthetic socket size for people with transtibial amputation: Implementation and evaluation. IEEE Trans. Biomed. Eng. 2021, 68, 36–46. [Google Scholar] [CrossRef]
- Paternò, L.; Ibrahimi, M.; Gruppioni, E.; Menciassi, A.; Ricotti, L. Sockets for limb prostheses: A review of existing technologies and open challenges. IEEE Trans. Biomed. Eng. 2018, 65, 1996–2010. [Google Scholar] [CrossRef]
- Almeida-Galárraga, D.; Ros-Felip, A.; Álvarez Sánchez, V.; Marco-Martinez, F.; Serrano-Mateo, L. Kinematics based physical modelling and experimental analysis of the shoulder joint complex. Ing. Investig. 2017, 37, 115–123. [Google Scholar] [CrossRef]
- Sánchez Otero, J.; Hernández, R.J.; Torres, J.E. The mechanical design of a transfemoral prosthesis using computational tools and design methodology. Ing. Investig. 2012, 32, 14–18. [Google Scholar] [CrossRef]
- Martin, J.J. Anatomically Configured Hip Level Prosthetic Socket System. U.S. Patent 7,300,466, 27 November 2007. [Google Scholar]
- Valyi-Nagy, T.; Kulcsar, G.; Szilagyi, I.; Valu, G.; Magyar, K.; Kiss, G.H.; Horvath, I. Process for Producing Primycin. U.S. Patent 3,498,884, 3 March 1970. [Google Scholar]
- Sengeh, D.M.; Herr, H. A variable-impedance prosthetic socket for a transtibial amputee designed from magnetic resonance imaging data. JPO J. Prosthet. Orthot. 2013, 25, 129–137. [Google Scholar] [CrossRef]
- Steer, J.W.; Grudniewski, P.A.; Browne, M.; Worsley, P.R.; Sobey, A.J.; Dickinson, A.S. Predictive prosthetic socket design: Part 2—generating person-specific candidate designs using multi-objective genetic algorithms. Biomech. Model. Mechanobiol. 2019, 19, 1347–1360. [Google Scholar] [CrossRef]
- Cammarata, A.; Lacagnina, M.; Sinatra, R. Closed-form solutions for the inverse kinematics of the Agile Eye with constraint errors on the revolute joint axes. In Proceedings of the 2016 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Daejeon, Republic of Korea, 9–14 October 2016; pp. 317–322. [Google Scholar] [CrossRef]
- Cammarata, A.; Sinatra, R.; Maddìo, P.D. Static condensation method for the reduced dynamic modeling of mechanisms and structures. Arch. Appl. Mech. 2019, 89, 2033–2051. [Google Scholar] [CrossRef]
- Nam, J.; Choi, H.; Kang, J. Finite element analysis for friction noise of simplified hip joint and its experimental validation. J. Mech. Sci. Technol. 2016, 30, 3453–3460. [Google Scholar] [CrossRef]
- Lin, Y.T.; Wu, J.S.S.; Chen, J.H. The study of wear behaviors on abducted hip joint prostheses by an alternate finite element approach. Comput. Methods Programs Biomed. 2016, 131, 143–155. [Google Scholar] [CrossRef] [PubMed]
- Gindre, J.; Bel-Brunon, A.; Rochette, M.; Lucas, A.; Kaladji, A.; Haigron, P.; Combescure, A. Patient-specific finite-element simulation of the insertion of guidewire during an EVAR procedure: Guidewire position prediction validation on 28 cases. IEEE Trans. Biomed. Eng. 2017, 64, 1057–1066. [Google Scholar] [CrossRef] [PubMed]
- Dickinson, A.S.; Steer, J.W.; Worsley, P.R. Finite element analysis of the amputated lower limb: A systematic review and recommendations. Med. Eng. Phys. 2017, 43, 1–18. [Google Scholar] [CrossRef] [PubMed]
- Ashkanfar, A.; Langton, D.J.; Joyce, T.J. A large taper mismatch is one of the key factors behind high wear rates and failure at the taper junction of total hip replacements: A finite element wear analysis. J. Mech. Behav. Biomed. Mater. 2017, 69, 257–266. [Google Scholar] [CrossRef]
- Hakim, R.A.N.A.; Edwan, A.; Jamari, J.; Ismail, R.; Bayuseno, A.; Tauviqirrahman, M.; Kurdi, O.; Saputra, E.; Anwar, I.B.; Dahlan, S. Simulation load parameter on bipolar artificial hip joint using finite element method (FEM). Mater. Today Proc. 2019, 13, 305–310. [Google Scholar] [CrossRef]
- Lim, J.; Kim, Y.; Kim, N. Mechanical effects of cochlear implants on residual hearing loss: A finite element analysis. IEEE Trans. Biomed. Eng. 2020, 67, 3253–3261. [Google Scholar] [CrossRef]
- N., C.K.; Ogulcan, G.; N., S.B.; Zuber, M.; B., S.S. Wear estimation of trapezoidal and circular shaped hip implants along with varying taper trunnion radiuses using finite element method. Comput. Methods Programs Biomed. 2020, 196, 105597. [Google Scholar] [CrossRef]
- Meng, Z.; Wong, D.W.C.; Zhang, M.; Leung, A.K.L. Analysis of compression/release stabilized transfemoral prosthetic socket by finite element modelling method. Med. Eng. Phys. 2020, 83, 123–129. [Google Scholar] [CrossRef]
- Camero Sanabria, H.E. A novel finite element method for designing floor slabs on grade and pavements with loads at edges. Ing. Investig. 2015, 35, 15–22. [Google Scholar] [CrossRef]
- Ren, S.; Shi, H.; Liu, Z.; Zhang, J.; Li, H.; Huang, H.; Ao, Y. Finite Element Analysis and Experimental Validation of the Anterior Cruciate Ligament and Implications for the Injury Mechanism. Bioengineering 2022, 9, 590. [Google Scholar] [CrossRef]
- Byun, S.H.; Seo, J.H.; Cho, R.Y.; Yi, S.M.; Kim, L.K.; Han, H.S.; On, S.W.; Kim, W.H.; An, H.W.; Yang, B.E. Finite Element Analysis of a New Non-Engaging Abutment System for Three-Unit Implant-Supported Fixed Dental Prostheses. Bioengineering 2022, 9, 483. [Google Scholar] [CrossRef]
- Vieira, M.M.; Neves-Amado, J.; Deodato, S. 12th International Seminar on Nursing Research Proceedings. In Proceedings of the 12th International Seminar on Nursing Research Proceedings, Porto, Spain, 3–4 May 2018. [Google Scholar]
- Tse, K.M.; Holder, D. A Biomechanical Evaluation of a Novel Airbag Bicycle Helmet Concept for Traumatic Brain Injury Mitigation. Bioengineering 2021, 8, 173. [Google Scholar] [CrossRef]
- Nappi, F.; Mazzocchi, L.; Spadaccio, C.; Attias, D.; Timofeva, I.; Macron, L.; Iervolino, A.; Morganti, S.; Auricchio, F. CoreValve vs. Sapien 3 Transcatheter Aortic Valve Replacement: A Finite Element Analysis Study. Bioengineering 2021, 8, 52. [Google Scholar] [CrossRef]
- García-Vilana, S.; Sánchez-Molina, D.; Llumà, J.; Galtés, I.; Velázquez-Ameijide, J.; Rebollo-Soria, M.C.; Arregui-Dalmases, C. Viscoelastic Characterization of Parasagittal Bridging Veins and Implications for Traumatic Brain Injury: A Pilot Study. Bioengineering 2021, 8, 145. [Google Scholar] [CrossRef]
- Escamilla-Nunez, R.; Michelini, A.; Andrysek, J. Biofeedback systems for gait rehabilitation of individuals with lower-limb amputation: A systematic review. Sensors 2020, 20, 1628. [Google Scholar] [CrossRef]
- Chigblo, P.; Tidjani, I.F.; Alagnidé, E.; Lawson, E.; Madougou, S.; Agbessi, O.; Akué, A.H.M. Outcomes of lower limb amputees at Cotonou. J. Clin. Orthop. Trauma 2019, 10, 191–194. [Google Scholar] [CrossRef]
- Kline, P.W.; Murray, A.M.; Miller, M.J.; So, N.; Fields, T.; Christiansen, C.L. Step length symmetry adaptation to split-belt treadmill walking after acquired non-traumatic transtibial amputation. Gait Posture 2020, 80, 162–167. [Google Scholar] [CrossRef]
- Eshraghi, A.; Safaeepour, Z.; Geil, M.D.; Andrysek, J. Walking and balance in children and adolescents with lower-limb amputation: A review of literature. Clin. Biomech. 2018, 59, 181–198. [Google Scholar] [CrossRef]
- Namwongsa, S.; Puntumetakul, R.; Neubert, M.S.; Chaiklieng, S.; Boucaut, R. Ergonomic risk assessment of smartphone users using the Rapid Upper Limb Assessment (RULA) tool. PLoS ONE 2018, 13, e0203394. [Google Scholar] [CrossRef]
- Joshi, M.; Deshpande, V. Investigative study and sensitivity analysis of Rapid Entire Body Assessment (REBA). Int. J. Ind. Ergon. 2020, 79, 103004. [Google Scholar] [CrossRef]


| Reference/Year | Contribution to the Field of Study |
|---|---|
| [26] | Friction-induced instability in the hip joint system was analyzed, using the finite element method. |
| [27] | In the study, a finite element approach, with contact transformation, was proposed, which required less computational effort. |
| [28] | The authors performed a numerical simulation that was capable of predicting variations in vascular geometry. |
| [29] | This systematic literature review investigated the state of the art in residual limb finite element analyses published since 2000. |
| [30] | Finite element 3D models from an interface perfectly adapted to large conical misalignments, and a wear algorithm, were used to investigate the degree of wear that could occur. |
| [31] | The results of the reaction force of the hip joint during salat were used for the simulation load parameter in the simulation of the bipolar artificial hip joint UNDIP, with those loads using the finite element method. |
| [32] | The effects of cochlear implants on residual hearing loss were investigated through a finite element model of human auditory periphery, consisting of the cochlea and the middle ear. |
| [33] | Estimation of hip implant wear, using the finite element method. |
| [34] | This work investigated the residual limb tension of the compression/release stabilized socket of a transfemoral amputee, using finite element modeling. |
| Activity | Answers | No. Items | Comfort |
|---|---|---|---|
| Walk | 9 | 12 | 25% |
| Sit down | 10 | 12 | 17% |
| Get up | 10 | 12 | 17% |
| Up or down | 11 | 12 | 8% |
| Customer Requirements | Design Requirements | Concepts | Importance |
|---|---|---|---|
| Autonomy | Stability | Independence, Support, Material | 1% |
| Safety | Resistance | Material, Simulation Test | 2% |
| Comfort | Ergonomics | Soft material, Non-intrusive, Intuitive design | 4% |
| Esthetics | Color | Material | 5% |
| Usability | Shape | Function, Replicable | 3% |
| Model 1 | Model 2 | Model 3 | |
|---|---|---|---|
| Body | Surface thickness: 5 mm | Solid | Solid |
| Material | 30% wt glass-fiber-reinforced polypropylene 1.3 GPa 0.4 41 MPa 950 kg/m | 30% wt glass-fiber-reinforced polypropylene 1.3 GPa 0.4 41 MPa 950 kg/m | 30% wt glass-fiber-reinforced polypropylene 1.3 GPa 0.4 41 MPa 950 kg/m Aluminum alloy 71 GPa 0.33 280 MPa 2770 kg/m |
| Element Type | Shell 101 | SOLID 187 | SOLID 187 |
| Elements | 291,972.00 | 254,482.00 | 829,810.00 |
| Nodes | 293,865.00 | 969,298.00 | 3,060,273.00 |
| Loads | Force 1 −543.72 N −26.94 N −542.58 N 22.52 N Force 2 −127.34 N −78.65 N −0.744 N 100.13 N Force 3 −205.68 N −204.9 N −9.91 N 14.86 N | Force 1 −543.72 N Force 2 −205.68 N Force 3 −127.34 N | Force 1 −543.72 N; Force 2 −205.68 N Force 3 −127.34 N |
| Supports | Fixed support, two edges, to attach the prosthesis or artificial limb. | Frictionless support, six faces, to attach the belt for hip. Cylindrical support, two faces, to secure the aluminum bracket. | Frictionless support, six faces, to attach the belt for hip. Cylindrical support, two faces, to secure the aluminum bracket. Fixed support, two faces, to attach the prosthesis or artificial limb. |
| Activity | Answers | No. Items | Comfort |
|---|---|---|---|
| Walk | 1 | 12 | 92% |
| Sit down | 3 | 12 | 75% |
| Get up | 3 | 12 | 75% |
| Up or down | 4 | 12 | 67% |
| Ranks | Consistencies |
|---|---|
| Excellent | |
| Good | |
| Acceptable | |
| Questionable | |
| Poor | |
| Unacceptable |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
González, A.K.; Rodríguez-Reséndiz, J.; Gonzalez-Durán, J.E.E.; Olivares Ramírez, J.M.; Estévez-Bén, A.A. Development of a Hip Joint Socket by Finite-Element-Based Analysis for Mechanical Assessment. Bioengineering 2023, 10, 268. https://doi.org/10.3390/bioengineering10020268
González AK, Rodríguez-Reséndiz J, Gonzalez-Durán JEE, Olivares Ramírez JM, Estévez-Bén AA. Development of a Hip Joint Socket by Finite-Element-Based Analysis for Mechanical Assessment. Bioengineering. 2023; 10(2):268. https://doi.org/10.3390/bioengineering10020268
Chicago/Turabian StyleGonzález, Ana Karen, Juvenal Rodríguez-Reséndiz, José Eli Eduardo Gonzalez-Durán, Juan Manuel Olivares Ramírez, and Adyr A. Estévez-Bén. 2023. "Development of a Hip Joint Socket by Finite-Element-Based Analysis for Mechanical Assessment" Bioengineering 10, no. 2: 268. https://doi.org/10.3390/bioengineering10020268
APA StyleGonzález, A. K., Rodríguez-Reséndiz, J., Gonzalez-Durán, J. E. E., Olivares Ramírez, J. M., & Estévez-Bén, A. A. (2023). Development of a Hip Joint Socket by Finite-Element-Based Analysis for Mechanical Assessment. Bioengineering, 10(2), 268. https://doi.org/10.3390/bioengineering10020268








