Design Optimization of a Phototherapy Extracorporeal Membrane Oxygenator for Treating Carbon Monoxide Poisoning
Abstract
:1. Introduction
2. Study Design and Methods
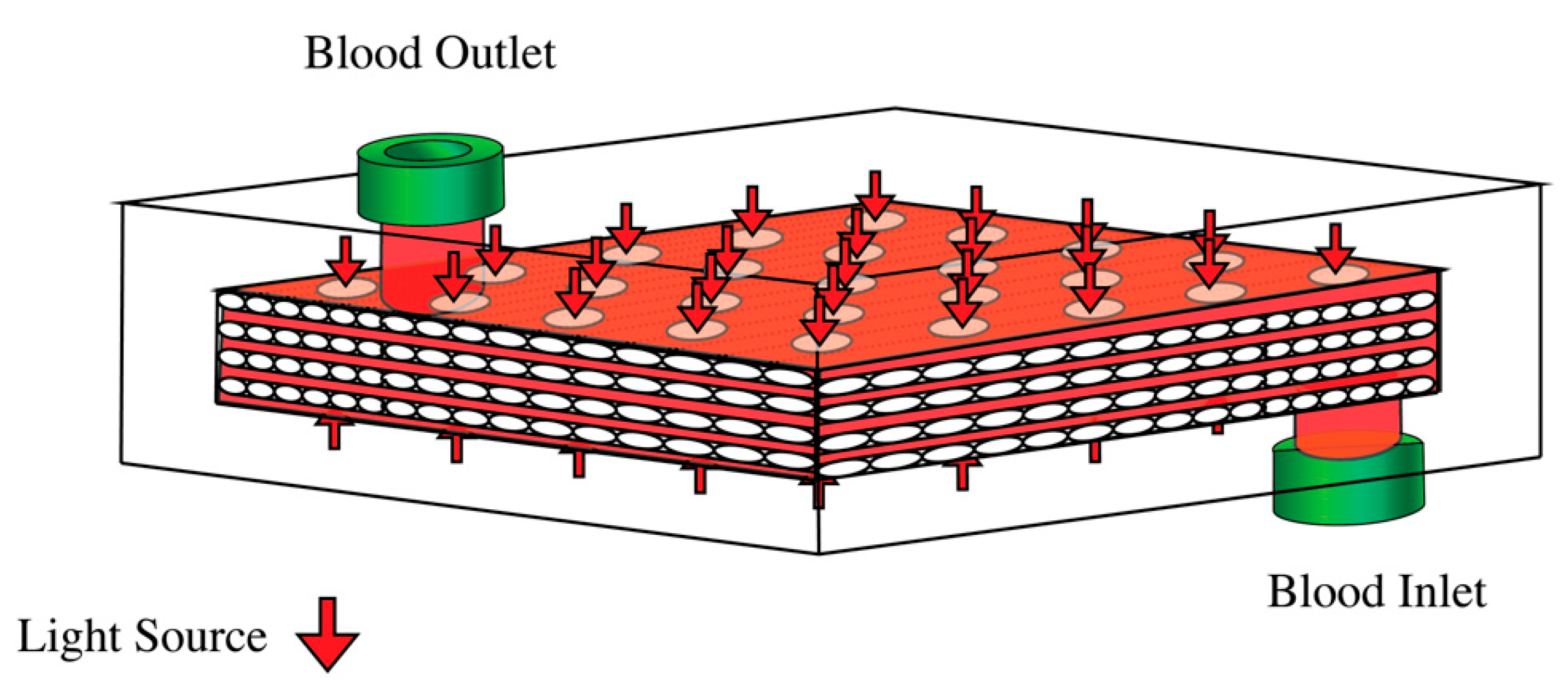
2.1. The Photo-ECMO Device
2.2. Light Propagation
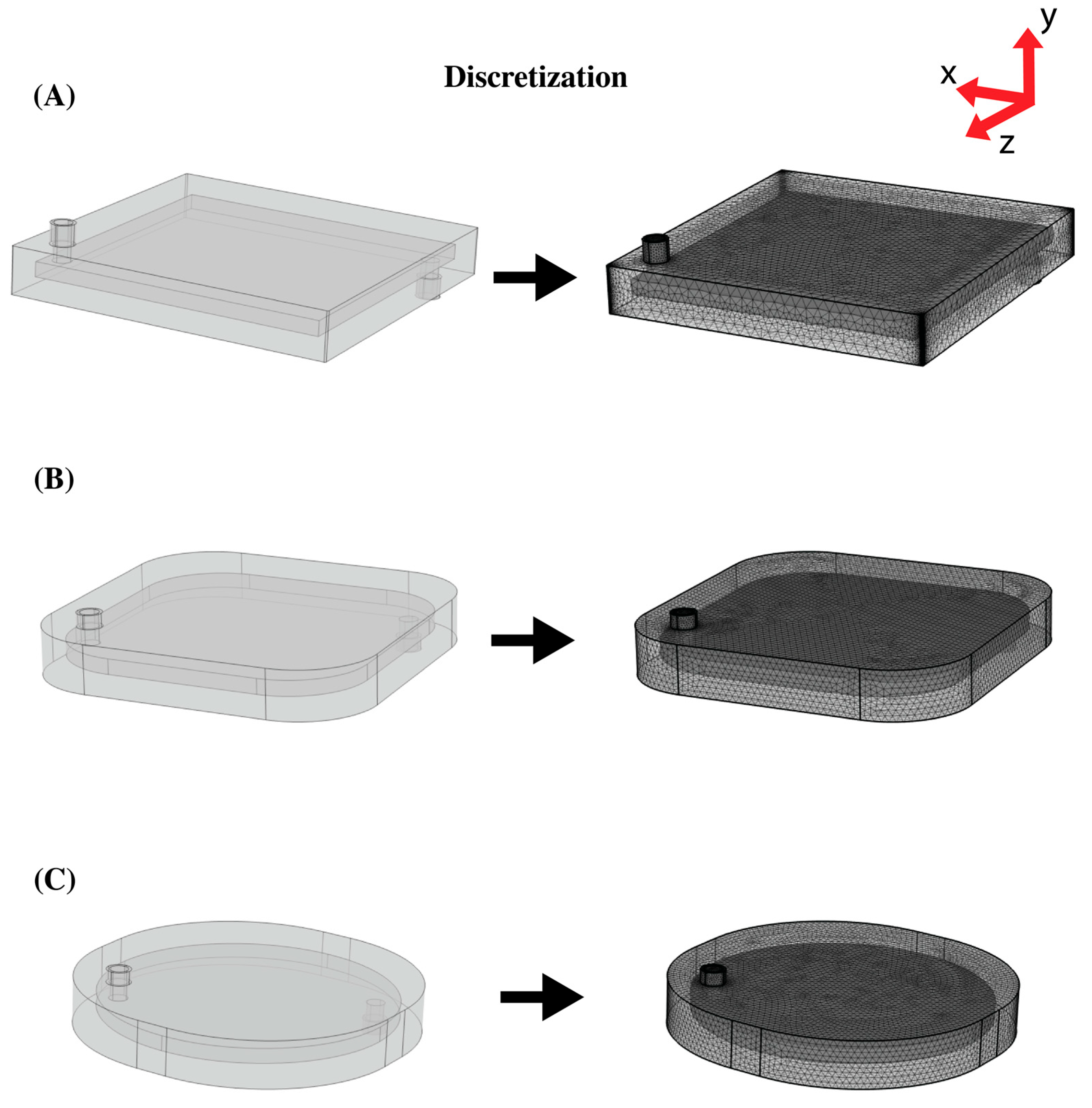
2.3. Modeling Geometries
2.4. Numerical Analysis
2.5. Blood Flow
2.6. Particle Tracing
2.7. Blood Heating
3. Results
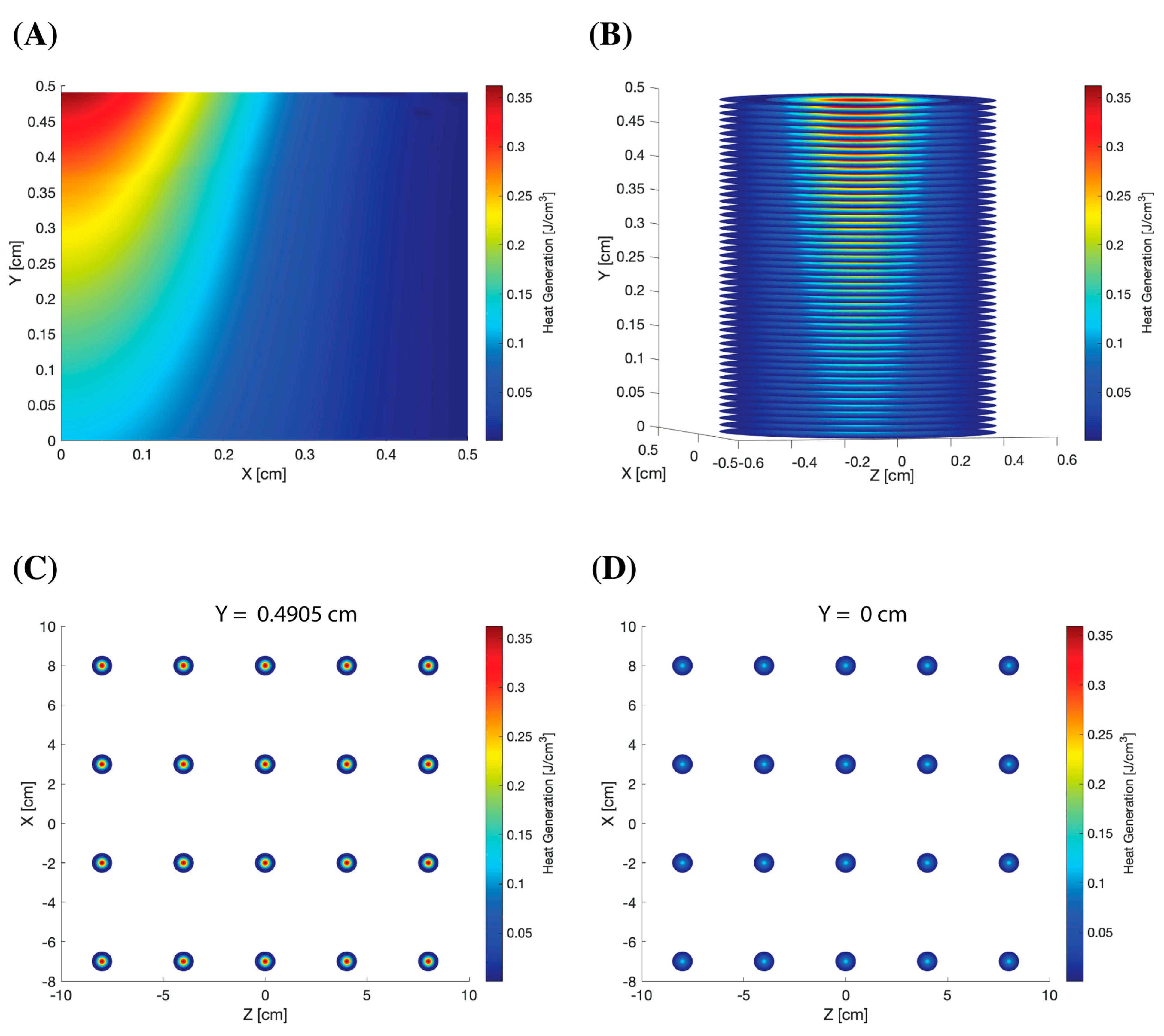
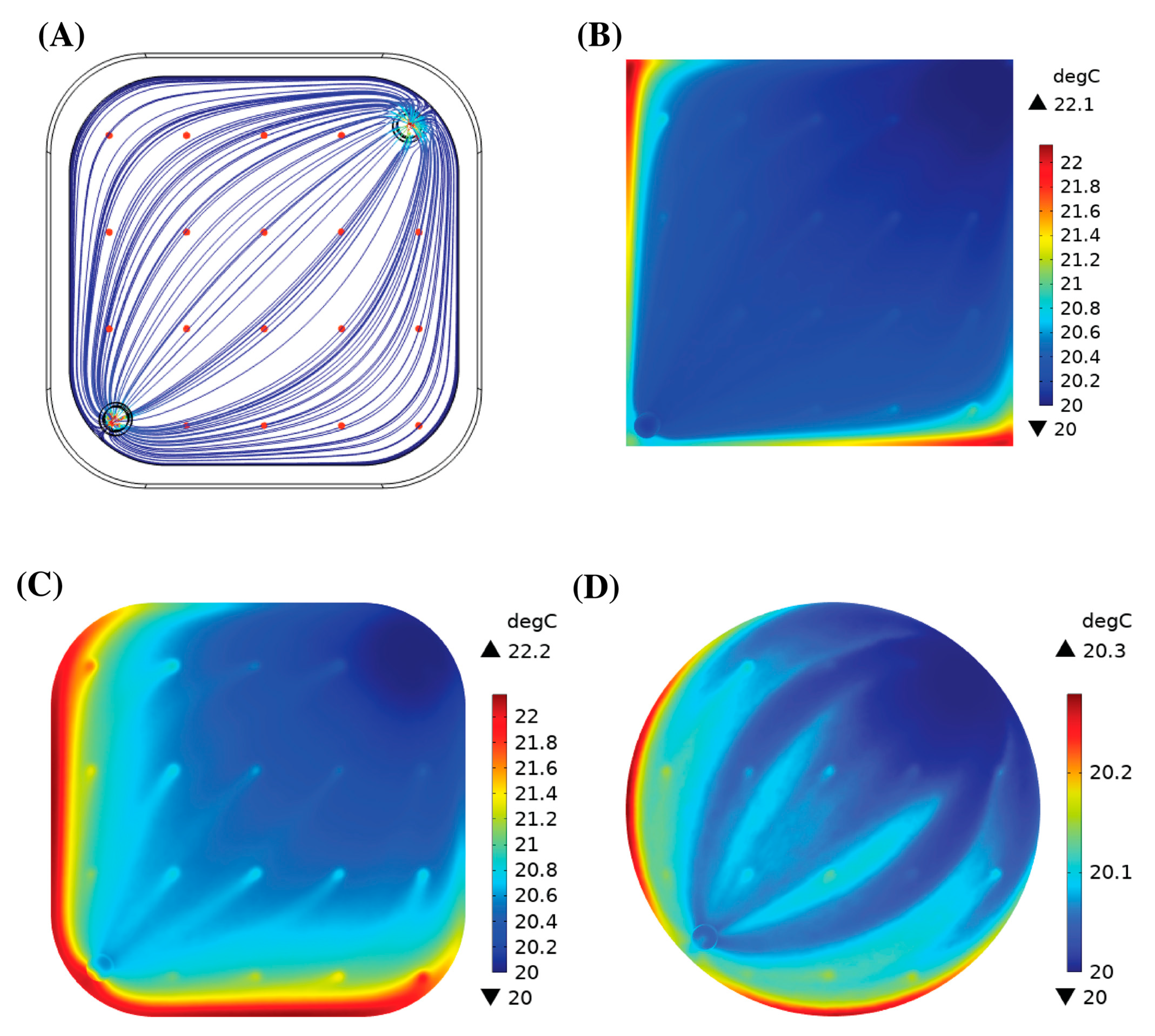
3.1. Light Propagation
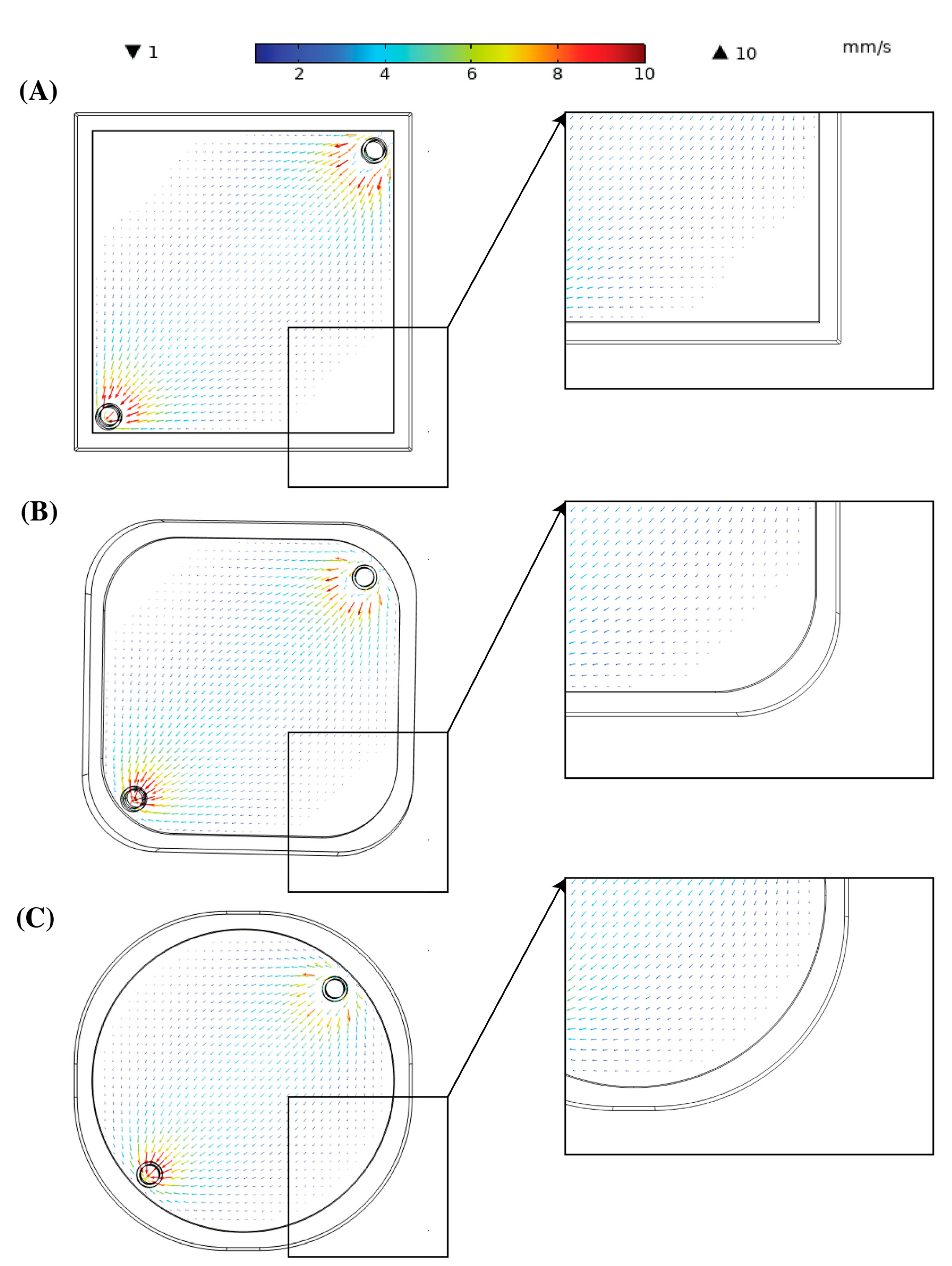
3.2. Blood Flow
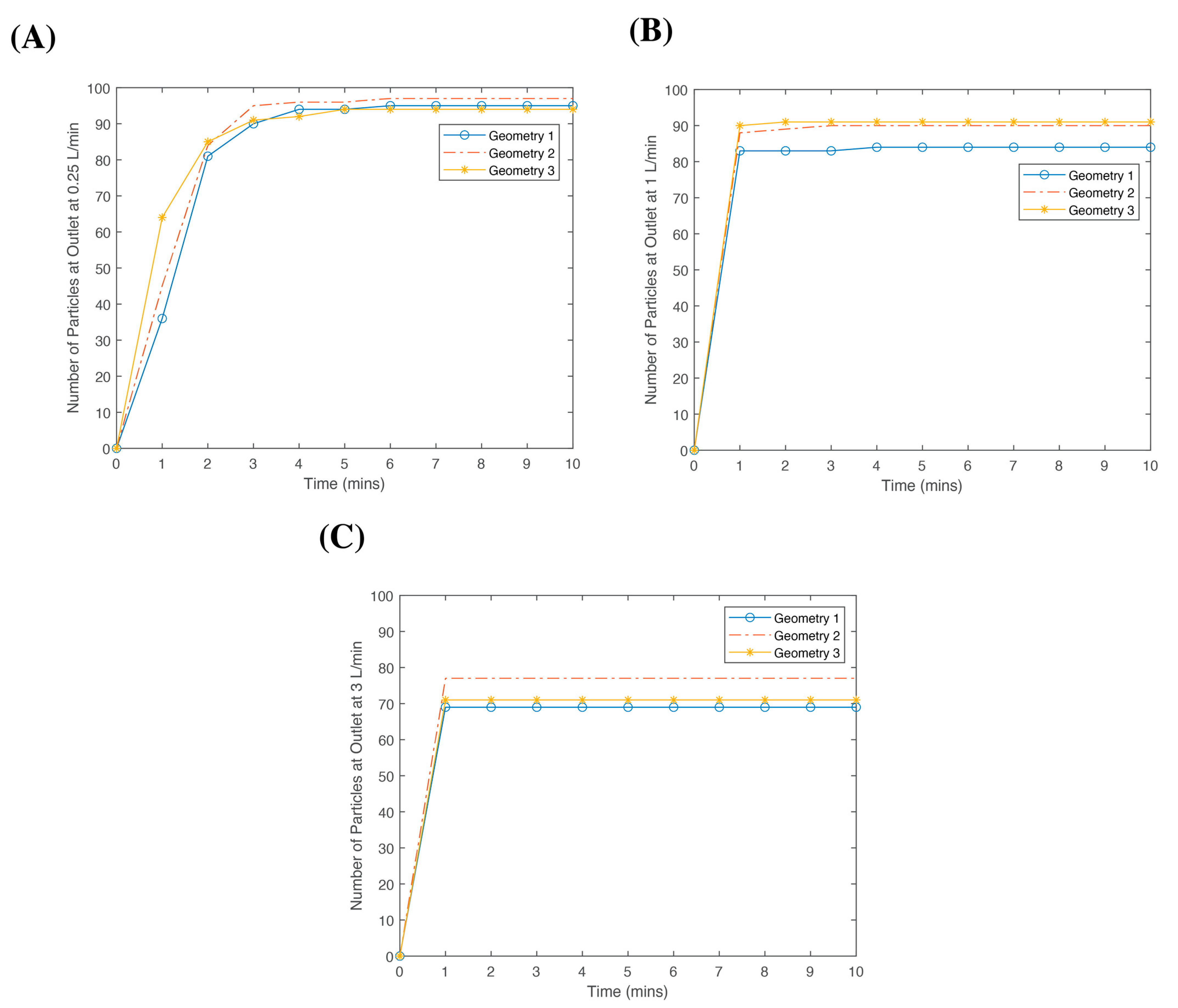
3.3. Particle Tracing
3.4. Heat Generation
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kinoshita, H.; Türkan, H.; Vucinic, S.; Naqvi, S.; Bedair, R.; Rezaee, R.; Tsatsakis, A. Carbon monoxide poisoning. Toxicol. Rep. 2020, 7, 169–173. [Google Scholar] [CrossRef] [PubMed]
- Hampson, N.B.; Weaver, L.K. Carbon monoxide poisoning: A new incidence for an old disease. Undersea Hyperb. Med. 2007, 34, 163–168. [Google Scholar] [PubMed]
- Hampson, N.B. Cost of accidental carbon monoxide poisoning: A preventable expense. Prev. Med. Rep. 2016, 3, 21–24. [Google Scholar] [CrossRef] [PubMed]
- Nañagas, K.A.; Penfound, S.J.; Kao, L.W. Carbon Monoxide Toxicity. Emerg. Med. Clin. North Am. 2022, 40, 283–312. [Google Scholar] [CrossRef] [PubMed]
- Chenoweth, J.A.; Albertson, T.E.; Greer, M.R. Carbon Monoxide Poisoning. Crit. Care Clin. 2021, 37, 657–672. [Google Scholar] [CrossRef] [PubMed]
- Peterson, J.E. Postexposure Relationship of Carbon Monoxide in Blood and Expired Air. Arch. Environ. Health Int. J. 1970, 21, 172–173. [Google Scholar] [CrossRef] [PubMed]
- Guzman, J.A. Carbon monoxide poisoning. Crit. Care Clin. 2012, 28, 537–548. [Google Scholar] [CrossRef] [PubMed]
- Schneir, A.; Rentmeester, L. Carbon monoxide poisoning and pulmonary injury from the mixture of formic and sulfuric acids. Clin. Toxicol. 2016, 54, 450–453. [Google Scholar] [CrossRef]
- Drinker, P.A. Progress in Membrane Oxygenator Design. Anesthesiology 1972, 37, 242–260. [Google Scholar] [CrossRef]
- Gourlay, T.; Fleming, J.; Taylor, K.; Aslam, M. Evaluation of a range of extracorporeal membrane oxygenators. Perfusion 1990, 5, 117–133. [Google Scholar] [CrossRef]
- Iwahashi, H.; Yuri, K.; Nosé, Y. Development of the oxygenator: Past, present, and future. J. Artif. Organs 2004, 7, 111–120. [Google Scholar] [CrossRef] [PubMed]
- Teber, O.O.; Altinay, A.D.; Mehrabani, S.A.N.; Tasdemir, R.S.; Zeytuncu, B.; Genceli, E.A.; Dulekgurgen, E.; Pekkan, K.; Koyuncu, I. Polymeric hollow fiber membrane oxygenators as artificial lungs: A review. Biochem. Eng. J. 2022, 180, 108340. [Google Scholar] [CrossRef]
- Evseev, A.K.; Zhuravel, S.V.; Alentiev, A.Y.; Goroncharovskaya, I.V.; Petrikov, S.S. Membranes in Extracorporeal Blood Oxygenation Technology. Membr. Membr. Technol. 2019, 1, 201–211. [Google Scholar] [CrossRef]
- Chen, W.; Zheng, H.; Yan, Z.; Chen, R. Shape design of an artificial pump-lung using high-resolution hemodynamic simulation with high-performance computing. Phys. Fluids 2023, 35, 031909. [Google Scholar] [CrossRef]
- Han, D.; Leibowitz, J.L.; Han, L.; Wang, S.; He, G.; Griffith, B.P.; Wu, Z.J. Computational fluid dynamics analysis and experimental hemolytic performance of three clinical centrifugal blood pumps: Revolution, Rotaflow and CentriMag. Med. Nov. Technol. Devices 2022, 15, 100153. [Google Scholar] [CrossRef] [PubMed]
- Tang, T.-Q.; Hsu, S.-Y.; Dahiya, A.; Soh, C.H.; Lin, K.C. Numerical modeling of pulsatile blood flow through a mini-oxygenator in artificial lungs. Comput. Methods Programs Biomed. 2021, 208, 106241. [Google Scholar] [CrossRef] [PubMed]
- Turri, F.; Yanagihara, J.I. Computer-Assisted Numerical Analysis for Oxygen and Carbon Dioxide Mass Transfer in Blood Oxygenators. Artif. Organs 2011, 35, 579–592. [Google Scholar] [CrossRef]
- Messai, E.; Bouguerra, A.; Harmelin, G.; Di Lascio, G.; Bonizzoli, M.; Bonacchi, M. A numerical model of blood oxygenation during veno-venous ECMO: Analysis of the interplay between blood oxygenation and its delivery parameters. J. Clin. Monit. Comput. 2016, 30, 327–332. [Google Scholar] [CrossRef]
- Conrad, S.A.; Wang, D. Evaluation of Recirculation During Venovenous Extracorporeal Membrane Oxygenation Using Computational Fluid Dynamics Incorporating Fluid-Structure Interaction. ASAIO J. 2021, 67, 943–953. [Google Scholar] [CrossRef]
- Stevens, M.; Callaghan, F.; Forrest, P.; Bannon, P.; Grieve, S. Flow mixing during peripheral veno-arterial extra corporeal membrane oxygenation—A simulation study. J. Biomech. 2017, 55, 64–70. [Google Scholar] [CrossRef]
- Nezami, F.R.; Khodaee, F.; Edelman, E.R.; Keller, S.P. A Computational Fluid Dynamics Study of the Extracorporeal Membrane Oxygenation-Failing Heart Circulation. ASAIO J. 2021, 67, 276–283. [Google Scholar] [CrossRef]
- Fragomeni, G.; Caruso, M.V.; Rossi, M. Flow Analysis in VA ECMO Support: A CFD Study. In 2020 IEEE International Conference on Bioinformatics and Biomedicine (BIBM); IEEE Computer Society: Washington, DC, USA, 2020; pp. 1440–1441. [Google Scholar]
- Haldane, J.; Smith, J.L. The Oxygen Tension of Arterial Blood. J. Physiol. 1896, 20, 497–520. [Google Scholar] [CrossRef]
- Fischbach, A.; Wiegand, S.B.; Zazzeron, L.; Traeger, L.; Fenza, R.; Bagchi, A.; Farinelli, W.A.; Franco, W.; Korupolu, S.; Arens, J.; et al. Veno-venous extracorporeal blood phototherapy increases the rate of carbon monoxide (CO) elimination in CO-poisoned pigs. Lasers Surg. Med. 2022, 54, 256–267. [Google Scholar] [CrossRef] [PubMed]
- Zazzeron, L.; Fischbach, A.; Franco, W.; Farinelli, W.A.; Ichinose, F.; Bloch, D.B.; Anderson, R.R.; Zapol, W.M. Phototherapy and extracorporeal membrane oxygenation facilitate removal of carbon monoxide in rats. Sci. Transl. Med. 2019, 11, eaau4217. [Google Scholar] [CrossRef] [PubMed]
- Fischbach, A.; Traeger, L.; Farinelli, W.A.; Ezaka, M.; Wanderley, H.V.; Wiegand, S.B.; Franco, W.; Bagchi, A.; Bloch, D.B.; Anderson, R.R.; et al. Hyperbaric phototherapy augments blood carbon monoxide removal. Lasers Surg. Med. 2022, 54, 426–432. [Google Scholar] [CrossRef] [PubMed]
- Goulopoulos, A.; Etim, E.; Korupolu, S.; Farinelli, W.; Sierra, H.; Anderson, R.R.; Fischbach, A.; Franco, W. Optical, flow, and thermal analysis of a phototherapy extracorporeal membrane oxygenator for treating carbon monoxide poisoning. Lasers Surg. Med. 2023, 55, 390–404. [Google Scholar] [CrossRef] [PubMed]
- Childs, J.; Fischbach, A.; Smirnov, A.; Farinelli, B.; Bühl, T.; Franco, W.; Anderson, R. Extracorporeal membrane oxygenators with light-diffusing fibers for treatment of carbon monoxide poisoning: Experiments, mathematical modeling, and performance assessment with unit cells. Lasers Surg. Med. 2023, 55, 590–600. [Google Scholar] [CrossRef]
- Wang, L.; Jacques, S.L.; Zheng, L. MCML—Monte Carlo modeling of light transport in multi-layered tissues. Comput. Methods Programs Biomed. 1995, 47, 131–146. [Google Scholar] [CrossRef]
- Franco, W.; Childers, M.; Nelson, J.S.; Aguilar, G. Laser surgery of port wine stains using local vaccum pressure: Changes in calculated energy deposition (Part II). Lasers Surg. Med. 2007, 39, 118–127. [Google Scholar] [CrossRef]
- Bejan, A. Heat Transfer; John Wiley & Sons: New York, NY, USA, 1993. [Google Scholar]
- Incropera, F.P.; DeWitt, D.P.; Bergman, T.L.; Lavine, A.S. Fundamentals of Heat and Mass Transfer, 8th ed.; Wiley: New York, NY, USA, 2017. [Google Scholar]
- Hesselmann, F.; Focke, J.M.; Schlanstein, P.C.; Steuer, N.B.; Kaesler, A.; Reinartz, S.D.; Schmitz-Rode, T.; Steinseifer, U.; Jansen, S.V.; Arens, J. Introducing 3D-potting: A novel production process for artificial membrane lungs with superior blood flow design. Bio-Des. Manuf. 2022, 5, 141–152. [Google Scholar] [CrossRef]
- Bartlett, R.H. ECMO: The next ten years. Egypt. J. Crit. Care Med. 2016, 4, 7–10. [Google Scholar] [CrossRef]
- Gartner, M.J.; Wilhelm, C.R.; Gage, K.L.; Fabrizio, M.C.; Wagner, W.R. Modeling flow effects on thrombotic deposition in a membrane oxygenator. Artif. Organs 2000, 24, 29–36. [Google Scholar] [CrossRef]
- Conway, R.G.; Zhang, J.; Jeudy, J.; Evans, C.; Li, T.; Wu, Z.J.; Griffith, B.P. Computed tomography angiography as an adjunct to computational fluid dynamics for prediction of oxygenator thrombus formation. Perfusion 2021, 36, 285–292. [Google Scholar] [CrossRef]
- Herron, D.M.; Grabowy, R.; Connolly, R.; Schwaitzberg, S.D. The limits of bloodwarming: Maximally heating blood with an inline microwave bloodwarmer. J. Trauma 1997, 43, 219–228. [Google Scholar] [CrossRef]

| Year | Model Type | Oxygen Pressure Status of the Gas Compartment | Capable of Animal Rescue | Number of ECMO Devices | CO Half-Life in 1 L of Blood | Refernces |
|---|---|---|---|---|---|---|
| 2019 | Rat | Normobaric | Yes | 1 | 36 ± 5.5 min | [25] |
| 2021 | Pig | Normobaric | Yes | 6 | 6.3 ± 1.2 min | [24] |
| 2021 | In Vitro | Hyperbaric | N/A | 4 | 5.2 ± 0.4 min | [26] |
| 2023 | Numerical Model | Normobaric | N/A | 1 | NA | [27] |
| 2023 | In Vitro and Mathematical Model | Normobaric | N/A | 1 | 1.5 min | [28] |
| Domain | Geometry 1 | Geometry 2 | Geometry 3 |
|---|---|---|---|
| Blood compartment (without tubes) | Extra fine mesh with a maximum growth rate of 1 | Extremely fine mesh with maximum element size of 2 mm | Extremely fine mesh |
| Blood in tubes | Extremely fine mesh | Normal mesh | Extremely fine mesh |
| Plexiglass casing | Extra fine mesh | Extremely fine mesh | Extremely fine mesh |
| Plexiglass | Blood in Tube | Channel | Computation Time | Average Velocity in Photo-ECMO Device (mm/s) | Average Velocity in Tubes (mm/s) | Pressure Drop (Pa) | Max Temperature @ 5 min (C) | Number of Particles at Outlet |
|---|---|---|---|---|---|---|---|---|
| General physics, Extremely fine | Fluid Dynamics, Normal | Fluid Dynamics, Normal | Flow—00:04:26 | 2.98 | 32.86 | 6.4726 | 22.81 | 99 |
| Heat—00:38:05 | ||||||||
| Particle tracing—00:08:44 | ||||||||
| General physics, Extremely fine | Fluid Dynamics, Finer | Fluid Dynamics, Finer | Flow—00:04:30 | 2.99 | 32.89 | 6.4538 | 22.81 | 97 |
| Heat—00:45:24 | ||||||||
| Particle tracing—00:08:04 | ||||||||
| General physics, Extremely fine | Fluid Dynamics, Extremely Fine | Fluid Dynamics, Extremely fine | Flow—00:06:48 | 3 | 32.91 | 6.4340 | 22.83 | 95 |
| Heat—00:58:32 | ||||||||
| Particle tracing—00:09:52 |
| Blood Flow Rate (L/min) | Average Velocity in Photo-ECMO (mm/s) | Maximum Velocity in Photo-ECMO (mm/s) | Average Velocity in Inlet and Outlet Tubes (mm/s) | Pressure Drop (Pa) | |
|---|---|---|---|---|---|
| Geometry 1 | 0.25 | 2.90 | 57.17 | 32.95 | 6.4025 |
| 1 | 12.04 | 237.59 | 132.13 | 34.1191 | |
| 3 | 38.46 | 596.44 | 396.72 | 240.9999 | |
| Geometry 2 | 0.25 | 2.74 | 57.02 | 32.87 | 5.3801 |
| 1 | 11.57 | 226.34 | 131.77 | 30.1926 | |
| 3 | 36.42 | 558.37 | 395.44 | 210.3300 | |
| Geometry 3 | 0.25 | 2.80 | 56.82 | 32.92 | 4.9975 |
| 1 | 11.97 | 235.67 | 131.87 | 29.1249 | |
| 3 | 39.29 | 585.71 | 395.73 | 208.1257 |
| Blood Flow Rate (L/min) | Maximum Temperature in Photo-ECMO Device after 5 Minutes (°C) | Maximum Temperature in Photo-ECMO at a Steady State (°C) | Average Temperature in Photo-ECMO at a Steady State (°C) | Average Temperature at the Blood Outlet at a Steady State (°C) |
|---|---|---|---|---|
| 0.25 | 21.83 | 21.59 | 20.07 | 20.08 |
| 1 | 21.95 | 23.99 | 20.77 | 21.05 |
| 3 | 22.3 | 22.17 | 20.22 | 20.27 |
| 0.25 | 20.83 | 22.19 | 20.58 | 20.91 |
| 1 | 21.94 | 20.86 | 20.16 | 20.23 |
| 3 | 21.68 | 20.68 | 20.05 | 20.07 |
| 0.25 | 20.57 | 20.28 | 20.04 | 20.06 |
| 1 | 21.57 | 22.53 | 20.60 | 20.80 |
| 3 | 21.32 | 20.93 | 20.16 | 20.20 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Etim, E.; Goulopoulos, A.; Fischbach, A.; Franco, W. Design Optimization of a Phototherapy Extracorporeal Membrane Oxygenator for Treating Carbon Monoxide Poisoning. Bioengineering 2023, 10, 969. https://doi.org/10.3390/bioengineering10080969
Etim E, Goulopoulos A, Fischbach A, Franco W. Design Optimization of a Phototherapy Extracorporeal Membrane Oxygenator for Treating Carbon Monoxide Poisoning. Bioengineering. 2023; 10(8):969. https://doi.org/10.3390/bioengineering10080969
Chicago/Turabian StyleEtim, Edidiong, Anastasia Goulopoulos, Anna Fischbach, and Walfre Franco. 2023. "Design Optimization of a Phototherapy Extracorporeal Membrane Oxygenator for Treating Carbon Monoxide Poisoning" Bioengineering 10, no. 8: 969. https://doi.org/10.3390/bioengineering10080969
APA StyleEtim, E., Goulopoulos, A., Fischbach, A., & Franco, W. (2023). Design Optimization of a Phototherapy Extracorporeal Membrane Oxygenator for Treating Carbon Monoxide Poisoning. Bioengineering, 10(8), 969. https://doi.org/10.3390/bioengineering10080969







