Experimentally Validated Finite Element Analysis of Thoracic Spine Compression Fractures in a Porcine Model
Abstract
:1. Introduction
2. Materials and Methods
2.1. Sample Selection and Preparation
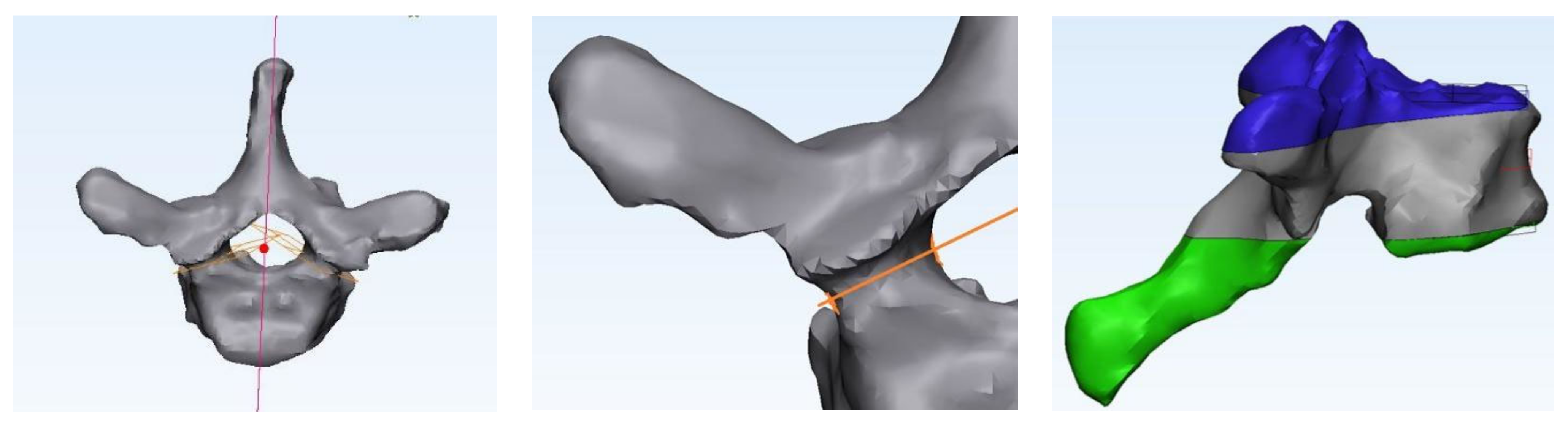
2.2. CT and Numerical Modeling
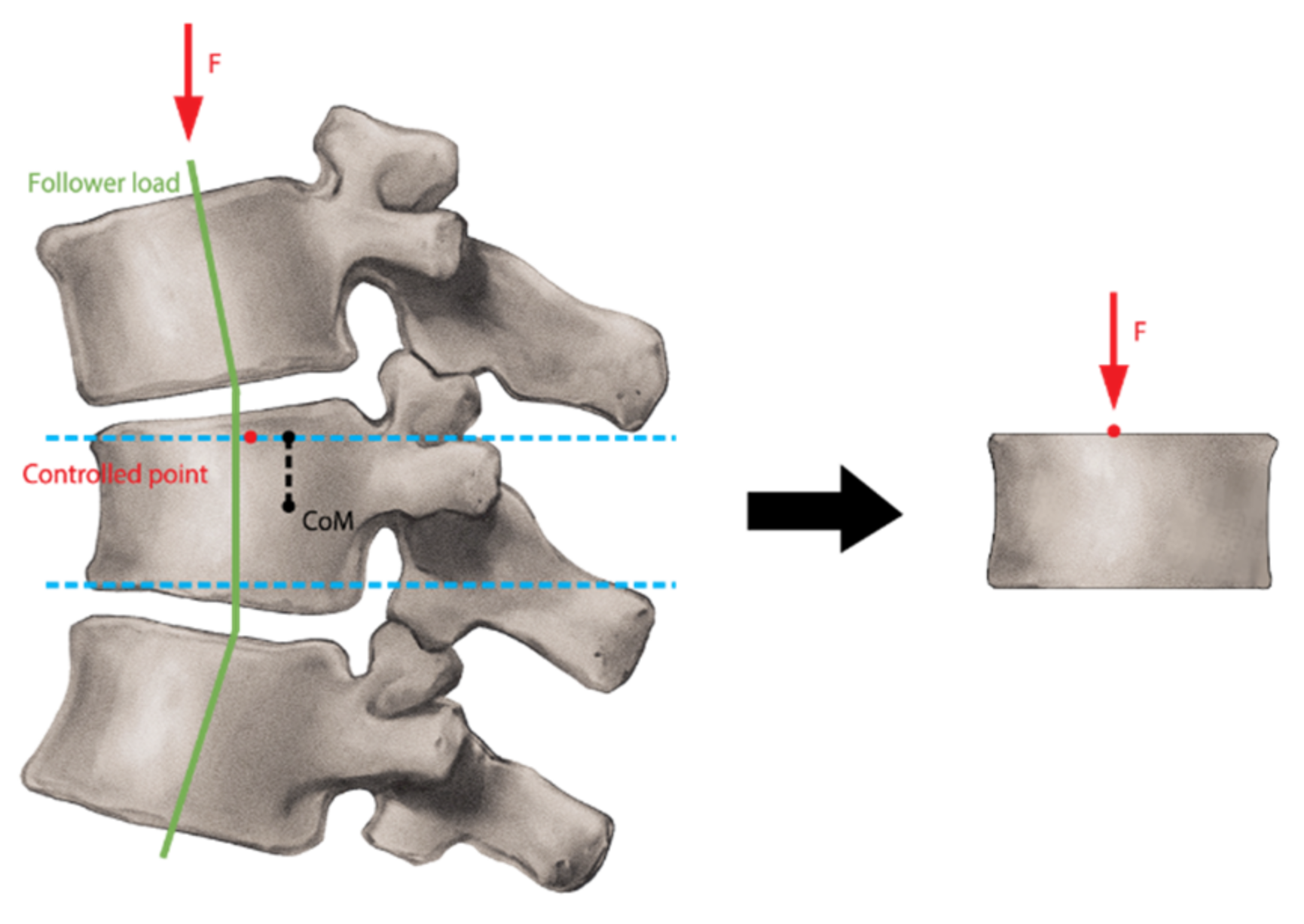
2.3. Finite Element Analysis (FEA)
2.4. Experimental Testing
2.4.1. Apparatus and Configuration of the Vertebrae in the MTS Machine
2.4.2. Data Collection and Measurements
3. Results
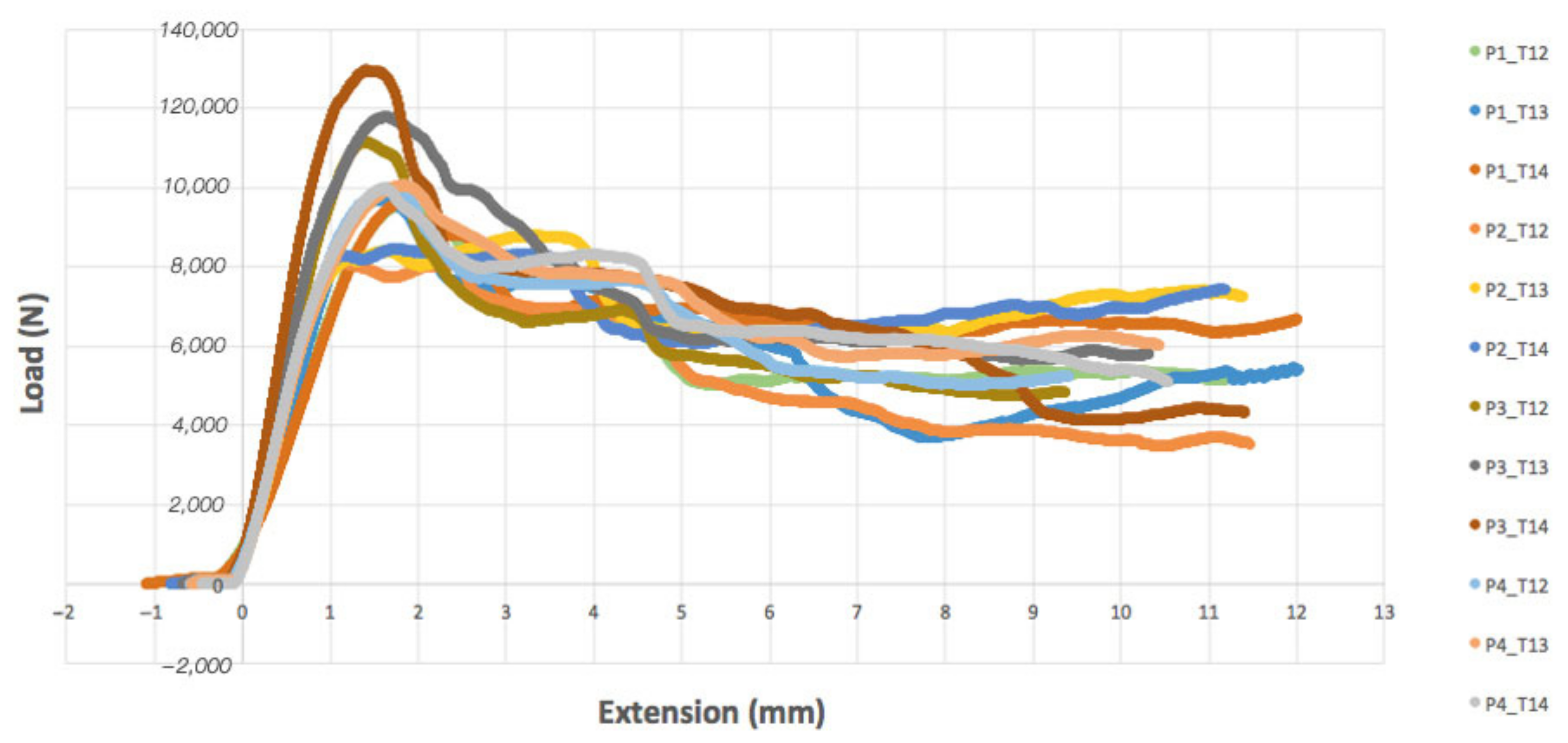
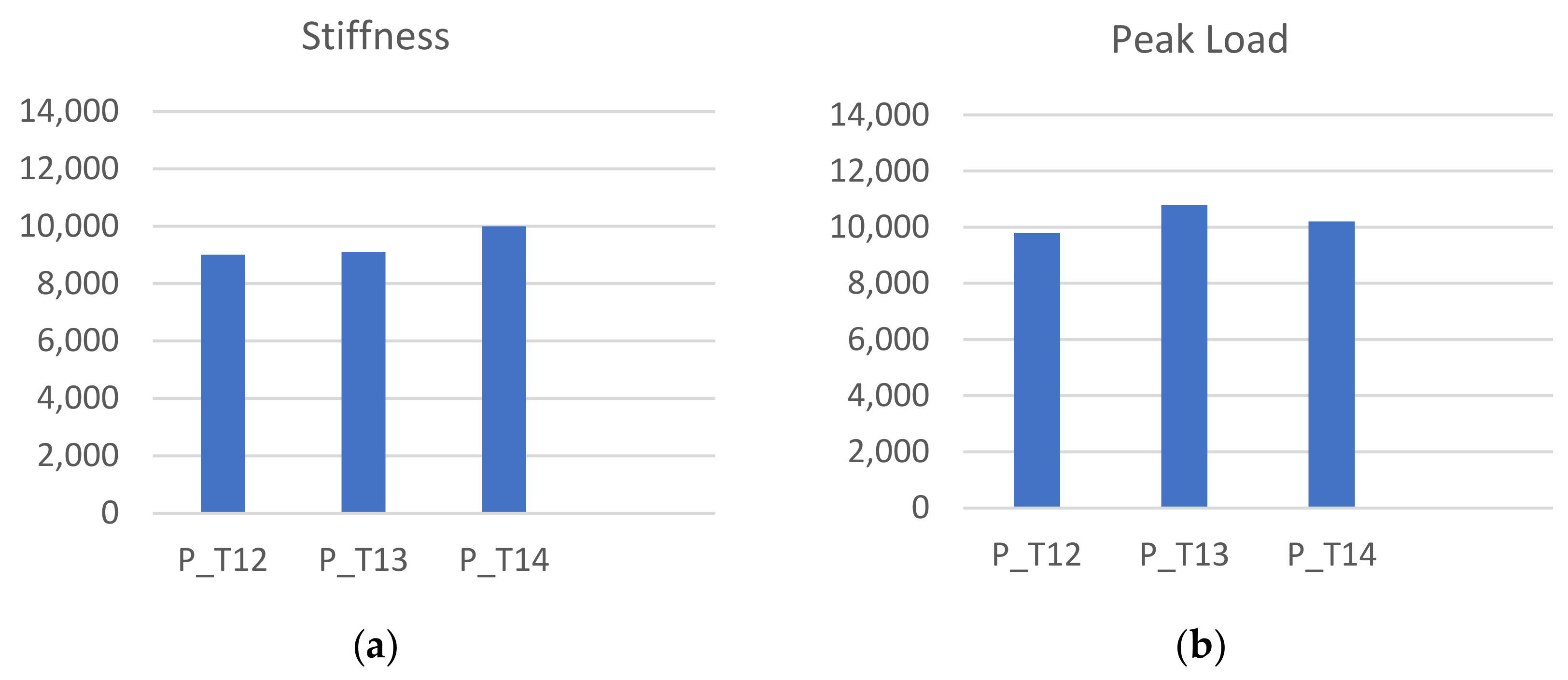
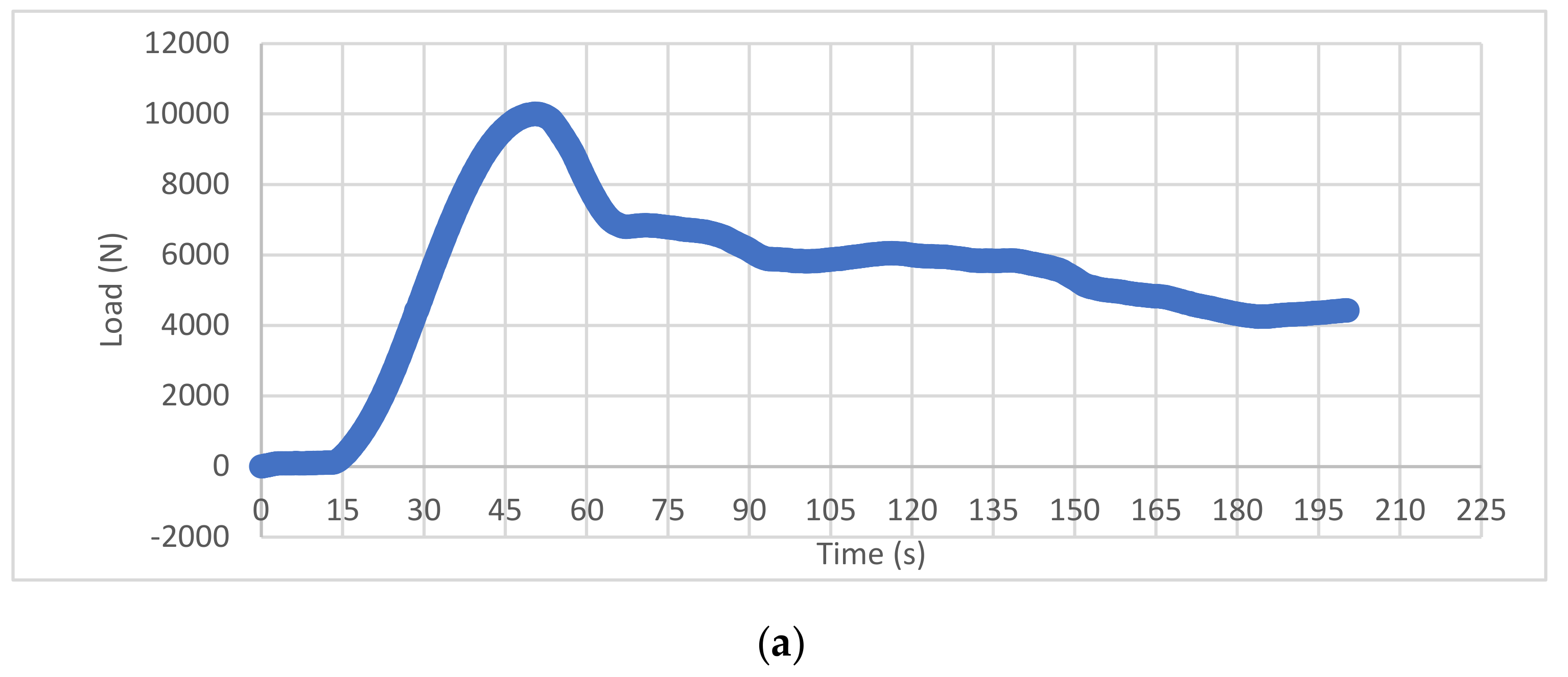
3.1. Experimental Compression
3.2. Video Imaging Analysis
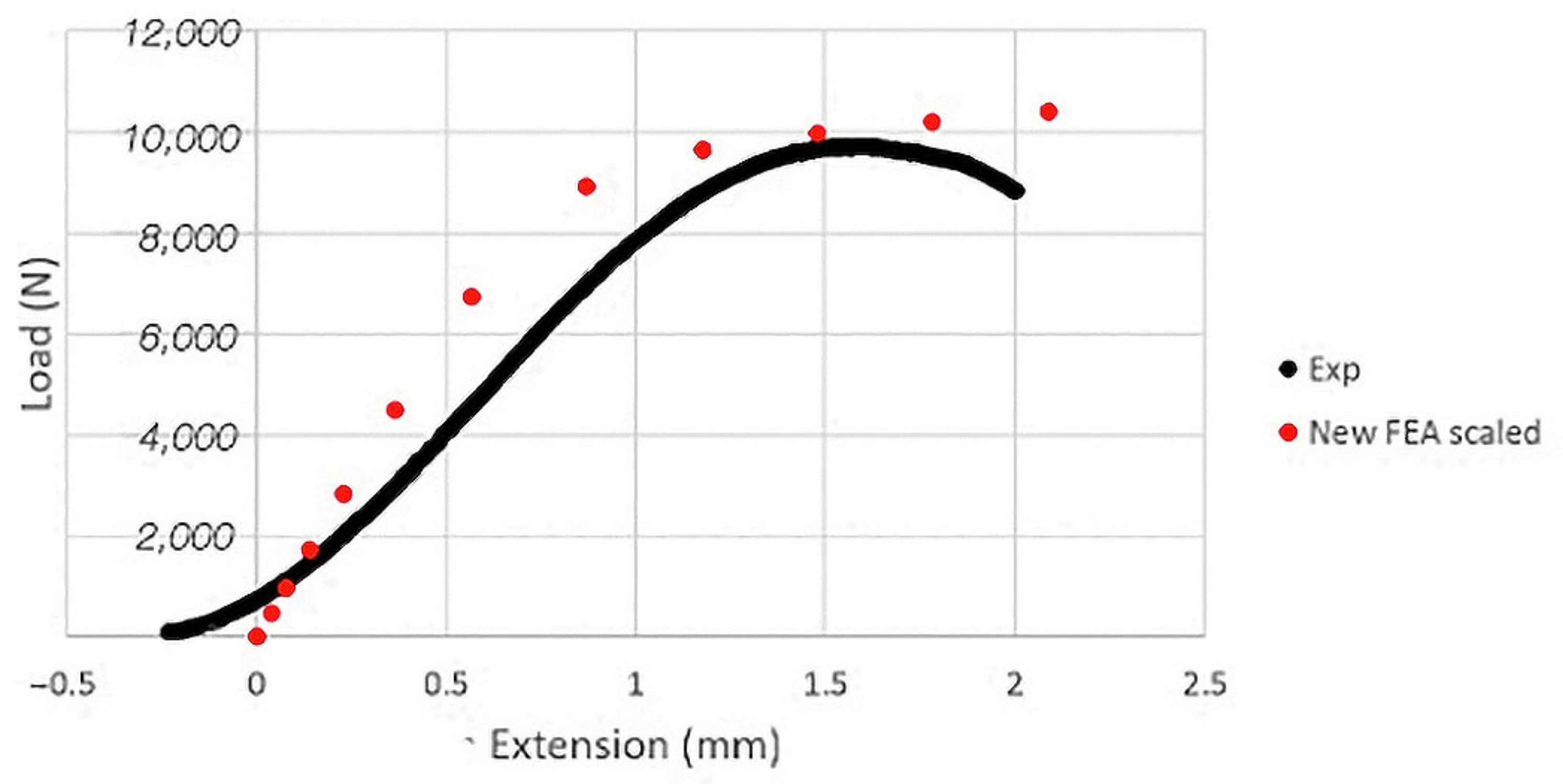
3.3. FEA Analysis
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Donnally, C.J., III; DiPompeo, C.M.; Varacallo, M. Vertebral Compression Fractures; StatPearls: Treasure Island, FL, USA, 2022. Available online: https://www.ncbi.nlm.nih.gov/books/NBK448171/ (accessed on 16 November 2022).
- Alexandru, D.; So, W. Evaluation and Management of Vertebral Compression Fractures. Perm. J. 2012, 16, 46. [Google Scholar] [CrossRef]
- Wood, K.B.; Li, W.; Lebl, D.S.; Ploumis, A. Management of thoracolumbar spine fractures. Spine J. 2014, 14, 145–164. [Google Scholar] [CrossRef]
- Ong, K.L.; Beall, D.P.; Frohbergh, M.; Lau, E.; Hirsch, J.A. Were VCF patients at higher risk of mortality following the 2009 publication of the vertebroplasty “sham” trials? Osteoporos. Int. 2018, 29, 375. [Google Scholar] [CrossRef]
- McCall, T.; Cole, C.; Dailey, A. Vertebroplasty and kyphoplasty: A comparative review of efficacy and adverse events. Curr. Rev. Musculoskelet. Med. 2008, 1, 17–23. [Google Scholar] [CrossRef]
- Potet, J.; Weber-Donat, G.; Curis, E.; Arnaud, F.X.; Thome, A.; Valbousquet, L.; Peroux, E.; Geffroy, Y.; Bouzad, C.; Kervella, Y.; et al. Incidence of pulmonary cement embolism after real-time ct fluoroscopy-guided vertebroplasty. J. Vasc. Interv. Radiol. 2013, 24, 1853–1860. [Google Scholar] [CrossRef] [PubMed]
- Kurra, S.; Metkar, U.; Lieberman, I.H.; Lavelle, W.F. The effect of kyphoplasty on mortality in symptomatic vertebral compression fractures: A review. Int. J. Spine Surg. 2018, 12, 543–548. [Google Scholar] [CrossRef]
- Clarençon, F.; Fahed, R.; Cormier, E.; Haffaf, I.; Spano, J.P.; Shotar, E.; Premat, K.; Bonaccorsi, R.; Degos, V.; Chiras, J. Safety and effectiveness of cervical vertebroplasty: Report of a large cohort and systematic review. Eur. Radiol. 2020, 30, 1571–1583. [Google Scholar] [CrossRef]
- Kallmes, D.F. Percutaneous Vertebroplasty Causing an Increase in Retropulsion of Bone Fragments. J. Vasc. Interv. Radiol. 2007, 18, 1333–1334. [Google Scholar] [CrossRef]
- Lai, P.L.; Tai, C.L.; Chen, L.H.; Nien, N.Y. Cement leakage causes potential thermal injury in vertebroplasty. BMC Musculoskelet. Disord. 2011, 12, 116. [Google Scholar] [CrossRef]
- Dar, F.H.; Meakin, J.R.; Aspden, R.M. Statistical methods in finite element analysis. J. Biomech. 2002, 35, 1155–1161. [Google Scholar] [CrossRef] [PubMed]
- Fries, T.P.; Belytschko, T. The extended/generalized finite element method: An overview of the method and its applications. Int. J. Numer. Methods Eng. 2010, 84, 253–304. [Google Scholar] [CrossRef]
- Sabat, L.; Kundu, C.K. History of Finite Element Method: A Review. In Lecture Notes in Civil Engineering; Springer: Singapore, 2021; Volume 75. [Google Scholar]
- Tenek, L.T.; Argyris, J. A Brief History of FEM; Springer: Dordrecht, The Netherlands, 1998. [Google Scholar]
- Stein, E. History of the Finite Element Method—Mathematics Meets Mechanics—Part I: Engineering Developments; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Morris, E.T.; Black, R.G.; Tobriner, S.O. Report on the Application of Finite Element Analysis to Historic Structures: Westminster Hall, London. J. Soc. Archit. Hist. 1995, 54, 336–347. [Google Scholar] [CrossRef]
- Hirschhorn, M.; Tchantchaleishvili, V.; Stevens, R.; Rossano, J.; Throckmorton, A. Fluid–structure interaction modeling in cardiovascular medicine—A systematic review 2017–2019. Med. Eng. Phys. 2020, 78, 1–13. [Google Scholar] [CrossRef]
- Pirmoradian, M.; Naeeni, H.A.; Firouzbakht, M.; Toghraie, D.; Khabaz, M.K.; Darabi, R. Finite element analysis and experimental evaluation on stress distribution and sensitivity of dental implants to assess optimum length and thread pitch. Comput. Methods Programs Biomed. 2020, 187, 105258. [Google Scholar] [CrossRef] [PubMed]
- Belwanshi, M.; Jayaswal, P.; Aherwar, A. A study on finite element analysis methodologies and approaches used for total hip arthroplasty. Mater. Today Proc. 2022, 56, 2596–2604. [Google Scholar] [CrossRef]
- Cai, X.Y.; Sang, D.; Yuchi, C.X.; Cui, W.; Zhang, C.; Du, C.F.; Liu, B. Using finite element analysis to determine effects of the motion loading method on facet joint forces after cervical disc degeneration. Comput. Biol. Med. 2020, 116, 103519. [Google Scholar] [CrossRef]
- Costa, M.C.; Tozzi, G.; Cristofolini, L.; Danesi, V.; Viceconti, M.; Dall’Ara, E. Micro finite element models of the vertebral body: Validation of local displacement predictions. PLoS ONE 2017, 12, e0180151. [Google Scholar] [CrossRef] [PubMed]
- Oravec, D.; Flynn, M.J.; Zauel, R.; Rao, S.; Yeni, Y.N. Digital tomosynthesis based digital volume correlation: A clinically viable noninvasive method for direct measurement of intravertebral displacements using images of the human spine under physiological load. Med. Phys. 2019, 46, 4553–4562. [Google Scholar] [CrossRef] [PubMed]
- Hussein, A.I.; Louzeiro, D.T.; Unnikrishnan, G.U.; Morgan, E.F. Differences in Trabecular Microarchitecture and Simplified Boundary Conditions Limit the Accuracy of Quantitative Computed Tomography-Based Finite Element Models of Vertebral Failure. J. Biomech. Eng. 2018, 140, 0210041. [Google Scholar] [CrossRef]
- Patwardhan, A.G.; Havey, R.M.; Meade, K.P.; Lee, B.; Dunlap, B. A follower load increases the load-carrying capacity of the lumbar spine in compression. Spine 1999, 24, 1003–1009. [Google Scholar] [CrossRef]
- Rohlmann, A.; Neller, S.; Claes, L.; Bergmann, G.; Wilke, H.J. Influence of a follower load on intradiscal pressure and intersegmental rotation of the lumbar spine. Spine 2001, 26, E557–E561. [Google Scholar] [CrossRef]
- Imai, K. Analysis of Vertebral Bone Strength, Fracture Pattern, and Fracture Location: A Validation Study Using a Computed Tomography-Based Nonlinear Finite Element Analysis. Aging Dis. 2015, 6, 180. [Google Scholar] [CrossRef]
- Crawford, R.P.; Cann, C.E.; Keaveny, T.M. Finite element models predict in vitro vertebral body compressive strength better than quantitative computed tomography. Bone 2003, 33, 744–750. [Google Scholar] [CrossRef] [PubMed]
- Dall’Ara, E.; Schmidt, R.; Pahr, D.; Varga, P.; Chevalier, Y.; Patsch, J.; Kainberger, F.; Zysset, P. A nonlinear finite element model validation study based on a novel experimental technique for inducing anterior wedge-shape fractures in human vertebral bodies in vitro. J. Biomech. 2010, 43, 2374–2380. [Google Scholar] [CrossRef] [PubMed]
- Busscher, I.; Ploegmakers, J.J.W.; Verkerke, G.J.; Veldhuizen, A.G. Comparative anatomical dimensions of the complete human and porcine spine. Eur. Spine J. 2010, 19, 1104. [Google Scholar] [CrossRef]
- Sheng, S.R.; Xu, H.Z.; Wang, Y.L.; Zhu, Q.A.; Mao, F.M.; Lin, Y.; Wang, X.Y. Comparison of Cervical Spine Anatomy in Calves, Pigs and Humans. PLoS ONE 2016, 11, e0148610. [Google Scholar] [CrossRef]
- Sheng, S.R.; Wang, X.Y.; Xu, H.Z.; Zhu, G.Q.; Zhou, Y.F. Anatomy of large animal spines and its comparison to the human spine: A systematic review. Eur. Spine J. 2010, 19, 46–56. [Google Scholar] [CrossRef] [PubMed]
- Wilke, H.J.; Geppert, J.; Kienle, A. Biomechanical in vitro evaluation of the complete porcine spine in comparison with data of the human spine. Eur. Spine J. 2011, 20, 1859. [Google Scholar] [CrossRef]
- Kim, B.G.; Dan, J.M.; Shin, D.E. Treatment of thoracolumbar Fracture. Asian Spine J. 2015, 9, 133–146. [Google Scholar] [CrossRef]
- Zhang, X.; Li, S.; Zhao, X.; Christiansen, B.A.; Chen, J.; Fan, S.; Zhao, F. The mechanism of thoracolumbar burst fracture may be related to the basivertebral foramen. Spine J. 2018, 18, 472–481. [Google Scholar] [CrossRef]
- Rudol, G.; Gummerson, N.W. (ii) Thoracolumbar spinal fractures: Review of anatomy, biomechanics, classification and treatment. Orthop. Trauma 2014, 28, 70–78. [Google Scholar] [CrossRef]
- Yoganandan, N.; Khandelwal, P.; Porwal, V.; Humm, J.; Banerjee, A. Human Thoracolumbar Spine Tolerance to Injury and Mechanisms From Caudo-Cephalad Loading: A Parametric Modeling Study. J. Eng. Sci. Med. Diagn. Ther. 2021, 4, 011007. [Google Scholar] [CrossRef] [PubMed]
- Chen, D.; Chen, C.-H.; Tang, L.; Wang, K.; Li, Y.-Z.; Phan, K.; Wu, A.-M. Three-dimensional reconstructions in spine and screw trajectory simulation on 3D digital images: A step by step approach by using Mimics software. J. Spine Surg. 2017, 3, 650–656. [Google Scholar] [CrossRef]
- Yesildal, R.; Karabudak, F.; Bayindir, F.; Zamanlou, H.; Yildirim, M.P.; Sagsoz, N.P.; Sen, S. Effect of Implant Diameter and Length on Stress Distribution for Titanium and Zirconia Implants by Using Finite Element Analysis (FEA). OALib 2015, 2, 1–7. [Google Scholar] [CrossRef]
- Eltes, P.E.; Bartos, M.; Hajnal, B.; Pokorni, A.J.; Kiss, L.; Lacroix, D.; Varga, P.P.; Lazary, A. Development of a Computer-Aided Design and Finite Element Analysis Combined Method for Affordable Spine Surgical Navigation with 3D-Printed Customized Template. Front. Surg. 2021, 7, 583386. [Google Scholar] [CrossRef] [PubMed]
- Wang, P.; Hu, X. Biomechanical finite element analysis of superior endplate collapse after thoracolumbar fracture surgery. Ann. Transl. Med. 2020, 8, 753. [Google Scholar] [CrossRef]
- Wu, W.; Han, Z.; Hu, B.; Du, C.; Xing, Z.; Zhang, C.; Gao, J.; Shan, B.; Chen, C. A graphical guide for constructing a finite element model of the cervical spine with digital orthopedic software. Ann. Transl. Med. 2021, 9, 169. [Google Scholar] [CrossRef]
- Silva, M.J.; Keaveny, T.M.; Hayes, W.C. Computed tomography-based finite element analysis predicts failure loads and fracture patterns for vertebral sections. J. Orthop. Res. 1998, 16, 300–308. [Google Scholar] [CrossRef]
- Giambini, H.; Qin, X.; Dragomir-Daescu, D.; An, K.N.; Nassr, A. Specimen-specific vertebral fracture modeling: A feasibility study using the extended finite element method. Med. Biol. Eng. Comput. 2016, 54, 583–593. [Google Scholar] [CrossRef]
- Barbero, E.J. Finite Element Analysis of Composite Materials Using AbaqusTM; CRC Press: Boca Raton, FL, USA, 2013. [Google Scholar]
- Miguel, A.L.R.; Moreiraa, R.P.L.; de Oliveira, A.F. ISO/IEC 17025: History and introduction of concepts. Quim. Nova 2021, 44, 792–796. [Google Scholar] [CrossRef]
- Eswaran, S.K.; Gupta, A.; Adams, M.F.; Keaveny, T.M. Cortical and trabecular load sharing in the human vertebral body. J. Bone Miner. Res. 2006, 21, 307–314. [Google Scholar] [CrossRef] [PubMed]
- Roux, J.P.; Wegrzyn, J.; Arlot, M.E.; Guyen, O.; Delmas, P.D.; Chapurlat, R.; Bouxsein, M.L. Contribution of trabecular and cortical components to biomechanical behavior of human vertebrae: An ex vivo study. J. Bone Miner. Res. 2010, 25, 356–361. [Google Scholar] [CrossRef] [PubMed]
- Jackman, T.M.; DelMonaco, A.M.; Morgan, E.F. Accuracy of finite element analyses of CT scans in predictions of vertebral failure patterns under axial compression and anterior flexion. J. Biomech. 2016, 49, 267–275. [Google Scholar] [CrossRef]
- Palanca, M.; Oliviero, S.; Dall’Ara, E. MicroFE models of porcine vertebrae with induced bone focal lesions: Validation of predicted displacements with digital volume correlation. J. Mech. Behav. Biomed. Mater. 2022, 125, 104872. [Google Scholar] [CrossRef] [PubMed]
- Yingling, V.R.; Callaghan, J.P.; McGill, S.M. The porcine cervical spine as a model of the human lumbar spine: An anatomical, geometric, and functional comparison. J. Spinal Disord. 1999, 12, 415–423. [Google Scholar] [CrossRef]







| Specification | Title 2 |
|---|---|
| X-ray Tube Current | 200 mA |
| Tube peak voltage (kVp) | 120 kV |
| Slice thickness | max = 0.5 mm |
| Pixel slice | max = 0.27 mm |
| Slide width | min = 512 px |
| Slice height | min = 512 px |
| a | b | Number FE |
|---|---|---|
| 0.48 | 4.6 × 104 | 162,799–200,758 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guitteny, S.; Lee, C.F.; Amirouche, F. Experimentally Validated Finite Element Analysis of Thoracic Spine Compression Fractures in a Porcine Model. Bioengineering 2024, 11, 96. https://doi.org/10.3390/bioengineering11010096
Guitteny S, Lee CF, Amirouche F. Experimentally Validated Finite Element Analysis of Thoracic Spine Compression Fractures in a Porcine Model. Bioengineering. 2024; 11(1):96. https://doi.org/10.3390/bioengineering11010096
Chicago/Turabian StyleGuitteny, Sacha, Cadence F. Lee, and Farid Amirouche. 2024. "Experimentally Validated Finite Element Analysis of Thoracic Spine Compression Fractures in a Porcine Model" Bioengineering 11, no. 1: 96. https://doi.org/10.3390/bioengineering11010096
APA StyleGuitteny, S., Lee, C. F., & Amirouche, F. (2024). Experimentally Validated Finite Element Analysis of Thoracic Spine Compression Fractures in a Porcine Model. Bioengineering, 11(1), 96. https://doi.org/10.3390/bioengineering11010096





