Three-Dimensional Analysis of Vocal Fold Oscillations: Correlating Superior and Medial Surface Dynamics Using Ex Vivo Human Hemilarynges
Abstract
:1. Introduction
2. Materials and Methods
2.1. Hemilarynges
2.2. Measurement Setup
2.3. Measurement Protocol
2.4. Data Analysis
2.4.1. Three-Dimensional Reconstruction

2.4.2. General Phonation Parameters
2.4.3. Three-Dimensional Parameters
2.4.4. Empirical Eigenfunctions
2.4.5. Mucosal Wave
2.4.6. Statistical Analysis
3. Results
3.1. General Phonation Parameters
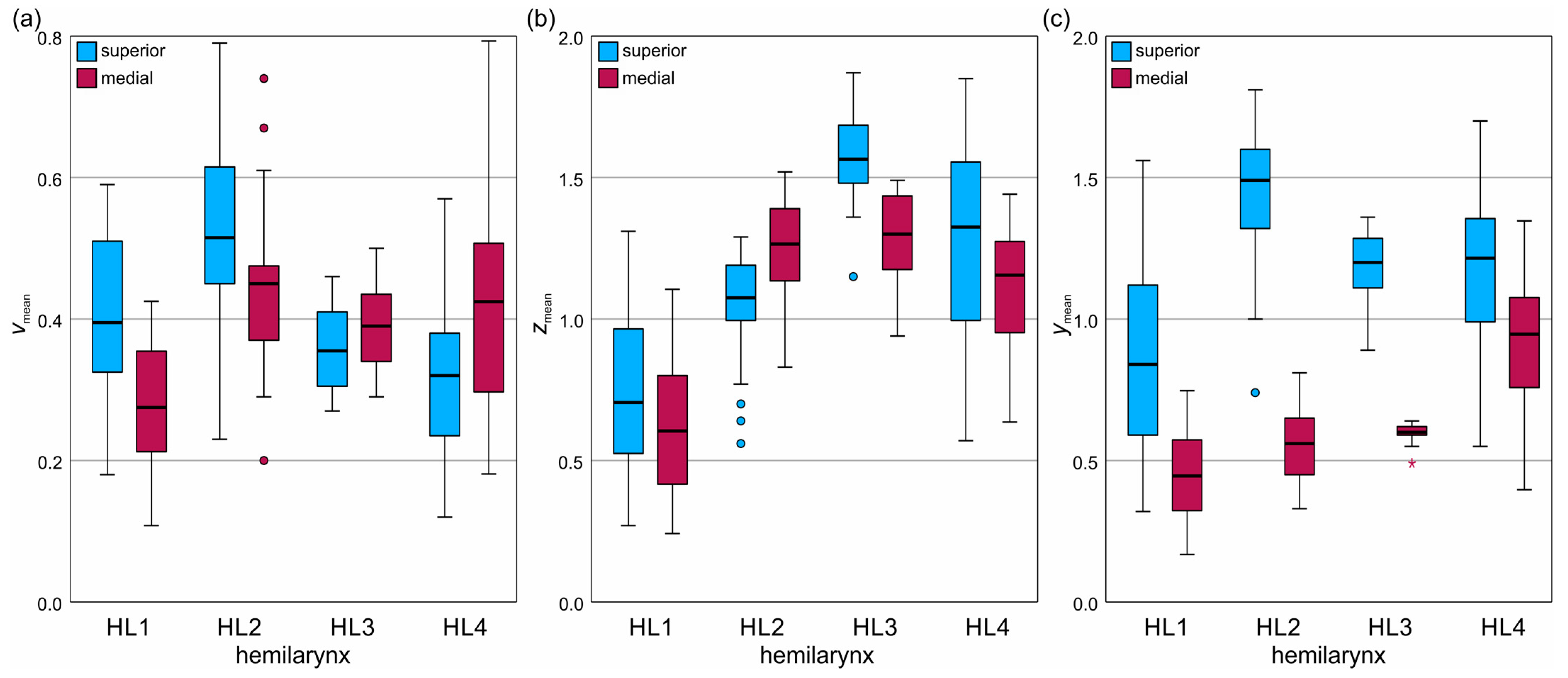
3.2. Three-Dimensional Parameter Results
3.3. Correlation Analysis
3.4. Regression Analysis
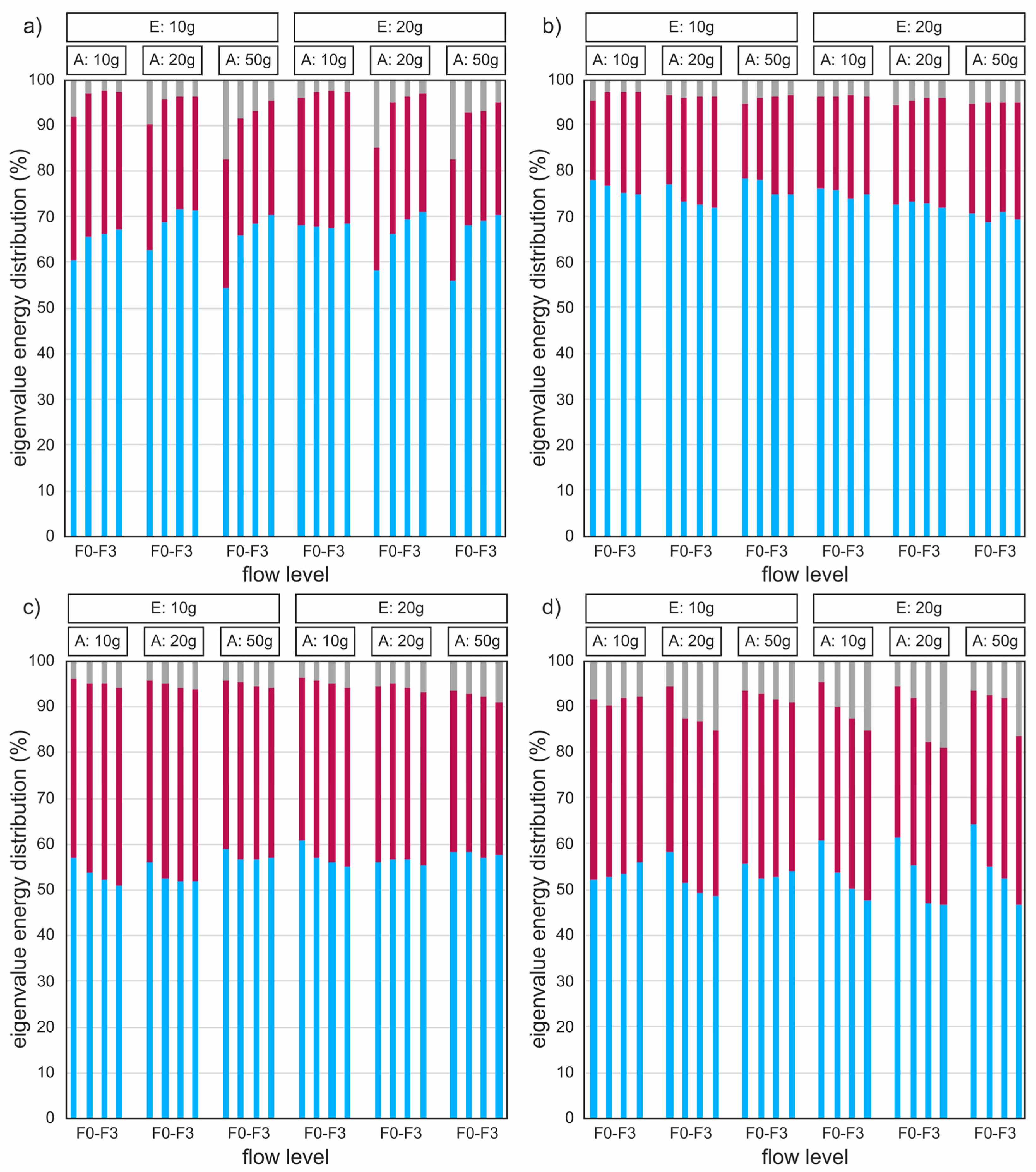
3.5. Empirical Eigenfunctions
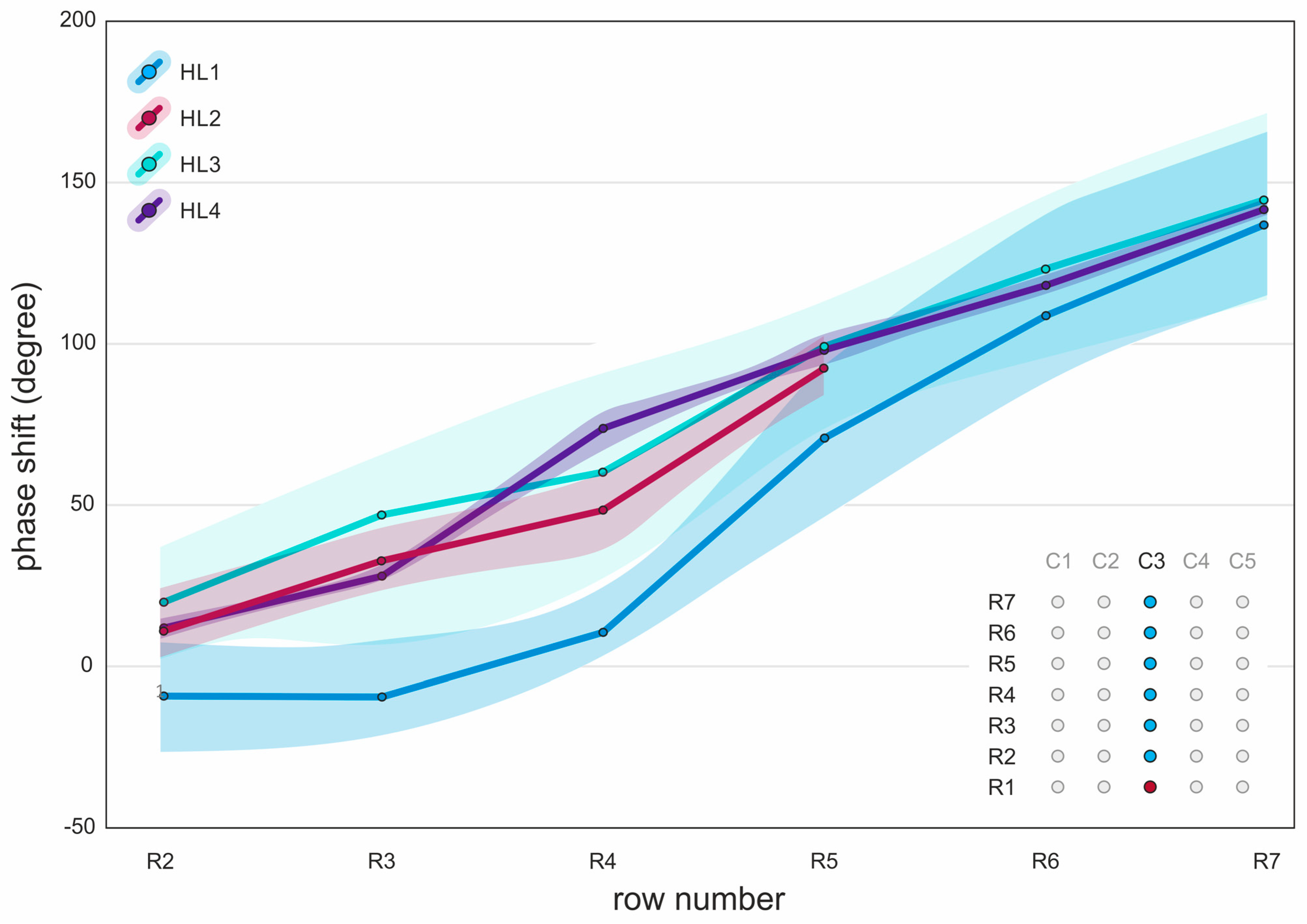
3.6. Mucosal Wave
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Roy, N.; Merrill, R.M.; Thibeault, S.; Parsa, R.A.; Gray, S.D.; Smith, E.M. Prevalence of Voice Disorders in Teachers and the General Population. J. Speech Lang. Hear. Res. 2004, 47, 281–293. [Google Scholar] [CrossRef] [PubMed]
- Ruben, R.J. Redefining the Survival of the Fittest: Communication Disorders in the 21st Century. Laryngoscope 2000, 110, 241. [Google Scholar] [CrossRef] [PubMed]
- Stevens, K.N. Acoustic Phonetics; Current Studies in Linguistics Series; 1. Paperback edition; MIT Press: Cambridge, MA, USA, 2000; ISBN 978-0-262-69250-2. [Google Scholar]
- Yamauchi, A.; Imagawa, H.; Yokonishi, H.; Sakakibara, K.-I.; Tayama, N. Multivariate Analysis of Vocal Fold Vibrations in Normal Speakers Using High-Speed Digital Imaging. J. Voice 2024, 38, 10–17. [Google Scholar] [CrossRef] [PubMed]
- Echternach, M.; Döllinger, M.; Sundberg, J.; Traser, L.; Richter, B. Vocal Fold Vibrations at High Soprano Fundamental Frequencies. J. Acoust. Soc. Am. 2013, 133, EL82–EL87. [Google Scholar] [CrossRef] [PubMed]
- Schneider, B.; Bigenzahn, W. Influence of Glottal Closure Configuration on Vocal Efficacy in Young Normal-Speaking Women. J. Voice 2003, 17, 468–480. [Google Scholar] [CrossRef]
- Doellinger, M.; Lohscheller, J.; McWhorter, A.; Kunduk, M. Variability of Normal Vocal Fold Dynamics for Different Vocal Loading in One Healthy Subject Investigated by Phonovibrograms. J. Voice 2009, 23, 175–181. [Google Scholar] [CrossRef]
- Kist, A.M.; Dürr, S.; Schützenberger, A.; Döllinger, M. OpenHSV: An Open Platform for Laryngeal High-Speed Videoendoscopy. Sci. Rep. 2021, 11, 13760. [Google Scholar] [CrossRef]
- Semmler, M.; Döllinger, M.; Patel, R.R.; Ziethe, A.; Schützenberger, A. Clinical Relevance of Endoscopic Three-dimensional Imaging for Quantitative Assessment of Phonation. Laryngoscope 2018, 128, 2367–2374. [Google Scholar] [CrossRef]
- Sommer, D.E.; Tokuda, I.T.; Peterson, S.D.; Sakakibara, K.-I.; Imagawa, H.; Yamauchi, A.; Nito, T.; Yamasoba, T.; Tayama, N. Estimation of Inferior-Superior Vocal Fold Kinematics from High-Speed Stereo Endoscopic Data in Vivo. J. Acoust. Soc. Am. 2014, 136, 3290–3300. [Google Scholar] [CrossRef]
- Patel, R.R.; Donohue, K.D.; Lau, D.; Unnikrishnan, H. In Vivo Measurement of Pediatric Vocal Fold Motion Using Structured Light Laser Projection. J. Voice 2013, 27, 463–472. [Google Scholar] [CrossRef]
- George, N.A.; De Mul, F.F.M.; Qiu, Q.; Rakhorst, G.; Schutte, H.K. Depth-Kymography: High-Speed Calibrated 3D Imaging of Human Vocal Fold Vibration Dynamics. Phys. Med. Biol. 2008, 53, 2667–2675. [Google Scholar] [CrossRef] [PubMed]
- Veltrup, R.; Angerer, S.; Gessner, E.; Matheis, F.; Sümmerer, E.; Döllinger, M.; Semmler, M. Synchronous 3D Imaging of the Medial and Superior Vocal Fold Surface in an Excised Human Hemilarynx. IEEE Trans. Biomed. Eng. 2024, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Schlegel, P.; Chung, H.R.; Döllinger, M.; Chhetri, D.K. Reconstruction of Vocal Fold Medial Surface 3D Trajectories: Effects of Neuromuscular Stimulation and Airflow. Laryngoscope 2023, 134, 1249–1257. [Google Scholar] [CrossRef] [PubMed]
- Lodermeyer, A.; Becker, S.; Döllinger, M.; Kniesburges, S. Phase-Locked Flow Field Analysis in a Synthetic Human Larynx Model. Exp. Fluids 2015, 56, 77. [Google Scholar] [CrossRef]
- Döllinger, M.; Berry, D.A.; Kniesburges, S. Dynamic Vocal Fold Parameters with Changing Adduction in Ex-Vivo Hemilarynx Experiments. J. Acoust. Soc. Am. 2016, 139, 2372–2385. [Google Scholar] [CrossRef]
- Semmler, M.; Kniesburges, S.; Birk, V.; Ziethe, A.; Patel, R.; Dollinger, M. 3D Reconstruction of Human Laryngeal Dynamics Based on Endoscopic High-Speed Recordings. IEEE Trans. Med. Imaging 2016, 35, 1615–1624. [Google Scholar] [CrossRef]
- Semmler, M.; Kniesburges, S.; Parchent, J.; Jakubaß, B.; Zimmermann, M.; Bohr, C.; Schützenberger, A.; Döllinger, M. Endoscopic Laser-Based 3D Imaging for Functional Voice Diagnostics. Appl. Sci. 2017, 7, 600. [Google Scholar] [CrossRef]
- Doellinger, M.; Berry, D.A. Visualization and Quantification of the Medial Surface Dynamics of an Excised Human Vocal Fold During Phonation. J. Voice 2006, 20, 401–413. [Google Scholar] [CrossRef]
- Alipour, F.; Scherer, R.C.; Finnegan, E. Pressure-Flow Relationships during Phonation as a Function of Adduction. J. Voice Off. J. Voice Found. 1997, 11, 187–194. [Google Scholar] [CrossRef]
- Döllinger, M.; Tayama, N.; Berry, D.A. Empirical Eigenfunctions and Medial Surface Dynamics of a Human Vocal Fold. Methods Inf. Med. 2005, 44, 384–391. [Google Scholar]
- Kist, A.M.; Gómez, P.; Dubrovskiy, D.; Schlegel, P.; Kunduk, M.; Echternach, M.; Patel, R.; Semmler, M.; Bohr, C.; Dürr, S.; et al. A Deep Learning Enhanced Novel Software Tool for Laryngeal Dynamics Analysis. J. Speech Lang. Hear. Res. 2021, 64, 1889–1903. [Google Scholar] [CrossRef] [PubMed]
- Larsson, H.; Hertegård, S. Calibration of High-Speed Imaging by Laser Triangulation. Logop. Phoniatr. Vocology 2004, 29, 154–161. [Google Scholar] [CrossRef] [PubMed]
- Patel, R.R.; Döllinger, M.; Jakubaß, B.; Pinhack, H.; Katz, U.; Semmler, M. Analyzing Vocal Fold Frequency Dynamics Using High-Speed 3D Laser Video Endoscopy. Laryngoscope 2024, 134, 3267–3276. [Google Scholar] [CrossRef] [PubMed]
- Boessenecker, A.; Berry, D.A.; Lohscheller, J.; Eysholdt, U.; Doellinger, M. Mucosal Wave Properties of a Human Vocal Fold. Acta Acust. United Acust. 2007, 93, 815–823. [Google Scholar]
- Berry, D.A.; Montequin, D.W.; Tayama, N. High-Speed Digital Imaging of the Medial Surface of the Vocal Folds. J. Acoust. Soc. Am. 2001, 110, 2539–2547. [Google Scholar] [CrossRef]
- Luegmair, G.; Mehta, D.D.; Kobler, J.B.; Dollinger, M. Three-Dimensional Optical Reconstruction of Vocal Fold Kinematics Using High-Speed Video with a Laser Projection System. IEEE Trans. Med. Imaging 2015, 34, 2572–2582. [Google Scholar] [CrossRef]
- Luegmair, G.; Kniesburges, S.; Zimmermann, M.; Sutor, A.; Eysholdt, U.; Döllinger, M. Optical Reconstruction of High-Speed Surface Dynamics in an Uncontrollable Environment. IEEE Trans. Med. Imaging 2010, 29, 1979–1991. [Google Scholar] [CrossRef]
- Kramer, E.; Linder, R.; Schönweiler, R. A Study of Subharmonics in Connected Speech Material. J. Voice 2013, 27, 29–38. [Google Scholar] [CrossRef]
- Sun, X. A Pitch Determination Algorithm Based on Subharmonic-to-Harmonic Ratio. In Proceedings of the 6th International Conference on Spoken Language Processing (ICSLP 2000), Beijing, China, 16 October 2000; ISCA: Singapore, 2000; Volume 4, pp. 676–679. [Google Scholar] [CrossRef]
- Omori, K.; Kojima, H.; Kakani, R.; Slavit, D.H.; Blaugrund, S.M. Acoustic Characteristics of Rough Voice: Subharmonics. J. Voice 1997, 11, 40–47. [Google Scholar] [CrossRef]
- Henningson, J.-O.; Stamminger, M.; Döllinger, M.; Semmler, M. Real-Time 3D Reconstruction of Human Vocal Folds via High-Speed Laser-Endoscopy. In Medical Image Computing and Computer Assisted Intervention—MICCAI 2022; Wang, L., Dou, Q., Fletcher, P.T., Speidel, S., Li, S., Eds.; Lecture Notes in Computer Science; Springer Nature: Cham, Switzerland, 2022; Volume 13437, pp. 3–12. ISBN 978-3-031-16448-4. [Google Scholar]
- Aichinger, P.; Kumar, S.P.; Lehoux, S.; Švec, J.G. Simulated Laryngeal High-Speed Videos for the Study of Normal and Dysphonic Vocal Fold Vibration. J. Speech Lang. Hear. Res. 2022, 65, 2431–2445. [Google Scholar] [CrossRef]
- Zhang, Z. Cause-Effect Relationship between Vocal Fold Physiology and Voice Production in a Three-Dimensional Phonation Model. J. Acoust. Soc. Am. 2016, 139, 1493–1507. [Google Scholar] [CrossRef] [PubMed]
- Gomez, P.; Schutzenberger, A.; Semmler, M.; Dollinger, M. Laryngeal Pressure Estimation with a Recurrent Neural Network. IEEE J. Transl. Eng. Health Med. 2019, 7, 2000111. [Google Scholar] [CrossRef] [PubMed]
- Doellinger, M.; Berry, D.A.; Berke, G.S. A Quantitative Study of the Medial Surface Dynamics of an In Vivo Canine Vocal Fold during Phonation. Laryngoscope 2005, 115, 1646–1654. [Google Scholar] [CrossRef] [PubMed]
- Titze, I.R.; Jiang, J.J.; Hsiao, T.-Y. Measurement of Mucosal Wave Propagation and Vertical Phase Difference in Vocal Fold Vibration. Ann. Otol. Rhinol. Laryngol. 1993, 102, 58–63. [Google Scholar] [CrossRef]




| ID | Sex | Age (Years) | Height (cm) | Weight (kg) |
|---|---|---|---|---|
| HL1 | Male | 81 | 165 | 52.1 |
| HL2 | Male | 90 | 185 | 68 |
| HL3 | Male | 73 | 168 | 54.4 |
| HL4 | Male | 76 | 163 | 63.5 |
| Parameter (unit) | f0,audio (Hz) | f0,Psub (Hz) | Psub (Pa) | Flow Rate (SLM) | RB (Pa/SLM) | SPL (dB) |
|---|---|---|---|---|---|---|
| Phonation onset (n = 24) | 139 ± 21 | 140 ± 21 | 1149 ± 808 | 26 ± 8 | 49 ± 9 | 68 ± 6 |
| All recordings (n = 96) | 145 ± 19 | 145 ± 19 | 1657 ± 293 | 34 ± 9 | 50 ± 6 | 72 ± 3 |
| Minimum values | 101 | 102 | 609 | 15 | 31 | 59 |
| Maximum values | 216 | 217 | 2804 | 53 | 94 | 78 |
| vmean,med | vmax,med | ymean,med | zmean,med | ymax,med | zmax,med | EV1 | EV2 | |
|---|---|---|---|---|---|---|---|---|
| Elongation | 0.02 ± 0.23 | 0.15 ± 0.23 | 0.06 ± 0.17 | −0.14 ± 0.39 | 0.03 ± 0.22 | −0.16 ± 0.39 | 0.013 ± 0.43 | −0.27 ± 0.48 ** |
| Adduction | 0.16 ± 0.32 | 0.07 ± 0.27 | −0.14 ± 0.33 | −0.34 ± 0.19 | −0.01 ± 0.34 | −0.25 ± 0.20 | 0.1 ± 0.31 | −0.1 ± 0.37 |
| flow | 0.80 ± 0.17 ** | 0.81 ± 0.17 ** | 0.70 ± 0.14 ** | 0.65 ± 0.14 ** | 0.69 ± 0.13 ** | 0.68 ± 0.15 ** | −0.57 ± 0.17 * | 0.27 ± 0.18 |
| vmean,sup | 0.95 ± 0.03 ** | 0.90 ± 0.08 ** | 0.84 ± 0.17 ** | 0.70 ± 0.21 * | 0.87 ± 0.11 ** | 0.75 ± 0.23 * | −0.57 ± 0.14 * | 0.35 ± 0.29 |
| vmax,sup | 0.94 ± 0.03 ** | 0.91 ± 0.07 ** | 0.79 ± 0.24 * | 0.71 ± 0.19 * | 0.83 ± 0.14 ** | 0.76 ± 0.20 ** | −0.56 ± 0.1 ** | 0.31 ± 0.3 |
| ymean,sup | 0.79 ± 0.12 ** | 0.69 ± 0.15 ** | 0.85 ± 0.10 ** | 0.93 ± 0.05 ** | 0.84 ± 0.10 ** | 0.92 ± 0.05 ** | −0.46 ± 0.16 | 0.51 ± 0.17 |
| zmean,sup | 0.74 ± 0.10 ** | 0.59 ± 0.23 * | 0.76 ± 0.16 ** | 0.82 ± 0.12 ** | 0.80 ± 0.11 ** | 0.83 ± 0.13 ** | −0.27 ± 0.22 | 0.5 ± 0.12 ** |
| ymax,sup | 0.63 ± 0.16 ** | 0.55 ± 0.25 * | 0.56 ± 0.28 * | 0.68 ± 0.06 ** | 0.60 ± 0.16 * | 0.71 ± 0.08 ** | −0.45 ± 0.3 | 0.52 ± 0.2 |
| zmax,sup | 0.69 ± 0.14 ** | 0.52 ± 0.22 | 0.73 ± 0.20 ** | 0.92 ± 0.07 ** | 0.74 ± 0.17 ** | 0.92 ± 0.08 ** | −0.35 ± 0.23 | 0.58 ± 0.14 ** |
| Hemilarynx ID | Three-Dimensional Parameter | B (Medial var.) | B (const.) | Std. Error | T-Value | p-Value | R2 (Medial var.) |
|---|---|---|---|---|---|---|---|
| HL1 | vmean,sup | 0.74 | −0.02 | 0.02 | 32.0 | 0.001 | 0.98 |
| vmax,sup | 0.68 | 0.01 | 0.03 | 20.9 | 0.001 | 0.95 | |
| ymean,sup | 0.46 | 0.04 | 0.02 | 26.3 | 0.001 | 0.97 | |
| zmean,sup | 0.88 | −0.01 | 0.03 | 26.8 | 0.001 | 0.97 | |
| ymax,sup | 0.45 | 0.14 | 0.07 | 6.5 | 0.001 | 0.41 | |
| zmax,sup | 1.12 | 0.04 | 0.05 | 22.9 | 0.001 | 0.90 | |
| HL2 | vmean,sup | 0.86 | −0.01 | 0.08 | 11.6 | 0.001 | 0.85 |
| vmax,sup | 0.81 | −0.03 | 0.08 | 10.2 | 0.001 | 0.82 | |
| ymean,sup | 0.38 | 0.01 | 0.06 | 6.3 | 0.001 | 0.63 | |
| zmean,sup | 0.78 | 0.44 | 0.11 | 6.9 | 0.001 | 0.67 | |
| ymax,sup | 0.14 | 0.43 | 0.03 | 4.1 | 0.001 | 0.41 | |
| zmax,sup | 0.88 | 0.64 | 0.1 | 14.8 | 0.001 | 0.90 | |
| HL3 | vmean,sup | 0.83 | 0.09 | 0.08 | 11.1 | <0.001 | 0.84 |
| vmax,sup | 0.69 | 0.12 | 0.04 | 16.7 | <0.001 | 0.92 | |
| ymean,sup | 0.19 | 0.37 | 0.04 | 4.7 | <0.001 | 0.48 | |
| zmean,sup | 0.81 | 0.02 | 0.11 | 7.2 | <0.001 | 0.69 | |
| ymax,sup | 0.10 | 1.46 | 0.05 | 1.8 | 0.085 | 0.09 | |
| zmax,sup | 0.75 | 0.79 | 0.04 | 18.9 | <0.001 | 0.94 | |
| HL4 | vmean,sup | 1.29 | 0.02 | 0.09 | 14.4 | 0.001 | 0.90 |
| vmax,sup | 0.90 | 0.21 | 0.15 | 6.1 | 0.001 | 0.61 | |
| ymean,sup | 0.73 | 0.06 | 0.08 | 9.3 | 0.001 | 0.79 | |
| zmean,sup | 0.44 | 0.54 | 0.11 | 4.0 | 0.001 | 0.40 | |
| ymax,sup | 0.28 | 0.78 | 0.09 | 3.2 | 0.001 | 0.28 | |
| zmax,sup | 0.96 | 0.48 | 0.16 | 6.0 | 0.001 | 0.61 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Veltrup, R.; Angerer, S.; Gessner, E.; Matheis, F.; Sümmerer, E.; Henningson, J.-O.; Döllinger, M.; Semmler, M. Three-Dimensional Analysis of Vocal Fold Oscillations: Correlating Superior and Medial Surface Dynamics Using Ex Vivo Human Hemilarynges. Bioengineering 2024, 11, 977. https://doi.org/10.3390/bioengineering11100977
Veltrup R, Angerer S, Gessner E, Matheis F, Sümmerer E, Henningson J-O, Döllinger M, Semmler M. Three-Dimensional Analysis of Vocal Fold Oscillations: Correlating Superior and Medial Surface Dynamics Using Ex Vivo Human Hemilarynges. Bioengineering. 2024; 11(10):977. https://doi.org/10.3390/bioengineering11100977
Chicago/Turabian StyleVeltrup, Reinhard, Susanne Angerer, Elena Gessner, Friederike Matheis, Emily Sümmerer, Jann-Ole Henningson, Michael Döllinger, and Marion Semmler. 2024. "Three-Dimensional Analysis of Vocal Fold Oscillations: Correlating Superior and Medial Surface Dynamics Using Ex Vivo Human Hemilarynges" Bioengineering 11, no. 10: 977. https://doi.org/10.3390/bioengineering11100977
APA StyleVeltrup, R., Angerer, S., Gessner, E., Matheis, F., Sümmerer, E., Henningson, J.-O., Döllinger, M., & Semmler, M. (2024). Three-Dimensional Analysis of Vocal Fold Oscillations: Correlating Superior and Medial Surface Dynamics Using Ex Vivo Human Hemilarynges. Bioengineering, 11(10), 977. https://doi.org/10.3390/bioengineering11100977







