Computational Study of Abdominal Aortic Aneurysm Walls Accounting for Patient-Specific Non-Uniform Intraluminal Thrombus Thickness and Distinct Material Models: A Pre- and Post-Rupture Case
Abstract
:1. Introduction
2. Materials and Methods
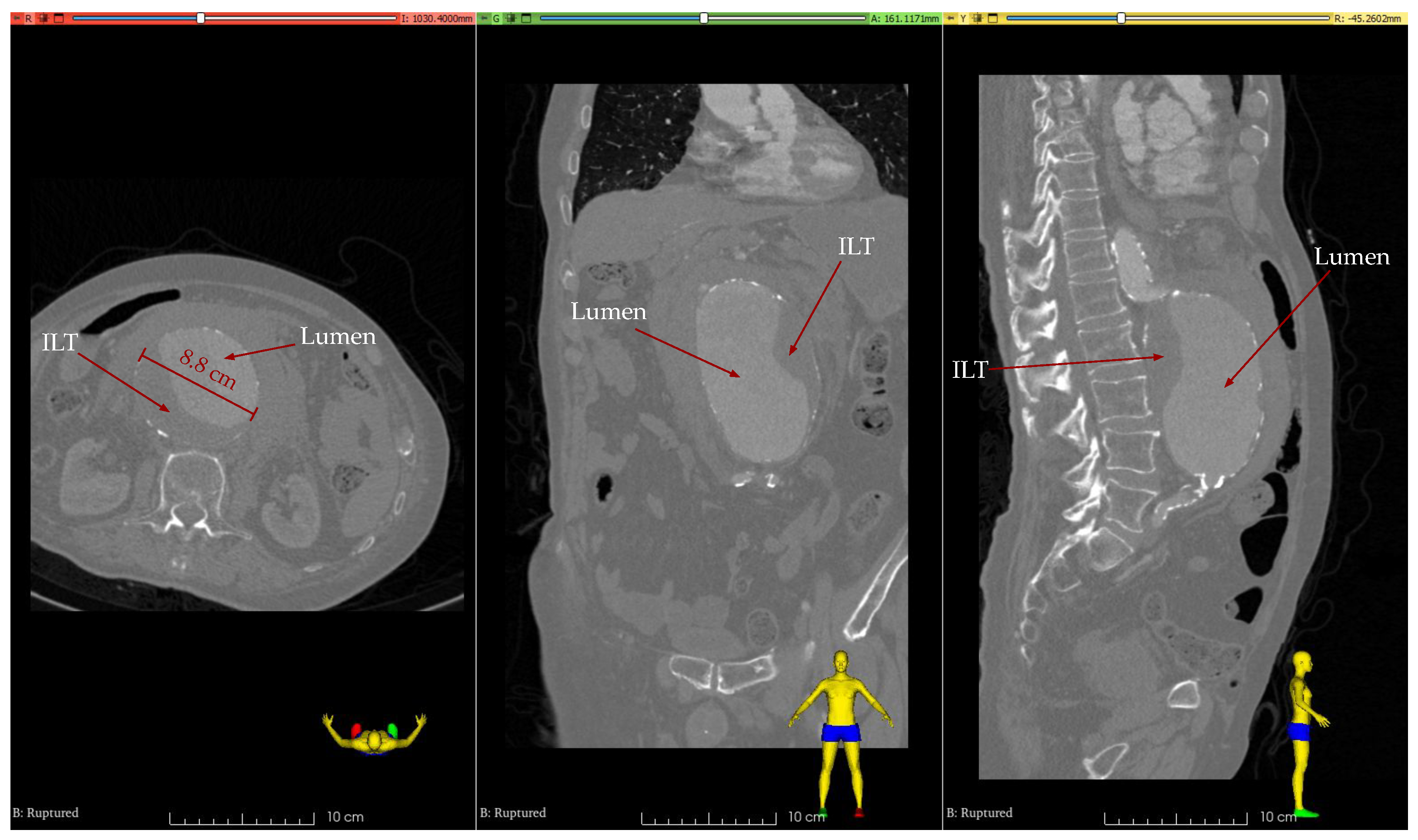
2.1. Clinical Case
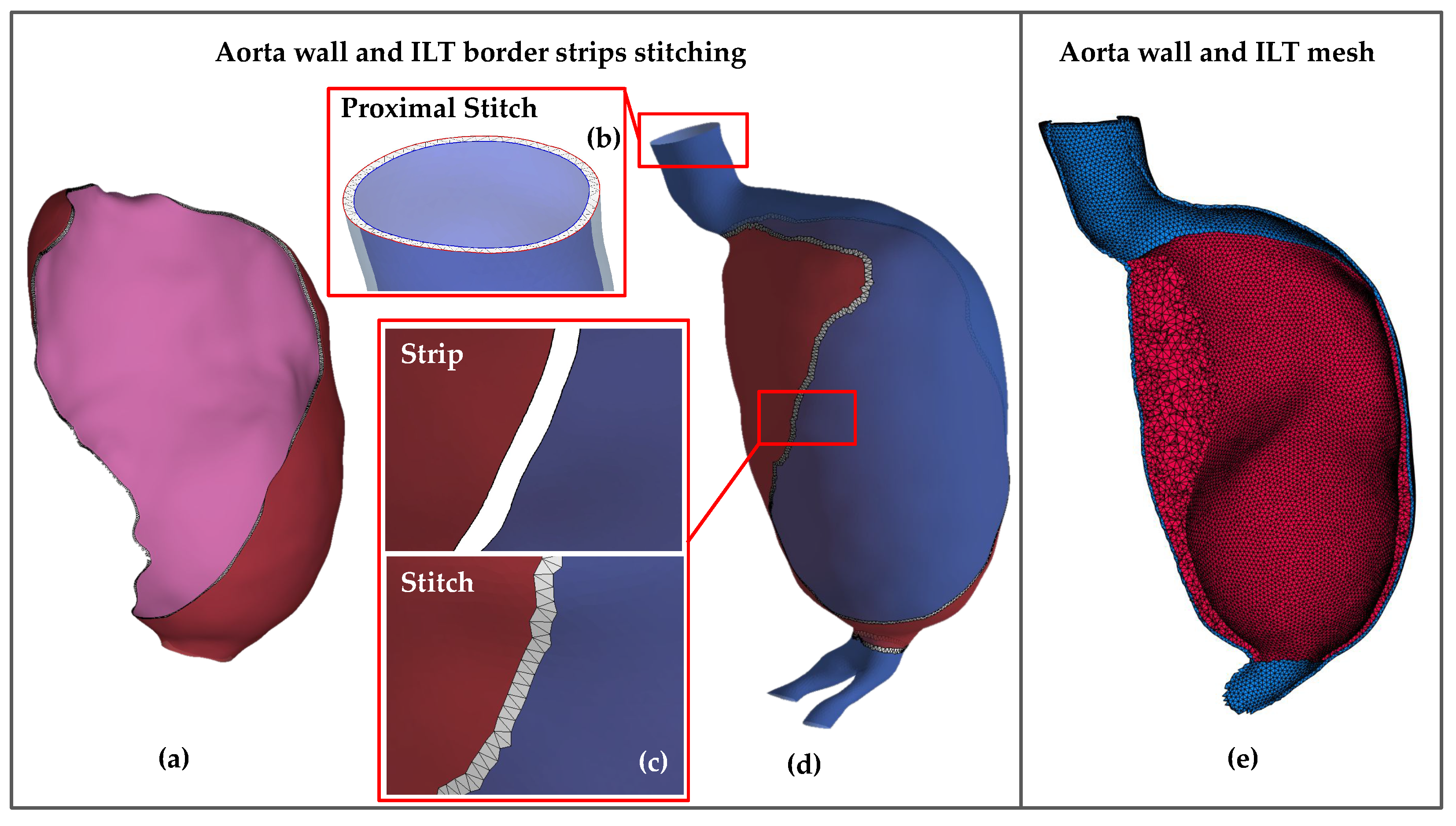
2.2. Segmentation, Reconstruction, and Smoothing
2.3. Meshing
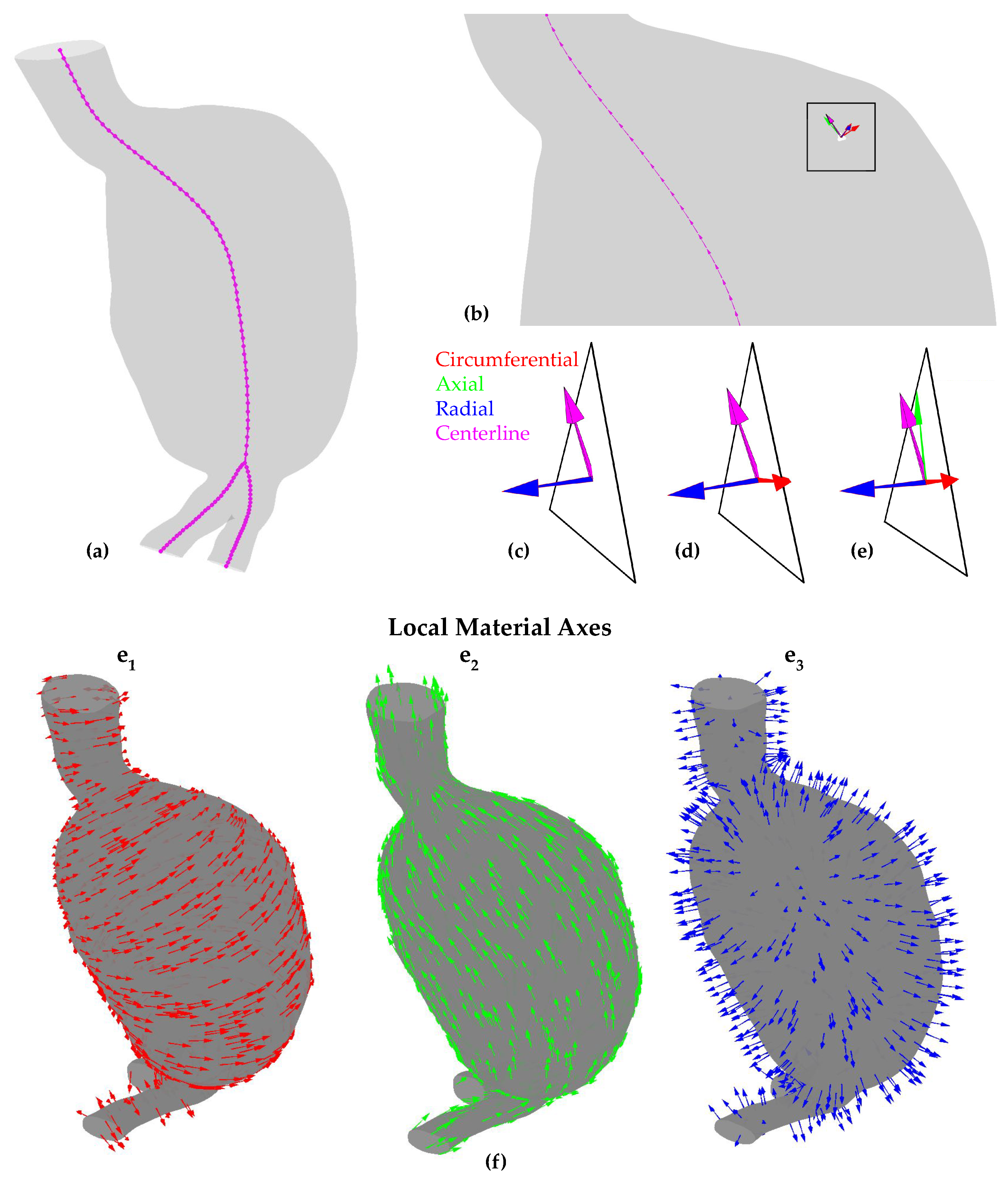
2.4. Local Material Axes
2.5. Material Model
2.5.1. Intraluminal Thrombus
2.5.2. Aortic Wall
HGO Model
Mooney–Rivlin Model
2.6. Finite Element Analysis
3. Results
3.1. Mesh Independence Study
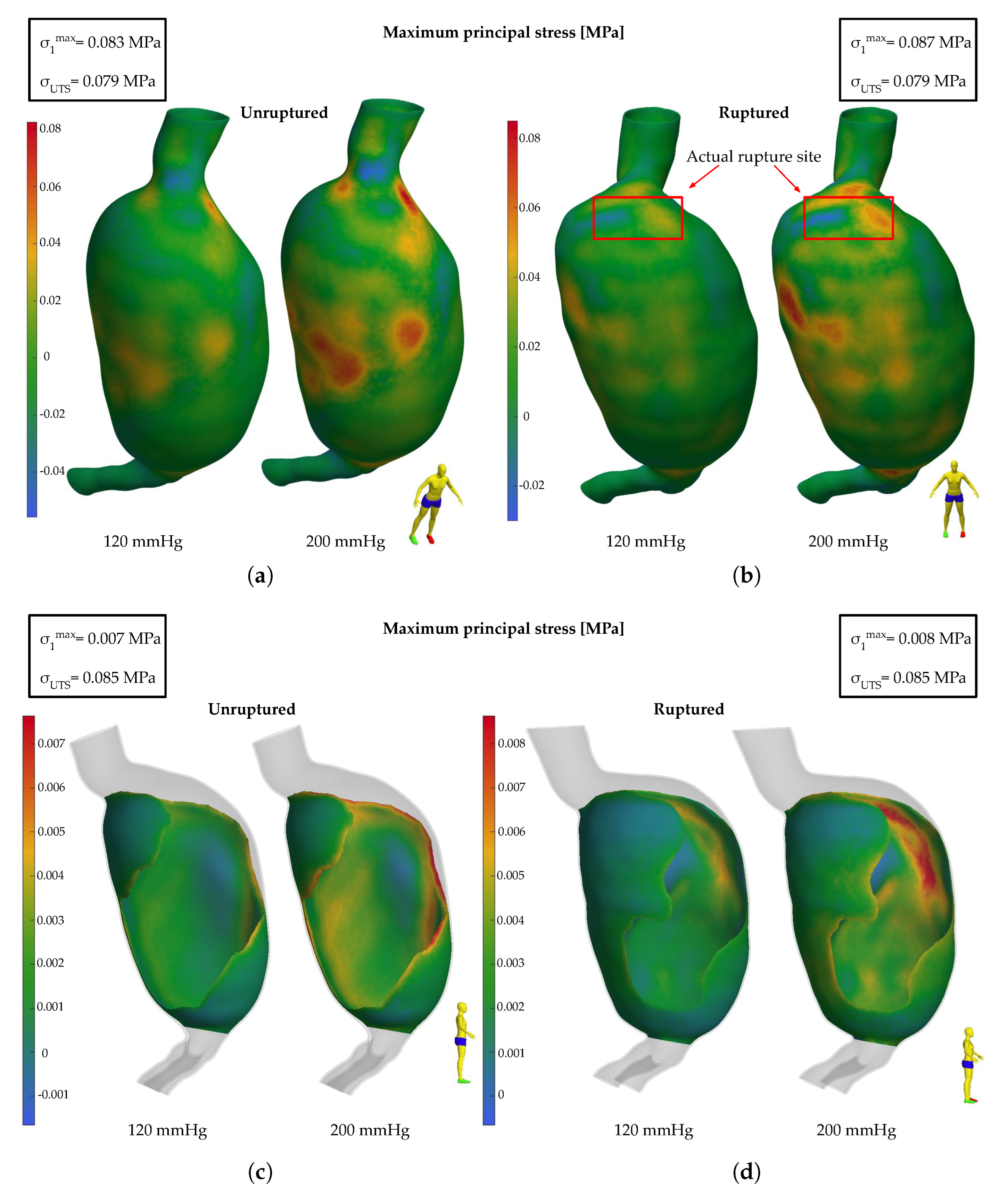
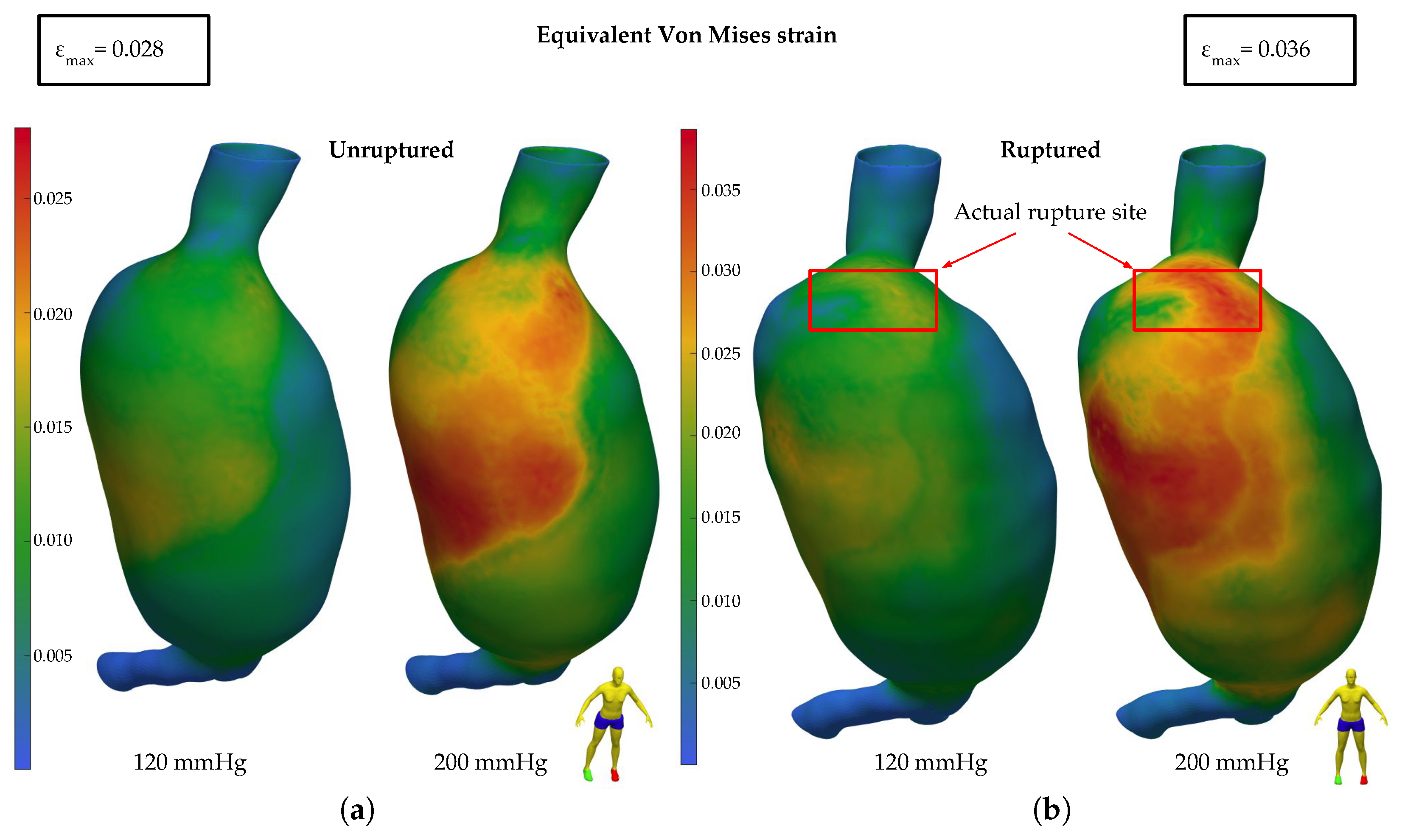
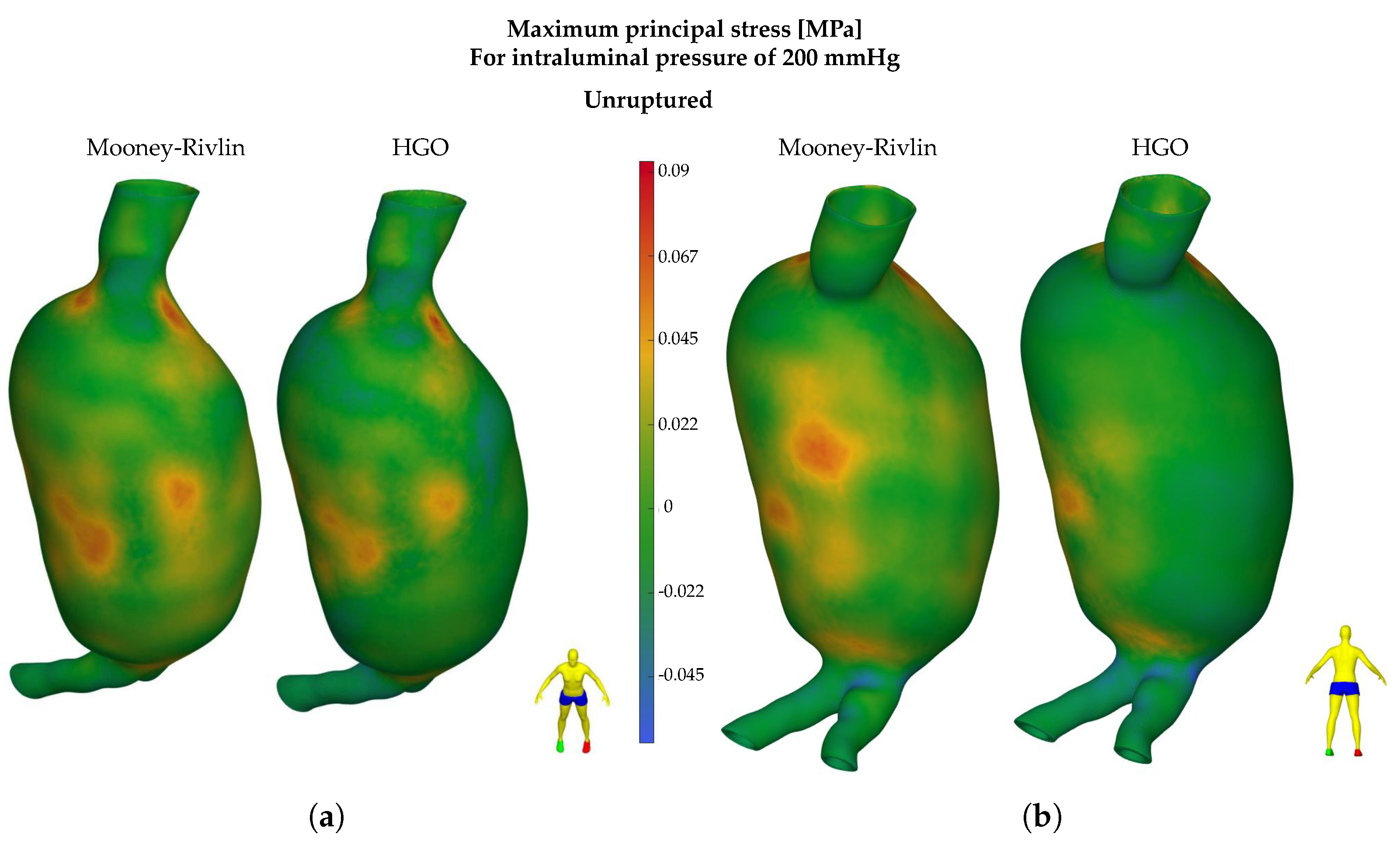
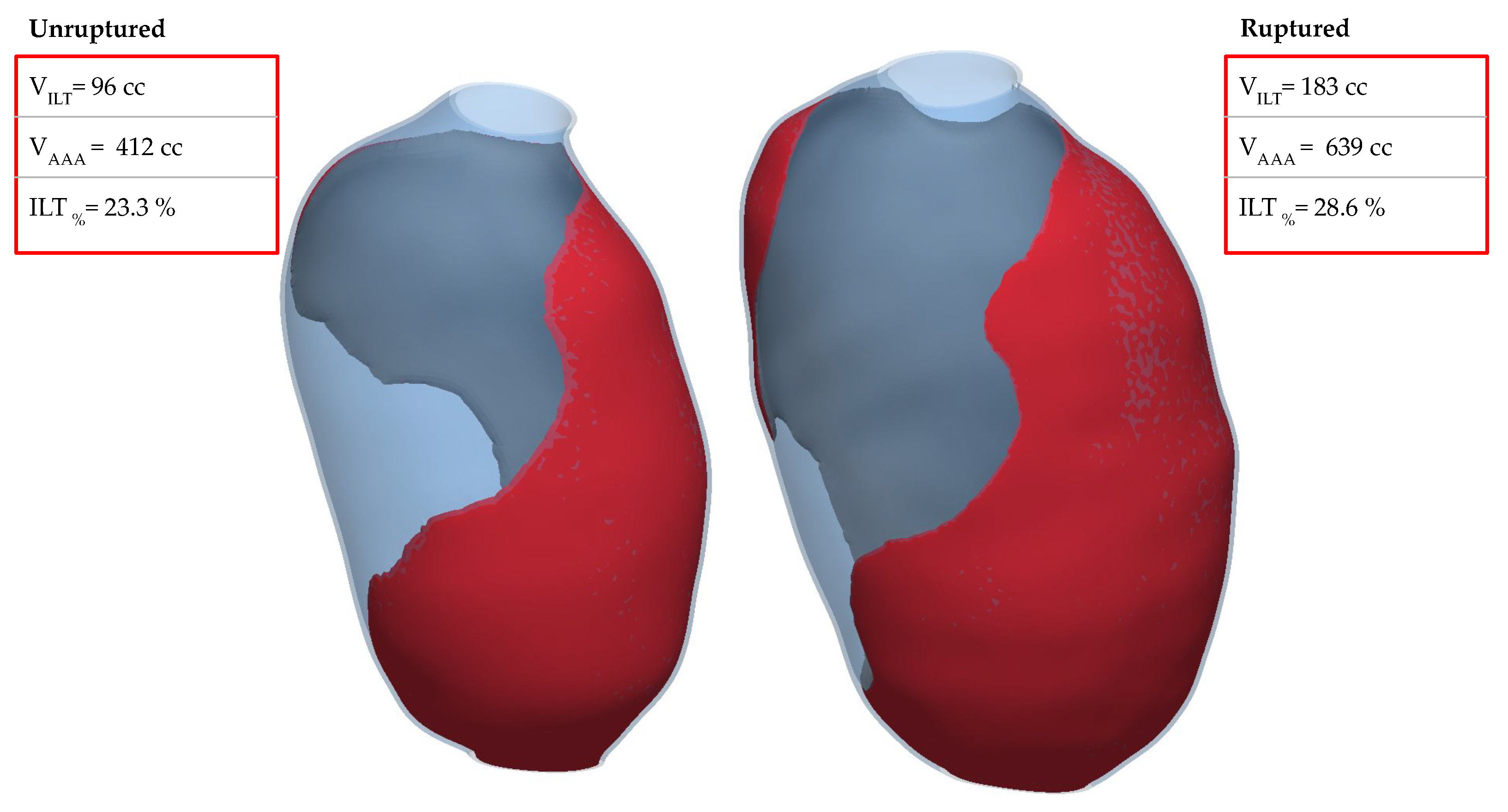
3.2. Finite Element Analysis Results
3.2.1. HGO Model
3.2.2. Mooney–Rivlin Model
4. Discussion
5. Limitations
6. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Correction Statement
References
- Lederle, F.A.; Johnson, G.R.; Wilson, S.E.; Chute, E.P.; Littooy, F.N.; Bandyk, D.F.; Krupski, W.C.; Barone, G.W.; Acher, C.W.; Ballard, D.J. Prevalence and associations of abdominal aortic aneurysm detected through screening. Ann. Intern. Med. 1997, 126, 441. [Google Scholar] [CrossRef]
- Locham, S.; Lee, R.E.; Nejim, B.; Aridi, H.D. Mortality after endovascular versus open repair of abdominal aortic aneurysm in the elderly. J. Surg. Res. 2017, 215, 153–159. [Google Scholar] [CrossRef]
- Daye, D.; Walker, T. Complications of endovascular aneurysm repair of the thoracic and abdominal aorta: Evaluation and management. Cardiovasc. Diagn. Ther. 2018, 8, S138–S156. [Google Scholar] [CrossRef]
- Dakour-Aridi, H.; Paracha, N.Z.; Locham, S.; Nejim, B. Assessment of failure to rescue after abdominal aortic aneurysm repair using the National Surgical Quality Improvement Program procedure-targeted data set. J. Vasc. Surg. 2018, 68, 1335–1344.e1. [Google Scholar] [CrossRef]
- Darling, R.; Messina, C.; Brewster, D.; Ottinger, L. Autopsy study of unoperated abdominal aortic aneurysms. The case for early resection. Circulation 1977, 56, II161–II164. [Google Scholar]
- Sterpetti, A.; Cavallaro, A.; Cavallari, N.; Allegrucci, P.; Tamburelli, A.; Agosta, F.; Bartoli, S. Factors influencing the rupture of abdominal aortic aneurysms. Surg. Gynecol. Obstet. 1991, 173, 175–178. [Google Scholar]
- Powell, J.; Brown, L.; Forbes, J.F.; Fowkes, F.G.R.; Greenhalgh, R.M.; Ruckley, C.V.; Thompson, S.G. Final 12-year follow-up of surgery vs surveillance in the UK Small Aneurysm Trial. Br. J. Surg. 2007, 94, 702–708. [Google Scholar] [CrossRef]
- Sweeting, M.; Thompson, S.G.; Brown, L.; Powell, J. Meta-analysis of individual patient data to examine factors affecting growth and rupture of small abdominal aortic aneurysms. Br. J. Surg. 2012, 99, 655–665. [Google Scholar] [CrossRef]
- Lederle, F.A.; Johnson, G.R.; Wilson, S.E. Abdominal aortic aneurysm in women. J. Vasc. Surg. 2001, 34, 122–126. [Google Scholar] [CrossRef]
- Johnston, K. Influence of sex on the results of abdominal aortic aneurysm repair. J. Vasc. Surg. 1994, 20, 914–926. [Google Scholar] [CrossRef]
- Bukač, M.; Shadden, S.C. Quantifying the effects of intraluminal thrombi and their poroelastic properties on abdominal aortic aneurysms. Arch. Appl. Mech. 2022, 92, 435–446. [Google Scholar] [CrossRef]
- Riveros, F.; Martufi, G.; Gasser, T.C.; Rodriguez-Matas, J.F. On the impact of intraluminal thrombus mechanical behavior in AAA passive mechanics. Ann. Biomed. Eng. 2015, 43, 2253–2264. [Google Scholar] [CrossRef] [PubMed]
- Qiu, Y.; Wang, Y.; Fan, Y.; Peng, L.; Liu, R.; Zhao, J.; Yuan, D.; Zheng, T. Role of intraluminal thrombus in abdominal aortic aneurysm ruptures: A hemodynamic point of view. Med. Phys. 2019, 46, 4263–4275. [Google Scholar] [CrossRef] [PubMed]
- Biasetti, J.; Hussain, F.; Gasser, T.C. Blood flow and coherent vortices in the normal and aneurysmatic aortas: A fluid dynamical approach to intra-Luminal thrombus formation. J. R. Soc. Interface 2011, 8, 1449–1461. [Google Scholar] [CrossRef] [PubMed]
- Zambrano, B.A.; Gharahi, H.; Lim, C.; Jaberi, F.A.; Choi, J.; Lee, W.; Baek, S. Association of intraluminal thrombus, hemodynamic forces, and abdominal aortic aneurysm expansion using longitudinal CT images. Ann. Biomed. Eng. 2015, 44, 1502–1514. [Google Scholar] [CrossRef] [PubMed]
- Franck, G.; Dai, J.; Fifre, A.; Ngo, S.; Justine, C.; Michineau, S.; Allaire, E.; Gervais, M. Reestablishment of the endothelial lining by endothelial cell therapy stabilizes experimental abdominal aortic aneurysms. Circulation 2013, 127, 1877–1887. [Google Scholar] [CrossRef] [PubMed]
- Vorp, D.A.; Lee, P.C.; Wang, D.H.J.; Makaroun, M.S.; Nemoto, E.M.; Ogawa, S.; Webster, M.W. Association of intraluminal thrombus in abdominal aortic aneurysm with local hypoxia and wall weakening. J. Vasc. Surg. 2001, 34, 291–299. [Google Scholar] [CrossRef] [PubMed]
- Wang, D.H.J.; Makaroun, M.S.; Webster, M.W.; Vorp, D.A. Mechanical properties and microstructure of intraluminal thrombus from abdominal aortic aneurysm. J. Biomech. Eng. 2001, 123, 536–539. [Google Scholar] [CrossRef]
- Harter, L.P.; Gross, B.H.; Callen, P.W.; Barth, R.A. Ultrasonic evaluation of abdominal aortic thrombus. J. Ultrasound Med. 1982, 1, 315–318. [Google Scholar] [CrossRef]
- Wang, D.H.J.; Makaroun, M.S.; Webster, M.W.; Vorp, D.A. Effect of intraluminal thrombus on wall stress in patient-specific models of abdominal aortic aneurysm. J. Vasc. Surg. 2002, 36, 598–604. [Google Scholar] [CrossRef]
- Gasser, T.C.; Auer, M.T.; Labruto, F.; Swedenborg, J.; Roy, J. Biomechanical rupture risk assessment of abdominal aortic aneurysms: Model complexity versus predictability of finite element simulations. Eur. J. Vasc. Endovasc. Surg. 2010, 40, 176–185. [Google Scholar] [CrossRef]
- Larsson, E.; Labruto, F.; Gasser, T.C.; Swedenborg, J.; Hultgren, R. Analysis of aortic wall stress and rupture risk in patients with abdominal aortic aneurysm with a gender perspective. J. Vasc. Surg. 2011, 54, 295–299. [Google Scholar] [CrossRef]
- Vorp, D.A.; Mandarino, W.A.; Webster, M.W.; Gorcsan, J. Potential influence of intraluminal thrombus on abdominal aortic aneurysm as assessed by a new non-invasive method. Cardiovasc. Surg. 1996, 4, 732–739. [Google Scholar] [CrossRef]
- Schurink, G.W.H.; Van Baalen, J.M.; Visser, M.J.; Van Bockel, J. Thrombus within an aortic aneurysm does not reduce pressure on the aneurysmal wall. J. Vasc. Surg. 2000, 31, 501–506. [Google Scholar] [CrossRef]
- Martino, E.S.D.; Vorp, D.A. Effect of variation in intraluminal thrombus constitutive properties on abdominal aortic aneurysm wall stress. Ann. Biomed. Eng. 2003, 31, 804–809. [Google Scholar] [CrossRef]
- Toungara, M.; Geindreau, C. Influence of a poro-mechanical modeling of the intraluminal thrombus and the anisotropy of the arterial wall on the prediction of the abdominal aortic aneurysm rupture. Cardiovasc. Eng. Technol. 2013, 4, 192–208. [Google Scholar] [CrossRef]
- Polzer, S.; Gasser, T.C.; Markert, B.; Bursa, J.; Skacel, P. Impact of poroelasticity of intraluminal thrombus on wall stress of abdominal aortic aneurysms. BioMed. Eng. OnLine 2012, 11, 62. [Google Scholar] [CrossRef]
- Arslan, A.; Salman, H.E. Effect of intraluminal thrombus burden on the risk of abdominal aortic aneurysm rupture. J. Cardiovasc. Dev. Dis. 2023, 10, 233. [Google Scholar] [CrossRef]
- Molony, D.; Broderick, S.P.; Callanan, A.; McGloughlin, T.; Walsh, M.T. Fluid–Structure Interaction in Healthy, Diseased and Endovascularly Treated Abdominal Aortic Aneurysms. In Biomechanics and Mechanobiology of Aneurysms; Springer: Berlin/Heidelberg, Germany, 2011; pp. 163–179. [Google Scholar] [CrossRef]
- Raghavan, M.L.; Webster, M.W.; Vorp, D.A. Ex vivo biomechanical behavior of abdominal aortic aneurysm: Assessment using a new mathematical model. Ann. Biomed. Eng. 1996, 24, 573–582. [Google Scholar] [CrossRef]
- Raghavan, M.L.; Vorp, D.A. Toward a biomechanical tool to evaluate rupture potential of abdominal aortic aneurysm: Identification of a finite strain constitutive model and evaluation of its applicability. J. Biomech. 2000, 33, 475–482. [Google Scholar] [CrossRef]
- Doyle, B.; Callanan, A.; McGloughlin, T.M. A comparison of modelling techniques for computing wall stress in abdominal aortic aneurysms. Biomed. Eng. Online 2007, 6, 38. [Google Scholar] [CrossRef]
- Rissland, P.; Alemu, Y.; Einav, S.; Ricotta, J.J.; Bluestein, D. Abdominal aortic aneurysm risk of rupture: Patient-specific FSI simulations using anisotropic model. J. Biomech. Eng. 2008, 131, 031001. [Google Scholar] [CrossRef]
- Holzapfel, G.; Gasser, T.C.; Ogden, R.W. A new constitutive framework for arterial wall mechanics and a comparative study of material models. J. Elast. 2000, 61, 1–48. [Google Scholar] [CrossRef]
- Di Martino, E.S.; Guadagni, G.; Fumero, A.; Ballerini, G.; Spirito, R.; Biglioli, P.; Redaelli, A. Fluid–structure interaction within realistic three-dimensional models of the aneurysmatic aorta as a guidance to assess the risk of rupture of the aneurysm. Med. Eng. Phys. 2001, 23, 647–655. [Google Scholar] [CrossRef]
- Auer, M.T.; Gasser, T.C. Reconstruction and finite element mesh generation of abdominal aortic aneurysms from computerized tomography angiography data with minimal user interactions. IEEE Trans. Med. Imaging 2010, 29, 1022–1028. [Google Scholar] [CrossRef]
- Doyle, B.; Callanan, A.; Grace, P.A.; Kavanagh, E.G. On the influence of patient-specific material properties in computational simulations: A case study of a large ruptured abdominal aortic aneurysm. Int. J. Numer. Methods Biomed. Eng. 2012, 29, 150–164. [Google Scholar] [CrossRef]
- De Lucio, M.; García, M.F.; Garcia, J.D.; Rodríguez, L.E.; Marcos, F. On the importance of tunica intima in the aging aorta: A three-layered in silico model for computing wall stresses in abdominal aortic aneurysms. Comput. Methods Biomech. Biomed. Eng. 2020, 24, 467–484. [Google Scholar] [CrossRef]
- Fedorov, A.; Beichel, R.; Kalpathy-Cramer, J.; Finet, J.; Fillion-Robin, J.C.; Pujol, S.; Bauer, C.; Jennings, D.; Fennessy, F.M.; Sonka, M.; et al. 3D Slicer as an image computing platform for the quantitative imaging network. Magn. Reson. Imaging 2012, 30, 1323–1341. [Google Scholar] [CrossRef]
- Moerman, K.M. GIBBON: The geometry and image-Based bioengineering add-on. J. Open Source Softw. 2018, 3, 506. [Google Scholar] [CrossRef]
- Maas, S.A.; Ellis, B.J.; Ateshian, G.A.; Weiss, J.A. FEBio: Finite elements for biomechanics. J. Biomech. Eng. 2012, 134. [Google Scholar] [CrossRef]
- Raut, S.S.; Jana, A.; De Oliveira, V.; Muluk, S.C.; Finol, E.A. The importance of patient-specific regionally varying wall thickness in abdominal aortic aneurysm biomechanics. J. Biomech. Eng. 2013, 135. [Google Scholar] [CrossRef] [PubMed]
- Shum, J.; Martufi, G.; Di Martino, E.S.; Washington, C.; Grisafi, J.L.; Muluk, S.C.; Finol, E.A. Quantitative assessment of abdominal aortic aneurysm geometry. Ann. Biomed. Eng. 2010, 39, 277–286. [Google Scholar] [CrossRef] [PubMed]
- Raghavan, M.; Vorp, D.A.; Federle, M.P.; Makaroun, M.S.; Webster, M.W. Wall stress distribution on three-dimensionally reconstructed models of human abdominal aortic aneurysm. J. Vasc. Surg. 2000, 31, 760–769. [Google Scholar] [CrossRef] [PubMed]
- Kazi, M.; Thyberg, J.; Religa, P.; Roy, J.; Eriksson, P.; Hedin, U.; Swedenborg, J. Influence of intraluminal thrombus on structural and cellular composition of abdominal aortic aneurysm wall. J. Vasc. Surg. 2003, 38, 1283–1292. [Google Scholar] [CrossRef] [PubMed]
- Gasser, T.C.; Ogden, R.W.; Holzapfel, G. Hyperelastic modelling of arterial layers with distributed collagen fibre orientations. J. R. Soc. Interface 2005, 3, 15–35. [Google Scholar] [CrossRef]
- Di Martino, E.S.; Mantero, S.; Inzoli, F.; Melissano, G.; Astore, D.; Chiesa, R.; Fumero, R. Biomechanics of abdominal aortic aneurysm in the presence of endoluminal thrombus: Experimental characterisation and structural static computational analysis. Eur. J. Vasc. Endovasc. Surg. 1998, 15, 290–299. [Google Scholar] [CrossRef]
- Ng, E.; Looi, L.J.C. Numerical analysis of biothermal-fluids and cardiac thermal pulse of abdominal aortic aneurysm. Math. Biosci. Eng. 2022, 19, 10213–10251. [Google Scholar] [CrossRef]
- Niestrawska, J.A.; Viertler, C.; Regitnig, P.; Cohnert, T.; Sommer, G.; Holzapfel, G. Microstructure and mechanics of healthy and aneurysmatic abdominal aortas: Experimental analysis and modelling. J. R. Soc. Interface 2016, 13, 20160620. [Google Scholar] [CrossRef]
- Wilson, J.S.; Virag, L.; Di Achille, P.; Karšaj, I.; Humphrey, J.D. Biochemomechanics of intraluminal thrombus in abdominal aortic aneurysms. J. Biomech. Eng. 2013, 135. [Google Scholar] [CrossRef]
- Xenos, M.; Rambhia, S.H.; Alemu, Y.; Einav, S.; Labropoulos, N.; Tassiopoulos, A.; Ricotta, J.J.; Bluestein, D. Patient-Based abdominal aortic aneurysm rupture risk prediction with fluid structure interaction modeling. Ann. Biomed. Eng. 2010, 38, 3323–3337. [Google Scholar] [CrossRef]
- Liljeqvist, M.L.; Hultgren, R.; Gasser, T.C.; Roy, J. Volume growth of abdominal aortic aneurysms correlates with baseline volume and increasing finite element analysis-derived rupture risk. J. Vasc. Surg. 2016, 63, 1434–1442.e3. [Google Scholar] [CrossRef] [PubMed]
- Kontopodis, N.; Metaxa, E.; Papaharilaou, Y.; Georgakarakos, E.; Tsetis, D.; Ioannou, C.V. Value of volume measurements in evaluating abdominal aortic aneurysms growth rate and need for surgical treatment. Eur. J. Radiol. 2014, 83, 1051–1056. [Google Scholar] [CrossRef] [PubMed]
- Singh, T.P.; Wong, S.A.; Moxon, J.V.; Gasser, T.C.; Golledge, J. Systematic review and meta-analysis of the association between intraluminal thrombus volume and abdominal aortic aneurysm rupture. J. Vasc. Surg. 2019, 70, 2065–2073. [Google Scholar] [CrossRef] [PubMed]
- Koncar, I.; Nikolic, D.; Milosevic, Z.; Bogavac-Stanojevic, N.; Ilic, N.; Dragas, M.; Sladojevic, M.; Markovic, M.; Vujcic, A.; Filipovic, N.; et al. Abdominal aortic aneurysm volume and relative intraluminal thrombus volume might be auxiliary predictors of rupture—An observational cross-sectional study. Front. Surg. 2023, 10, 1095224. [Google Scholar] [CrossRef] [PubMed]
- Throop, A.; Bukac, M.; Zakerzadeh, R. Prediction of wall stress and oxygen flow in patient-specific abdominal aortic aneurysms: The role of intraluminal thrombus. Biomech. Model. Mechanobiol. 2022, 21, 761–1779. [Google Scholar] [CrossRef] [PubMed]
- Maier, A.; Gee, M.W.; Reeps, C.; Eckstein, H.; Wall, W.A. Impact of calcifications on patient-specific wall stress analysis of abdominal aortic aneurysms. Biomech. Model. Mechanobiol. 2010, 9, 511–521. [Google Scholar] [CrossRef]
- Sethi, A.; Taylor, D.L.; Ruby, J.G.; Venkataraman, J.; Sorokin, E.P.; Cule, M.; Melamud, E. Calcification of the abdominal aorta is an under-appreciated cardiovascular disease risk factor in the general population. Front. Cardiovasc. Med. 2022, 9, 1003246. [Google Scholar] [CrossRef]
- Zelaya, J.E.; Goenezen, S.; Dargon, P.; Azarbal, A.F.; Rugonyi, S. Improving the efficiency of abdominal aortic aneurysm wall stress computations. PLoS ONE 2014, 9, e101353. [Google Scholar] [CrossRef]
- Chandra, S.; Gnanaruban, V.; Riveros, F.; Rodriguez, J.F.; Finol, E.A. A Methodology for the derivation of unloaded abdominal aortic aneurysm geometry with experimental validation. J. Biomech. Eng. 2016, 138, 101005. [Google Scholar] [CrossRef]
- Johnston, R.D.; Ghasemi, M.; Lally, C. Inverse material parameter estimation of patient-specific finite element models at the carotid bifurcation: The impact of excluding the zero-pressure configuration and residual stress. Int. J. Numer. Methods Biomed. Eng. 2022, 39, e3663. [Google Scholar] [CrossRef]
- Long, A.; Rouet, L.; Bissery, A.; Rossignol, P.; Mouradian, D.; Sapoval, M. Compliance of abdominal aortic aneurysms evaluated by tissue Doppler imaging: Correlation with aneurysm size. J. Vasc. Surg. 2005, 42, 18–26. [Google Scholar] [CrossRef] [PubMed]
- Krüger, T.; Veseli, K.; Lausberg, H.; Vöhringer, L.; Schneider, W.; Schlensak, C. Regional and directional compliance of the healthy aorta: Anex vivostudy in a porcine model. Interact. Cardiovasc. Thorac. Surg. 2016, 23, 104–111. [Google Scholar] [CrossRef] [PubMed]
- Buja, L.M.L.; Butany, J. Cardiovascular Pathology; Academic Press: Cambridge, MA, USA, 2015. [Google Scholar]
- Tsamis, A.; Krawiec, J.T.; Vorp, D.A. Elastin and collagen fibre microstructure of the human aorta in ageing and disease: A review. J. R. Soc. Interface 2013, 10, 20121004. [Google Scholar] [CrossRef] [PubMed]



| Body | Material Model | Parameter | Value | Dimensions |
|---|---|---|---|---|
| ILT | Linear elastic | E | MPa | |
| (-) | ||||
| Aortic wall | HGO | c | MPa | |
| MPa | ||||
| (-) | ||||
| (-) | ||||
| (°) | ||||
| Mooney–Rivlin | MPa | |||
| MPa |
| Elements | Nodes | Max Stress Value (MPa) | Absolute Deviation at Max Stress | |
|---|---|---|---|---|
| Coarse | 247,948 | 64,939 | 0.0808 | 2.18% |
| Fine | 427,252 | 107,054 | 0.0826 | - |
| Finer | 559,152 | 138,285 | 0.0837 | 1.42% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sarantides, P.; Raptis, A.; Mathioulakis, D.; Moulakakis, K.; Kakisis, J.; Manopoulos, C. Computational Study of Abdominal Aortic Aneurysm Walls Accounting for Patient-Specific Non-Uniform Intraluminal Thrombus Thickness and Distinct Material Models: A Pre- and Post-Rupture Case. Bioengineering 2024, 11, 144. https://doi.org/10.3390/bioengineering11020144
Sarantides P, Raptis A, Mathioulakis D, Moulakakis K, Kakisis J, Manopoulos C. Computational Study of Abdominal Aortic Aneurysm Walls Accounting for Patient-Specific Non-Uniform Intraluminal Thrombus Thickness and Distinct Material Models: A Pre- and Post-Rupture Case. Bioengineering. 2024; 11(2):144. https://doi.org/10.3390/bioengineering11020144
Chicago/Turabian StyleSarantides, Platon, Anastasios Raptis, Dimitrios Mathioulakis, Konstantinos Moulakakis, John Kakisis, and Christos Manopoulos. 2024. "Computational Study of Abdominal Aortic Aneurysm Walls Accounting for Patient-Specific Non-Uniform Intraluminal Thrombus Thickness and Distinct Material Models: A Pre- and Post-Rupture Case" Bioengineering 11, no. 2: 144. https://doi.org/10.3390/bioengineering11020144
APA StyleSarantides, P., Raptis, A., Mathioulakis, D., Moulakakis, K., Kakisis, J., & Manopoulos, C. (2024). Computational Study of Abdominal Aortic Aneurysm Walls Accounting for Patient-Specific Non-Uniform Intraluminal Thrombus Thickness and Distinct Material Models: A Pre- and Post-Rupture Case. Bioengineering, 11(2), 144. https://doi.org/10.3390/bioengineering11020144









