Evaluating Machine Learning-Based MRI Reconstruction Using Digital Image Quality Phantoms
Abstract
:1. Introduction
2. Materials and Methods
2.1. Digital Phantom Creation
- Simple Disk Phantom:
- 2.
- Resolution Phantom
- 3.
- Low-Contrast Phantom
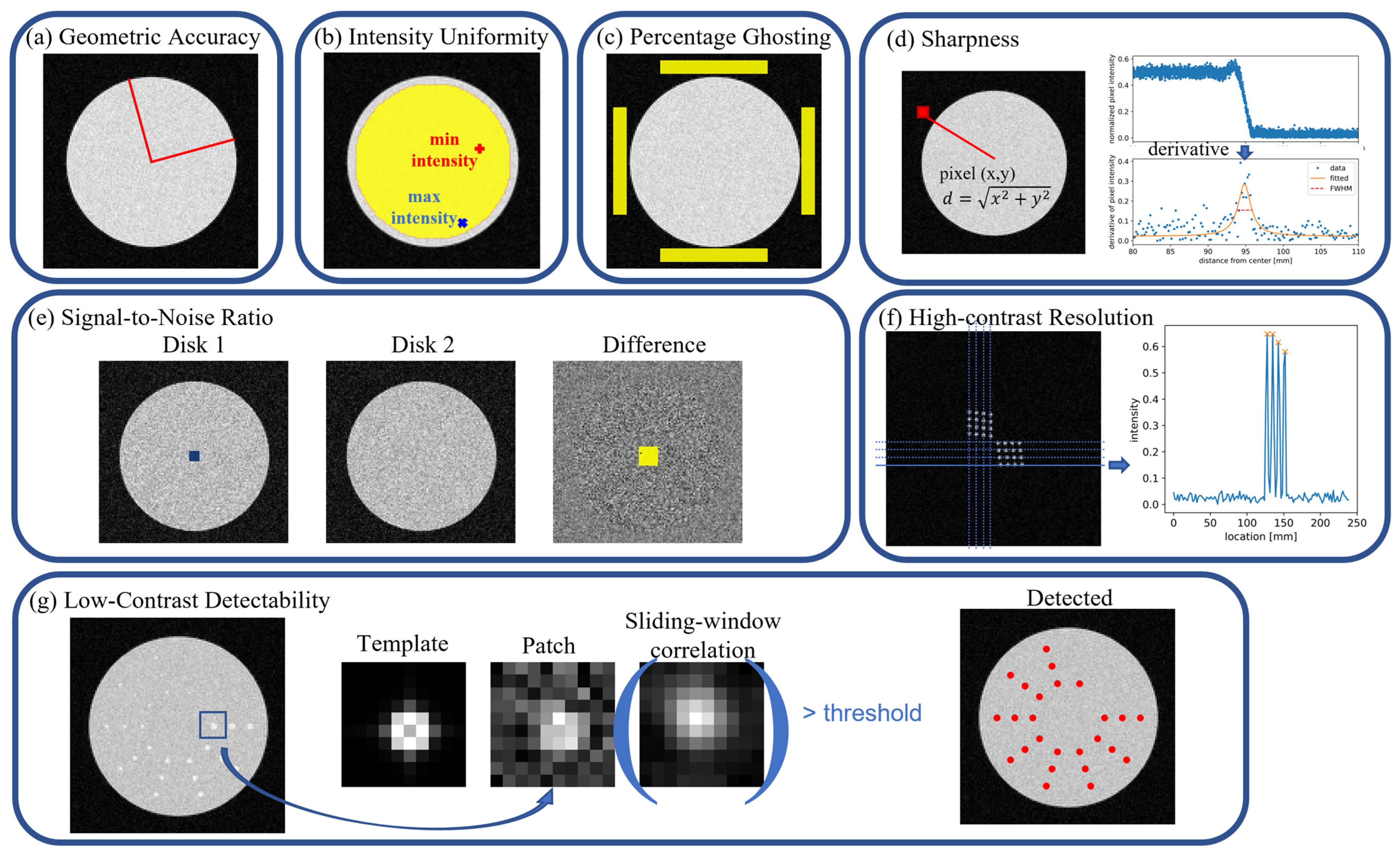
2.2. Evaluation Metrics
2.2.1. Geometric Accuracy
2.2.2. Intensity Uniformity
2.2.3. Percentage Ghosting
2.2.4. Sharpness
2.2.5. Signal-to-Noise Ratio
2.2.6. High-Contrast Resolution
2.2.7. Low-Contrast Detectability
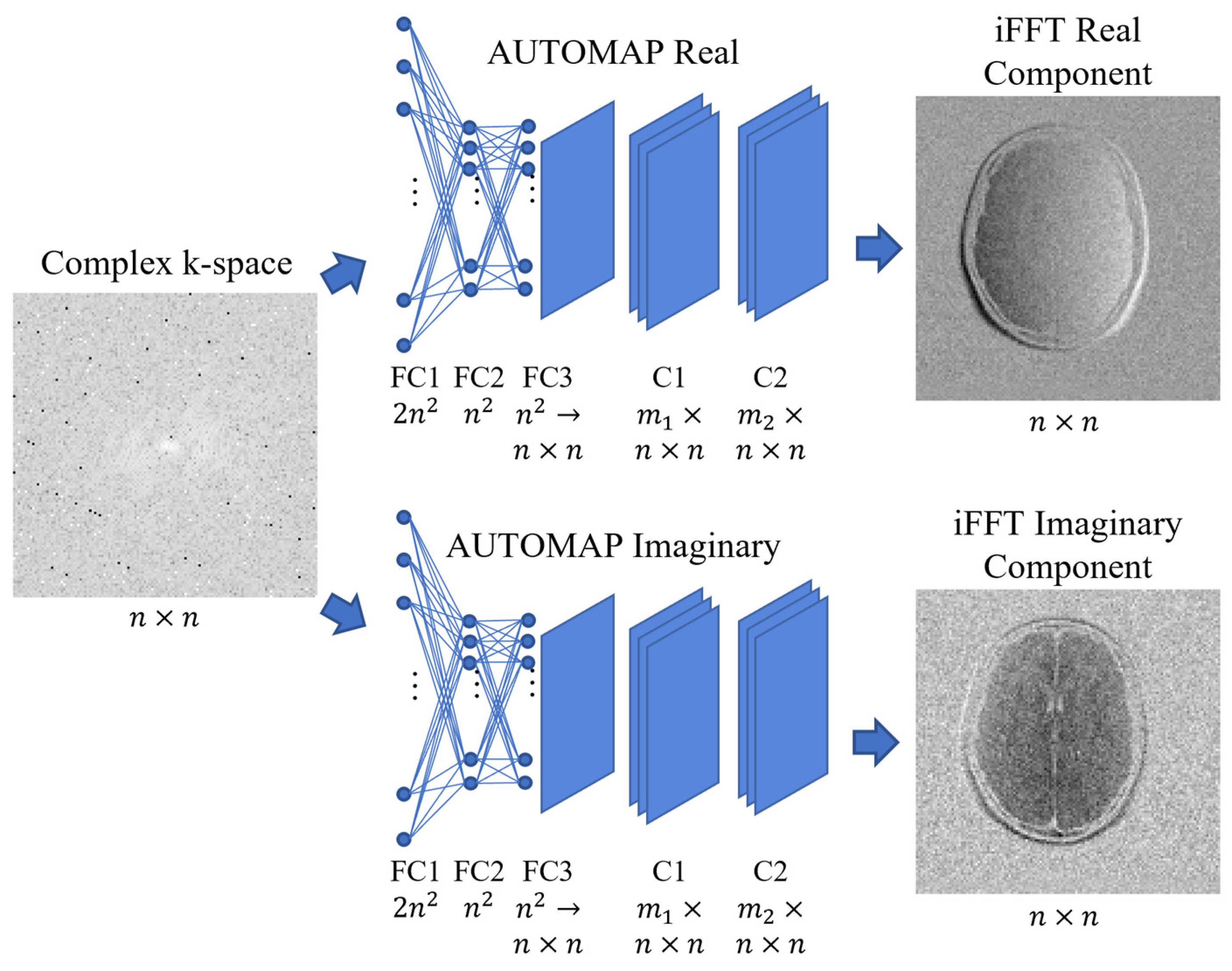
2.3. AUTOMAP Network
2.4. Training Data
2.4.1. M4Raw Dataset
2.4.2. Fast MRI Dataset
2.4.3. Preprocessing
2.5. Test Set
2.6. Experiments
- Comparison of Fully Sampled vs. Undersampled Training Data:
- 2.
- Two Noise Levels for the Testing Phantom:
- 3.
- Comparison of 3T vs. 0.3T MR Training Data:
3. Results
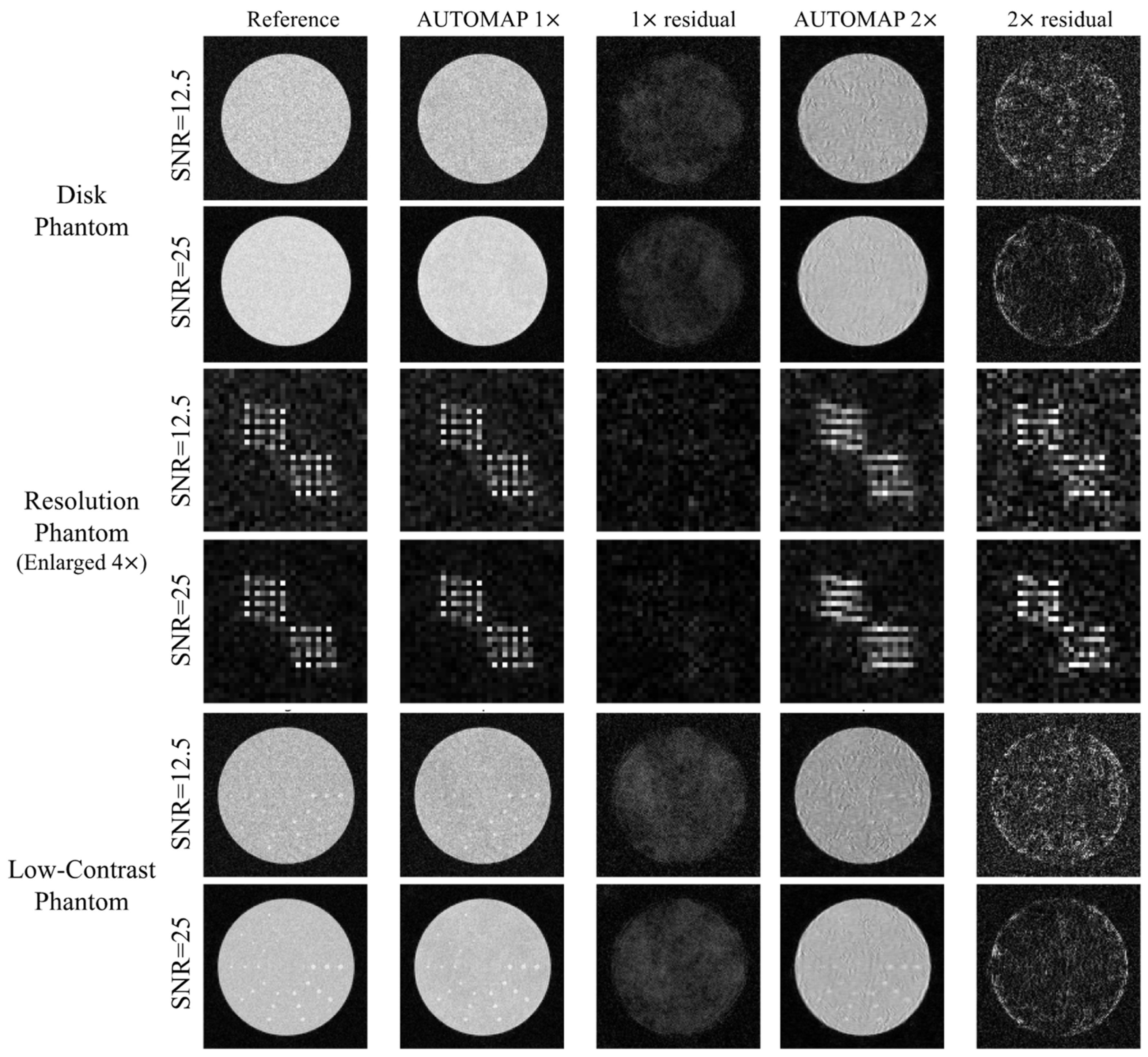
3.1. Reference iFFT Reconstruction, Fully and UnderSampled AUTOMAP
3.2. Impact of SNR in Test Images
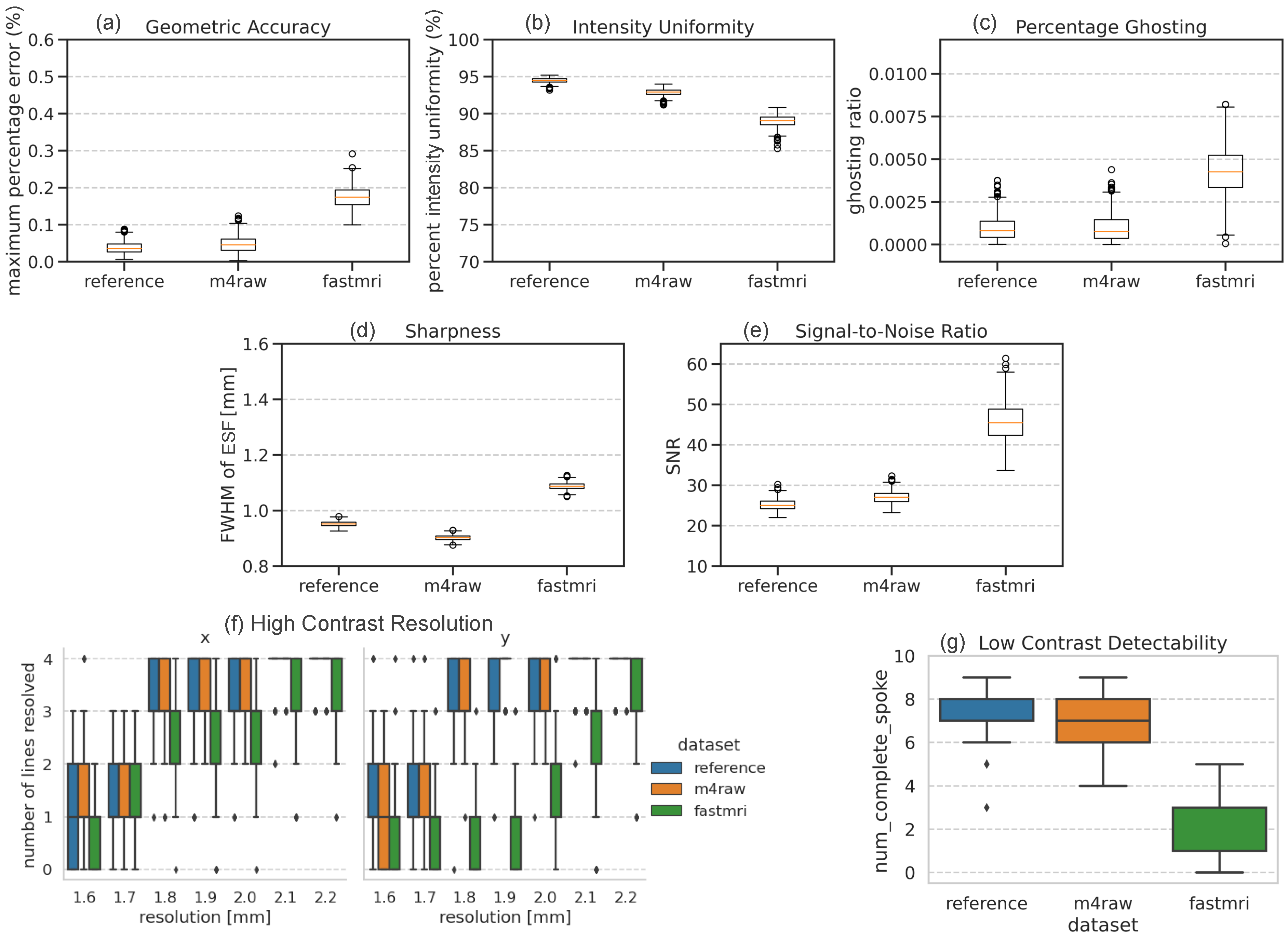
3.3. Impact of Dataset
3.4. Conventional Metrics
4. Discussion
4.1. Performance Difference in M4Raw- and FastMRI-Trained Networks
4.2. Limitations
4.3. Future Work
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Disclaimer
References
- Montalt-Tordera, J.; Muthurangu, V.; Hauptmann, A.; Steeden, J.A. Machine learning in Magnetic Resonance Imaging: Image reconstruction. Phys. Med. 2021, 83, 79–87. [Google Scholar] [CrossRef] [PubMed]
- Zhu, B.; Liu, J.Z.; Cauley, S.F.; Rosen, B.R.; Rosen, M.S. Image reconstruction by domain-transform manifold learning. Nature 2018, 555, 487–492. [Google Scholar] [CrossRef]
- Schlemper, J.; Caballero, J.; Hajnal, J.V.; Price, A.N.; Rueckert, D. A Deep Cascade of Convolutional Neural Networks for Dynamic MR Image Reconstruction. IEEE Trans. Med. Imaging 2018, 37, 491–503. [Google Scholar] [CrossRef]
- Zein, M.E.; Laz, W.E.; Laza, M.; Wazzan, T.; Kaakour, I.; Adla, Y.A.; Baalbaki, J.; Diab, M.O.; Sabbah, M.; Zantout, R. A Deep Learning Framework for Denoising MRI Images using Autoencoders. In Proceedings of the 2023 5th International Conference on Bio-engineering for Smart Technologies (BioSMART), Online, 7–9 June 2023; pp. 1–4. [Google Scholar]
- American College of Radiology. Phantom Test Guidance for Use of the Large MRI Phantom for the ACR.
- Ihalainen, T.M.; Lonnroth, N.T.; Peltonen, J.I.; Uusi-Simola, J.K.; Timonen, M.H.; Kuusela, L.J.; Savolainen, S.E.; Sipila, O.E. MRI quality assurance using the ACR phantom in a multi-unit imaging center. Acta Oncol. 2011, 50, 966–972. [Google Scholar] [CrossRef] [PubMed]
- Chen, C.C.; Wan, Y.L.; Wai, Y.Y.; Liu, H.L. Quality assurance of clinical MRI scanners using ACR MRI phantom: Preliminary results. J. Digit. Imaging 2004, 17, 279–284. [Google Scholar] [CrossRef] [PubMed]
- Alaya, I.B.; Mars, M. Automatic Analysis of ACR Phantom Images in MRI. Curr. Med. Imaging 2020, 16, 892–901. [Google Scholar] [CrossRef]
- Jhonata, E.; Ramos, H.Y.K.; Tancredi, F.B. Automation of the ACR MRI Low-Contrast Resolution Test Using Machine Learning. In Proceedings of the 2018 11th International Congress on Image and Signal Processing, BioMedical Engineering and Informatics (CISP-BMEI 2018), Beijing, China, 13–15 October 2018. [Google Scholar]
- Sun, J.; Barnes, M.; Dowling, J.; Menk, F.; Stanwell, P.; Greer, P.B. An open source automatic quality assurance (OSAQA) tool for the ACR MRI phantom. Australas. Phys. Eng. Sci. Med. 2015, 38, 39–46. [Google Scholar] [CrossRef] [PubMed]
- Epistatou, A.C.; Tsalafoutas, I.A.; Delibasis, K.K. An Automated Method for Quality Control in MRI Systems: Methods and Considerations. J. Imaging 2020, 6, 111. [Google Scholar] [CrossRef]
- Alfano, B.; Comerci, M.; Larobina, M.; Prinster, A.; Hornak, J.P.; Selvan, S.E.; Amato, U.; Quarantelli, M.; Tedeschi, G.; Brunetti, A.; et al. An MRI digital brain phantom for validation of segmentation methods. Med. Image Anal. 2011, 15, 329–339. [Google Scholar] [CrossRef]
- Collins, D.L.; Zijdenbos, A.P.; Kollokian, V.; Sled, J.G.; Kabani, N.J.; Holmes, C.J.; Evans, A.C. Design and construction of a realistic digital brain phantom. IEEE Trans. Med. Imaging 1998, 17, 463–468. [Google Scholar] [CrossRef]
- Wulkerr, C.; Gessert, N.T.; Doneva, M.; Kastryulin, S.; Ercan, E.; Nielsen, T. Digital reference objects for evaluating algorithm performance in MR image formation. Magn. Reson. Imaging 2023, 105, 67–74. [Google Scholar] [CrossRef] [PubMed]
- Mohan, S.; Kadkhodaie, Z.; Simoncelli, E.P.; Fernandez-Granda, C. Robust and interpretable blind image denoising via bias-free convolutional neural networks. arXiv 2019, arXiv:1906.05478. [Google Scholar] [CrossRef]
- National Electrical Manufacturers Association. NEMA Standards Publication MS 3-2008 (R2014, R2020): Determination of Image Uniformity in Diagnostic Magnetic Resonance Images; NEMA: Rosslyn, VA, USA, 2021. [Google Scholar]
- National Electrical Manufacturers Association. NEMA Standards Publication MS 6-2008 (R2014, R2020): Determination of Signal-to-Noise Ratio and Image Uniformity for Single-Channel Non-Volume Coils in Diagnostic MR Imaging; NEMA: Rosslyn, VA, USA, 2021. [Google Scholar]
- John Eng, M. Sample Size Estimation: How Many Individuals Should Be Studied? Radiology 2003, 227, 309–313. [Google Scholar] [CrossRef] [PubMed]
- Richard, S.; Husarik, D.B.; Yadava, G.; Murphy, S.N.; Samei, E. Towards task-based assessment of CT performance: System and object MTF across different reconstruction algorithms. Med. Phys. 2012, 39, 4115–4122. [Google Scholar] [CrossRef] [PubMed]
- Bazin, P.L.; Nijsse, H.E.; van der Zwaag, W.; Gallichan, D.; Alkemade, A.; Vos, F.M.; Forstmann, B.U.; Caan, M.W.A. Sharpness in motion corrected quantitative imaging at 7T. Neuroimage 2020, 222, 117227. [Google Scholar] [CrossRef] [PubMed]
- Reeder, S.B.; Wintersperger, B.J.; Dietrich, O.; Lanz, T.; Greiser, A.; Reiser, M.F.; Glazer, G.M.; Schoenberg, S.O. Practical approaches to the evaluation of signal-to-noise ratio performance with parallel imaging: Application with cardiac imaging and a 32-channel cardiac coil. Magn. Reson. Med. 2005, 54, 748–754. [Google Scholar] [CrossRef]
- Otsu, N. A Threshold Selection Method from Gray-Level Histograms. IEEE Trans. SMC 1979, 9, 62–66. [Google Scholar] [CrossRef]
- Dufour, R.M.; Miller, E.L.; Galatsanos, N.P. Template matching based object recognition with unknown geometric parameters. IEEE Trans. Image Process. 2002, 11, 1385–1396. [Google Scholar] [CrossRef] [PubMed]
- Koonjoo, N.; Zhu, B.; Bagnall, G.C.; Bhutto, D.; Rosen, M.S. Boosting the signal-to-noise of low-field MRI with deep learning image reconstruction. Sci. Rep. 2021, 11, 8248. [Google Scholar] [CrossRef]
- Lyu, M.; Mei, L.; Huang, S.; Liu, S.; Li, Y.; Yang, K.; Liu, Y.; Dong, Y.; Dong, L.; Wu, E.X. M4Raw: A multi-contrast, multi-repetition, multi-channel MRI k-space dataset for low-field MRI research. Sci. Data 2023, 10, 264. [Google Scholar] [CrossRef]
- Knoll, F.; Zbontar, J.; Sriram, A.; Muckley, M.J.; Bruno, M.; Defazio, A.; Parente, M.; Geras, K.J.; Katsnelson, J.; Chandarana, H.; et al. fastMRI: A Publicly Available Raw k-Space and DICOM Dataset of Knee Images for Accelerated MR Image Reconstruction Using Machine Learning. Radiol. Artif. Intell. 2020, 2, e190007. [Google Scholar] [CrossRef] [PubMed]
- Muckley, M.J.; Riemenschneider, B.; Radmanesh, A.; Kim, S.; Jeong, G.; Ko, J.; Jun, Y.; Shin, H.; Hwang, D.; Mostapha, M.; et al. Results of the 2020 fastMRI Challenge for Machine Learning MR Image Reconstruction. IEEE Trans. Med. Imaging 2021, 40, 2306–2317. [Google Scholar] [CrossRef] [PubMed]
- Yang, G.; Yu, S.; Dong, H.; Slabaugh, G.; Dragotti, P.L.; Ye, X.; Liu, F.; Arridge, S.; Keegan, J.; Guo, Y.; et al. DAGAN: Deep De-Aliasing Generative Adversarial Networks for Fast Compressed Sensing MRI Reconstruction. IEEE Trans. Med. Imaging 2018, 37, 1310–1321. [Google Scholar] [CrossRef] [PubMed]
- Sriram, A.; Zbontar, J.; Murrell, T.; Defazio, A.; Zitnick, C.L.; Yakubova, N.; Knoll, F.; Jonhson, P. End-to-End Variational Networks for Accelerated MRI Reconstruction. arXiv 2020, arXiv:2004.06688. [Google Scholar]
- Eo, T.; Jun, Y.; Kim, T.; Jang, J.; Lee, H.J.; Hwang, D. KIKI-net: Cross-domain convolutional neural networks for reconstructing undersampled magnetic resonance images. Magn. Reson. Med. 2018, 80, 2188–2201. [Google Scholar] [CrossRef] [PubMed]
- Solomon, J.; Samei, E. Correlation between human detection accuracy and observer model-based image quality metrics in computed tomography. J. Med. Imaging 2016, 3, 035506. [Google Scholar] [CrossRef] [PubMed]
- Leng, S.; Yu, L.; Zhang, Y.; Carter, R.; Toledano, A.Y.; McCollough, C.H. Correlation between model observer and human observer performance in CT imaging when lesion location is uncertain. Med. Phys. 2013, 40, 081908. [Google Scholar] [CrossRef]
- O’Neill, A.G.; Lingala, S.G.; Pineda, A.R. Predicting human detection performance in magnetic resonance imaging (MRI) with total variation and wavelet sparsity regularizers. Proc. SPIE Int. Soc. Opt. Eng. 2022, 12035. [Google Scholar] [CrossRef]


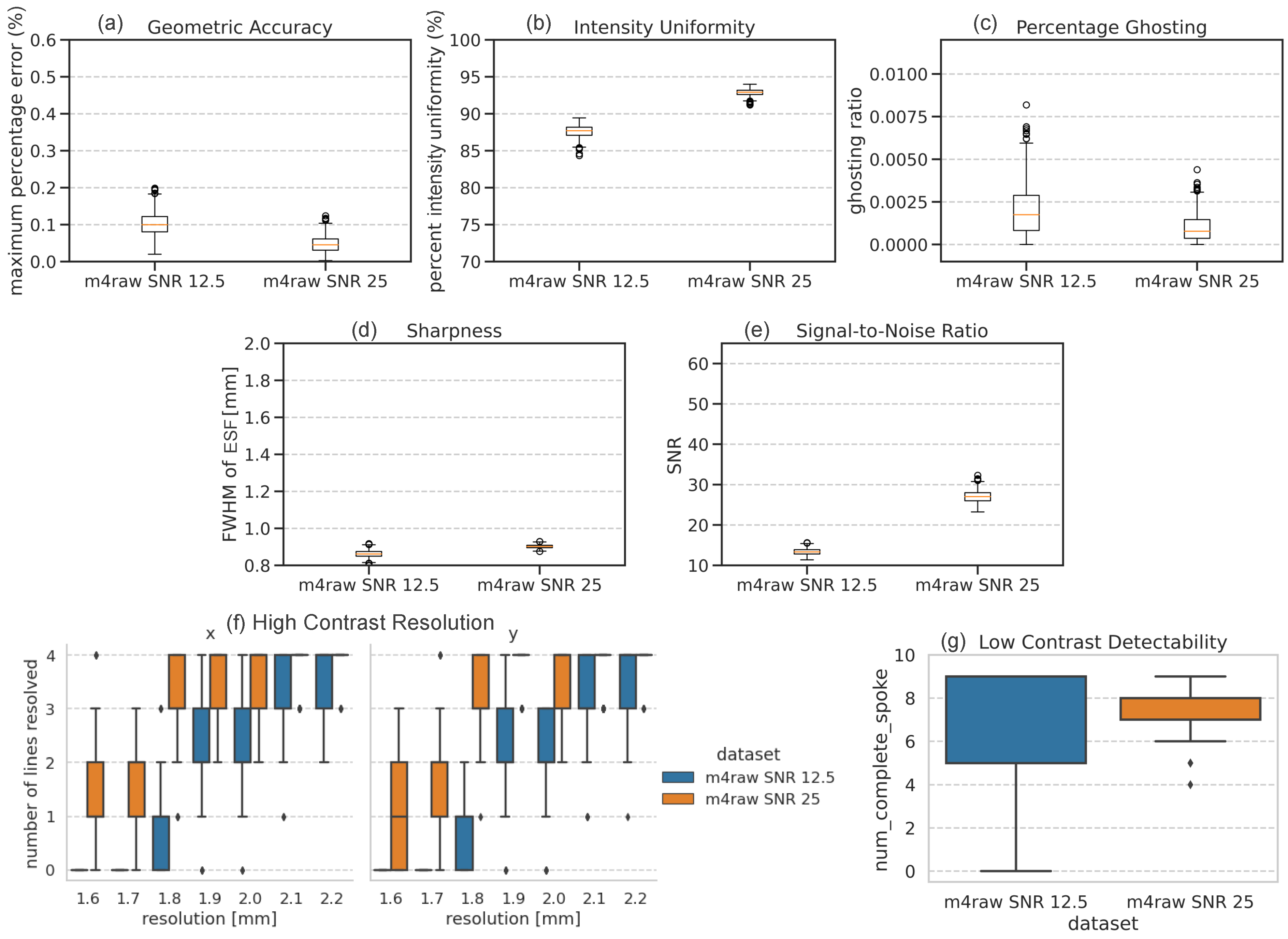

| Training Set | Test Set SNR | Geometric Accuracy (%) | Intensity Uniformity (%) | Ghosting Ratio * | Sharpness [mm] | SNR | Low-Contrast Detectability |
|---|---|---|---|---|---|---|---|
| M4Raw 1× | 12.5 | 0.10 ± 0.03 | 87.6 ± 0.8 | 0.002 ± 0.002 | 0.86 ± 0.02 ** | 13.4 ± 0.8 | 7.0 ± 2.6 |
| 25 | 0.05 ± 0.02 | 92.9 ± 0.5 | 0.001 ± 0.001 | 0.90 ± 0.01 | 27.1 ± 1.6 | 7.1 ± 0.9 | |
| M4Raw 2× | 12.5 | 0.29 ± 0.06 | 80.6 ± 2.2 | 0.003 ± 0.002 | 1.26 ± 0.06 | 14.4 ± 1.8 | 3.6 ± 2.5 |
| 25 | 0.21 ± 0.05 | 87.0 ± 1.5 | 0.002 ± 0.001 | 1.23 ± 0.05 | 29.5 ± 4.0 | 3.3 ± 1.3 | |
| FastMRI 1× | 12.5 | 0.21 ± 0.03 | 83.1 ± 1.3 | 0.005 ± 0.003 | 1.10 ± 0.02 | 19.7 ± 2.1 | 1.5 ± 1.7 |
| 25 | 0.17 ± 0.03 | 89.0 ± 0.8 | 0.004 ± 0.001 | 1.09 ± 0.01 | 45.7 ± 4.7 | 1.4 ± 1.2 | |
| FastMRI 2× | 12.5 | 0.37 ± 0.07 | 79.1 ± 2.2 | 0.004 ± 0.003 | 1.65 ± 0.06 | 23.2 ± 3.4 | 1.2 ± 1.2 |
| 25 | 0.32 ± 0.05 | 85.1 ± 1.5 | 0.004 ± 0.002 | 1.64 ± 0.05 | 48.1 ± 7.2 | 0.8 ± 0.6 | |
| Reference (iFFT) | 12.5 | 0.09 ± 0.03 | 88.9 ± 0.7 | 0.002 ± 0.001 | 0.91 ± 0.02 | 12.6 ± 0.7 | 8.0 ± 1.9 |
| 25 | 0.04 ± 0.02 | 94.5 ± 0.3 | 0.001 ± 0.001 | 0.95 ± 0.01 | 25.2 ± 1.4 | 7.6 ± 0.7 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tan, F.; Delfino, J.G.; Zeng, R. Evaluating Machine Learning-Based MRI Reconstruction Using Digital Image Quality Phantoms. Bioengineering 2024, 11, 614. https://doi.org/10.3390/bioengineering11060614
Tan F, Delfino JG, Zeng R. Evaluating Machine Learning-Based MRI Reconstruction Using Digital Image Quality Phantoms. Bioengineering. 2024; 11(6):614. https://doi.org/10.3390/bioengineering11060614
Chicago/Turabian StyleTan, Fei, Jana G. Delfino, and Rongping Zeng. 2024. "Evaluating Machine Learning-Based MRI Reconstruction Using Digital Image Quality Phantoms" Bioengineering 11, no. 6: 614. https://doi.org/10.3390/bioengineering11060614
APA StyleTan, F., Delfino, J. G., & Zeng, R. (2024). Evaluating Machine Learning-Based MRI Reconstruction Using Digital Image Quality Phantoms. Bioengineering, 11(6), 614. https://doi.org/10.3390/bioengineering11060614





