The Effect of the TiO2 Anodization Layer in Pedicle Screw Conductivity: An Analytical, Numerical, and Experimental Approach
Abstract
1. Introduction
2. Materials and Methods
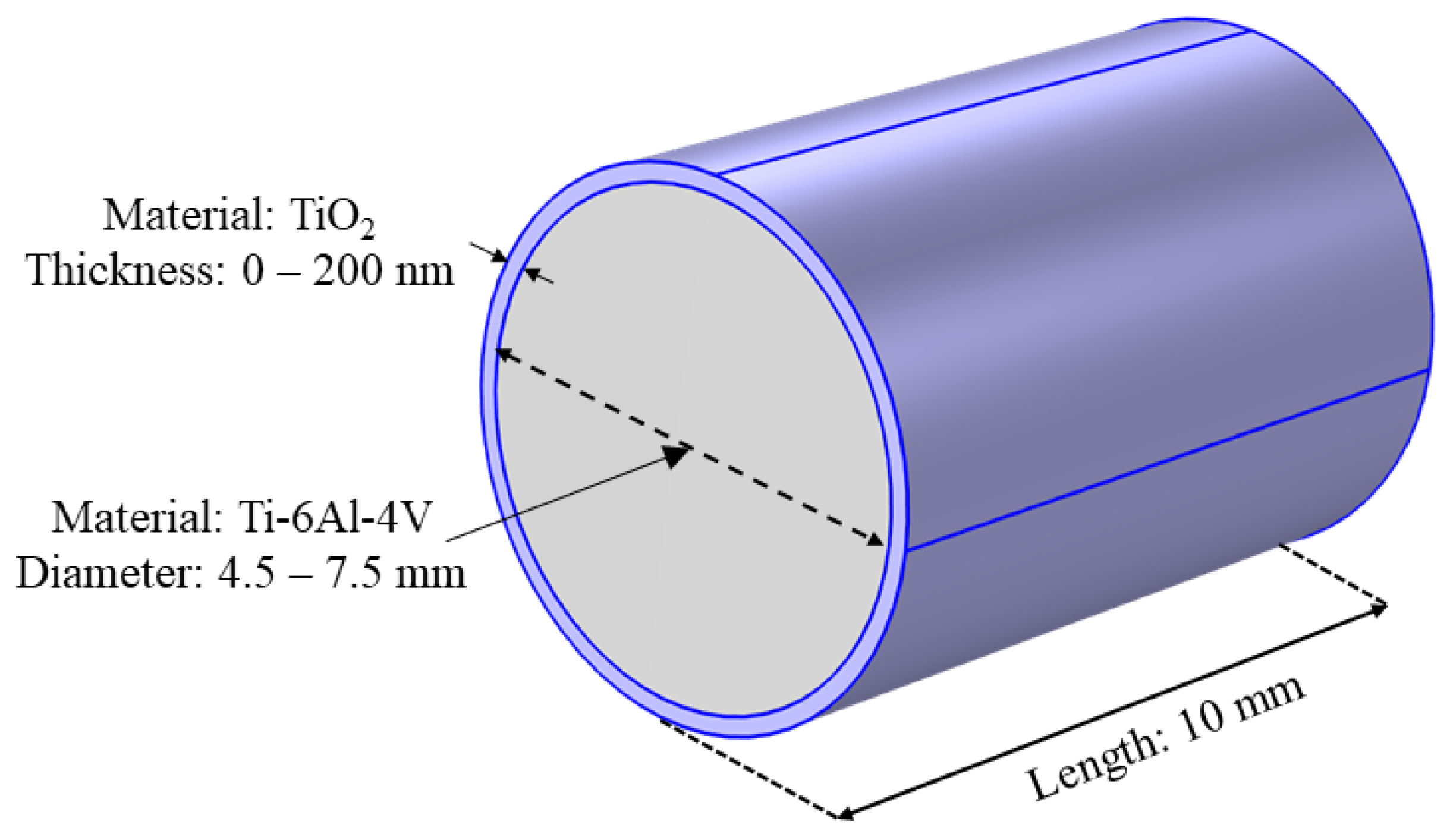
2.1. Analytical Approach
2.2. Numerical Approach
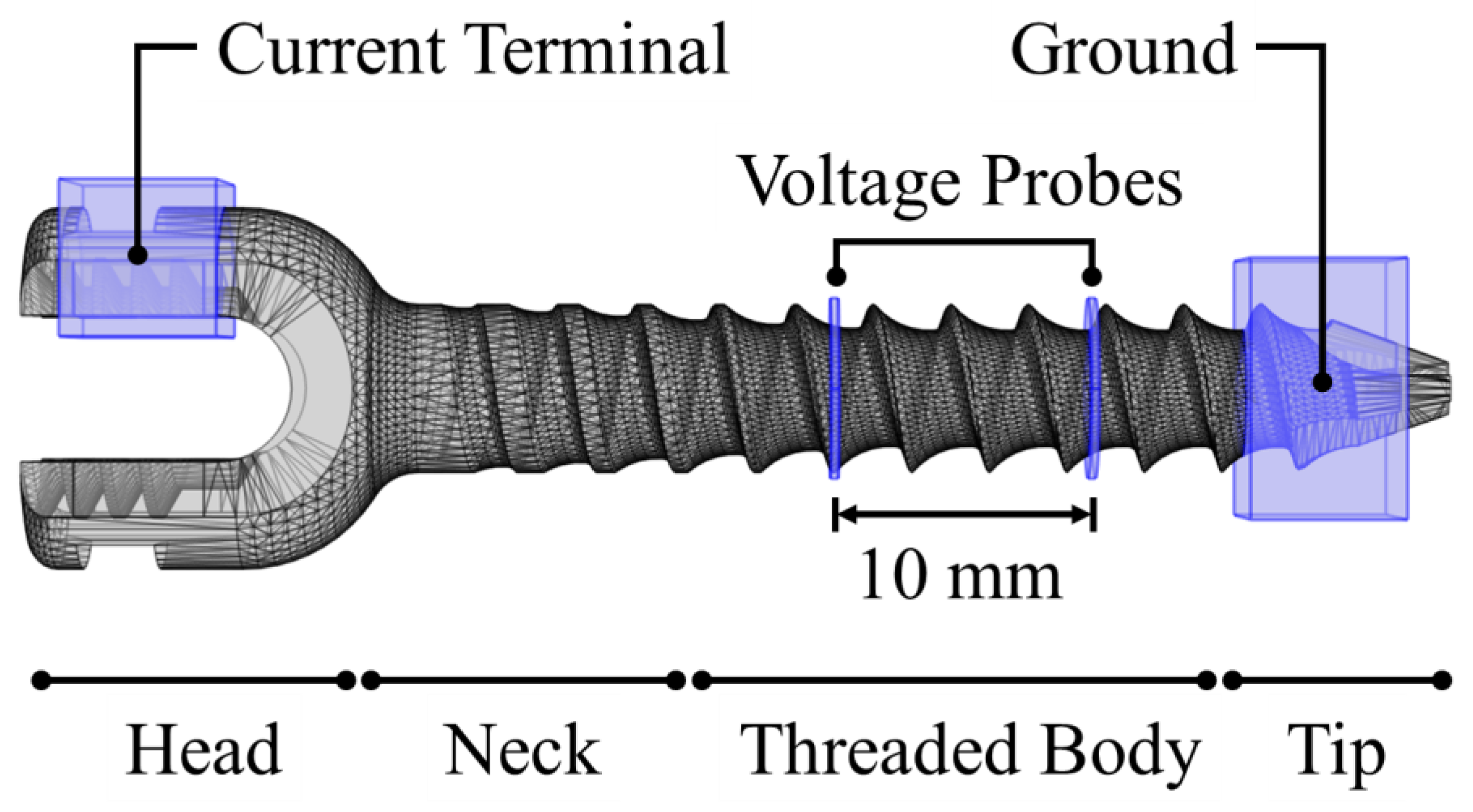
2.3. Experimental Approach
2.4. Statistical Analysis
3. Results
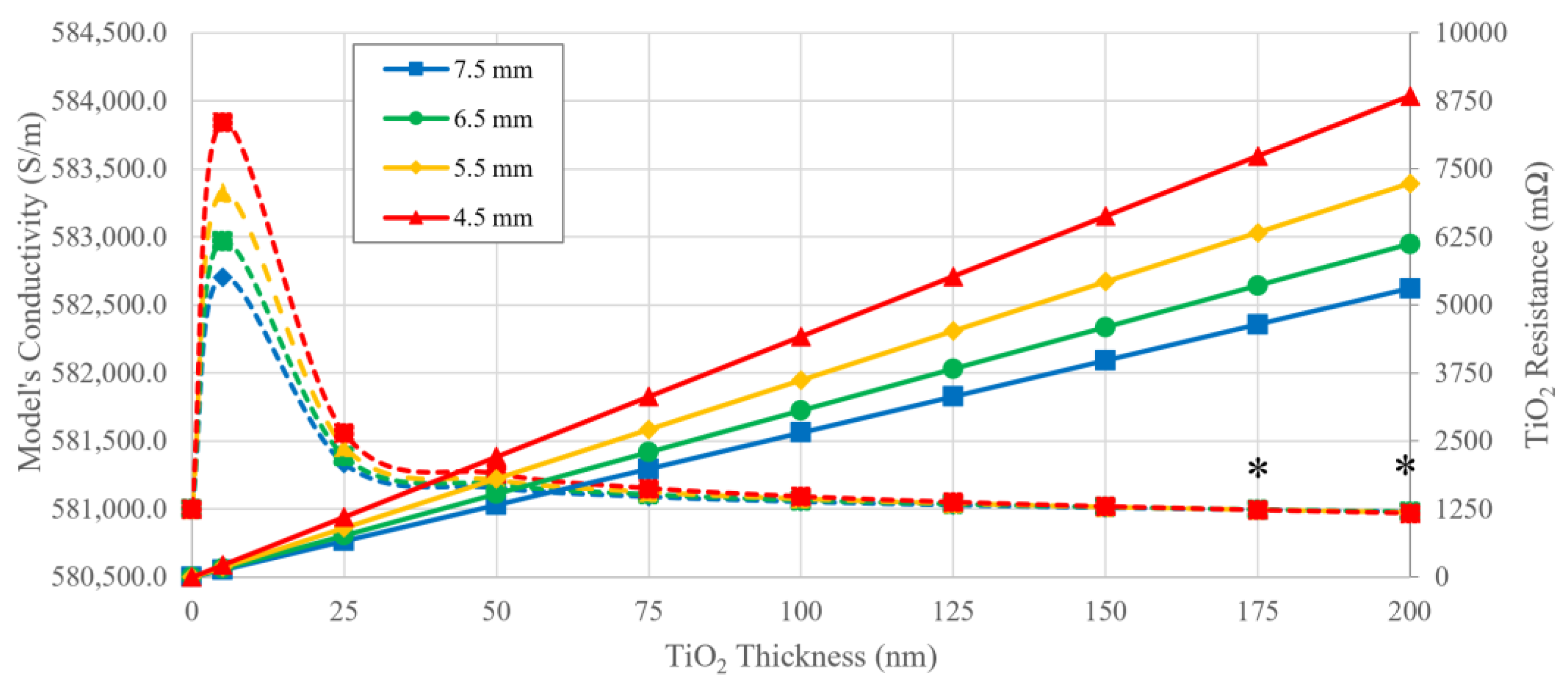
3.1. Analytical Approach
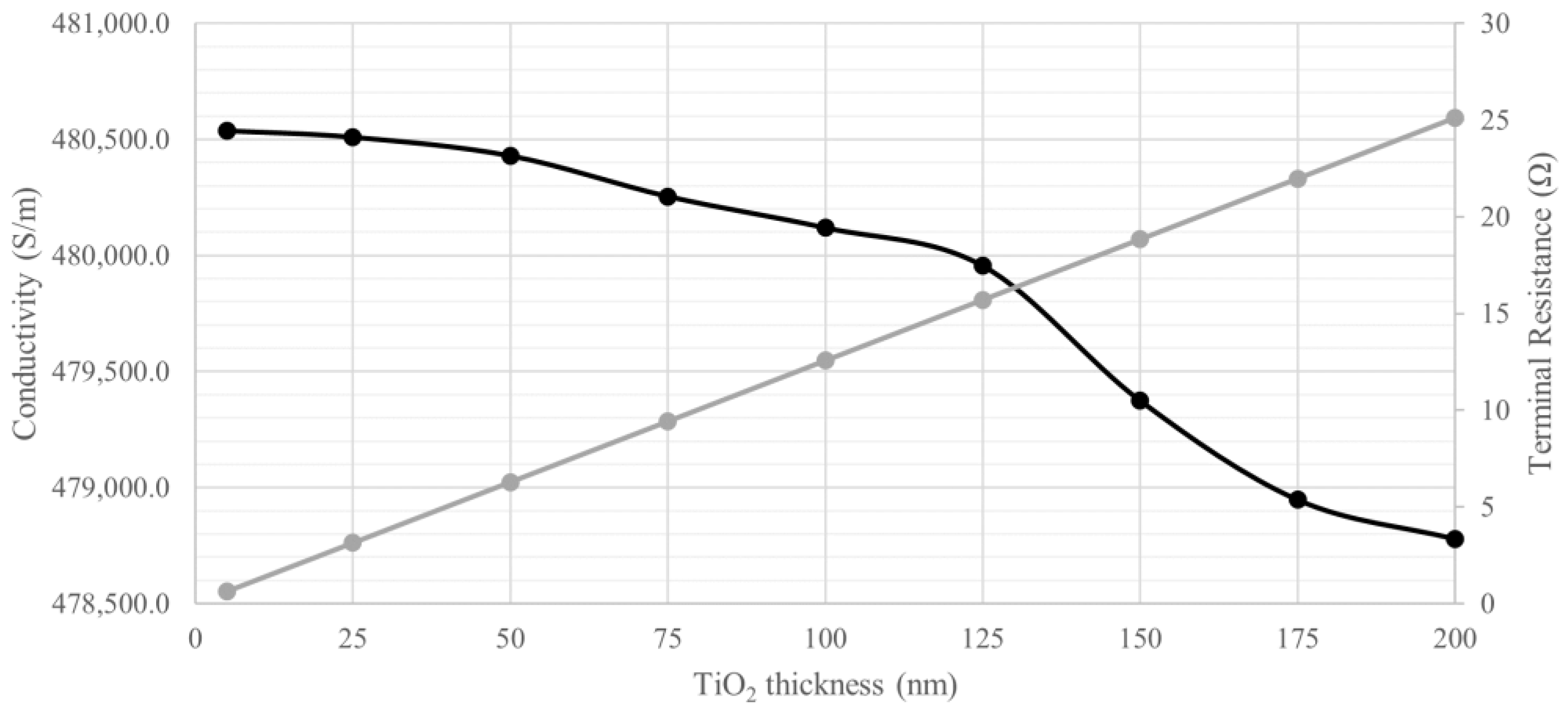
3.2. Numerical Approach
3.3. Experimental Approach
4. Discussion
4.1. Analytical Approach
4.2. Numerical Approach
4.3. Experimental Approach
4.4. Practical Implications
4.5. Limitations
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Basu, S.; Gohil, K. Intraoperative Neuromonitoring in Spine Surgery: Does it Reduce Neural Complications? Current Evidence. Indian. Spine J. 2023, 6, 15. [Google Scholar]
- Calancie, B.; Lebwohl, N.; Madsen, P.; Klose, K.J. Intraoperative evoked EMG monitoring in an animal model. A new technique for evaluating pedicle screw placement. Spine 1992, 17, 1229–1235. [Google Scholar] [CrossRef] [PubMed]
- Calancie, B.; Madsen, P.; Lebwohl, N. Stimulus-Evoked EMG Monitoring During Transpedicular Lumbosacral Spine Instrumentation: Initial Clinical Results. Spine 1994, 19, 2780–2786. [Google Scholar] [CrossRef] [PubMed]
- Donohue, M.L.; Swaminathan, V.; Gilbert, J.L.; Fox, C.W.; Smale, J.; Moquin, R.R.; Calancie, B. Intraoperative neuromonitoring: Can the results of direct stimulation of titanium-alloy pedicle screws in the thoracic spine be trusted? J. Clin. Neurophysiol. 2012, 29, 502–508. [Google Scholar] [CrossRef] [PubMed]
- Fonseca, P.; Goethel, M.; Vilas-Boas, J.P.; Gutierres, M.; Correia, M.V. A systematic review with meta-analysis of the diagnostic test accuracy of pedicle screw electrical stimulation. Eur. Spine J. 2022, 31, 1599–1610. [Google Scholar] [CrossRef] [PubMed]
- Anderson, D.G.; Wierzbowski, L.R.; Schwartz, D.M.; Hilibrand, A.S.; Vaccaro, A.R.; Albert, T.J. Pedicle screws with high electrical resistance: A potential source of error with stimulus-evoked EMG. Spine 2002, 27, 1577–1581. [Google Scholar] [CrossRef] [PubMed]
- Fonseca, P.; Goethel, M.F.; Sebastião, R.; Sousa, M.V.; Vilas-Boas, J.P.; Correia, M.V.; Gutierres, M. A New Coupling Method for Accurate Measurement of Pedicle Screw Electrical Properties for Surgical Procedures. Appl. Sci. 2021, 11, 9861. [Google Scholar] [CrossRef]
- Limthongkul, W.; Savage, J.; Nenonene, E.K.; Karaikovic, E.E. Evaluation of the intrinsic properties of pedicle screws: Do diameter, manufacturing and screw design affect resistance and/or resistivity. Bosn. J. Basic. Med. Sci. 2009, 9 (Suppl. 1), S77–S82. [Google Scholar] [CrossRef]
- Norton, J.; Kindrachuk, M.; Fourney, D.R. Considering Pedicle Screw Resistance in Electromyography of the Spine. Oper. Neurosurg. 2020, 20, 69–73. [Google Scholar] [CrossRef]
- Davis, S.; Walsh, J.P.; Crosby, S.; Kabins, M.; Weyand, T.; Lee, D. The effect of hydroxyapatite on titanium pedicle screw resistance: An electrical model. Spine J. 2022, 22, 869–876. [Google Scholar] [CrossRef]
- Davis, T.T.; Tadlock, S.; Bernbeck, J.; Fung, D.A.; Molinares, D.M. Can triggered electromyography be used to evaluate pedicle screw placement in hydroxyapatite-coated screws: An electrical examination. J. Clin. Neurophysiol. 2014, 31, 138–142. [Google Scholar] [CrossRef]
- Diamanti, M.V.; Del Curto, B.; Pedeferri, M. Anodic Oxidation of Titanium: From Technical Aspects to Biomedical Applications. J. Appl. Biomater. Biomech. 2011, 9, 55–69. [Google Scholar] [CrossRef]
- Prando, D.; Brenna, A.; Diamanti, M.V.; Beretta, S.; Bolzoni, F.; Ormellese, M.; Pedeferri, M. Corrosion of titanium: Part 2: Effects of surface treatments. J. Appl. Biomater. Funct. Mater. 2018, 16, 3–13. [Google Scholar] [CrossRef] [PubMed]
- Zaniolo, K.M.; Biaggio, S.R.; Bocchi, N.; Rocha-Filho, R.C. Properties of colored oxide films formed electrochemically on titanium in green electrolytes under ultrasonic stirring. J. Mater. Sci. 2018, 53, 7294–7304. [Google Scholar] [CrossRef]
- Yan, Z.M.; Guo, T.W.; Pan, H.; Yu, J.J. Influences of Electrolyzing Voltage on Chromatics of Anodized Titanium Dentures. Mater. Trans. 2002, 43, 3142–3145. [Google Scholar] [CrossRef][Green Version]
- Diamanti, M.V.; Pozzi, P.; Randone, F.; Del Curto, B.; Pedeferri, M. Robust anodic colouring of titanium: Effect of electrolyte and colour durability. Mater. Des. 2016, 90, 1085–1091. [Google Scholar] [CrossRef]
- Ross, A.P.; Webster, T.J. Anodizing color coded anodized Ti6Al4V medical devices for increasing bone cell functions. Int. J. Nanomed. 2013, 8, 109–117. [Google Scholar] [CrossRef] [PubMed]
- Ju, Y.; Wang, M.; Wang, Y.; Wang, S.; Fu, C. Electrical Properties of Amorphous Titanium Oxide Thin Films for Bolometric Application. Adv. Condens. Matter Phys. 2013, 2013, 365475. [Google Scholar] [CrossRef]
- Ibach, H.; Lüth, H. The Electrical Conductivity of Metals. In Solid-State Physics: An Introduction to Principles of Materials Science, 4th ed.; Ibach, H., Lüth, H., Eds.; Springer: Berlin/Heidelberg, Germany, 2009; pp. 255–261. [Google Scholar]
- Stephen, L. Titanium Dioxide Versatile Solid Crystalline: An Overview. In Assorted Dimensional Reconfigurable Materials; Dongre, R.P., Dilip, R., Eds.; IntechOpen: Rijeka, Croatia, 2020. [Google Scholar]
- Lin, Y.-J.; Yang, S.-H. Carrier transport and photoresponse for heterojunction diodes based on the reduced graphene oxide-based TiO2 composite and p-type Si. Appl. Phys. A 2014, 116, 91–95. [Google Scholar] [CrossRef]
- Bak, T.; Nowotny, J.; Rekas, M.; Sorrell, C.C. Defect chemistry and semiconducting properties of titanium dioxide: III. Mobility of electronic charge carriers. J. Phys. Chem. Solids 2003, 64, 1069–1087. [Google Scholar] [CrossRef]
- ABNT NBR 15408-2:2020; Implantes para Cirurgia—Passivação de Titânio e de Ligas de Titânio por Revestimento Eletrolítico. Parte 2: Tratamento Anódico em Solução com pH Inferior a 13. Associação Brasileira de Normas Técnicas: Rio de Janeiro, Brazil, 2020.
- Sarah, M.S.P.; Musa, M.Z.; Asiah, M.N.; Rusop, M. Electrical conductivity characteristics of TiO2 thin film. In Proceedings of the 2010 International Conference on Electronic Devices, Systems and Applications, Kuala Lumpur, Malaysia, 11–14 April 2010; pp. 361–364. [Google Scholar]
- Rådegran, G.; Lausmaa, J.; Mattsson, L.; Rolander, U.; Kasemo, B. Preparation of ultra-thin oxide windows on titanium for tem analysis. J. Electron. Microsc. Technol. 1991, 19, 99–106. [Google Scholar] [CrossRef] [PubMed]
- Nunez, P.; Richter, M.H.; Piercy, B.D.; Roske, C.W.; Cabán-Acevedo, M.; Losego, M.D.; Konezny, S.J.; Fermin, D.J.; Hu, S.; Brunschwig, B.S.; et al. Characterization of Electronic Transport through Amorphous TiO2 Produced by Atomic Layer Deposition. J. Phys. Chem. C 2019, 123, 20116–20129. [Google Scholar] [CrossRef]
- Ohtsuka, T.; Guo, J.; Sato, N. Raman Spectra of the Anodic Oxide Film on Titanium in Acidic Sulfate and Neutral Phosphate Solutions. J. Electrochem. Soc. 1986, 133, 2473. [Google Scholar] [CrossRef]
- Gomez Sanchez, A.; Schreiner, W.; Duffó, G.; Ceré, S. Surface modification of titanium by anodic oxidation in phosphoric acid at low potentials. Part 1. Structure, electronic properties and thickness of the anodic films. Surf. Interface Anal. 2013, 45, 1037–1046. [Google Scholar] [CrossRef]
- Gilani, T.H.; Rabchuk, D. Electrical resistivity of gold thin film as a function of film thickness. Can. J. Phys. 2018, 96, 272–274. [Google Scholar] [CrossRef]
- Lacy, F. Developing a theoretical relationship between electrical resistivity, temperature, and film thickness for conductors. Nanoscale Res. Lett. 2011, 6, 636. [Google Scholar] [CrossRef]
- Edwin, A. Thin Films/Properties and Applications. In Thin Films; Alicia Esther, A., Ed.; IntechOpen: Rijeka, Croatia, 2021; Chapter 1. [Google Scholar]
- Sellers, M.C.K.; Seebauer, E.G. Measurement method for carrier concentration in TiO2 via the Mott–Schottky approach. Thin Solid Films 2011, 519, 2103–2110. [Google Scholar] [CrossRef]
- Sun, H.; Xu, Z.-t.; Zhang, D. First-principles calculations to investigate doping effects on electrical conductivity and interfacial contact resistance of TiO2. Appl. Surf. Sci. 2023, 614, 156202. [Google Scholar] [CrossRef]
- Chanda, M. (Ed.) Electrical, Electronic and Optical Properties. In Science of Engineering Materials: Volume 3 Engineering Properties; Macmillan Education UK: London, UK, 1980; pp. 61–126. [Google Scholar]
- Prasad, K.; Bally, A.R.; Schmid, P.E.; Lévy, F.; Benoit, J.; Barthou, C.; Benalloul, P. Ce-doped TiO2 Insulators in Thin Film Electroluminescent Devices. Jpn. J. Appl. Phys. 1997, 36, 5696. [Google Scholar] [CrossRef]
- Leonard, W.F.; Lin, S.F. The validity of Matthiessen’s rule for metallic films. Thin Solid Films 1975, 28, L9–L12. [Google Scholar] [CrossRef]
- Policastro, S.A.; Anderson, R.M.; Hangarter, C.M.; Arcari, A.; Iezzi, E.B. Incorporating Physics-Based Models into Equivalent Circuit Analysis of EIS Data from Organic Coatings. Coatings 2023, 13, 1285. [Google Scholar] [CrossRef]
- Gudić, S.; Vrsalović, L.; Kvrgić, D.; Nagode, A. Electrochemical Behaviour of Ti and Ti-6Al-4V Alloy in Phosphate Buffered Saline Solution. Materials 2021, 14, 7495. [Google Scholar] [CrossRef] [PubMed]
- Tsao, B.H.; Carr, S.F.; Weimer, J.A. Ultra-thin TiO2 dielectric film for high capacitance capacitor. AIP Conf. Proc. 1995, 324, 117–122. [Google Scholar] [CrossRef]
- Wang, H.; Liao, X.; Ma, X.; Li, C.; Han, J.; Zhou, Y. Solid and hollow pedicle screws affect the electrical resistance: A potential source of error with stimulus-evoked electromyography. Indian J. Orthop. 2013, 47, 352–356. [Google Scholar] [CrossRef] [PubMed]
- Han, S.; Yu, J.L.; Lee, S.Y. Optical and Electrical Properties of Oxide Multilayers. Trans. Electr. Electron. Mater. 2016, 17, 235–237. [Google Scholar] [CrossRef]
- Zhou, J.; Wu, Z.; Liu, Z. Optical and electrical properties of TiO2/Au/TiO2 multilayer coatings in large area deposition at room temperature. Rare Met. 2008, 27, 457–462. [Google Scholar] [CrossRef]
- Sharma, A.K. Anodizing titanium for space applications. Thin Solid Films 1992, 208, 48–54. [Google Scholar] [CrossRef]
- Benea, L.; Simionescu-Bogatu, N. Reactivity and Corrosion Behaviors of Ti6Al4V Alloy Implant Biomaterial under Metabolic Perturbation Conditions in Physiological Solutions. Materials 2021, 14, 7404. [Google Scholar] [CrossRef]
 |  |  |  |  |  |  |  | ||
|---|---|---|---|---|---|---|---|---|---|
| Group I | Group II | Group III | Group IV | ||||||
| Name | DB1 | DB2 | DB3 | SB | BG1 | BG2 | BG3 | DG | |
| Anodization Voltage (V) | 15 | 35 | 60 | 75 | |||||
| Theoretical TiO2 thickness (nm) | 30 | 75 | 120 | 150 | |||||
| Nominal Diameter (mm) | 6.5 | 4.5 | 5.5 | 7.5 | |||||
| Cross-sectional Area (mm2) | 24.50 | 11.74 | 17.54 | 32.61 | |||||
| Head-to-tip length (mm) | 60 | 55 | 45 | 50 | 55 | 50 | 45 | 55 | |
| Thread length (mm) | 45 | 40 | 30 | 35 | 40 | 35 | 30 | 40 | |
| TiO2 Thickness (nm) | Terminal Voltage (mV) | Terminal Resistance (mΩ) | Section Resistance (mΩ) | Calculated Conductivity (S/m) |
|---|---|---|---|---|
| 0 | 0.03 | 2.58 | 0.8405 | 485,615 |
| 5 | 6.31 | 630 | 0.8494 | 480,537 |
| 25 | 31.4 | 3140 | 0.8494 | 480,509 |
| 50 | 62.8 | 6280 | 0.8496 | 480,429 |
| 75 | 94.2 | 9420 | 0.8499 | 480,254 |
| 100 | 125.6 | 12,560 | 0.8501 | 480,119 |
| 125 | 157.0 | 15,700 | 0.8504 | 479,955 |
| 150 | 188.3 | 18,830 | 0.8515 | 479,374 |
| 175 | 219.7 | 21,970 | 0.8522 | 478,947 |
| 200 | 251.1 | 25,110 | 0.8525 | 478,778 |
| Group | Screw | Total Resistance (mΩ) | Section Parameters | Screw Results | Group Results | ||||
|---|---|---|---|---|---|---|---|---|---|
| Cross-Sectional Area (mm2) | Effective Lead Distance (mm) | Resistance (mΩ) | Calculated Conductivity (MS/m) | 95% CI | Calculated Conductivity (MS/m) | 95% CI (MS/m) | |||
| I | DB1 | 62.6 ± 2.1 | 24.50 | 10.19 | 0.74 ± 0.05 | 0.564 ± 0.041 | [0.564; 0.565] | 0.556 ± 0.037 2,3,4 | [0.555; 0.557] |
| DB2 | 48.4 ± 4.8 | 10.84 | 0.82 ± 0.05 | 0.540 ± 0.030 * | [0.539; 0.540] | ||||
| DB3 | 17.4 ± 1.1 | 10.19 | 0.74 ± 0.06 | 0.564 ± 0.041 | [0.563; 0.564] | ||||
| II | SB | 73.4 ± 3.0 | 11.74 | 10.04 | 1.56 ± 0.05 | 0.549 ± 0.019 | [0.548; 0.549] | 0.549 ± 0.019 1,3,4 | [0.548; 0.550] |
| III | BG1 | 239.2 ± 1.9 | 17.54 | 9.41 | 1.04 ± 0.05 | 0.517 ± 0.026 * | [0.517; 0.518] | 0.533 ± 0.026 1,2,4 | [0.532; 0.533] |
| BG2 | 119.6 ± 1.9 | 12.10 | 1.30 ± 0.00 | 0.531 ± 0.001 * | [0.530; 0.532] | ||||
| BG3 | 59.6 ± 2.1 | 9.22 | 0.96 ± 0.05 | 0.549 ± 0.032 * | [0.548; 0.550] | ||||
| IV | DG | 259.4 ± 3.6 | 32.61 | 9.64 | 0.60 ± 0.00 | 0.492 ± 0.000 | [0.492; 0.493] | 0.492 ± 0.000 1,2,3 | [0.492; 0.493] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fonseca, P.; Goethel, M.F.; Vilas-Boas, J.P.; Gutierres, M.; Correia, M.V. The Effect of the TiO2 Anodization Layer in Pedicle Screw Conductivity: An Analytical, Numerical, and Experimental Approach. Bioengineering 2024, 11, 634. https://doi.org/10.3390/bioengineering11070634
Fonseca P, Goethel MF, Vilas-Boas JP, Gutierres M, Correia MV. The Effect of the TiO2 Anodization Layer in Pedicle Screw Conductivity: An Analytical, Numerical, and Experimental Approach. Bioengineering. 2024; 11(7):634. https://doi.org/10.3390/bioengineering11070634
Chicago/Turabian StyleFonseca, Pedro, Márcio Fagundes Goethel, João Paulo Vilas-Boas, Manuel Gutierres, and Miguel Velhote Correia. 2024. "The Effect of the TiO2 Anodization Layer in Pedicle Screw Conductivity: An Analytical, Numerical, and Experimental Approach" Bioengineering 11, no. 7: 634. https://doi.org/10.3390/bioengineering11070634
APA StyleFonseca, P., Goethel, M. F., Vilas-Boas, J. P., Gutierres, M., & Correia, M. V. (2024). The Effect of the TiO2 Anodization Layer in Pedicle Screw Conductivity: An Analytical, Numerical, and Experimental Approach. Bioengineering, 11(7), 634. https://doi.org/10.3390/bioengineering11070634








