Numerical Simulation of Thermal Therapy for Melanoma in Mice
Abstract
1. Introduction
2. Materials and Models
2.1. Digital Mouse Model
2.2. Helmholtz Coil Model
3. Principles and Methods
3.1. Introduction to the Software
- Regional discretization or sub-domain delineation;
- An interpolating function that approximates the unknown solution in a cell;
- Establish unit equations and introduce boundary conditions to form a system of equations;
- Solve the system of equations.
3.2. Principles of Magnetic Induction Hyperthermia
3.3. Principle Verification
4. Results and Analysis
4.1. Electromagnetic Field Distribution in Space
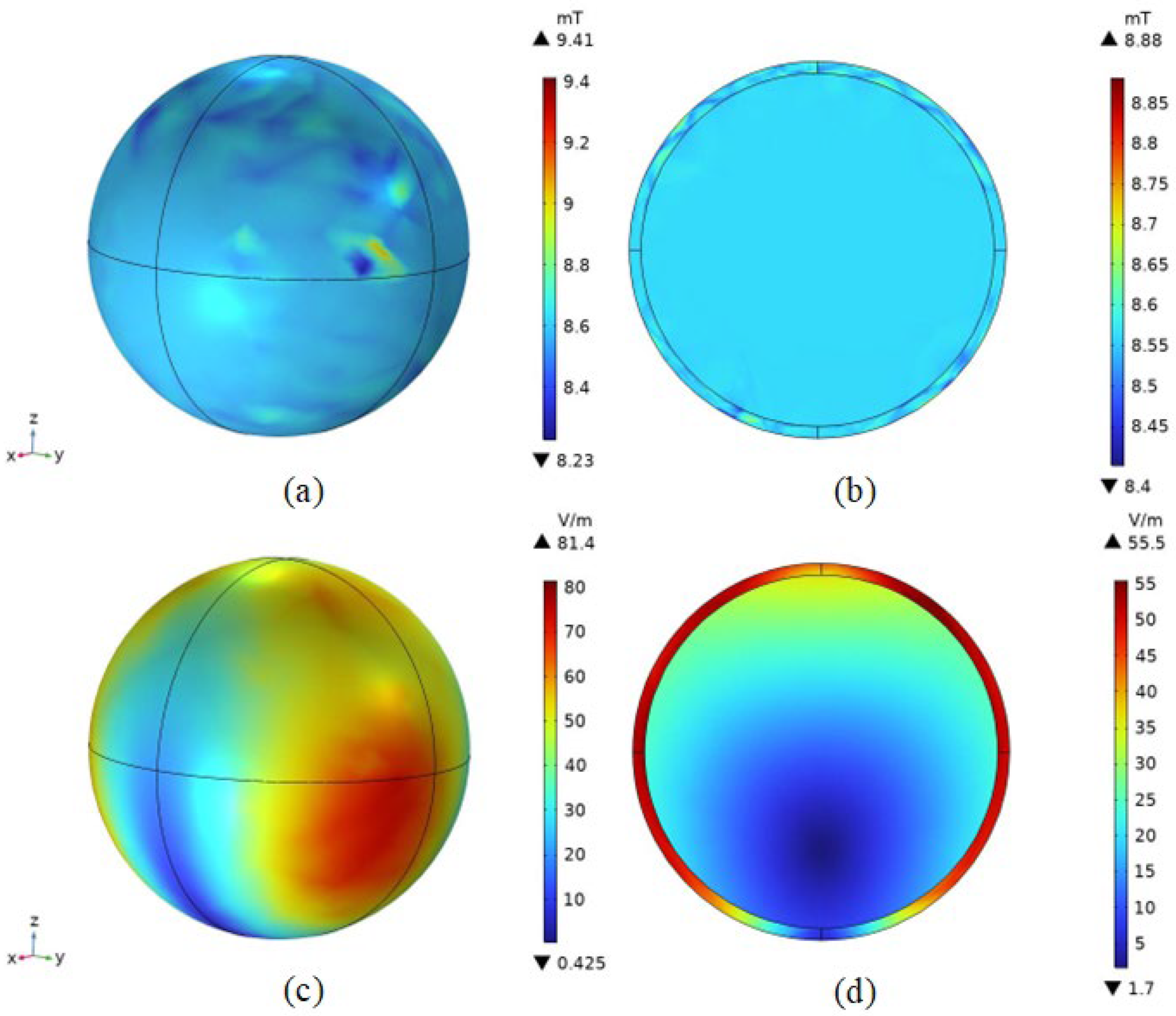
4.2. Spatial Electromagnetic Field Distribution after Adding the Mouse Model
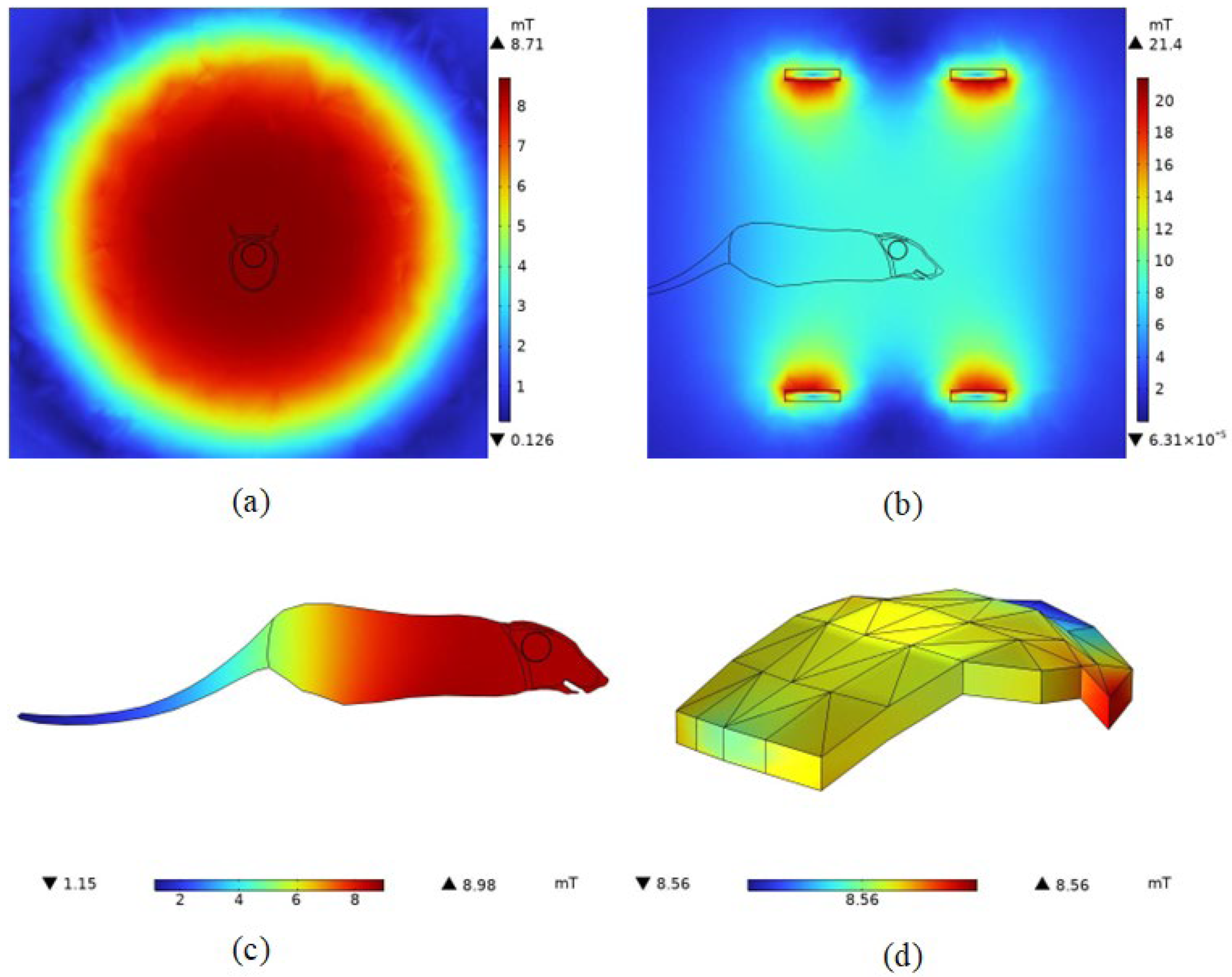
4.2.1. Magnetic Field Density Distribution
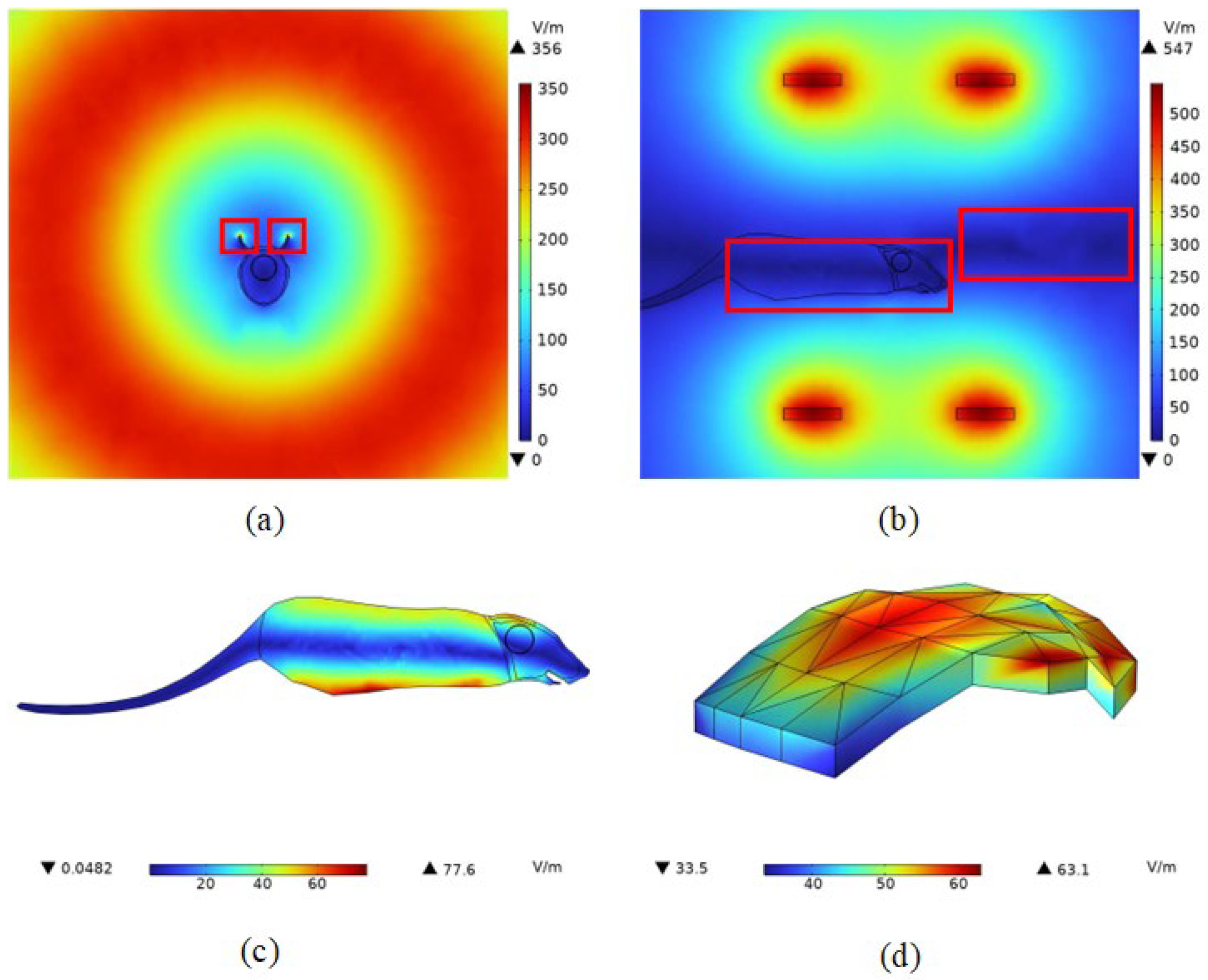
4.2.2. Induced Electric Field Strength Distribution
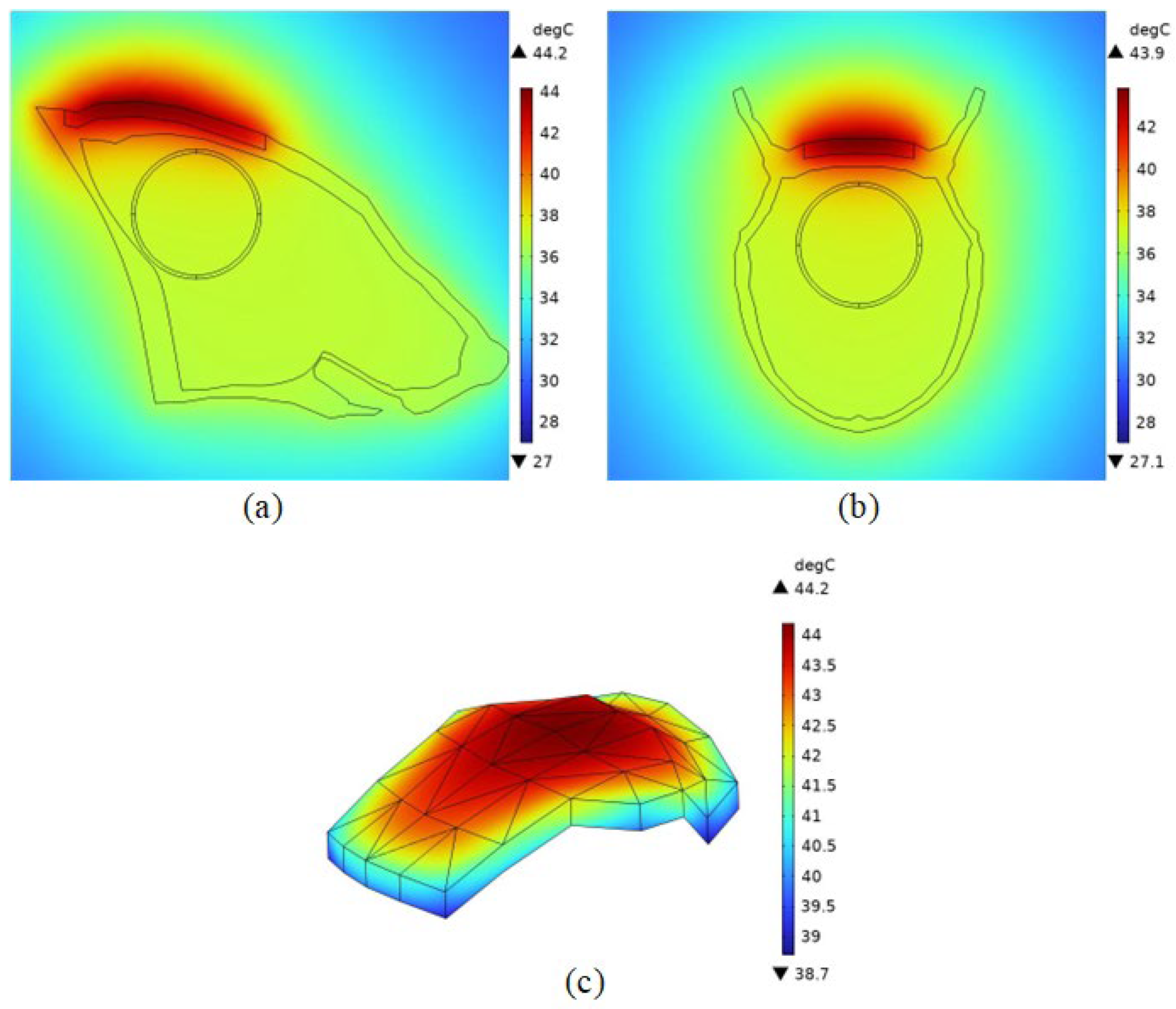
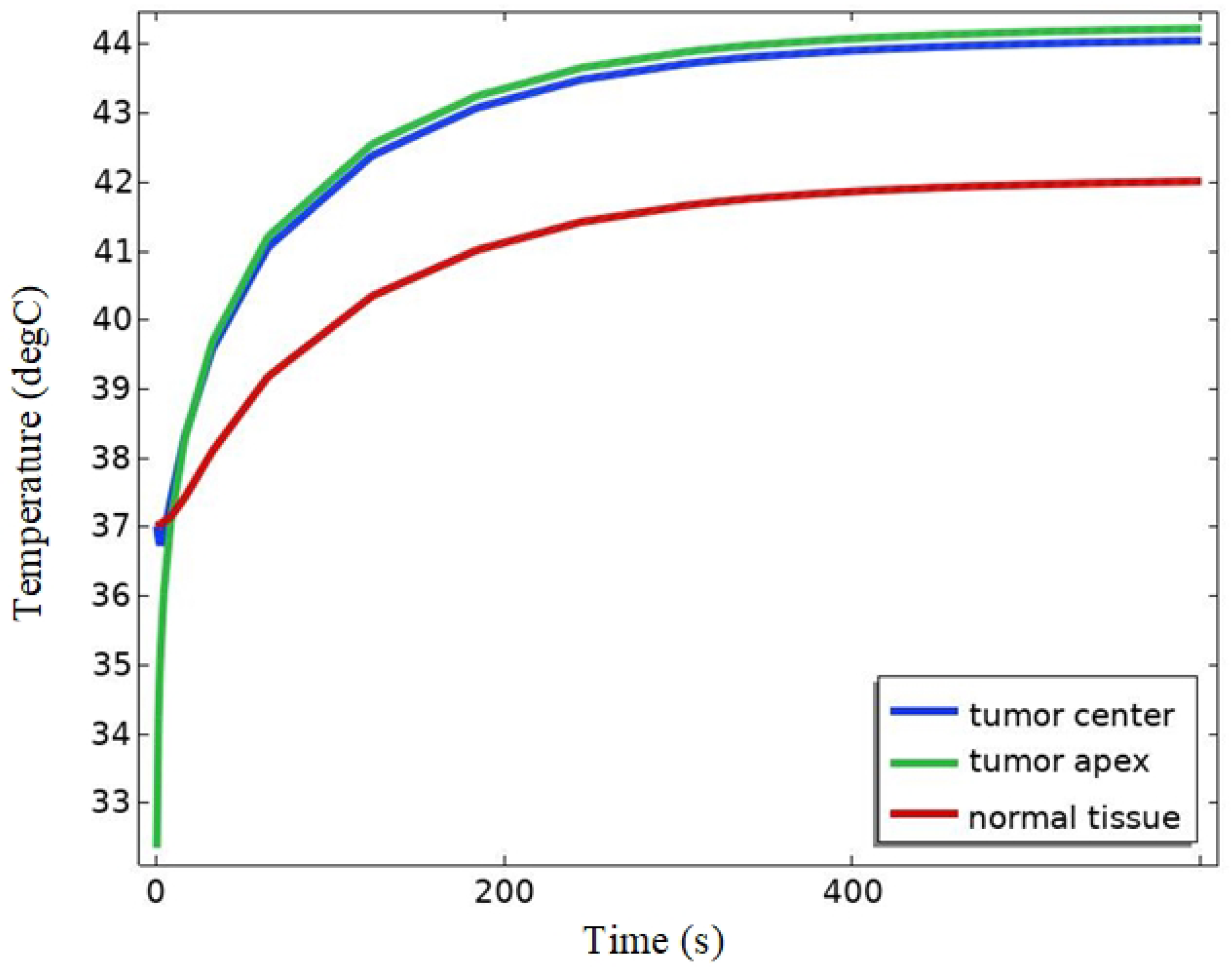
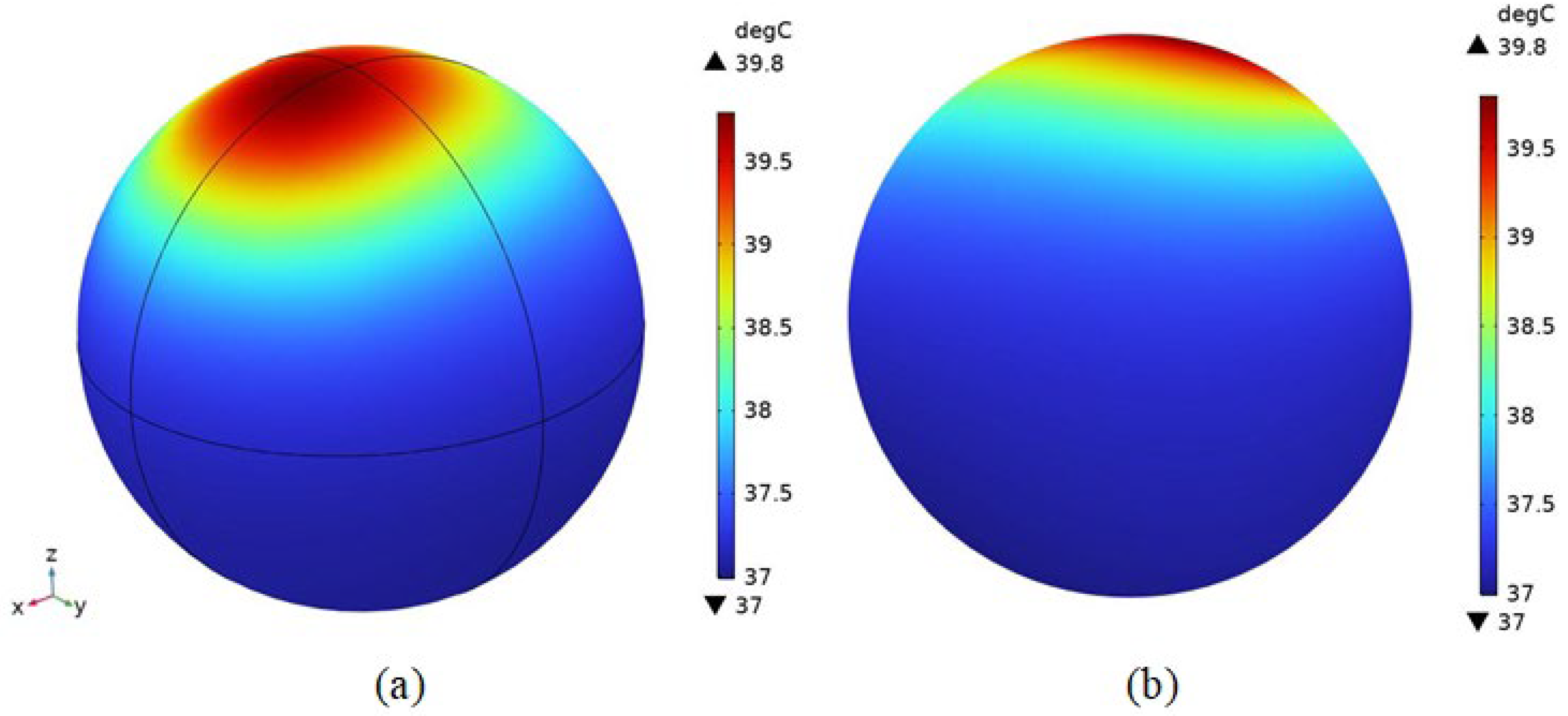
4.2.3. Temperature Field Simulation
4.2.4. Distribution of Physical Fields within the Brain Tissue of an Organism
5. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Han, B.; Zheng, R.; Zeng, H.; Wang, S.; Sun, K.; Chen, R.; Li, L.; Wei, W.; He, J. Cancer incidence and mortality in China, 2022. J. Natl. Cancer Cent. 2024, 4, 47–53. [Google Scholar] [CrossRef]
- Leonardi, G.C.; Falzone, L.; Salemi, R.; Zanghì, A.; Spandidos, D.A.; Mccubrey, J.A.; Candido, S.; Libra, M. Cutaneous melanoma: From pathogenesis to therapy. Int. J. Oncol. 2018, 52, 1071–1080. [Google Scholar] [CrossRef] [PubMed]
- Arnold, M.; de Vries, E.; Whiteman, D.C.; Jemal, A.; Bray, F.; Parkin, D.M.; Soerjomataram, I. Global burden of cutaneous melanoma attributable to ultraviolet radiation in 2012. Int. J. Cancer 2018, 143, 1305–1314. [Google Scholar] [CrossRef] [PubMed]
- Balch, C.M.; Buzaid, A.C.; Soong, S.-J.; Atkins, M.B.; Cascinelli, N.; Coit, D.G.; Fleming, I.D.; Gershenwald, J.E.; Houghton, A., Jr.; Kirkwood, J.M. Final version of the American Joint Committee on Cancer staging system for cutaneous melanoma. J. Clin. Oncol. 2001, 19, 3635–3648. [Google Scholar] [CrossRef] [PubMed]
- Dai, J.; Wu, S.; Kong, Y.; Chi, Z.; Si, L.; Sheng, X.; Cui, C.; Fang, J.; Zhang, J.; Guo, J. Nanosecond pulsed electric fields enhance the anti-tumour effects of the mTOR inhibitor everolimus against melanoma. Sci. Rep. 2017, 7, 39597. [Google Scholar] [CrossRef]
- Arnold, M.; Singh, D.; Laversanne, M.; Vignat, J.; Vaccarella, S.; Meheus, F.; Cust, A.E.; De Vries, E.; Whiteman, D.C.; Bray, F. Global burden of cutaneous melanoma in 2020 and projections to 2040. JAMA Dermatol. 2022, 158, 495–503. [Google Scholar] [CrossRef] [PubMed]
- Wu, Y.; Wang, Y.; Wang, L.; Yin, P.; Lin, Y.; Zhou, M. Burden of melanoma in China, 1990–2017: Findings from the 2017 global burden of disease study. Int. J. Cancer 2020, 147, 692–701. [Google Scholar] [CrossRef]
- Cassano, R.; Cuconato, M.; Calviello, G.; Serini, S.; Trombino, S. Recent advances in nanotechnology for the treatment of melanoma. Molecules 2021, 26, 785. [Google Scholar] [CrossRef] [PubMed]
- Vogl, T.J.; Naguib, N.N.; Lehnert, T.; Nour-Eldin, N.-E.A. Radiofrequency, microwave and laser ablation of pulmonary neoplasms: Clinical studies and technical considerations. Eur. J. Radiol. 2011, 77, 346–357. [Google Scholar] [CrossRef]
- Chu, K.F.; Dupuy, D.E. Thermal ablation of tumours: Biological mechanisms and advances in therapy. Nat. Rev. Cancer 2014, 14, 199–208. [Google Scholar] [CrossRef]
- Gilchrist, R.; Medal, R.; Shorey, W.D.; Hanselman, R.C.; Parrott, J.C.; Taylor, C.B. Selective inductive heating of lymph nodes. Ann. Surg. 1957, 146, 596–606. [Google Scholar] [CrossRef] [PubMed]
- Weber, K. Differences in types and incidence of neoplasms in Wistar Han and Sprague-Dawley rats. Toxicol. Pathol. 2017, 45, 64–75. [Google Scholar] [CrossRef] [PubMed]
- Kacew, S. Invited review: Role of rat strain in the differential sensitivity to pharmaceutical agents and naturally occurring substances. J. Toxicol. Environ. Health Part A 1996, 47, 1–30. [Google Scholar] [CrossRef]
- Ouyang, W.; Gao, F.; Wang, L.; Xie, X.; Lei, F.; Zhou, J.; Liao, Y.; Zhong, M.; Tang, J. Thermoseed hyperthermia treatment of mammary orthotopic transplantation tumors in rats and impact on immune function. Oncol. Rep. 2010, 24, 973–979. [Google Scholar] [PubMed]
- Tabatabaei, S.N.; Duchemin, S.; Girouard, H.; Martel, S. Towards MR-navigable nanorobotic carriers for drug delivery into the brain. In Proceedings of the 2012 IEEE International Conference on Robotics and Automation, St Paul, MN, USA, 14–18 May 2012; pp. 727–732. [Google Scholar]
- Huang, C.-F.; Lin, X.-Z.; Lo, W.-H. Design and construction of a hyperthermia system with improved interaction of magnetic induction-heating. In Proceedings of the 2010 Annual International Conference of the IEEE Engineering in Medicine and Biology, Buenos Aires, Argentina, 31 August–4 September 2010; pp. 3229–3232. [Google Scholar]
- Xia, Q.-S.; Liu, X.; Xu, B.; Zhao, T.-D.; Li, H.-Y.; Chen, Z.-H.; Xiang, Q.; Geng, C.-Y.; Pan, L.; Hu, R.-L. Feasibility study of high-temperature thermoseed inductive hyperthermia in melanoma treatment. Oncol. Rep. 2011, 25, 953–962. [Google Scholar] [PubMed]
- Kok, H.P.; Cressman, E.N.; Ceelen, W.; Brace, C.L.; Ivkov, R.; Grüll, H.; Ter Haar, G.; Wust, P.; Crezee, J. Heating technology for malignant tumors: A review. Int. J. Hyperth. 2020, 37, 711–741. [Google Scholar] [CrossRef]
- Dogdas, B.; Stout, D.; Chatziioannou, A.F.; Leahy, R.M. Digimouse: A 3D whole body mouse atlas from CT and cryosection data. Phys. Med. Biol. 2007, 52, 577. [Google Scholar] [CrossRef] [PubMed]
- Bai, B.; Chow, P.; Chatziioannou, A.; Leahy, R.M. Fully 3D uniform resolution transmission microPET image reconstruction. In Proceedings of the 2002 IEEE Nuclear Science Symposium Conference Record, Norfolk, VA, USA, 10–16 November 2002; pp. 1470–1473. [Google Scholar]
- Bernabei, J.M.; Lee, W.H.; Peterchev, A.V. Modeling transcranial electric stimulation in mouse: A high resolution finite element study. In Proceedings of the 2014 36th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Chicago, IL, USA, 26–30 August 2014; pp. 406–409. [Google Scholar]
- Patel, V.R.; Roberson, M.L.; Pignone, M.P.; Adamson, A.S. Risk of mortality after a diagnosis of melanoma in situ. JAMA Dermatol. 2023, 159, 703–710. [Google Scholar] [CrossRef]
- Shaopeng, L.; Meng, X.; Lisheng, Z.; Jinghui, G. Study on dielectric properties of SD rat tissues in vitro. In Proceedings of the 2013 Annual Report Conference on Electrical Insulation and Dielectric Phenomena, Chenzhen, China, 20–23 October 2013; pp. 1332–1335. [Google Scholar]
- Hasgall, P.A.; Di Gennaro, F.; Baumgartner, C.; Neufeld, E.; Lloyd, B.; Gosselin, M.C.; Payne, D.; Klingenböck, A.; Kuster, N. IT’IS Database for Thermal and Electromagnetic Parameters of Biological Tissues, Version 4.1; IT’IS Foundation: Zürich, Switzerland, 2022. [Google Scholar] [CrossRef]
- Gong, Y.; Capstick, M.; Tillmann, T.; Dasenbrock, C.; Samaras, T.; Kuster, N. Desktop exposure system and dosimetry for small scale in vivo radiofrequency exposure experiments. Bioelectromagnetics 2016, 37, 49–61. [Google Scholar] [CrossRef]
- Holmes, K.R. Thermal properties. Cortex 1983, 491, 16. [Google Scholar]
- Wessapan, T.; Srisawatdhisukul, S.; Rattanadecho, P. Numerical analysis of specific absorption rate and heat transfer in the human body exposed to leakage electromagnetic field at 915 MHz and 2450 MHz. Heat Transf. 2011, 133, 051101. [Google Scholar] [CrossRef]
- Wu, L.; Cheng, J.; Liu, W.; Chen, X. Numerical analysis of electromagnetically induced heating and bioheat transfer for magnetic fluid hyperthermia. IEEE Trans. Magn. 2015, 51, 1–4. [Google Scholar]
- Suleman, M.; Riaz, S. 3D in silico study of magnetic fluid hyperthermia of breast tumor using Fe3O4 magnetic nanoparticles. J. Therm. Biol. 2020, 91, 102635. [Google Scholar] [CrossRef]
- Mier, Y.H.; Hernandez, A.V.; Salas, L.L. Magnetic induction heating system for local hyperthermia research. In Proceedings of the Second Joint 24th Annual Conference and the Annual Fall Meeting of the Biomedical Engineering Society Engineering in Medicine and Biology, Houston, TX, USA, 23–26 October 2002; pp. 1744–1745. [Google Scholar]
- Rosensweig, R.E. Heating magnetic fluid with alternating magnetic field. J. Magn. Magn. Mater. 2002, 252, 370–374. [Google Scholar] [CrossRef]
- Feng, C.; Ma, X. Introduction to Engineering Electromagnetic Fields; Monographs of the High Education Press: Beijing, China, 2000. [Google Scholar]
- Pennes, H.H. Analysis of tissue and arterial blood temperatures in the resting human forearm. J. Appl. Physiol. 1948, 1, 93–122. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Ye, Y.; Lin, Z.; Wang, Z.; Chen, Y.; Li, G.; Ouyang, Z.; Li, J. Application of a new self-regulating temperature magnetic material Fe83Zr10B7 in magnetic induction hyperthermia. Int. J. Hyperth. 2023, 40, 2211269. [Google Scholar] [CrossRef]
- Lin, C.-T.; Liu, K.-C. Estimation for the heating effect of magnetic nanoparticles in perfused tissues. Int. Commun. Heat Mass Transf. 2009, 36, 241–244. [Google Scholar] [CrossRef]
- Wang, X.; Tang, J.; Shi, L. Induction heating of magnetic fluids for hyperthermia treatment. IEEE Trans. Magn. 2009, 46, 1043–1051. [Google Scholar] [CrossRef]
- Thiesen, B.; Jordan, A. Clinical applications of magnetic nanoparticles for hyperthermia. Int. J. Hyperth. 2008, 24, 467–474. [Google Scholar] [CrossRef]
- Sharma, A.; Jangam, A.; Shen, J.L.Y.; Ahmad, A.; Arepally, N.; Rodriguez, B.; Borrello, J.; Bouras, A.; Kleinberg, L.; Ding, K. Validation of a temperature-feedback controlled automated magnetic hyperthermia therapy device. Cancers 2023, 15, 327. [Google Scholar] [CrossRef]
- Liu, X.; Zheng, J.; Sun, W.; Zhao, X.; Li, Y.; Gong, N.; Wang, Y.; Ma, X.; Zhang, T.; Zhao, L.-Y. Ferrimagnetic vortex nanoring-mediated mild magnetic hyperthermia imparts potent immunological effect for treating cancer metastasis. ACS Nano 2019, 13, 8811–8825. [Google Scholar] [CrossRef] [PubMed]
- Moise, S.; Byrne, J.M.; El Haj, A.J.; Telling, N.D. The potential of magnetic hyperthermia for triggering the differentiation of cancer cells. Nanoscale 2018, 10, 20519–20525. [Google Scholar] [CrossRef] [PubMed]
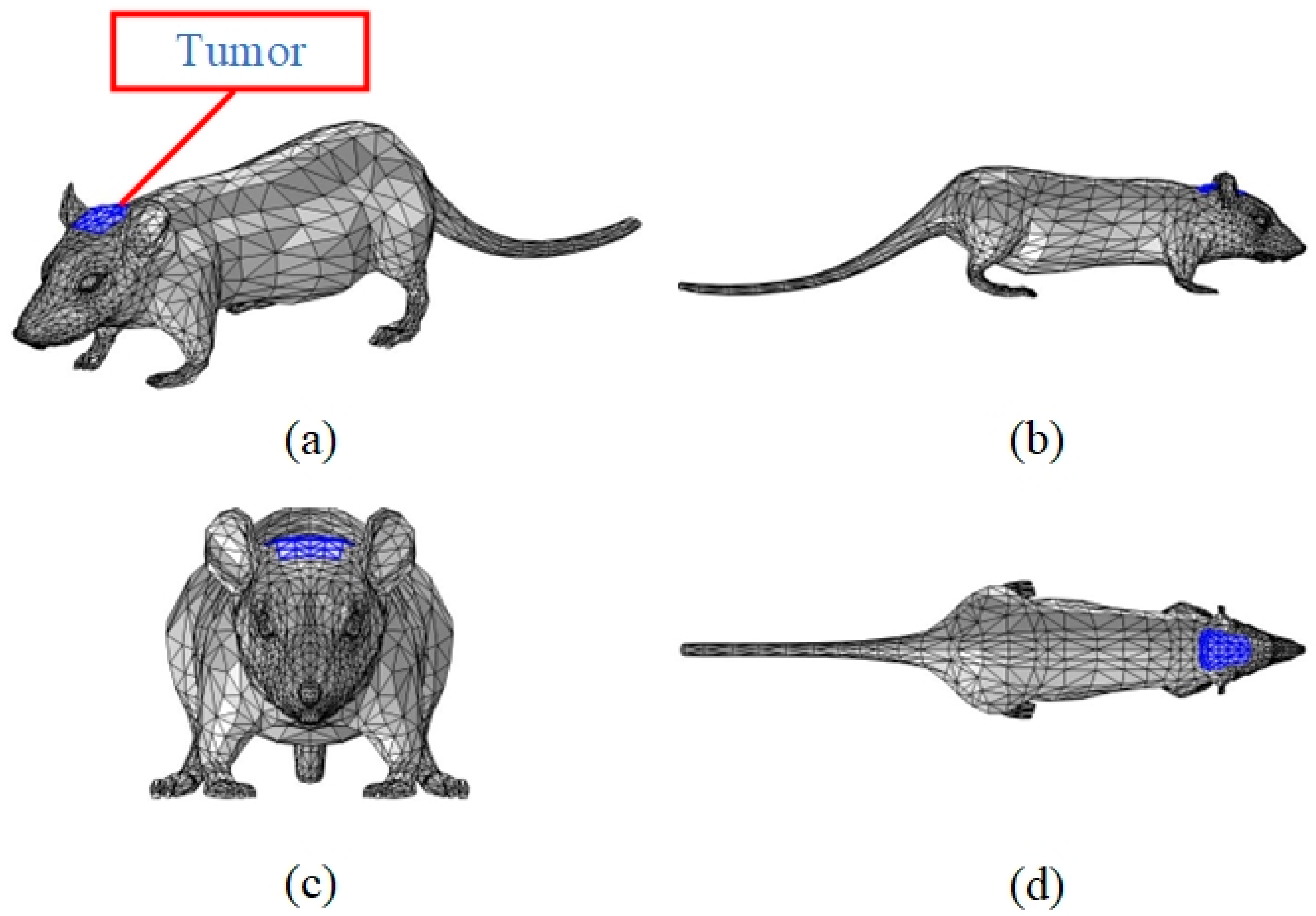
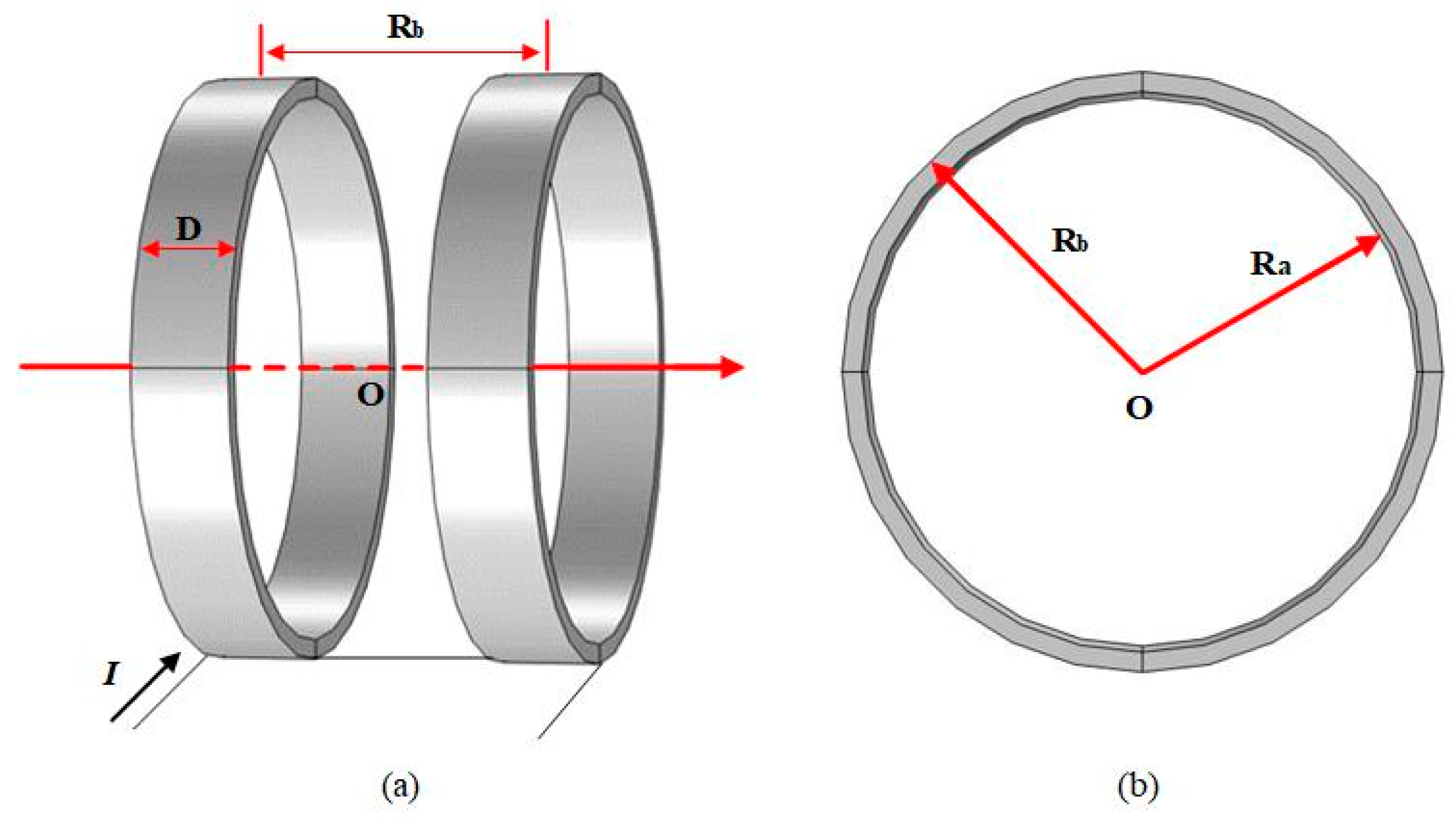
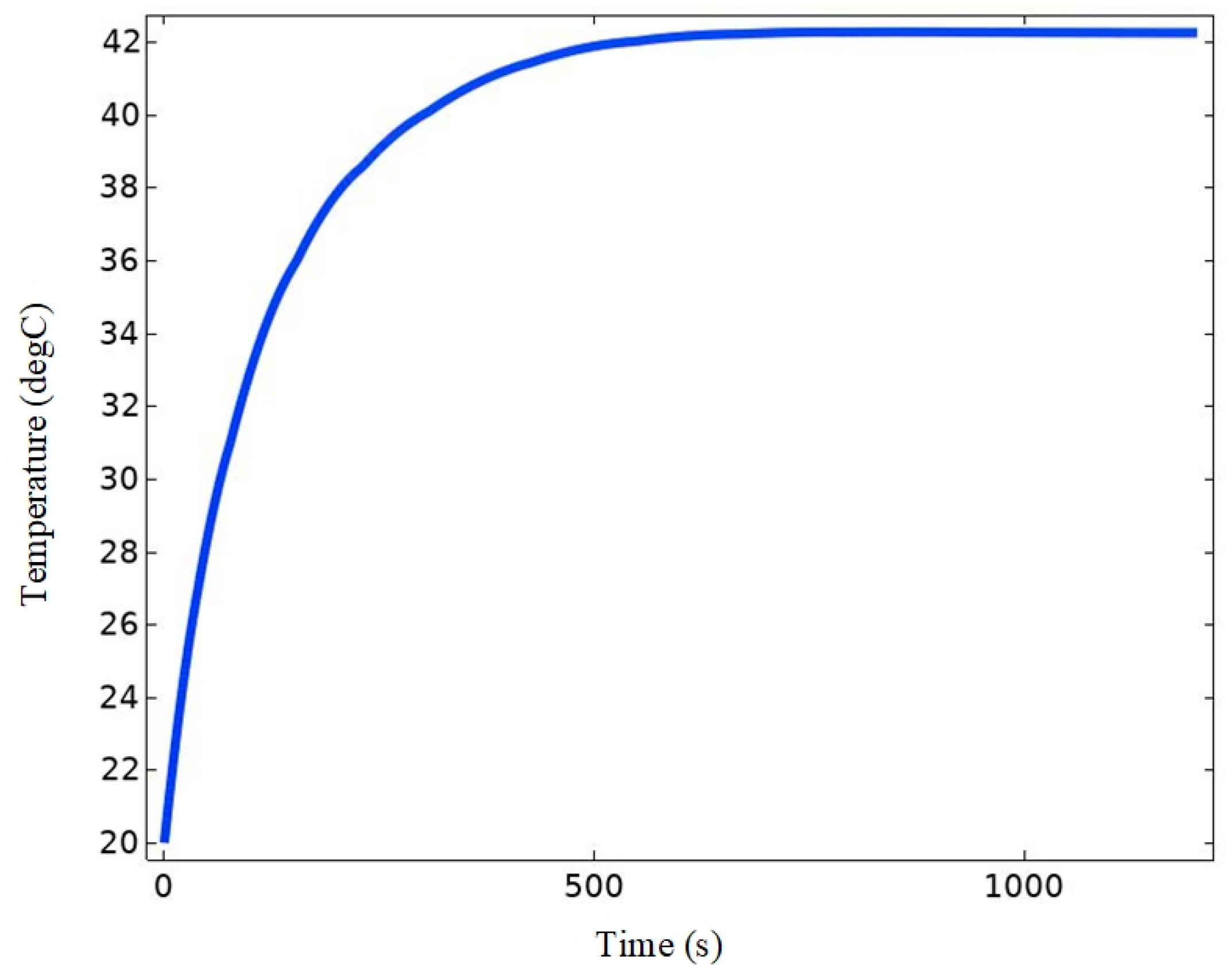
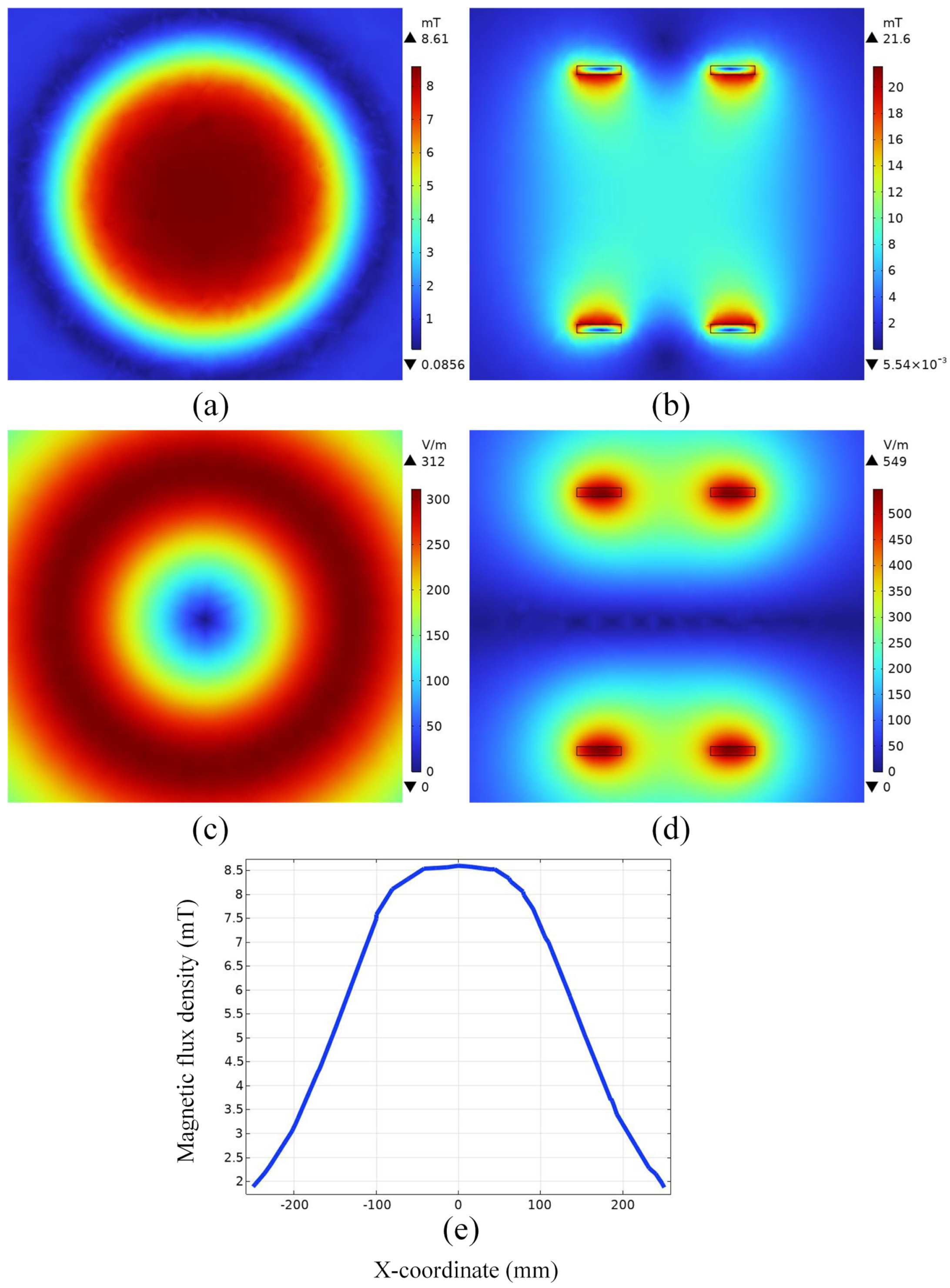
| Dimension | Numeric (mm) |
|---|---|
| length (including tail) | 335 |
| width | 67 |
| height | 69 |
| Tissue | Conductivity (σ/(S·m−1)) | Relative Permittivity |
|---|---|---|
| scalp | 0.000451 | 1120 |
| torso | 0.304169 | 5411.25 |
| limbs | 0.27945 | 3670 |
| skull | 0.0208 | 228 |
| brain tissue | 0.1079 | 2665 |
| muscle | 0.362 | 8090 |
| Tissue | Density (kg·m−1) | Specific Heat Capacity (J·kg−1·K−1) | Thermal Conductivity (W·m−1·K−1) | Perfusion (s−1) | Metabolic Fever (W·m−1) |
|---|---|---|---|---|---|
| scalp | 1109 | 3391 | 0.37 | 0.02 | 1620 |
| muscle | 1090 | 3421 | 0.49 | 0.00869 | 480 |
| skull | 1908 | 1313 | 0.32 | 0.000436 | 610 |
| brain tissue | 1043 | 3639.5 | 0.515 | 0.00883 | 7100 |
| Tissue | Density (kg·m−1) | Specific Heat Capacity (J·kg−1·K−1) | Thermal Conductivity (W·m−1·K−1) | Perfusion (s−1) | Metabolic Fever (W·m−1) |
|---|---|---|---|---|---|
| magnetic nanofluids | 5180 | 4000 | 40 | - | - |
| tumor tissue | 1060 | 3650 | 0.535 | 0.01392 | 5790 |
| mixed tissue | 1072.4 | 3651.1 | 0.5316 | - | - |
| magnetic nanofluids | 5180 | 4000 | 40 | - | - |
| Turns of Each Coil | Width (D) | Outer Diameter (Ra) | Inner Diameter (Rb) |
|---|---|---|---|
| 180 | 0.05 m | 0.15 m | 0.14 m |
| Frequency | Amplitude of Current | Relative Permeability | Relative Permittivity | Conductivity |
|---|---|---|---|---|
| 100 kHz | 8 A | 1 | 1 | 5.998e7 S/m |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Lu, M. Numerical Simulation of Thermal Therapy for Melanoma in Mice. Bioengineering 2024, 11, 694. https://doi.org/10.3390/bioengineering11070694
Zhang Y, Lu M. Numerical Simulation of Thermal Therapy for Melanoma in Mice. Bioengineering. 2024; 11(7):694. https://doi.org/10.3390/bioengineering11070694
Chicago/Turabian StyleZhang, Yunfei, and Mai Lu. 2024. "Numerical Simulation of Thermal Therapy for Melanoma in Mice" Bioengineering 11, no. 7: 694. https://doi.org/10.3390/bioengineering11070694
APA StyleZhang, Y., & Lu, M. (2024). Numerical Simulation of Thermal Therapy for Melanoma in Mice. Bioengineering, 11(7), 694. https://doi.org/10.3390/bioengineering11070694







