Mixture Theory-Based Finite Element Approach for Analyzing the Edematous Condition of Biological Soft Tissues
Abstract
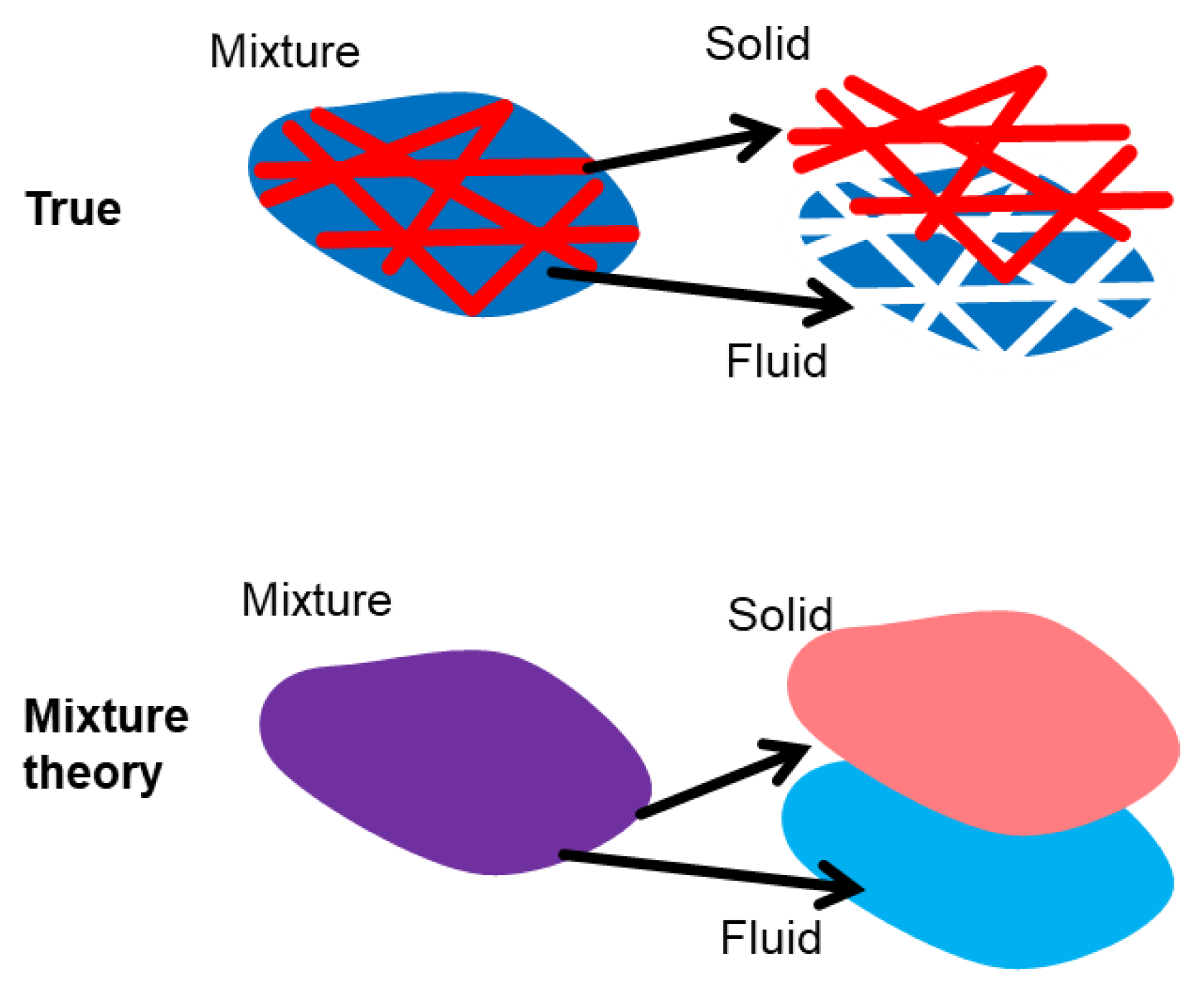
:1. Introduction
2. Methods
2.1. Theoretical Formulations
2.2. Numerical Verification
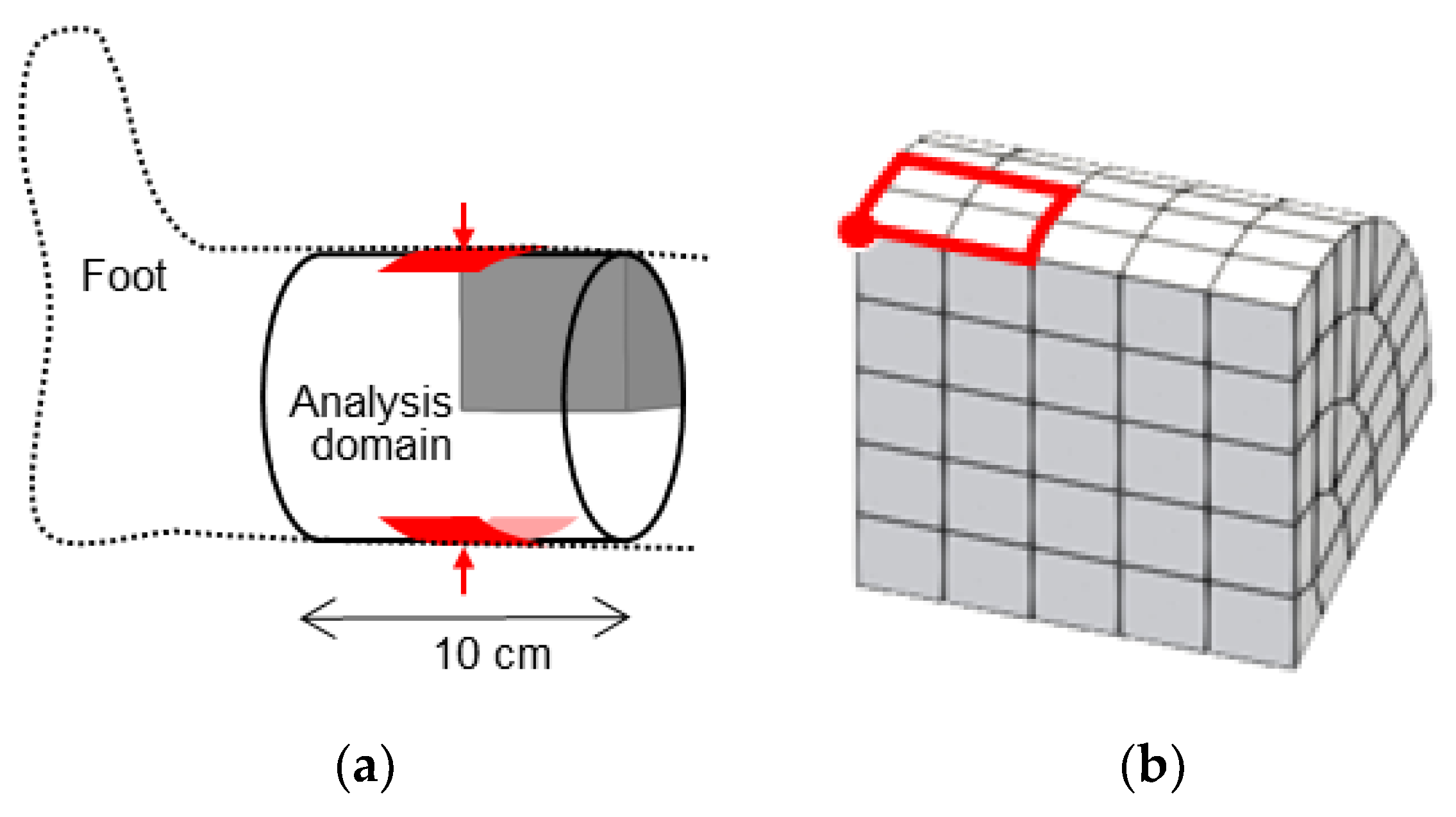
2.3. Reproduction of Indentation Test under Pitting Edema
3. Results
3.1. Numerical Verification
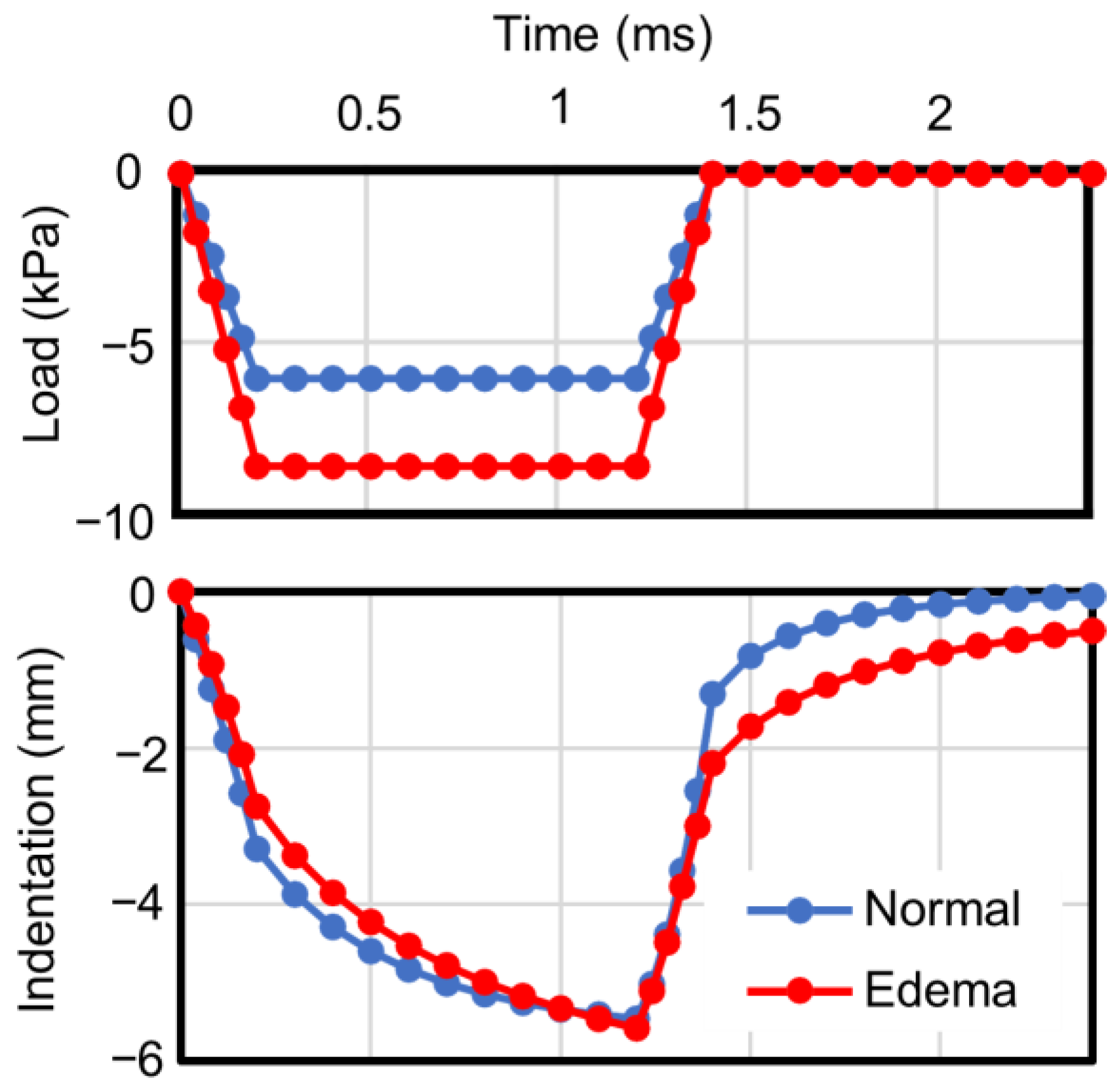
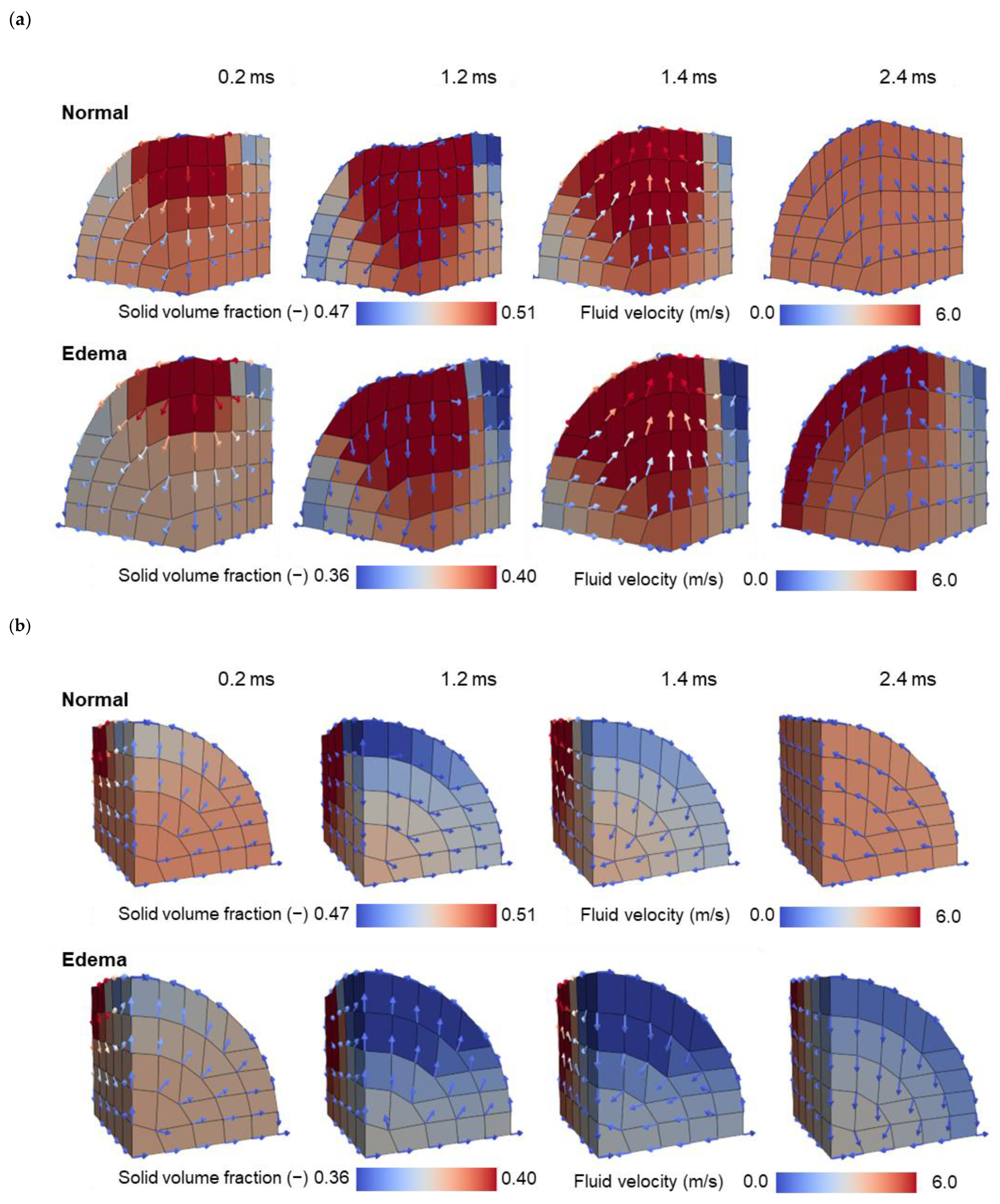
3.2. Indentation Test under Pitting Edema
4. Discussion
4.1. New Approach for Simulating Edematous Condition of Soft Biological Tissues
4.2. Pitting Edema Indentation Test
4.3. Factors Influencing Recovery Time in Edematous Tissues
4.4. Future Research
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
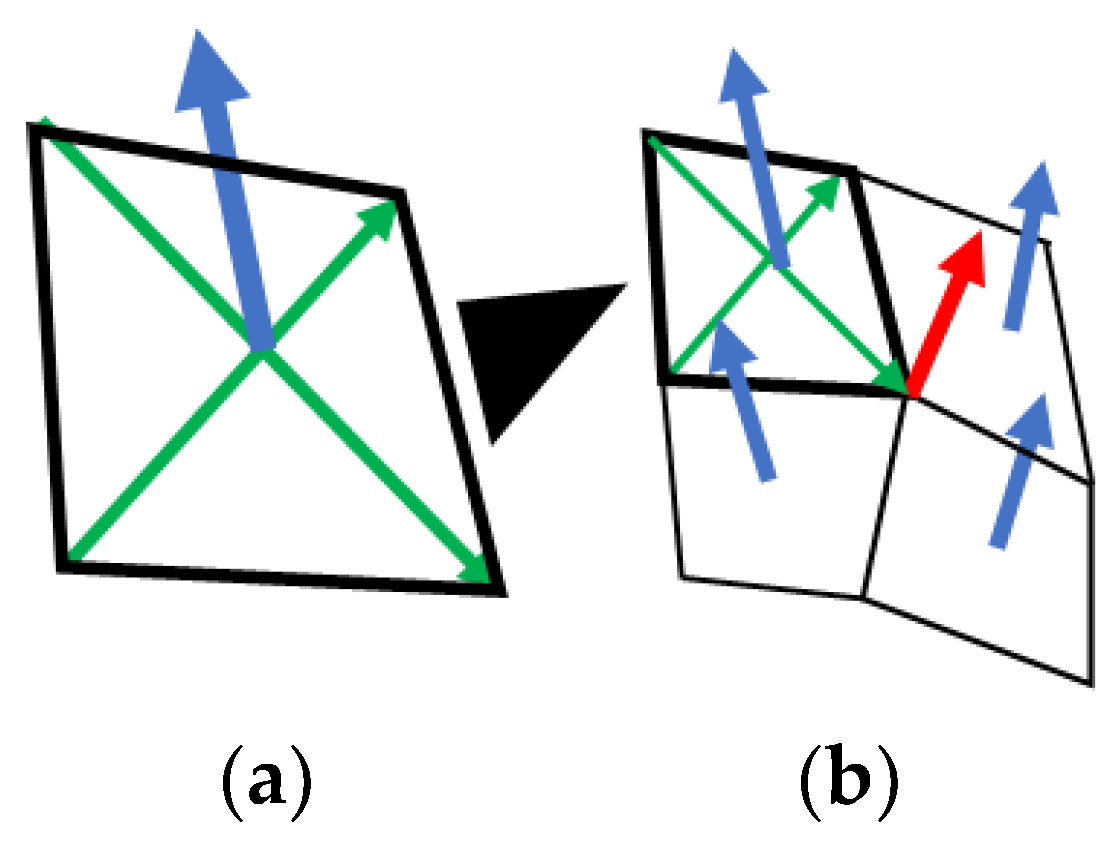
Appendix A. Governing Equations
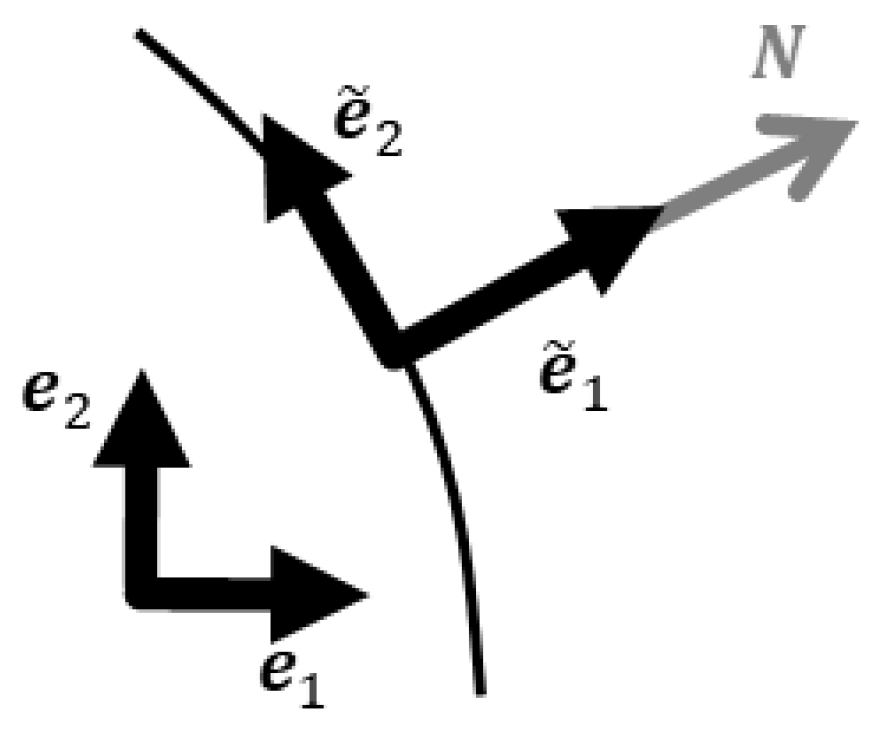
Appendix A.1. Piola Transformation
Appendix A.2. Momentum Equation
Appendix A.3. Continuity Equation
Appendix A.4. Darcy’s Law
Appendix B. Solid Volume Fraction
References
- Dongaonkar, R.M.; Quick, C.M.; Stewart, R.H.; Drake, R.E.; Cox, C.S., Jr.; Laine, G.A. Edemagenic gain and interstitial fluid volume regulation. Am. J. Physiol. Regul. Integr. Comp. Physiol. 2008, 294, R651–R659. [Google Scholar] [CrossRef] [PubMed]
- Dongaonkar, R.M.; Laine, G.A.; Stewart, R.H.; Quick, C.M. Balance point characterization of interstitial fluid volume regulation. Am. J. Physiol. Regul. Integr. Comp. Physiol. 2009, 297, R6–R16. [Google Scholar] [CrossRef]
- Liang, D.; Bhatta, S.; Gerzanich, V.; Simard, J.M. Cytotoxic edema: Mechanisms of pathological cell swelling. Neurosurg. Focus 2007, 22, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Trayes, K.P.; Studdiford, J.S.; Pickle, S.; Tully, A.S. Edema: Diagnosis and management. Am. Fam. Physician 2013, 88, 102–110. Available online: https://www.aafp.org/pubs/afp/issues/2013/0715/p102.html (accessed on 11 June 2024). [PubMed]
- Hirabayashi, S.; Iwamoto, M. Finite element analysis of biological soft tissue surrounded by a deformable membrane that controls transmembrane flow. Theor. Biol. Med. Model. 2018, 15, 21. [Google Scholar] [CrossRef]
- Klahr, B.; Thiesen, J.L.; Pinto, O.T.; Carniel, T.A.; Fancello, E.A. A variational RVE-based multiscale poromechanical formulation applied to soft biological tissues under large deformations. Eur. J. Mech. A Solids 2023, 99, 104937. [Google Scholar] [CrossRef]
- Zienkiewicz, O.C.; Chan, A.H.C.; Pastor, M.; Paul, D.K.; Shiomi, T. Static and dynamic behaviour of soils: A rational approach to quantitative solutions. I. Fully saturated problems. Proc. R. Soc. Lond. A 1990, 429, 285–309. [Google Scholar] [CrossRef]
- Schrefler, B.A.; Scotta, R. A fully coupled dynamic model for two-phase fluid flow in deformable porous media. Comput. Methods Appl. Mech. Eng. 2001, 190, 3223–3246. [Google Scholar] [CrossRef]
- Almeida, E.S.; Spilker, R.L. Mixed and penalty finite element models for the nonlinear behavior of biphasic soft tissues in finite deformation: Part I—Alternate formulations. Comput. Methods Biomech. Bio. Med. Eng. 1997, 1, 151–170. [Google Scholar] [CrossRef]
- Oomens, C.W.; van Campen, D.H.; Grootenboer, H.J. A mixture approach to the mechanics of skin. J. Biomech. 1987, 20, 877–885. [Google Scholar] [CrossRef]
- Vermilyea, M.E.; Spilker, R.L. Hybrid and mixed-penalty finite elements for 3-D analysis of soft hydrated tissue. Int. J. Numer. Methods Eng. 1993, 36, 4223–4243. [Google Scholar] [CrossRef]
- Vankan, W.J.; Huyghe, J.M.; Janssen, J.D.; Huson, A. Poroelasticity of saturated solids with an application to blood perfusion. Int. J. Eng. Sci. 1996, 34, 1019–1031. [Google Scholar] [CrossRef]
- Levenston, M.E.; Frank, E.H.; Grodzinsky, A.J. Variationally derived 3-field finite element formulations for quasistatic poroelastic analysis of hydrated biological tissues. Comput. Methods Appl. Mech. Eng. 1998, 156, 231–246. [Google Scholar] [CrossRef]
- Chen, Y.; Chen, X.; Hisada, T. Non-linear finite element analysis of mechanical electrochemical phenomena in hydrated soft tissues based on triphasic theory. Int. J. Numer. Methods Eng. 2006, 65, 147–173. [Google Scholar] [CrossRef]
- Hassan, C.R.; Lee, W.; Komatsu, D.E.; Qin, Y.X. Evaluation of nucleus pulposus fluid velocity and pressure alteration induced by cartilage endplate sclerosis using a poro-elastic finite element analysis. Biomech. Model. Mechanobiol. 2021, 20, 281–291. [Google Scholar] [CrossRef]
- Jiang, F.; Hirano, T.; Liang, C.; Zhang, G.; Matsunaga, K.; Chen, X. Multi-scale simulations of pulmonary airflow based on a coupled 3D-1D-0D model. Comput. Biol. Med. 2024, 171, 108150. [Google Scholar] [CrossRef]
- Cheng, S.; Bilston, L.E. Unconfined compression of white matter. J. Biomech. 2007, 40, 117–124. [Google Scholar] [CrossRef]
- Franceschini, G.; Bigoni, D.; Regitnig, P.; Holzapfel, G.A. Brain tissue deforms similarly to filled elastomers and follows consolidation theory. J. Mech. Phys. Solids 2006, 54, 2592–2620. [Google Scholar] [CrossRef]
- Stastna, M.; Tenti, G.; Sivaloganathan, S.; Drake, J.M. Brain biomechanics: Consolidation theory of hydrocephalus. Variable permeability and transient effects. Can. Appl. Math. Q. 1999, 7, 93–109. [Google Scholar]
- Taylor, Z.; Miller, K. Reassessment of brain elasticity for analysis of biomechanisms of hydrocephalus. J. Biomech. 2004, 37, 1263–1269. [Google Scholar] [CrossRef]
- Soltz, M.A.; Ateshian, G.A. Experimental verification and theoretical prediction of cartilage interstitial fluid pressurization at an impermeable contact interface in confined compression. J. Biomech. 1998, 31, 927–934, Erratum in J. Biomech. 2006, 39, 594. [Google Scholar] [CrossRef] [PubMed]
- Riken; The Shizuoka Prefecture Industrial Technology Institute. Mechanical Property Database. Computational Biomechanics-Human Organs Property Database for Computer Simulation. Available online: http://cfd-duo.riken.jp/cbms-mp/index.htm (accessed on 9 May 2024).
- Holmes, M.H.; Mow, V.C. The nonlinear characteristics of soft gels and hydrated connective tissues in ultrafiltration. J. Biomech. 1990, 23, 1145–1156. [Google Scholar] [CrossRef] [PubMed]
- Suh, J.K.; Spilker, R.; Holmes, M.H. A penalty finite element analysis for nonlinear mechanics of biphasic hydrated soft tissue under large deformation. Int. J. Numer. Methods Eng. 1991, 32, 1411–1439. [Google Scholar] [CrossRef]



| Normal | Edema | |
|---|---|---|
| Total volume (L) | 0.785 | 1.02 |
| Solid volume (L) | 0.393 | 0.393 |
| Fluid volume (L) | 0.393 | 0.628 |
| Initial pore water pressure (kPa) | 0.00 | 4.50 |
| Maximum load (kPa) | 5.95 | 8.50 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hirabayashi, S.; Iwamoto, M.; Chen, X. Mixture Theory-Based Finite Element Approach for Analyzing the Edematous Condition of Biological Soft Tissues. Bioengineering 2024, 11, 702. https://doi.org/10.3390/bioengineering11070702
Hirabayashi S, Iwamoto M, Chen X. Mixture Theory-Based Finite Element Approach for Analyzing the Edematous Condition of Biological Soft Tissues. Bioengineering. 2024; 11(7):702. https://doi.org/10.3390/bioengineering11070702
Chicago/Turabian StyleHirabayashi, Satoko, Masami Iwamoto, and Xian Chen. 2024. "Mixture Theory-Based Finite Element Approach for Analyzing the Edematous Condition of Biological Soft Tissues" Bioengineering 11, no. 7: 702. https://doi.org/10.3390/bioengineering11070702







