Abstract
The quest for novel materials with extraordinary electronic and plasmonic properties is an ongoing pursuit in the field of materials science. The dataset provides the results of a computational study that used ab initio and semi-analytical computations to model freestanding nanosystems. We delve into the world of ribbon-like materials, specifically graphene nanoribbons, silicene nanoribbons, and germanene nanoribbons, comparing their electronic and plasmonic characteristics. Our research reveals a myriad of insights, from the tunability of band structures and the influence of an atomic number on electronic properties to the adaptability of nanoribbons for optoelectronic applications. Further, we uncover the promise of these materials for biosensing, demonstrating their plasmon frequency tunability based on charge density and Fermi velocity modification. Our findings not only expand the understanding of these quasi-1D materials but also open new avenues for the development of cutting-edge devices and technologies. This data presentation holds immense potential for future advancements in electronics, optics, and molecular sensing.
Dataset License: CC-BY-4.0
Keywords:
graphene; silicene; germanene; plasmons; electronics; semi-analytical model; DFT; GW approximation 1. Introduction
In recent years, extensive research has been dedicated to exploring two-dimensional (2D) hexagonal materials arranged in a honeycomb-like lattice [1]. While graphene stands out as the most prominent paradigm of such materials, the inherent incompatibility of carbon-based materials with predominant silicon-based and germanium-based electronics renders graphene currently impractical for widespread application [2]. Consequently, significant research attention has turned towards alternative candidates within the group IV elements, namely silicene and germanene, which serve as analogs to graphene for silicon and germanium elements [3].
While carbon (C), silicon (Si), and germanium (Ge) are classified within the same group IV on the periodic table, their structural characteristics diverge, primarily due to variations in orbital hybridization patterns [4]. Specifically, the energy required for s and p orbital hybridization in C significantly exceeds that in Si and Ge. Consequently, C tends to favor sp2 hybridization [5], leading to a configuration where all C atoms reside within the same plane. In contrast, silicene and germanene, featuring Si and Ge atoms, respectively, exhibit a mixed sp2-sp3 hybridization [6]. This leads to the formation of a characteristic buckled honeycomb lattice structure, wherein silicene and germanene deviate from a coplanar arrangement [7].
Additionally, the electronic band structures of these materials reveal linear bands that give rise to Dirac cones at the K and K′ points within the 2D hexagonal Brillouin zone (BZ) [8]. While graphene comprises lightweight C atoms, silicene and germanene comprise heavier Si and Ge atoms. Consequently, the role of the spin–orbit interaction in their behavior becomes increasingly significant [9], paving the way for remarkable new physics insights, particularly in the context of topological insulators [10].
In the realm of 2D material-based electronic devices, one of the crucial electronic parameters influencing their performance is the bandgap [11]. Consequently, the ability to adjust the bandgap of 2D materials, such as graphene, silicene, and germanene, is a critical effort for their effective utilization in optoelectronic devices [12]. Notably, graphene, silicene, and germanene inherently possess zero bandgaps. Nevertheless, they do exhibit a finite bandgap when transitioning into a nanoribbon configuration [13] (i.e., quasi-1D systems), namely graphene nanoribbons (GNRs), silicene nanoribbons (SiNRs), and germanene nanoribbons (GeNRs). Interestingly, the bandgap of these nanoribbons can be readily adjusted through processes such as hydrogenation or altering the ribbon width [14].
From the plasmonics viewpoint, the concept of plasmon-enhanced infrared optical absorption, leveraging graphene, holds significant promise as a spectroscopic method for investigating the vibrational modes within intricate biopolymers (such as proteins, nucleic acids, and synthetic polymers) [15]. In pursuit of enhancing the 2D plasmon excitation of graphene, GNRs have been arranged into 2D periodic arrays [16,17,18]. This technique has demonstrated its efficacy in discerning the vibrational modes of gas molecules [19]. Particularly, GNRs exhibit two distinct plasmon modes [20]: a 2D plasmon and an edge plasmon. The first mode, the 2D plasmon, is noteworthy due to its high tunability and versatile applications in the infrared and terahertz domains. Conversely, the second mode (observed at the eV scale) is solely modifiable by adjusting the ribbon width and is linked to quantum charge confinement.
While extensive research, both experimental and theoretical, has been conducted on the electronic and plasmonic characteristics of graphene and GNRs, there is a growing interest in exploring these properties within the realm of SiNRs and GeNRs. This heightened focus is driven by their potential versatility within current semiconductor technology. From a theoretical perspective, the prevalent approaches for probing the electronic and plasmonic properties of such systems encompass the density functional theory (DFT) [21], time-dependent density functional theory (TDDFT) [22,23], and Green’s function method [24]. Nonetheless, these ab initio methods face challenges when addressing more intricate systems, such as experimentally realized GNRs spanning from 100 to 500 nm, involving a substantial number of atoms [20]. This limitation can be overcome by adopting semi-analytical models [25], which have demonstrated favorable agreement with prior experimental findings and theoretical predictions.
The data presented and discussed in this study offer a comparative analysis of the electronic and plasmonic characteristics of GNRs, SiNRs, and GeNRs, all with a consistent ribbon width of 155 nm. Our modeling approach enables the estimation of essential parameters such as effective mass, bandgap, density of states (DOS), and plasmon frequency tunability. We explore ground state properties within a few meV and demonstrate plasmon tunability at the terahertz (THz) scale, a crucial domain for prominent 2D materials-based plasmonic effects. The key input parameter in our semi-analytical model is the Fermi velocity of graphene, silicene, and germanene in their freestanding configurations, which we determined through DFT calculations and refined using the GW approximation. To emulate the effect of nanoribbon systems deposited on various substrates, we increased the Fermi velocity by up to 75%, aligning with prior observations in the case of graphene on h-BN substrates [26]. Our findings underscore the potential effectiveness of this combined density functional computations and straightforward semi-analytical model by setting experimental parameters or supplementing data from more sophisticated theoretical frameworks.
2. Theoretical Framework
Before delving into the theoretical framework, it is worth noting that we initially employed a comparable approach using conventional DFT computations based on local density approximation (LDA) to calculate the Fermi velocity [27]. However, in this approach, the calculated Fermi velocity ( m/s) fell below the experimental value for graphene ( m/s) [28]. Despite this, we proceeded to explore the potential applications of wide GNRs in biosensing using this approach [29,30]. Recently, we have enhanced our calculations by employing the GW approximation method to investigate silicene and germanene strips [31,32]. Therefore, in this current study, our aim is not to reiterate the previously stated findings but rather to present a comparative analysis of the electronic properties and plasmon characteristics of GNRs, SiNRs, and GeNRs, all possessing a ribbon width of 155 nm.
We chose a ribbon width of 155 nm because of two important points from the experimental perspective:
- GNRs of the same width order have been synthesized in [20] using high-quality chemical vapor deposited (CVD) graphene on Al2O3 substrates;
- Minimize the effects of quantum confinement. For instance, it has been reported by Yang et al. [33] that GNRs with widths less than 57 nm exhibit pronounced sensitivity to quantum confinement. In our present study, our systems are nearly four times larger than the threshold where such effects become prominent, ensuring that the semi-analytical model can be applied without constraints.
2.1. Semi-Analytical Framework
To begin, we use the approach introduced by Popov et al. [25] (see Refs. inside). The underlying principle of the semi-analytical model is rooted in the linear dispersion of charge carriers in 2D Dirac-like materials (such as graphene, silicene, and germanene), particularly in the vicinity of the Fermi level and around the K points in the first BZ. The dispersion relation for charge carriers (e.g., electrons or holes) in this approximation is given using [6,25]:
- is the energy of the charge carrier as a function of the wave vector k;
- is the reduced Planck constant;
- is the Fermi velocity of electrons/holes;
- is the magnitude of the wave vector k, representing the momentum of the charge carrier.
By calculating the first derivative of with respect to k in Equation (1), one can determine the Fermi velocity using the following expression [6,27]:
Applying the concept of Equation (2), the Fermi velocity can be extracted through a linear fit conducted on the band structure data obtained using the DFT-GW method (see next subsection). This analysis involves calculating the slope of the linear fit and subsequently multiplying it by 1/.
On the other hand, the effective mass () in 2D Dirac-like materials as [25,27]:
By extracting from Equation (1), Equation (3) can be expressed as:
where is the Fermi energy. In the context of nanoribbons, the effective mass is often calculated using the bandgap value () instead of the Fermi energy because nanoribbons typically have a finite (direct) bandgap, resulting in the following expression [25,27]:
where the bandgap is calculated using Equations (3) and (5), and taking for simplicity , as follows [25]:
Here, is the ribbon width. After determining the bandgap and effective mass as functions of the ribbon width and the Fermi velocity, we can estimate the energy band structure of GNRs, SiNRs, and GeNRs using the following expression [25,28]:
where is the 1D integer band index number. It is worth emphasizing that in Equation (6), as the ribbon width increases (), both the bandgap and Equation (7) approach zero ( and , respectively, as the case of ideal 2D Dirac-like materials). This observation indicates that quantum confinement becomes progressively less significant. Now, we can analyze the DOS spectrum by analyzing the band structure data through a conventional histogram with evenly sized bins.
In the previous Equations (3)–(7), the electronic properties are calculated for an isolated nanoribbon. Plasmonic properties, on the other hand, can be investigated for both isolated systems and periodic arrangements, with the latter taking the form of 2D arrays. To achieve this, we can employ the following expression [25]:
Compared to our previous works, Equation (8) considers an electron relaxation rate of in this study, indicating the absence of electron scattering or relaxation within the material. However, it is worth noting that a comprehensive analysis of these parameters can be found in Refs. [31,32].
In Equation (8), , , , , and represent the electron charge, dielectric constant, wave vector, excitation angle, and 2D charge density, respectively. Specifically, the 2D charge density can be employed to customize Equation (8) and analyze the ribbons as either isolated systems or periodic arrays using the following expression [13,25,31,32]:
Here, is the one-dimensional (1D) charge density, and is the vacuum distance between attached ribbons. Subsequently, Equation (8) can be formulated as follows [32]:
However, as mentioned above, when the nanoribbons are organized as 2D periodic arrays, the response of the 2D plasmon mode is notably improved, and this is the main motivation for using Equation (8) as written.
In this context, the 2D charge density can be calculated from the Fermi level approach, as follows [29,30]:
Reorganizing Equation (11), the 2D charge density can be expressed as [29,30]:
As noted, the Fermi velocity of 2D Dirac-like materials plays a crucial role in Equations (1)–(12) and, more broadly, in the entire semi-analytical modeling approach.
2.2. DFT-GW Approach
For further details, see Refs. [31,32]. The ground-state properties of 2D Dirac-like materials (i.e., graphene, silicene, and germanene) were determined through DFT using the Abinit software (Version 6.3) [34], with a specific focus on the LDA [35]. The number of plane waves (PWs) is limited by the energy cut-off of ~680 eV. To cancel the effect of core electrons, norm-conserving pseudopotentials of the Troullier–Martins type were utilized [36]. To satisfy the 3D periodicity necessary for PW-DFT calculations, we set a vacuum separation of 20 along the z-axis. This study focuses on freestanding systems, and the need for geometric optimization was deemed unnecessary, as its influence on the determination of charge carrier velocity was found to be negligible, extending to no more than the third significant digit. The structural parameters (lattice constant and buckling) are reported in Table 1. To compute the band structure of all systems, we prepared a high-resolution Monkhorst–Pack grid [37] of 540 × 540 × 1, enabling the calculation of the linear band structure of graphene, silicene, and germanene near the K point and incorporating up to eight bands. The Kohn–Sham electronic structure, encompassing the ground-state energy and electronic density, serves as the initial input for the subsequent GW calculation.

Table 1.
Summary of structural parameters of freestanding systems under study.
To enhance the precision of DFT calculations, it becomes crucial to account for many-body effects, and one effective method to achieve this is by employing the many-body GW self-energy approach [38]. The GW method is a well-established technique for enhancing the accuracy of DFT calculations, and this improvement is achieved by incorporating the many-body GW self-energy formulation. In our computations, we simplify the approach by omitting vertex corrections in both polarizability and self-energy calculations. As mentioned earlier, we build upon the Kohn–Sham (KS) electronic structure to construct the G and W components as part of the GW procedure. Finally, to facilitate efficient integration across frequencies, we adopt the contour deformation (CD) scheme [39].
To emphasize, we solely implemented the one-shot G0W0 approach, a non-self-consistent method. This technique involves computing the Green’s function (G0) and the screened Coulomb interaction (W0) directly from the initial density functional theory (DFT) outcomes without engaging in any subsequent iterative refinement. Additionally, our calculations did not incorporate any form of (partial) self-consistent GW methodologies.
We point out this in our GW calculations for graphene. We chose LDA for its computational efficiency and proven accuracy in this specific context [13,32]. While generalized gradient approximation (GGA) or hybrid functionals might offer certain advantages in modeling complex exchange-correlation effects, the LDA-GW approach is less computationally demanding, allowing for more extensive sampling or larger systems within the same computational budget. Notably, in our study, LDA-GW achieved a Fermi velocity within 1.6% of the experimental value for graphene, underscoring its effectiveness. This precision, combined with computational simplicity, makes LDA-GW particularly suitable for materials like graphene, where key electronic properties are captured accurately without the need for more complex functionals.
Furthermore, all refined DFT-GW computations were carried out on the tier-0 high-performance computing (HPC) facility known as Marconi, which is operated by the CINECA Consortium in Italy. Given the advanced capabilities of this facility, each calculation was completed in less than 0.5 real hours (non-computational hours), though this was preceded using several preparatory tests.
3. Data Description
3.1. Data Generation
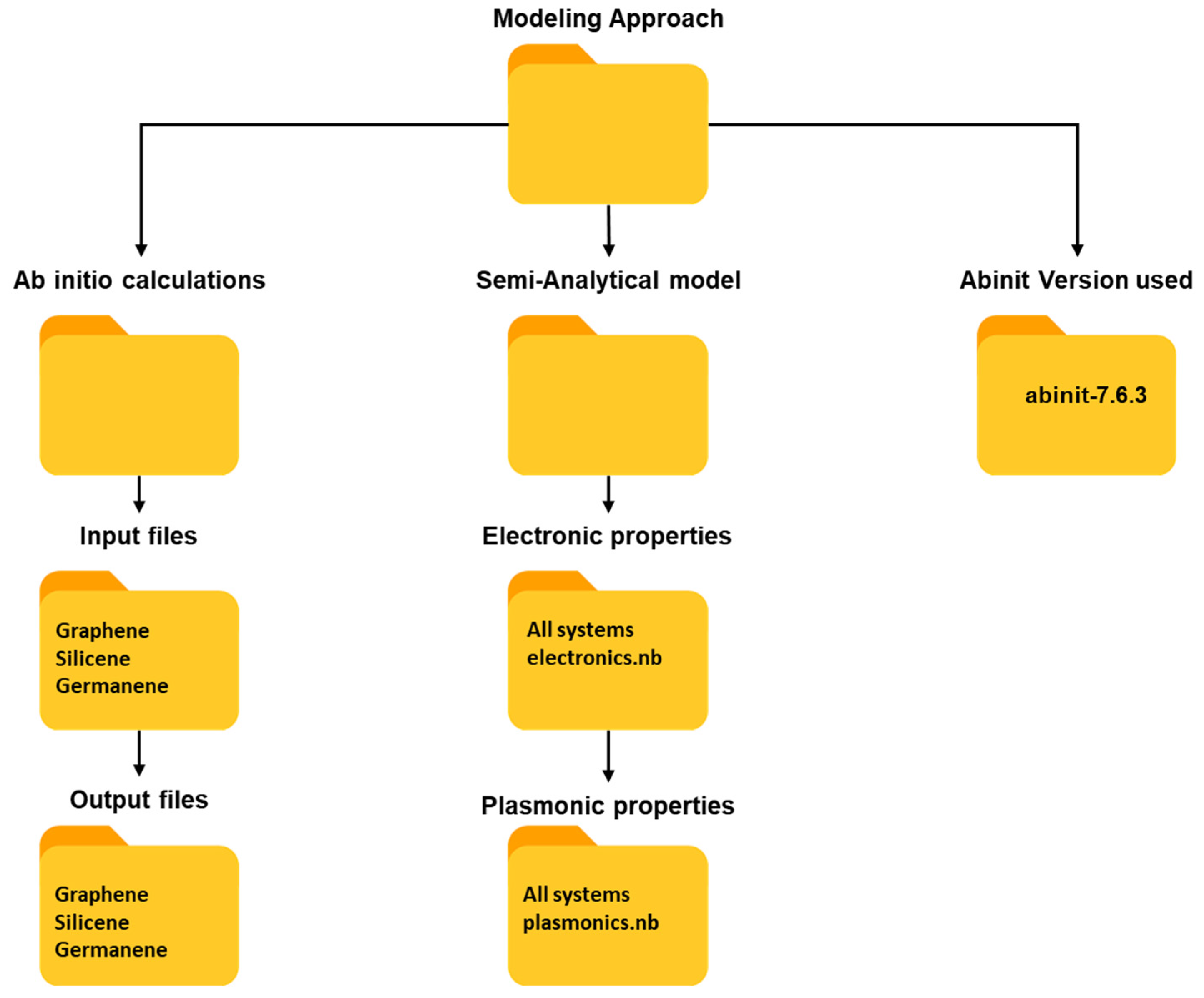
The datasets accompanying this study as supplementary files provide the data compiled during the computational studies in [13,27,31,32]. The primary file is separated into subfolders that are denoted in Scheme 1. A root directory has been established, comprising three distinct subdirectories. The first, titled ‘Ab initio calculations’, contains both the input and output files pertinent to density functional theory calculations. The second subdirectory, named the ‘Semi-analytical model’, houses files associated with the semi-analytical model employed to analyze electronic and plasmonic properties. Lastly, the third folder, labeled ‘Abinit Version Used’, contains the specific version of the Abinit software that was utilized.
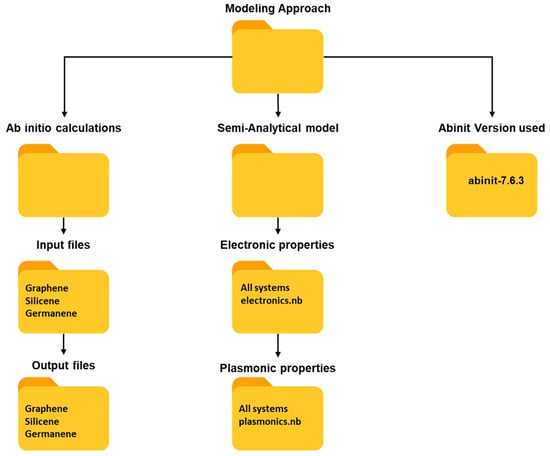
Scheme 1.
Scheme of generated data for ab initio and semi-analytical computations.
Within the ‘Input files’ subfolder, as an example for silicene, there are five key files. The first is a pseudopotential file for silicon of the Troullier–Martins type. The second, ‘silicene.files’, interfaces with the Abinit software to set up calculations. The third file, ‘silicene_den.in’, is dedicated to computing electron density. The fourth file, ‘silicene_bnd.in’, calculates the band structure. Lastly, the ‘KSS.in’ file is responsible for determining the refined Kohn–Sham electron structure. The results of all these calculations are in the respective output folder.
After completing the ab initio calculations for the various systems under investigation, we extract the primary parameter of the semi-analytical model: the Fermi velocity. For ease of calculation and result visualization, this model is implemented in a Mathematica worksheet. However, the simplicity of the model’s underlying equations allows for the use of alternative software for analysis and data plotting. With this in mind, two folders have been created, each containing specific files for analyzing electronic and plasmonic properties. These are named ‘All systems electronics.nb’ and ‘All systems plasmonics.nb’, respectively.
Note that all numerical data and figures in this study were generated conventionally using Mathematica software. Specifically, all fittings and computations were performed using Mathematica 12, licensed in 2019 through CEDIA: https://www.cedia.edu.ec/es/licencias-wolfram.
3.2. Electronics Properties: Freestanding Systems
We point out that while the semi-analytical model effectively derives the properties of nanostrips, our focus on GW calculations is driven by the need for accurate Fermi velocity estimation. As an example, for graphene [13], the conventionally used Fermi velocity ( m/s [28]) notably varies from experimental and GW-calculated values. These variations are crucial at the THz scale (0.1 eV), where our research is focused, as they can significantly impact the predicted electronics and plasmonics. Therefore, GW calculations are essential for the accuracy and predictive validity of our results at this scale, aligning with future experimental verifications and applications.
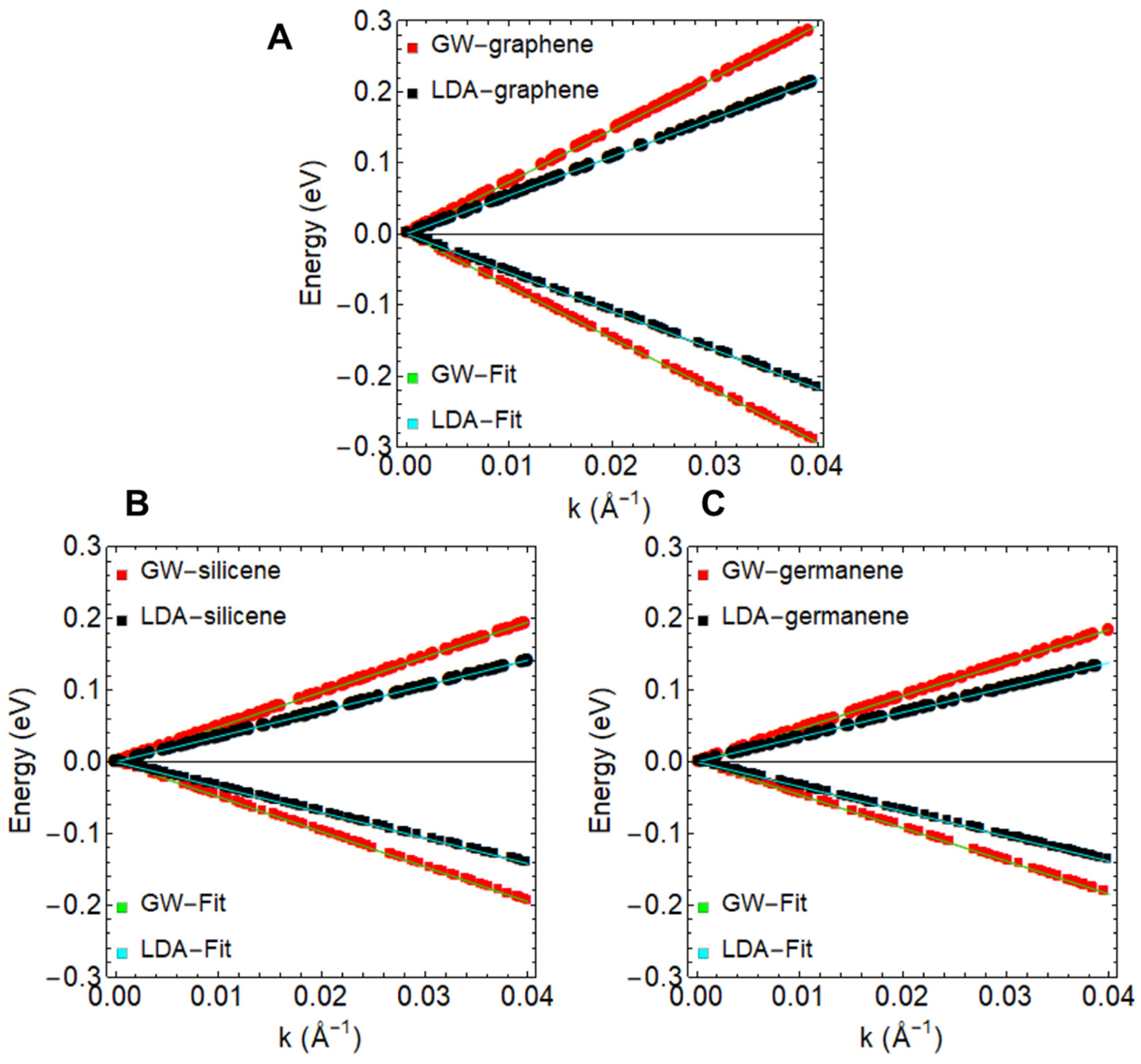
Figure 1 presents a comparative analysis of the band structures of freestanding graphene (Figure 1A), silicene (Figure 1B), and germanene (Figure 1C) along the path at the Fermi level and in the vicinity of the K point, obtained using both the LDA (black points) and GW (red points) approaches. While all these systems exhibit linear band dispersion, it is noteworthy that the slopes derived from GW calculations are consistently vertical than those obtained from LDA computations. This outcome suggests a higher Fermi velocity in all cases (see Table 2).
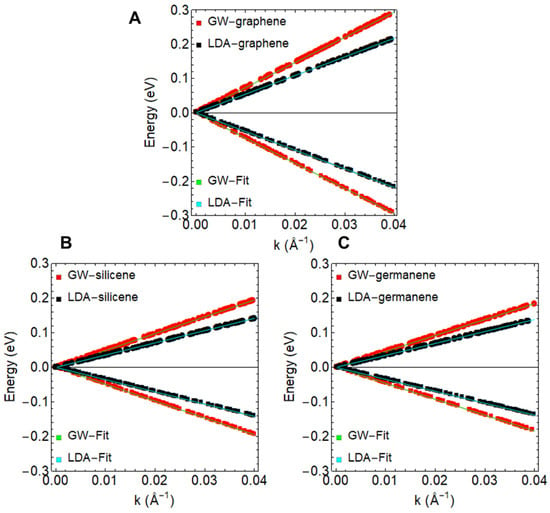
Figure 1.
Electronic band structure computed using the LDA (black points) and GW (red points) methods: (A) graphene, (B) silicene, and (C) germanene. Green and cyan lines represent the linear fit.

Table 2.
Summary of estimated parameters of freestanding 2D systems under study. The effective mass and bandgap values were calculated using Equations (5) and (6), respectively, for a ribbon width of 155 nm.
Through DFT data fitting using Equation (2), we determined the Fermi velocity of graphene to be m/s, aligning closely with the experimental value of m/s [28]. In the case of silicene and germanene, Fermi velocities were determined to be m/s and m/s, respectively (see Table 2). As depicted in Figure 1, the slopes of the band structures for silicene and germanene, in comparison to graphene, are less pronounced, indicating a reduction in Fermi velocities by approximately 33.4% and 37.2%, respectively.
3.3. Electronic Properties: Freestanding Ribbon Systems
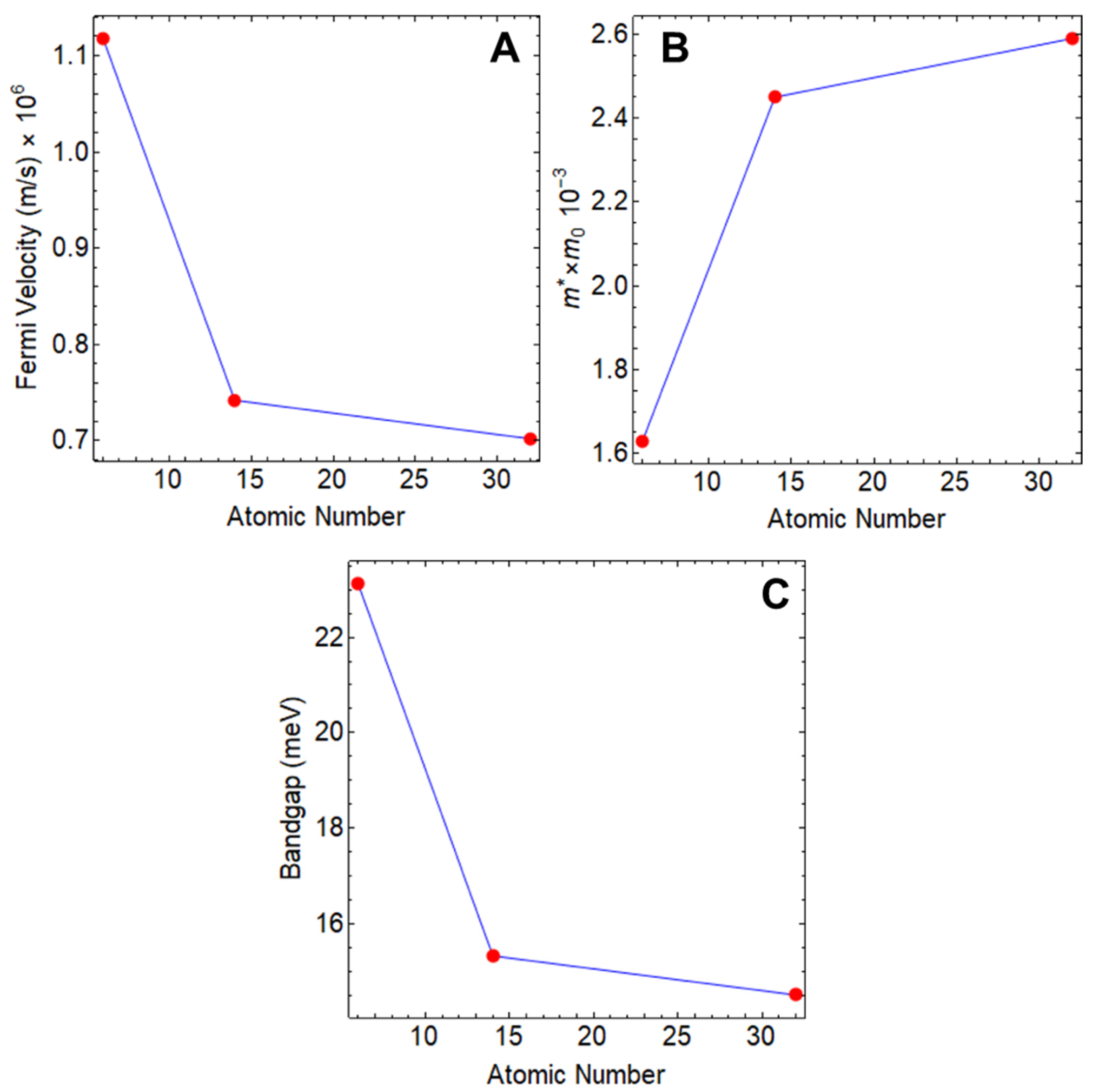
In Figure 2 (and Table 2), we observe the variation of the Fermi velocity (Figure 2A), effective electron mass (Figure 2B), and bandgap (Figure 2C) in relation to the atomic number for a 155 nm wide nanoribbon. These data provide valuable insights into the behavior of these crucial electronic properties as we move up the periodic table and increase the atomic weight. While atomic nuclei fundamentally shape a system’s structural (geometry) properties, there is a discernible trend in the variations of these properties with the ascending atomic number.
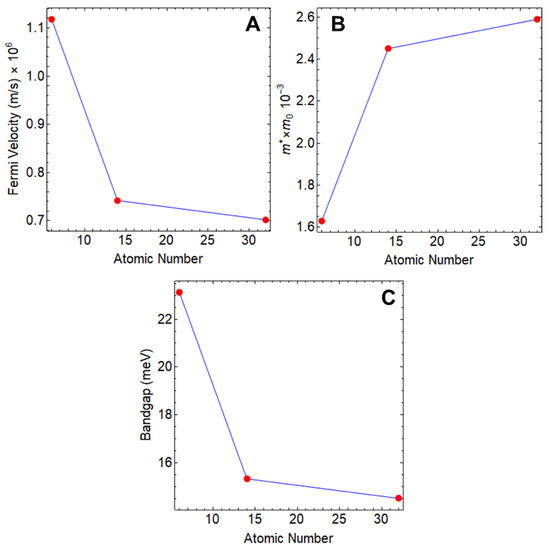
Figure 2.
Estimated parameters of (A) Fermi velocity, (B) electron effective mass, and (C) bandgap as a function of the atomic number: C6, Si14, and Ge32. The ribbon width was fixed at 155 nm.
In particular, we can observe a notable reduction in both the Fermi velocity and bandgap, following a decreasing exponential trend as the atomic number increases. In the context of bandgap and considering nanoribbons with identical widths (155 nm), there is a reduction of 33.6% for SiNR and 37.0% for GeNR. Concurrently, the effective mass experiences an increase, with increments of 33.5% and 37.1%, respectively, compared to that of the GNR.
While the electronic properties of materials are primarily governed by their electronic structures, it is worth noting that the atomic number’s significance comes into play due to its influence on the nature of atomic orbitals. Atomic orbitals, determined via the atomic number, have the potential to impact the degree of overlap between neighboring atoms within the material. With a higher atomic number, the orbitals tend to be more extensive, fostering stronger orbital overlap. This increased overlap can, in turn, broaden the energy bands within the material, potentially resulting in a reduction of the bandgap and affecting other related properties.
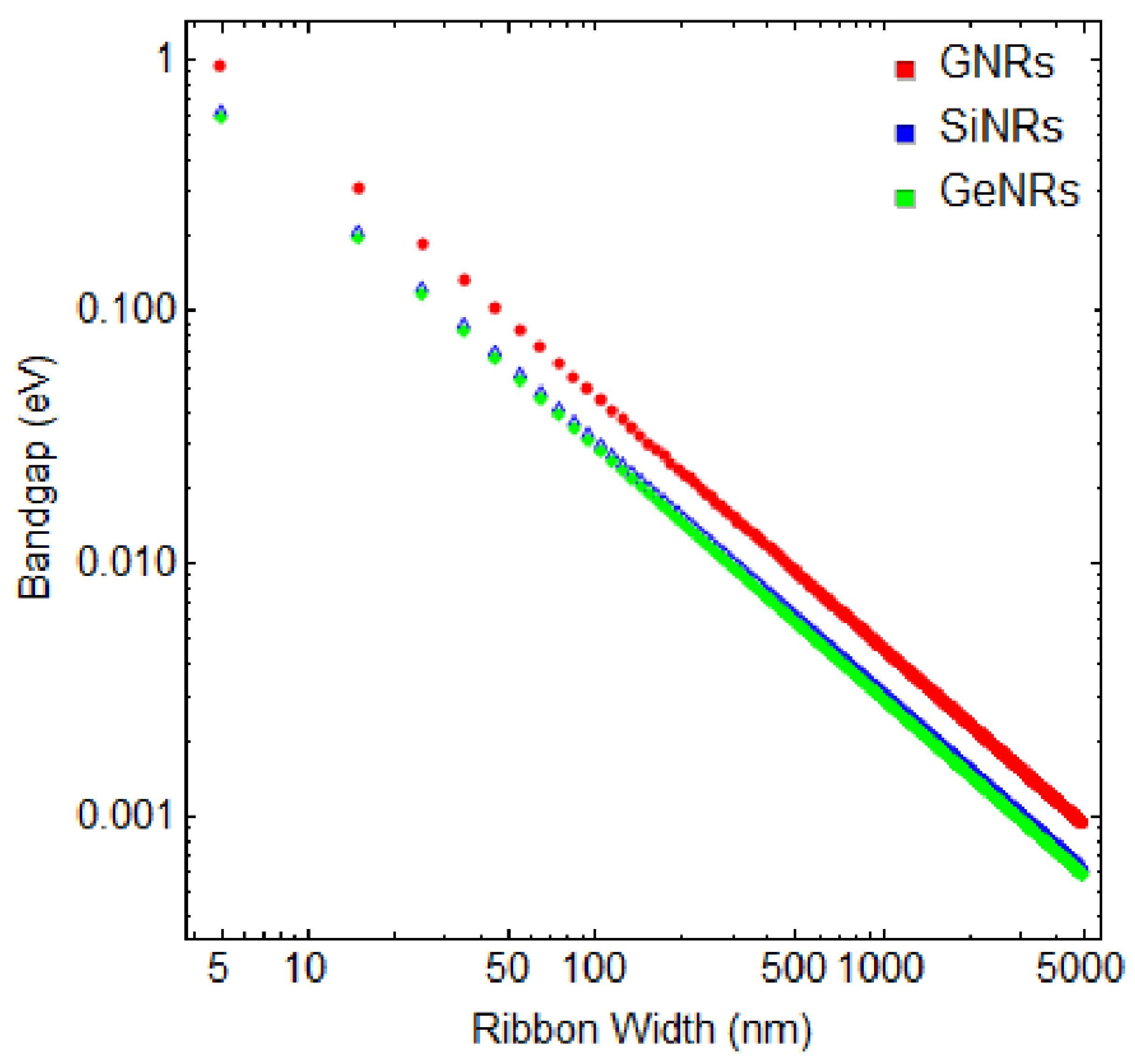
Figure 3 provides a helpful depiction of the bandgap variations in GNRs (red points), SiNRs (blue points), and GeNRs (green points) in response to changes in nanoribbon width, spanning from 5 nm to 5 µm, calculated using Equation (6). Notably, the bandgap of a 5 nm GNR approaches nearly 1 eV, aligning remarkably closely with the experimentally measured value for a GNR on Ge(001) substrates [40]. This observation underscores the potential adaptability of such systems concerning bandgap adjustments, a prospect that holds significant relevance in the context of current semiconductor technology rooted in silicon, which boasts a bandgap of 1.1 eV.
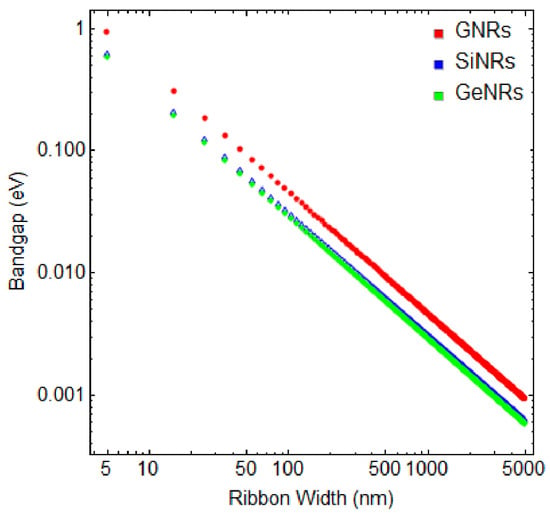
Figure 3.
Bandgap variation as a function of the ribbon width from 5 nm to 5 μm for GNRs (red points), SiNRs (blue points), and GeNRs (green points).
While Equation (6) may appear straightforward, its simplicity is quite powerful in enabling accurate predictions that align well with experimental findings. This simplicity serves as a valuable tool for forecasting the bandgap values for SiNRs and GeNRs based on their respective widths. An intriguing observation is that the bandgap of these nanoribbons undergoes a significant reduction, transitioning from the eV scale to the realm of just a few meV. This phenomenon underscores the adaptability of these nanoribbon systems, mainly in contexts where extremely small bandgaps are required, such as in the domains of photonics and plasmonics, to operate at THz frequencies [41,42,43].
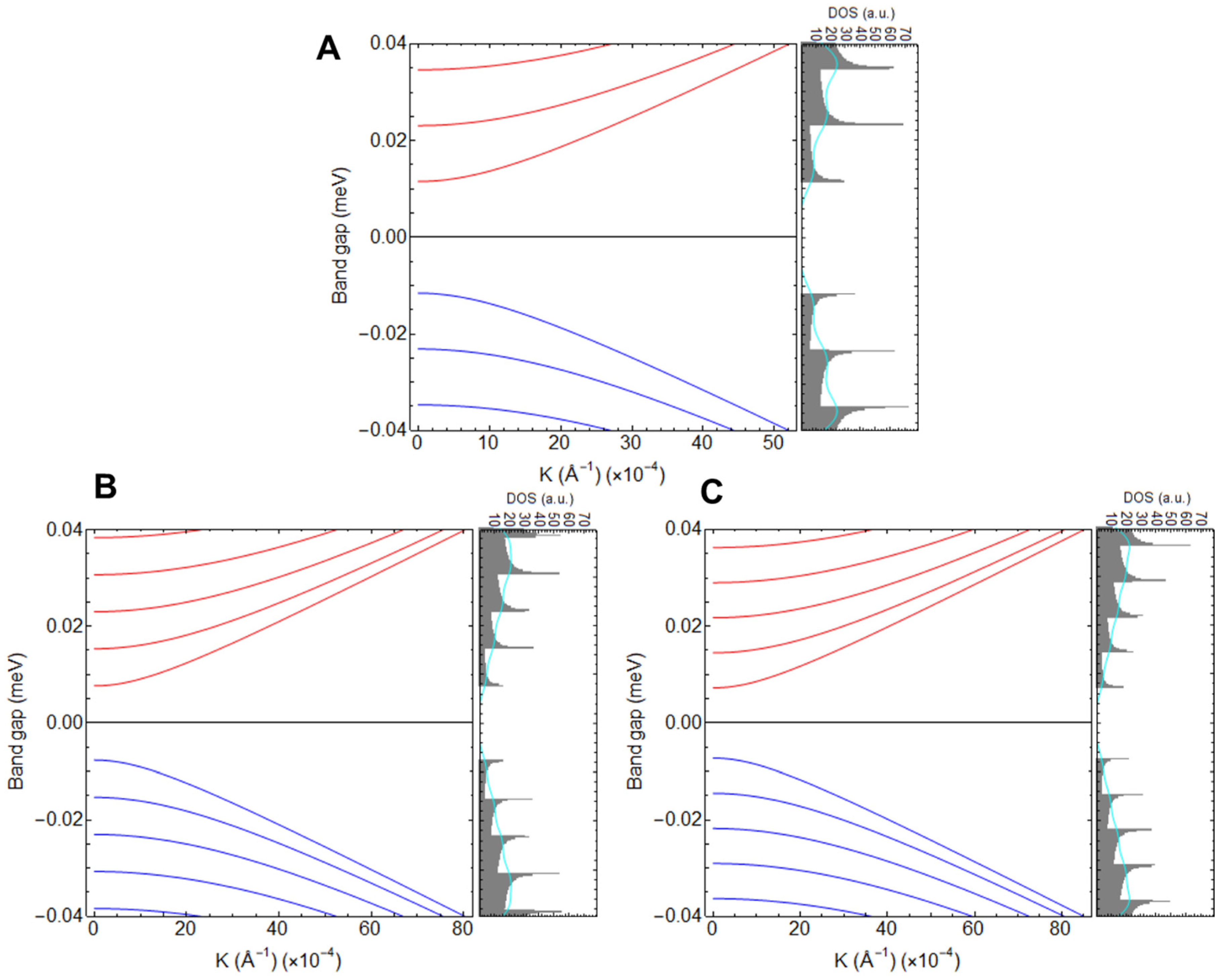
In Figure 4, utilizing Equation (7), we gain valuable insights into the band structures and DOS of the GNR (Figure 4A), SiNR (Figure 4B), and GeNR (Figure 4C) while maintaining a constant width of 155 nm. One of the most significant observations is that as we examine the region around 0.04 eV, a change in the atomic element () leads to an increase in the number of bands, subsequently impacting the DOS. To illustrate, in the case of the GNR, we discern the presence of three conduction bands and three valence bands, whereas, in SiGNR and GeNR, we encounter five conduction bands and five valence bands. It is worth that, as mentioned, the bandgap for the 155 nm wide SiNR (23.12 meV) and 155 nm wide GeNR (15.34 meV) is smaller when compared to that of the 155 nm wide GNR (14.52 meV). This distinctive alteration in electronic properties emphasizes the role of atomic composition in shaping the band structure and DOS.
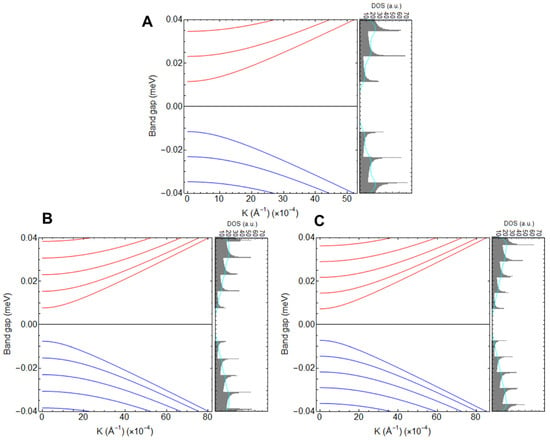
Figure 4.
Electronic band structure and density of states (DOS) of (A) GNR, (B) SiNR, and (C) GeNRs. The ribbon width was fixed at 155 nm. The cyan line represents the smoothed DOS.
3.4. Plasmonic Properties: Freestanding Ribbon Systems
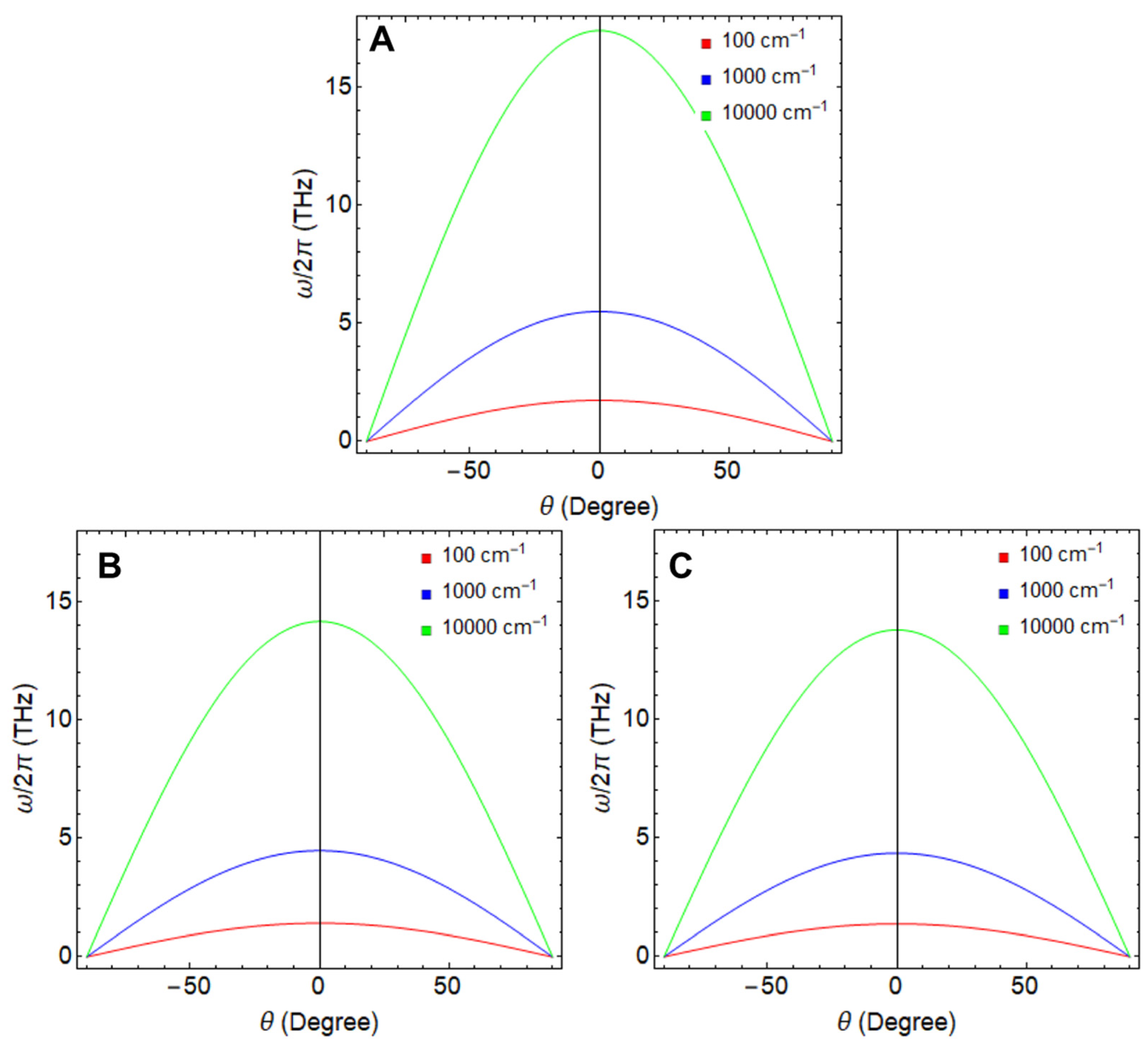
We now focus on the plasmonic properties of nanoribbons in the THz scale, all featuring a width of 155 nm and using Equation (8). Figure 5 presents the tunability of the plasmon frequency on both the excitation angle () and three different momentum values: cm−1 (red line), cm−1 (blue line), and cm−1 (green line).
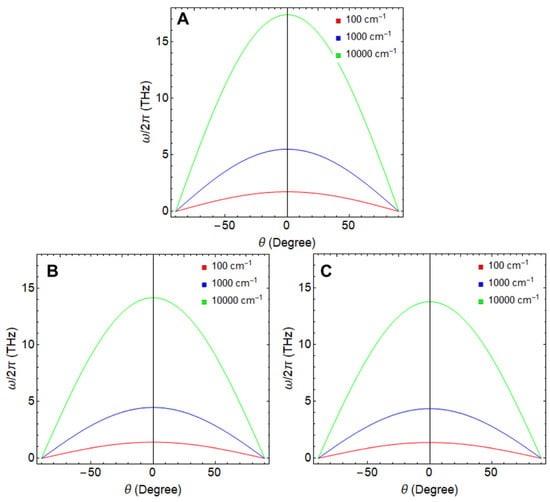
Figure 5.
Plasmon frequency as a function of the angle variation () considering different plasmon momenta: cm−1, 0 cm−1, and cm−1. The ribbon width was fixed at 155 nm. (A) GNR, (B) SiNR, and (C) GeNR.
In the context of a GNR (Figure 5A), we can discern a distinctive pattern in the plasmonic frequency. At a momentum of 100 cm−1 (red line) and an angle of , the plasmonic frequency exhibits a pronounced minimum, hovering around the 2 THz range. As we endeavor into higher momentum values, this frequency increases, surging to nearly 5 THz at 1000 cm−1 (blue line) and a notable 17 THz at 10,000 cm−1 (green line), all while maintaining an angle of . A noteworthy trend across all these scenarios is the frequency attenuation as the angle progresses toward , consistent with the behavior predicted using Equation (8), which hinges on the cosine function.
Likewise, when we turn our attention to SiNR (Figure 5B) and GeNR (Figure 5C), a parallel trend unfolds. Increasing the momentum while maintaining yields a distinct peak in the plasmonic frequency. However, it is noteworthy that the frequency maxima for SiNR and GeNR fall on the lower end of the spectrum compared to the GNR. Specifically, SiNR reaches an approximate maximum of 14 THz, while GeNR achieves nearly 13 THz.
Our next parameter of scrutiny is the 2D charge density. While this value can be computed using Equation (12), for the sake of clarity and visualization, we have opted to employ three distinct magnitudes: cm−2 (green line), cm−2 (blue line), and cm−2 (red line). Furthermore, as stated, this parameter can be controlled by employing Equation (9), specifically by adjusting the separation distance between nanoribbons.
It is worth noting that from an experimental perspective, these alterations in charge density can be achieved through charge-transfer mechanisms during interactions between nanoribbons and the substrate on which they are placed. A similar effect unfolds in biosensor applications, where nanoribbons interface with the target molecule, leading to potential shifts in charge density due to nucleophilic or electrophilic interactions.
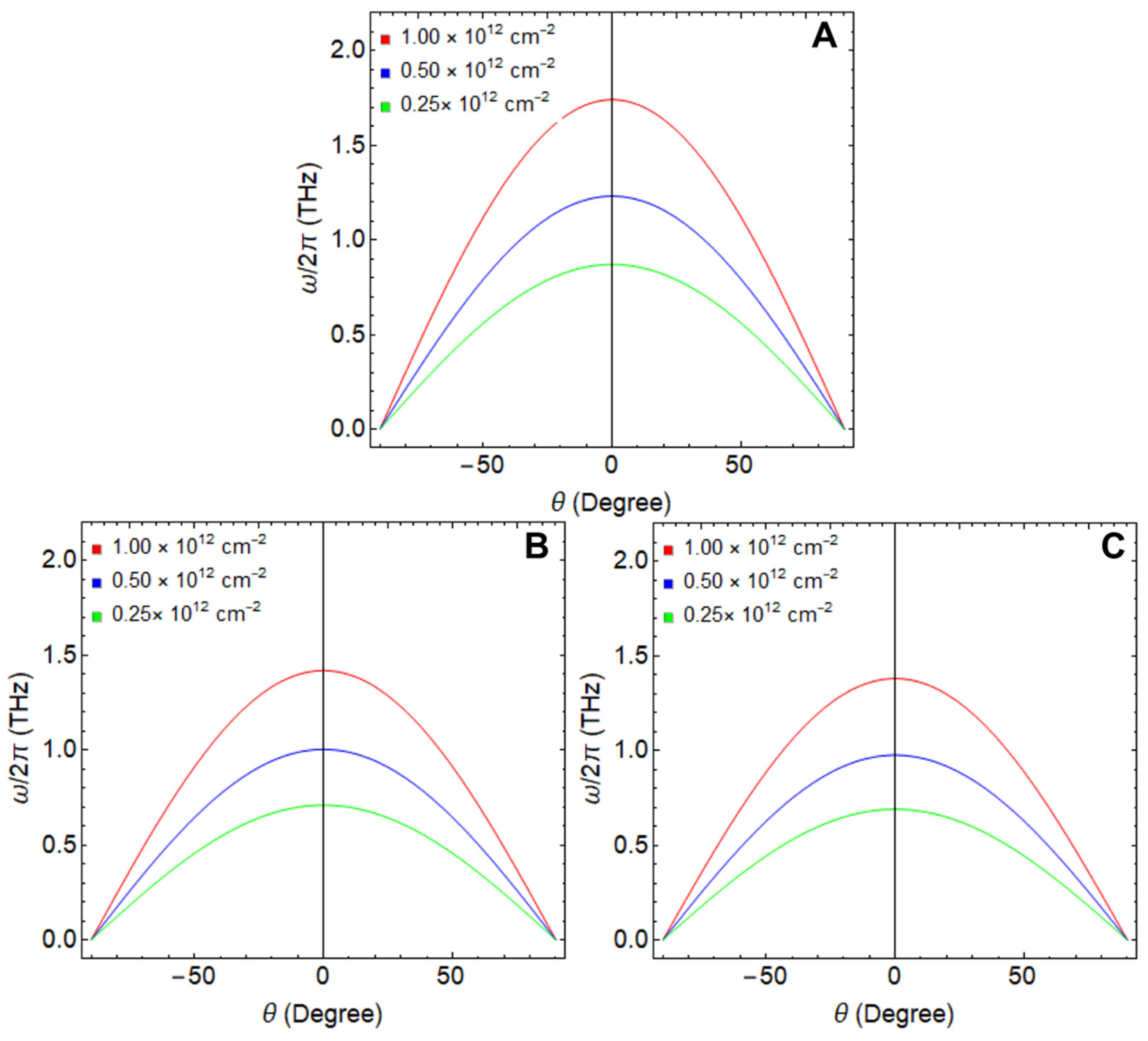
In light of this, we delve into the plasmon frequency behavior, as depicted in Figure 6, for the GNR (Figure 6A), SiNR (Figure 6B), and GeNR (Figure 6C). As previously discussed, the GNR demonstrates its maximum peak frequency at . However, when we test a momentum value of cm−1, we observe a noteworthy shift in these maxima. Specifically, for a charge density of cm−2 (red line), the maximum hits almost 1.8 THz, reducing to nearly 1 THz for a charge density of cm−2 (blue line), and further declining to approximately 0.8 THz for a charge density of cm−2 (green line). Aside from highlighting the material adaptability, these findings unveil resonances occurring at frequencies below 2 THz, a region highly relevant for numerous biosensing applications.
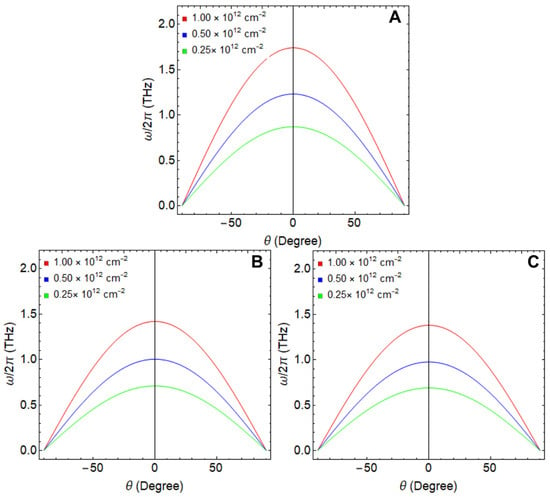
Figure 6.
Plasmon frequency as a function of the angle variation () considering different charge densities: cm−2, cm−2, and cm−2. The ribbon width was fixed at 155 nm and cm−1. (A) GNR, (B) SiNR, and (C) GeNR.
As an example, consider the challenge of detecting molecules in aqueous environments. The significant hurdle here is the interference caused by water, which exhibits a resonance at nearly 1 THz. This underscores the need for ultra-sensitive materials operating within this frequency range to pinpoint and identify the molecules of interest effectively.
Interestingly, SiNR and GeNR exhibit resonances within a similar frequency range at the same moment ( cm−1) and . This observation strongly indicates that these materials hold significant promise for a wide array of applications, particularly in the realm of molecular sensing. Nevertheless, we point out that the plasmon frequency in both materials is slightly lower compared to the GNR. Their maximum frequencies are approximately 1.4 THz, with minimums at around 0.6 THz. This can be attributed to the relationship outlined in Equation (10), which indicates an inverse proportionality between the plasmon frequency and effective mass (). In simpler terms, the higher the effective mass, the lower the plasmon frequency, or a lower Fermi velocity results in lower plasmon frequencies. It is essential to highlight that the plasmon frequency can be enhanced and raised by increasing the charge density or the transferred charge, which, in turn, relies on the specific molecule of interest or substrate. We will delve into this aspect further in the following analysis (Table 3 and Figure 7). As stated, we observed a decrease in Fermi velocity and plasmon frequency as we transitioned between different systems (GNR→SiNR→GeNR). To gain a deeper understanding, we will now examine individual cases to analyze the influence of the substrate in GNR (Figure 7A), SiNR (Figure 7B), and GeNR (Figure 7C).

Table 3.
Summary of estimated parameters by increasing the Fermi velocity.
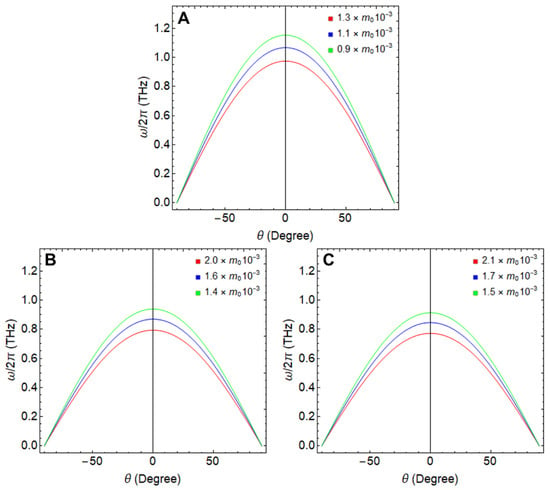
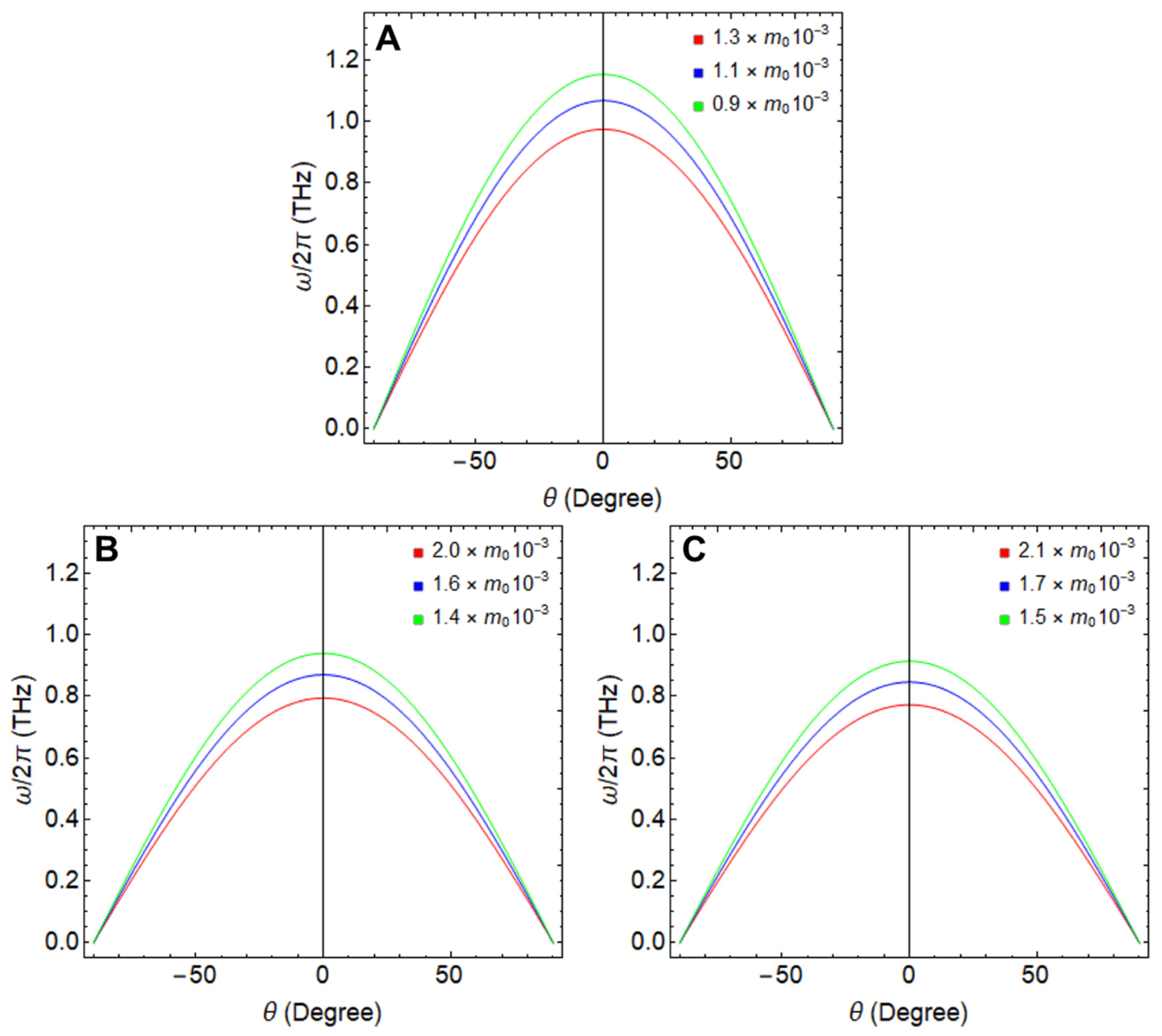
Figure 7.
Plasmon frequency as a function of the angle variation () considering different effective masses, which were varied by increasing the Fermi velocity from 25% to 75% (see Table 2). The ribbon width was fixed at 155 nm and cm−1. (A) GNR, (B) SiNR, and (C) GeNR.
Hwang et al. [26] have demonstrated the tunability of the Fermi velocity of graphene through substrate engineering. They achieved these results by depositing graphene on different substrates, resulting in distinct Fermi velocities while maintaining the electronic properties. Specifically, graphene deposited on SiC(000-1), hBN, and Quartz exhibited Fermi velocities of m/s, m/s, and m/s, respectively. In other words, graphene can significantly enhance its Fermi velocity by up to approximately 150% without sacrificing its Dirac-like behavior. Similar expectations could be extended to silicene and germanene.
In Table 3, we have conservatively increased the Fermi velocity from 25% to 75%, as achieving a 150% boost in silicene and germanene might be more challenging due to their buckled structures, which could potentially disrupt symmetry. Also, Table 3 provides the calculated effective masses for various increments in Fermi velocity. These values serve as essential inputs for determining the plasmon frequencies across different nanoribbons, all while keeping their ribbon width constant at 155 nm and cm−1.
Across all systems, an increase in Fermi velocity results in a decreased effective mass, which in turn spurs the plasmon frequency to rise. For the GNR and , we observe a maximum frequency of nearly 1.1 THz at (green line) and a minimum of 0.9 THz at (red line). Meanwhile, for SiNR and GeNR, the plasmon frequency remains slightly lower, with a maximum of approximately 0.9 THz and a minimum of around 0.7 THz, alongside similar effective mass values.
3.5. Comparison with the Literature
Our results expand additional relevance in light of recent advancements in the production of graphene, silicene, and germanene nanostrips, which can now be manufactured in wide or narrow dimensions, as indicated in Refs. [20,40]. This technological progress is complemented by our demonstration of the adjustable band gaps in these materials. The success in manipulating these properties has spurred further research into more complex structures. A notable example is the investigation into two-dimensional (2D) metallic transition metal dichalcogenide nanoclusters, such as MoTe2 in its metallic (1T’ phase) form embedded within a semiconducting polymorph (MoTe2 in 1H phase), as discussed in Ref. [44].
While extended tight-binding models incorporating third-nearest-neighbor hopping and a Hubbard mean-field interaction term [45], as well as density-functional computations based on the generalized gradient approximation (GGA) [46], are viable for understanding the electronic properties of narrower graphene, silicene, and germanene nanoribbons, they have a significant limitation. These approaches are typically constrained to systems of only a few nanometers. This restriction becomes particularly challenging for ab initio methods when modeling larger systems, such as the 155 nm systems described in our data descriptor article, which align with experimental observations [20]. Consequently, while these methods offer valuable insights, their applicability is limited in the context of our larger-scale studies.
On the other hand, the effectiveness of our modeling approach was demonstrated through its alignment with the previous literature. For example, Ref. [27] provides a comparison of the bandgap values predicted using our semi-analytical model against experimental measurements, focusing on graphene nanoribbons with widths ranging from 15 to 90 nm. This comparison highlighted a notable agreement between our model predictions and experimental data [47]. Furthermore, we have also compared our results with those obtained using the GW approximation for various widths of graphene nanoribbons [48]. This comparison is particularly insightful, showing a remarkable correlation for nanoribbons wider than 1.5 nm.
In Ref. [32], we applied the semi-analytical model to estimate the bandgap of a 2.7 nm wide graphene nanoribbon, as experimentally observed by Kiraly et al. [40] on Ge(001). Our findings indicate that this nanoribbon exhibits a bandgap of approximately 1.7 eV. Remarkably, the smoothed curve of the density of states (DOS) histogram from our model aligns perfectly with the results obtained using scanning tunneling spectroscopy (STS).
Finally, and of equal significance, in Ref. [13], we compared our predictions with those in Ref. [18], which reports on a freestanding, narrow-wide five-armchair graphene nanoribbon (5AGNR) with similar plasmonic properties. In this comparison, we explicitly establish a relationship and observe a perfect alignment between the semi-analytical model and time-dependent density functional theory (TDDFT) results. All this concordance highlights the robustness of the semi-analytical approach, demonstrating its capability to accurately predict complex plasmonic behaviors in nanoribbons or nanostrips.
4. Conclusions
The data presented were produced in [13,27,31,32], and the findings are discussed as a comparative analysis of the electronic and plasmonic properties of freestanding and ribbon-like structures of graphene, silicene, and germanene with a constant ribbon width of 155 nm.
From the perspective of electronic properties:
- Freestanding graphene, silicene, and germanene all exhibit linear band dispersion, with higher Fermi velocities obtained from GW calculations compared to LDA calculations;
- The Fermi velocity for freestanding graphene, silicene, and germanene was determined to be m/s, m/s, and m/s, respectively;
- As we move up the periodic table, we observe a reduction in both Fermi velocity and bandgap, highlighting the influence of the atomic number on these electronic properties;
- The bandgap of nanoribbons (GNRs, SiNRs, and GeNRs) can be significantly adjusted by changing the ribbon width, showing potential applications in optoelectronics and current semiconductor technology.
From the perspective of plasmonic properties:
- Plasmon frequencies were investigated for GNRs, SiNRs, and GeNRs at various excitation angles and momentum values. GNRs exhibited a pronounced plasmon frequency variation with angle and momentum, while SiNRs and GeNRs showed lower maximum frequencies;
- The plasmon frequency can be controlled by adjusting charge density, making these materials suitable for biosensing applications;
- The plasmon frequency can be enhanced by increasing charge density or modifying the substrate, demonstrating their adaptability for specific applications.
An important outcome is that the Fermi velocity can be increased, and effective mass can be reduced through substrate engineering, similar to observations in graphene. The increase in Fermi velocity resulted in higher plasmon frequencies. This suggests that silicene and germanene also hold promise for Fermi velocity tuning and plasmonic applications.
The intent of this study is to increase the reproducibility of the work achieved in [27,31,32]. We hope to elucidate our methods and computational models to create a framework that other researchers can follow to build on or validate our work. The data are published in a text file format to make it accessible to researchers who may not have access to or experience with the Abinit package. The base semi-analytical model is also made available for other work that may want to use and modify it for new geometries and studies. We hope that other sophisticated computational methods can produce similar results and thus encourage more research, particularly in the field of bandgap engineering and plasmonics.
Author Contributions
Conceptualization, S.B. and C.V.G.; methodology, N.B.G., J.V. and M.Á.S.P.; validation, C.V.G. and M.G.; writing—original draft preparation, T.T. and C.V.G.; writing—review and editing, C.V.G.; visualization, J.V.and M.G.; supervision, S.B.; project administration, T.T.; funding acquisition, T.T. All authors have read and agreed to the published version of the manuscript.
Funding
This work was funded by Universidad Técnica Particular de Loja (“Análisis de las propiedades térmicas del grafeno y zeolita” Grand No.: PROY_INV_QU_2022_362).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data provided in the article are accompanied by a detailed methodology, making it possible for readers to reproduce and generate similar data using the described approach.
Acknowledgments
T.T., M.G. and C.V.G. wish to thank the Ecuadorian National Department of Sciences and Technology (SENESCYT). This work was partially supported by LNF-INFN: Progetto HPSWFOOD Regione Lazio-CUP I35F20000400005.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Cao, J.M.; Zatovsky, I.V.; Gu, Z.Y.; Yang, J.L.; Zhao, X.X.; Guo, J.Z.; Haiyang, X.; Wu, X.L. Two-dimensional MXene with Multidimensional Carbonaceous Matrix: A Platform for General-Purpose Functional Materials. Prog. Mater. Sci. 2023, 135, 101105. [Google Scholar] [CrossRef]
- Elbanna, A.; Jiang, H.; Fu, Q.; Zhu, J.F.; Liu, Y.; Zhao, M.; Liu, D.; Lai, S.; Chua, X.W.; Pan, J.; et al. 2D material infrared photonics and plasmonics. ACS Nano 2023, 17, 4134–4179. [Google Scholar] [CrossRef]
- Zia, A.; Cai, Z.-P.; Naveed, A.B.; Chen, J.-S.; Wang, K.-X. MXene, silicene and germanene: Preparation and energy storage applications. Mater. Today Energy 2022, 30, 1011144. [Google Scholar] [CrossRef]
- Kremer, L.F.; Baierle, R.J. Stability, electronic and optical properties of group IV graphenylene-like materials. An ab initio investigation. Diam. Relat. Mater. 2024, 141, 110689. [Google Scholar] [CrossRef]
- Yang, G.; Li, L.; Lee, W.B.; Ng, M.C. Structure of graphene and its disorders: A review. Sci. Technol. Adv. Mater. 2018, 19, 613–648. [Google Scholar] [CrossRef]
- Trivedi, S.; Anurag, S.; Rajnish, K. Silicene and germanene: A first principle study of electronic structure and effect of hydrogenation-passivation. J. Comput. Theor. Nanosci. 2014, 11, 781–788. [Google Scholar] [CrossRef]
- Davis, J.M.; Gustavo, S.; Orozco, G.; Barraza-Lopez, S. Thermally driven phase transitions in freestanding low-buckled silicene, germanene, and stanene. Phys. Rev. Mater. 2023, 7, 054008. [Google Scholar] [CrossRef]
- Novoselov, K.S.; Jiang, D.; Schedin, F.; Geim, A.K. Two-dimensional atomic crystals. Proc. Natl. Acad. Sci. USA 2005, 102, 10451–10453. [Google Scholar] [CrossRef]
- Kurpas, M.; Faria, P.E.; Gmitra, M.; Jaroslav, F. Spin-orbit coupling in elemental two-dimensional materials. Phys. Rev. B 2019, 100, 125422. [Google Scholar] [CrossRef]
- Ezawa, M. Monolayer topological insulators: Silicene, germanene, and stanene. J. Phys. Soc. Jpn. 2015, 84, 121003. [Google Scholar] [CrossRef]
- Chaves, A.; Azadani, J.G.; Alsalman, H.; Da Costa, D.R.; Frisenda, R.; Chaves, A.J.; Song, H.S.; Kim, Y.D.; He, D.; Zhou, J.; et al. Bandgap engineering of two-dimensional semiconductor materials. Npj 2D Mater. Appl. 2020, 4, 29. [Google Scholar] [CrossRef]
- An, J.; Zhao, X.; Zhang, Y.; Liu, M.; Yuan, J.; Sun, X.; Zhang, Z.; Wang, B.; Li, S.; Liet, D. Perspectives of 2D materials for optoelectronic integration. Adv. Funct. Mater. 2022, 32, 2110119. [Google Scholar] [CrossRef]
- Tene, T.; Guevara, M.; Moreano, G.; Calderón, E.; García, N.B.; Gomez, C.V.; Bellucci, S. Modeling Plasmonics and Electronics in Semiconducting Graphene Nanostrips. Emerg. Sci. J. 2023, 7, 1459–1477. [Google Scholar] [CrossRef]
- Sung, Y.; Vejayan, H.; Baddeley, C.J.; Richardson, N.V.; Grillo, F.; Schaubet, R. Surface confined hydrogenation of graphene nanoribbons. ACS Nano 2022, 16, 10281–10291. [Google Scholar] [CrossRef] [PubMed]
- Chen, R.; Peng, F.; Yan, Z.; Yang, Z.; Chen, S.; Chang, Z.; Wang, Y.; Liu, Z.; Huanget, X. Plasmon-enhanced infrared absorption in graphene nanodot array. Plasmonics 2023, 18, 2205–2212. [Google Scholar] [CrossRef]
- Sindona, A.; Pisarra, M.; Belluci, S.; Tene, T.; Guevara, M.; Vacacela Gomez, C. Plasmon oscillations in two-dimensional arrays of ultranarrow graphene nanoribbons. Phys. Rev. B 2019, 100, 235422. [Google Scholar] [CrossRef]
- Nekuee, S.; Khavasi, A. A Novel Method for Fast and Accurate Extraction of Surface Plasmon Modes in Periodic Arrays of Graphene Nanoribbons. IEEE Photonics Technol. Lett. 2024, 36, 297–300. [Google Scholar] [CrossRef]
- Xia, S.; Zhang, D.; Zhai, X.; Wang, L.; Wen, S. Phase-controlled topological plasmons in 1D graphene nanoribbon array. Appl. Phys. Lett. 2023, 123, 101102. [Google Scholar] [CrossRef]
- Khaliji, K.; Biswas, S.R.; Hu, H.; Yang, X.; Dai, Q.; Oh, S.; Avouris, P.; Low, T. Plasmonic gas sensing with graphene nanoribbons. Phys. Rev. Appl. 2020, 13, 011002. [Google Scholar] [CrossRef]
- Fei, Z.; Goldflam, M.D.; Wu, J.-S.; Dai, S.; Wagner, M.; McLeod, A.S.; Liu, M.K.; Post, K.W.; Zhu, S.; Janssen, G.C.A.M.; et al. Edge and surface plasmons in graphene nanoribbons. Nano Lett. 2015, 15, 8271–8276. [Google Scholar] [CrossRef]
- Moon, H.; Yun, J.; Kim, K.H.; Jangd, S.S.; Lee, S.G. Investigations of the band structures of edge-defect zigzag graphene nanoribbons using density functional theory. RSC Adv. 2016, 6, 39587–39594. [Google Scholar] [CrossRef]
- Pengfei, L.; Shi, R.; Lin, P.; Ren, X. First-principles calculations of plasmon excitations in graphene, silicene, and germanene. Phys. Rev. B 2023, 107, 035433. [Google Scholar] [CrossRef]
- Despoja, V.; Mowbray, D.J.; Vlahović, D.; Marušić, L. TDDFT study of time-dependent and static screening in graphene. Phys. Rev. B 2012, 86, 195429. [Google Scholar] [CrossRef]
- Souto, A.; Cunha, D.; Vasilevskiy, M. Modeling of a Plasmonic Biosensor Based on a Graphene Nanoribbon Superlattice. Phys. Status Solidi (B) 2022, 259, 2200055. [Google Scholar] [CrossRef]
- Popov, V.V.; Bagaeva, T.Y.; Otsuji, T.; Ryzhii, V. Oblique terahertz plasmons in graphene nanoribbon arrays. Phys. Rev. B 2010, 81, 073404. [Google Scholar] [CrossRef]
- Hwang, C.; Siegel, D.A.; Mo, S.-K.; Regan, W.; Ismach, A.; Zhang, Y.; Zettl, A.; Lanzara, A. Fermi velocity engineering in graphene by substrate modification. Sci. Rep. 2012, 2, 590. [Google Scholar] [CrossRef]
- Tene, T.; Guevara, M.; Viteri, E.; Maldonado, A.; Pisarra, M.; Sindona, A.; Vacacela Gomez, C.; Bellucci, S. Calibration of Fermi Velocity to Explore the Plasmonic Character of Graphene Nanoribbon Arrays by a Semi-Analytical Model. Nanomaterials 2022, 12, 2028. [Google Scholar] [CrossRef]
- Zhang, Y.; Tan, Y.-W.; Stormer, H.L.; Kim, P. Experimental observation of the quantum Hall effect and Berry’s phase in graphene. Nature 2005, 438, 201–204. [Google Scholar] [CrossRef]
- Tene, T.; Guevara, M.; Svozilík, J.; Coello-Fiallos, D.; Briceño, J.; Vacacela Gomez, C. Proving Surface Plasmons in Graphene Nanoribbons Organized as 2D Periodic Arrays and Potential Applications in Biosensors. Chemosensors 2022, 10, 514. [Google Scholar] [CrossRef]
- Tene, T.; Guevara, M.; Cevallos, Y.; Sáez Paguay, M.Á.; Bellucci, S.; Vacacela Gomez, C. THz Surface Plasmons in Wide and Freestanding Graphene Nanoribbon Arrays. Coatings 2023, 13, 28. [Google Scholar] [CrossRef]
- Tene, T.; Guevara, M.; Borja, M.; Mendoza Salazar, M.J.; Palacios Robalino, M.; Vacacela Gomez, C.; Bellucci, S. Modeling semiconducting silicene nanostrips: Electronics and THz plasmons. Front. Phys. 2023, 11, 1198214. [Google Scholar] [CrossRef]
- Tene, T.; Guevara, M.; Tubon-Usca, G.; Villacrés Cáceres, O.; Moreano, G.; Vacacela Gomez, C.; Bellucci, S. THz plasmonics and electronics in germanene nanostrips. J. Semicond. 2023, 44, 102001. [Google Scholar] [CrossRef]
- Yang, Y.; Murali, R. Impact of size effect on graphene nanoribbon transport. IEEE Electron. Device Lett. 2010, 31, 237–239. [Google Scholar] [CrossRef]
- Gonze, X.; Amadon, B.; Antonius, G.; Arnardi, F.; Baguet, L.; Beuken, J.-M.; Bieder, J.; Bottin, F.; Bouchet, J.; Bousquet, E.; et al. The ABINIT project: Impact, environment and recent developments. Comput. Phys. Commun. 2020, 248, 107042. [Google Scholar] [CrossRef]
- Perdew, J.P.; Zunger, A. Self-interaction correction to density-functional approximations for many-electron systems. Phys. Rev. B 1981, 23, 5048. [Google Scholar] [CrossRef]
- Troullier, N.; Martins, J.L. Efficient pseudopotentials for plane-wave calculations. Phys. Rev. B 1991, 43, 1993. [Google Scholar] [CrossRef]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188. [Google Scholar] [CrossRef]
- Aryasetiawan, F.; Gunnarsson, O. The GW method. Rep. Prog. Phys. 1998, 61, 237. [Google Scholar] [CrossRef]
- Golze, D.; Wilhelm, J.; Van Setten, M.J.; Rinke, P. Core-level binding energies from GW: An efficient full-frequency approach within a localized basis. J. Chem. Theory Comput. 2018, 14, 4856–4869. [Google Scholar] [CrossRef]
- Kiraly, B.; Mannix, A.J.; Jacobberger, R.M.; Fisher, B.L.; Arnold, M.S.; Hersam, M.C.; Guisinger, N.P. Sub-5 nm, globally aligned graphene nanoribbons on Ge (001). Appl. Phys. Lett. 2016, 108, 213101. [Google Scholar] [CrossRef]
- Li, Z.-T.; Li, X.; Liu, G.-D.; Wang, L.-L.; Linet, Q. Analytical investigation of unidirectional reflectionless phenomenon near the exceptional points in graphene plasmonic system. Opt. Express 2023, 31, 30458–30469. [Google Scholar] [CrossRef] [PubMed]
- Nejad, H.E.; Lorestaniweiss, Z.; Farmani, A.; Talebzadeh, R. First designing of a silicene-based optical MOSFET with outstanding performance. Sci. Rep. 2023, 13, 6563. [Google Scholar] [CrossRef] [PubMed]
- Shirkani, H.; Sadeghi, Z.; Yektaparast, B.; Fadaei, N. Design and study of phosphorene nanoribbons as a perfect absorber and polarizer in mid-IR range. Phys. E Low-Dimens. Syst. Nanostruct. 2022, 137, 115066. [Google Scholar] [CrossRef]
- Yuan, J.; Chen, Y.; Xie, Y.; Cai, Y. Squeezed metallic droplet with tunable Kubo gap and charge injection in transition metal dichalcogenides. Proc. Natl. Acad. Sci. USA 2020, 117, 6362–6369. [Google Scholar] [CrossRef] [PubMed]
- Hancock, Y.; Uppstu, A.; Saloriutta, K.; Harju, A.; Puska, M.J. Generalized tight-binding transport model for graphene nanoribbon-based systems. Phys. Rev. B 2010, 81, 245402. [Google Scholar] [CrossRef]
- Song, Y.-L.; Zhang, Y.; Zhang, J.M.; Lu, D.-B. Effects of the edge shape and the width on the structural and electronic properties of silicene nanoribbons. Appl. Surf. Sci. 2010, 256, 6313–6317. [Google Scholar] [CrossRef]
- Han, M.Y.; Ozyilmaz, B.; Zhang, Y.; Kim, P. Energy band-gap engineering of graphene nanoribbons. Phys. Rev. Lett. 2007, 98, 206805. [Google Scholar] [CrossRef]
- Yang, L.; Park, C.H.; Son, Y.W.; Cohen, M.L.; Louie, S.G. Quasiparticle energies and band gaps in graphene nanoribbons. Phys. Rev. Lett. 2007, 99, 186801. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).