Quantitative Macromolecular Modeling Assay of Biopolymer-Based Hydrogels
Abstract
:1. Introduction
2. Results and Discussion
2.1. Compressive Stress–Strain Response: Hyperelastic PI
2.2. Swelling Experiments
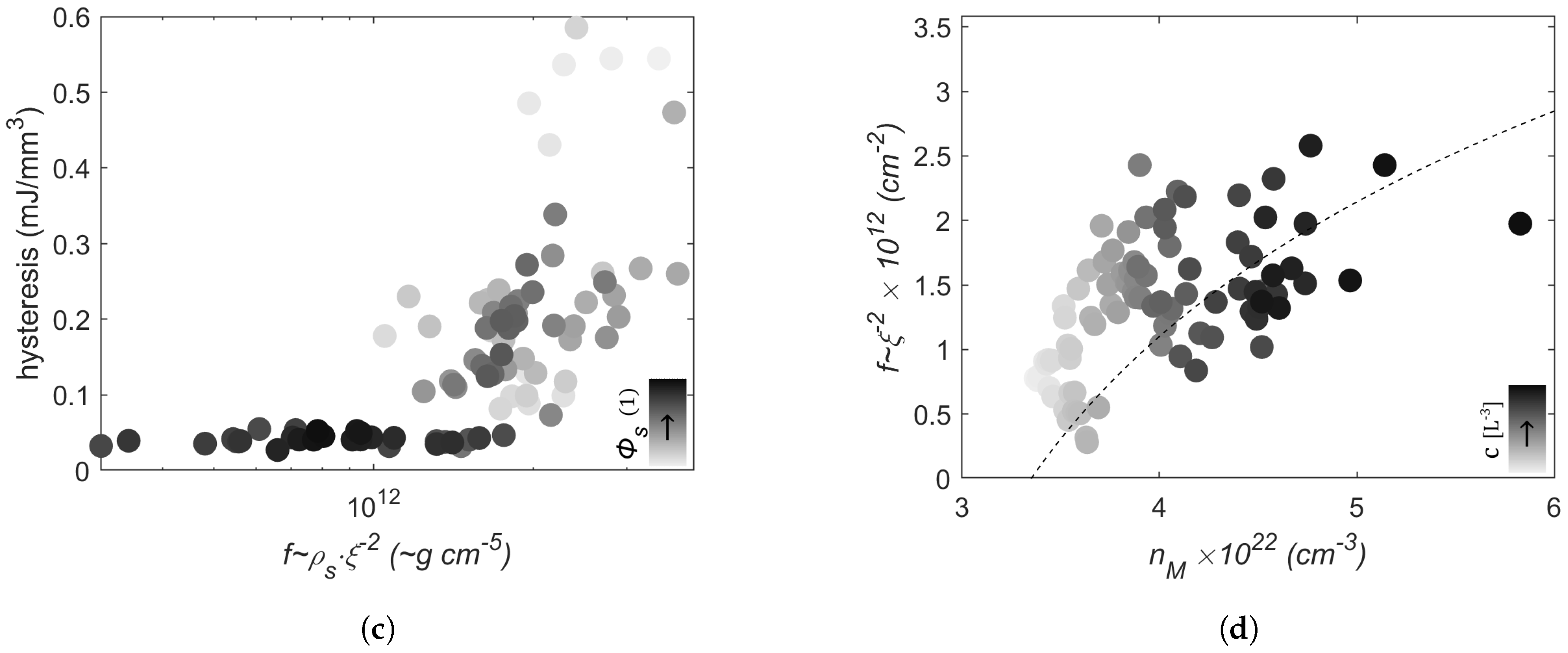
2.3. Discussion
3. Conclusions
4. Materials and Methods
4.1. Hydrogel Specimens
4.2. Swelling Experiment
4.2.1. Components’ Contents and Average Densities
4.2.2. Molar Properties of the Interstitial Fluid Phase
4.3. Unconfined Constant Strain-Rate Cyclic Compression Tests
4.4. Polymer Average Structural Parameters
4.4.1. Molecular Models of Hyperelastic Strain Energy Density Function
Neo-Hookean Model
Arruda–Boyce 8-Chain Model
4.4.2. Characteristic Length of the Polymer Network
4.4.3. Equilibrium Swelling
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Samples | Time (d) | (-) | (%) | (kPa) | (kPa) | (nm) | () | () | Wdiss () |
|---|---|---|---|---|---|---|---|---|---|
| algGEl0 | 0 | 16.36 | 1.57 | 7.9 | |||||
| 1 | 9.55 | 4.43 | 0.31 | 12.2 | |||||
| algGEL1 | 0 | 20.18 | 2.11 | 7.4 | |||||
| 1 | 2 | 20.17 | 1.66 | 7.4 | |||||
| 2 | 1.9 | 10.27 | 1.05 | 9.2 | |||||
| 3 | 1.74 | 10.42 | 1.06 | 9.2 | |||||
| ADAGEL0 | 0 | 12.83 | 0.95 | 8.6 | |||||
| 1 | 5.15 | 7.65 | 0.56 | 10.2 | |||||
| 2 | 8.6 | 7.00 | 0.6 | 10.5 | |||||
| 3 | 11.9 | 5.57 | 0.46 | 11.3 | |||||
| ADAGEL1 | 0 | 11.84 | 0.90 | 8.9 | |||||
| 1 | 2.05 | 15.02 | 0.99 | 8.1 | |||||
| 2 | 1.97 | 15.94 | 1.20 | 8.0 | |||||
| 3 | 2 | 14.97 | 1.09 | 8.2 | |||||
| ADAGEL2 | 0 | 16.57 | 1.12 | 7.9 | |||||
| 1 | 2.7 | 11.96 | 0.98 | 8.8 | |||||
| 2 | 3.86 | 13.92 | 1.32 | 8.4 | |||||
| 3 | 4.64 | 10.69 | 1.08 | 9.1 | |||||
| ADAGEL3 | 0 | 7.36 | 1.36 | 8.0 | |||||
| 1 | 0.92 | 2.93 | 2.1 | 7.0 | |||||
| 2 | 0.72 | 2.29 | 2.63 | 6.5 | |||||
| 3 | 0.59 | 3.13 | 2.01 | 7.0 | |||||
| ADAGEL4 | 0 | 13.26 | 0.77 | 10.3 | |||||
| 1 | 3.94 | 18.94 | 0.29 | 14.0 | |||||
| 2 | 3.81 | 18.31 | 0.24 | 15.3 | |||||
| 3 | 3.62 | 23.40 | 0.25 | 13.7 | |||||
| ADAGEL5 | 0 | 13.26 | 1.4 | 8.5 | |||||
| 1 | 1.77 | 18.94 | 2.35 | 7.5 | |||||
| 2 | 1.65 | 18.31 | 2.38 | 7.6 | |||||
| 3 | 1.44 | 23.4 | 2.11 | 7.0 |
References
- Sánchez-Cid, P.; Jiménez-Rosado, M.; Romero, A.; Pérez-Puyana, V. Novel Trends in Hydrogel Development for Biomedical Applications: A Review. Polymers 2022, 14, 3023. [Google Scholar] [CrossRef] [PubMed]
- Hashemi-Afzal, F.; Fallahi, H.; Bagheri, F.; Collins, M.N.; Eslaminejad, M.B.; Seitz, H. Advancements in hydrogel design for articular cartilage regeneration: A comprehensive review. Bioact. Mater. 2025, 43, 1–31. [Google Scholar] [CrossRef] [PubMed]
- Cheng, A.H.D. Poroelasticity; Springer International Publishing: Cham, Switzerland, 2016. [Google Scholar] [CrossRef]
- Caccavo, D.; Lamberti, G. PoroViscoElastic model to describe hydrogels’ behavior. Mater. Sci. Eng. C 2017, 76, 102–113. [Google Scholar] [CrossRef] [PubMed]
- Sakai, T. Physics of Polymer Gels; Wiley-VCH Verlag: Weinheim, Germany, 2020. [Google Scholar] [CrossRef]
- Boyce, M.C.; Arruda, E.M. Constitutive Models of Rubber Elasticity: A Review. Rubber Chem. Technol. 2000, 73, 504–523. [Google Scholar] [CrossRef]
- Flory, J.P. Principles of Polymer Chemistry; Cornell University Press: New York, NY, USA, 1953. [Google Scholar]
- Flory, P.J.; Rehner, J. Statistical Mechanics of Cross-Linked Polymer Networks II. Swelling. J. Chem. Phys. 1943, 11, 521–526. [Google Scholar] [CrossRef]
- Weizel, A.; Distler, T.; Detsch, R.; Boccaccini, A.; Bräuer, L.; Paulsen, F.; Seitz, H.; Budday, S. Hyperelastic parameter identification of human articular cartilage and substitute materials. J. Mech. Behav. Biomed. Mater. 2022, 133, 105292. [Google Scholar] [CrossRef]
- Arruda, E.M.; Boyce, M.C. A three-dimensional constitutive model for the large stretch behavior of rubber elastic materials. J. Mech. Phys. Solids 1993, 41, 389–412. [Google Scholar] [CrossRef]
- Obukhov, S.P.; Rubinstein, M.; Colby, R.H. Network Modulus and Superelasticity. Macromolecules 1994, 27, 3191–3198. [Google Scholar] [CrossRef]
- Mikhailov, O.V. Gelatin as It Is: History and Modernity. Int. J. Mol. Sci. 2023, 24, 3583. [Google Scholar] [CrossRef]
- Joardder, M.U.; Mourshed, M.; Hasan Masud, M. State of Bound Water: Measurement and Significance in Food Processing; Springer Nature: Cham, Switzerland, 2019. [Google Scholar] [CrossRef]
- Sarker, B.; Papageorgiou, D.G.; Silva, R.; Zehnder, T.; Gul-E-Noor, F.; Bertmer, M.; Kaschta, J.; Chrissafis, K.; Detsch, R.; Boccaccini, A.R. Fabrication of alginate–gelatin crosslinked hydrogel microcapsules and evaluation of the microstructure and physico-chemical properties. J. Mater. Chem. B 2014, 2, 1470. [Google Scholar] [CrossRef]
- Gomez, C.; Rinaudo, M.; Villar, M. Oxidation of sodium alginate and characterization of the oxidized derivatives. Carbohydr. Polym. 2007, 67, 296–304. [Google Scholar] [CrossRef]
- Zhang, G.; Steck, J.; Kim, J.; Ahn, C.H.; Suo, Z. Hydrogels of arrested phase separation simultaneously achieve high strength and low hysteresis. Sci. Adv. 2023, 9, eadh7742. [Google Scholar] [CrossRef] [PubMed]
- Karunaratne, N. The Complex World of Polysaccharides; IntechOpen: London, UK, 2012. [Google Scholar] [CrossRef]
- Distler, T.; Solisito, A.A.; Schneidereit, D.; Friedrich, O.; Detsch, R.; Boccaccini, A.R. 3D printed oxidized alginate-gelatin bioink provides guidance for C2C12 muscle precursor cell orientation and differentiation via shear stress during bioprinting. Biofabrication 2020, 12, 045005. [Google Scholar] [CrossRef] [PubMed]
- Russo, R.; Malinconico, M.; Santagata, G. Effect of Cross-Linking with Calcium Ions on the Physical Properties of Alginate Films. Biomacromolecules 2007, 8, 3193–3197. [Google Scholar] [CrossRef]
- Quinn, F.X.; Kampff, E.; Smyth, G.; McBrierty, V.J. Water in hydrogels. 1. A study of water in poly(N-vinyl-2-pyrrolidone/methyl methacrylate) copolymer. Macromolecules 1988, 21, 3191–3198. [Google Scholar] [CrossRef]
- Dargaville, B.L.; Hutmacher, D.W. Water as the often neglected medium at the interface between materials and biology. Nat. Commun. 2022, 13, 4222. [Google Scholar] [CrossRef]
- Karakaya, E.; Schöbel, L.; Zhong, Y.; Hazur, J.; Heid, S.; Forster, L.; Teßmar, J.; Boccaccini, A.R.; Detsch, R. How to Determine a Suitable Alginate for Biofabrication Approaches using an Extensive Alginate Library. Biomacromolecules 2023, 24, 2982–2997. [Google Scholar] [CrossRef]
- Tokita, M.; Tanaka, T. Friction coefficient of polymer networks of gels. J. Chem. Phys. 1991, 95, 4613–4619. [Google Scholar] [CrossRef]
- Brochard, F.; de Gennes, P.G. Dynamical Scaling for Polymers in Theta Solvents. Macromolecules 1977, 10, 1157–1161. [Google Scholar] [CrossRef]
- Richbourg, N.R.; Peppas, N.A. The swollen polymer network hypothesis: Quantitative models of hydrogel swelling, stiffness, and solute transport. Prog. Polym. Sci. 2020, 105, 101243. [Google Scholar] [CrossRef]
- Topuz, F.; Henke, A.; Richtering, W.; Groll, J. Magnesium ions and alginate do form hydrogels: A rheological study. Soft Matter 2012, 8, 4877. [Google Scholar] [CrossRef]
- Zhao, J.; Wu, H.; Wang, L.; Jiang, D.; Wang, W.; Yuan, G.; Pei, J.; Jia, W. The beneficial potential of magnesium-based scaffolds to promote chondrogenesis through controlled Mg2+ release in eliminating the destructive effect of activated macrophages on chondrocytes. Biomater. Adv. 2022, 134, 112719. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Zheng, X.; Wang, Y.; Tao, T.; Wang, Z.; Yuan, L.; Han, B. The Biomimetics of Mg2+-Concentration-Resolved Microenvironment for Bone and Cartilage Repairing Materials Design. Biomimetics 2022, 7, 227. [Google Scholar] [CrossRef] [PubMed]
- Wan, L.Q.; Jiang, J.; Arnold, D.E.; Guo, X.E.; Lu, H.H.; Mow, V.C. Calcium Concentration Effects on the Mechanical and Biochemical Properties of Chondrocyte-Alginate Constructs. Cell. Mol. Bioeng. 2008, 1, 93–102. [Google Scholar] [CrossRef] [PubMed]
- Shen, X.; Hu, L.; Li, Z.; Wang, L.; Pang, X.; Wen, C.Y.; Tang, B. Extracellular Calcium Ion Concentration Regulates Chondrocyte Elastic Modulus and Adhesion Behavior. Int. J. Mol. Sci. 2021, 22, 10034. [Google Scholar] [CrossRef]
- Kozanecki, M.; Halagan, K.; Matyjaszewki, K.; Ulanski, J. Intermolecular Interactions in Selected Polymer-Water Systems as Seen by Raman Spectroscopy. In Proceedings of the 2018 12th International Conference on Electromagnetic Wave Interaction with Water and Moist Substances (ISEMA), Lublin, Poland, 4–7 June 2018; pp. 1–9. [Google Scholar] [CrossRef]
- Sahoo, D.R.; Biswal, T. Alginate and its application to tissue engineering. SN Appl. Sci. 2021, 3, 30. [Google Scholar] [CrossRef]
- Lukin, I.; Erezuma, I.; Maeso, L.; Zarate, J.; Desimone, M.F.; Al-Tel, T.H.; Dolatshahi-Pirouz, A.; Orive, G. Progress in Gelatin as Biomaterial for Tissue Engineering. Pharmaceutics 2022, 14, 1177. [Google Scholar] [CrossRef]
- Distler, T.; McDonald, K.; Heid, S.; Karakaya, E.; Detsch, R.; Boccaccini, A.R. Ionically and Enzymatically Dual Cross-Linked Oxidized Alginate Gelatin Hydrogels with Tunable Stiffness and Degradation Behavior for Tissue Engineering. ACS Biomater. Sci. Eng. 2020, 6, 3899–3914. [Google Scholar] [CrossRef]
- Howard, R.M. Analytical approximations for the inverse Langevin function via linearization, error approximation, and iteration. Rheol. Acta 2020, 59, 521–544. [Google Scholar] [CrossRef]
- Petrosyan, R. Improved approximations for some polymer extension models. Rheol. Acta 2016, 56, 21–26. [Google Scholar] [CrossRef]

| Sample Designations | Average Parameters | ||||||
|---|---|---|---|---|---|---|---|
| Qv,eq | ϕp,0 | ϕp,eq | * | * | |||
| (%) | [1] | [1] | [-] | ||||
| algGEL0 | 2000 | 0.182 | 0.008 | 4.030 | 0.703 | 17.777 | 0.504 |
| algGEL1 | 235 | 0.155 | 0.077 | 4.970 | 0.664 | 17.755 | 0.527 |
| ADAGEL0 | 2421 | 0.134 | 0.006 | 3.160 | 0.827 | 17.777 | 0.505 |
| ADAGEL1 | 220 | 0.137 | 0.063 | 2.915 | 1.006 | 17.759 | 0.522 |
| ADAGEL2 | 776 | 0.140 | 0.018 | 4.081 | 0.566 | 17.773 | 0.507 |
| ADAGEL3 | 100 | 0.135 | 0.133 | 3.943 | 1.031 | 17.737 | 0.550 |
| ADAGEL4 | 417 | 0.134 | 0.030 | 1.812 | 1.556 | 17.770 | 0.510 |
| ADAGEL5 | 169 | 0.126 | 0.084 | 3.265 | 1.156 | 17.753 | 0.530 |
| Sample Designations | Cross-Linking * | Swelling Medium | ||
|---|---|---|---|---|
| 0.1 M CaCl2 |
50% w/v
mTG (In Situ) Enzymatic Activity ∼ 7.5 U/g |
Schiff’s Base Formation Due to Formed Aldehyde Groups | ||
| Ionic | Covalent | Reversible Covalent | ||
| algGEL0 | - | - | - | UPW |
| algGEL1 | √ | - | - | 0.1 M CaCl2 |
| ADAGEL0 | - | - | √ | UPW |
| ADAGEL1 | √ | - | √ | 0.1 M CaCl2 |
| ADAGEL2 | - | √ | √ | UPW |
| ADAGEL3 | √ | √ | √ | 0.1 M CaCl2 |
| ADAGEL4 | √ (in situ) | - | √ | UPW |
| ADAGEL5 | √ (in situ) | √ | √ | UPW |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abroug, N.; Schöbel, L.; Boccaccini, A.R.; Seitz, H. Quantitative Macromolecular Modeling Assay of Biopolymer-Based Hydrogels. Gels 2024, 10, 676. https://doi.org/10.3390/gels10110676
Abroug N, Schöbel L, Boccaccini AR, Seitz H. Quantitative Macromolecular Modeling Assay of Biopolymer-Based Hydrogels. Gels. 2024; 10(11):676. https://doi.org/10.3390/gels10110676
Chicago/Turabian StyleAbroug, Nada, Lisa Schöbel, Aldo R. Boccaccini, and Hermann Seitz. 2024. "Quantitative Macromolecular Modeling Assay of Biopolymer-Based Hydrogels" Gels 10, no. 11: 676. https://doi.org/10.3390/gels10110676
APA StyleAbroug, N., Schöbel, L., Boccaccini, A. R., & Seitz, H. (2024). Quantitative Macromolecular Modeling Assay of Biopolymer-Based Hydrogels. Gels, 10(11), 676. https://doi.org/10.3390/gels10110676









