Diffusion Correction in Fricke Hydrogel Dosimeters: A Deep Learning Approach with 2D and 3D Physics-Informed Neural Network Models
Abstract
1. Introduction
2. Results and Discussion
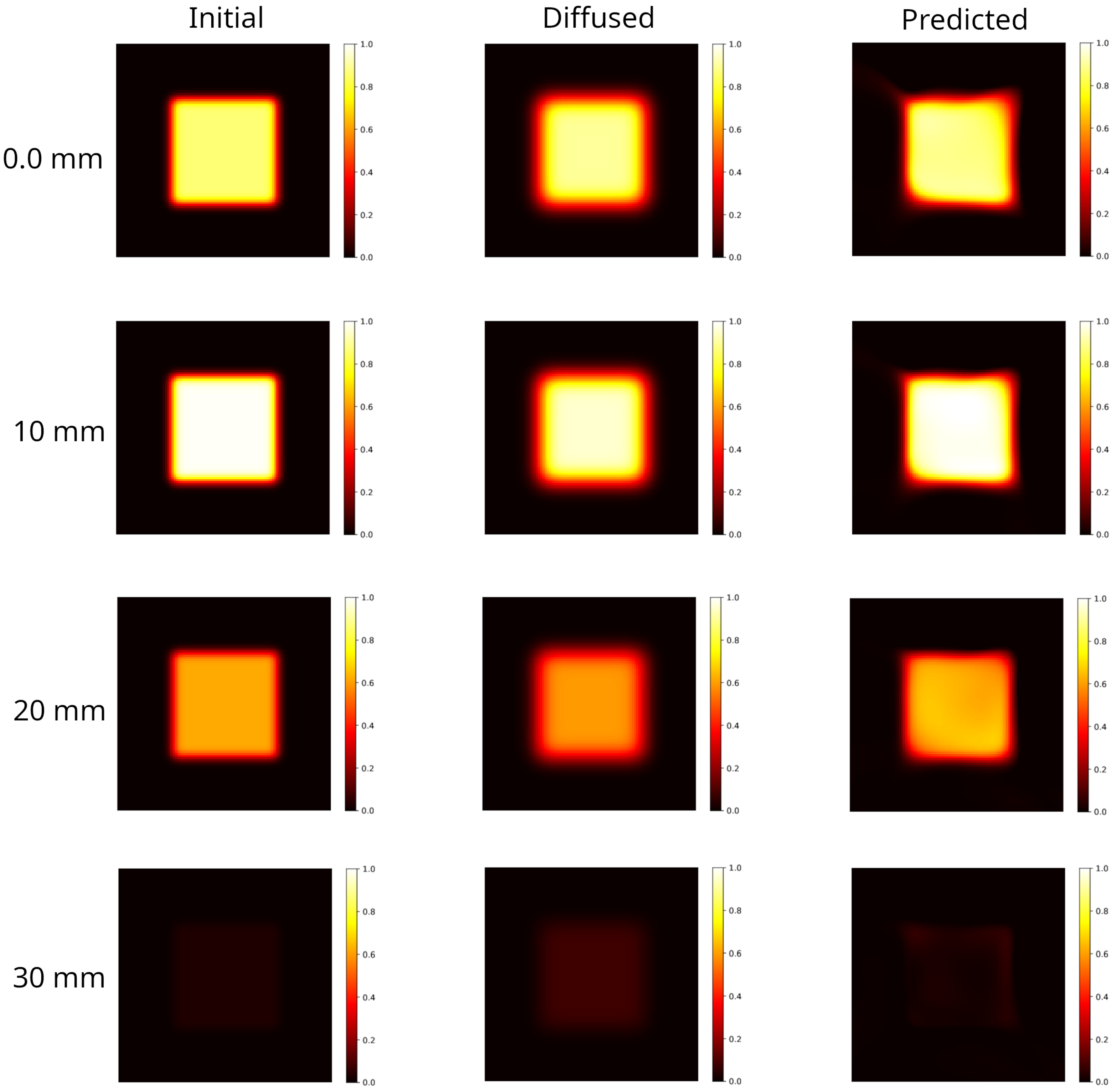
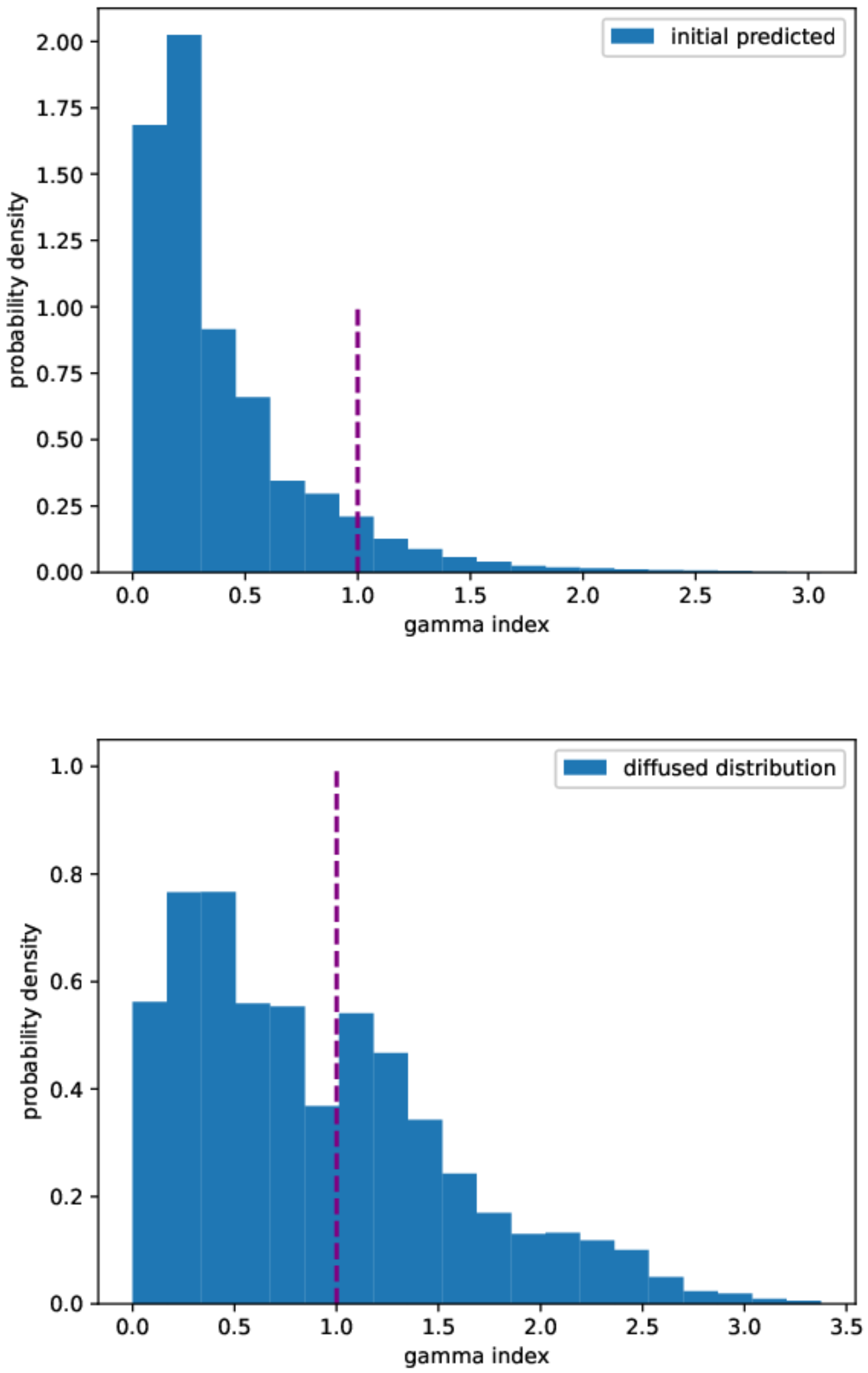
2.1. 2D PINN Model Predictions: Rectangular Distribution
2.2. 2D PINN Model Predictions: Circular Distribution
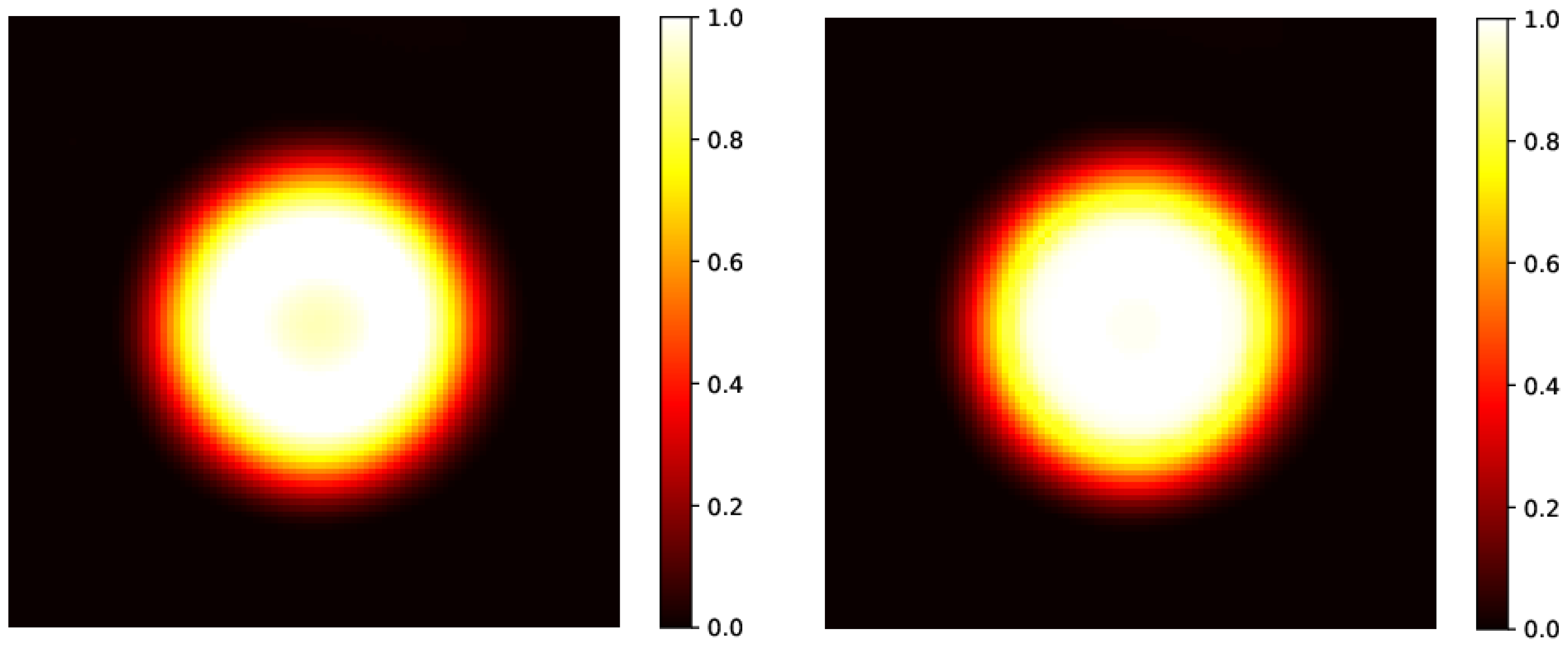
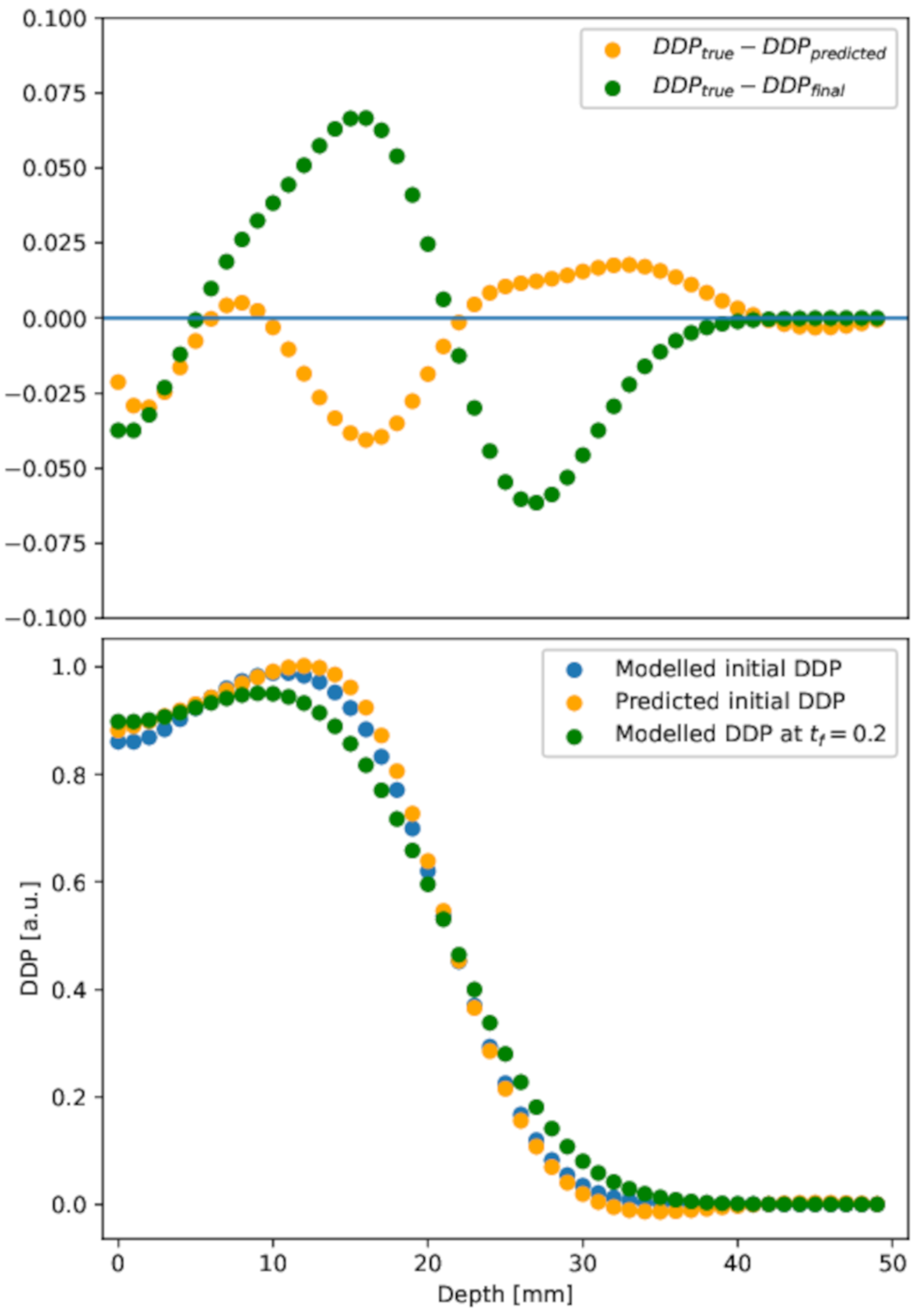
2.3. 3D PINN Model Predictions: A DDP Model Distribution
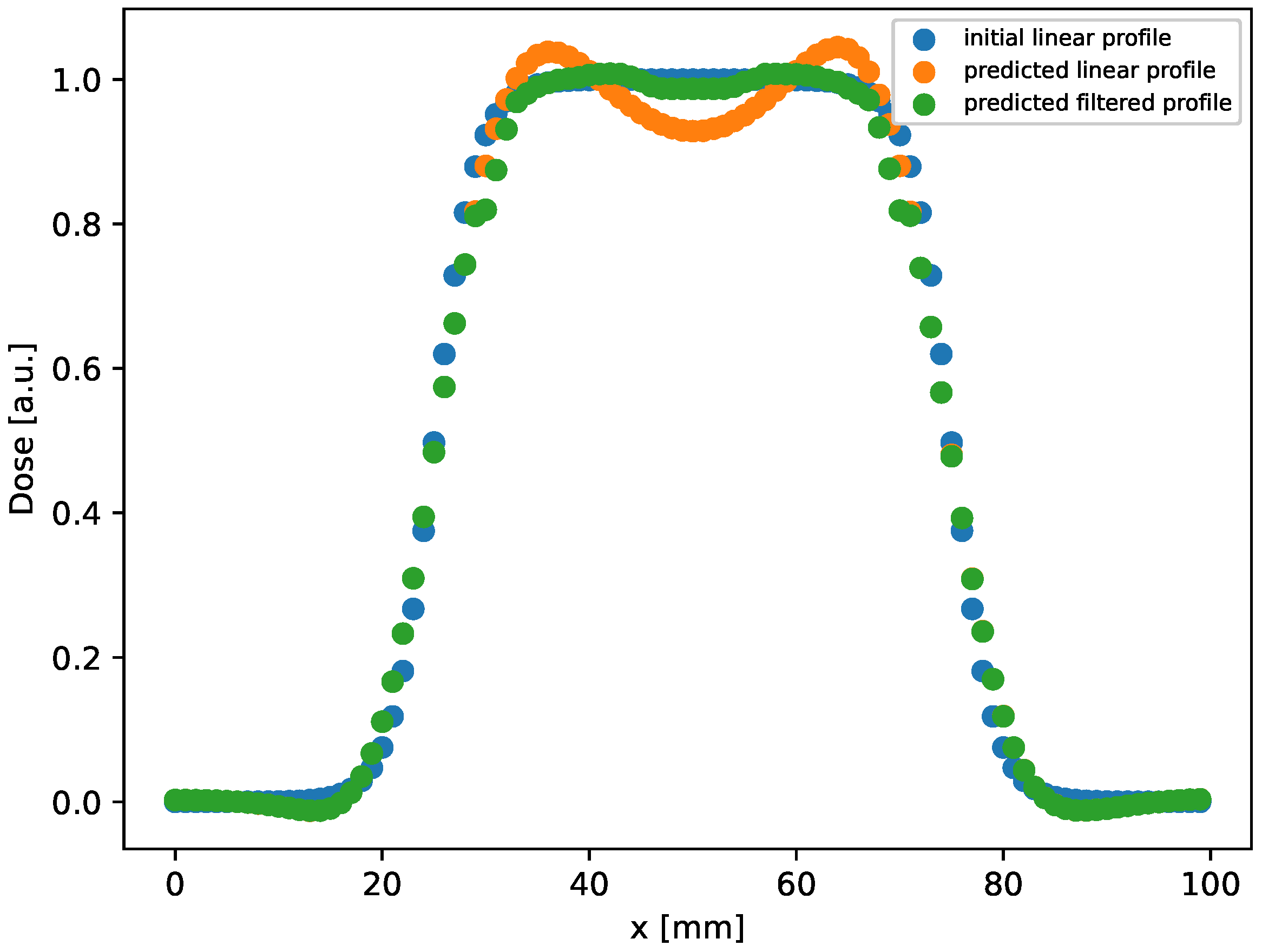
2.4. Discussion
3. Conclusions
4. Materials and Methods
4.1. Sample Model Design
4.2. Numerical Integration of the Forward Diffusion Equation
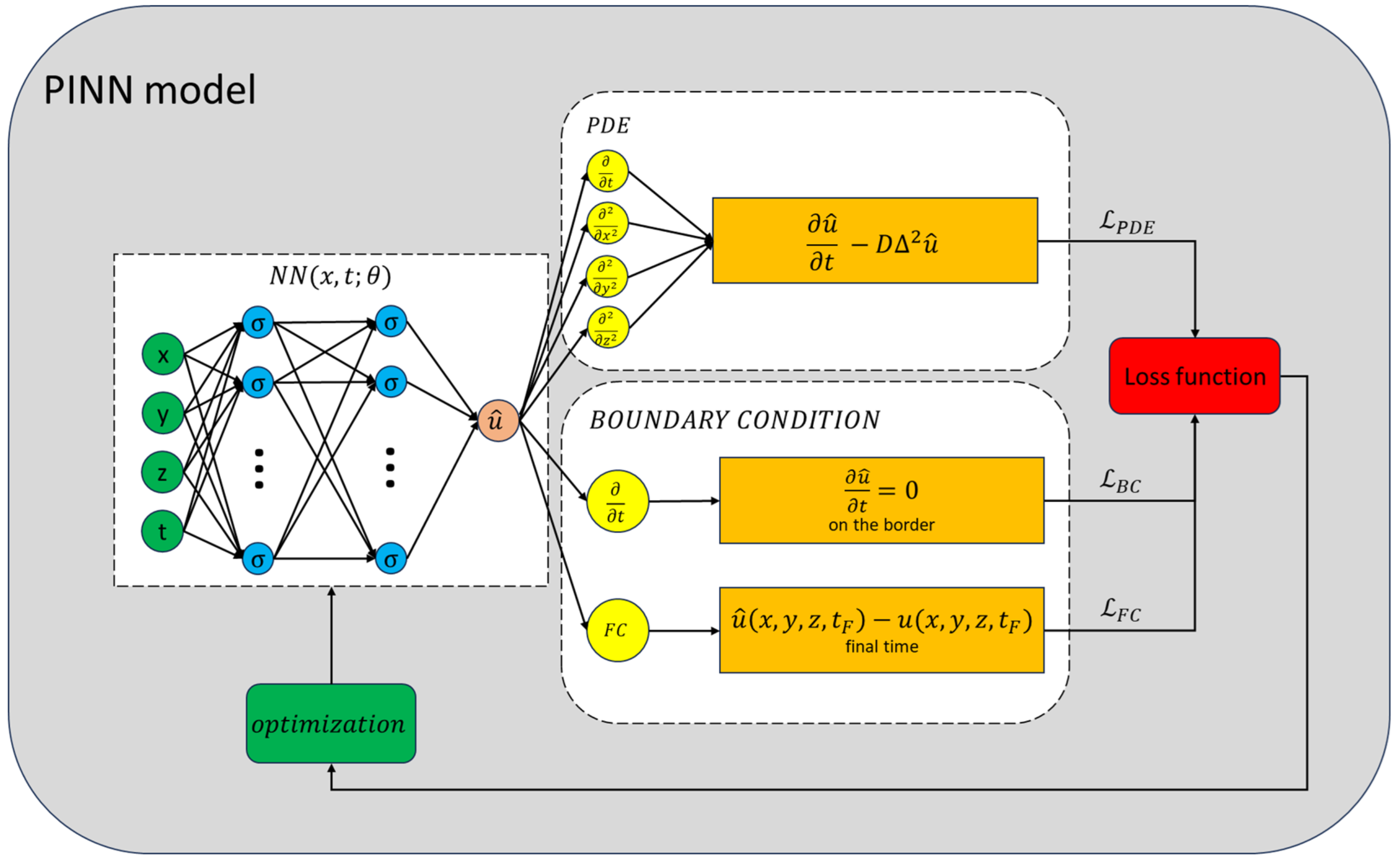
4.3. PINN Model
- Sample N couples , couples in and couples in ;
- calculate , and ;
- calculate ;
- optimize the parameters of the network ;
- repeat the above steps time.
4.4. Evaluation Criteria of the PINN Model Prediction
4.4.1. Gamma Analysis
- is the true initial (or reference) dose distribution at the position ;
- is the predicted initial dose distribution at the position ;
- is the threshold value of the dose, calculated as a percentage of the maximum value of the true initial dose distribution (global index [85]);
- is the distance threshold value in millimeters;
- is the spatial domain as stated in the above sections.
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kron, T.; Fox, C.; Ebert, M.A.; Thwaites, D. Quality management in radiotherapy treatment delivery. J. Med. Imaging Radiat. Oncol. 2022, 66, 279–290. [Google Scholar] [CrossRef] [PubMed]
- Fleckenstein, J.; Poettgen, C.; Reinmuth, N. Modern definitive radiochemotherapy-state of the art implementation and new consolidation strategies. ONKOLOGIE 2022, 28, 1071–1077. [Google Scholar] [CrossRef]
- Marrale, M.; d’Errico, F. Hydrogels for three-dimensional ionizing-radiation dosimetry. Gels 2021, 7, 74. [Google Scholar] [CrossRef] [PubMed]
- De Deene, Y. Radiation dosimetry by use of radiosensitive hydrogels and polymers: Mechanisms, state-of-the-art and perspective from 3D to 4D. Gels 2022, 8, 599. [Google Scholar] [CrossRef] [PubMed]
- Fricke, H.; Morse, S. The chemical action of roentgen rays on dilute ferrosulphate solutions as a measure of dose. Am. J. Roentgenol. Radium Ther. 1927, 18, 430–432. [Google Scholar]
- Schulz, R.; DeGuzman, A.; Nguyen, D.; Gore, J. Dose-response curves for Fricke-infused agarose gels as obtained by nuclear magnetic resonance. Phys. Med. Biol. 1990, 35, 1611. [Google Scholar] [CrossRef]
- Gore, J.; Kang, Y. Measurement of radiation dose distributions by nuclear magnetic resonance (NMR) imaging. Phys. Med. Biol. 1984, 29, 1189. [Google Scholar] [CrossRef]
- Duzenli, C.; Sloboda, R.; Robinson, D. A spin-spin relaxation rate investigation of the gelatin ferrous sulphate NMR dosimeter. Phys. Med. Biol. 1994, 39, 1577. [Google Scholar] [CrossRef]
- Gambarini, G.; Arrigoni, S.; Cantone, M.; Molho, N.; Facchielli, L.; Sichirollo, A. Dose-response curve slope improvement and result reproducibility of ferrous-sulphate-doped gels analysed by NMR imaging. Phys. Med. Biol. 1994, 39, 703. [Google Scholar] [CrossRef]
- Audet, C.; Schreiner, L. Multiple-site fast exchange model for spin–lattice relaxation in the Fricke-gelatin dosimeter. Med. Phys. 1997, 24, 201–209. [Google Scholar] [CrossRef]
- Hazle, J.; Hefner, L.; Nyerick, C.; Wilson, L.; Boyer, A. Dose-response characteristics of a ferrous-sulphate-doped gelatin system for determining radiation absorbed dose distributions by magnetic resonance imaging (Fe MRI). Phys. Med. Biol. 1991, 36, 1117. [Google Scholar] [CrossRef] [PubMed]
- Kron, T.; Metcalfe, P.; Pope, J. Investigation of the tissue equivalence of gells used for NMR dosimetry. Phys. Med. Biol. 1993, 38, 139. [Google Scholar] [CrossRef]
- Luciani, A.; Di Capua, S.; Guidoni, L.; Ragona, R.; Rosi, A.; Viti, V. Multiexponential relaxation in Fricke agarose gels: Implications for NMR dosimetry. Phys. Med. Biol. 1996, 41, 509. [Google Scholar] [CrossRef]
- Appleby, A.; Leghrouz, A. Imaging of radiation dose by visible color development in ferrous-agarose-xylenol orange gels. Med. Phys. 1991, 18, 309–312. [Google Scholar] [CrossRef] [PubMed]
- Healy, B.; Zahmatkesh, M.; Nitschke, K.; Baldock, C. Effect of saccharide additives on response of ferrous–agarose–xylenol orange radiotherapy gel dosimeters. Med. Phys. 2003, 30, 2282–2291. [Google Scholar] [CrossRef]
- Scotti, M.; Arosio, P.; Brambilla, E.; Gallo, S.; Lenardi, C.; Locarno, S.; Orsini, F.; Pignoli, E.; Pedicone, L.; Veronese, I. How xylenol orange and ferrous ammonium sulphate influence the dosimetric properties of PVA–GTA Fricke gel dosimeters: A spectrophotometric study. Gels 2022, 8, 204. [Google Scholar] [CrossRef] [PubMed]
- Gallo, S.; Lizio, D.; Monti, A.F.; Veronese, I.; Brambilla, M.G.; Lenardi, C.; Torresin, A.; Gambarini, G. Temperature behavior of radiochromic poly (vinyl-alcohol)-glutaraldehyde Fricke gel dosimeters in practice. J. Phys. D Appl. Phys. 2020, 53, 365003. [Google Scholar] [CrossRef]
- Rabaeh, K.A.; Eyadeh, M.M.; Hailat, T.F.; Aldweri, F.M.; Alheet, S.M.; Eid, R.M. Characterization of ferrous-methylthymol blue-polyvinyl alcohol gel dosimeters using nuclear magnetic resonance and optical techniques. Radiat. Phys. Chem. 2018, 148, 25–32. [Google Scholar] [CrossRef]
- Rabaeh, K.A.; Eyadeh, M.M.; Hailat, T.F.; Madas, B.G.; Aldweri, F.M.; Almomani, A.M.; Awad, S.I. Improvement on the performance of chemically cross-linked fricke methylthymol-blue radiochromic gel dosimeter by addition of dimethyl sulfoxide. Radiat. Meas. 2021, 141, 106540. [Google Scholar] [CrossRef]
- Alves, A.V.S.; de Almeida, W.S.; Sussuchi, E.M.; Lazzeri, L.; d’Errico, F.; de Souza, S.O. Investigation of chelating agents/ligands for Fricke gel dosimeters. Radiat. Phys. Chem. 2018, 150, 151–156. [Google Scholar] [CrossRef]
- De Almeida, W.d.S.; Alves, A.V.S.; Oliveira, W.F.; da Silveira, M.A.L.; de Souza, S.O.; d’Errico, F.; Sussuchi, E.M. Radiochromic Fricke gels with eriochrome cyanine R for radiotherapy dosimetry. Radiat. Phys. Chem. 2022, 191, 109830. [Google Scholar] [CrossRef]
- Bengtsson, M.; Furre, T.; Rødal, J.; Skretting, A.; Olsen, D.R. Measurement of dynamic wedge angles and beam profiles by means of MRI ferrous sulphate gel dosimetry. Phys. Med. Biol. 1996, 41, 269. [Google Scholar] [CrossRef]
- Johansson, S.Å.; Magnusson, P.; Fransson, A.; Olsson, L.E.; Christoffersson, J.O.; Montelius, A.; Mattsson, S. Dosimeter gel and MR imaging for verification of calculated dose distributions in clinical radiation therapy. Acta Oncol. 1997, 36, 283–290. [Google Scholar] [CrossRef] [PubMed]
- Chan, M.F.; Ayyangar, K.M. Confirmation of target localization and dosimetry for 3D conformal radiotherapy treatment planning by MR imaging of a ferrous sulfate gel head phantom. Med. Phys. 1995, 22, 1171–1175. [Google Scholar] [CrossRef] [PubMed]
- Gum, F.; Scherer, J.; Bogner, L.; Solleder, M.; Rhein, B.; Bock, M. Preliminary study on the use of an inhomogeneous anthropomorphic Fricke gel phantom and 3D magnetic resonance dosimetry for verification of IMRT treatment plans. Phys. Med. Biol. 2002, 47, N67. [Google Scholar] [CrossRef]
- Schreiner, L.; Crooks, I.; Evans, M.; Keller, B.; Parker, W. Imaging of HDR brachytherapy dose distributions using NMR Fricke-gelatin dosimetry. Magn. Reson. Imaging 1994, 12, 901–907. [Google Scholar] [CrossRef]
- Olsen, D.; Hellesnes, J. Absorbed dose distribution measurements in brachytherapy using ferrous sulphate gel and magnetic resonance imaging. Br. J. Radiol. 1994, 67, 1121–1126. [Google Scholar] [CrossRef]
- Knutsen, B.H.; Skretting, A.; Hellebust, T.P.; Olsen, D.R. Determination of 3D dose distribution from intracavitary brachytherapy of cervical cancer by MRI of irradiated ferrous sulphate gel. Radiother. Oncol. 1997, 43, 219–227. [Google Scholar] [CrossRef]
- Schulz, R.; Maryanski, M.; Ibbott, G.; Bond, J. Assessment of the accuracy of stereotactic radiosurgery using Fricke-infused gels and MRI. Med. Phys. 1993, 20, 1731–1734. [Google Scholar] [CrossRef]
- Olsson, L.; Arndt, J.; Fransson, A.; Nordell, B. Three-dimensional dose mapping from gamma knife treatment using a dosimeter gel and MR-imaging. Radiother. Oncol. 1992, 24, 82–86. [Google Scholar] [CrossRef]
- Bäck, S.Å.J.; Medin, J.; Magnusson, P.; Olsson, P.; Grusell, E.; Olsson, L.E. Ferrous sulphate gel dosimetry and MRI for proton beam dose measurements. Phys. Med. Biol. 1999, 44, 1983. [Google Scholar] [CrossRef] [PubMed]
- Maeyama, T.; Fukunishi, N.; Ishikawa, K.L.; Fukasaku, K.; Fukuda, S. Radiological properties of nanocomposite Fricke gel dosimeters for heavy ion beams. J. Radiat. Res. 2016, 57, 318–324. [Google Scholar] [CrossRef]
- Bäck, S.Å.J.; Magnusson, P.; Fransson, A.; Olsson, L.E.; Montelius, A.; Holmberg, O.; Andreo, P.; Mattsson, S. Improvements in absorbed dose measurements for external radiation therapy using ferrous dosimeter gel and MR imaging (FeMRI). Phys. Med. Biol. 1998, 43, 261. [Google Scholar] [CrossRef]
- Bero, M.; Zahili, M. Radiochromic gel dosimeter (FXG) chemical yield determination for dose measurements standardization. J. Phys. Conf. Ser. 2009, 164, 012011. [Google Scholar] [CrossRef]
- Olding, T.; Salomons, G.; Darko, J.; Schreiner, L. A practical use for FXG gel dosimetry. J. Phys. Conf. Ser. 2010, 250, 012003. [Google Scholar] [CrossRef]
- Olding, T.; Darko, J.; Schreiner, L. Effective management of FXG gel dosimetry. J. Phys. Conf. Ser. 2010, 250, 012028. [Google Scholar] [CrossRef]
- Vaiente, M.; Molina, W.; Silva, L.C.; Figueroa, R.; Malano, F.; Pérez, P.; Santibañez, M.; Vedelago, J. Fricke gel dosimeter with improved sensitivity for low-dose-level measurements. J. Appl. Clin. Med. Phys. 2016, 17, 402–417. [Google Scholar] [CrossRef]
- Ibbott, G.S.; Roed, Y.; Lee, H.; Alqathami, M.; Wang, J.; Pinsky, L.; Blencowe, A. Gel dosimetry enables volumetric evaluation of dose distributions from an MR-guided linac. In Proceedings of the AIP Conference Proceedings; AIP Publishing: New York, NY, USA, 2016; Volume 1747. [Google Scholar]
- McDonald, B.A.; Lee, H.J.; Ibbott, G.S. Low-density gel dosimeter for measurement of the electron return effect in an MR-linac. Phys. Med. Biol. 2019, 64, 205016. [Google Scholar] [CrossRef]
- Lee, H.J.; Kadbi, M.; Bosco, G.; Ibbott, G.S. Real-time volumetric relative dosimetry for magnetic resonance—Image-guided radiation therapy (MR-IGRT). Phys. Med. Biol. 2018, 63, 045021. [Google Scholar] [CrossRef]
- Kron, T.; Jonas, D.; Pope, J.M. Fast T1 imaging of dual gel samples for diffusion measurements in NMR dosimetry gels. Magn. Reson. Imaging 1997, 15, 211–221. [Google Scholar] [CrossRef]
- Chu, K.; Jordan, K.; Battista, J.; Van Dyk, J.; Rutt, B. Polyvinyl alcohol-Fricke hydrogel and cryogel: Two new gel dosimetry systems with low Fe3+ diffusion. Phys. Med. Biol. 2000, 45, 955. [Google Scholar] [CrossRef] [PubMed]
- Hill, B.; Bäck, S.Å.J.; Lepage, M.; Simpson, J.; Healy, B.; Baldock, C. Investigation and analysis of ferrous sulfate polyvinyl alcohol (PVA) gel dosimeter. Phys. Med. Biol. 2002, 47, 4233. [Google Scholar] [CrossRef]
- Mansur, H.S.; Sadahira, C.M.; Souza, A.N.; Mansur, A.A. FTIR spectroscopy characterization of poly (vinyl alcohol) hydrogel with different hydrolysis degree and chemically crosslinked with glutaraldehyde. Mater. Sci. Eng. C 2008, 28, 539–548. [Google Scholar] [CrossRef]
- Marrale, M.; Collura, G.; Brai, M.; Toschi, N.; Midiri, F.; La Tona, G.; Lo Casto, A.; Gagliardo, C. Physics, techniques and review of neuroradiological applications of diffusion kurtosis imaging (DKI). Clin. Neuroradiol. 2016, 26, 391–403. [Google Scholar] [CrossRef] [PubMed]
- d’Errico, F.; Lazzeri, L.; Dondi, D.; Mariani, M.; Marrale, M.; Souza, S.O.; Gambarini, G. Novel GTA-PVA Fricke gels for three-dimensional dose mapping in radiotherapy. Radiat. Meas. 2017, 106, 612–617. [Google Scholar] [CrossRef]
- Lazzeri, L.; Marini, A.; Cascone, M.G.; d’Errico, F. Dosimetric and chemical characteristics of Fricke gels based on PVA matrices cross-linked with glutaraldehyde. Phys. Med. Biol. 2019, 64, 085015. [Google Scholar] [CrossRef]
- Collura, G.; Gallo, S.; Tranchina, L.; Abbate, B.F.; Bartolotta, A.; d’Errico, F.; Marrale, M. Analysis of the response of PVA-GTA Fricke-gel dosimeters with clinical magnetic resonance imaging. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. Atoms 2018, 414, 146–153. [Google Scholar] [CrossRef]
- Gallo, S.; Gambarini, G.; Veronese, I.; Argentiere, S.; Gargano, M.; Ianni, L.; Lenardi, C.; Ludwig, N.; Pignoli, E.; d’Errico, F. Does the gelation temperature or the sulfuric acid concentration influence the dosimetric properties of radiochromic PVA-GTA Xylenol Orange Fricke gels? Radiat. Phys. Chem. 2019, 160, 35–40. [Google Scholar] [CrossRef]
- Wang, K.; Zhang, W.; Qi, Y.; Hu, X.; Zhang, X.; Chang, S.; Zhang, H. Radiation-sensitive nanogel-incorporated Fricke hydrogel dosimeters with reduced diffusion rates. Polym. Adv. Technol. 2023, 34, 539–548. [Google Scholar] [CrossRef]
- Gallo, S.; Locarno, S.; Brambilla, E.; Lenardi, C.; Pignoli, E.; Veronese, I. Dosimetric characterization of double network Fricke hydrogel based on PVA-GTA and phenylalanine peptide derivative. J. Phys. D Appl. Phys. 2023, 57, 075303. [Google Scholar] [CrossRef]
- Rabaeh, K.A.; Hailat, T.F.; Eyadeh, M.M.; Al-Shorman, M.Y.; Aldweri, F.M.; Alheet, S.M.; Madas, B.G.; Awad, S.I. Dosimetric properties of sulfosalicylic acid-ferrous-polyvinyl alcohol-glutaraldehyde hydrogel dosimeters using magnetic and optical techniques. Radiat. Phys. Chem. 2020, 177, 109106. [Google Scholar] [CrossRef]
- Romeo, M.; Cottone, G.; D’Oca, M.; Bartolotta, A.; Miraglia, R.; Gerasia, R.; Gagliardo, C.; d’Errico, F.; Marrale, M. Deep learning approach for diffusion correction in Fricke hydrogel dosimeters. Radiat. Meas. 2024, 175, 107171. [Google Scholar] [CrossRef]
- Karniadakis, G.E.; Kevrekidis, I.G.; Lu, L.; Perdikaris, P.; Wang, S.; Yang, L. Physics-informed machine learning. Nat. Rev. Phys. 2021, 3, 422–440. [Google Scholar] [CrossRef]
- Raissi, M.; Perdikaris, P.; Karniadakis, G.E. Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J. Comput. Phys. 2019, 378, 686–707. [Google Scholar] [CrossRef]
- Lagaris, I.E.; Likas, A.; Fotiadis, D.I. Artificial neural networks for solving ordinary and partial differential equations. IEEE Trans. Neural Netw. 1998, 9, 987–1000. [Google Scholar] [CrossRef]
- Lee, H.; Kang, I.S. Neural algorithm for solving differential equations. J. Comput. Phys. 1990, 91, 110–131. [Google Scholar] [CrossRef]
- Cuomo, S.; Di Cola, V.S.; Giampaolo, F.; Rozza, G.; Raissi, M.; Piccialli, F. Scientific machine learning through physics–informed neural networks: Where we are and what’s next. J. Sci. Comput. 2022, 92, 88. [Google Scholar] [CrossRef]
- Kim, D.; Lee, J. A review of physics informed neural networks for multiscale analysis and inverse problems. Multiscale Sci. Eng. 2024, 6, 1–11. [Google Scholar] [CrossRef]
- Lawal, Z.K.; Yassin, H.; Lai, D.T.C.; Che Idris, A. Physics-informed neural network (PINN) evolution and beyond: A systematic literature review and bibliometric analysis. Big Data Cogn. Comput. 2022, 6, 140. [Google Scholar] [CrossRef]
- Viana, F.A.; Subramaniyan, A.K. A survey of Bayesian calibration and physics-informed neural networks in scientific modeling. Arch. Comput. Methods Eng. 2021, 28, 3801–3830. [Google Scholar] [CrossRef]
- Blechschmidt, J.; Ernst, O.G. Three ways to solve partial differential equations with neural networks—A review. GAMM-Mitteilungen 2021, 44, e202100006. [Google Scholar] [CrossRef]
- Antonion, K.; Wang, X.; Raissi, M.; Joshie, L. Machine Learning Through Physics–Informed Neural Networks: Progress and Challenges. Acad. J. Sci. Technol. 2024, 9, 46–49. [Google Scholar] [CrossRef]
- Sutar, A.; Kulkarni, A.; Jain, A.; Jadhav, P.; Gohokar, V. Physics informed neural networks–a methodology review. In Proceedings of the 2022 6th International Conference on Computing, Communication, Control And Automation (ICCUBEA), Pune, India, 26–27 August 2022; pp. 1–4. [Google Scholar]
- Uddin, Z.; Ganga, S.; Asthana, R.; Ibrahim, W. Wavelets based physics informed neural networks to solve non-linear differential equations. Sci. Rep. 2023, 13, 2882. [Google Scholar] [CrossRef] [PubMed]
- Hornik, K.; Stinchcombe, M.; White, H. Multilayer feedforward networks are universal approximators. Neural Netw. 1989, 2, 359–366. [Google Scholar] [CrossRef]
- Miften, M.; Olch, A.; Mihailidis, D.; Moran, J.; Pawlicki, T.; Molineu, A.; Li, H.; Wijesooriya, K.; Shi, J.; Xia, P.; et al. Tolerance limits and methodologies for IMRT measurement-based verification QA: Recommendations of AAPM Task Group No. 218. Med. Phys. 2018, 45, e53–e83. [Google Scholar] [CrossRef]
- Jin, C.; Chen, J.; Yang, L.; Luo, W.; Wu, G.; Zha, Y. Effect of DMSO on the sensitivity and diffusion of FPGX gel dosimeter. Radiat. Phys. Chem. 2012, 81, 879–883. [Google Scholar] [CrossRef]
- Eyadeh, M.M.; Rabaeh, K.A.; Aldweri, F.M.; Al-Shorman, M.Y.; Alheet, S.M.; Awad, S.I.; Hailat, T.F. Nuclear magnetic resonance analysis of a chemically cross-linked ferrous–methylthymol blue–polyvinyl alcohol radiochromic gel dosimeter. Appl. Radiat. Isot. 2019, 153, 108812. [Google Scholar] [CrossRef] [PubMed]
- Zhang, W.; Wang, K.; Zeng, Y.; Hu, X.; Zhang, X.; Chang, S.; Zhang, H. Low-diffusion Fricke gel dosimeters with core-shell structure based on spatial confinement. Materials 2021, 14, 3932. [Google Scholar] [CrossRef]
- Zhang, W.; Wang, K.; Hu, X.; Zhang, X.; Chang, S.; Zhang, H. Preparation of W1/O/W2 emulsion to limit the diffusion of Fe3+ in the Fricke gel 3D dosimeter. Polym. Adv. Technol. 2020, 31, 2127–2135. [Google Scholar] [CrossRef]
- Li, S.; Wang, G.; Di, Y.; Wang, L.; Wang, H.; Zhou, Q. A physics-informed neural network framework to predict 3D temperature field without labeled data in process of laser metal deposition. Eng. Appl. Artif. Intell. 2023, 120, 105908. [Google Scholar] [CrossRef]
- Mostajeran, F.; Mokhtari, R. DeepBHCP: Deep neural network algorithm for solving backward heat conduction problems. Comput. Phys. Commun. 2022, 272, 108236. [Google Scholar] [CrossRef]
- Chen, M.; Niu, R.; Zheng, W. Adaptive multi-scale neural network with resnet blocks for solving partial differential equations. Nonlinear Dyn. 2023, 111, 6499–6518. [Google Scholar] [CrossRef]
- Maczuga, P.; Paszyński, M. Influence of activation functions on the convergence of physics-informed neural networks for 1d wave equation. In Proceedings of the International Conference on Computational Science; Springer: Berlin/Heidelberg, Germany, 2023; pp. 74–88. [Google Scholar]
- Liu, Y.; Liu, W.; Yan, X.; Guo, S.; Zhang, C.a. Adaptive transfer learning for PINN. J. Comput. Phys. 2023, 490, 112291. [Google Scholar] [CrossRef]
- Di Martino, F.; Del Sarto, D.; Bass, G.; Capaccioli, S.; Celentano, M.; Coves, D.; Douralis, A.; Marinelli, M.; Marrale, M.; Masturzo, L.; et al. Architecture, flexibility and performance of a special electron linac dedicated to Flash radiotherapy research: ElectronFlash with a triode gun of the centro pisano flash radiotherapy (CPFR). Front. Phys. 2023, 11, 1268310. [Google Scholar] [CrossRef]
- Landau, R.H.; Páez, M.J.; Bordeianu, C.C. Computational Physics: Problem Solving with Python; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Moin, P. Fundamentals of Engineering Numerical Analysis; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Virtanen, P.; Gommers, R.; Oliphant, T.E.; Haberland, M.; Reddy, T.; Cournapeau, D.; Burovski, E.; Peterson, P.; Weckesser, W.; Bright, J.; et al. SciPy 1.0: Fundamental Algorithms for Scientific Computing in Python. Nat. Methods 2020, 17, 261–272. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Abadi, M.; Agarwal, A.; Barham, P.; Brevdo, E.; Chen, Z.; Citro, C.; Corrado, G.S.; Davis, A.; Dean, J.; Devin, M.; et al. TensorFlow: Large-Scale Machine Learning on Heterogeneous Systems, 2015. Available online: https://www.tensorflow.org (accessed on 1 February 2022).
- Keras. 2015. Available online: https://keras.io (accessed on 1 February 2022).
- Low, D.A.; Harms, W.B.; Mutic, S.; Purdy, J.A. A technique for the quantitative evaluation of dose distributions. Med. Phys. 1998, 25, 656–661. [Google Scholar] [CrossRef] [PubMed]
- Hussein, M.; Clark, C.; Nisbet, A. Challenges in calculation of the gamma index in radiotherapy–towards good practice. Phys. Medica 2017, 36, 1–11. [Google Scholar] [CrossRef]
- Huttenlocher, D.P.; Klanderman, G.A.; Rucklidge, W.J. Comparing images using the Hausdorff distance. IEEE Trans. Pattern Anal. Mach. Intell. 1993, 15, 850–863. [Google Scholar] [CrossRef]
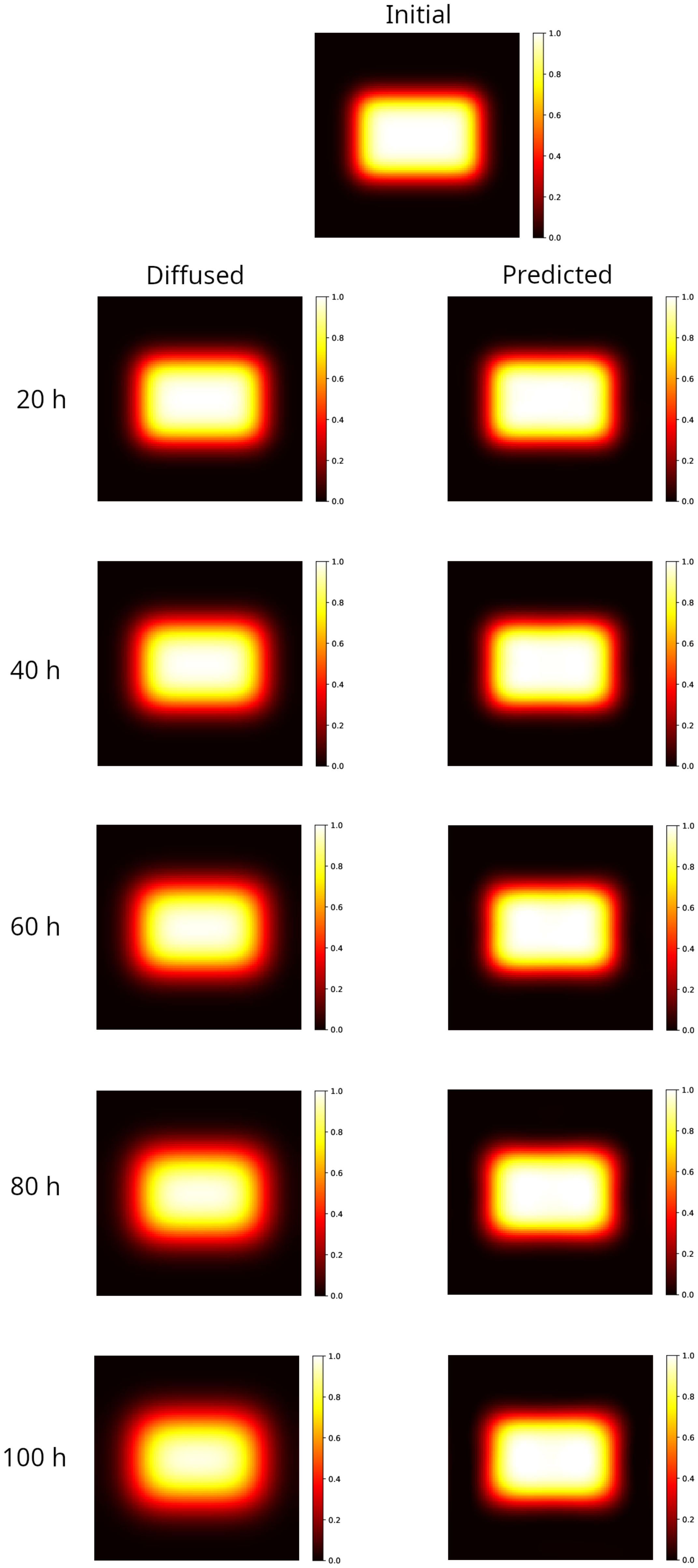
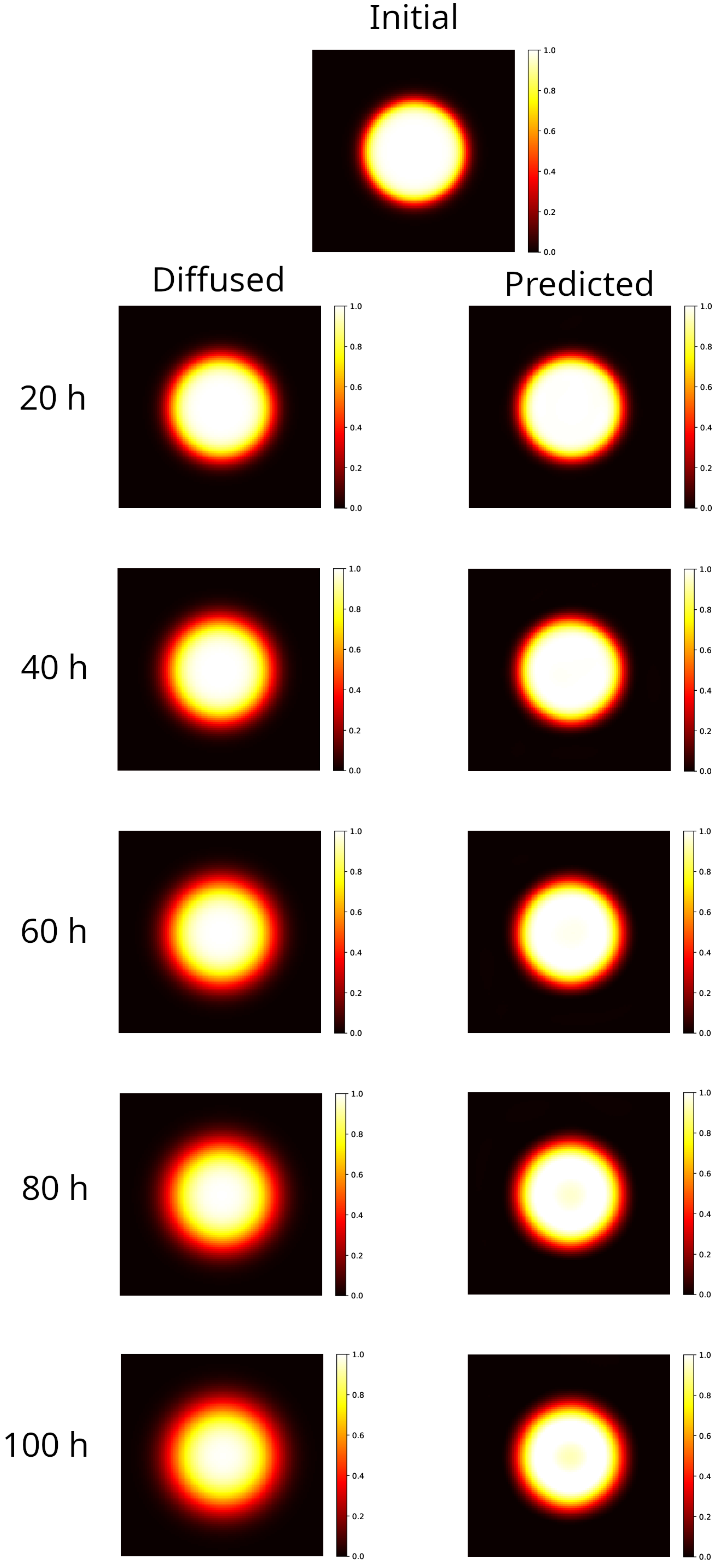


| Time (h) | Distribution | MSE | ||
|---|---|---|---|---|
| 20 | diffused | 100% | 0.339 | |
| predicted | 100% | 0.0681 | ||
| 40 | diffused | 82.9% | 0.626 | |
| predicted | 100% | 0.0869 | ||
| 60 | diffused | 58.7% | 0.899 | |
| predicted | 100% | 0.0992 | ||
| 80 | diffused | 44.9% | 1.16 | |
| predicted | 100% | 0.128 | ||
| 100 | diffused | 34.6% | 1.41 | |
| predicted | 100% | 0.153 |
| Time (h) | Distribution | MSE | ||
|---|---|---|---|---|
| 20 | diffused | 100% | 0.465 | |
| predicted | 100% | 0.118 | ||
| 40 | diffused | 58.5% | 0.845 | |
| predicted | 100% | 0.188 | ||
| 60 | diffused | 42.1% | 1.20 | |
| predicted | 100% | 0.288 | ||
| 80 | diffused | 32.8% | 1.53 | |
| predicted | 91.4% | 0.437 | ||
| 100 | diffused | 25.0% | 1.84 | |
| predicted | 84.9% | 0.538 |
| Time (h) | Distribution | MSE | ||
|---|---|---|---|---|
| 40 | diffused | 59.8% | 0.905 | |
| predicted | 92.4% | 0.403 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Romeo, M.; Cottone, G.; D’Oca, M.C.; Bartolotta, A.; Gallo, S.; Miraglia, R.; Gerasia, R.; Milluzzo, G.; Romano, F.; Gagliardo, C.; et al. Diffusion Correction in Fricke Hydrogel Dosimeters: A Deep Learning Approach with 2D and 3D Physics-Informed Neural Network Models. Gels 2024, 10, 565. https://doi.org/10.3390/gels10090565
Romeo M, Cottone G, D’Oca MC, Bartolotta A, Gallo S, Miraglia R, Gerasia R, Milluzzo G, Romano F, Gagliardo C, et al. Diffusion Correction in Fricke Hydrogel Dosimeters: A Deep Learning Approach with 2D and 3D Physics-Informed Neural Network Models. Gels. 2024; 10(9):565. https://doi.org/10.3390/gels10090565
Chicago/Turabian StyleRomeo, Mattia, Grazia Cottone, Maria Cristina D’Oca, Antonio Bartolotta, Salvatore Gallo, Roberto Miraglia, Roberta Gerasia, Giuliana Milluzzo, Francesco Romano, Cesare Gagliardo, and et al. 2024. "Diffusion Correction in Fricke Hydrogel Dosimeters: A Deep Learning Approach with 2D and 3D Physics-Informed Neural Network Models" Gels 10, no. 9: 565. https://doi.org/10.3390/gels10090565
APA StyleRomeo, M., Cottone, G., D’Oca, M. C., Bartolotta, A., Gallo, S., Miraglia, R., Gerasia, R., Milluzzo, G., Romano, F., Gagliardo, C., Di Martino, F., d’Errico, F., & Marrale, M. (2024). Diffusion Correction in Fricke Hydrogel Dosimeters: A Deep Learning Approach with 2D and 3D Physics-Informed Neural Network Models. Gels, 10(9), 565. https://doi.org/10.3390/gels10090565











