Unsteady RANS Simulations of Strong and Weak 3D Stall Cells on a 2D Pitching Aerofoil
Abstract
:1. Introduction
2. Methodology
2.1. Governing Equations
2.2. Flow Configuration
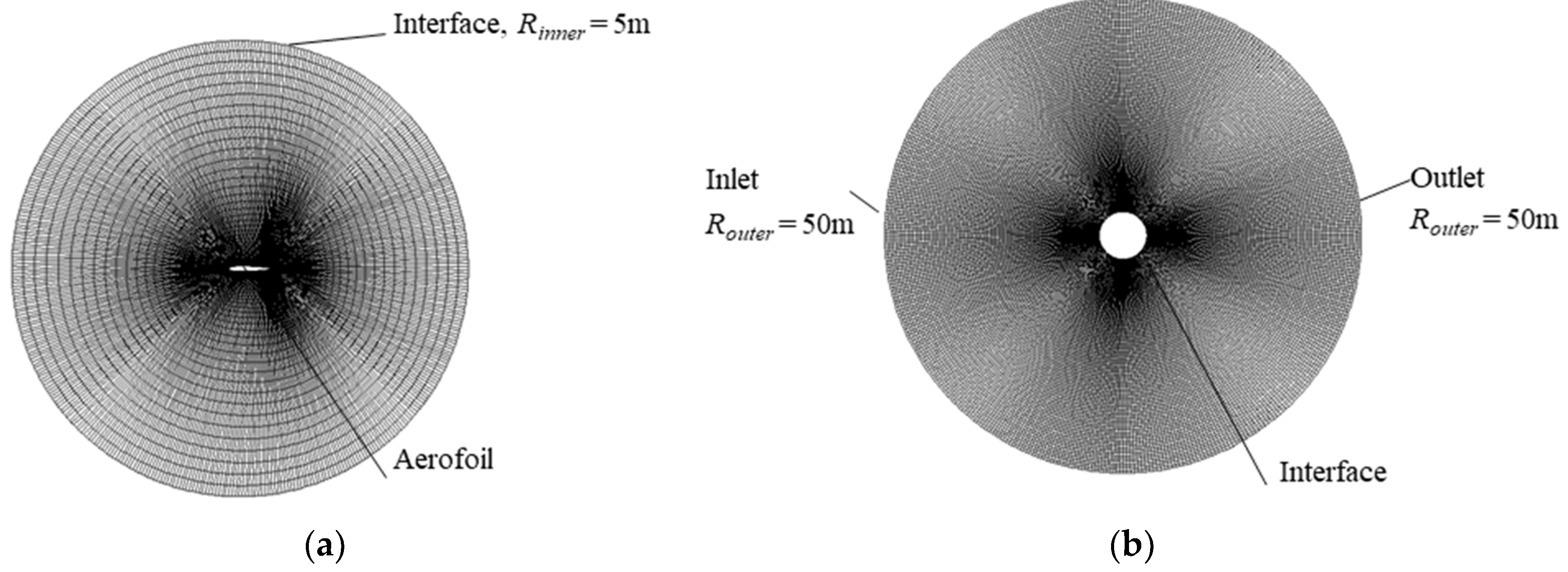
2.3. Computational Mesh
2.4. Computational Details
3. Sensitivity Analysis
4. Results
4.1. Cases with f = 0.1
4.1.1. Lift Coefficient (CL) Hysteresis Loop
4.1.2. Leading-Edge Vortex (LEV) and Trailing-Edge Separation
4.1.3. 3D Flow Structures
4.2. Cases with f = 0.025
4.2.1. CL Hysteresis Loop
4.2.2. LEV and Trailing-Edge Separation
4.2.3. Stall Cell Formation
4.3. Cases with f = 0.01
4.3.1. CL Hysteresis Loop
4.3.2. LEV and Trailing-Edge Separation
4.3.3. Stall Cell Formation
5. Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| AoA | = | angle of attack |
| AR | = | aspect ratio |
| c | = | chord length |
| CFD | = | computational fluid dynamics |
| CD | = | drag coefficient |
| CL | = | lift coefficient |
| f | = | reduced frequency |
| G | = | grid |
| LEV | = | leading-edge vortex |
| LSB | = | laminar separation bubble |
| U∞ | = | free-stream velocity |
| VAWT | = | vertical axis wind turbine |
| R | = | computational domain radius |
| RANS | = | Reynolds-averaged Navier–Strokes |
| Re | = | Reynolds number |
| SST | = | shear stress transport |
| α | = | pitching angle |
| αm | = | mean angle |
| α1 | = | pitching range |
| k | = | turbulent kinetic energy |
| t | = | flow time |
| x, y, z | = | Cartesian coordinate |
| Ω | = | angular velocity |
| ω | = | specific dissipation rate |
References
- Ham, N.D.; Garelick, M.S. Dynamic stall considerations in helicopter rotors. J. Am. Helicopter Soc. 1968, 13, 49–55. [Google Scholar] [CrossRef]
- McCroskey, W.J. The Phenomenon of Dynamic Stall; National Aeronautic and Space Administration AMES Research Center: Moffett Field, CA, USA, 1981.
- Brandon, J.M. Dynamic stall effects and applications to high performance aircraft. In Aircraft Dynamics at High Angles of Attack: Ezperiments and Modelling; NASA Langley Reserch Center: Hampton, VA, USA, 1991. [Google Scholar]
- Akbari, M.; Price, S.J. Simulation of dynamic stall for a NACA 0012 airfoil using a vortex method. J. Fluids Struct. 2003, 17, 855–874. [Google Scholar] [CrossRef]
- Choudhry, A.; Leknys, R.; Arjomandi, M.; Kelso, R. An insight into the dynamic stall lift characteristics. Exp. Therm. Fluid Sci. 2014, 58, 188–208. [Google Scholar] [CrossRef]
- Alrefai, M.; Mukund, A. Controlled leading-edge suction for management of unsteady separation over pitching airfoils. AIAA J. 1996, 34, 2327–2336. [Google Scholar] [CrossRef]
- Lee, T.; Gerontakos, P. Investigation of flow over an oscillating airfoil. J. Fluid Mech. 2004, 512, 313–341. [Google Scholar] [CrossRef]
- Ducoin, A.; Astolfi, J.A.; Deniset, F.; Sigrist, J.F. Computational and experimental investigation of flow over a transient pitching hydrofoil. Eur. J. Mech. B/Fluids 2009, 28, 728–743. [Google Scholar] [CrossRef] [Green Version]
- Panda, J.; Zaman, K. Experimental investigation of the flow field of an oscillating airfoil and estimation of lift from wake surveys. J. Fluid Mech. 1994, 265, 65–95. [Google Scholar] [CrossRef]
- Wang, S.; Ingham, D.B.; Ma, L.; Pourkashanian, M.; Tao, Z. Turbulence modeling of deep dynamic stall at relatively low Reynolds number. J. Fluids Struct. 2012, 33, 191–209. [Google Scholar] [CrossRef]
- Niu, Y.-Y.; Chang, C.-C. How do aerodynamic forces of the pitching rigid and flexible airfoils evolve? AIAA J. 2013, 51, 2946–2952. [Google Scholar] [CrossRef]
- Wernert, P.; Geissler, W.; Raffel, M.; Kompenhans, J. Experimental and numerical investigations of dynamic stall on a pitching airfoil. AIAA J. 1996, 34, 982–989. [Google Scholar] [CrossRef]
- Disotell, K.J.; Nikoueeyan, P.; Naughton, J.W. Global surface pressure measurements of static and dynamic stall on a wind turbine airfoil at low Reynolds number. Exp. Fluids 2016, 57, 82. [Google Scholar] [CrossRef]
- Zanotti, A.; Melone, S.; Nilifard, R.; D’Andrea, A. Experimental-numerical investigation of a pitching airfoil in deep dynamic stall. J. Aerosp. Eng. 2014, 228, 557–566. [Google Scholar] [CrossRef]
- Zanotti, A.; Nilifard, R.; Gibertini, G.; Guardone, A.; Quaranta, G. Assessment of 2D/3D numerical modeling for deep dynamic stall experiments. J. Fluids Struct. 2014, 51, 97–115. [Google Scholar] [CrossRef]
- Howel, R.; Qin, N.; Edwards, J.; Durrani, N. Wind tunnel and numerical study of a small vertical axis wind turbine. Renew. Energy 2010, 35, 412–422. [Google Scholar] [CrossRef] [Green Version]
- Li, C.; Zhu, S.; Xu, Y.-L.; Xiao, Y. 2.5D large eddy simulation of vertical axis wind turbine in consideration of high angle of attack flow. Renew. Energy 2013, 51, 317–330. [Google Scholar] [CrossRef] [Green Version]
- Drofelnik, J.; Campobasso, M.S. Comparative turbulent three-dimensional Navier-Stokes hydrodynamic analysis and performance assessment of oscillating wings for renewable energy applications. Int. J. Mar. Energy 2016, 16, 100–115. [Google Scholar] [CrossRef]
- Spentzos, A.; Barakos, G.N.; Badcock, K.J.; Richards, B.; Coton, F.; Galbraith, R.; Berton, E.; Favier, D. Computational Fluid Dynamics Study of Three-Dimensional Dynamic Stall of Various Planform Shapes. J. Aircr. 2007, 44, 1118–1128. [Google Scholar] [CrossRef]
- Spentzos, A.; Barakos, G.; Badcock, K.; Richards, B.; Wernert, P.; Schreck, S.; Raffel, M. Investigation of Three-Dimensional Dynamic Stall Using Computational Fluid Dynamics. AIAA J. 2005, 43, 1023–1033. [Google Scholar] [CrossRef]
- Visbal, M.R.; Garmann, D.J. High-Fidelity Simulations of Dynamic Stall over a Finite-Aspect-Ratio Wing. In Proceedings of the 8th AIAA Flow Control Conference, Washington, DC, USA, 13–17 June 2016. [Google Scholar]
- Moss, G.F.; Murdin, P.M. Two-Dimensional Low-Speed Tunnel Tests on the NACA 0012 Section Including Measurements Made during Pitching Oscillations at the Stall; Royal Aircraft Establishment: Farnborough, UK, 1971. [Google Scholar]
- Gregory, N.; Quincey, V.; O’Reilly, C.; Hall, D. Progress Rport on Observations of Three-Dimensional Flow Patterns Obtained during Stall Development on Aerofoils, and on the Problem of Measuring Two-Dimensional Characteristics; HM Stationary Office: London, UK, 1971. [Google Scholar]
- Winkelmann, A.; Barlow, J.; Saini, J.; Anderson, J.; Jones, E. The Effects of Leading Edge Modifications on the Post-Stall Characteristics of Wings. In Proceedings of the 18th Aerospace Sciences Meeting, Pasadena, CA, USA, 14–16 January 1980. [Google Scholar]
- Winkelmann, A.E.; Barlow, J.B. Flowfield model for a rectangular planform wing beyond stall. AIAA J. 1980, 18, 1006–1008. [Google Scholar] [CrossRef]
- Yon, S.A.; Katz, J. Study of the unsteady flow features on a stalled wing. AIAA J. 1998, 36, 305–312. [Google Scholar] [CrossRef]
- Liu, D.; Nishino, T. Numerical analysis on the oscillation of stall cells over a NACA 0012 aerofoil. Comput. Fluids 2018, 175, 246–259. [Google Scholar] [CrossRef]
- Manni, L.; Nishino, T.; Delafin, P.-L. Numerical study of airfoil stall cells using a very wide computational domain. Comput. Fluids 2016, 140, 260–269. [Google Scholar] [CrossRef]
- Menter, F.R. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef] [Green Version]
- Danao, L.A.; Qin, N.; Howell, R. A numerical study of blade thickness and camber effects on vertical axis wind turbines. J. Power Energy 2012, 226, 867–881. [Google Scholar] [CrossRef]
- Gharali, K.; Johnson, D.A. Dynamic stall simulation of a pitching airfoil under unsteady freestream velocity. J. Fluids Struct. 2013, 42, 228–244. [Google Scholar] [CrossRef]
- Martinat, G.; Braza, M.; Hoarau, Y.; Harran, G. Turbulence modelling of the flow past a pitching NACA0012 airfoil at 100,000 and 1,000,000 Reynolds numbers. J. Fluids Struct. 2008, 24, 1294–1303. [Google Scholar] [CrossRef]
- Wang, S.; Ingham, D.B.; Ma, L.; Pourkashanian, M.; Tao, Z. Numerical investigations on dynamic stall of low Reynolds number flow around oscillating airfoils. Comput. Fluids 2010, 39, 1529–1541. [Google Scholar] [CrossRef]
- Fluent, A.N. ANSYS Fluent 18.2 ‘Theory Guide’; ANSYS Inc.: Canonsburg, PA, USA, 2017. [Google Scholar]
- Worstell, M.H. Aerodynamic performance of the DOE/Sandia 17-m-diameter vertical-axis wind turbine. J. Energy 1981, 5, 39–42. [Google Scholar] [CrossRef]
- Blonk, D. Conceptual Design and Evaluation of Economic Feasibility of Floating Vertical Axis Wind Turbines; Delft University of Technology: Delft, The Netherlands, 2010. [Google Scholar]
- Kjellin, J.; Bulow, F.; Eriksson, S.; Deglaire, P.; Leijon, M.; Bernhoff, H. Power coefficient measurement on a 12 kW straight bladed vertical axis wind turbine. Renew. Energy 2011, 36, 3050–3053. [Google Scholar] [CrossRef]
- Brusca, S.; Lanzafame, R.; Messina, M. Design of a vertical-axis wind turbine: How the aspect ratio affects the turbine’s performance. Int. J. Energy Environ. Eng. 2014, 5, 333–340. [Google Scholar] [CrossRef]
- Li, Q.; Maeda, T.; Kamada, Y.; Murata, J.; Furukawa, K.; Yamamoto, M. Measurement of the flow field around straight-bladed vertical axis wind turbine. J. Wind Eng. Ind. Aerodyn. 2016, 151, 70–78. [Google Scholar] [CrossRef]
- Patankar, S. Numerical Heat Transfer and Fluid Flow; CRC Press: Boca Raton, FL, USA, 1980. [Google Scholar]
- Weihs, D.; Katz, J. Cellular Patterns in Poststall Flow over Unswept Wings. AIAA J. 1983, 21, 1757–1758. [Google Scholar] [CrossRef]
- Crow, S. Stability Theory for a Pair of Trailing Vortices. AIAA J. 1970, 8, 2172–2179. [Google Scholar] [CrossRef]
- Disotell, K.J.; Gregory, J.W. Time-Resolved Measurements of Cellular Separation on a Stalling Airfoil. In Proceedings of the 53rd AIAA Aerospace Sciences Meeting, Kissimmee, FL, USA, 5–9 January 2015. [Google Scholar]
- Spalart, P.R. Prediction of lift cells for stalling wings by lifting-line theory. AIAA J. 2014, 52, 1817–1821. [Google Scholar] [CrossRef]
- Gross, A.; Fasel, H.F.; Gaster, M. Criterion for spanwise spacing of stall cells. AIAA J. 2014, 53, 272–274. [Google Scholar] [CrossRef]


















| Reduced Frequency f | Mean Pitching Angle (°) | Pitching Range (°) | Maximum Angle (°) | Minimum Angle (°) |
|---|---|---|---|---|
| 0.01 | 6, 6.5, 7, … 10 | 22, 23, 24, … 30 | 17, 18, 19, … 25 | −5 |
| 0.025 | 6.5, 7, 7.5, … 10 | 23, 24, 25, … 30 | 18, 19, 20, … 25 | −5 |
| 0.1 | 7.5, 8, 8.5, … 10 | 25, 26, 27, … 30 | 20, 21, 22, … 25 | −5 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, D.; Nishino, T. Unsteady RANS Simulations of Strong and Weak 3D Stall Cells on a 2D Pitching Aerofoil. Fluids 2019, 4, 40. https://doi.org/10.3390/fluids4010040
Liu D, Nishino T. Unsteady RANS Simulations of Strong and Weak 3D Stall Cells on a 2D Pitching Aerofoil. Fluids. 2019; 4(1):40. https://doi.org/10.3390/fluids4010040
Chicago/Turabian StyleLiu, Dajun, and Takafumi Nishino. 2019. "Unsteady RANS Simulations of Strong and Weak 3D Stall Cells on a 2D Pitching Aerofoil" Fluids 4, no. 1: 40. https://doi.org/10.3390/fluids4010040
APA StyleLiu, D., & Nishino, T. (2019). Unsteady RANS Simulations of Strong and Weak 3D Stall Cells on a 2D Pitching Aerofoil. Fluids, 4(1), 40. https://doi.org/10.3390/fluids4010040





