Abstract
Large eddy simulations were performed to characterize the flow and mass transport mechanisms in the interior of two Pocillopora coral colonies with different geometries, one with a relatively loosely branched morphology (P. eydouxi), and the other with a relatively densely branched structure (P. meandrina). Detailed velocity vector and streamline fields were obtained inside both corals for the same unidirectional oncoming flow, and significant differences were found between their flow profiles and mass transport mechanisms. For the densely branched P. meandrina colony, a significant number of vortices were shed from individual branches, which passively stirred the water column and enhanced the mass transport rate inside the colony. In contrast, vortices were mostly absent within the more loosely branched P. eydouxi colony. To further understand the impact of the branch density on internal mass transport processes, the non-dimensional Stanton number for mass transfer, St, was calculated based on the local flow time scale and compared between the colonies. The results showed up to a increase in St when the mean vortex diameter was used to calculate St, compared to calculations based on the mean branch diameter. Turbulent flow statistics, including the fluctuating velocity components, the mean Reynolds stress, and the variance of the velocity components were calculated and compared along the height of the flow domain. The comparison of turbulent flow statistics showed similar Reynolds stress profiles for both corals, but higher velocity variations, in the interior of the densely branched coral, P. meandrina.
1. Introduction
Determining hydrodynamic properties in the interior of coral colonies is essential for understanding growth and mass transport process in branching corals [1,2]. Because of each colony’s unique geometric structure, distinct flow fields evolve in different individual colonies, both in the interior and at the exterior of the colony. The characteristics of internal flow field depends upon morphological parameters such as the porosity, branch diameter, inter-branch distance, and the Reynolds number. The mean flow profiles inside the colony influence the exchange of solutes across the coral tissue-water interface, control the nutrient transport, and determine the dissolved oxygen concentration near the coral surface [3].
Reef corals depend on the surrounding water for nourishment and their morphology affects food availability. In an early flume experiment, Chamberline et al. visualized the flow around different coral morphologies and concluded that loosely branched colonies likely have a relatively higher probability of obtaining suspended food particles inside the colony. In contrast, tightly branched colonies must contend with the reduced access to food inside the coral due to their complex branching structures that impede the flow [4]. The suspended particles serve as supplemental nourishment when the symbiotic relationship between algae and coral polyps provides insufficient nutrition. Chamberlain also brought attention to the effect of colony orientation on the flow field and discussed the hydrodynamic adaptation of branching corals. Sebens et al. [5] analyzed the impact of branch spacing on the particulate capturing capabilities of corals. The authors of that study analyzed the maximum particulate capturing cases within the low and high density aggregate corals from low to high flow conditions, and found that the location of maximum consumption depends on the internal flow conditions. In some cases, the corals changed morphological structure to gain better access to nutrients. Similarly, Hunter et al. investigated the effects of colony bushiness on the feeding effectiveness for unidirectional and wavy flows [6]. Thus, we see that nutrient availability changes significantly in corals with changes in internal hydrodynamics, which need to be explored in detail to understand their impact on colony growth and transport processes. To examine this relationship, Mass and Genin conducted a controlled study and demonstrated the development of an asymmetrical branching pattern as a consequence of an asymmetry in the oncoming flow conditions [7]. Kandorp and Kubler also discuss how the flow conditions can change the internal branch density of corals [8].
Experimental studies show that the growth and development of coral and reef systems are influenced by metabolic responses, which directly depend on the internal flow dynamics [2,9]. Physiological processes like photosynthesis and respiration depend on the thickness of the diffusive boundary layer (DBL), which is a strong function of the internal hydrodynamics [10,11]. To understand this relationship, Bruno et al. conducted an experiment and found that coral respiration rates depend on the inter-branch distance and flow magnitude inside the corals. The authors suggested that an increase in inter-branch distance enhances the transport rate due to the corresponding reduction in the thickness of the DBL [12]. Similarly, Jimenez et al. measured the thickness of the thermal boundary layer (TBL) in low flow conditions and showed that the TBL at the coral surface is a strong function of the flow magnitude [13]. In a recent paper, Chan et al. hypothesized that the tissue surface pH of a coral is also a function of the flow microenvironment inside the colony structure [14].
Reidenbach et al. [15] performed laboratory experiments on mass transport over rough coral beds and found that the mass transfer rate increased sharply for wavy flow in comparison to the unidirectional flow condition. The authors concluded that the increase in turbulent stress also increased the mass transfer rate. Later, Stocking et al. took flow field measurements above one healthy and one algae-covered coral colony and found differences in the velocity profiles and Reynolds stresses at the top of the colonies [16]. Similarly, Hench et al. investigated spatial flow patterns on a single colony, and on several adjacent colonies (at resolutions of 0.1–10 m) using acoustic Doppler velocimetry (ADV). Here, the flow profile and turbulent statistics were calculated from measurements obtained at the minimum spatial resolution of 0.2 m in the horizontal and vertical directions [17]. Pomeroy et al. used ADV to obtain velocity profile, shear stress, and suspended sediment transport rates over the rough boundary of coral reef [18]. Similarly, Sous et al. characterized the spatial evolution of a reef structure using spectral analysis [19]. In a flume study, Asher et al. calculated drag force on a model reef composed of 81 Pocillopora colonies and determined the drag force as a function of colony height at several points inside the model reef. The authors also determined the mean velocity profile and Reynolds stresses from the velocity measurements at the same measurement points, both inside and above the model reef [20]. These analyses provide an excellent picture of the character of turbulent flow fields throughout a coral reef, but complete, detailed, three-dimensional flow fields inside an entire coral colony remain exceedingly difficult to obtain. In recent years, new flow visualization and measurement techniques like magnetic resonance velocimetry (MRV) have been used to obtain the flow field inside complex geometries. Chang et al. used MRV to obtain the first detailed flow profile in the interior of a colony and compared the mean velocity profile between low and high flow coral geometries with different inter-branch distances [21]. This is the first study where detailed velocity fields were used for analyzing flow inside a colony and the authors emphasized how intra-colonial variability plays an important role in mass transfer. In another study, Chang et al. computed the flow profile inside Pocillopora and Stylophora colonies and derived a correlation between the local shear stress and the rate of scalar transport. The authors suggested a similarity in mass transfer characteristics despite differences in their physical shapes and hydrodynamic conditions [22]. Recently, Shapiro et al. showed that the cilia of a coral can stir the water column and create vortices which can enhance the mass transport rate by up to compared to diffusion through an unstirred boundary layer near the coral surface [23].
The current study builds upon the foundational studies by Chang and Shapiro, and tries to address the question of whether the internal geometry plays an important role in mass transfer in the interior of coral. In a recent paper, Hossain and Staples computed the detailed, three-dimensional velocity field inside a P. meandrina colony and documented the existence of passively formed vortices within the densely branched colony, which enhanced mass transport inside the complex geometry [24]. In the current study, we want to extend this analysis further by comparing flow fields between two different branching coral species in the same genus to evaluate if the same mass transport characteristics and mechanisms hold for densely and loosely branched colonies. The first part of the paper discusses how internal hydrodynamics control the transport process for branching corals. To quantify the mass transfer rate in coral colonies, engineering correlations for heat and mass transfer serve as as an important tool. Atkinson and Bilger et al. were pioneers in such analyses. They used the mass Stanton number to compute the uptake of phosphate in corals and compared their experimental flume study data with the engineering correlations from classical heat and mass transfer applications [25,26]. The mass Stanton number is a dimensionless number that represents the ratio of mass transfer rate to the advection rate on the surface. Similarly, the Sherwood number has been used to calculate mass transfer rates from submerged canopies of arrays of cylinders for both unidirectional and oscillatory flows [27]. Both the mass Stanton and Sherwood number can be used to estimate the mass transfer rate between the complex geometry of a coral colony and the surrounding water as both these numbers are the functions of the Reynolds and Schmidt numbers, roughness parameters, and the surface geometry [22,26]. In the current study the mass Stanton number used to calculate average mass transfer rates along the length of both colonies was based on the mathematical formulation by Atkinson and Bilger et al. [25].
The mass transport between the surrounding water columns and the interior of the coral reef also depends on the turbulent flow profile both at the exterior and interior of the reef [15,28]. For example, the transport of eggs and sperm from the surface of an Acropora reef to the surrounding water and the transport of nutrients from the water to the interior of the reef depends on the turbulent stress at the top of the reef. Turbulent flow statistics are also important for calculating the Reynolds stress and the bed shear stress, and determining the transport momentum and sedimentation rate in the bottom layer of the reef or over a colony or reef [16,29,30]. Though numerous studies have explored the effects of these quantities on coral reef systems, we reiterate here that computing the detailed, local turbulent flow in the interior of a reef or a single colony is still a challenging task.
Canopy flow theory can be used to compute the turbulent flow characteristics through complex coral reef structures and to understand the macroscopic turbulent flow field around the structure. Nepf et al. performed an open channel flume study and described the transition between emerged and submerged canopies and explained the impact on mean momentum and turbulence [31]. Generally, the double-averaged Navier–Stokes equations are used to solve the spatio-temporally averaged velocity components and turbulent statistics from the flow field [32]. The averaging procedure creates a new term, the dispersive stress, which needs a closure model in order to solve the complete set of equations [33]. The closure models that exist were developed for homogeneous structures, and the accuracy of these models inside a complex coral reef geometry is still not clear. Though it is an excellent tool for large-scale flow analysis, more detailed flow information for a single colony is needed to obtain the micro-scale flow field and to understand the mass transport mechanisms, and local turbulent statistics within coral colonies with different branching patterns. In addition, we still depend on empirical and semi-empirical data for calculating drag forces inside reefs [34]. If we can resolve the flow field inside the reef, the drag forces and the closure models used for the calculation of dispersive stress can be evaluated more accurately. To achieve this, we continue our analysis of the turbulent stress and momentum transfer through both structures in the second part of this paper.
To assist us in achieving both of these objectives, we implement a numerical approach to solving for the flow field inside the coral colonies. Capturing the arbitrary boundary of a coral is a challenging task. Different numerical approaches have been used to solve this issue, but problems arise due to the complex natural morphology of corals, and the turbulent flow. Therefore, a new interest in the numerical simulation of hydrodynamics of real corals has emerged. In a recent paper, Stocking et al. numerically investigated heat and mass transport for flow over the exterior of natural and modeled coral structures and discussed the effect of roughness on heat and mass transport [35]. Similarly, Cano et al. performed a drag force analysis on a real coral geometry with an open-branched structure [36]. These analyses provide an excellent view of the flow dynamics in real corals, but did not calculate the structure of the turbulence, including the fluctuation components of the velocity, the detailed velocity vectors, or the development of local shear stresses inside the coral structures. Kaandorp et al. used the lattice Boltzman method to calculate flow pattern inside Maracis mirabilis [37,38] and, similarly, Chindapol et al. used COMSOL Multiphysics to model the effect of flow on the growth of Pocillopora verrucosa [39]. But these simulations were performed in a laminar flow framework. The immersed boundary method (IBM) is suitable for handling complex geometries and turbulent flows, and the governing equations are discretized on fixed Cartesian grids with an external force. Chang et al. were the first to use the immersed boundary method to simulate the flow inside the arbitrary branches of coral colonies [22]. In the current analysis, we have used the similar IB algorithm to perform all of these simulations in a large eddy simulation (LES) framework.
2. Materials and Methods
2.1. Immersed Boundary Method with Large Eddy Simulation
The turbulent flow over these complex geometries was computed with an incompressible immersed boundary solver, developed in the large eddy simulation framework. In LES, the large scales in the flow are resolved whereas the small scales are modeled. The filtered Navier–Stokes equations used in the current analysis are shown below:
where the bar represents the filtering operations. The velocity components are defined by and P represents the dynamic pressure. The term is used for the external forcing used in the immersed boundary method. Here the subgrid stress tensor is defined by and must be modeled to solve the velocity field. There are different techniques to parameterize the subgrid stress. In the current study, a Lagrangian dynamic Smaogrorinsky [40] model has been used for the complex structure. Here the coefficients of subgrid scale(SGS) stress model are adjusted dynamically which is suitable for LES of complex geometry [41]. In the current simulation, a uniform grid spacing has been used in the X, Y and Z coordinates.A finite difference algorithm with the second order accuracy in space and time has been used to discretize the N-S equations. Here the time Step was advanced explicitly with a second-order Adams–Bashforth time marching algorithm. A uniform incoming velocity boundary condition at the inlet and a convective boundary condition have been used at the outlet of the domain. Slip boundary conditions are assumed in the lateral direction and at the top of the flow domain.
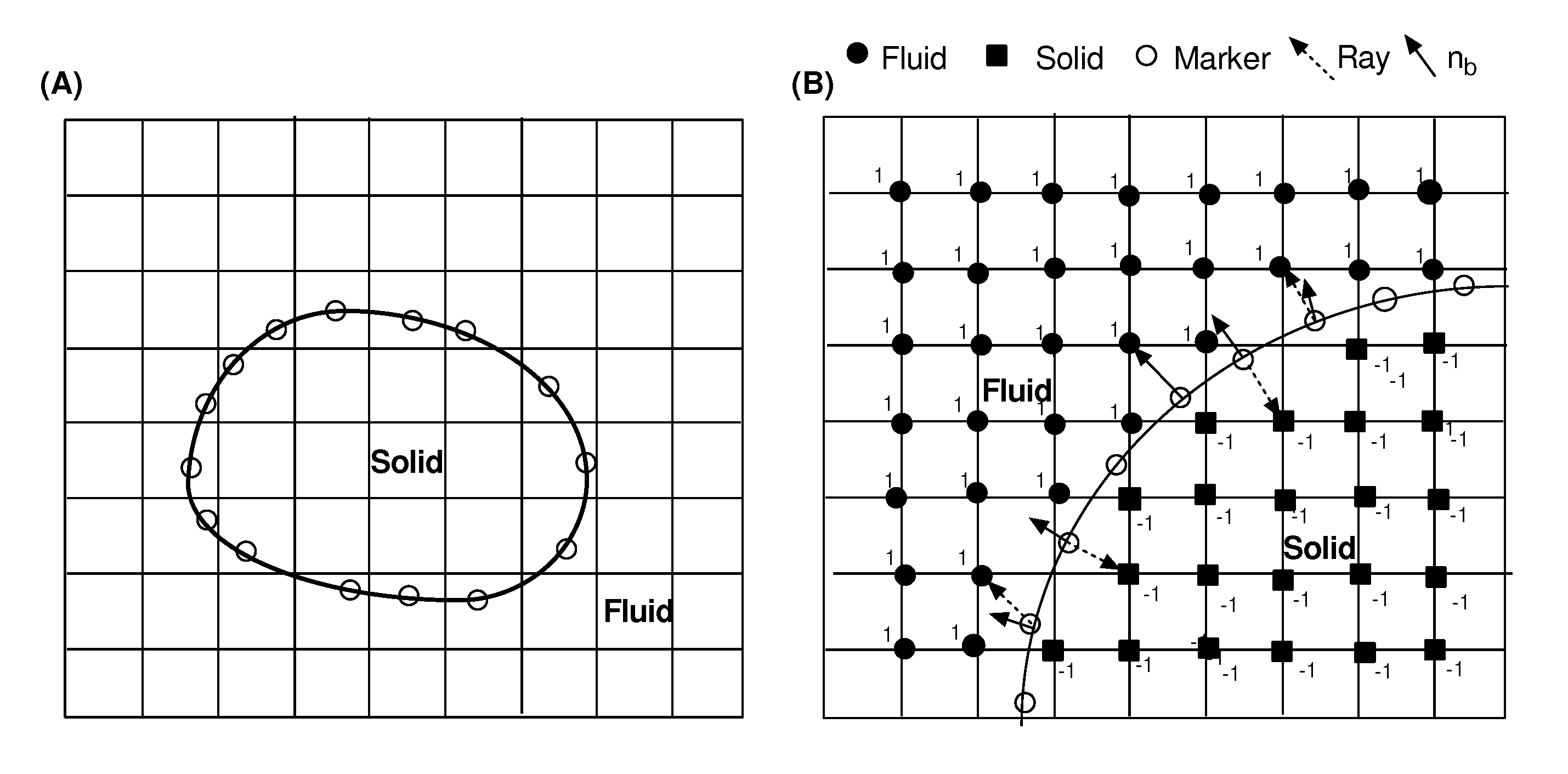
Performing LES in a complex geometry is still a challenging task. The process requires high quality mesh generation, which is not easy even for simple geometry. In comparison, immersed boundary with an arbitrary shape can be modeled on a fixed nonconforming grid by using an external force field. The IB method was first introduced by Peskin et al. [42] and is used mainly for low Reynolds number biological flows by modeling the boundary as a set of interconnected spring elements. But this approach causes stiffness at the stationary boundary. Later Mohd-Yusof et al. [43] and Fadlun et al. [44] solved this issue by introducing a direct forcing approach to this algorithm. In the direct forcing method, forcing is implemented in such a way that the appropriate boundary conditions are enforced on the boundary itself. The IB method used in the current study was developed by Balaras et al. [45] and the details of the implementation and accuracy of the method can be found in the referenced papers. Here a brief description is introduced to describe the main features of the algorithm. In the current IB method, a ray-tracing algorithm was implemented to capture the interface of solid and fluid in the Cartesian grid. To provide a short description, different stages used in the IB method are shown in Figure 1.
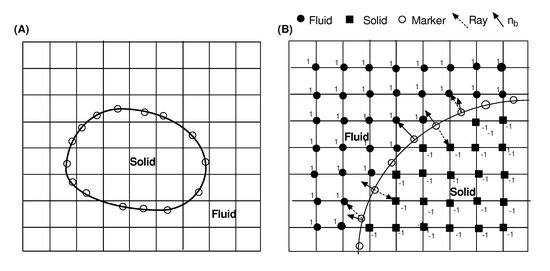
Figure 1.
(A) An arbitrary object immersed in Cartesian coordinates. (B) A ray tracing algorithm is utilized in the immersed boundary algorithm [45,46] to identify solid and fluid grid points in the computational domain.
Figure 1 shows a solid object submerged in the Cartesian grids. The boundary is described by a series of markers. In the Stereolithography (STL) file, the boundary of the solid object is composed of millions of triangles. A search algorithm is used to identify the nearest grid points around the marker particles. To find the phase of grid points, ray is sent from these markers to the nearest grid points and normal is calculated on these markers. Then the dot product of the normal and the ray determines if the location of the grid point is inside the solid or not. In the case of the stationary boundary, this process is performed at the beginning of the simulation. Then the closest grid points near the boundary in the fluid are chosen for the implementation of the forcing function. The velocity of the forcing points is interpolated from the surrounding fluid. Different techniques are available for interpolation to reconstruct the velocity field near the solid boundary. The reconstruction procedure and the implementation of the immersed boundary method can be found in detail in the referenced paper of Balaras and Young et al. [46].
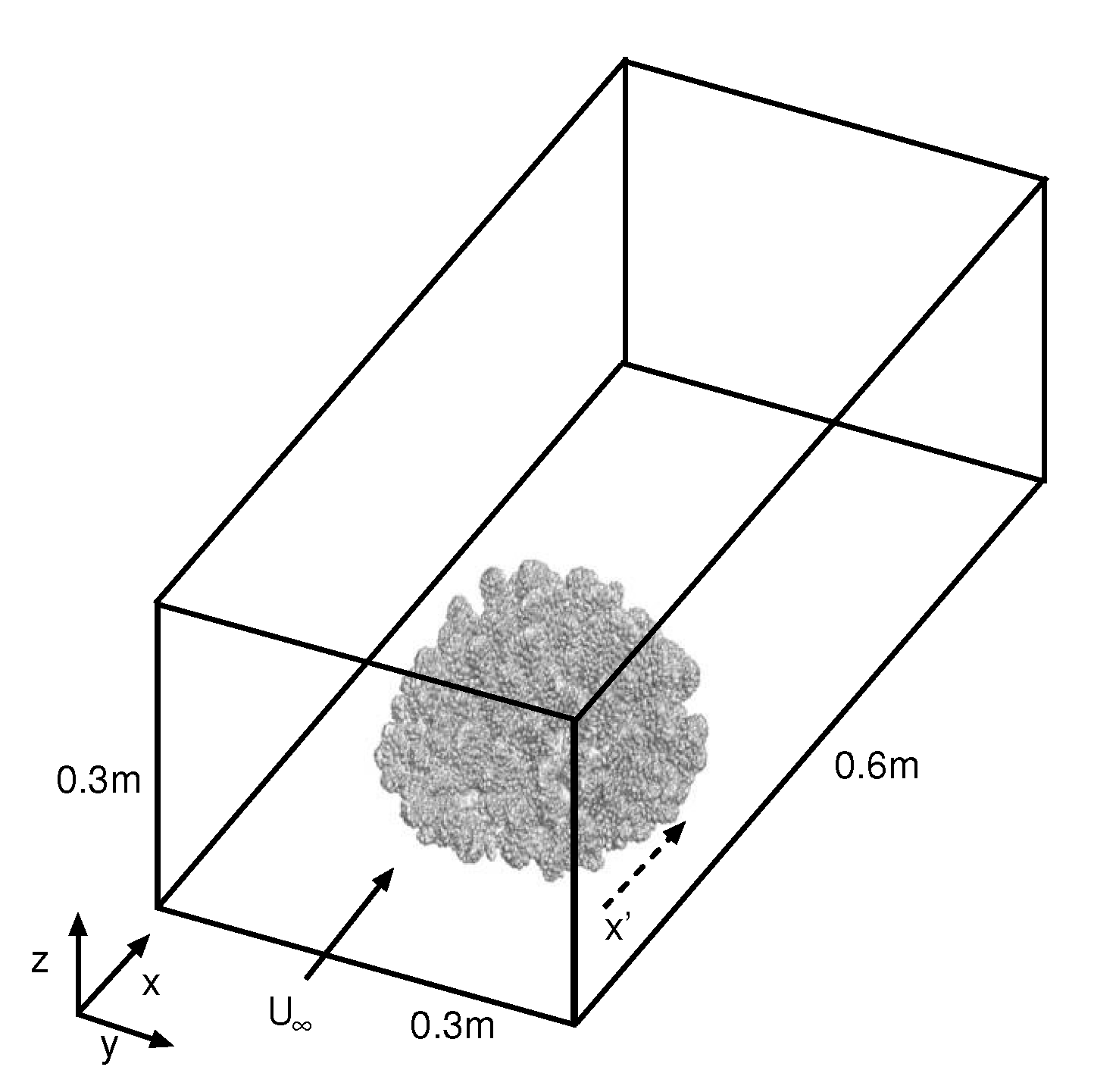
In addition to the main features of the current algorithm, we also want to discuss the limitations of the current study. The experimental studies show that mass and flow dynamics change significantly in oscillatory flow conditions [47]. In the current analysis, only the uniform flow condition was considered in studying the impact of coral structure on hydrodynamics. In addition, coral grows in a natural reef environment and the colony sitting in the wake region of another coral will have different flow dynamics than the one in front of it. A single coral, sitting in an open flow condition, does not represent a typical flow condition in nature. However, resolving the flow field with a fine-scale resolution in the interior of a reef is extremely computationally expensive. Even for a single coral, 54 million grids were used for all of the simulations performed in the current study. This illustrates how expensive the simulation would be if the computation were performed on a larger scale. In addition, the sidewall of the domain may constrain the flow. However, the presence of the close neighboring corals may have a similar effects on the flow profile. Overall, the objective of the current study is to find the detailed hydrodynamics and mass transport mechanisms inside two different coral geometries where the maximum length scale of the analysis is the height of the coral. In addition, the simulation performed in the current study was not fine enough to resolve the diffusive boundary layer, which is approximately a few hundred microns from the coral surface [48]. We believe that the current setup of the flow domain shown in Figure 2 and the resolution of the simulation will be sufficient to meet the aforementioned objectives.
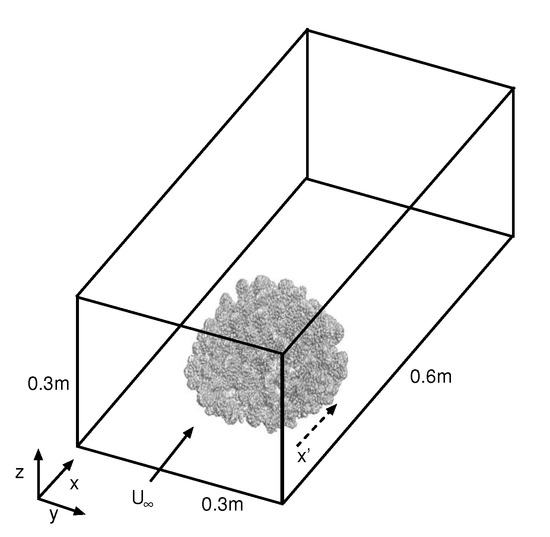
Figure 2.
Schematic of flow domain used in the simulation (not to scale). indicates the beginning of the flow domain, while represents the beginning (front edge) of the coral in the flow domain.
2.2. Coral Geometries
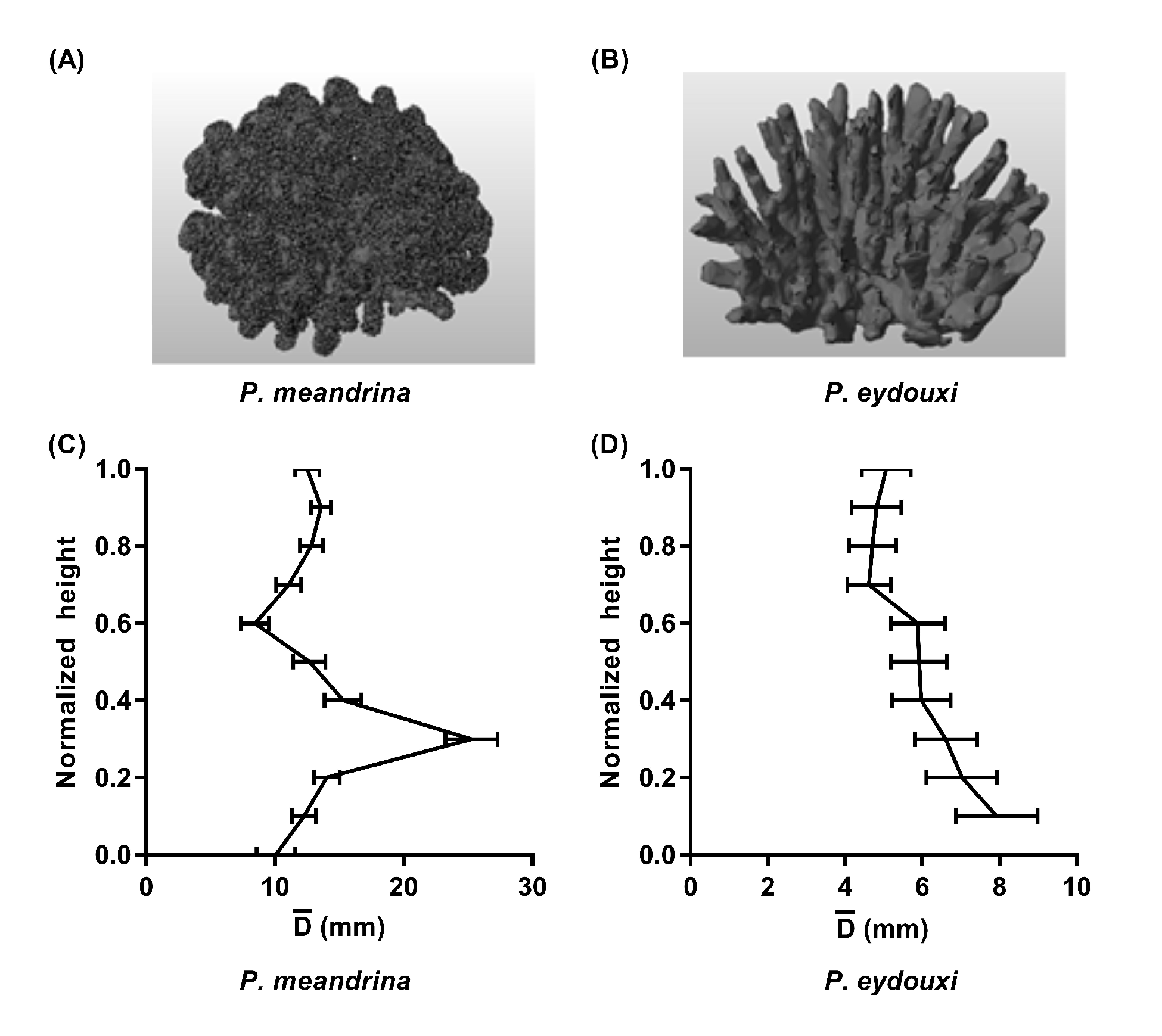
From the previous discussion, it is clear that the current analysis needs to be performed on real coral geometries with different branching patterns. To achieve this, Stereolithography (STL) files of two Pocillopora colonies were used for the current simulations. The densely branched P. meandrina also known as Cauliflower coral, is generally found in the Indo and eastern Pacific and grows in strong flow conditions. In contrast, there is relatively more space between the branches of P. eydouxi, which is found in the frontal reef area. The size of these coral structure depends on the physiological factors, hydrodynamic condition, and species-specific demographic location. So, there exists spatial heterogeneity in their population size. The STL file of P. meandrina, used for the current simulations, were obtained from the computed tomography (CT) scan of the real coral skeleton and shared by Dr. Uri Shavit from Technion—Israel Institute of Technology. The dimension and the geometric features of both of these colonies can be found in Table 1. In addition to the geometrical dimensions, the mean branch diameter was plotted as a function of colony height for both structures in Figure 3. These are Stony corals, where the tissue makes little contribution to the body mass index. Therefore, using coral skeletons instead of real coral geometries will have a little impact on the computational results.

Table 1.
Geometrical features of the Pocillopora colonies.
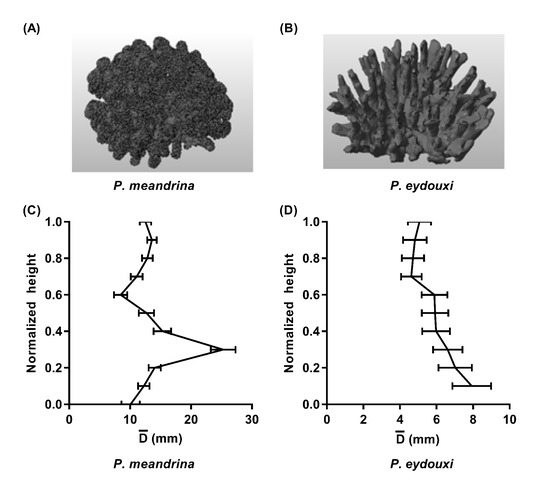
Figure 3.
(A,B) Rendered stereolithography files of the P. meandrina and P. eydouxi colony geometries used in the simulations. (C,D) Mean branch diameter at normalized height from the base of the Pocillopora colonies. Horizontal bars indicate the variance.
3. Results
3.1. Validation of the Simulation Results
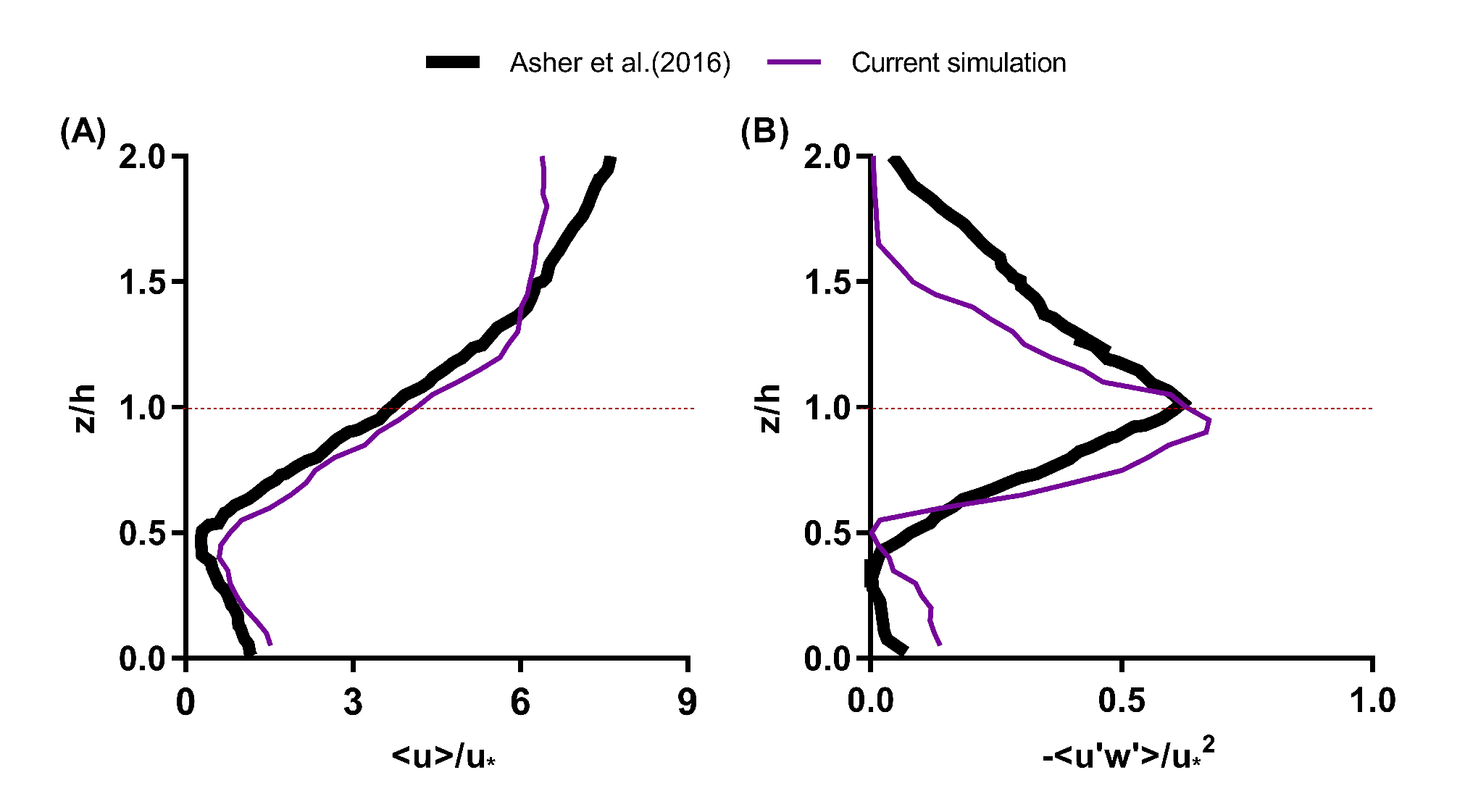
The current simulation was validated by two experimental results from Chang et al. [21] and Asher et al. [20], respectively. A detailed comparison between the experimental results of Chang et al. and the results from current numerical techniques can be found in Hossain and Staples [49]. Only a brief description of the main features of the comparison is discussed here. Chang et al. utilized MRV to obtain a detailed velocity at the interior of the densely branched coral (high flow morphology) of Styolophora. The experiment was performed at the Reynolds number 5000 based on the incoming flow magnitude and height of the colony. For the numerical simulation, the computation was performed on P. meandrina at the same Re number based on the height and incoming uniform flow. The geometrical features of colonies and the dimensions of the flow domains were similar for both cases. For qualitative comparison, velocity slices were extracted from the same normalized height and compared between the experimental and simulation results. The comparison shows similar flow characteristics at both the interior and exterior of the colony. As the densely branched structure worked as a baffle, most of the incoming flow was diverted outside and toward the top of the colony for both structures. In addition, a quantitative comparison was performed by measuring the mean velocity magnitude as a function of radial distance from the exterior to the center of the colony, and the result showed similar velocity trends for both structures.
The second comparison was performed with the experimental results of Asher et al. [20] who analyzed the P. meandrina colony, similar to the current simulation to measure the vertical variations of drag forces. In the experimental study, eighty-one P. menadrina coral skeletons were used for calculating mean streamwise velocity profiles and the Reynolds stress developed over the colony. These velocity profiles were obtained by laser Doppler anemometry, using 19 locations inside and around the P. meandrina. In this flume study, the ratio of the height of the water column to the colony height was three, which represents the optimum depth after which the flow structure does not change with an increase in the depth to coral height ratio [50]. The magnitude of the Reynolds number was based on the uniform incoming flow and the height of the colony. The mean velocity and Reynolds stress profiles were obtained by double averaging the respective magnitude in the streamwise and lateral directions and normalized by the friction velocity, which was calculated with the equation of Pokrajac et al. [51]. For the simulation, the same water depth to coral height ratio and Reynolds number were used in the flow domain. Here the Reynolds number was calculated based on the height and uniform flow at the inlet of magnitude m/s. To match the dimension of the experiment, the height of the colony used in the simulation was extended up to m. Similar to the experimental study, a double averaging was implemented here in the streamwise and lateral direction up to the dimension of the P. menadrina to obtain the mean streamwise velocity and Reynolds stress profiles developed through the colony. Both mean profiles were normalized by the friction velocity calculated from the square root of the maximum values of Reynolds stress [33] found at the top of the colony. Figure 4 shows the comparison of mean streamwise velocity and Reynolds stress profiles between the flume study and the current simulation through the P. menadrina. In general, the comparison shows a close match between the experiment and the current simulation results for both of these profiles. For the streamwise velocity, both results showed an inflection point located near at the interior of the colony, and the profiles matched well up to ≈ above the coral. Above , the experimental result displayed a relatively higher velocity magnitude in comparison to the simulation.
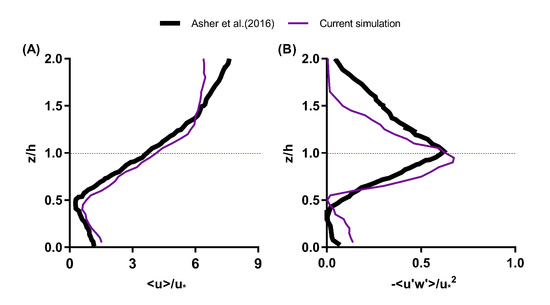
Figure 4.
Comparison of (A) the normalized streamwise velocity and (B) Reynolds stress over a single P. meandrina colony from the current simulation with the experimental results over 81 P. meandrina colonies at by Asher et al. [20]. The dotted line represents the top of the colony. The experimental data were obtained using GRABIT in MATLAB [52] and reproduced with permission from Asher et al. Vertical variations of coral reef drag forces. Journal of Geophysical Research: Oceans 2016, 121, 3549–3563. For both data sets, the mean velocity and Reynolds stress were normalized by the friction velocity.
To capture the turbulent mixing and shear, Reynolds stress was also plotted along with the height of the colony and averaged, in the same manner discussed earlier. The Reynolds stress exhibited the maximum magnitude at the top of the colony for both cases, which indicates higher mixing and momentum transport at the top of the coral. For the Reynolds stress, the results show a close match from the base up to in the flow domain, and beyond this height, the simulation result reached zero magnitude more quickly than the experiment. One reason for these discrepancies might be the number of corals analyzed. The slip boundary condition used at the top of the colony might also affect the overlying water column. The third reason might be the length of the flow domain where the averaging was computed. In the experiment, the averaging was performed on 81 P. menadrina colonies, whereas only a single coral was analyzed in the simulation. To demonstrate the grid independence of the the numerical results, we preformed the validation simulation at two different grid resolutions ( and 300) in the vertical direction. As we are averaging the simulation data in the horizontal and lateral directions, similar to the experimental procedure discussed earlier, we changed the grid resolution only in vertical direction. We did not find any difference in the simulated results at the two grid resolutions and the profiles were similar to the computational results shown in Figure 4. It is interesting to note that both the velocity and Reynolds stress profiles matched well within the colony up to the crest height. This might be interesting for future analysis if the simulation results on multiple colonies can be used to simulate flow inside large-scale reef. Though the results show a good match between the experiment and numerical studies, the comparison between only one set of geometry is not sufficient to draw such a conclusion.
3.2. Comparison of Flow Profiles and Transport Mechanism between Pocillopra Geometries
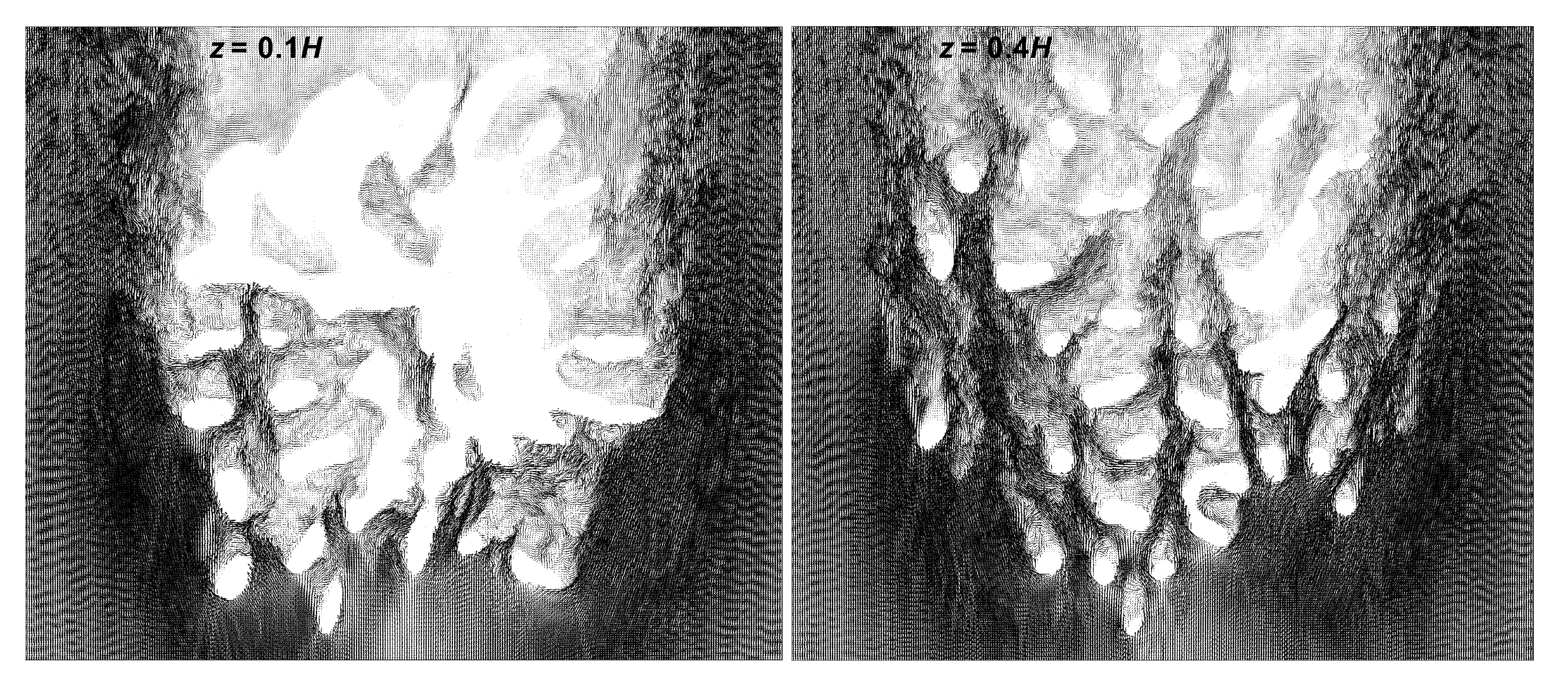
To understand the variation of the flow field within the colonies, comparison of flow profiles was performed between the two Pocillopora geometries at Reynolds number . The Reynolds number was determined based on the uniform flow magnitude at the inlet and the height of the colony. The incoming velocity was selected based on the computational experiments performed on Pocillopora by Chang et al. [22], for the purposes of comparison. For the internal flow comparison between these two branching corals, detailed vector profiles were obtained inside different sections of coral. Figure 5 and Figure 6 show a comparison of the top view of the vectors profile in the interior of both colonies obtained at the same normalized height from the base of the coral. For the densely branched P. menadrina, the velocity vector profile shows the interaction of the incoming flow with the branches of the colony. Comparatively large and higher concentrations of velocity vector were observed at the frontal section of the coral in comparison of the rear section, which indicates the difference in flow magnitude and the nutrient distribution between the front and rear sections of the coral. Here most of the flow was diverted outside because of the dense branch structure of the colony. From this observation, it seems that the dense branches at the frontal section of P. menadrina channel the flow to the outer periphery. In contrast, the vector profiles inside P. eydouxi show better penetration in the deep interior of the colony due to the openness of the structure. One of the interesting features of the flow profile of P. eydouxi was the formation of the wake region behind the individual branches in addition to a large wake region behind the coral. Though these vector profiles provide a qualitative comparison of the distinct flow features exhibited by the two different branching patterns, the transport mechanism in the interior of the colony is still not clear. To understand the transport mechanism, streamlines were plotted on the planes perpendicular to the flow direction from the front to the back of the colony. Figure 7A shows the formation of local vortices in the interior of P. meanndrina plotted at L perpendicular to the flow direction. For this densely branched colony, a highly vortical flow was observed from the L to the back of the colony, specifically in the middle where the mean flow magnitude started to drop in the interior. These passively formed vortices stirred the water near the coral surface and enhanced the mass transport rate. Similar formation of vortices at the exterior of the colony due to ciliary beating was cited by Shapiro et al. [23]. In a recent paper, Hossain et al. mentioned the formation of these vortices for the same P. menadrina colony [24]. The authors calculated the advection timescale along the length of the coral. They suggested that these passive vortices compensate for the reduction of the flow speed in the interior of coral. In the current study, we wanted to extend this analysis for relatively open uniform branching coral like P. eydouxi and determine whether these local vortices formed in a large number as found in P. meandrina. To achieve this, streamlines were also plotted at the same normalized location in the interior of P. eydouxi (Figure 7B). In this case, the formation of these local vortices decreased substantially. Similar slices were obtained at different sections from the front to the back of the coral and most of the slices did not show these vortices, except for a couple of small ones. This corroborates our previous assumption [24] that passive geometric features generate highly vortical flow in the interior of densely branched coral. When the branching pattern becomes relatively open and uniform, coral does not need to compensate for the drop in velocity magnitude by generating vortical fields inside the colony.
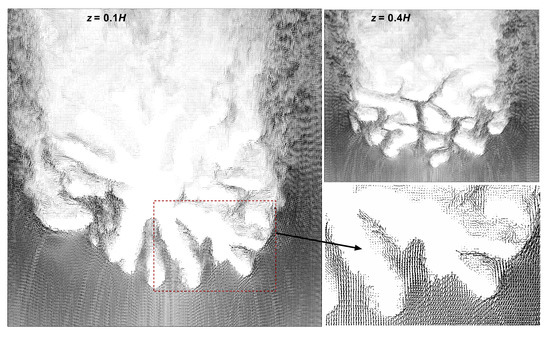
Figure 5.
Top view of the instantaneous velocity vector fields at two different heights ( and , where H is the height of the colony) inside the P. meandrina colony. These vector fields show the detailed interaction of the oncoming flow with the individual branches of the colony. The lower right figure shows a zoomed-in view of the velocity vectors at the frontal section of the colony at . The difference in vector fields at the front and rear halves of the densely branched coral, P. menadrina is clearly observable from the figure.
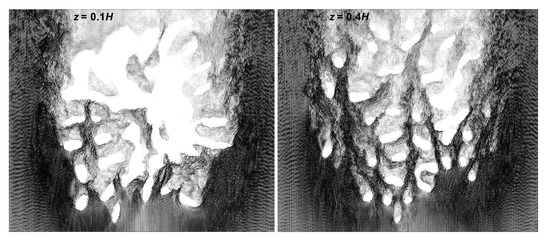
Figure 6.
Top view of the instantaneous velocity vector fields at two different heights ( and , where H is the height of the colony) inside the P. eydouxi colony. In comparison to P. meandrina, the velocity vector field demonstrates relatively higher flow penetration into the P. eydouxi colony because of the openness of the structure. The formation of wakes can be observed behind individual branches.
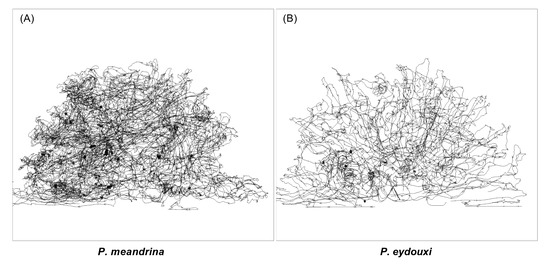
Figure 7.
Front-view streamline sections plotted at L for both Pocillopora colonies. The formation of vortices can clearly be seen in the inter-branch velocity field of P. meandrina in (A), whereas relatively few vortices are formed around the branches of P. eydouxi, as seen in (B).
We want to further investigate the transport rate for both these branching structures. Atkinson and Bilger et al. [25] previously used the Stanton number to compute the phosphate uptake in the reef environment. The mass Stanton number is the ratio of the mass transfer rate to the advection rate at the surface. Here we used the mathematical formulation of Atkinson and Bilger [25] to calculate the Stanton number along the length of both of geometries. The Stanton number can be defined as:
where m is the mass transfer rate, is the mean velocity magnitude, and and are concentrations of the substance at the surface and in the far water, respectively. If we consider a control volume (CV) around the coral, where the dimensions of the CV are equal to the maximum length, width and height of the coral, and assume that the concentration of the substance is zero () in the surrounding water, the transport of the substance will balance the decay in the concentration as described in the equation here:
where A is the surface area of the coral, V is the volume of water in the control volume and k is the first order decay rate which is defined as follows:
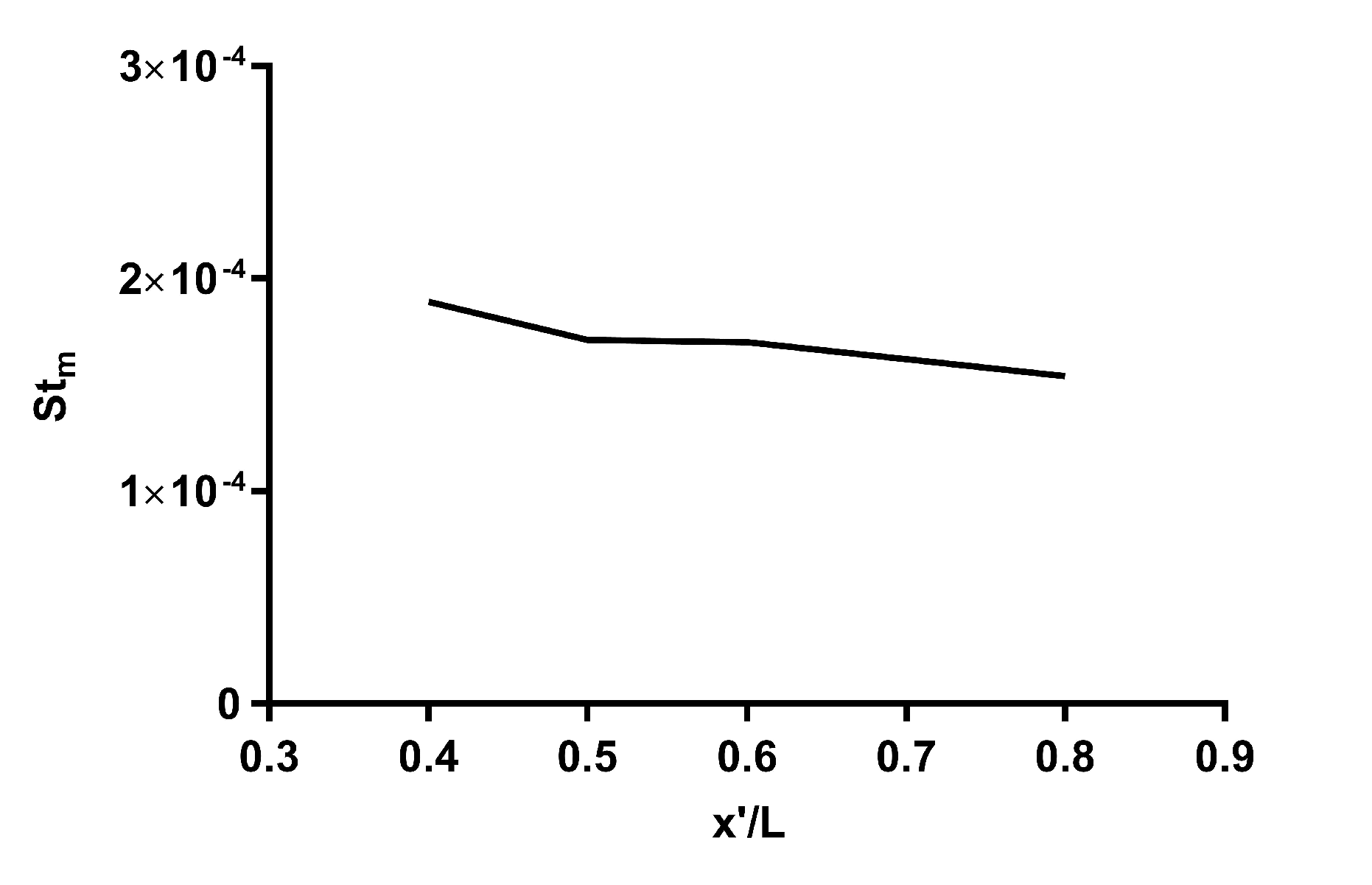
To make a fair comparison of the mass transfer rate between the two colonies, the transport of the same substance was compared, and the mass Stanton number was estimated along their lengths. Calcification is one of the most important physiological processes that stony corals carry out, and it controls the formation of their calcium carbonate skeletons. Here, we calculated St based on the transport of the same quantity of Ca from the coral surface for a given advection timescale at different sections of the colonies. To calculate St from Equations (3)–(5), we need the magnitude of the concentration of Ca in the reef, the mean velocity magnitude, and the advection timescale value along the length of the coral. The concentration of Ca is approx. 15 mol/m at 16 to 17 C in water [27]. is the magnitude of decay, which is on the order of mmol/m inside a coral colony [53]. Here, we used the advection timescale inside the colony as . The mean velocity and the advection time scale calculated at different sections of both colonies are shown in Table 2. The advection time scale was calculated based on two different characteristic length scales. For P. meandrina, the advection time was calculated from the mean diameter of the vortices (except for at L). As the number and the size of the vortices were not significant inside P. eydouxi, the advection time scale was calculated from the mean branch diameter and velocity magnitude along the length of the colony.If we consider the decay of the same quantity of Ca at the different advection time scales, estimates of the Stanton number can be obtained from Equations (3)–(5). In natural environments, the assumption of the decay of the same quantity of a substance at the advection time scale along the length of the colony may not hold everywhere in the colony [27]. If more than one coral were used in the analysis, the result might show significant variations in the Stanton number as the corals in the wake region of a reef might have a different mean flow profile than the frontal corals; however, these simplifying approximations were used to compare the transfer rates under idealized conditions between two different branching corals for the same flow conditions. Figure 8 shows the Stanton number obtained along the length of the P. meandrina colony, and Table 2 shows the values used for calculating St for both colonies. Due to the small number of vortices at the frontal and rear sections of the colony, the calculations of St were started and ended at L and L, respectively, in the interior of the P. meandrina colony. The calculations demonstrate an increase in the Stanton number of up to compared to the St magnitude calculated from an advection timescale based on the average branch diameter of P. meandrina; however, the P. eydouxi colony exhibits St values that are almost twice the magnitude of the maximum St value within the P. meandrina colony. It should be noted that the Stanton number calculated in the current study matches well with the St number measured in the flume study by Atkinson and Bilger [25] for the transfer of phosphate within coral colonies, and the magnitude varies from to , when studied for the velocity range to m/s.

Table 2.
Stanton number calculated along the length of the P. meandrina colony in the flow direction using two different methods (top and middle values) and the Stanton number calculated along the length of the P. eydouxi colony using the first method only (bottom values). Key: * The mean branch diameter was used as a length scale to calculate these values. † The mean diameter of the vortices was used as a length scale to calculate these values.
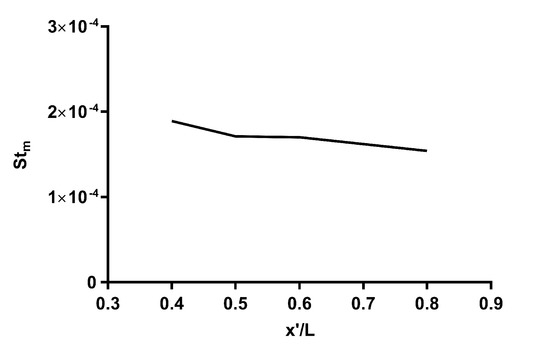
Figure 8.
The Stanton number calculated in the interior of the P. meandrina colony based on the mean flow magnitude and advection time scale at Reynolds number 15,000. Here, the advection time scale was calculated based one the mean vortex diameter at different sections of P. meandrina perpendicular to the flow direction, and the mean velocity value in those sections.
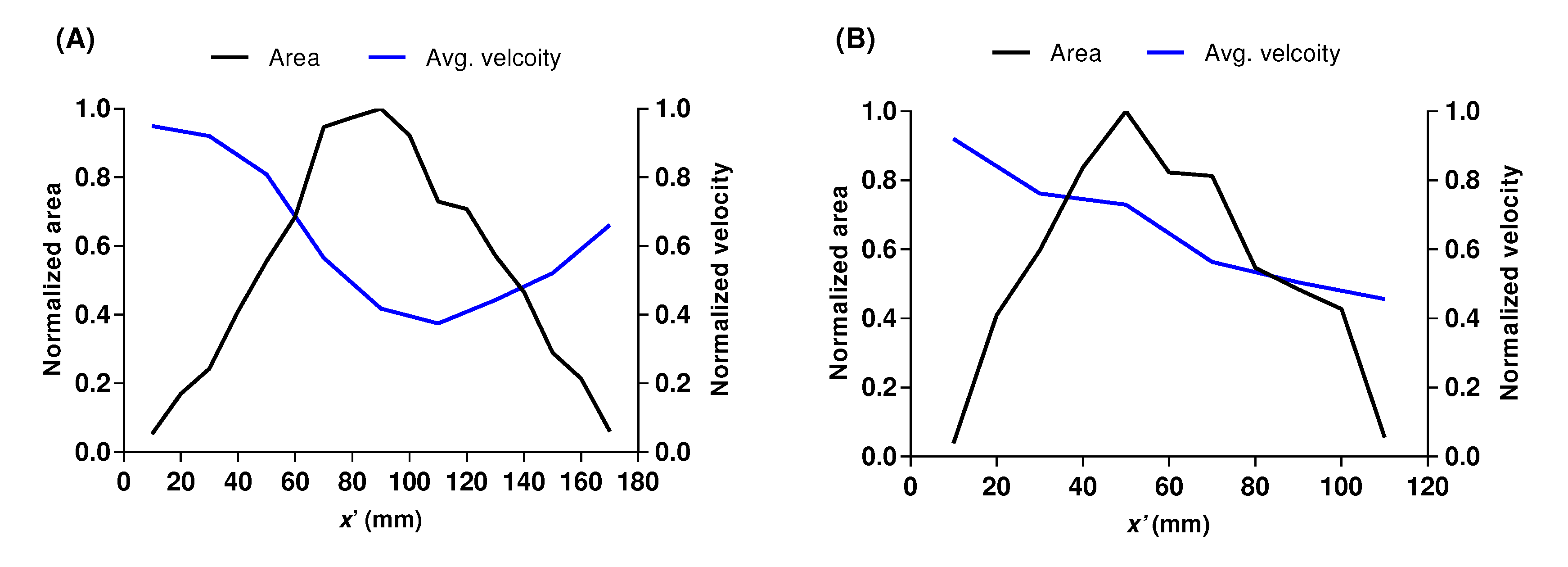
In addition to the transport mechanism, mean velocity profiles were computed and compared inside both these colonies from front to back for a similar incoming flow condition. The mean velocity profile averaged in the lateral direction within the coral is plotted along the length of the coral in Figure 9. To understand the variation of mean velocity with the internal geometry, the cross-sectional areas of the coral on the y-z plane were also included in the same plot. Almost in the middle of the colony, the mean velocity magnitude dropped to 60% within the densely-branched P. meandrina. In comparison, a relatively higher velocity profile was observed along the length of P. eydouxi, which ensures a higher probability of obtaining suspended food and relatively fast mass transfer in comparison to P. meandrina. It will be interesting to find the variation of the mean velocity profile with the change in incoming flow magnitude within the colony. In a previous study, Chang et al. performed a similar numerical experiment and found that the mean velocity profiles collapsed within Pocillopora when they were normalized by their respective incoming flow velocity [22].
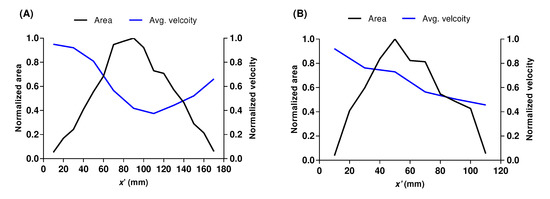
Figure 9.
Mean velocity profile and internal cross-sectional area (y-z plane) along the length of (A) the densely branched P. meandrina colony and (B) the loosely branched P. eydouxi colony. Here, the area and velocity are normalized by the maximum cross-sectional area and oncoming velocity magnitude, respectively.
3.3. Turbulent Momentum Flux
Numerous experiments and numerical studies were performed to understand the effects of canopy density on the mean velocity profile and turbulence statistics and have concluded that the turbulent momentum flux inside the canopy is strongly influenced by the canopy density [41,54,55]. In one study, Nepf et al. measured the mean velocity profile over a submerged canopy and described that the mean velocity and location of the inflection points depend on the sparsity of canopy elements [56]. Similarly, Dupont et al. used large eddy simulations to calculate the variation in turbulence characteristics for the variation in leaf-area index (LAI) parameters for the canopy elements. Though these turbulent analyses provide an excellent overview of the impact of canopy density on turbulent flow fields, measuring the fluctuating components and the subsequent calculation of turbulence moments within a single coral structure, as we have done here, has not been done before. In the current study, we were able to obtain this detailed fluctuating velocity field around both structures. Figure 10 shows a comparison of the instantaneous and fluctuating vector fields inside and above P. eydouxi. Figure 10 (left) shows the lateral view of the relatively high concentration of velocity vectors at the front and along the top surface of the colony. These velocity fluctuations contributed to the development of turbulent stress on the top of the surface of the coral. Maximum velocity fluctuations were observed both at the top and inside the colony, which indicates a significant contribution of the turbulent stress within the coral.
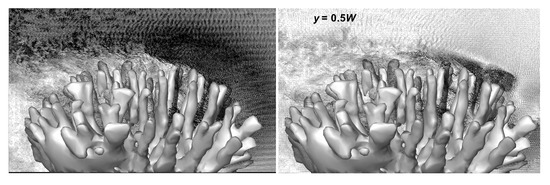
Figure 10.
Side view of instantaneous mean (left) and fluctuating (right) velocity vector components above P. eydouxi at , where W is the width of the colony. Here, the flow is moving from right to left. The instantaneous mean vector field (left) shows a higher concentration of velocity vectors above the colony as most of the flow is diverted to the top and sides of the colony. The fluctuating vector field was obtained by subtracting mean velocity from the instantaneous velocity field. These fluctuating velocity components also appear denser at the top surface of colony and contribute, to the Reynolds stress which controls mass transport to and from the top surface of the colony.
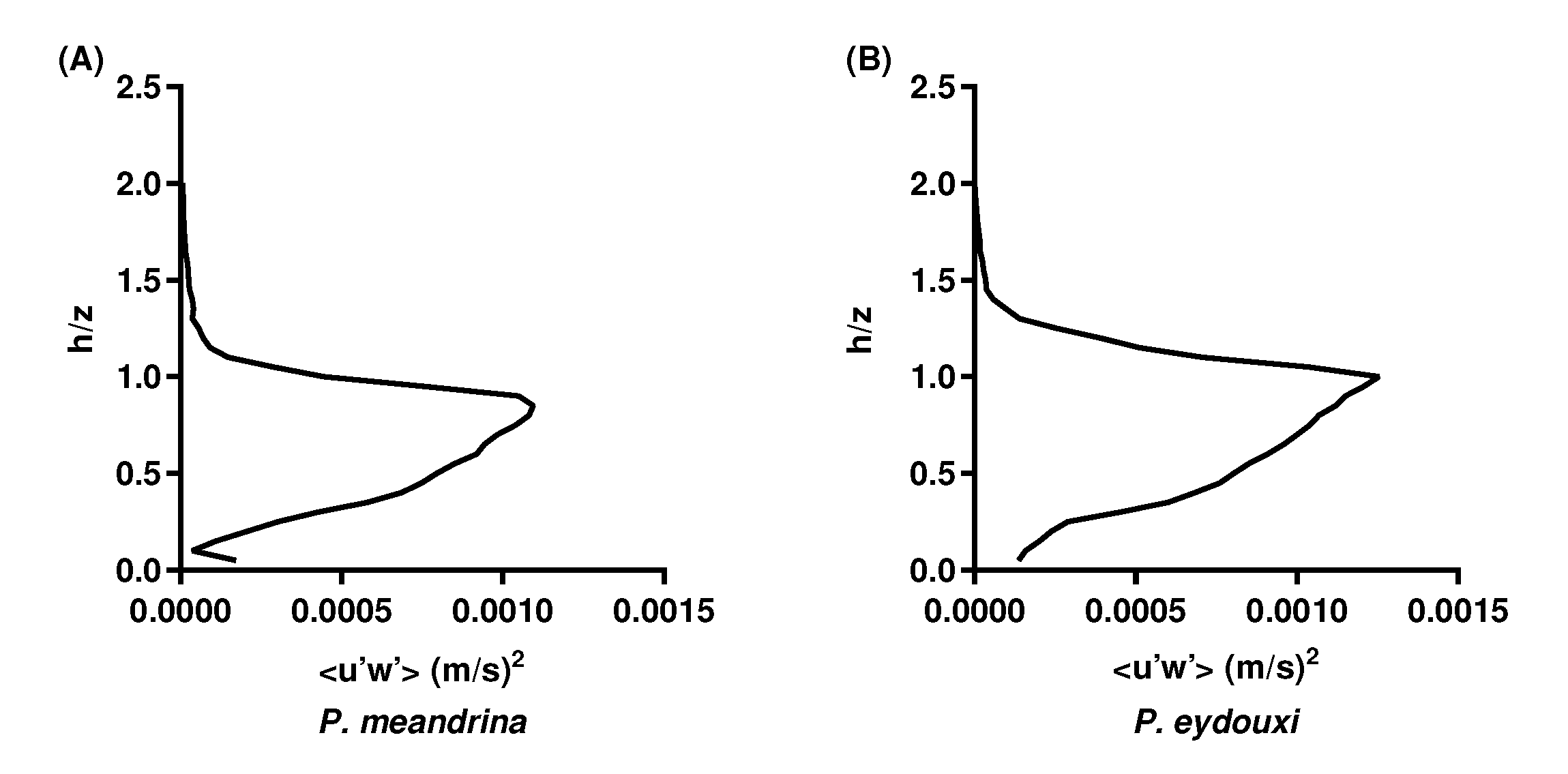
From these detailed fluctuating flow fields, we were able to calculate Reynolds stress for these corals. Figure 11 shows the formation of the Reynolds stress over both structures at Reynolds number 15,000. Here, the Reynolds stress showed similar profiles over the geometries, and the maximum magnitude was found at the crest of the colony, which matches the relatively higher fluctuating vector components described earlier over the top of the colonies in Figure 10. Even though there was a slight difference in the magnitude, the internal branching pattern did not alter the general profile of Reynolds stress too much in the interior of the colony. This is a very interesting finding in the sense that the Reynolds stress controls the mixing, transport of nutrients, and the transfer of scalar to and from the coral colony. Therefore, the influence of the Reynolds stress on the mass transfer was almost the same for both Pocillopora colonies despite significant differences in their branching patterns. It may be tempting to use this finding to contradict the common assumption that densely branched strictures may dampen the turbulent stress in the interior of the colony. But with only two geometrical structures, it is difficult to come to such a conclusion. Similar studies in the future should include more geometries. The same magnitude of Reynolds stress at the top of the colony indicated similar frictional velocity above both colonies, and the magnitude of the stress reached the zero value at nearly the same height.
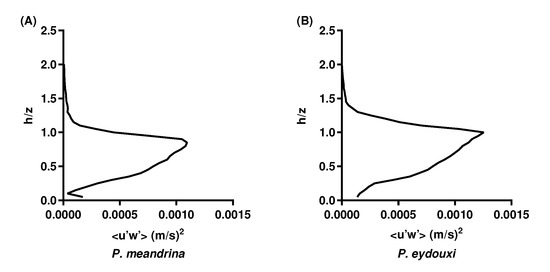
Figure 11.
Mean Reynolds stress plotted as a function of normalized height above the top surface of the colony for (A) P. meandrina and (B) P. eydouxi at a Reynolds number of 15,000. Similar Reynolds stresses were observed above both colonies, despite their differences in branching patterns.
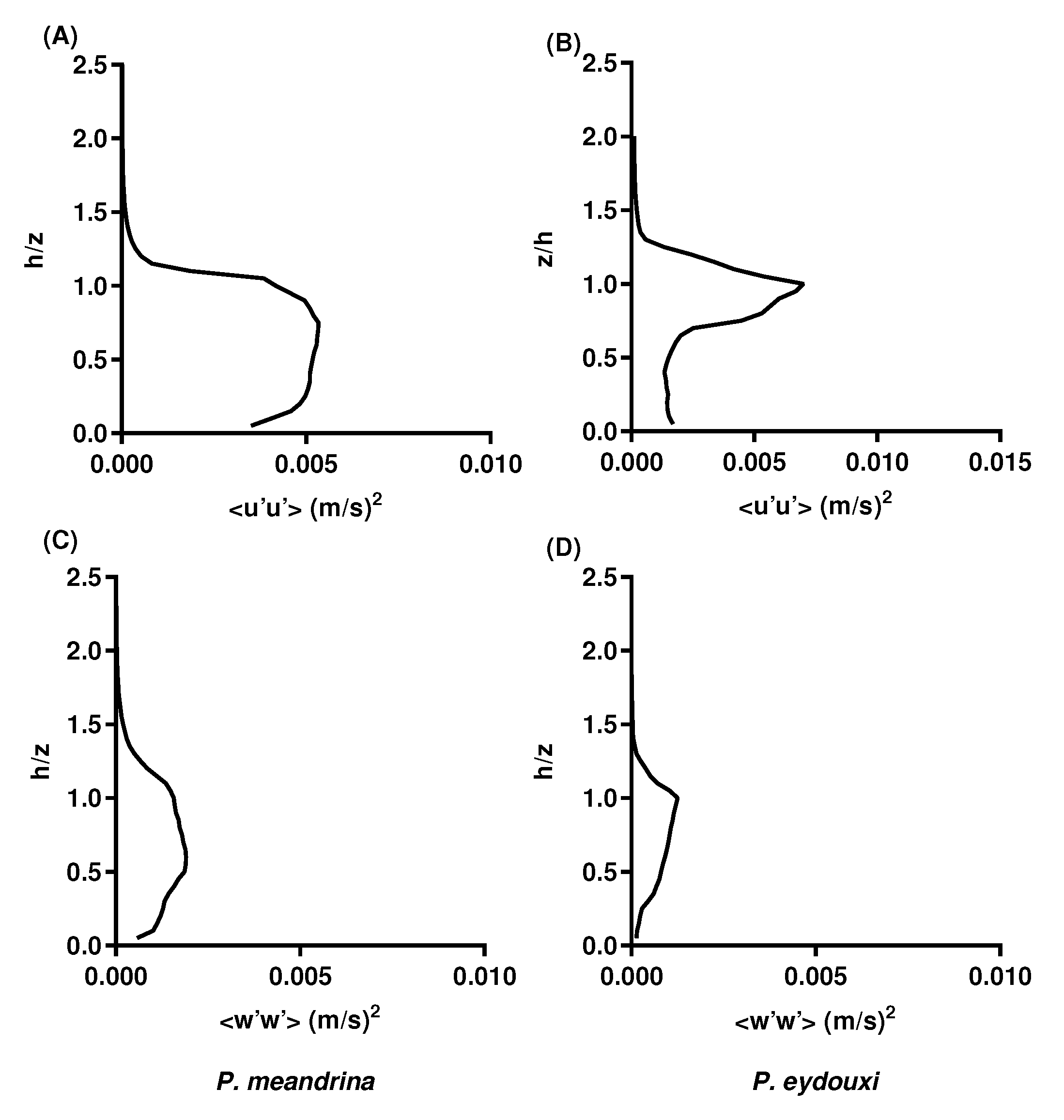
In addition to Reynolds stress, streamwise and vertical velocity variances were computed over both Pocillopora structures (Figure 12). Here, the streamwise velocity variance showed relatively greater magnitudes above the tops of these heterogeneous structures, which was expected for open branched colonies like P. eydouxi. But within the canopies, the streamwise variance did not vary monotonically with the increase or decrease in branch density for both corals. For densely branched P. meandrina, the magnitudes remained constant up to the height of the colony. In contrast, the magnitude of streamwise variance was relatively small up to the mid-height of the colony in P. eydouxi and the variance increased sharply above this height. Similarly, relatively higher vertical velocity variance was observed in the densely branched heterogeneous structure of P. meandrina.
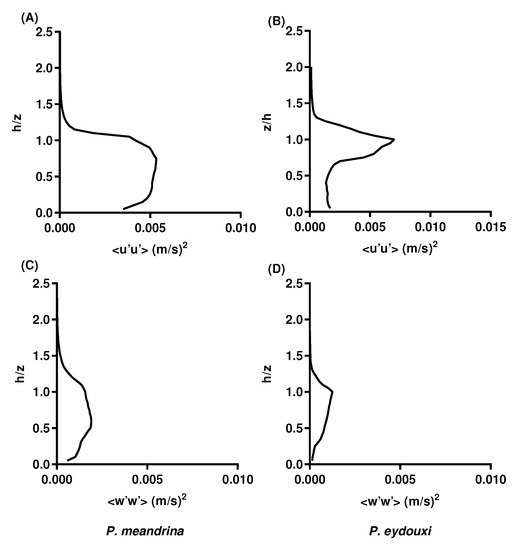
Figure 12.
(A,B) streamwise, and (C,D), vertical velocity variance computed over P. meandrina and P. eydouxi, respectively. In both cases, the magnitude of the variance was found to be higher for P. meandrina where the inter-branch distance was smaller than for P. eydouxi.
4. Discussion
Mass transport mechanisms were compared for two Pocillopora branching coral colonies with different branch densities and the Stanton number was used to compare the efficacy of mass transfer in the two colonies. The advection time scale used to calculate the Stanton number within the colonies was found in two different ways. First, when then were a large number of vortices in the flow field at the interior of the colony, the mean vortex diameter was used as the characteristic length to calculate the advection time scale following [23,24]. Alternatively, when the number of vortices in the colony interior was not significant, and hence using the mean vortex diameter was not feasible, the mean branch diameter was used as the characteristic length scale for the advection time scale. The branch diameter was also used by Chang et al. [27] for the calculation of the Sherwood (Sh) number from the direct measurement of the dissolution rate of gypsum from a coated coral colony.
Figure 8 and Table 2 show the Stanton number calculated along the flow direction in the densely branched P. meandrina colony based on the mean vortex diameter. These results demonstrate a significant increase in the Stanton number compared to the Stanton number calculated using the branch diameter, as tabulated in column 7 of Table 2. When the mean branch diameter was used along the length of coral, the results showed a nearly constant Stanton number throughout the colony in the flow direction, which is the upper bound of mass transfer for the whole colony. Meanwhile, experimental results in a similar colony geometry showed a decreasing trend in the interior of the colony [27]).
But even the upper-bound transfer rate may not meet the large mass transport requirement within the densely branched colony, which is due to the large internal surface area (), to keep the internal polyps healthy. The transport mechanism for the loosely branched P. eydouxi colony, where the velocity magnitude is comparatively higher within the larger inter-branch spaces, may use a constant mass transfer rate, but this mechanism perhaps would not meet the mass transfer requirement for the densely branched P. meandrina colony. Densely branched corals might be utilizing an additional mass transport mechanism in order to meet their nutritional needs. The observed passively-generated vortices within P. meandrina might help bridge this mass transfer rate gap by stirring the overlying water column, which enhances mass transport. Recently Shapiro [23] and Pacherres et al. [57] visualized the formation of vortices near the coral surface due to ciliary beating. Stony corals might use passive vortex shedding from branches, ciliary beating, or both, to generate vortical fields deep inside the colony where a high transport rate is required, in order to enhance mass transport there.
The detailed velocity vector fields also help to explain the requirement for an alternative method to increase the transfer processes within a densely branched colony. For example, the mean vector magnitude at the frontal section (up to L) of P. meandrina is higher than at the downstream side. Therefore, there exists a mean velocity gradient along the densely branched colony, which also generates a mass transfer gradient within the colony [21,27]. The blockage of the flow increases with the thickness of the branches and Figure 9 shows substantial reduction in mean velocity inside P. meandrina. The situation will be worse for any coral living in the wake region of another coral. If a reef is large enough, the transport process may become stagnant within the interior. Corals adapt to the local flow environment to adjust their metabolic processes [7] and the local flow information found within P. meandrina might help us to understand how such adaptation occurs.
When the number of vortices is small within the branching colony, the branch diameter might be another alternative for calculating the St number. The time required for one particle to move through the diffusion boundary layer from the coral surface to a position one branch diameter away within the colony will require approximately seconds. For P. eydouxi the value of was s for the mean branch diameter of at , whereas at same location the magnitude of was s based on the mean branch diameter. This means that P. meandrina required almost times longer to travel one branch diameter distance from the surface. To reach the same branch diameter distance as P. eydouxi, P. meandrina needed almost s, which is approximately times longer than the time required for P. eydouxi. The extra time required for transport inside P. meandrina may significantly affect the thickness of diffusive boundary layers as well as the metabolic processes. Therefore, there should exist a mechanism that helps the interior of dense colonies remain healthy. Now, from the comparison of the Stanton numbers and the advection time scales, it is clear that the mass transfer rate is higher within P. eydouxi than within the densely branched P. meandrina. Reidenbach et al. [28] measured the mass transfer rate from coral with different inter-branch spacing and found similar results showing a lower mass transport rate for the more densely branched colony.
The effects of the internal structure of the colony on the turbulent stresses were also studied for these two Pocillopora colony geometries. The Reynolds stress and variance were calculated for the two colonies. For the Reynolds stress, the profiles remained generally the same throughout the colony though there were substantial differences in their internal geometrical properties. The magnitude of the Reynolds stress has an important impact on quantities such as the friction velocity, mass transfer rate, bed shear stress, and drag developed on the corals. For example, the friction velocity directly depends on the maximum magnitude of the Reynolds stress over the colony and the results show a similar magnitude of friction velocity developed on both colonies. Similarly, the coefficient of the mass transfer rate is a direct function of shear stress over the colony, which shows an almost similar rate of transfer at the top of both colonies [3].
5. Conclusions
The mass transport mechanism and detailed vector profiles were analyzed for two different branching corals. The vector profile shows a relatively higher flow penetration for the front half of densely branched P. meandrina than for the rear half. In contrast, the flow penetrated deep into the interior of P. eydouxi due to the relative openness of the structure. The mean velocity magnitude was computed along the length of coral and used for calculating the Stanton number for the estimation of the mass transfer rate. streamlines were plotted inside the coral to understand the transport mechanisms for two different branching patterns. The results showed the formation of passive vortices inside densely branched P.meandrina, which stirred the water column and enhanced the transfer rate. In contrast, a relatively small number of vortices were found in the more sparsely branched colony of P. eydouxi. To quantify the transfer rate, Stanton numbers were calculated and compared along the length of both corals. The results show a constant mass transfer rate for P. eydouxi from the front to the back of the colony, which corresponds to the better flow penetration in the interior. For the densely branched P. menadrina, the magnitudes of the Stanton numbers were calculated based on the two different time scales. The results show up to a 219% increase in the Stanton number when the mean vortices diameters were used as length instead of the mean branch diameter inside P. menadrina. However, in both cases, the magnitude of the Stanton number was relatively smaller than the P. eydouxi for the same incoming flow. In addition, turbulent statistics were calculated for both Pocillopra geometries at Re = 15,000. The vector field displayed a relatively large number of velocity fluctuations near the top of the colony, which makes significant contributions in the mixing and momentum transfer from the top of the coral. This flow information was used for the calculation of mean Reynolds stress and velocity variance along with the height of both colonies. The results exhibit almost the same magnitude of Reynolds stress and variance above the top of the colonies with maximum magnitude at the crest, but in the interior, these parameters show a significant difference in magnitude due to the difference in branching patterns.
Author Contributions
M.M.H. designed and performed the numerical experiments, analyzed the computational data, and wrote the paper. A.E.S. supervised the work and edited the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
This work was partially supported by the United States Department of State’s Bureau of Educational and Cultural Affairs through the Fulbright Program.
Acknowledgments
We would like to thank Uri Shavit of the Technion—Israel Institute of Technology for the use of his P. meandrina geometry file and Elias Balaras of George Washington University for the use of his immersed boundary code.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Fabricius, K.E.; Genin, A.; Benayahu, Y. Flow-dependent herbivory and growth in zooxanthellae-free soft corals. Limnol. Oceanogr. 1995, 40, 1290–1301. [Google Scholar] [CrossRef]
- Mass, T.; Genin, A.; Shavit, U.; Grinstein, M.; Tchernov, D. Flow enhances photosynthesis in marine benthic autotrophs by increasing the efflux of oxygen from the organism to the water. Proc. Natl. Acad. Sci. USA 2010, 107, 2527–2531. [Google Scholar] [CrossRef]
- Hondzo, M. Dissolved oxygen transfer at the sediment-water interface in a turbulent flow. Water Resour. Res. 1998, 34, 3525–3533. [Google Scholar] [CrossRef]
- Chamberlain, J.A., Jr.; Graus, R.R. Water flow and hydromechanical adaptations of branched reef corals. Bull. Mar. Sci. 1975, 25, 112–125. [Google Scholar]
- Sebens, K.P.; Witting, J.; Helmuth, B. Effects of water flow and branch spacing on particle capture by the reef coral Madracis mirabilis (Duchassaing and Michelotti). J. Exp. Mar. Biol. Ecol. 1997, 211, 1–28. [Google Scholar] [CrossRef]
- Hunter, T. Suspension feeding in oscillating flow: The effect of colony morphology and flow regime on plankton capture by the hydroid Obelia longissima. Biol. Bull. 1989, 176, 41–49. [Google Scholar] [CrossRef]
- Mass, T.; Genin, A. Environmental versus intrinsic determination of colony symmetry in the coral Pocillopora verrucosa. Mar. Ecol. Prog. Ser. 2008, 369, 131–137. [Google Scholar] [CrossRef]
- Kaandorp, J.A.; Kübler, J.E. The Algorithmic Beauty of Seaweeds, Sponges and Corals; Springer: Berlin, Germany, 2001. [Google Scholar]
- Patterson, M.R.; Sebens, K.P.; Olson, R.R. In situ measurements of flow effects on primary production and dark respiration in reef corals. Limnol. Oceanogr. 1991, 36, 936–948. [Google Scholar] [CrossRef]
- Shashar, N.; Kinane, S.; Jokiel, P.; Patterson, M. Hydromechanical boundary layers over a coral reef. J. Exp. Mar. Biol. Ecol. 1996, 199, 17–28. [Google Scholar] [CrossRef]
- Larkum, A.W.; Koch, E.M.; Kühl, M. Diffusive boundary layers and photosynthesis of the epilithic algal community of coral reefs. Mar. Biol. 2003, 142, 1073–1082. [Google Scholar] [CrossRef]
- Bruno, J.F.; Edmunds, P.J. Metabolic consequences of phenotypic plasticity in the coral Madracis mirabilis (Duchassaing and Michelotti): The effect of morphology and water flow on aggregate respiration. J. Exp. Mar. Biol. Ecol. 1998, 229, 187–195. [Google Scholar] [CrossRef]
- Jimenez, I.M.; Kühl, M.; Larkum, A.W.; Ralph, P.J. Heat budget and thermal microenvironment of shallow-water corals: Do massive corals get warmer than branching corals? Limnol. Oceanogr. 2008, 53, 1548–1561. [Google Scholar] [CrossRef]
- Chan, N.; Wangpraseurt, D.; Kühl, M.; Connolly, S.R. Flow and coral morphology control coral surface pH: Implications for the effects of ocean acidification. Front. Mar. Sci. 2016, 3, 10. [Google Scholar] [CrossRef]
- Reidenbach, M.A.; Koseff, J.R.; Monismith, S.G. Laboratory experiments of fine-scale mixing and mass transport within a coral canopy. Phys. Fluids 2007, 19, 075107. [Google Scholar] [CrossRef]
- Stocking, J.B.; Rippe, J.P.; Reidenbach, M.A. Structure and dynamics of turbulent boundary layer flow over healthy and algae-covered corals. Coral Reefs 2016, 35, 1047–1059. [Google Scholar] [CrossRef]
- Hench, J.L.; Rosman, J.H. Observations of spatial flow patterns at the coral colony scale on a shallow reef flat. J. Geophys. Res. Ocean. 2013, 118, 1142–1156. [Google Scholar] [CrossRef]
- Pomeroy, A.W.; Lowe, R.J.; Ghisalberti, M.; Storlazzi, C.; Symonds, G.; Roelvink, D. Sediment transport in the presence of large reef bottom roughness. J. Geophys. Res. Ocean. 2017, 122, 1347–1368. [Google Scholar] [CrossRef]
- Sous, D.; Bouchette, F.; Doerflinger, E.; Meulé, S.; Certain, R.; Toulemonde, G.; Dubarbier, B.; Salvat, B. On the small-scale fractal geometrical structure of a living coral reef barrier. Earth Surf. Process. Landf. 2020. [Google Scholar] [CrossRef]
- Asher, S.; Niewerth, S.; Koll, K.; Shavit, U. Vertical variations of coral reef drag forces. J. Geophys. Res. Ocean. 2016, 121, 3549–3563. [Google Scholar] [CrossRef]
- Chang, S.; Elkins, C.; Alley, M.; Eaton, J.; Monismitha, S. Flow inside a coral colony measured using magnetic resonance velocimetry. Limnol. Oceanogr. 2009, 54, 1819–1827. [Google Scholar] [CrossRef]
- Chang, S.; Iaccarino, G.; Ham, F.; Elkins, C.; Monismith, S. Local shear and mass transfer on individual coral colonies: Computations in unidirectional and wave-driven flows. J. Geophys. Res. Ocean. 2014, 119, 2599–2619. [Google Scholar] [CrossRef]
- Shapiro, O.H.; Fernandez, V.I.; Garren, M.; Guasto, J.S.; Debaillon-Vesque, F.P.; Kramarsky-Winter, E.; Vardi, A.; Stocker, R. Vortical ciliary flows actively enhance mass transport in reef corals. Proc. Natl. Acad. Sci. USA 2014, 111, 13391–13396. [Google Scholar] [CrossRef] [PubMed]
- Hossain, M.M.; Staples, A.E. Passive vortical flows enhance mass transport in the interior of a coral colony. Phys. Fluids 2019, 31, 061701. [Google Scholar] [CrossRef]
- Atkinson, M.; Bilger, R. Effects of water velocity on phosphate uptake in coral reef-hat communities. Limnol. Oceanogr. 1992, 37, 273–279. [Google Scholar] [CrossRef]
- Bilger, R.; Atkinson, M. Anomalous mass transfer of phosphate on coral reef flats. Limnol. Oceanogr. 1992, 37, 261–272. [Google Scholar] [CrossRef]
- Chang, S.; Elkins, C.; Eaton, J.K.; Monismith, S. Local mass transfer measurements for corals and other complex geometries using gypsum dissolution. Exp. Fluids 2013, 54, 1563. [Google Scholar] [CrossRef]
- Reidenbach, M.A.; Koseff, J.R.; Monismith, S.G.; Steinbuckc, J.V.; Genin, A. The effects of waves and morphology on mass transfer within branched reef corals. Limnol. Oceanogr. 2006, 51, 1134–1141. [Google Scholar] [CrossRef]
- Reidenbach, M.A.; Monismith, S.G.; Koseff, J.R.; Yahel, G.; Genin, A. Boundary layer turbulence and flow structure over a fringing coral reef. Limnol. Oceanogr. 2006, 51, 1956–1968. [Google Scholar] [CrossRef]
- Asher, S.; Shavit, U. The effect of water depth and internal geometry on the turbulent flow inside a coral reef. J. Geophys. Res. Ocean. 2019, 124, 3508–3522. [Google Scholar] [CrossRef]
- Nepf, H.; Vivoni, E. Flow structure in depth-limited, vegetated flow. J. Geophys. Res. Ocean. 2000, 105, 28547–28557. [Google Scholar] [CrossRef]
- Finnigan, J. Turbulence in plant canopies. Annu. Rev. Fluid Mech. 2000, 32, 519–571. [Google Scholar] [CrossRef]
- Moltchanov, S.; Bohbot-Raviv, Y.; Shavit, U. Dispersive stresses at the canopy upstream edge. Bound.-Layer Meteorol. 2011, 139, 333–351. [Google Scholar] [CrossRef]
- Rosman, J.H.; Hench, J.L. A framework for understanding drag parameterizations for coral reefs. J. Geophys. Res. Ocean. 2011, 116. [Google Scholar] [CrossRef]
- Stocking, J.B.; Laforsch, C.; Sigl, R.; Reidenbach, M.A. The role of turbulent hydrodynamics and surface morphology on heat and mass transfer in corals. J. R. Soc. Interface 2018, 15, 20180448. [Google Scholar] [CrossRef]
- Osorio-Cano, J.D.; Osorio, A.F.; Alcérreca-Huerta, J.C.; Oumeraci, H. Drag and inertia forces on a branched coral colony of Acropora palmata. J. Fluids Struct. 2019, 88, 31–47. [Google Scholar] [CrossRef]
- Kaandorp, J.A.; Koopman, E.A.; Sloot, P.M.; Bak, R.P.; Vermeij, M.J.; Lampmann, L.E. Simulation and analysis of flow patterns around the scleractinian coral Madracis mirabilis (Duchassaing and Michelotti). Philos. Trans. R. Soc. Lond. Ser. B Biol. Sci. 2003, 358, 1551–1557. [Google Scholar] [CrossRef]
- Kaandorp, J.A.; Sloot, P.M.; Merks, R.M.; Bak, R.P.; Vermeij, M.J.; Maier, C. Morphogenesis of the branching reef coral Madracis mirabilis. Proc. R. Soc. B Biol. Sci. 2005, 272, 127–133. [Google Scholar] [CrossRef]
- Chindapol, N.; Kaandorp, J.A.; Cronemberger, C.; Mass, T.; Genin, A. Modelling growth and form of the scleractinian coral Pocillopora verrucosa and the influence of hydrodynamics. PLoS Comput. Biol. 2013, 9, e1002849. [Google Scholar] [CrossRef]
- Meneveau, C.; Lund, T.S.; Cabot, W.H. A Lagrangian dynamic subgrid-scale model of turbulence. J. Fluid Mech. 1996, 319, 353–385. [Google Scholar] [CrossRef]
- Bailey, B.N.; Stoll, R. Turbulence in sparse, organized vegetative canopies: A large-eddy simulation study. Bound.-Layer Meteorol. 2013, 147, 369–400. [Google Scholar] [CrossRef]
- Peskin, C.S. The immersed boundary method. Acta Numer. 2002, 11, 479–517. [Google Scholar] [CrossRef]
- Mohd-Yusof, J. methods for complex geometries. Annu. Res. Briefs 1998, 325. [Google Scholar]
- Fadlun, E.; Verzicco, R.; Orlandi, P.; Mohd-Yusof, J. Combined immersed-boundary finite-difference methods for three-dimensional complex flow simulations. J. Comput. Phys. 2000, 161, 35–60. [Google Scholar] [CrossRef]
- Balaras, E. Modeling complex boundaries using an external force field on fixed Cartesian grids in large-eddy simulations. Comput. Fluids 2004, 33, 375–404. [Google Scholar] [CrossRef]
- Yang, J.; Balaras, E. An embedded-boundary formulation for large-eddy simulation of turbulent flows interacting with moving boundaries. J. Comput. Phys. 2006, 215, 12–40. [Google Scholar] [CrossRef]
- Lowe, R.J.; Koseff, J.R.; Monismith, S.G.; Falter, J.L. Oscillatory flow through submerged canopies: 2. Canopy mass transfer. J. Geophys. Res. Ocean. 2005, 110. [Google Scholar] [CrossRef]
- Jørgensen, B.B.; Revsbech, N.P. Diffusive boundary layers and the oxygen uptake of sediments and detritus 1. Limnol. Oceanogr. 1985, 30, 111–122. [Google Scholar] [CrossRef]
- Hossain, M.M.; Staples, A.E. Effects of coral colony morphology on turbulent flow dynamics. bioRxiv 2019, 839902. [Google Scholar] [CrossRef]
- Lowe, R.J.; Shavit, U.; Falter, J.L.; Koseff, J.R.; Monismith, S.G. Modeling flow in coral communities with and without waves: A synthesis of porous media and canopy flow approaches. Limnol. Oceanogr. 2008, 53, 2668–2680. [Google Scholar] [CrossRef]
- Pokrajac, D.; Finnigan, J.; Manes, C.; McEwan, I.; Nikora, V. On the definition of the shear velocity in rough bed open channel flows. River Flow 2006, 1, 89–98. [Google Scholar]
- Jiro. GRABIT. Available online: https://www.mathworks.com/matlabcentral/fileexchange/7173-grabit (accessed on 3 September 2020).
- Langdon, C.; Takahashi, T.; Sweeney, C.; Chipman, D.; Goddard, J.; Marubini, F.; Aceves, H.; Barnett, H.; Atkinson, M.J. Effect of calcium carbonate saturation state on the calcification rate of an experimental coral reef. Glob. Biogeochem. Cycles 2000, 14, 639–654. [Google Scholar] [CrossRef]
- Poggi, D.; Katul, G. The ejection-sweep cycle over bare and forested gentle hills: A laboratory experiment. Bound.-Layer Meteorol. 2007, 122, 493–515. [Google Scholar] [CrossRef]
- Finnigan, J.J.; Shaw, R.H.; Patton, E.G. Turbulence structure above a vegetation canopy. J. Fluid Mech. 2009, 637, 387–424. [Google Scholar] [CrossRef]
- Nepf, H.M. Flow and transport in regions with aquatic vegetation. Annu. Rev. Fluid Mech. 2012, 44, 123–142. [Google Scholar] [CrossRef]
- Pacherres, C.O.; Ahmerkamp, S.; Schmidt-Grieb, G.M.; Holtappels, M.; Richter, C. Ciliary vortex flows and oxygen dynamics in the coral boundary layer. Sci. Rep. 2020, 10, 1–10. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).