Dynamic Behaviours of a Filament in a Viscoelastic Uniform Flow

Abstract

The dynamic behaviours of a filament in a viscoelastic uniform flow were investigated by an immersed boundary-lattice Boltzmann method. The effects of the Reynolds numbers ($Re$, ranging from 10 to 200) and the Weissenberg number ($Wi$, ranging from 0 to 1.2) on the filament flapping motion and the drag and lift coefficients on the filament were studied. It was found that a higher inertial effect (larger $Re$) promotes the flapping motion of the filament. In addition, the major effect of the viscoelasticity of the Giesekus fluid is to decrease the critical Reynolds number for the flapping motion of the filament and to promote the flapping motion. The drag coefficient on the filament in a Giesekus uniform flow decreases with the increase of $Wi$ at low $Re$ ($Re<100$), and experiences oscillations with similar amplitudes at all $Wi$ at a sufficiently high $Re$ ($Re>100$). In contrast, the viscoelasticity of the FENE-CR fluid increases the critical Reynolds number at lower $Wi$ ($Wi<0.8$), and shows little influence on the critical Reynolds number at higher $Wi$ ($Wi\ge 0.8$). In addition, the viscoelasticity of the FENE-CR fluid hinders the flapping motion of the filament, and increases the drag coefficient on the filament at low $Re$ ($Re<100$).

1. Introduction

The behaviour of a filament (or a flexible fibre) in fluids has attracted growing attention recently, as it is closely related to many biological and industrial systems. Until now, many investigations have been conducted on filament behaviours in Newtonian fluids by experimental [1,2] and numerical methods [3,4,5,6,7,8], and different behaviours of the filament have been identified (e.g., straight configuration [1,3,4,6], periodic oscillation [1,3,4,6] and chaotic flapping motion [8]). In contrast, much less effort has been made regarding filament behaviours in non-Newtonian flows, especially the passive behaviours of a filament. However, it is still necessary to investigate the motion of a filament in non-Newtonian fluids, since a filament can be involved in many non-Newtonian flow scenarios. For example, in the mucociliary clearance system in the human lung, cilia (filaments) and the mucus layer (a viscoelastic fluid) work together to transport inhaled external particles out of the lung [9]. In addition, the motion of fibres may have a significant influence on the papermaking process [10,11,12], in which viscoelastic fluid (pulp suspension) is normally involved.

Early attempts to investigate filament behaviours in non-Newtonian fluids have been mainly focused on collective behaviours of multiple filaments in shear flows by experimental methods [13,14,15]. It was reported that filaments may experience different final orientations (e.g., along the flow direction, along the vorticity direction or aligned at an angle with the flow direction) depending on the elasticity of the fluid [13,14,15]. Most recently, the behaviours of a single filament were numerically investigated in different flow conditions of viscoelastic fluids (e.g., in a cellular flow [10] and in a uniform flow [16]). Specifically, Yang and Fauci [10] investigated the transport properties of a filament in a FENE-P cellular flow (generated by four counter-rotating vortices), and it was found that the filament tends to stay in cellular regions with the inclusion of the viscoelasticity of the fluid [10]. This is different from the behaviour of a filament in a Newtonian cellular flow, where the filament tends to escape cellular regions [17]. In addition, the dynamic behaviours of a filament in a FENE-MCR uniform flow were studied by Lu et al. [16], who found that the viscoelasticity of the fluid may hinder the flapping motion of the filament. However, they only focused on the filament motion at a fixed Reynolds number ($Re=165$), and the viscoelasticity of the fluid may have different effects on the filament behaviour at different Reynolds numbers. In this work, effects of the fluid viscoelasticity and the Reynolds number on the filament behaviours were investigated.

The fluid-filament system was solved by using the immersed boundary-lattice Boltzmann method (IB-LBM) proposed by us [18], which is based on non-conformal meshes. Compared with traditional methods for fluid–structure interaction (FSI) problems involving non-Newtonian fluids based on body conformal meshes (e.g, the arbitrary Lagrangian Eulerian finite element method (ALE-FEM), and the deforming-spatial-domain/stabilised space-time method [19,20,21,22]), IB-LBM has an important advantage: the generation of mesh is simple, especially for complex geometries [23]. It does not require mesh movement or regeneration when handling problems with large deformations and displacements. Due to the explicit FSI coupling and the simplicity of mesh treatment, the efficiency of solving FSI problems by IB-LBM is very high [23]. Therefore, it has been extensively used to study FSI problems in Newtonian and non-Newtonian fluids recently [24,25,26,27]. In addition, in our method, an artificial damping is introduced to enhance the numerical stability in solving the constitutive equations of viscoelastic fluids. The artificial viscosity does not affect the numerical results if the damping effect is much weaker than the relaxation and the convective effects [18].

The organisation of the rest of this paper is as follows. The governing equations and the numerical method used in this paper are introduced in Section 2. In Section 3, validation cases are presented. Section 4 gives the numerical results and discussion. Final conclusions are provided in Section 5.

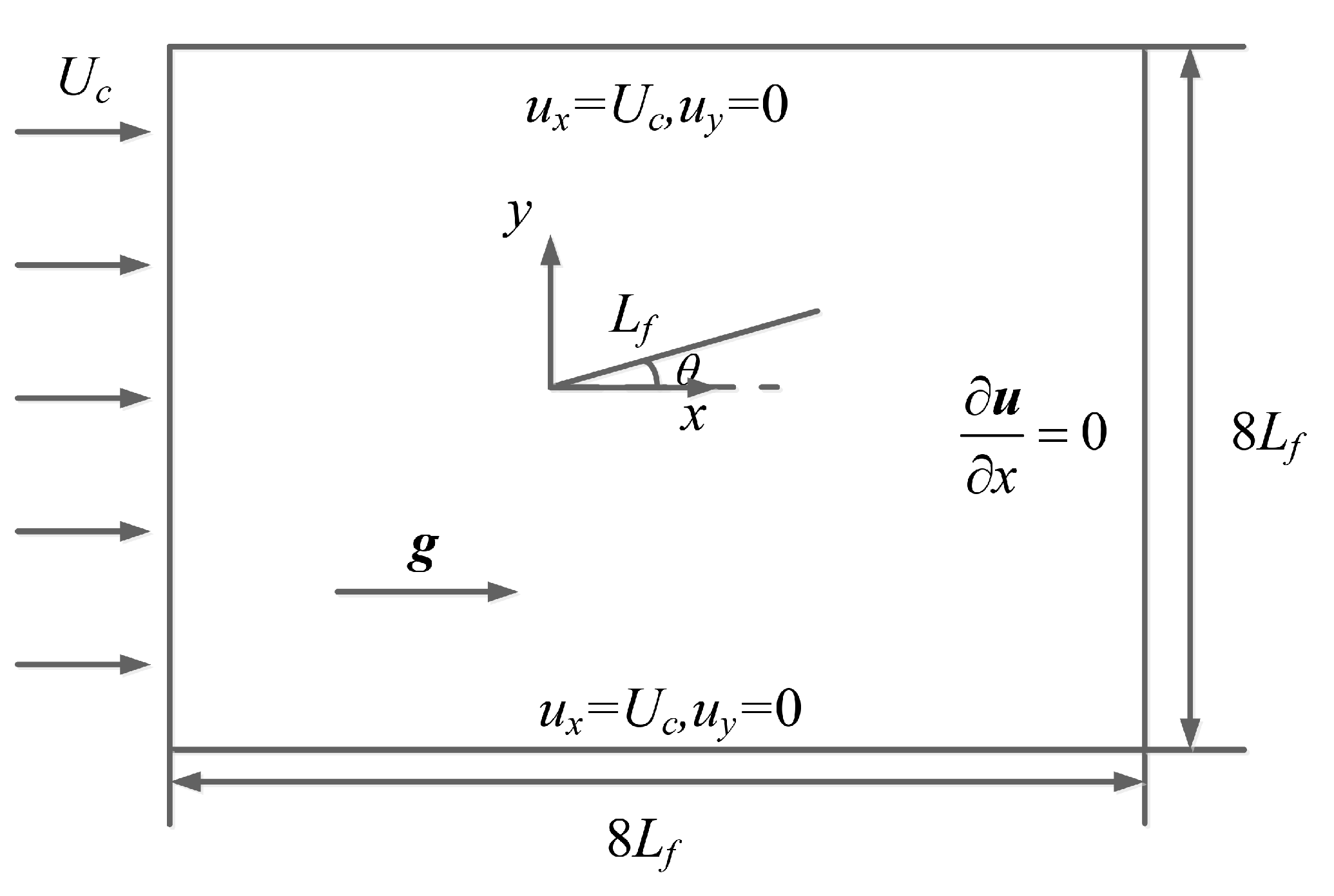
2. Mathematical Model and Numerical Method

A flexible filament with the length of $L_f$ in a viscoelastic uniform flow is shown in Figure 1. Simulations were conducted in a square domain of $(-2L_f,6L_f)\times (-4L_f,4L_f)$. The leading edge of the filament was pinned (the tip of a pinned filament was fixed in its position but was free to rotate) and positioned at the origin, and the filament was initially inclined at $\theta =0.1\pi$ from the positive x-axis direction to provide an initial asymmetry and to reduce the computational time to reach oscillatory flapping motion. A uniform flow ($u_x=U_c$, $u_y=0$) was applied to the inlet of the domain, and the filament in the flow could exhibit damped or stable flapping motion depending on the values of the Reynolds number and the Weissenberg number (defined at the end of this section). The Dirichlet boundary conditions ($u_x=U_c$, $u_y=0$) were applied to the upper and lower boundaries, and the Neumann boundary condition ($\frac{\partial \mathit{u}}{\partial x}=0$) was used at the outlet.

The dynamics of the fluid were governed by the continuity and Navier–Stokes equations:

$$\nabla ·\mathit{u}=0,$$

(1)

$$\frac{\partial \mathit{u}}{\partial t}+(\mathit{u}·\nabla )\mathit{u}=\frac{1}{\rho }\nabla ·(-p\mathit{I}+2{\mu }_s\mathit{D}+{\mathit{\tau }}_{\mathit{p}}),$$

(2)

where $\rho$ is the fluid density, $\mathit{u}$ is the fluid velocity, p is the pressure, ${\mu }_s$ is the solvent dynamic viscosity, $\mathit{I}$ is the identity tensor, $\mathit{D}=\frac{1}{2}(\nabla \mathit{u}+{\left(\nabla \mathit{u}\right)}^T)$ is the strain rate tensor and ${\mathit{\tau }}_{\mathit{p}}$ is the viscoelastic stress tensor, which accounts for the effect of the polymers on the solvent. Here, we consider two types of viscoelastic fluids (i.e., FENE-CR and Giesekus fluids), as these two models are widely used to describe the properties of constant viscosity (FENE-CR model) [28] and shear-thinning viscoelastic (Giesekus model) [29,30] fluids. In these models, the viscoelastic stress tensor ${\mathit{\tau }}_{\mathit{p}}$ can be described by the conformation tensor $\mathit{C}$ (a statistical indicator of the orientation of the polymer molecules) [18,31,32]:

$${\mathit{\tau }}_{\mathit{p}}=\frac{{\mu }_p}{\lambda }(\mathit{C}-\mathit{I})\left(\mathrm{Giesekus}\right),$$

(3)

$${\mathit{\tau }}_{\mathit{p}}=\frac{{\mu }_p}{\lambda }F\left(\mathit{C}\right)(\mathit{C}-\mathit{I})(\mathrm{FENE}-\mathrm{CR}),$$

(4)

where ${\mu }_p$ and $\lambda$ are the dynamic viscosity and relaxation time of the polymer, respectively, and $F\left(\mathit{C}\right)=\frac{1}{1-tr\left(\mathit{C}\right)/L_p^2}$ is the “spring function” with $L_p$ being the maximum extension length of the spring and tr(C) being the trace of the tensor $\mathit{C}$. The conformation of tensor $\mathit{C}$ is determined by the following transport equations [18,31,32]:

$$\frac{\partial \mathit{C}}{\partial t}+(\mathit{u}·\nabla )\mathit{C}=-\frac{1}{\lambda }(\mathit{C}-\mathit{I})-\frac{\alpha }{\lambda }(\mathit{C}-\mathit{I})·(\mathit{C}-\mathit{I})+\mathit{C}·\nabla \mathit{u}+{\left(\nabla \mathit{u}\right)}^T·\mathit{C}\left(\mathrm{Giesekus}\right),$$

(5)

$$\frac{\partial \mathit{C}}{\partial t}+(\mathit{u}·\nabla )\mathit{C}=-\frac{F\left(\mathit{C}\right)}{\lambda }(\mathit{C}-\mathit{I})+\mathit{C}·\nabla \mathit{u}+{\left(\nabla \mathit{u}\right)}^T·\mathit{C}(\mathrm{FENE}-\mathrm{CR}),$$

(6)

where $\alpha$ is the mobility parameter. The Oldroyd-B model can be recovered from the Giesekus model for the case of $\alpha =0$ and from the FENE-CR model for the case of $L_p^2\to \infty$. $\alpha =0.2$ and $L_p^2=10$ are used in this work, as those values were used and validated in our previous work [18],

The dynamics of the filament are described by [4,27,33,34]

$$m_s\frac{{\partial }^2\mathbf{X}}{\partial t^2}=\frac{\partial }{\partial s}\left[T\frac{\partial \mathbf{X}}{\partial s}\right]-E_b\frac{{\partial }^4\mathbf{X}}{\partial s^4}+m_s\mathit{g}+{\mathit{F}}_H,$$

(7)

where $m_s$ is the linear density of the filament, X is the position vector of a point on the filament, s is the Lagrangian coordinate along the filament, $T=E_s\left(\left|\frac{\partial \mathbf{X}}{\partial s_0}\right|-1\right)$ is the tensile stress, $E_s$ is the stretching coefficient, $s_0$ is the Lagrangian coordinate of the undeformed filament, $E_b$ is the bending rigidity, $\mathit{g}$ is the gravitational acceleration, and ${\mathit{F}}_H$ is the hydrodynamic force exerted on the filament by the ambient fluid.

In this study, the immersed boundary-lattice Boltzmann method was employed to solve the fluid–structure system [4,18,23,35,36]. In this method, the multi relaxation time (MRT) lattice Boltzmann method is utilised to solve the Navier–Stokes equations to improve the computational efficiency of simulations [33,37], and the single relaxation time (SRT) lattice Boltzmann method is used to solve the constitutive equations of the viscoelastic models [18,31,32,38,39]. It should be noted that a diffusion parameter $\kappa$ is normally involved in this method (in the transport equations of the conformation tensor $\mathit{C}$) to improve the stability of simulations, and more details can be found in [18,31]. The interaction between the fluid and the solid structure is achieved by using the immersed boundary method [4,18,23,33,40,41,42,43]. It should be noted that the “dynamic Eulerian–Lagrangian coupling strategy” is employed in this work, as the filament is a solid structure with mass (please refer to [18,25,44,45] for more details). The immersed boundary-lattice Boltzmann method used in this work has been extensively validated in different flows in our previous work [18], and details of this method and validation cases can be found in our previous studies [4,18].

The filament is discretised into $N_f$ initially equally spaced nodal points, and the tensile and bending forces exerted on these nodal points are computed by the finite difference method. To calculate the tensile force at the kth point, the following finite-difference scheme is used [4],

$${\left.\frac{\partial }{\partial s}\left[T\frac{\partial \mathbf{X}}{\partial s}\right]\right|}_k=\frac{T_{k+\frac{1}{2}}{\mathbf{t}}_{k+\frac{1}{2}}-T_{k-\frac{1}{2}}{\mathbf{t}}_{k-\frac{1}{2}}}{\Delta s},$$

(8)

where $\Delta s$ is the arc length along the filament; and the tensile force T and the tangent vector $\mathbf{t}=\frac{\partial \mathbf{X}}{\partial s}$, at the segment centre, $k+\frac{1}{2}$, are both computed using a second-order central difference scheme. The bending force at kth point is also computed using a central difference scheme by [4]

$$E_b\frac{{\partial }^4\mathbf{X}}{\partial s^4}=E_b\frac{{\mathbf{X}}_{k+2}-4{\mathbf{X}}_{k+1}+6{\mathbf{X}}_k-4{\mathbf{X}}_{k-1}+{\mathbf{X}}_{k-2}}{\Delta s^4}.$$

(9)

The non-dimensional parameters involved in this problem are: the Reynolds number $Re=\rho U_c{L}_f/{\mu }_0$, the Weissenberg number $Wi=\lambda U_c/L_f$, the viscosity ratio $\beta ={\mu }_s/{\mu }_0$, the Prandtl number $Pr=\kappa /\left(U_c{L}_f\right)$, the density ratio ${\rho }_r=m_s/\left(\rho L_f\right)$, the non-dimensional bending modulus $e_b=E_b/\left(\rho U_c^2{L}_f^3\right)$, the non-dimensional stretching modulus $e_s=E_s/\left(\rho U_c^2{L}_f\right)$ and the Froude number $Fr=g{L}_f/U_c^2$, where ${\mu }_0\equiv {\mu }_s+{\mu }_p$ is the zero-shear viscosity of the fluid. It should be noted that the Prandlt number $Pr$ is used to quantify the artificial diffusion effect involved in the numerical method, and it should be very small in practice [18,31] (please refer to Section 3.3 for the determination of $Pr$ adopted in this work).

3. Validation

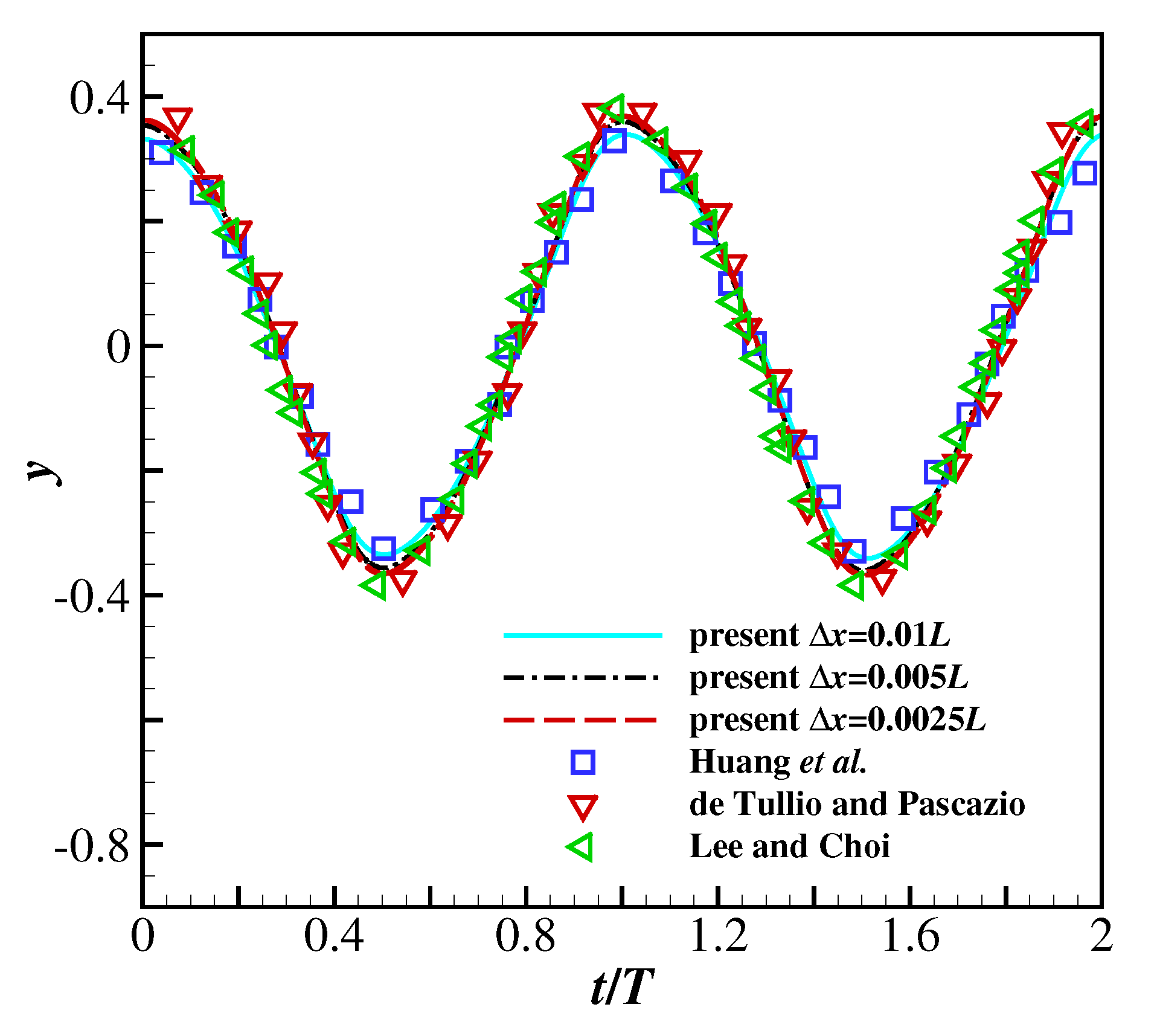
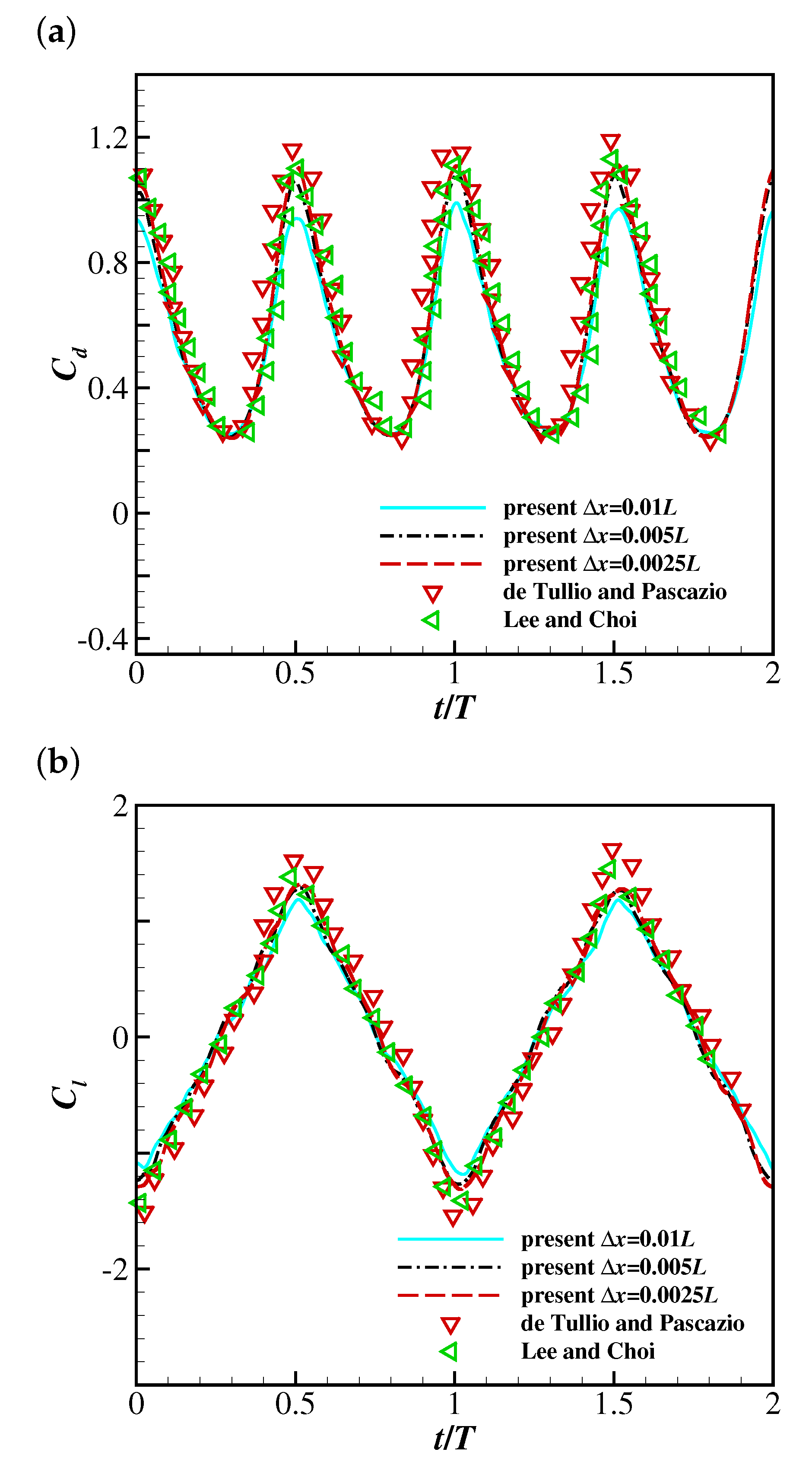
3.1. A 2D Filament Flapping in a Newtonian Uniform Flow

The motion of a 2D filament in a Newtonian uniform flow is studied here to validate the present numerical method. The definitions of the computational domain, the associated coordinate system and the boundary conditions used are the same as shown in Figure 1. The non-dimensional parameters are: the Reynolds number $Re=\rho U_c{L}_f/{\mu }_s$, the Froude number $Fr=g{L}_f/U_c^2$, the non-dimensional bending modulus $e_b=E_b/\left(\rho U_c^2{L}_f^3\right)$, the non-dimensional stretching modulus $e_s=E_s/\left(\rho U_c^2{L}_f\right)$ and the density ratio ${\rho }_r=m_s/\left(\rho L_f\right)$.

Three uniform grids are used with nodes—$801\times 801$, $1601\times 1601$ and $3201\times 3201$, corresponding to grid spacings, $h=\Delta x=\Delta y$, of 0.01$L_f$, 0.005$L_f$ and 0.0025$L_f$—to verify the mesh independence of the present method. Following the research by Huang et al. [3], the parametric values are $Re=200$, $Fr=0.5$, $e_b=0.0015$ and ${\rho }_r=1.5$. The filament is assumed to be inextensible, achieved by applying a large value of non-dimensional stretching modulus: $e_s=1000$. Figure 2 and Figure 3 illustrate the time history of the transverse displacement of the trailing edge, and the drag and lift coefficients of the filament, respectively. The present results are compared with the results of Huang et al. [3], de Tullio and Pascazio [46] and Lee and Choi [47]. It is shown the present solver predicts virtually identical transverse displacement of the trailing edge and drag and lift coefficients at grid spacings $h/L_f=$ 0.005 and 0.0025, but the drag and lift coefficients at grid spacing $h/L_f=0.01$ are slightly different. This confirms that the grid spacing $h/L_f=0.005$ is sufficient to simulate the filament’s motion in Newtonian uniform flow.

The effect of the domain size on the flapping motion of the filament in a Newtonian uniform flow was verified by conducting three computational domains: $8L_f\times 8L_f$, $12L_f\times 12L_f$ and $16L_f\times 16L_f$. Figure 4 shows the time history of the transverse displacement of the filament trailing edge at $Re=200$. It was found that the filament experiences oscillations with similar amplitudes when the domain size ranges from $8L_f$ to $16L_f$, which confirms that a domain of $8L_f\times 8L_f$ is sufficiently large for the investigation of a filament flapping motion in a uniform flow.

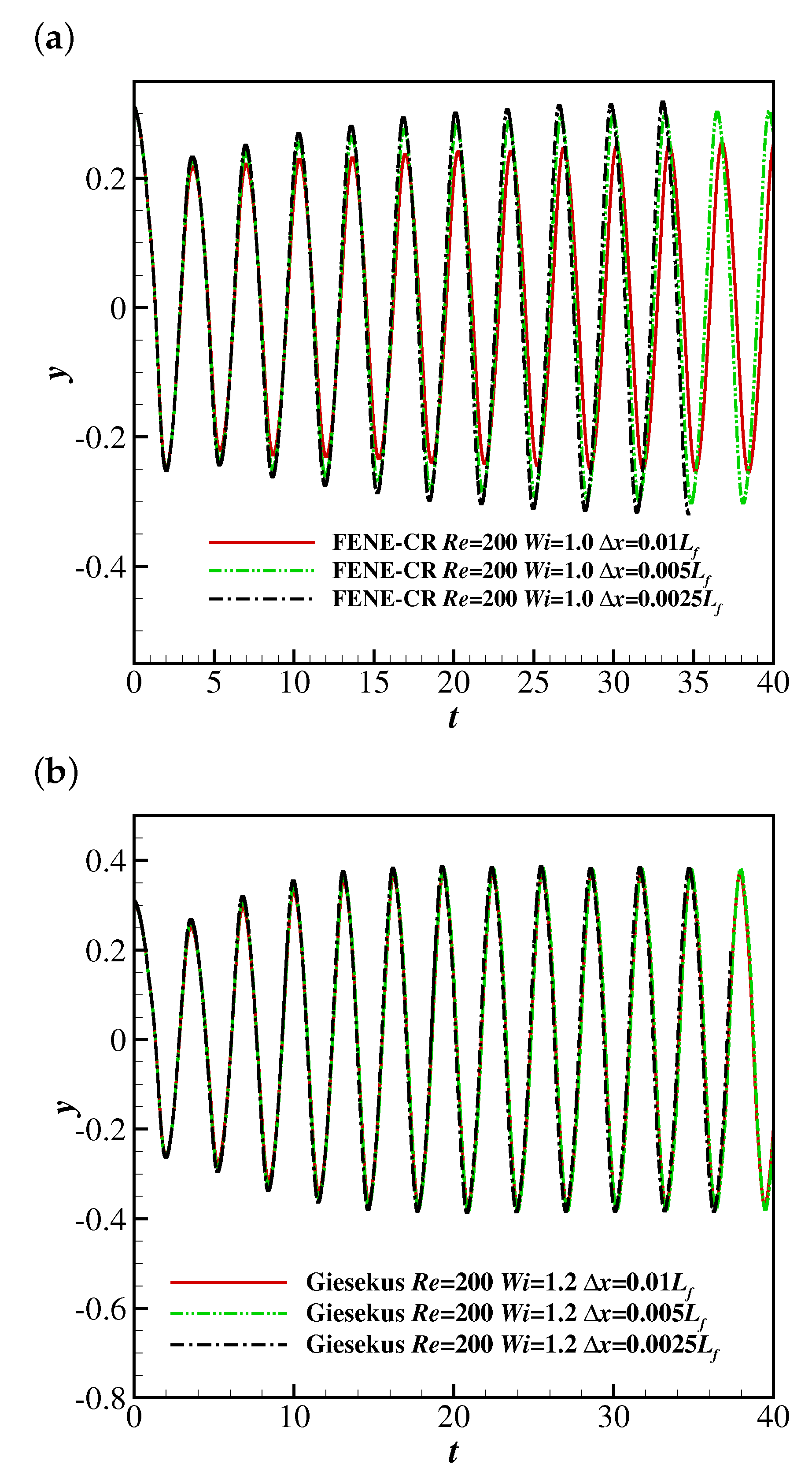
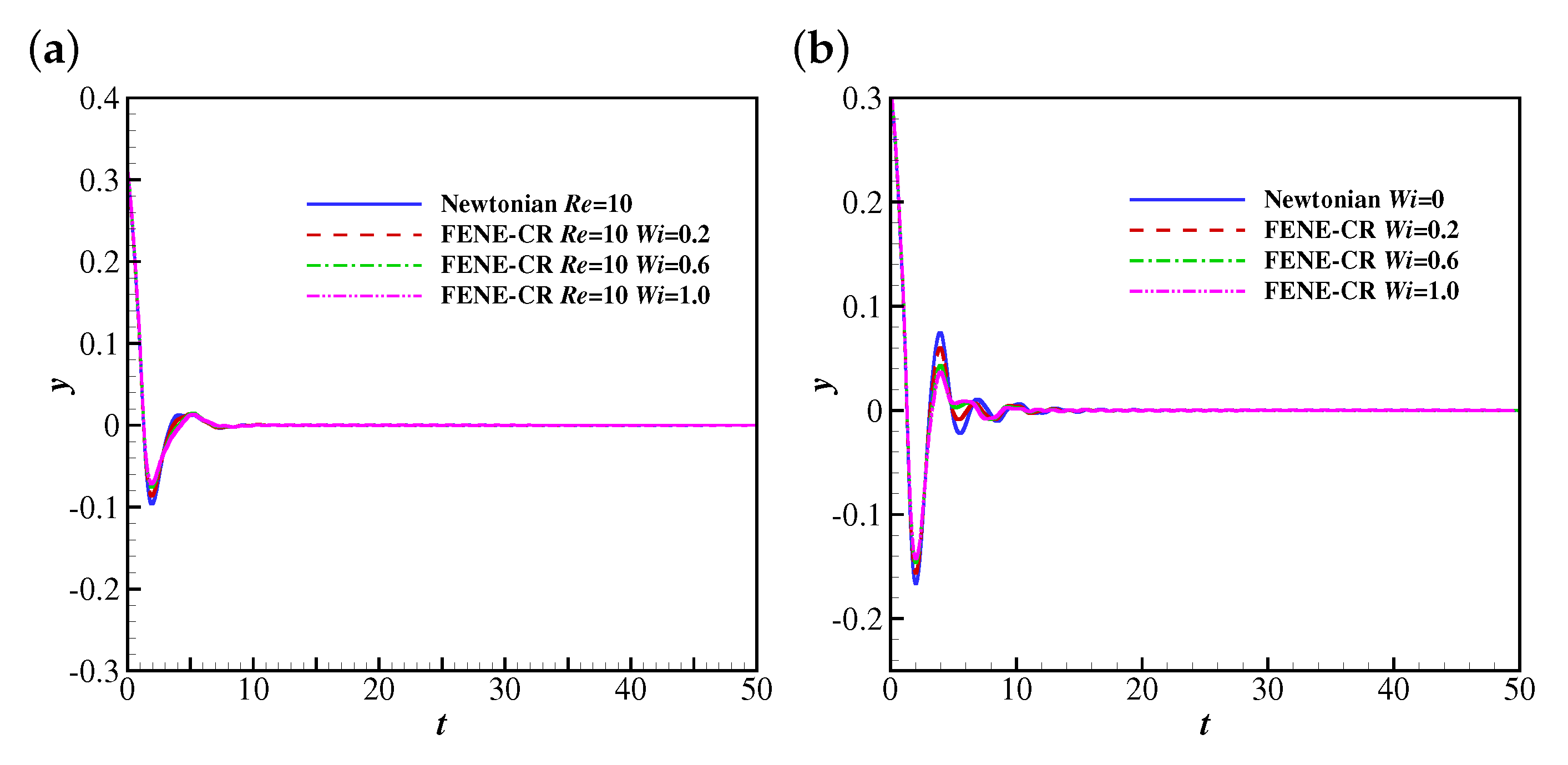
3.2. Grid Convergence Study of the Filament Flapping Motion in a Viscoelastic Uniform Flow

The effect of the grid spacing on the filament motion in a viscoelastic uniform flow was evaluated, and three grid spacings were used as in Section 3.1 ($h=$ 0.01$L_f$, 0.005$L_f$ and 0.0025$L_f$). Figure 5 shows the time histories of the free-end position of the filament in FENE-CR (at $Wi=1.0$) and Giesekus (at $Wi=1.2$) uniform flows at $Re=200$ and $Pr=2.0\times {10}^{-4}$ (as validated in Section 3.3). It was observed that the filament experiences oscillations with similar amplitudes at all grid spacings in the Giesekus uniform flow. In addition, the grid spacing shows a weak influence on the filament flapping motion at $h=$ 0.005$L_f$ and 0.0025$L_f$, but the behaviour of the filament is remarkably different when the grid spacing increases to 0.001$L_f$. This means the grid spacing should be smaller than 0.001$L_f$ to simulate the filament flapping motion in a viscoelastic uniform flow. Therefore, the grid spacing $h=0.005L_f$ was used in the present research.

3.3. Determination of the Prandlt Number $Pr$

To determine a suitable value of the Prandtl number $Pr$ involved in this problem, several simulations were conducted with different values of $Pr$ at $Re=200$ and $Wi=1.0$ for FENE-CR and Giesekus fluids.

Figure 6 shows the time histories of the free-end position of the filament in the FENE-CR and Giesekus uniform flows at $Re=200$, and $Pr=2.5\times {10}^{-4}$, $5.0\times {10}^{-4}$, $1.0\times {10}^{-3}$ and $1.0\times {10}^{-2}$. It was found that the Prandlt number $Pr$ does not influence the simulation results when $Pr$ is less than $1.0\times {10}^{-3}$. Therefore, Prandtl number $Pr=2.0\times {10}^{-4}$ was used in the simulations.

4. Results and Discussion

As stated in Section 1, the objective of this work was to investigate effects of the fluid viscoelasticity and the Reynolds number on the filament behaviour. Therefore, different values of the Reynolds number ($10\le Re\le 200$) and the Weissenberg number ($0\le Wi\le 1.2$ where $Wi=0$ corresponds to the Newtonian fluid) were employed, and other parameters were set to be fixed values (as used in the validations): the viscosity ratio $\beta =0.5$, the Prandtl number $Pr=2.0\times {10}^{-4}$, the density ratio ${\rho }_r=1.5$, the non-dimensional bending modulus $e_b=0.0015$, the non-dimensional stretching stiffness $e_s=1000$ and the Froude number $Fr=0.5$. The grid spacing $h=\Delta x=\Delta y=0.005L_f$ was used in the simulations (as validated in Section 3.1 and Section 3.2).

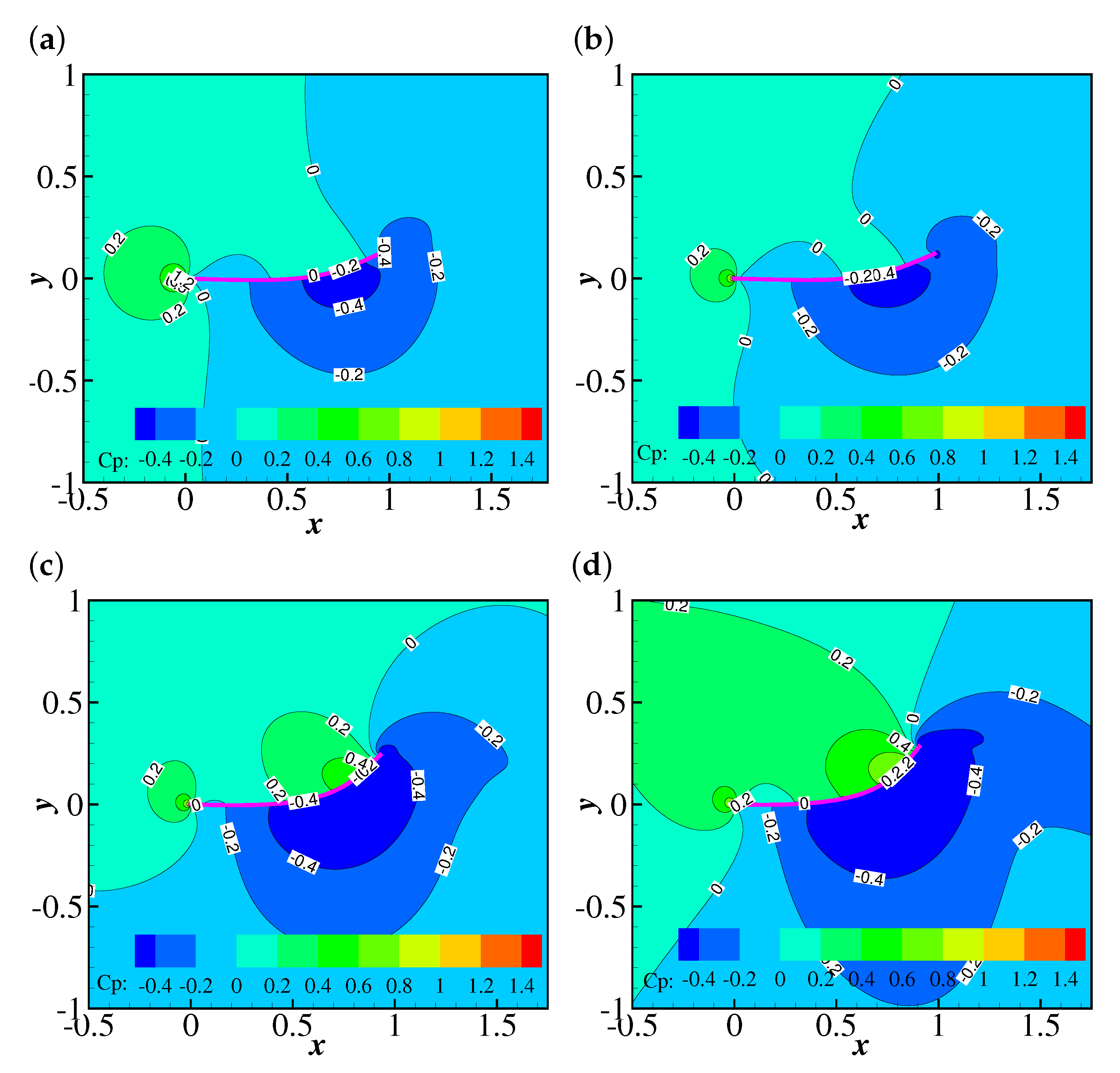
4.1. The Filament Behaviours in a Giesekus Uniform Flow

In this section, the behaviour of the filament in a Giesekus uniform flow is examined, and effects of the Reynolds number $Re$ and the Weissenberg number $Wi$ on the the filament flapping motion and the drag and lift coefficients on the filament are studied.

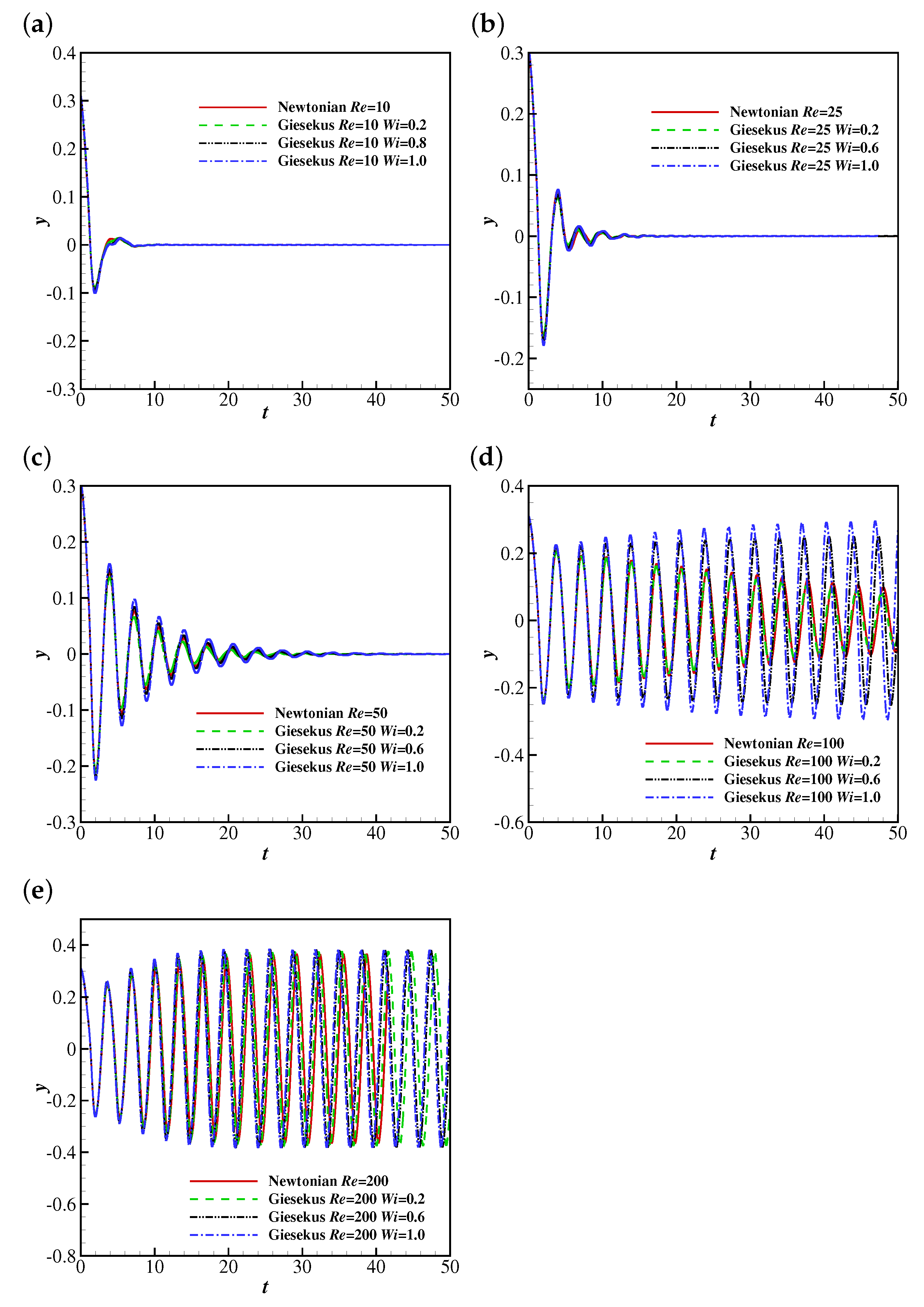
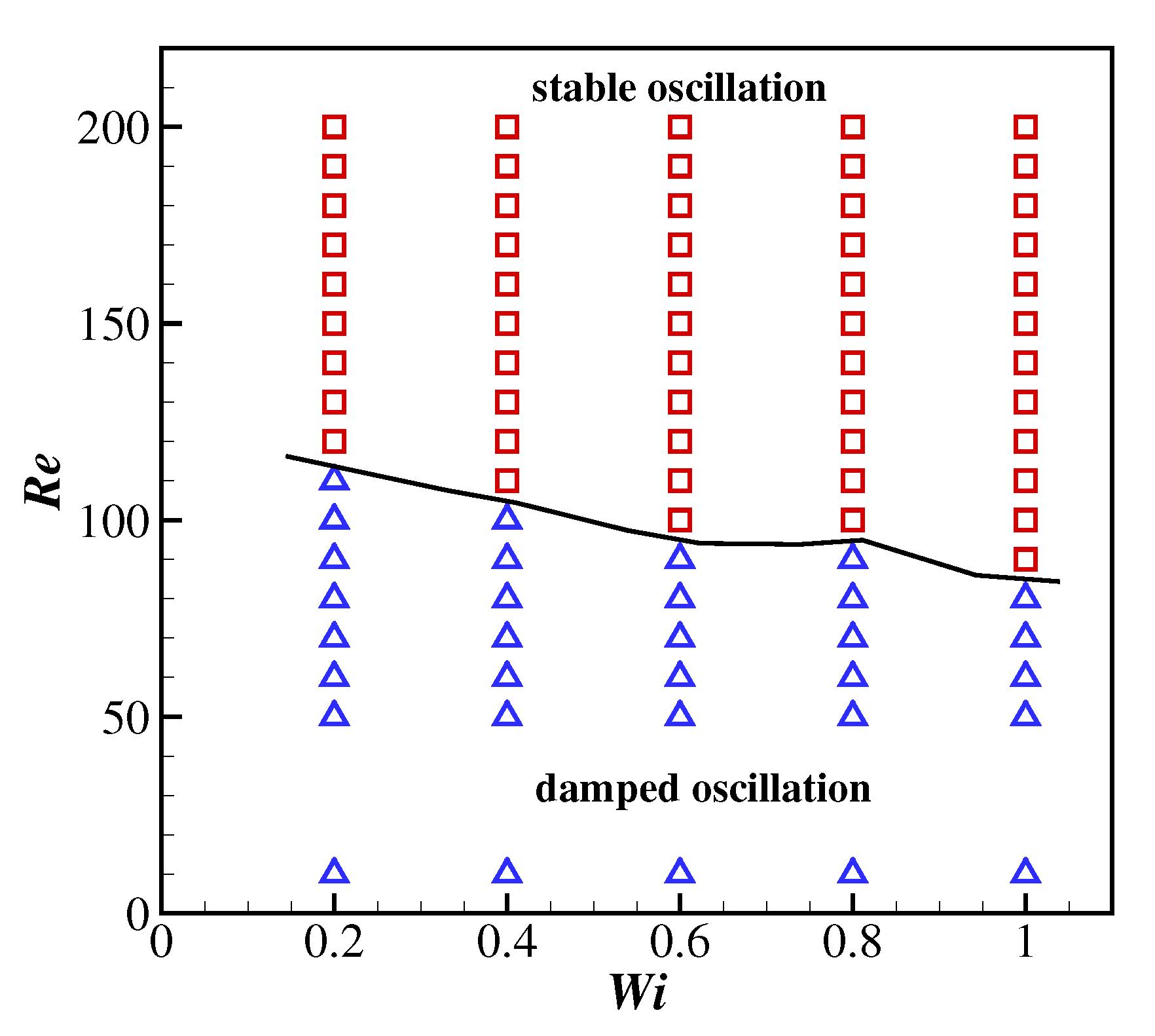
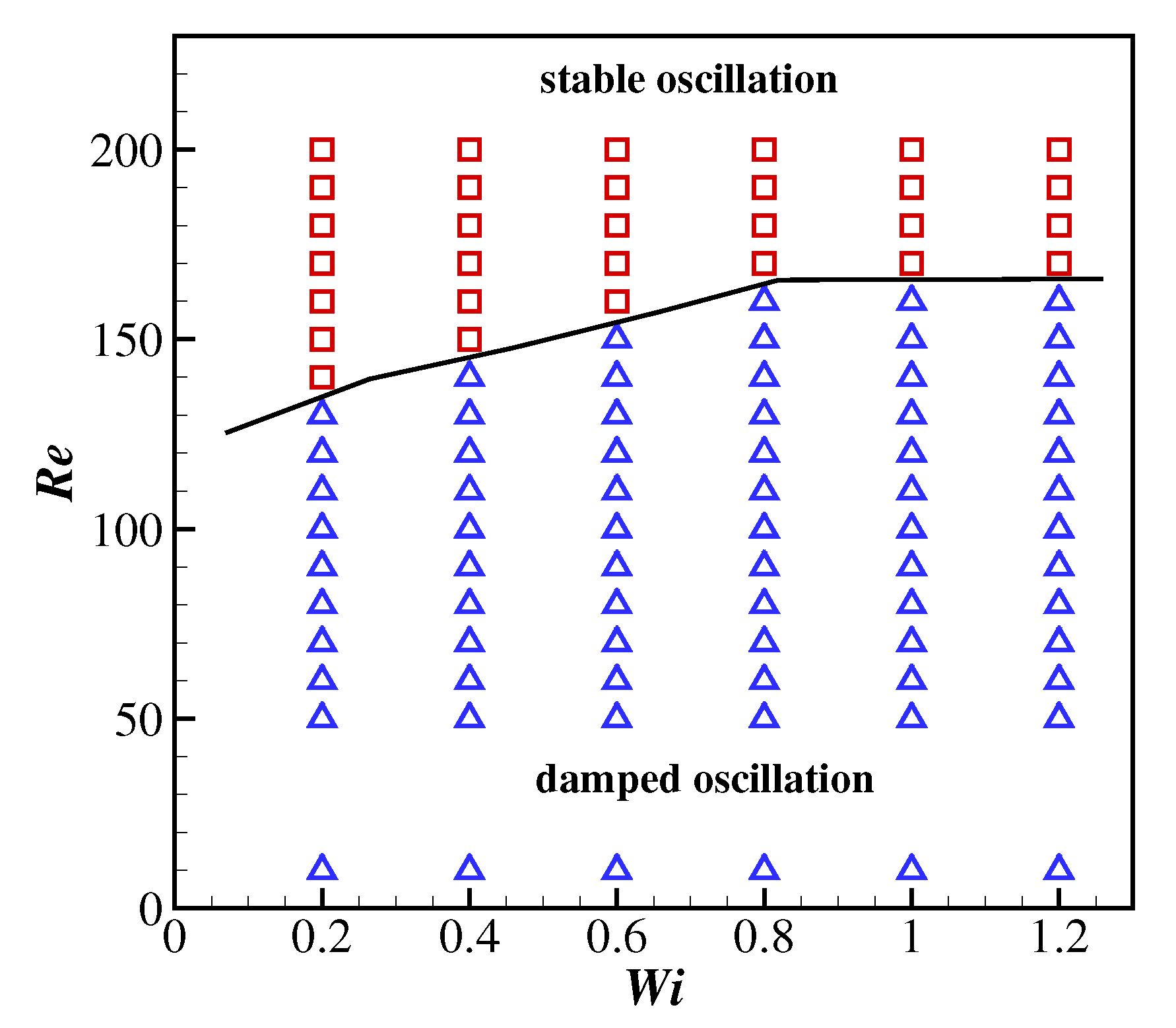
4.1.1. The Effects of Wi and Re on the Flapping Motion of the Filament

First, the effects of $Wi$ and $Re$ on the filament flapping motion are considered. The time histories of the free-end position of the filament at $Re=$ 10, 25, 50, 100 and 200 are shown in Figure 7. The Weissenberg numbers considered are $Wi=$0, 0.2, 0.6 and 1.0, where $Wi=0$ represents the Newtonian case.

It was found that the filament tends to reach a steady horizontal configuration at low Reynolds numbers ($Re=$ 10 and 25) for all $Wi$ considered in the simulations. With the increase of $Re$, the filament experiences damped oscillations at $Re=50$, and stable oscillations with similar amplitudes when $Re$ is sufficiently high (e.g., 200). This indicates the inertial effect promotes the flapping motion the filament.

As shown in Figure 7a–c, the viscoelasticity of the Giesekus fluid seems to have a weak effect on the flapping motion of the filament at lower Reynolds numbers ($Re=$ 10, 25 and 50) by slightly increasing the flapping amplitude. However, the filament behaviours are quite different at higher Reynolds numbers (e.g., $Re=100$, Figure 7d). Specifically, the filament experiences damped oscillations at $Wi=$ 0 and 0.2, and it shows stable oscillations at $Wi=$ 0.6 and 1.0. This is caused by higher lift forces exerted on the filament due to larger pressure differences across the filament at $Wi=0.6$ and 1.0 (please refer to the discussion in Section 4.1.2 for more details). In addition, this means the viscoelasticity of the Giesekus fluid reduces the critical Reynolds number for stable oscillations of the filament, and the stronger viscoelasticity promotes oscillations of the filament. This is understandable, since the Giesekus fluid shows shear-thinning characteristics [29,48], and the effective viscosity of the fluid is smaller, causing a higher “effective Reynolds number”. When $Re$ increases to 200, the filament shows stable oscillations at all $Wi$ considered.

To further illustrate the effects of $Wi$ and $Re$ on the filament flapping motion, the states of the filament behaviours as functions of the Reynolds number and Weissenberg number are shown in Figure 8. The behaviours of the filament can be classified into two states depending on the evolution of the magnitude of the oscillation: stable (the magnitude increases and then reaches a steady value) and damped (the magnitude experiences a monotonic decrease). It was observed that the filament tends to experience damped oscillations at lower Reynolds numbers and stable oscillations at higher Reynolds numbers. In addition, the viscoelasticity of the Giesekus fluid can alter the behaviours of the filament, and the critical Reynolds number for the stable oscillations is lower at higher $Wi$ due to the stronger shear-thinning effects of the fluid (leading to a smaller apparent viscosity).

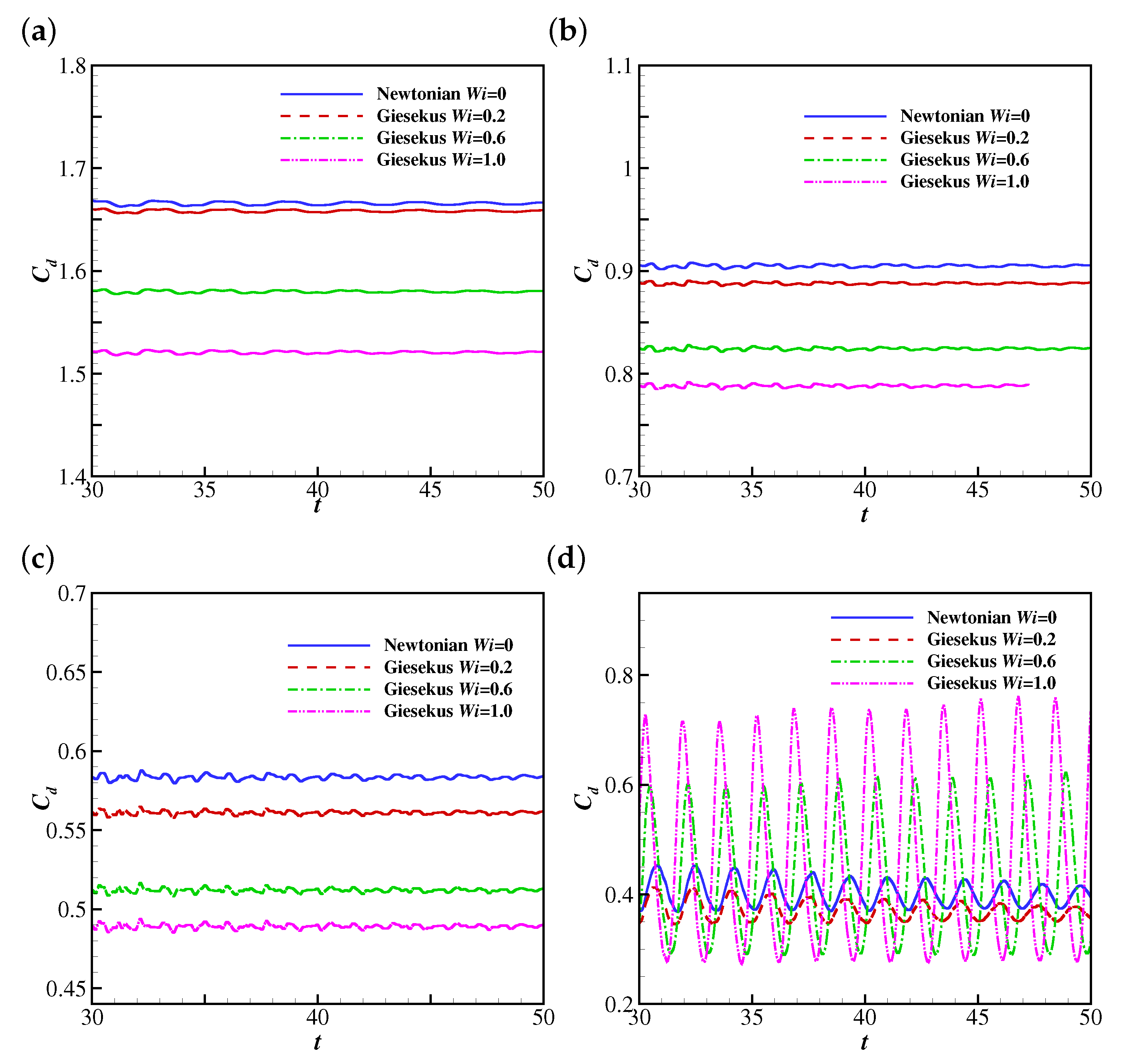
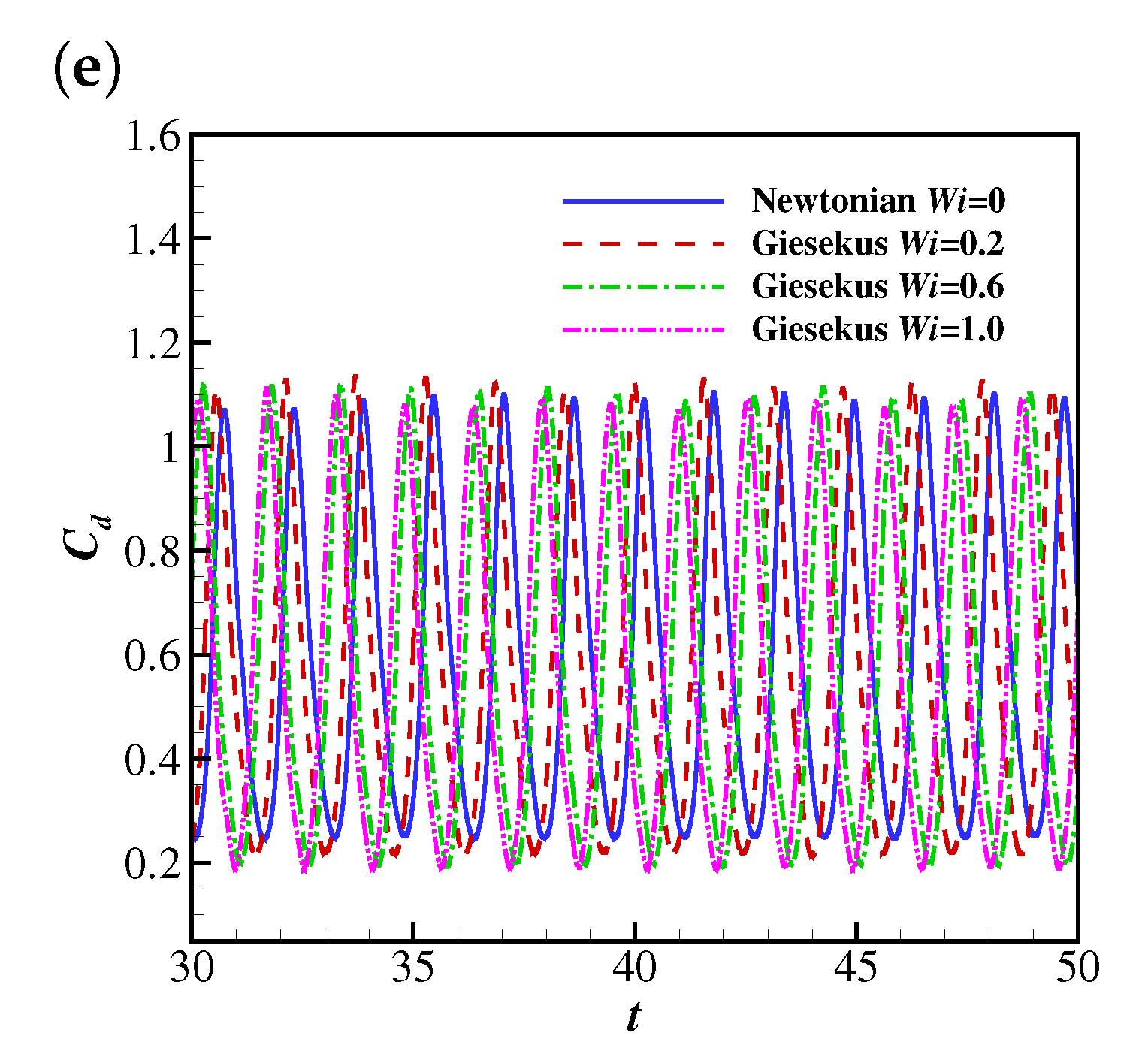
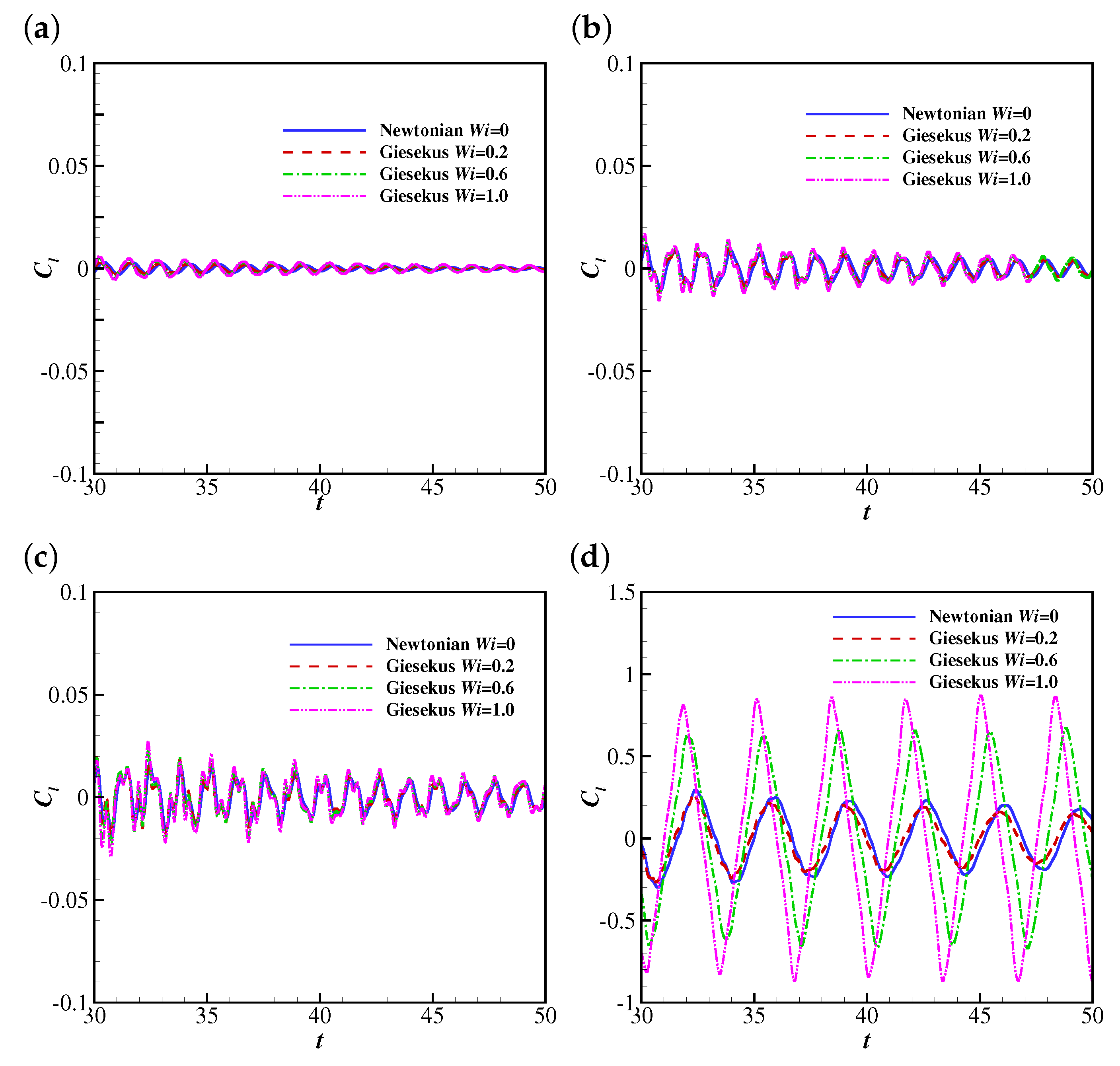
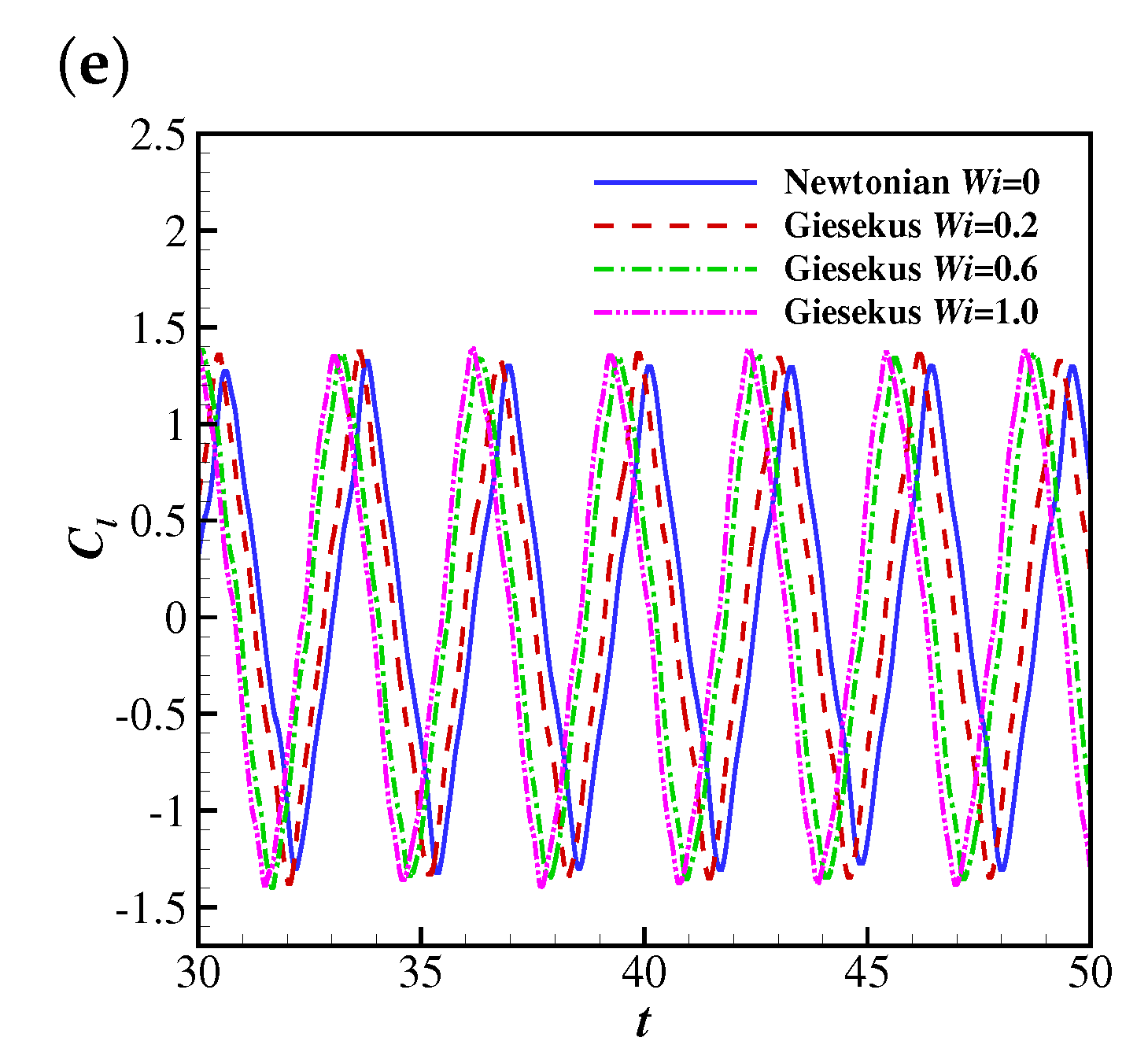
4.1.2. The Effects of Wi and Re on the Drag and Lift Coefficients of the Filament

The temporal evolutions of the drag coefficient (from $t=30$ to 50) on the filament are shown in Figure 9. At lower Reynolds numbers (e.g., $Re=10$, 25 and 50), the filament finally reaches the steady horizontal configuration, and correspondingly the drag coefficient converges to constant values. The drag coefficient decreases with $Wi$, which is reasonable since the Giesekus fluid shows shear-thinning characteristics (as the filament reaches the steady horizontal configuration, the shear stress becomes the major component of the drag force exerted on the filament). To further confirm the shear-thinning effect of the Giesekus fluid leading to the decreasing drag, the non-dimensional shear rates, ${\dot{\gamma }}^{*}=\frac{\partial u_x}{\partial y}/\frac{U_c}{L_f}$ (at the upper side), along the filament at $Re=10$, $Wi=0$, 0.2, 0.6 and 1.0 and $t=50$ is compared (as shown in Figure 10). It was found that ${\dot{\gamma }}^{*}$ is normally larger when the stronger viscoelasticity of the Giesekus fluid is included (at higher $Wi$). Considering that the drag coefficient decreases with increasing $Wi$, the shear-thinning effect of the Giesekus fluid can be confirmed. When $Re$ increases to 100, the drag coefficient shows damped oscillations at $Wi=0$ and 0.2 and stable oscillations at $Wi=0.6$ and 1.0. It was also found that the maximum drag coefficient at $Wi=1.0$ is larger than that at $Wi=0.6$. These are caused by the different pressure differences across the filament at different $Wi$. Figure 11 illustrates contours of the pressure coefficient at $Re=100$ and $Wi=$ 0, 0.2, 0.6 and 1.0 at a time when the displacement of the filament is at a peak (i.e., at $t=$ 30.935 for $Wi=0$, $t=$ 30.825 for $Wi=0.2$, $t=$ 30.605 for $Wi=0.6$ and $t=$ 30.375 for $Wi=1.0$). It was observed that the pressure difference across the filament does not show great difference (with a slight shrink of the higher pressure region at the upper side of the filament) when $Wi$ increases from 0 to 0.2. That explains why the displacement of the filament and the drag coefficient exerted on the filament experience similar oscillations at $Wi=0$ and 0.2. However, the situation is different at $Wi=0.6$ where a high pressure region appears and the low pressure region experiences a great expansion. This pressure differential produces a large force on the filament causing a larger drag force on the filament. That is why the displacement of filament and the drag coefficient show stable oscillation at $Wi=0.6$ (in contrast to the damped oscillation at $Wi=0$ and 0.2). When $Wi$ increases to 1.0, the pressure difference is further increased and the high pressure and low pressure regions further expand. Thus, the drag coefficient experiences oscillations larger in amplitude at $Wi=1.0$ compared with those at $Wi=0.6$. The drag coefficients on the filament at $Re=200$ show stable oscillations at all $Wi$, and the oscillation amplitudes at all $Wi$ are quite close to each other, which means the shear-thinning characteristic of the Giesekus fluid does not have significant influence on the drag coefficient when the Reynolds number is sufficiently high.

The temporal evolutions of the lift coefficient (from $t=30$ to 50) on the filament are shown in Figure 12. The lift coefficient at lower Reynolds numbers (e.g., $Re=10$, 25 and 50) shows oscillations with small amplitudes corresponding to the steady horizontal configuration of the filament. At $Re=100$, the lift coefficient experiences damped oscillations at $Wi=0$ and 0.2 (corresponding to damped oscillations of the filament) and stable oscillations at $Wi=0.6$ and 1.0 (corresponding to stable oscillations of the filament). The mechanism behind this is similar to that of the drag coefficient (the increase of the pressure difference across the filament leads to a larger lift force). Similarly to the drag coefficient, the lift coefficient also shows stable oscillations with similar amplitudes at all $Wi$ at $Re=200$. This means the lift coefficient of the filament at a sufficiently high $Re$ (e.g., 200) is not significantly influenced by the shear-thinning property of the Giesekus fluid.

4.2. The Filament Motion in a Uniform FENE-CR Flow.

The filament behaviours in a FENE-CR uniform flow are studied in this section, and the effects of Wi and Re on the filament flapping motion and the drag and lift coefficients are investigated.

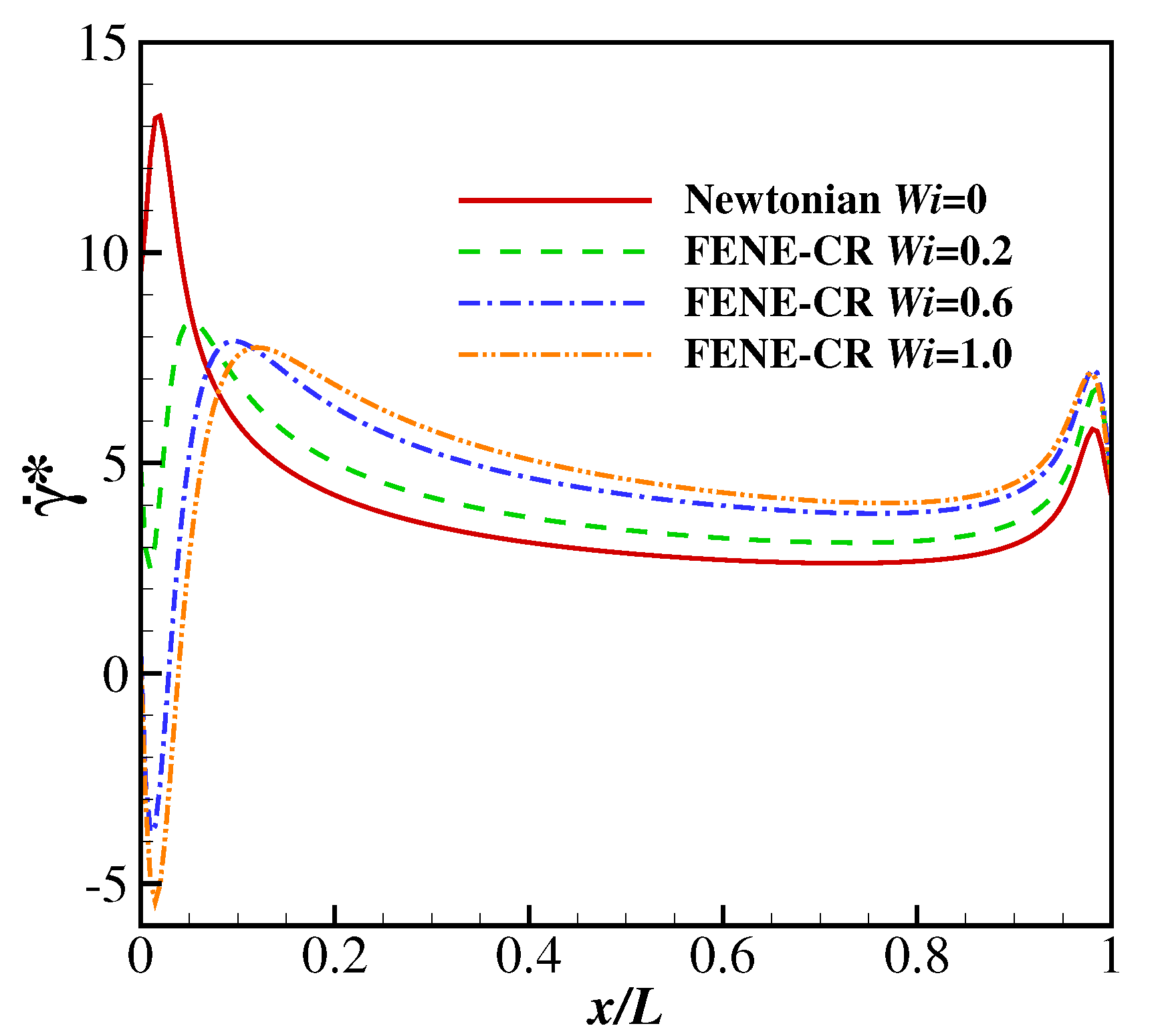
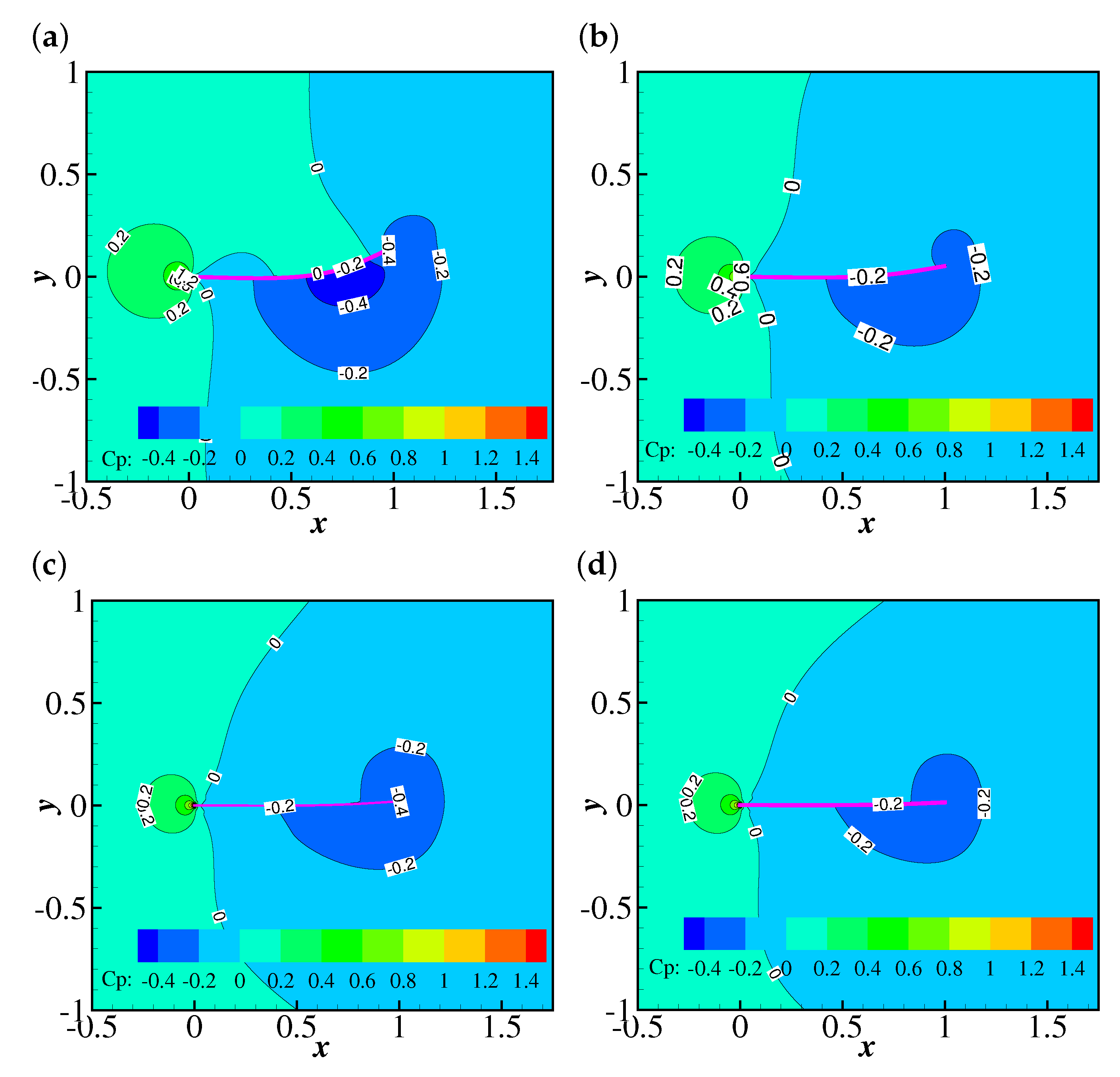
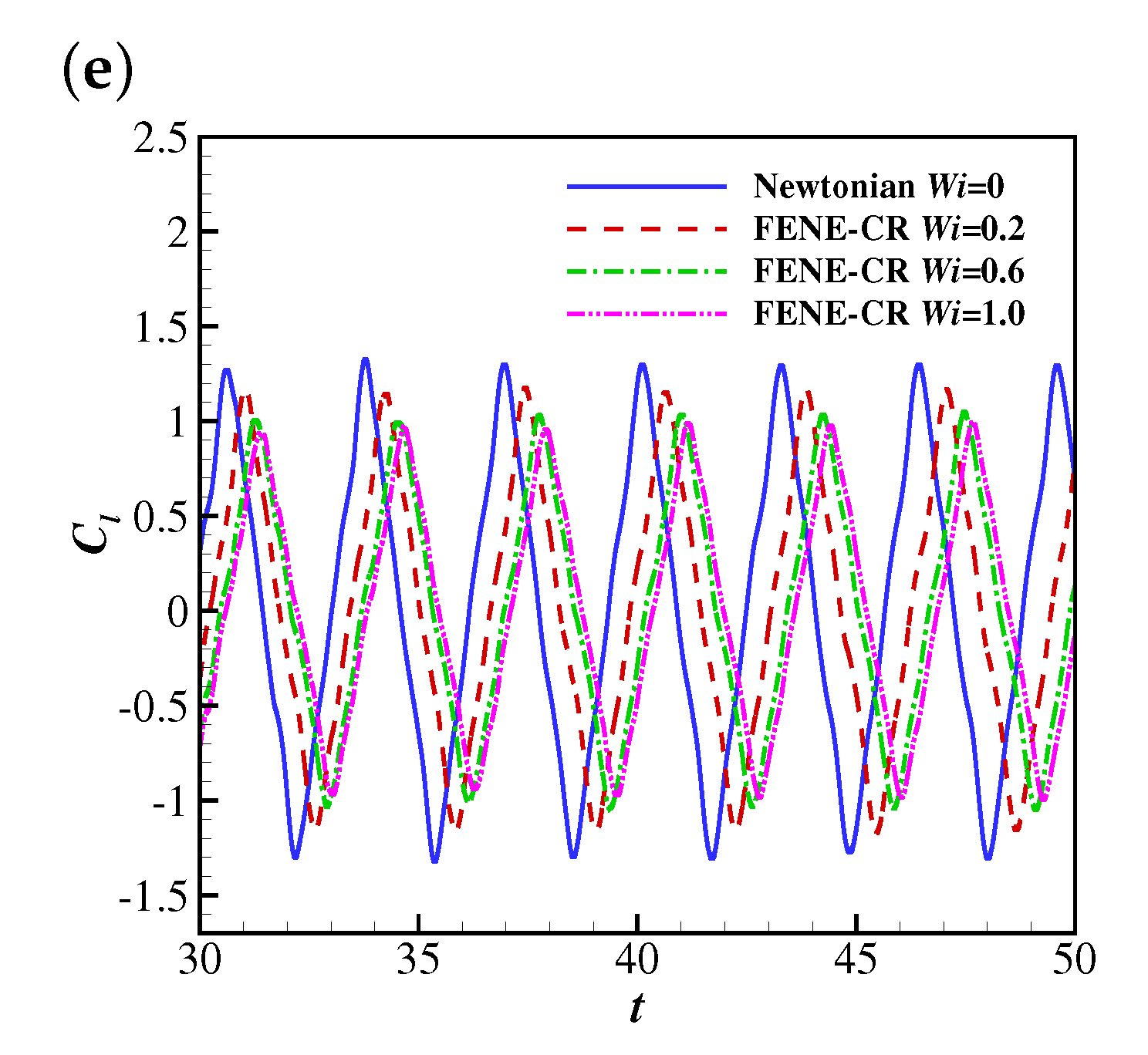
4.2.1. The Effects of Wi and Re on the Flapping Motion of the Filament

The temporal evolutions of the free-end position of the filament at $Re=10$, 25, 50, 100 and 200 are shown in Figure 13. It was observed that the filament reaches the steady horizontal configuration at lower Reynolds numbers (e.g., $Re=10$, 25 and 50), which is similar to the behaviour of the filament in the Giesekus fluid. The filament undergoes oscillations with smaller amplitudes in FENE-CR fluids than those in a Newtonian fluid. This is different from the behaviour of the filament in Giesekus uniform flows, where it experiences oscillations with larger amplitudes. This means the viscoelasticity of the FENE-CR fluid hinders the flapping motion of the filament. A similar trend was also observed at $Re=100$. The filament experiences stable oscillations at $Re=200$ at all $Wi$ considered.

The states of the filament behaviours in the FENE-CR fluid as a function of the Reynolds number and Weissenberg number are shown in Figure 14. It was observed that the critical $Re$ for the stable oscillation of the filament increases with the increase of $Wi$ at lower $Wi$ ($Wi\le 0.8$). However, the viscoelasticity of the FENE-CR fluid does not have significant influence on the flapping behaviour of the filament at higher $Wi$ ($Wi>0.8$).

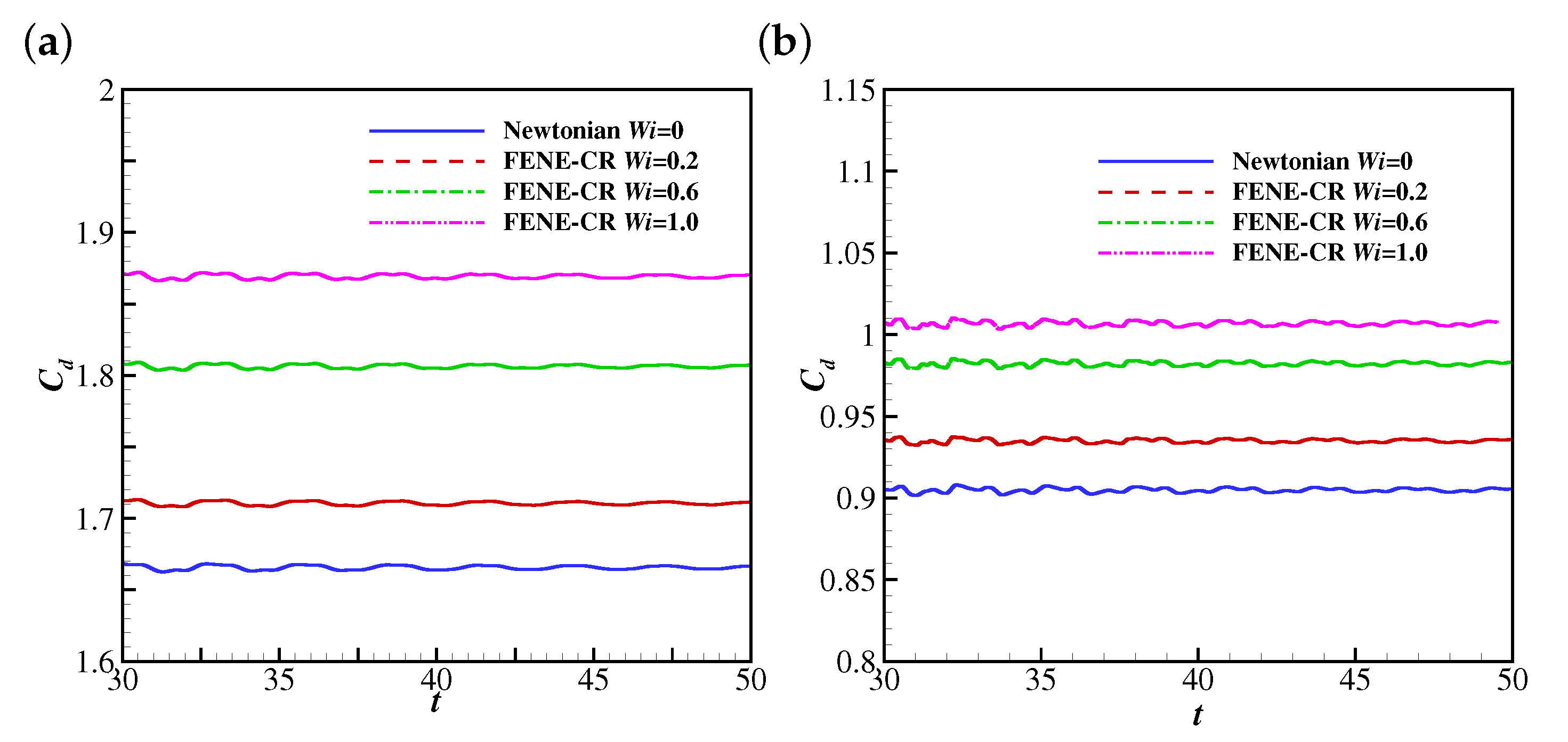
4.2.2. The Effects of Wi and Re on the Drag and Lift Coefficients of the Filament

Figure 15 illustrates the time evolutions of the drag coefficient (from $t=30$ to 50) of the filament at $Re=10$, 25, 50, 100 and 200. The drag coefficient increases with $Wi$ at lower Reynolds numbers (e.g., $Re=10$, 25 and 50). This trend is different from those reported by previous studies on the FENE-CR flow over a confined cylinder [49,50]. For example, Kim et al. [49] suggested that the cylinder experiences a reduction in the drag coefficient with the increase of $Wi$ at $L_p^2=10$. Further simulations showed a different tendency of the drag coefficient is caused by a blockage of the flow. The effect of the blockage of the channel was observed in the investigation on the Oldroyd-B fluid over a stationary cylinder by Huang and Feng [51]. To explain the tendency of the viscoelasticity of the FENE-CR fluid leading to the increase of the drag coefficient, the non-dimensional shear rates ${\dot{\gamma }}^{*}$ (at the upper side) along the filament at $Re=10$, $Wi=0$, 0.2, 0.6 and 1.0 and $t=50$ are compared (as shown in Figure 16). It is clear that the shear rate is larger at higher $Wi$ (except in the leading edge region of filament). Since the FENE-CR is a type of viscoelastic fluid with constant viscosity [28], it is understandable that the filament experiences a larger drag at higher $Wi$. In addition, the drag coefficient shows damped oscillations at all $Wi$ at $Re=100$, and the oscillation amplitude shows a significant reduction when $Wi$ increases from 0 to 0.2. A further decrease in the oscillation amplitude was observed at $Wi=0.6$, and the drag coefficient showed an oscillation with a similar amplitude to that at $Wi=0.2$. Similarly to the discussion in the Giesekus case, the pressure distribution leads to the different oscillation amplitudes at different $Wi$. Figure 17 illustrates the contours of the pressure coefficient at $Re=100$ and $Wi=$ 0, 0.2, 0.6 and 1.0 at a time when the displacement of the filament is at a peak (i.e., at $t=$ 30.935 for $Wi=0$, $t=$ 30.87 for $Wi=0.2$, $t=$ 30.825 for $Wi=0.6$ and $t=$ 30.795 for $Wi=1.0$). It is clear that the higher pressure region (at the upper side of the filament) experiences a marked reduction in size when $Wi$ increases from 0 to 0.2, causing a decrease of the pressure difference across the filament (a lower drag force on the filament). When $Wi$ increases to 0.6, the lower pressure region the upper side of the filament expands further, causing the reduction of the pressure difference, and there is no significant difference between the pressure distribution at $Wi=0.6$ and 1.0. That explains the tendency of the stronger viscoelasticity of the FENE-CR fluid causing the smaller oscillation amplitude of the drag coefficient. At $Re=200$, the drag coefficients at all $Wi$ experience stable oscillations, and the amplitudes of the oscillations and the time-averaged values of the drag coefficient reduce with the increase of $Wi$. This means the drag force on the filament is smaller than that in a Newtonian fluid at $Re=200$ when the viscoelasticity of the FENE-CR fluid is included.

The time histories of the lift coefficient of the filament are shown in Figure 18. The lift coefficients experience oscillations with small amplitudes at lower Reynolds numbers (e.g., $Re=10$, 25 and 50), which is similar to those in the Giesekus case. Similarly to the drag coefficient, the lift coefficient experiences an oscillation with a smaller amplitude when the viscoelasticity of the FENE-CR fluid is included ($Wi>0$), and it is caused by the decrease of the pressure difference across the filament. At $Re=200$, the lift coefficient showed stable oscillations at all $Wi$ simulated, and the oscillation amplitude reduced with the increase of $Wi$ in contrast to the similar amplitudes in the Giesekus cases.

5. Concluding Remarks

In this work, the dynamic behaviours of the a filament in Newtonian, FENE-CR and Giesekus uniform flows have been studied. The fluid–structure system was solved by employing the multi-relaxation time lattice Boltzmann method combined with the finite-difference method and the immersed boundary method. This method is based on non-conformal meshes, which can significantly improve the efficiency of solving FSI problems involving large deformation and displacement by avoiding the regeneration of the mesh. The effects of the Reynolds number and Weissenberg number on the flapping motion, drag coefficient and lift coefficient of the filament were investigated. It was found that the Reynolds number promotes the flapping motion of the filament. The major effect of the viscoelasticity of the Giesekus fluid is to decrease the critical Reynolds number for the flapping motion of the filament. In addition, the filament experiences lower drag in a Giesekus uniform flow compared with that in a Newtonian uniform flow at low $Re$ ($Re<100$), and the drag coefficient shows periodic oscillation when $Re$ is sufficiently large ($Re>100$). In contrast, the viscoelasticity of the FENE-CR fluid normally hinders the flapping motion of the filament, and it increases the critical Reynolds number for the flapping motion of the filament at lower $Wi$ ($Wi<0.8$) and shows little influence on the critical Reynolds number at higher $Wi$ ($Wi\ge 0.8$). In addition, the viscoelasticity of the FENE-CR fluid enhances the drag force on the filament at low Reynolds numbers ($Re<100$) and the flapping amplitude of the drag decreases when the Reynolds number is sufficiently high ($Re=200$).

It should be noted that the results obtained in this work may provide guidance for some practical applications. For example, paints (viscoelastic fluids) are normally manufactured to have shear-thinning properties. This is because paints are normally expected to have low viscosities at high shear rates (e.g., painting motion) to smoothly spread over the wall and high viscosities to stick to the paintbrush (flexible fibres) at low shear rates (e.g., after painting motion) [52]. Hence, Giesekus fluids could be suitable choices for paints.