PIV-Measurements of Centrifugal Instabilities in a Rectangular Curved Duct with a Small Aspect Ratio
Abstract
:1. Introduction
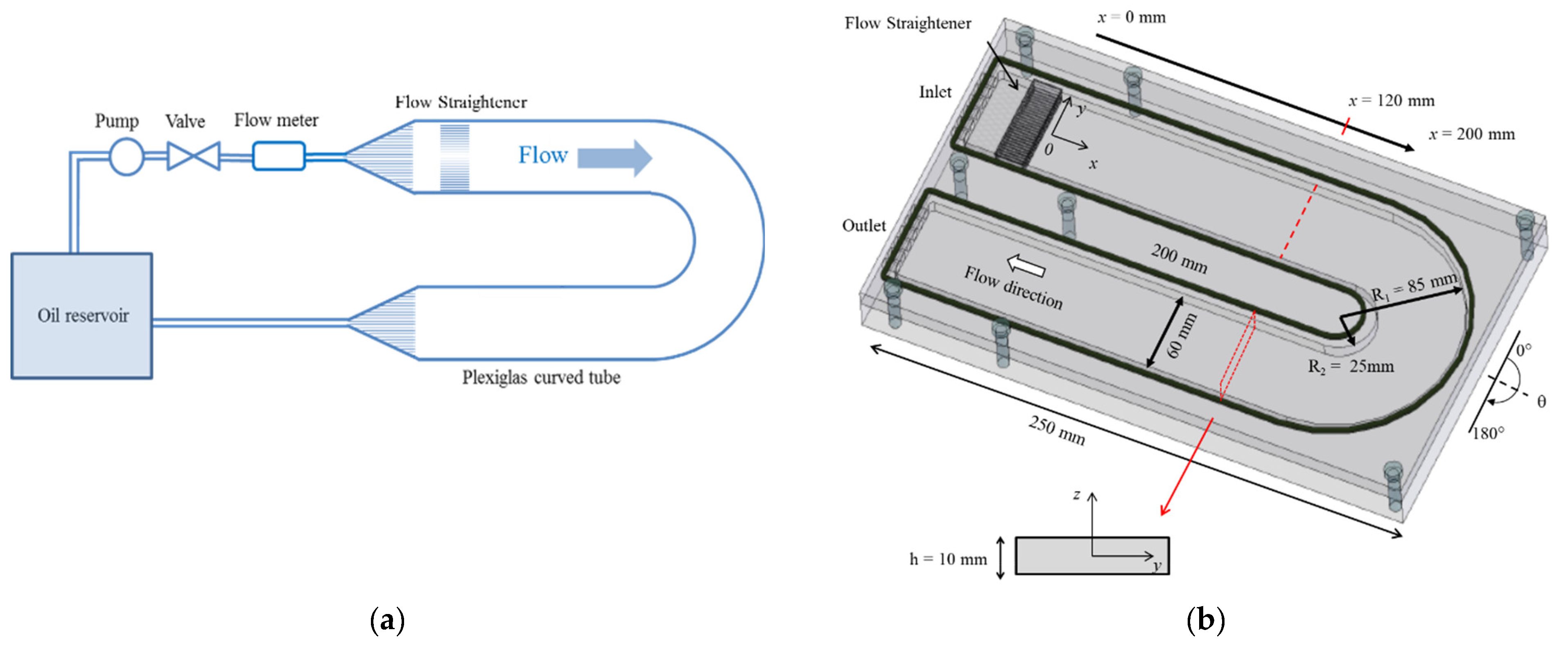
2. Experimental Conditions
Flow Visualization
3. Experimental Results
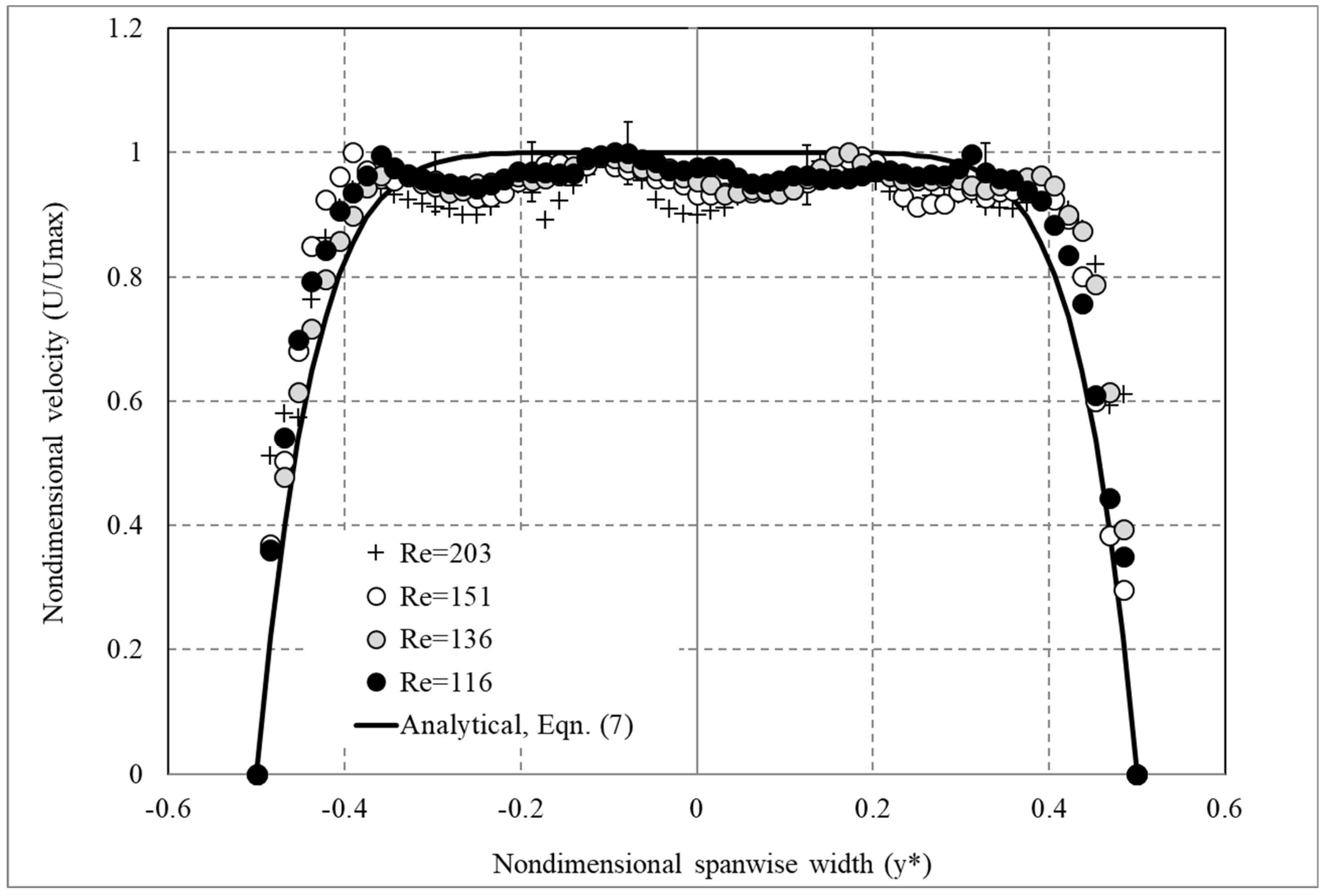
3.1. Experimental Validation
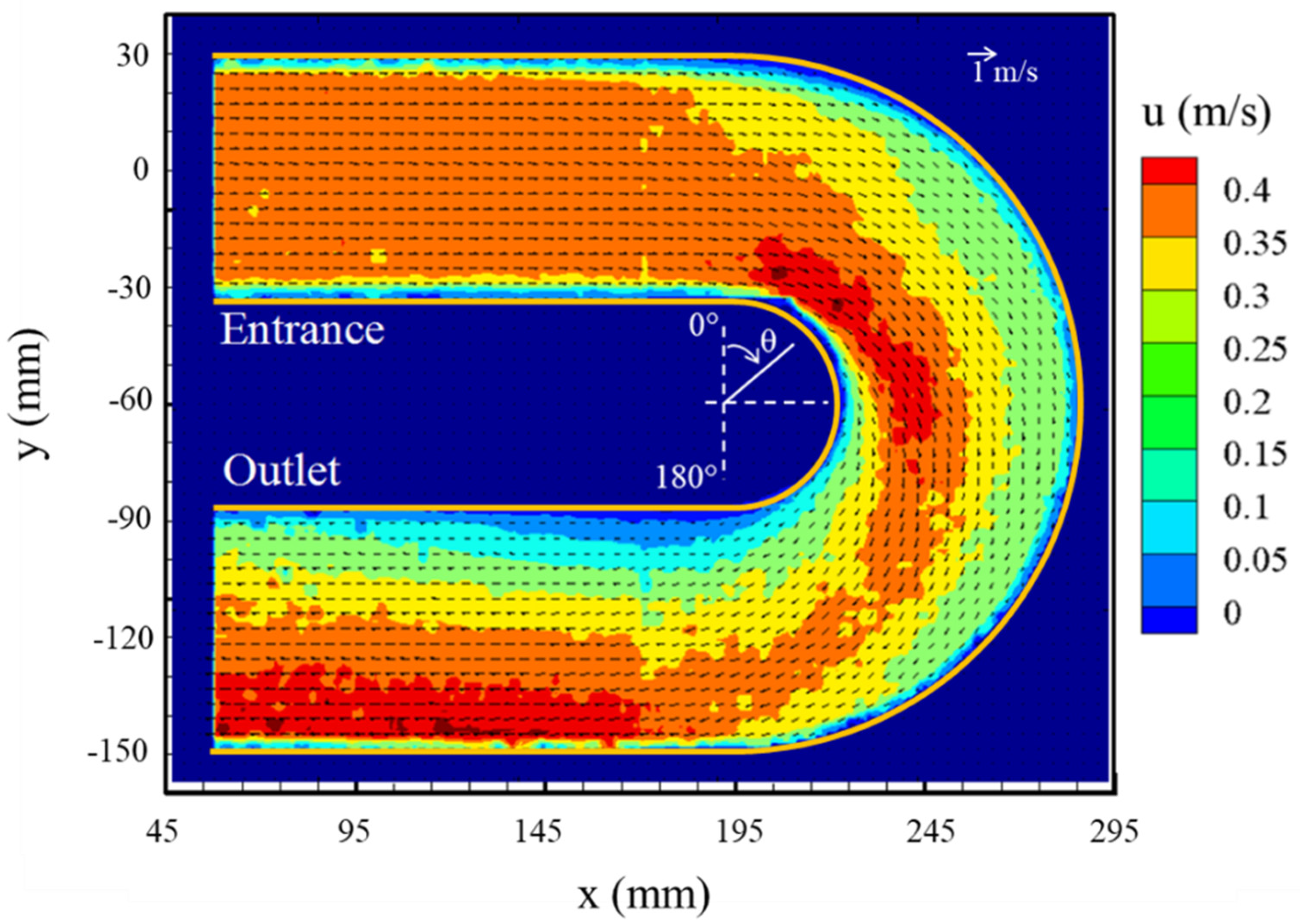
3.2. Two-Dimensional Velocity Distributions
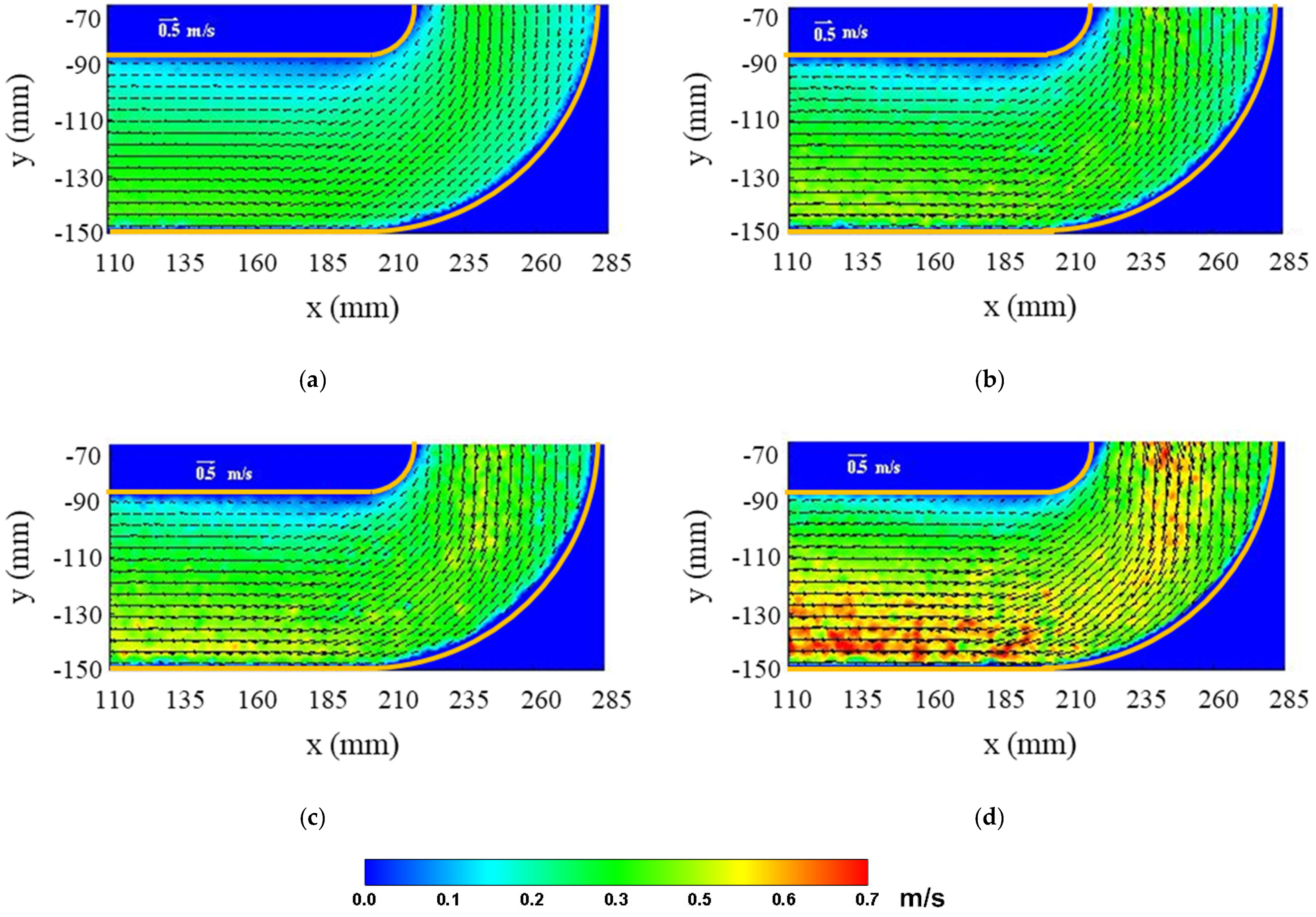
3.3. Flow Pattern along the Curved Channel
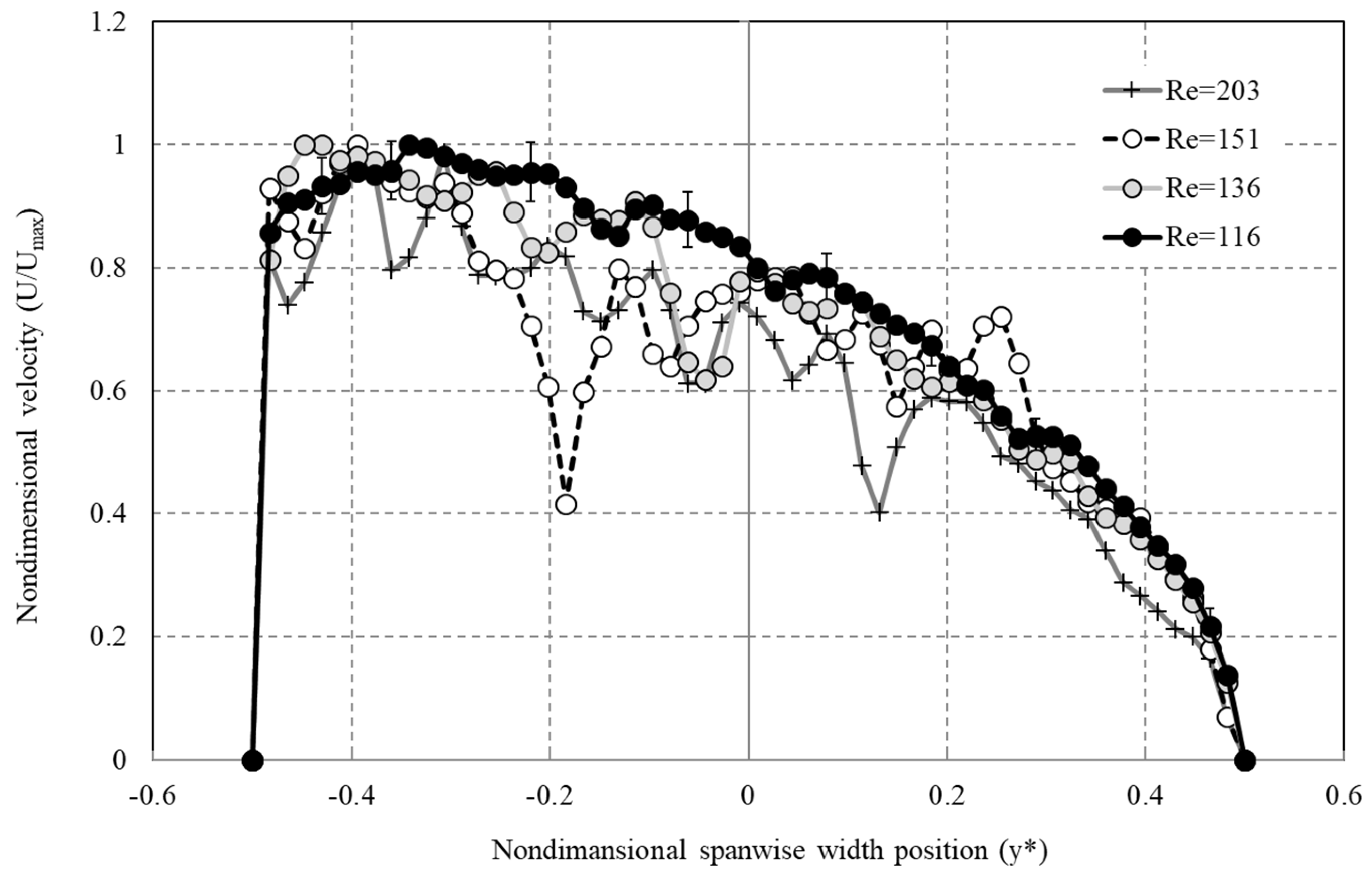
3.4. Spanwise Velocity Distribution
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Martin, J.; Oshkai, P.; Djilili, N. Flow structure in a u-shaped fuel cell flow channel: Quantitative visualization using particle image velocimetry. Trans. ASME J. Fuel Cell Sci. Tech. 2005, 2, 70. [Google Scholar] [CrossRef]
- Ligrani, P.M.; Hedlund, C.R. Experimental surface heat transfer and flow structure in a curved channel with laminar, transitional, and turbulent flows. Trans. ASME J. Turbomach. 2004, 126, 414. [Google Scholar] [CrossRef]
- Kumar, V.; Aggarwal, M.; Nigam, K.D.P. Mixing in curved tubes. Chem. Eng. Sci. 2006, 61, 5742. [Google Scholar] [CrossRef]
- Bruschewski, M.; Scherhag, C.; Schiffer, H.P.; Grundmann, S. Influence of Channel Geometry and Flow Variables on Cyclone Cooling of Turbine Blades. Trans. ASME J. Turbomach. 2016, 138, 061005. [Google Scholar] [CrossRef]
- Couette, M. Études sur le frottement des liquids. Ann. Chim. Phys. 1890, 21, 433–510. [Google Scholar]
- Taylor, G.I. VIII. Stability of a viscous liquid contained between two rotating cylinders. Phil. Trans. R. Soc. Lond. A 1923, 223, 289–343. [Google Scholar] [CrossRef]
- Dean, W.R. Flow motion in a curved channel. Proc. R. Soc. Lond. A 1928, 121, 402. [Google Scholar]
- Berger, S.A.; Yao, L.S. Entry flow in a curved pipe. J. Fluid Mech. 1975, 67, 177–196. [Google Scholar]
- Patankar, S.V.; Pratap, V.S.; Spalding, D.B. Prediction of turbulent flow in curved pipes. J. Fluid Mech. 1975, 67, 583–595. [Google Scholar] [CrossRef] [Green Version]
- Agrawal, Y.; Talbot, L.; Gong, K. Laser anemometer study of flow development in curved circular pipes. J. Fluid Mech. 1978, 85, 497–518. [Google Scholar] [CrossRef]
- Lin, J.Y.; Tarbell, J.M. An experimental and numerical study of periodic flow in a curved tube. J. Fluid Mech. 1980, 100, 623–638. [Google Scholar] [CrossRef]
- Berger, S.A.; Talbot, L.; Yao, L.S. Flow in curved pipes. Annu. Rev. Fluid Mech. 1983, 15, 461–512. [Google Scholar] [CrossRef]
- Olson, D.E.; Snyder, B. The upstream scale of flow development in curved circular pipes. J. Fluid Mech. 1985, 150, 139–158. [Google Scholar] [CrossRef]
- Ghia, K.N.; Sokhey, J.S. Laminar incompressible viscous flow in curved ducts of regular cross-sections. J. Fluids Eng. 1977, 99, 640–648. [Google Scholar] [CrossRef]
- Sugiyama, S.; Hayashi, T.; Yamazaki, K. Flow characteristics in the curved rectangular channels: Visualization of secondary flow. JSME Int. J. Ser. B 1983, 26, 532–552. [Google Scholar] [CrossRef]
- Humphrey, J.A.C.; Taylor, A.M.K.; Whitelaw, J.H. Laminar flow in a square duct of strong curvature. J. Fluid Mech. 1977, 83, 509–527. [Google Scholar] [CrossRef]
- Bara, B.; Nandakumar, K.; Masliyah, J.H. An experimental and numerical study of the dean problem: Flow development towards two-dimensional multiple solutions. J. Fluid Mech. 1992, 244, 339–376. [Google Scholar] [CrossRef]
- Arnal, M.P.; Goering, D.J.; Humphrey, J.A.C. Unsteady laminar flow developing in a curved duct. Int. J. Heat Fluid Flow 1992, 13, 347–357. [Google Scholar] [CrossRef]
- Mees, P.A.J.; Nandakumar, K.; Masliyah, J.H. Instability and transitions of flow in a curved square duct: The development of two pairs of dean vortices. J. Fluid Mech. 1996, 314, 227–246. [Google Scholar] [CrossRef]
- Gauthier, G.; Gondret, P.; Thome, H.; Rabaud, M. Centrifugal instabilities in a curved rectangular duct of small aspect ratio. Phys. Fluids 2001, 13, 2831–2834. [Google Scholar] [CrossRef] [Green Version]
- Boutabaa, M.; Helin, L.; Mompean, G.; Thais, L. Numerical study of Dean vortices in developing Newtonian and viscoelastic flows through a curved duct of square cross-section. Comptes Rendus Mécanique 2009, 337, 40–47. [Google Scholar] [CrossRef]
- Wu, X.; Lai, S.; Yamamoto, K.; Yanase, S. Vortex patterns of the flow in a curved duct. Energy Procedia 2011, 12, 920–927. [Google Scholar] [CrossRef] [Green Version]
- Yamamoto, K.; Wub, X.; Hyakutake, T.; Yanase, S. Taylor–Dean flow through a curved duct of square cross section. Fluid Dyn. Res. 2004, 35, 67–86. [Google Scholar] [CrossRef]
- Yamamoto, K.; Wub, X.; Nozaki, K.; Hayamizu, Y. Visualization of Taylor–Dean flow in a curved duct of square cross-section. Fluid Dyn. Res. 2006, 38, 1–18. [Google Scholar] [CrossRef]
- Norouzi, M.; Biglari, N. An analytical solution for Dean flow in curved ducts with rectangular cross section. Phys. Fluids 2013, 25, 053602. [Google Scholar] [CrossRef]
- Yanase, S.; Kaga, Y.; Daikai, R. Laminar flows through a curved rectangular duct over a wide range of the aspect ratio. Fluid Dyn. Res. 2002, 31, 151–183. [Google Scholar] [CrossRef]
- Facao, J.; Oliveira, A.C. Modeling laminar heat transfer in a curved rectangular duct with a computational fluid dynamics code. Numer. Heat Trans. A 2005, 48, 165–177. [Google Scholar] [CrossRef]
- Chandratilleke, T.T.; Nadim, N.; Narayanaswamy, R. Vortex structure-based analysis of laminar flow behaviour and thermal characteristics in curved ducts. Int. J. Sci. 2012, 59, 75–86. [Google Scholar] [CrossRef]
- Li, Y.; Wang, X.; Yuan, S.; Tan, S.K. Flow development in curved rectangular ducts with continuously varying curvature. Exp. Fluid Sci. 2016, 75, 1–15. [Google Scholar] [CrossRef]
- Raffle, M.; Willert, C.; Werely, S.; Kompenhans, J. Particle Image Velocimetry—A Practical Guide, 3rd ed.; Springer: Berlin, Germany, 2018. [Google Scholar]
- Ebadian, M.A.; Dong, Z.F. Forced convection, internal flow in ducts. In Handbook of Heat Transfer, 3rd ed.; McGraw-Hill: New York, NY, USA, 1998. [Google Scholar]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Goharzadeh, A.; Rodgers, P. PIV-Measurements of Centrifugal Instabilities in a Rectangular Curved Duct with a Small Aspect Ratio. Fluids 2021, 6, 184. https://doi.org/10.3390/fluids6050184
Goharzadeh A, Rodgers P. PIV-Measurements of Centrifugal Instabilities in a Rectangular Curved Duct with a Small Aspect Ratio. Fluids. 2021; 6(5):184. https://doi.org/10.3390/fluids6050184
Chicago/Turabian StyleGoharzadeh, Afshin, and Peter Rodgers. 2021. "PIV-Measurements of Centrifugal Instabilities in a Rectangular Curved Duct with a Small Aspect Ratio" Fluids 6, no. 5: 184. https://doi.org/10.3390/fluids6050184
APA StyleGoharzadeh, A., & Rodgers, P. (2021). PIV-Measurements of Centrifugal Instabilities in a Rectangular Curved Duct with a Small Aspect Ratio. Fluids, 6(5), 184. https://doi.org/10.3390/fluids6050184






