Abstract
A variety of mathematical models have been developed to simulate the biochemical and physico-chemical aspects of the anaerobic digestion (AD) process to treat organic wastes and generate biogas. However, all these models, including the most widely accepted and implemented Anaerobic Digestion Model No.1, remain incapable of adequately representing the material balance of AD and are therefore inherently incapable of material conservation. The absence of robust mass conservation constrains reliable estimates of any kinetic parameters being estimated by regression of empirical data. To address this issue, the present work involved the development of a “framework” for a mass-conserving atomistic mathematical model which is capable of mass conservation, with a relative error in the range of machine precision value and an atom balance with a relative error of ±0.02% whilst obeying the Henry’s law and electroneutrality principle. Implementing the model in an Excel spreadsheet, the study calibrated the model using the empirical data derived from batch studies. Although the model shows high fidelity as assessed via inspection, considering several constraints including the drawbacks of the model and implementation platform, the study also provides a non-exhaustive list of limitations and further scope for development.
1. Introduction
Anaerobic digestion (AD) is recognised as a sustainable process to treat organic wastes (from food residues to agricultural waste) and generate biogas and digestate [1,2]. Biogas which typically contains ~60% methane is used as fuel to generate heat and electricity, whereas the nutrient rich residual material (digestate) is used as fertiliser or soil amendment [3,4]. Unlike most fermentation processes which have well-defined substrate and a single organism involved, AD involves a consortium of microbes, facilitating multiple biochemical reactions to convert diverse substrates consisting of various macromolecules [5,6]. With multiple reactions happening in series and in parallel, a typical anaerobic digester contains four broad categories of microorganisms—hydrolysers, acidogens, acetogens and methanogens. The hydrolysers convert macromolecules such as carbohydrates, proteins, lipids and fibres to relatively simple monomeric units such as sugars, amino acids, fatty acids and glycerol. These monomeric units are further converted to acetate through a set of reactions catalysed by acidogens and acetogens, simultaneously producing H2, H2S, NH3, CO2, etc. The acetoclastic methanogens finally convert acetate to CH4 and CO2, whereas the metabolites such as H2 and CO2 can undergo hydrogenotrophic methanogenesis to generate CH4 [7]. Recent work in the field has focused on developing process technologies and additive-based solutions to optimise the process for enhancing CH4 production and generating high quality nutrient rich digestates which could be used as an alternative to chemical fertilisers for land application [8,9,10]. To support this, considerable work has been carried out to model the AD process and optimise the process parameters to maximise the outputs [11].
AD has a long history of development as a unit operation in wastewater treatment [12]. However, more recently, interest in the technology for the production of renewable energy from biomass resources and bio-degradable wastes has become an additional motivation [13,14,15]. The application of the technology in the field of renewable energy brings a tight focus on the capital and operating economics, which in turn creates a demand for greater process productivity or intensity and the more rigorous models and methods required to design them [16,17,18,19,20]. Prior to the publication of the International Water Association’s (IWA) Anaerobic Digestion Model No. 1 (ADM1), the majority of models made no attempt to “conserve” matter [21,22,23]. This situation arose principally due to the almost overwhelming complexity of composition of relevant feedstocks. ADM1 deals with the complexity of feed and intermediate materials by describing them in terms of Chemical Oxygen Demand (COD), with particular fractions assigned additional characteristics such as “readily available” [22]. ADM1 belongs to a class of models which may be collectively termed Oxygen Demand Models (ODMs). Oxygen demand models and methods can be based on any of the common forms: Biochemical (BOD), Chemical (COD) or Theoretical (ThOD) [12,24,25]. However, only those based on COD or ThOD, when rigorously constructed, permit the conservation of redox to a “reasonable” degree of precision. Where the precision of COD methods is limited by the prescribed chemo-catalytic system, the empirical nature of COD determination and the variability of the terminal oxidation products [25], the degree of precision of ThOD-based methods and models is governed by the state of knowledge of the underlying stoichiometry. Where the stoichiometric knowledge is only partial, COD and ThOD data can be advantageously combined to improve the rigour of redox conservation of exclusively COD-based methods.
Whilst ODMs, particularly ADM1, have a broader applicability than their predecessors, they remain incapable of adequately representing the material balance of AD and therefore inherently incapable of material conservation. The absence of robust mass conservation also constrains any kinetic parameters estimated by regression of empirical data to an ODM to the system studied and very close analogues. For instance, the exclusion of system mass and volume reduction due to mass transfer (liquid–gas transfer), in ADM1 results in an inaccurate prediction of concentration of any given component in the system. With the concentration of components (for e.g., sugars) affecting the reaction rate (as per Monod kinetics), the regression of empirical data with the model would result in inaccurate estimates of kinetic parameters. Further to this, the resulting inaccurate prediction of the concentration of ionic components would result in the inaccurate prediction of physico-chemical characteristics. With the inaccurate prediction of physico-chemical characteristics such as pH, used to model inhibition functions (expressed together with Monod kinetics) in ADM1, the estimates of the kinetic parameters will ultimately be inaccurate.
Mass-conserving atomistic models (MAM) are generally limited to systems characterised by very simple feed and microbial consortia compositions. This limitation is imposed by the analytical load required to fully determine the composition of anything other than very simple, highly prescribed feed streams. In this work, a MAM is developed based on a conventional “food” analysis of the feed stock which is characterised in terms of its carbohydrate, protein and lipid content [26]. Yao [27], in a largely theoretical study, showed that each of the major food components were characterised by a relatively narrow range of stoichiometries. Thus, by inference, a reasonable estimate of the atomistic composition of a complex feed stock can be obtained through the application of three standard food analysis methods [27]. Typical mass-based determinations of the major food components can be readily and arbitrarily converted to the molar compositions required for modelling purposes by division by assumed molecular masses to yield the molar compositions of a carbohydrate polymer, a lipid and a protein polymer. The MAM framework is assembled on these three starting components to represent the classical steps of hydrolysis, acidogenesis, acetogenesis and methanogenesis. The objective of the framework is to represent the observed behaviours of AD, based on the minimum number of intermediate and final components linked by the minimum number of bio-chemical and physico-chemical processes. Table 1 provides key differences between the ADM1 model and MAM framework (present study).

Table 1.
Key differences between Anaerobic Digestion Model No. 1 (ADM1) and the mass-conserving atomistic model (present study).
2. Model Development
2.1. General Assumptions of the Model
- A batch AD process is considered to occur in a reactor with initial liquid volume VL and headspace volume of VH. The reactor is considered to be connected to a separate flexible gas bag which is replaced at regular time intervals equal in size to the time step used to integrate the bio-kinetic rate equations shown in Table 2.
- Initially (t0), the headspace is considered to be filled with N2, which is used to flush the reactors to generate anaerobic conditions.
- The total pressure of the system at any time point is assumed to be 1 atm.
- The density of any component (bulk density) in the aqueous phase is assumed as 1000 g/L.
2.2. Model Description
The model considers two major process families, biochemical and physico-chemical, to occur simultaneously, as described below. Biochemical processes are considered to occur at a finite rate between the electrochemically neutral species whilst the physico-chemical processes are considered to occur instantaneously. Figure 1 illustrates the MAM framework.
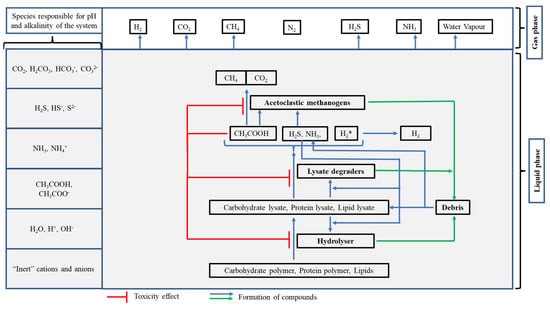
Figure 1.
Illustration of the mass-conserving atomistic model (MAM) framework.
2.2.1. Biochemical Processes
The anaerobic biochemical processes are considered to occur in three steps: hydrolysis, acetogenesis and acetoclastic methanogenesis.
Hydrolysis
The three substrates, carbohydrate polymer, protein polymer and lipid, are considered to undergo growth-independent hydrolysis, resulting in the production of carbohydrate lysate (monomers), protein lysate (amino acids) and lipid lysate (glycerol and long chain fatty acids). The rate of hydrolysis is assumed to be second order overall, dependent upon the concentration of specific hydrolysers and the concentration of the respective substrate constituent. The growth of hydrolysers (carbohydrate polymer hydrolyser, protein polymer hydrolyser and lipid hydrolyser) is considered to depend on the concentration of individual lysates and is described through Monod kinetics [28].
Acetogenesis
The lysates (monomeric units) produced in the hydrolysis step are considered to undergo acetogenesis, resulting in the production of acetate. The rate of acetogenesis is assumed to be dependent upon the concentration of respective lysate and the concentration of respective lysate degraders. The growth of specific lysate degraders, namely, carbohydrate lysate degraders, protein lysate degraders and lipid lysate degraders are considered to depend upon the concentration of individual (corresponding) lysates and are described through Monod kinetics [28].
Acetoclastic Methanogenesis
The acetate produced in the acetogenesis step is considered to undergo methanogenesis, resulting in production of methane and carbon dioxide. The rate of methanogenesis is assumed to be dependent upon the concentration of acetate and concentration of acetoclastic methanogens. The growth of acetoclastic methanogens is dependent upon the concentration of acetate and concentration of acetoclastic methanogens and is described through Monod kinetics [28].
Debris Formation and Disintegration
The hydrolysers, lysate degraders and acetoclastic methanogens are considered to undergo decay due to senility and the toxicity effect of acetate (volatile fatty acid), thus resulting in the production of debris. The debris is considered to undergo disintegration, resulting in the production of a fixed percentage of carbohydrate lysate, protein lysate and lipids lysate, as described through the balanced stoichiometric reactions.
Redox
Many of the steps in anaerobic degradation are considered to be redox reactions. When written in a conventional form, they appear to be thermodynamically highly unfavourable and give rise to substantial amounts of free hydrogen. Whilst hydrogen is observed in digester gases, the concentrations are orders of magnitude lower than would be expected from conventional stoichiometries. In biochemical systems, these twin issues are addressed by considering the exchange of , and . In the proposed model, the complex processes of redox and free energy exchanges are simplified into two forms of hydrogen: “combined” () and “free” ( gas). The rate of conversion of to (gas) is considered to depend upon the concentration of all the microbial species in the system and the concentration of .
Biochemical Processes and Components in the Framework
The biochemical processes occurring in the liquid phase involve seven bacterial species (three hydrolysers, three lysate degraders and one acetoclastic methanogen), debris (dead biomass), three polymeric materials (carbohydrate polymer, protein polymer and lipid), three lysates (carbohydrate lysate, protein lysate and lipid lysate), acetate, , , , , , , and . Table 2 describes the assumed molecular formula for the polymers, lysates and biomass, stoichiometric equations, and rate equations. The abbreviations and symbols used in Table 2 are described in the Supplementary Material (Table S1: Supplementary Material S1).

Table 2.
Balanced stoichiometric equations and rate equations based on assumed molecular formula for polymers, lysates and biomass (adapted or developed based on Refs. [27,29,30,31,32]).
Table 2.
Balanced stoichiometric equations and rate equations based on assumed molecular formula for polymers, lysates and biomass (adapted or developed based on Refs. [27,29,30,31,32]).
| Balanced Stoichiometric Reactions | ||
| Process/Reaction | Balanced Stoichiometric Reaction | Comments |
| Carbohydrate polymer hydrolysis | Assumed cellulose polymer of 360 monomeric units | |
| Protein polymer hydrolysis | Assumed protein polymer of 350 monomeric units | |
| Lipid hydrolysis | Assumed lipid consisting of 1 glycerol molecule attached with 3 molecules of 18C saturated fatty acid | |
| Formation of carbohydrate polymer hydrolysers | - | |
| Formation of carbohydrate lysate degraders | - | |
| Conversion of carbohydrate lysate to acetate | - | |
| Formation of protein polymer hydrolysers | - | |
| Formation of protein lysate degraders | - | |
| Conversion of protein lysate to acetate | - | |
| Formation of lipid hydrolysers | - | |
| Formation of lipid lysate degraders | - | |
| Conversion of lipid lysate to acetate | - | |
| Formation of acetoclastic methanogens | - | |
| Conversion of acetate to methane and carbon dioxide | Methane formation | |
| Conversion of to | Hydrogen (gas) formation from protons generated by oxidation of molecules such as and () | |
| Debris degradation | Debris degradation resulting in formation of carbohydrate lysate, protein lysate and lipid lysate | |
| Rate equations | ||
| Compound | Rate equation | |
| Carbohydrate polymer (CP) | ||
| Protein polymer (PP) | ||
| Lipid (LP) | ||
| Carbohydrate lysate (CL) | ||
| Protein lysate (PL) | ||
| Lipid lysate (LL) | ||
| Acetate (Ac) | ||
| Carbohydrate polymer hydrolyser (CP_Hy) | ||
| Protein polymer hydrolyser (PP_Hy) | ||
| Lipid hydrolyser (LP_Hy) | ||
| Carbohydrate lysate degrader (CL_De) | ||
| Protein lysate degrader (PL_De) | ||
| Lipid lysate degrader (LL_De) | ||
| Acetoclastic methanogens (AM_De) | ||
| Carbon dioxide () | ||
| Ammonia () | ||
| Hydrogen sulphide () | ||
| Water- “native form” () | ||
| Hydrogen () | ||
| Methane () | ||
| Debris (Deb) | ||
| Ash (Ash) | ||
| Lignin (Lignin) | ||
2.2.2. Physico-Chemical Processes
Two basic physico-chemical reactions are considered to occur in the system, namely, the aqueous phase and liquid–gas equilibrium processes. The aqueous phase and liquid–gas processes are interlinked, and the model below describes the conversion of the species in an ionic or non-ionic form and the transfer of the species from liquid to the gas phase.
Aqueous Processes
As shown in Table 3, the model incorporates eight acid-base reactions. These reactions are considered to occur simultaneously, along with the liquid–gas transfer.

Table 3.
Acid-base equilibrium constants and equations to determine concentration of particular species in the liquid phase [22,33].
The overall charge balance of the system is modelled in algebraic form, as described in ADM1 [22] and shown in Equation (1). The concentration of “inert” cations and anions are represented as and , respectively. Equation (1) is solved to determine the concentration of ions by substituting the concentration of respective species, as shown in Table 3. Based on the negative logarithm to base 10 of , the of the system can be determined.
Based on the molar concentration of ions and the equations described in Table 3, the molar concentration of other species (listed in Table 3) can be determined. However, it is important to consider that the formation of these species would result in either splitting or formation of water molecules. Therefore, the concentration of water molecules in the system will be altered when the equilibrium conditions are established.
The following sections describe the method developed and used to model (a) the initial composition of the components (substrate, inoculum, water) added to the system under equilibrium conditions and (b) the initial state composition of the mixture when the components are mixed in the reactor and the equilibrium conditions are re-established. Overall, the following sections describe the modelling method used to determine all the species that undergo aqueous phase physico-chemical reactions in the system.
- Modelling initial state of the components
Any component (substrate, inoculum or water) exists in an equilibrium state. This means that depending on the and molar concentration (of native form) of species in the component, a specific concentration of cations (e.g., ), anions (e.g., ) and neutral molecules (e.g., , ) will exist, such that the overall charge balance of the species sums to zero and the component remains electroneutral. As described above, the concentration of these ionic species can be modelled based on the molar concentration of ions as determined through Equation (1) and equations provided in Table 3. However, in order to model the concentration of molecules under established equilibrium conditions, the following hypothetical reactions are considered to occur within each individual component (Table 4).

Table 4.
Hypothetical reactions considered to occur within the component (substrate, inoculum or water), resulting in formation of native (neutral) form of the respective ionic species [24,33].
It is assumed that all the ionic species (except , , inert cations, and anions) and non-ionic species (such as ) are converted to their native form, as described through the hypothetical reactions in Table 4.
The hypothetical reactions mentioned in Table 4 result in the formation of and/or ions. As shown in Equation (2) and Equation (3), the “” or “” ions in component are described as (or ) (determined as per Equation (1)) minus the (or ) reacted in the hypothetical reactions, plus the (or ) generated through the hypothetical reactions (as shown in Table 4).
Based on Equation (2) and Equation (3), the total mass (grams) of molecules (native form) in the component is determined as shown in Equation (4).
The term in Equation (4) is the mass concentration (g/L) of molecules under equilibrium conditions, which is equal to 1000 minus the sum of the mass concentration (g/L) of all other constituents (carbohydrate polymer, protein polymer, lipids, carbohydrate lysate, protein lysate, lipid lysate, , , , , , , , , , , , , , biomass (hydrolysers, lysate degraders and acetoclastic methanogens), ash, and lignin) in the component . is the volume of component and is the molecular weight of .
The absolute difference between would indicate the excess of hypothetical ions, if , or the excess of hypothetical ions if in the given component when all molecules are converted into a native form. Thus, in order to maintain the electroneutrality of the component, the absolute difference between will always be equal to the absolute difference between the molar concentration of inert cationic and anionic species in the given component.
- Modelling initial equilibrium state (t0) of the mixture
For the ease of explanation and understanding, this section considers three components [substrate (), inoculum () and water ()] being instantaneously mixed in a reactor at time . In order to model the initial equilibrium state (), firstly, the model considers that, before mixing the three components, the constituents such as , , , , , and of each component are converted to the native form, as described in Table 4.
For further simplification, the modelling approach for this part is explained by using as an example. Based on the molar concentration of the native form of (, and ) in the components (, and ), the mass concentration (, and ) is calculated using the molecular weight () of the native form. Based on the mass concentration (g/L) of the native form, molecular weight, and the volume of particular component (, and ) in the mixture at , the molar concentration () of the native form in the mixture is formulated as per Equation (5).
Using equations similar to Equation (5), the molar concentration of native forms of other species (, and ) are determined. Together, based on the molar concentration of the native forms and using the equations in Table 3 and Equation (1), the molar concentration of other species such as , , , , , , , , , , , and , existing under equilibrium conditions at initial equilibrium state (), are determined.
Based on Equation (4), the mass (grams) of molecules in the mixture under equilibrium conditions at the initial equilibrium state () is formulated, as described in Equation (6).
In Equation (6), represents the moles of molecules (native form) at which react to form the different species (ionic/non-ionic) existing under the equilibrium state in the mixture as described in Equation (7), with the respective reactions shown in Table 5. represents the moles of ions generated in the mixture at due to the splitting of the molecules (native form) and other molecules such as , and (native form) as described in Equation (8), with respective reactions shown in Table 6. represents the excess moles of the ions in the mixture before the equilibrium is established at , as described in Equation (9). represents the moles of the ions in the mixture after the establishment of the equilibrium at , as described in Equation (10).

Table 5.
Reactions of molecules (in native form) to generate different species in the mixture [24,33].

Table 6.
Reactions resulting in generation of ions in the mixture due to splitting of molecules (native form) or other molecules (native form) [24,33].
In Equations (7)–(10), represents the volume of liquid at and is the sum of the volume of components added to the mixture (, and ).
Based on the mass (grams) of molecules in the mixture under equilibrium conditions (), the mass (grams) of molecules () (native form) at is formulated as shown in Equation (11). Importantly, is equal to only at the initial condition ().
In Equation (11), and are determined as shown in Equations (2) and (3), respectively.
It is important to consider that the approach for modelling the molecules (in native form) is based on mass (grams) basis, unlike the concentration basis used to determine the charge balance. This is carried out (a) to minimise the numerical errors and (b) because the molecules in the native form are considered to undergo reactions (described in Table 2) as like the other species (, , and ) in their respective native forms. This also implies that the rate equations (mentioned in Table 2) which describe the biochemical processes in the liquid phase are implemented on mass (grams) basis rather than mass concentration (g/L) basis. This further implies that the kinetic constants dependent upon the volume (such as saturation constant) are considered based on the total liquid volume of the system at .
- Modelling equilibrium state at any consecutive time point
For the purpose of simplification, this section describes the modelling approach used to determine the equilibrium state at time point (). Before the establishment of the equilibrium state at any time point, the integration of rate equations up to the desired time point () is performed with an increment of the desired time step, using the equations described in Table 2. Integrating the rate equations will provide the total mass (grams) of each molecule (in native form) for molecules such as , , and at time t. The mass (grams) of the molecule in the native form at time t will further undergo speciation and liquid–gas transfer (as described in Liquid–Gas Processes Section). At any time point, the mass (grams) of a particular molecule (in native form) in the liquid before the establishment of the equilibrium is formulated as shown in Equation (12) (for example, mass (grams) of ( at time point ).
In the above equation, represents the mass (grams) of (native form) in the liquid phase after the establishment of equilibrium and the occurrence of liquid–gas transfer at time , as described in Equation (13). Similarly, the mass (grams) of other molecules such as , , and is determined.
In Equation (13), is the mass (grams) of released in the gas phase after the establishment of the equilibrium at time and is determined in a similar manner as shown in the liquid–gas processes (Liquid–Gas Processes Section). Based on , the molar concentration of under equilibrium conditions is determined, as shown in Equation (14).
Similar to Equation (14), the molar concentration of and under equilibrium conditions is determined. Furthermore, the molar concentration (native form) of species that undergo ionisation but do not undergo liquid–gas transfer (e.g., ) is determined as shown in Equation (15), whereas the molar concentration of inert cations and inert anions is determined as shown in Equations (16) and (17). Based on all these molar concentrations, the molar concentration of other ionic and non-ionic species under equilibrium conditions is determined using equations shown in Table 3 and Equation (1).
The mass (grams) of molecules in the mixture under equilibrium conditions at is formulated as described in Equation (18).
In Equation (18), is determined as shown in Equation (11); represents the mass (grams) of released in the gas phase after the establishment of the equilibrium and occurrence of liquid–gas transfer at (Liquid–Gas Processes Section), whereas , , and are derived as shown in Equation (19)–(22).
Liquid–Gas Processes
The model considers seven species in the gas phase, namely, , , , , , and . Except , the other species are considered to undergo liquid–gas transfer. is included in the model because the start-up phase of the AD process includes the sparging of gas in the reactor to create the initial anaerobic condition. , , , , are considered to undergo liquid–gas transfer based on Henry’s law, whereas the liquid–gas transfer of is modelled based on Antoine’s equation. With an example of , based on Henry’s law, Equation (23) is formulated to determine the mass (grams) of transferred from the liquid to gas phase at . Similar equations are developed for other molecules undergoing liquid–gas transfer.
Equation (23) is further written in the form of , where represents .
In Equation (23), represents the sum of mass (grams) of , , , and released from the liquid phase into the gas phase at time point , as shown in Equation (24), represents the sum of the moles of , , , and released from the liquid phase into the gas phase at time point and the moles of , , , , and present in the headspace at time point , as shown in Equation (25), represents volume of liquid (litres) at time and , respectively, as shown in in Equation (26), and represents the total pressure of the system and is considered to be 1 atm.
Based on Equation (26), the headspace volume is determined as shown in Equation (27).
The mass (grams) of molecules released in the gas phase under equilibrium conditions at time is modelled using Antoine’s equation, as shown in Equation (28).
In Equation (28), , and are Antoine’s equation constants for water, is the temperature of the gas (°C) and is the total gas pressure (mm Hg).
Based on above set of equations, the total volume (litres) of in gas phase (headspace + gas bag) at time is determined as shown in Equation (29).
Similarly, the total volume of , , , and in the gas phase (headspace + gas bag) are determined. Based on these volumes, the total volume of gas (headspace + gas bag) is determined as shown in Equation (30).
As the model does not considers production of through biochemical processes, it is assumed that does not undergo liquid–gas transfer as per Henry’s law. Hence, the total volume of in the gas phase (headspace + gas bag) at time is determined as shown in Equation (31).
Based on the total volume (litres) of gas in the gas phase, the gas volume in the gas bag at is determined as shown in Equation (32).
Based on Equation (32), the volume (litres) of the specific gas in headspace and gas bag at is determined as shown (for example ) in Equation (33) and Equation (34). Further based on Equation (34), the cumulative volume (litres) of a particular gas is determined, as shown in Equation (35).
2.3. Model Implementation
The model is implemented in Microsoft Excel® for Microsoft 365 MSO (Version 2201 Build 16.0.14827.20198) 64-bit. Supplementary Material S2 shows the model implementation for the batch anaerobic digestion of the system with an inoculum to substrate ratio (ISR) of 1.00 [1]. The amount of materials (substrate, inoculum and water) added in the system with different ISRs used for the calibration of the model are provided in the Supplementary Material. To integrate the rate equations, the IVSOLVE function of the Excel add-in ExceLabTM 7.0 (ExcelWorks LCC, Boston, MA, USA) based on the Runge–Kutta method of order 5 is used. Iterative calculations are enabled with maximum iterations of 100 and a maximum change of 10−15, as several equations include circular references. In order to solve the charge balance equation and determine the molar concentration of ions, Newton–Raphson’s method is implemented with 14 iterations and an initial guess value (at ) of 10−9 moles/L, whereas the guess value at any consecutive time points is equal to the as determined through Newton–Raphson’s method at a previous time point. For the verification of the model, the mass balance, atomic balance, charge balance and compliance with Henry’s law is checked at all the time points in the system (Supplementary Material S2).
2.4. Model Calibration
The model was calibrated using the data generated from experimental investigations carried out in our previous study on batch AD of food waste (Gandhi et al. [1]) where batch experiments were performed in 5 l bioreactors (3.5 l working volume) placed in water baths maintained at 37 ± 1.5 °C [1]. Table S2 (Supplementary Material S3) shows the experimental setup (inoculum, substrate and deionised water added to the system) which includes six conditions (six different ISRs). Two reactors (n = 2) were setup for each experimental condition.
The analytical characterisation of the substrate and inoculum generated through experimental investigations (Table 7) was used as input data for the model. Arbitrary initial parameter values for substrate and inoculum are assumed in cases where certain analytical characteristics such as , , cations, anions, amino acids and biomass concentration are not determined through analytical methods. Considering a) limitations of implementation platform and the model and b) number of input parameters, the stoichiometric reactions, values of respective mass-based stoichiometric constants and values of biochemical constants ( are determined by trying several different values and changing them as required to achieve appropriate fits with the entire set (for all six ISRs) of experimental data. Overall, the calibration process was carried out based on a trial-and-error method and the fidelity of the model was assessed via inspection. The corelation coefficient was calculated to compare model output with the experimental observations as described by Li et al. [34].

Table 7.
Analytical characteristics of substrate and inoculum (mean ± standard deviation) obtained from experimental investigations: Gandhi et al. [1].
2.5. Model Limitations
This section includes the limitation of the present model and further scope to develop better quasi-mechanistic bio-kinetic models. The limitations mentioned below together explain the discrepancy between the experimental values and model output. The comparison between the model output and experimental observations is displayed in the Supplementary Material (Figures S1–S13; Supplementary Material S3).
- Model considers model substrates such as carbohydrates, proteins and lipids represented by specific molecular formulas. Although in actual digesters the molecular formula of the compounds can vary along with the chain length, this variation in the sub-type of macromolecule (for e.g., sub-types of carbohydrates such glucose, fructose, ribose, raffinose, etc.) and their respective degradation pathways could result in variable VFA profile which would in turn result in a variation in gas volume and composition.
- Model assumes that a fixed proportion of products are being produced as described through stoichiometric reactions. However, the product formation could vary depending upon other factors such as , which in turn influences the microbiology of the system and metabolic pathways adopted for degradation. Along with this, the products in turn could result in the alteration of parameters such as which would further have cascading effects.
- Model considers a fixed molecular formula to describe all the different bacterial species in the system. In a real scenario, the different bacterial species could have diverse molecular composition and the molecular composition of the same species could differ based on the growth stage, which in turn depends upon other factors such as or concentration of limiting compounds in the system or concentration of inhibitory or stimulatory substances [32]. For example, under conditions with high concentration of substrate, the production of specific enzymes could be upregulated, thus resulting in changes in the overall molecular composition of the bacterial species [35].
- Model considers fixed mass-based stoichiometric constants of the biomass formation (fixed stoichiometric reaction) along the entire duration of digestion, which in an actual scenario could vary based on the overall state of the system and other factors such as , the concentration of specific molecules, and metabolic pathways adopted to generate biomass under the given state of system [36].
- Model considers a single type of microbial biomass involved in the degradation of a specific compound and disregards the conversion of multiple types of molecules through the same type of microbial biomass. For example, the model does not consider that the carbohydrate polymer degraders could also result in degradation of proteins and vice versa.
- The biological reactions assumed in the model considers the production of only acetate and none of the other volatile fatty acids such as propionate, butyrate, valerate, etc., and organic acids such as lactate, pyruvate, succinate, etc. [37]. In actual digesters, the different types of VFAs are produced and the VFA profile depends upon the and overall microbiology of the system, which in turn is affected by the concentration of inhibitory molecules such as VFAs, ammonia and hydrogen sulphide [38,39].
- Model does not include the non-competitive type of inhibition but includes a process related to the toxicity effect of VFA (specifically acetate), which results in the death of microbial biomass (debris formation). Also, the toxicity effect on microbes is considered only due to acetate. In actual digesters, a range of VFAs would be produced at varying concentrations and the strength of toxicity or inhibitory effect of the VFAs would vary depending upon the type and concentration of specific VFAs [40,41]. In addition to this, there could be toxicity or inhibitory effects due to molecules such as ammonium ion/ammonia, hydrogen sulphide and other organic acids (lactate, pyruvate, etc.) and alcohols (ethanol, methanol, etc.), which are not included in the model [42,43,44,45,46].
- Model does not consider the effect of contact inhibition on the growth of biomass which may result in the excess growth of the microbial biomass, in turn diverting (or converting) a significant proportion of macromolecules as structural components of the biomass. This limits the conversion of macromolecules into products such as VFAs, and and the production of excess biomass [47].
- Model describes biomass growth through Monod kinetics, whereas the production of other products is assumed to be dependent upon the concentration of the limiting component and the concentration of biomass as of a second order reaction. However, in an actual scenario, the product formation could be growth linked or non-growth linked or combination of both, which could also depend upon the type of the reactant molecules [48,49].
- Model does not consider occurrence of hydrogenotrophic methanogenesis. Hydrogenotrophic methanogenesis is not included in the model, as the rate of hydrogenotrophic methanogenesis and biomass (hydrogenotrophic methanogens) growth is dependent upon on the concentration of hydrogen in the liquid phase which would change due to the liquid–gas transfer of hydrogen [22]. Hence, the rate of hydrogenotrophic methanogenesis (and biomass formation) which depends upon concentration of hydrogen would require accounting the hydrogen losses from the liquid phase at any given time point. Therefore, rate equations at each time point will depend upon the hydrogen concentration which remains in the liquid phase after establishment of the physico-chemical equilibrium and liquid–gas transfer of hydrogen. Implementing this in the present framework would require the determination of hydrogen concentration in the liquid phase at each time step and conducting a separate integration of the rate equations at each time point. Given this complexity, although easy to implement, the low computational power of the model implementation platform (Excel) makes it difficult to find appropriate parameter values and hence limits the implementation of the hydrogenotrophic methanogenesis reactions. Due to similar reasons, the toxicity effects of other molecules such as ammonia and hydrogen sulphide which can undergo gas–liquid liquid transfer on a microbial biomass is not considered.
- Model does not include homoacetogens and syntropic acetate oxidising bacterial species [50]. Although, several species of homoacetogens and syntropic acetate oxidising bacterial species have been identified in digesters, for the purpose of simplicity and due to limitations of the model implementation platform the model does not include these sets of bacterial groups and associated reactions.
- Model does not consider the occurrence of enzymatic reactions due to extracellular enzymes present in the liquid phase and the rate of degradation of any molecule (except debris) is dependent upon the concentration of microbes. In actual digesters, the enzymes released in the liquid phase (either due to inherent extracellular nature of particular enzyme (for e.g., proteases) or due to lysis of microbial cells) could still be active and conduct specific reactions even after the death of the microbial cell. This overall may lead to the underestimation of the rate of degradation of specific molecules in the system which are catalysed by such enzymes released in the liquid phase.
- Model assumes that the debris degradation occurs as per first order kinetics and results in the production of carbohydrate, proteins and lipids lysate (monomers). However, in an actual scenario, it could be mediated through the presence of certain enzymes which would result in the formation of rather complex products (for e.g., peptidoglycan, structural proteins, lipids, lipoproteins, etc.) whose individual degradation rates may vary depending upon the composition and other characteristics of the system such as , which in turn regulate the activity of these catalysing enzymes. Hence, first order kinetics may not be suitable to describe debris degradation [23,51].
- Model does not consider the dependence of microbial growth on the concentration of trace elements in the system, as well as the precipitation reactions that could occur in the system which would result in a lower concentration of the available forms of trace elements or nutrients such as . The precipitation reactions would further affect the concentration of ionizable components in the system and hence indirectly affect the of the system [52,53,54].
- The equation used to determine the concentration of hydrogen ions (and the ) in the system does not involve other major species such as amino acids (although included as one of the components of in biochemical reactions), organic acids such as lactate, other VFAs (except acetate) and certain anionic species such as phosphates present in the system [55,56,57]. As the values of amino acids vary depending upon the type of amino acid, and the molar concentration of ions would vary depending upon the VFA profile, the model losses accuracy for prediction [58]. In addition to this, other cationic (, , , ) and anionic (, , , ) species and their respective precipitation reactions could significantly affect the of the system [22].
- Model considers only single form of sulphur containing compound (). Other sulphur containing molecules such as sulphates and organisms and reactions resulting in the formation or reduction in sulphate are not included in the model [59].
- The modelling approach used in the present scenario models liquid–gas transfer in accordance to obey the Henry’s law instantaneously at any given time point. However, in an actual scenario, the Henry’s law may not hold true for such a system where a continuous transfer of gases from the liquid to gas phase occurs. Also, the model does not include the resistance factor for liquid–gas transfer and dependence of rate of transfer on the surface area of the liquid phase, as described using Whitman’s two-film theory [60].
- The model assumes that the liquid–gas transfer in the system complying with the Henry’s law is unidirectional. However, in actual systems, this could be bi-directional. This may lead to errors when the model is implemented for semi-continuously fed digesters where the gas collection bags are changed at regular intervals.
- The values of Henry’s law constants adopted in the present model are specifically determined for the systems where the aqueous phase is composed of water molecules. However, given the complex nature and composition of the aqueous phase, these values could differ for systems such as anaerobic digesters, which could in turn affect the liquid–gas transfer [61].
- Model does not consider condensation reaction for water molecules and assumes the gas phase is maintained at the same temperature as the liquid phase. This is carried out to reduce the complexity as the Antoine’s equation coefficient varies based on the temperature [62]. However, in actual digesters, the gas in the headspace of the digester and gas collection bag could be at different temperatures compared to the liquid phase.
- The model fails to express the continuous dynamic state of the system. This is because the acid-base equilibrium reactions and liquid–gas transfer reactions which result in a change in volume of the liquid phase and headspace of the system are modelled and implemented using a set of implicit algebraic equations.
- For the ease of implementation and understanding, the model is implemented and executed in Excel. Implementation in Excel limits the direct regression of a model with experimental data due to the complex structure of the model, which involves circular references.
3. Results and Discussion
3.1. Model Verification and Calibration
The developed model was implemented in Microsoft Excel® for Microsoft 365 MSO (Version 2201 Build 16.0.14827.20198) 64-bit. In comparison to previous models such as ADM1 which have been majorly implemented in MATLAB [53,54], the present work implements a highly complex model on one of the most basic and widely used platforms, making it accessible to a broader range of users, including those with limited programming knowledge. However, this implies that the model should be verified for any inaccuracies or errors. Unlike the previous models, which fail to prove/describe the mass balance, atomic balance, compliance with electroneutrality principle (charge balance) and Henry’s law, this work verified the model, providing proofs for compliance (Supplementary Material S2).
To verify the mass balance, the total mass of the system at any time point was compared with the total mass at initial time . The total mass of system at time and any time were calculated as described by Equation (36) and Equation (37), respectively. Compliant with law of mass conservation, the total mass of the systems at any time point was identical to that at the initial time , indicating a relative mass balance error less than the machine precision value (Supplementary Material S2; cells ES78:ES108). Similarly based on the Carbon, Hydrogen, Nitrogen, Sulphur and Oxygen content of individual molecules, the atomic balance was determined, and the maximum relative error was found to be ±0.02%, which was due to errors introduced as a result of numerical integration (Supplementary Material S2; cells EZ78:FD108).
In Equation (36), , , and represent the volume (L) of headspace, substrate, inoculum, and water, respectively, at . and (=1000 g/L; as per Section 2.1) represent the density of nitrogen at 37 ℃ and bulk density of the system, respectively.
The terms in Equation (37) represent entities as described in Section 2.2 and Supplementary Material S1. represents gas constant and is the reaction temperature (310.15 K).
The charge balance, indicating compliance with the electroneutrality principle [22], was determined for each time point based on the concentration of charged molecules in the system using Equation (1). Being compliant with the electroneutrality principle, the difference between total positive and negative charge in the system was found to be 0 (Supplementary Material S2; cells EY78:EY108).
Lastly, the compliance with Henry’s law [61] was determined by comparing the calculated Henry’s law coefficient for individual gases [for e.g., as per Equation (38) for ], with the actual Henry’s law constant (constant value for a specific gas at specific temperature and specific medium) for , , , and . Compliant with Henry’s law, the Henry’s law constant (at 37 ℃) at any given time was 0.001155 mol/L/atm for , 0.02469 mol/L/atm for , 0.07511 mol/L/atm for , 35.1086 mol/L/atm for and 0.0007402 mol/L/atm for (Supplementary Material S2; ET78:EX108) [61].
The terms in Equation (38) represent entities as described in Section 2.2 and the Supplementary Material S1. represents the sum of the moles of , , , and released from the liquid phase into the gas phase at time point and the moles of , , , , and present in the headspace at time point , as shown in Equation (25).
As described in Section 2.4, the calibration process was carried out based on a trial-and-error method and the fidelity of the model was assessed via inspection. Table 8 and Table 9 show values of the bio-kinetic parameters and mass-based stoichiometric constants (MBSC), respectively. Given a completely different modelling approach and basis (mass basis), the bio-kinetic parameter values in the present study cannot be directly compared with values from other models such as ADM1 (COD basis) [22]. However, very interestingly, the model was calibrated based on a single set of bio-kinetic parameters (Table 8) which describes both methanogenic and acidogenic systems well.

Table 8.
Calibration values of biokinetic parameters.

Table 9.
Values of mass-based stoichiometric constants (MBSC).
3.2. Comparison between Model Output and Experimental Observations
Table 10 provides the correlation coefficients for various parameters, indicating a comparison between the model output and experimental observations from 12 reactors (six conditions: six different inoculum to substrate ratios [1]). A very strong correlation (correlation coefficient > 0.75) was observed for most of the parameters. A relatively lower correlation coefficient of 0.65 and 0.50 was observed for the concentration of VFA (g/L) and ammonia-N (g/L), respectively.

Table 10.
Correlation coefficient for various parameters indicating comparison between model output and experimental observations.
As described in model limitations (Section 2.5), a lower correlation coefficient for VFA was mainly because the model only considers the production of acetate (as VFA) and none of the other VFAs or other non-volatile organic acids. As previously described by Gandhi et al. [1], the experimental data clearly indicated the production of VFAs other than acetic acid as well as production of lactic acid which is not considered in the present framework, whereas in the case of ammonia-N, a lower correlation coefficient could be due to the combined effect of multiple limitations (Section 2.5) of the model. For example, the model considers ammonia-N as the only nitrogen source for the formation of biomass [hydrolysers, lysate degraders (except protein polymer hydrolyser and protein lysate degraders) and acetoclastic methanogens], thus diverting a significant fraction of ammonia-N for biomass production and resulting in relatively lower predicted/modelled ammonia-N concentrations than that present in the actual digester. The model also considers a single type of microbial biomass involved in the degradation of a specific compound, disregarding the conversion/metabolism of multiple types of molecules (for e.g., carbohydrates, proteins, and lipids) by the same type of microbial biomass, as could happen in actual digesters. This implies a relatively higher amount of ammonia-N being utilised for the formation of a “function specific” microbial biomass, thus resulting in a lower predicted/model ammonia-N concentration in the system. Additionally, the model does not consider the effect of contact inhibition on the growth of microbial biomass, which may result in excess growth of the biomass, in turn diverting a significant fraction of ammonia-N. Furthermore, the lack of experimental data for amino acids (protein lysate) in the system, which upon degradation can produce ammonia, and uncertainty in the determination of proteins (experimental observations) due to interferences and limitations of the analytical technique [1], may have contributed to inaccurate analytical determinations, ultimately resulting in a lower correlation for ammonia-N.
Overall, to the best of the authors knowledge this work for the first times shows high correlation for multiple parameters, using a single set of bio-kinetic and stoichiometric parameters and describing (a) non-acidified methanogenic systems, (b) reversibly acidified systems, and (c) irreversibly acidified systems. This means that the developed model can describe both methanogenesis and acidogenesis well, using the same set of bio-kinetic parameters for batch anaerobic digesters.
4. Conclusions
The present work illustrates a methodology for the development of a mass-based atomistic mathematical model for the batch AD process. Upon calibrating the model using experimental data, the relative mass balance and charge balance error at any given time were found to be less than machine precision value, whereas the maximum relative atom balance error was found to be ±0.02% which was due to errors introduced as a result of numerical integration. Along with this, the liquid–gas transfer in the model was observed to comply with the Henry’s law. Together, the mass balance, atomic balance, charge balance and compliance with Henry’s law provide strong evidence for model verification. In addition to this, the calibration of the model with experimental data showed a high fidelity of the model as assessed via inspection. Thus, developing such models which account for and consider the degradation of multiple components in the system, as well as simulate the change in volume as a result of liquid–gas mass transfer, along with prediction of and alkalinity based on molar concentrations of different ionic species in the system, could help in hypothesis testing and determine reliable estimates of the bio-kinetic parameters when regressed with robustly acquired analytical data. Using these parameters which could be determined through relatively simple batch studies simulating the process under continuous or semi-continuous operations could be possible. However, further work is required to develop the MAM framework for a continuous or semi-continuous operational mode. To the authors’ knowledge, this study attempted for the first time to develop such a framework; however, further work to overcome the limitations of the present model is required. In general, the overall structure of the model could be adapted to understand other similar physico-chemical processes.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/fermentation10060299/s1, Supplementary Material S1: Table S1. Abbreviations and symbols used in the model framework; Supplementary Material S2: Excel file with model implementation for batch anaerobic digestion; Supplementary Material S3: Table S2. Batch experiment setup: The amount of substrate, inoculum, deionised water added to achieve respective substrate to inoculum ratios; Supplementary Material S3: Figures S1–S13. Comparison between model output and experimental observations.
Author Contributions
Conceptualisation, B.P.G., A.J.L.-B., K.T.S. and A.D.M.; methodology, B.P.G., A.J.L.-B., K.T.S. and A.D.M.; software, B.P.G. and A.D.M.; validation, A.J.L.-B.; formal analysis, B.P.G., A.J.L.-B., K.T.S. and A.D.M.; investigation, B.P.G., A.J.L.-B., K.T.S. and A.D.M.; resources, K.T.S. and A.D.M.; data curation, A.J.L.-B. and B.P.G.; writing—original draft preparation, B.P.G.; writing—review and editing, A.J.L.-B., L.I.E., K.T.S. and A.D.M.; visualisation, B.P.G., A.J.L.-B., L.I.E., K.T.S. and A.D.M.; supervision, A.J.L.-B., K.T.S. and A.D.M.; funding acquisition, L.I.E., K.T.S. and A.D.M. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by Global Challenge Research Fund (GCRF) funded RECIRCULATE project (Grant Ref.: ES/P010857/1) and Lancaster University, UK.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data are provided in Supplementary Materials.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Gandhi, B.P.; Otite, S.V.; Fofie, E.A.; Lag-Brotons, A.J.; Ezemonye, L.I.; Semple, K.T.; Martin, A.D. Kinetic Investigations into the Effect of Inoculum to Substrate Ratio on Batch Anaerobic Digestion of Simulated Food Waste. Renew. Energy 2022, 195, 311–321. [Google Scholar] [CrossRef]
- Xing, T.; Yun, S.; Li, B.; Wang, K.; Chen, J.; Jia, B.; Ke, T.; An, J. Coconut-shell-derived bio-based carbon enhanced microbial electrolysis cells for upgrading anaerobic co-digestion of cow manure and aloe peel waste. Bioresour. Technol. 2021, 338, 125520. [Google Scholar] [CrossRef]
- Otite, S.V.; Gandhi, B.P.; Agyabeng Fofie, E.; Lag-Brotons, A.J.; Ezemonye, L.I.; Martin, A.D.; Pickup, R.W.; Semple, K.T. Effect of the Inoculum-to-Substrate Ratio on Putative Pathogens and Microbial Kinetics during the Batch Anaerobic Digestion of Simulated Food Waste. Microorganisms 2024, 12, 603. [Google Scholar] [CrossRef]
- Huang, X.; Yun, S.; Zhu, J.; Du, T.; Zhang, C.; Li, X. Mesophilic anaerobic co-digestion of aloe peel waste with dairy manure in the batch digester: Focusing on mixing ratios and digestate stability. Bioresour. Technol. 2016, 218, 62–68. [Google Scholar] [CrossRef]
- Sharma, R.; Carg, P.; Kumar, P.; Bhatia, S.K.; Kulshrestha, S. Microbial fermentation and its role in quality improvement of fermented foods. Fermentation 2020, 6, 106. [Google Scholar] [CrossRef]
- Yun, S.; Xing, T.; Han, F.; Shi, J.; Wang, Z.; Fan, Q.; Xu, H. Enhanced direct interspecies electron transfer with transition metal oxide accelerants in anaerobic digestion. Bioresour. Technol. 2021, 320, 124294. [Google Scholar] [CrossRef]
- D’Silva, T.C.; Isha, A.; Chandra, R.; Vijay, V.K.; Subbarao, P.M.V.; Kumar, R.; Chaudhary, V.P.; Singh, H.; Khan, A.A.; Tyagi, V.K.; et al. Enhancing methane production in anaerobic digestion through hydrogen assisted pathways—A state-of-the-art review. Renew. Sustain. Energy Rev. 2021, 151, 111536. [Google Scholar] [CrossRef]
- Li, X.; Wang, Z.; He, Y.; Wang, Y.; Wang, S.; Zheng, Z.; Wang, S.; Xu, J.; Cai, Y.; Ying, H. A Comprehensive Review of the Strategies to Improve Anaerobic Digestion: Their Mechanism and Digestion Performance. Methane 2024, 3, 227–256. [Google Scholar] [CrossRef]
- Yun, S.; Xing, T.; Wang, Y.; Chen, R.; Han, F.; Zhang, C.; Zou, M. Mineral residue accelerant-enhanced anaerobic digestion of cow manure: An evaluation system of comprehensive performance. Sci. Total Environ. 2023, 858, 159840. [Google Scholar] [CrossRef]
- Abbas, Y.; Yun, S.; Wang, Z.; Zhang, Y.; Zhang, X.; Wang, K. Recent advances in bio-based carbon materials for anaerobic digestion: A review. Renew. Sustain. Energy Rev. 2021, 135, 110378. [Google Scholar] [CrossRef]
- Tsapekos, P.; Lovato, G.; Rodrigues, J.A.D.; Alvarado-Morales, M. Amendments to model frameworks to optimize the anaerobic digestion and support the green transition. Renew. Sustain. Energy Rev. 2024, 197, 114413. [Google Scholar] [CrossRef]
- Tchobanoglous, G.; Burton, F.L.; Stensel, H.D. Wastewater Engineering Treatment and Reuse; Metcalf & Eddy, Inc., McGraw-Hill: New York, NY, USA, 2003; p. 1771. ISBN 0-07-041878-0. [Google Scholar]
- Malhotra, M.; Aboudi, K.; Pisharody, L.; Singh, A.; Banu, J.R.; Bhatia, S.K.; Varjani, S.; Kumar, S.; González-Fernández, C.; Kumar, S.; et al. Biorefinery of Anaerobic Digestate in a Circular Bioeconomy: Opportunities, Challenges and Perspectives. Renew. Sustain. Energy Rev. 2022, 166, 112642. [Google Scholar] [CrossRef]
- Zhang, C.; Su, H.; Baeyens, J.; Tan, T. Reviewing the Anaerobic Digestion of Food Waste for Biogas Production. Renew. Sustain. Energy Rev. 2014, 38, 383–392. [Google Scholar] [CrossRef]
- Chiu, S.L.H.; Lo, I.M.C. Reviewing the Anaerobic Digestion and Co-Digestion Process of Food Waste from the Perspectives on Biogas Production Performance and Environmental Impacts. Environ. Sci. Pollut. Res. 2016, 23, 24435–24450. [Google Scholar] [CrossRef]
- Bhatt, A.H.; Tao, L. Economic Perspectives of Biogas Production via Anaerobic Digestion. Bioengineering 2020, 7, 74. [Google Scholar] [CrossRef]
- Kunatsa, T.; Xia, X. A Review on Anaerobic Digestion with Focus on the Role of Biomass Co-Digestion, Modelling and Optimisation on Biogas Production and Enhancement. Bioresour. Technol. 2022, 344, 126311. [Google Scholar] [CrossRef]
- Xiao, H.; Zhang, D.; Tang, Z.; Li, K.; Guo, H.; Niu, X.; Yi, L. Comparative Environmental and Economic Life Cycle Assessment of Dry and Wet Anaerobic Digestion for Treating Food Waste and Biogas Digestate. J. Clean. Prod. 2022, 338, 130674. [Google Scholar] [CrossRef]
- Vasco-Correa, J.; Khanal, S.; Manandhar, A.; Shah, A. Anaerobic Digestion for Bioenergy Production: Global Status, Environmental and Techno-Economic Implications, and Government Policies. Bioresour. Technol. 2018, 247, 1015–1026. [Google Scholar] [CrossRef]
- Batstone, D.J.; Virdis, B. The Role of Anaerobic Digestion in the Emerging Energy Economy. Curr. Opin. Biotechnol. 2014, 27, 142–149. [Google Scholar] [CrossRef]
- Lyberatos, G.; Skiadas, I. Modelling of Anaerobic Digestion—A Review. Glob. Nest Int. J. 1999, 1, 63–76. [Google Scholar]
- Batstone, D.J.; Keller, J.; Angelidaki, I.; Kalyuzhnyi, S.V.; Pavlostathis, S.G.; Rozzi, A.; Sanders, W.T.; Siegrist, H.; Vavilin, V.A. The IWA Anaerobic Digestion Model No 1 (ADM1). Water Sci. Technol. 2002, 45, 65–73. [Google Scholar] [CrossRef]
- Emebu, S.; Pecha, J.; Janáčová, D. Review on Anaerobic Digestion Models: Model Classification & Elaboration of Process Phenomena. Renew. Sustain. Energy Rev. 2022, 160, 112288. [Google Scholar] [CrossRef]
- Sawyer, C.N.; McCarty, P.L.; Parkin, G.F. Chemistry for Environmental Engineering; McGraw-Hill: New York, NY, USA, 1994. [Google Scholar]
- Eaton, A.D.; APHA; AWWA; WEF. Standard Methods for the Examination of Water and Wastewater, 21st ed.; American Public Works Association: Washington, DC, USA, 2005; ISBN 978-0875530475. [Google Scholar] [CrossRef]
- Roe, M.; Pinchen, H.; Church, S.; Finglas, P. McCance and Widdowson’s the Composition of Foods Seventh Summary Edition and Updated Composition of Foods Integrated Dataset. Nutr. Bull. 2015, 40, 36–39. [Google Scholar] [CrossRef]
- Yao, Y. Use of Carbohydrate, Protein and Fat to Characterise Wastewater in Terms of Its Major Elemental Constituents and Energy. Master’s Thesis, University of Manchester, Manchester, UK, 2014. Available online: https://pure.manchester.ac.uk/ws/portalfiles/portal/54552077/FULL_TEXT.PDF (accessed on 2 February 2021).
- Monod, J. The Growth of Bacterial Cultures. Annu. Rev. Microbiol. 1949, 3, 371–394. [Google Scholar] [CrossRef]
- Battley, E.H. On the Enthalpy of Formation of Escherichia Coli K-12 Cells. Biotechnol. Bioeng. 1992, 39, 5–12. [Google Scholar] [CrossRef]
- Nelson, D.L.; Cox, M.M. Lehninger Principles of Biochemistry, 4th ed.; W. H. Freeman and Company: New York, NY, USA, 2005. [Google Scholar]
- Torabizadeh, H. All Proteins Have a Basic Molecular Formula. World Acad. Sci. Eng. Technol. 2011, 78, 961–965. [Google Scholar]
- Popovic, M. Thermodynamic Properties of Microorganisms: Determination and Analysis of Enthalpy, Entropy, and Gibbs Free Energy of Biomass, Cells and Colonies of 32 Microorganism Species. Heliyon 2019, 5, E01950. [Google Scholar] [CrossRef]
- Lide, D.R. CRC Handbook of Chemistry and Physics, 88th ed.; Taylor & Francis Group: Boca Raton, FL, USA, 2007. [Google Scholar]
- Li, X.; Yang, Z.; Liu, G.; Ma, Z.; Wang, W. Modified anaerobic digestion model No. 1 (ADM 1) for modeling anaerobic digestion process at different ammonium concentrations. Water Environ. Res. 2019, 91, 700–714. [Google Scholar] [CrossRef]
- Temudo, M.F.; Mato, T.; Kleerebezem, R.; Van Loosdrecht, M.C.M. Xylose Anaerobic Conversion by Open-Mixed Cultures. Appl. Microbiol. Biotechnol. 2009, 82, 231–239. [Google Scholar] [CrossRef]
- Gomez-Pastor, R.; Perez-Torrado, R.; Garre, E.; Matall, E. Recent Advances in Yeast Biomass Production. In Biomass-Detection, Production and Usage; InTech: Rijeka, Croatia, 2011; pp. 202–222. [Google Scholar] [CrossRef]
- Zhou, M.; Yan, B.; Wong, J.W.C.; Zhang, Y. Enhanced Volatile Fatty Acids Production from Anaerobic Fermentation of Food Waste: A Mini-Review Focusing on Acidogenic Metabolic Pathways. Bioresour. Technol. 2018, 248, 68–78. [Google Scholar] [CrossRef]
- Krakat, N.; Anjum, R.; Dietz, D.; Demirel, B. Methods of Ammonia Removal in Anaerobic Digestion: A Review. Water Sci. Technol. 2017, 76, 1925–1938. [Google Scholar] [CrossRef]
- Meegoda, J.N.; Li, B.; Patel, K.; Wang, L.B. A Review of the Processes, Parameters, and Optimization of Anaerobic Digestion. Int. J. Environ. Res. Public Health 2018, 15, 2224. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, Y.; Wang, J.; Meng, L. Effects of Volatile Fatty Acid Concentrations on Methane Yield and Methanogenic Bacteria. Biomass Bioenergy 2009, 33, 848–853. [Google Scholar] [CrossRef]
- Candry, P.; Radić, L.; Favere, J.; Carvajal-Arroyo, J.M.; Rabaey, K.; Ganigué, R. Mildly Acidic pH Selects for Chain Elongation to Caproic Acid over Alternative Pathways during Lactic Acid Fermentation. Water Res. 2020, 186, 116396. [Google Scholar] [CrossRef]
- Hajarnis, S.R.; Ranade, D.R. Inhibition of Methanogens by N- and Iso-Volatile Fatty Acids. World J. Microbiol. Biotechnol. 1994, 10, 350–351. [Google Scholar] [CrossRef]
- Visser, A.; Nozhevnikova, A.N.; Lettinga, G. Sulphide Inhibition of Methanogenic Activity at Various PH Levels at 55 °C. J. Chem. Technol. Biotechnol. 1993, 57, 9–13. [Google Scholar] [CrossRef]
- Koster, I.W.; Rinzema, A.; de Vegt, A.L.; Lettinga, G. Sulfide Inhibition of the Methanogenic Activity of Granular Sludge at Various PH-Levels. Water Res. 1986, 20, 1561–1567. [Google Scholar] [CrossRef]
- Aguilar, A.; Casas, C.; Lema, J.M. Degradation of Volatile Fatty Acids by Differently Enriched Methanogenic Cultures: Kinetics and Inhibition. Water Res. 1995, 29, 505–509. [Google Scholar] [CrossRef]
- Astals, S.; Peces, M.; Batstone, D.J.; Jensen, P.D.; Tait, S. Characterising and Modelling Free Ammonia and Ammonium Inhibition in Anaerobic Systems. Water Res. 2018, 143, 127–135. [Google Scholar] [CrossRef]
- Ikryannikova, L.N.; Kurbatov, L.K.; Gorokhovets, N.V.; Zamyatnin, A.A. Contact-Dependent Growth Inhibition in Bacteria: Do Not Get Too Close! Int. J. Mol. Sci. 2020, 21, 7990. [Google Scholar] [CrossRef]
- Bouguettoucha, A.; Balannec, B.; Amrane, A. Unstructured Models for Lactic Acid Fermentation—A Review. Food Technol. Biotechnol. 2011, 49, 3. [Google Scholar]
- Kovárová-Kovar, K.; Egli, T. Growth Kinetics of Suspended Microbial Cells: From Single-Substrate-Controlled Growth to Mixed-Substrate Kinetics. Microbiol. Mol. Biol. Rev. 1998, 62, 646–666. [Google Scholar] [CrossRef]
- Pan, X.; Zhao, L.; Li, C.; Angelidaki, I.; Lv, N.; Ning, J.; Cai, G.; Zhu, G. Deep Insights into the Network of Acetate Metabolism in Anaerobic Digestion: Focusing on Syntrophic Acetate Oxidation and Homoacetogenesis. Water Res. 2021, 190, 116774. [Google Scholar] [CrossRef]
- Aldin, S.; Nakhla, G.; Ray, M.B. Modeling the Influence of Particulate Protein Size on Hydrolysis in Anaerobic Digestion. Ind. Eng. Chem. Res. 2011, 50, 10843–10849. [Google Scholar] [CrossRef]
- Maharaj, B.C.; Mattei, M.R.; Frunzo, L.; van Hullebusch, E.D.; Esposito, G. ADM1 Based Mathematical Model of Trace Element Complexation in Anaerobic Digestion Processes. Bioresour. Technol. 2019, 276, 253–259. [Google Scholar] [CrossRef]
- Maharaj, B.C.; Mattei, M.R.; Frunzo, L.; van Hullebusch, E.D.; Esposito, G. ADM1 Based Mathematical Model of Trace Element Precipitation/Dissolution in Anaerobic Digestion Processes. Bioresour. Technol. 2018, 267, 666–676. [Google Scholar] [CrossRef]
- Maharaj, B.C.; Mattei, M.R.; Frunzo, L.; van Hullebusch, E.D.; Esposito, G. A General Framework to Model the Fate of Trace Elements in Anaerobic Digestion Environments. Sci. Rep. 2021, 11, 7476. [Google Scholar] [CrossRef]
- Liu, H.; Chen, Y.; Ye, J.; Xu, H.; Zhu, Z.; Xu, T. Effects of Different Amino Acids and Their Configurations on Methane Yield and Biotransformation of Intermediate Metabolites during Anaerobic Digestion. J. Environ. Manag. 2021, 296, 113152. [Google Scholar] [CrossRef]
- Flores-Alsina, X.; Solon, K.; Kazadi Mbamba, C.; Tait, S.; Gernaey, K.V.; Jeppsson, U.; Batstone, D.J. Modelling Phosphorus (P), Sulfur (S) and Iron (Fe) Interactions for Dynamic Simulations of Anaerobic Digestion Processes. Water Res. 2016, 95, 370–382. [Google Scholar] [CrossRef]
- Fermoso, F.G.; van Hullebusch, E.; Collins, G.; Roussel, J.; Mucha, A.P.; Esposito, G. Trace Elements in Anaerobic Biotechnologies; IWA Publishing: London, UK, 2019; ISBN 9781789060225. [Google Scholar] [CrossRef]
- Ramsay, I.R. Modelling and Control of High-Rate Anaerobic Wastewater Treatment Systems. Ph.D. Thesis, University of Queensland, Brisbane, Australia, 1997. [Google Scholar]
- Kalyuzhnyi, S.V.; Fedorovich, V.V. Mathematical Modelling of Competition between Sulphate Reduction and Methanogenesis in Anaerobic Reactors. Bioresour. Technol. 1998, 65, 227–242. [Google Scholar] [CrossRef]
- Whitman, W.G. The Two Film Theory of Gas Absorption. Int. J. Heat Mass Transf. 1962, 5, 429–433. [Google Scholar] [CrossRef]
- Sander, R. Compilation of Henry’s Law Constants (Version 4.0) for Water as Solvent. Atmos. Chem. Phys. 2015, 15, 4399–4981. [Google Scholar] [CrossRef]
- Rodgers, R.C.; Hill, G.E. Equations for Vapour Pressure versus Temperature: Derivation and Use of the Antoine Equation on a Hand-Held Programmable Calculator. Br. J. Anaesth. 1978, 50, 415. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).