Modeling the Succinic Acid Bioprocess: A Review
Abstract
1. Introduction
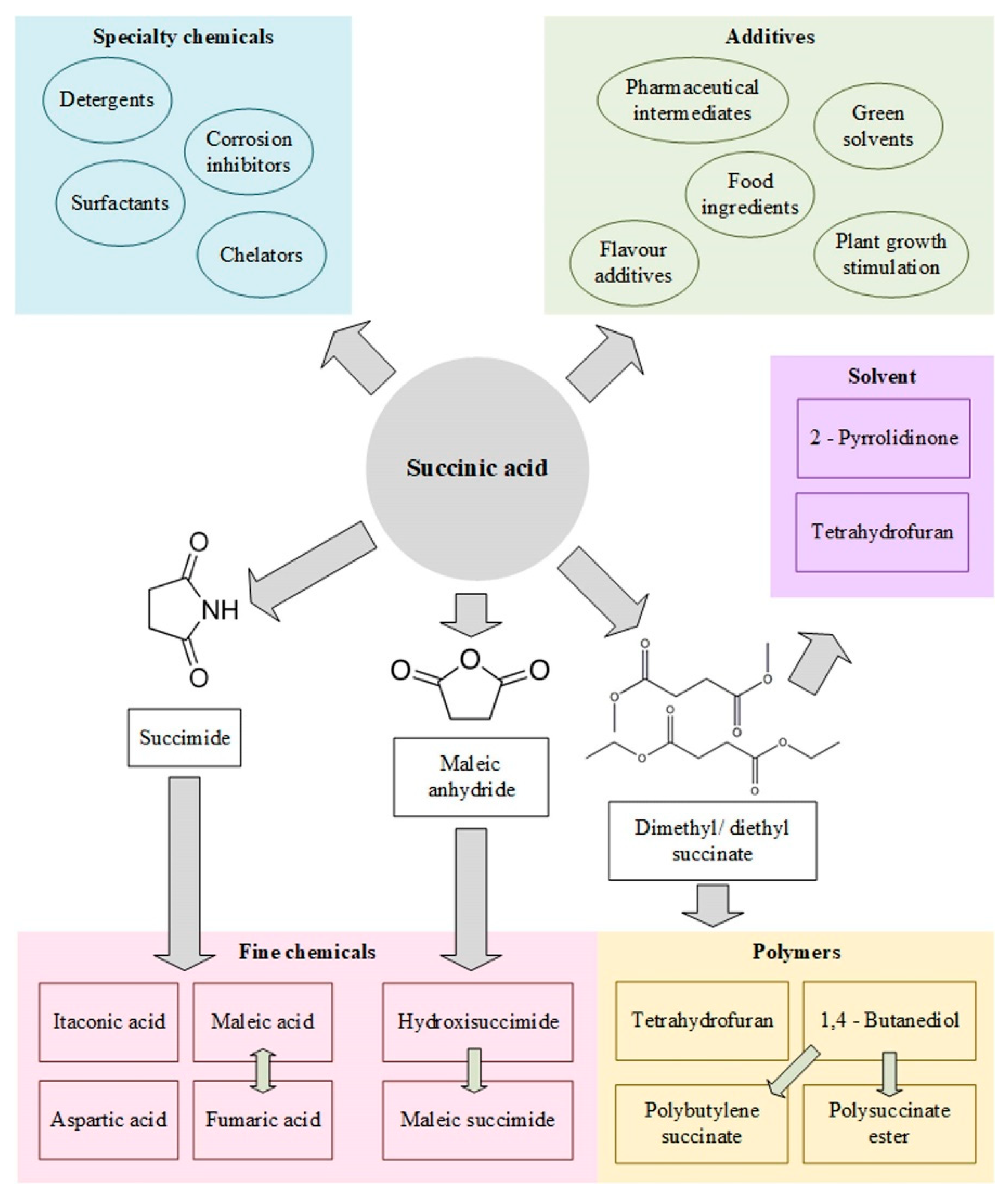
1.1. Succinic Acid Bioproduction
1.2. The Importance of Kinetic Modeling
- Reaction kinetics in the system. The description of a bacterial reaction network is very complex, although the evolution of the concentrations can be described through a kinetic model [62].
2. Kinetic Models
2.1. Non-Segregated, Unstructured Models
2.1.1. Biomass Growth Models
2.1.2. Substrate Consumption Models
2.1.3. Product Generation Models
3. Mass Transfer Phenomena
3.1. Mass Transport in the Liquid Phase
3.1.1. CO2—Carbonate Equilibrium
3.1.2. Gas–Liquid Equilibrium
3.1.3. Gas–Liquid Mass Transfer
3.2. Mass Transport and Biofilm
4. Coupling Dynamic Phenomena to Explain Succinic Acid Production
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| AA | Acetic Acid |
| ADP | Adenosine DiPhosphate |
| ATP | Adenosine TriPhosphate |
| CTR | Carbon dioxide Transfer Rate |
| C4 | 4 Carbon containing compound |
| C5 | 5 Carbon containing compound |
| C6 | 6 Carbon containing compound |
| ET | Ethanol |
| FAD+ | Flavin Adenine Dinocluotide |
| FA | Formic Acid |
| Fructose 1, 6–P | Fructose 1, 6–Phosphate |
| Fructose 6–P | Fructose 6–Phosphate |
| GDP | Gross Domestic Product |
| Glucose 6–P | Glucose 6 Phosphate |
| Glyceraldehyde 3–P | Glyceraldehyde 3–Phosphate |
| IB | Integrated Biorefineries |
| LA | Lactic Acid |
| NADH | Nicotinamide Adenine Dinucleotide reduced |
| NAD+ | Nicotinamide Adenine Dinucleotide |
| PA | Pyruvic Acid |
| PEP | Phosphoenol Pyruvate |
| PEPC | Phosphoenol Pyruvate Carboxylase |
| PEPCK | Phosphoenol Pyruvate Carboxykinase |
| PYC | Pyruvate Carboxylase |
| TCA | TriCarboxylic Acid Cycle |
| TRL | Technology Readiness Level |
| Ribose 5–P | Ribose 5–Phosphate |
| Ribulose 5–P | Ribulose 5–Phosphate |
| ROS | Reactive Oxygen Species |
| R+D+I | Research, Development and Innovation |
| SA | Succinic Acid |
| Sedoheptulose 7–P | Sedoheptulose 7–Phosphate |
| US DOE | United States Department of Energy |
| Xylulose 5–P | Xylulose 5–Phosphate |
| a | volumetric coefficient (m3), exponent in Equation (21). |
| b | Schenov constant of organic substances (m3‧kg−1), exponent in Equation (21) |
| B | number of blades |
| Bi | Biot number |
| C | concentration (mol‧L−1, kg L−1) |
| d | diameter of the reactor (m) |
| D | diffusivity (m2 s−1), dilution rate (g L−1) |
| De | effective diffusivity (m2 s−1) |
| E | Euler number |
| f | specific constant related to the geometry of the vessel |
| h | Schenov constant of salts (L mol−1) |
| H0 | Henry’s constant for CO2 in a pure solvent (kPa m3 kmol−1) |
| J | width of baffles (m) |
| k | mass transfer coefficient (m s−1) |
| K | equilibrium constants, kinetic constants (g L−1) |
| L | biofilm thickness, length of the reactor (m) |
| m | Pirt’s coefficient (s−1) |
| n | number of species, substrate flux (g m L−1 s−1), exponent of Equation (42) |
| N | stirring speed (rpm) |
| p | number of measurement points of surface average relative effective diffusivity |
| P | partial pressure in a gas mixture (kPa), power input under gassed conditions (W) |
| q | impeller type |
| Q | flow (L s−1, L min−1) |
| r | particle radius (m) |
| R | ideal gas constant (atm L mol−1 K−1), rate of metabolite production (g L−1 h−1), number of baffles |
| Re | Reynolds number |
| Sc | Schmidt number |
| Sh | Sherwood number |
| t | time (s, min, h) |
| T | temperature (°C, K) |
| v | gas velocity, velocity in the bulk liquid (m s−1) |
| V | volume of the liquid (L, m3) |
| w | average flow velocity (m s−1) |
| W | width of blades (m) |
| Y | yield (g g−1) |
| Z | distance from the bottom of the biofilm (m) |
| [CO2] | concentration of dissolved CO2 in the bulk liquid (mol L−1) |
| [CO32−] | concentration of carbonate ion (mol L−1) |
| [G] | glucose concentration (kg m−3) |
| [H2CO3] | carbonic acid concentration (mol L−1) |
| [HCO3−] | bicarbonate ion concentration (mol L−1) |
| [P] | product concentration (g L−1) |
| [S] | substrate concentration (g L−1) |
| [X] | biomass concentration (g L−1) |
| α | solubility of CO2, associated growth parameter in production generation models (g g−1), exponent in Equation (48). |
| β | non-associated growth parameter in production generation models (g g−1 h−1), exponent of Equation (51). |
| δ | associated growth parameter in substrate consumption models (g g−1) |
| γ | associated growth parameter in substrate consumption models (g g−1 h−1) |
| η | effectiveness factor |
| φ | Thiele modulus |
| λ | time of the latency phase (h), reduction factor |
| µ | specific growth rate (s−1, min−1, h−1), dynamic viscosity (kg m−1 s−1) |
| ν | reaction rate (kg kg−1 s−1), kinematic viscosity (m2 s−1) |
| ρ | density (kg m−3) |
| Ω | structure factor |
| aq | refers to aqueous |
| b | refers to biofilm |
| cells | refers to cells in biofilm |
| EPS | refers to extracellular polymeric substances |
| G | refers to gas |
| i | refers to ion I, to species i |
| IS | refers to inhibition per substrate |
| j | refers to species j |
| L | refers to bulk liquid |
| m | refers to maximum state |
| n | refers to organic substances |
| o | refers to non-gassed Newtonian fluids, refers to “cell free” extracellular polymeric substances/water matrix |
| P | refers to product, biocatalyst particle |
| s | refers to superficial gas, refers to the surface of the biofilm, refers to the surface of the biocatalyst particle |
| S | refers to substrate |
| TCO2 | refers to total CO2 |
| T | refers to a specific temperature |
| w | refers to working volume, refers to water in biofilm |
| 0 | refers to a pure solvent or ambient conditions |
| 1 | refers to Equation (1) |
| 2 | refers to Equation (2) |
| 3 | refers to Equation (3) |
| 4 | refers to Equation (4) |
| * | refers to a relative rate, refers to a saturation concentration |
References
- The World Bank Data GDP (Constant 2010 USD). Available online: https://data.worldbank.org/indicator/NY.GDP.MKTP.KD (accessed on 4 January 2022).
- Parry, I.; Black, S.; Vernon, N.; Blewer, P.; Fulwood, M.; Khanburg, T.; Peciccia, A.; Roaf, J.; Schulz, P.; Zhunussova, K. Still Not Getting Energy Prices Right: A Global and Country Update of Fossil Fuel Subsidies; Elsevier: Amsterdam, The Netherlands, 2021. [Google Scholar]
- Bechthold, I.; Bretz, K.; Kabasci, S.; Kopitzky, R.; Springer, A. Succinic Acid: A New Platform Chemical for Biobased Polymers from Renewable Resources. Chem. Eng. Technol. Ind. Chem. Plant Equip. Process Eng. Biotechnol. 2008, 31, 647–654. [Google Scholar] [CrossRef]
- Martins, F.; Felgueiras, C.; Smitkova, M.; Caetano, N. Analysis of Fossil Fuel Energy Consumption and Environmental Impacts in European Countries. Energies 2019, 12, 964. [Google Scholar] [CrossRef]
- Farrow, A.; Miller, K.A. Toxic Air: The Price of Fossil Fuels; Greenpeace: Amsterdam, The Netherlands, 2020. [Google Scholar]
- Kotcher, J.; Maibach, E.; Choi, W.T. Fossil Fuels Are Harming Our Brains: Identifying Key Messages about the Health Effects of Air Pollution from Fossil Fuels. BMC Public Health 2019, 19, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Lelieveld, J.; Klingmüller, K.; Pozzer, A.; Burnett, R.T.; Haines, A.; Ramanathan, V. Effects of Fossil Fuel and Total Anthropogenic Emission Removal on Public Health and Climate. Proc. Natl. Acad. Sci. USA 2019, 116, 7192–7197. [Google Scholar] [CrossRef]
- Kopel, J.; Brower, G.L. Impact of Fossil Fuel Emissions and Particulate Matter on Pulmonary Health. Bayl. Univ. Med. Cent. Proc. 2019, 32, 636–638. [Google Scholar] [CrossRef]
- FitzPatrick, M.; Champagne, P.; Cunningham, M.F.; Whitney, R.A. A Biorefinery Processing Perspective: Treatment of Lignocellulosic Materials for the Production of Value-Added Products. Bioresour. Technol. 2010, 101, 8915–8922. [Google Scholar] [CrossRef]
- Lipnizki, F.; Rudolph, G.; Thuvander, J. Membrane Processes in Lignocellulosic Biorefineries: Status, Potential and Challenges; Conference of Visegrad Countries. 2019. Available online: https://lup.lub.lu.se/record/55f7df81-6d21-41b7-ae47-31de95c3c88b (accessed on 7 January 2022).
- Hassan, S.S.; Williams, G.A.; Jaiswal, A.K. Lignocellulosic Biorefineries in Europe: Current State and Prospects. Trends Biotechnol. 2019, 37, 231–234. [Google Scholar] [CrossRef]
- Ubando, A.T.; Felix, C.B.; Chen, W.H. Biorefineries in Circular Bioeconomy: A Comprehensive Review. Bioresour. Technol. 2020, 299, 122585. [Google Scholar] [CrossRef]
- Ali, N.; Zhang, Q.; Liu, Z.Y.; Li, F.L.; Lu, M.; Fang, X.C. Emerging Technologies for the Pretreatment of Lignocellulosic Materials for Bio-Based Products. Appl. Microbiol. Biotechnol. 2020, 104, 455–473. [Google Scholar] [CrossRef]
- Usmani, Z.; Sharma, M.; Awasthi, A.K.; Lukk, T.; Tuohy, M.G.; Gong, L.; Nguyen-Tri, P.; Goddard, A.D.; Bill, R.M.; Nayak, S.C.; et al. Lignocellulosic Biorefineries: The Current State of Challenges and Strategies for Efficient Commercialization. Renew. Sustain. Energy Rev. 2021, 148, 111258. [Google Scholar] [CrossRef]
- Yousuf, A.; Pirozzi, D.; Sannino, F. Fundamentals of Lignocellulosic Materials for Bio-Based Products; Academic Press: Cambridge, MA, USA, 2020. [Google Scholar]
- Zuccaro, G.; Pirozzi, D.; Yousuf, A. Lignocellulosic Biomass to Biodiesel. In Lignocellulosic Biomass to Liquid Biofuels; Academic Press: Cambridge, MA, USA, 2020; pp. 127–167. [Google Scholar]
- Ma, S.; Wang, H.; Li, J.; Fu, Y.; Zhu, W. Methane Production Performances of Different Compositions in Lignocellulosic Biomass through Anaerobic Digestion. Energy 2019, 189, 116190. [Google Scholar] [CrossRef]
- Koupaie, E.H.; Dahadha, S.; Lakeh, A.B.; Azizi, A.; Elbeshbishy, E. Enzymatic Pretratment of Lignocellulosic Biomass for Enhanced Biomethane Production—A Review. J. Environ. Manag. 2019, 233, 774–784. [Google Scholar] [CrossRef]
- Salvachúa, D.; Mohagheghi, A.; Smith, H.; Bradfield, M.F.A.; Nicol, W.; Black, B.A.; Biddy, M.J.; Dowe, N.; Beckham, G.T. Succinic Acid Production on Xylose-Enriched Biorefinery Streams by Actinobacillus succinogenes in Batch Fermentation. Biotechnol. Biofuels 2016, 9, 28. [Google Scholar] [CrossRef]
- Hassan, S.S.; Williams, G.A.; Jaiswal, A.K. Moving towards the Second Generation of Lignocellulosic Biorefineries in the EU: Drivers, Challenges and Opportunities. Renew. Sustain. Energy Rev. 2019, 101, 590–599. [Google Scholar] [CrossRef]
- Pateraki, C.; Patsalou, M.; Vlysidis, A.; Kopsahelis, N.; Webb, C.; Koutinas, A.A.; Koutinas, M. Actinobacillus succinogenes: Advances on Succinic Acid Production and Prospects for Development of Integrated Biorefineries. Biochem. Eng. J. 2016, 112, 285–303. [Google Scholar] [CrossRef]
- Sahoo, K.K.; Datta, S.; Nayak, A.; Pranaw, K.; Dutta, D.; Goswami, G. Biological Production of Succinic Acid: State of the Art and Future Perspectives. In Industrial Microbiology and Biotechnology; Springer: Singapore, 2022; pp. 427–461. [Google Scholar]
- Bozell, J.J.; Petersen, G.R. Technology Development for the Production of Biobased Products from Biorefinery Carbohydrates—The US Department of Energy’s “Top 10” Revisited. Green Chem. 2010, 12, 539–554. [Google Scholar] [CrossRef]
- Werpy, T.; Petersen, G. Top Value Added Chemicals from Biomass: Volume I—Results of Screening for Potential Candidates from Sugars and Synthesis Gas (No. DOE/GO-102004-1992); National Renewable Energy Lab: Golden, CO, USA, 2004. [Google Scholar]
- Putri, D.N.; Sahlan, M.; Montastruc, L.; Meyer, M.; Negny, S.; Hermansyah, H. Progress of Fermentation Methods for Bio-Succinic Acid Production Using Agro-Industrial Waste by Actinobacillus succinogenes. Energy Rep. 2020, 6, 234–239. [Google Scholar] [CrossRef]
- McKinlay, J.B.; Vieille, C.; Zeikus, J.G. Prospects for a Bio-Based Succinate Industry. Appl. Microbiol. Biotechnol. 2007, 76, 727–740. [Google Scholar] [CrossRef]
- Song, H.; Lee, S.Y. Production of Succinic Acid by Bacterial Fermentation. Enzym. Microb. Technol. 2006, 39, 352–361. [Google Scholar] [CrossRef]
- Zeikus, J.G.; Jain, M.K.; Elankovan, P. Biotechnology of Succinic Acid Production and Markets for Derived Industrial Products. Appl. Microbiol. Biotechnol. 1999, 51, 545–552. [Google Scholar] [CrossRef]
- Mancini, E.; Mansouri, S.S.; Gernaey, K.V.; Luo, J.; Pinelo, M. From Second Generation Feed-Stocks to Innovative Fermentation and Downstream Techniques for Succinic Acid Production. Crit. Rev. Environ. Sci. Technol. 2019, 50, 1–45. [Google Scholar] [CrossRef]
- Akhtar, J.; Idris, A.; Aziz, R.A. Recent Advances in Production of Succinic Acid from Lignocellulosic Biomass. Appl. Microbiol. Biotechnol. 2014, 98, 987–1000. [Google Scholar] [CrossRef] [PubMed]
- Polly, O.L. Production of Succinic Acid. U.S. Patent No. 2,533,620, 12 December 1950. Available online: https://patents.google.com/patent/US2533620A/en (accessed on 10 January 2022).
- Cok, B.; Tsiropoulos, I.; Roes, A.L.; Patel, M.K. Succinic Acid Production Derived from Carbohydrates: An Energy and Greenhouse Gas Assessment of a Platform Chemical toward a Bio-Based Economy. Bioprod. Biorefining 2014, 8, 16–29. [Google Scholar] [CrossRef]
- Dai, Z.; Guo, F.; Zhang, S.; Zhang, W.; Yang, Q.; Dong, W.; Jiang, M.; Ma, J.; Xin, F. Bio-based Succinic Acid: An Overview of Strain Development, Substrate Utilization, and Downstream Purification. Biofuels Bioprod. Biorefining 2019, 14, 965–985. [Google Scholar] [CrossRef]
- Dienst, S.; Onderzoek, L. Strategic Thinking in Sustainable Energy from the Sugar Platform to Biofuels and Biochemicals Final Report for the European Commission Directorate—General Energy; Consorzio per La Ricerca e La Dimostrazione Sulle Energie Rinnovabili (RE-CORD): Florence, Italy, 2015. [Google Scholar]
- MRP Global Bio Succnic Acid Market Insights, Forescast to 2026. Available online: https://www.marketresearchplace.com/report/global-bio-succinic-acid-market-insights-forecast-to-192517.html (accessed on 11 January 2022).
- Mancini, E.; Dickson, R.; Fabbri, S.; Udugama, I.A.; Ullah, H.I.; Vishwanath, S.; Gernaey, K.V.; Luo, J.; Pinelo, M.; Mansouri, S.S. Economic and Environmental Analysis of Bio-Succinic Acid Production: From Established Processes to a New Continuous Fermentation Approach with in-Situ Electrolytic Extraction. Chem. Eng. Res. Des. 2022, 179, 401–414. [Google Scholar] [CrossRef]
- Almqvist, H.; Pateraki, C.; Alexandri, M.; Koutinas, A.; Lidén, G. Succinic Acid Production by Actinobacillus succinogenes from Batch Fermentation of Mixed Sugars. J. Ind. Microbiol. Biotechnol. 2016, 43, 1117–1130. [Google Scholar] [CrossRef]
- Lin, S.K.C.; Du, C.; Koutinas, A.; Wang, R.; Webb, C. Substrate and Product Inhibition Kinetics in Succinic Acid Production by Actinobacillus succinogenes. Biochem. Eng. J. 2008, 41, 128–135. [Google Scholar] [CrossRef]
- Ferone, M.; Raganati, F.; Olivieri, G.; Salatino, P.; Marzocchella, A. Biosuccinic Acid from Lignocellulosic-Based Hexoses and Pentoses by Actinobacillus succinogenes: Characterization of the Conversion Process. Appl. Biochem. Biotechnol. 2017, 183, 1465–1477. [Google Scholar] [CrossRef]
- Pateraki, C.; Almqvist, H.; Ladakis, D.; Lidén, G.; Koutinas, A.A.; Vlysidis, A. Modelling Succinic Acid Fermentation Using a Xylose Based Substrate. Biochem. Eng. J. 2016, 114, 26–41. [Google Scholar] [CrossRef]
- Cimini, D.; Zaccariello, L.; D’Ambrosio, S.; Lama, L.; Ruoppolo, G.; Pepe, O.; Faraco, V.; Schiraldi, C. Improved Production of Succinic Acid from Basfia succiniciproducens Growing on A. Donax and Process Evaluation through Material Flow Analysis. Biotechnol. Biofuels 2019, 12, 22. [Google Scholar] [CrossRef]
- Thuy, N.T.H.; Kongkaew, A.; Flood, A.; Boontawan, A. Fermentation and Crystallization of Succinic Acid from Actinobacillus succinogenes ATCC55618 Using Fresh Cassava Root as the Main Substrate. Bioresour. Technol. 2017, 233, 342–352. [Google Scholar] [CrossRef]
- Briki, A.; Kaboré, K.; Olmos, E.; Bosselaar, S.; Blanchard, F.; Fick, M.; Guedon, E.; Fournier, F.; Delaunay, S. Corynebacterium glutamicum, a Natural Overproducer of Succinic Acid? Eng. Life Sci. 2020, 20, 205–215. [Google Scholar] [CrossRef]
- Huang, M.; Cheng, J.; Chen, P.; Zheng, G.; Wang, D.; Hu, Y. Efficient Production of Succinic Acid in Engineered Escherichia coli Strains Controlled by Anaerobically-Induced NirB Promoter Using Sweet Potato Waste Hydrolysate. J. Environ. Manag. 2019, 237, 147–154. [Google Scholar] [CrossRef]
- Filippi, K.; Papapostolou, H.; Alexandri, M.; Vlysidis, A.; Myrtsi, E.D.; Ladakis, D.; Pateraki, C.; Haroutounian, S.A.; Koutinas, A. Integrated Biorefinery Development Using Winery Waste Streams for the Production of Bacterial Cellulose, Succinic Acid and Value-Added Fractions. Bioresour. Technol. 2022, 343, 125989. [Google Scholar] [CrossRef]
- Oreoluwa Jokodola, E.; Narisetty, V.; Castro, E.; Durgapal, S.; Coulon, F.; Sindhu, R.; Binod, P.; Rajesh Banu, J.; Kumar, G.; Kumar, V. Process Optimisation for Production and Recovery of Succinic Acid Using Xylose-Rich Hydrolysates by Actinobacillus succinogenes. Bioresour. Technol. 2022, 344, 126224. [Google Scholar] [CrossRef]
- Xu, C.; Alam, M.A.; Wang, Z.; Peng, Y.; Xie, C.; Gong, W.; Yang, Q.; Huang, S.; Zhuang, W.; Xu, J. Co-Fermentation of Succinic Acid and Ethanol from Sugarcane Bagasse Based on Full Hexose and Pentose Utilization and Carbon Dioxide Reduction. Bioresour. Technol. 2021, 339, 125578. [Google Scholar] [CrossRef]
- Ercole, A.; Raganati, F.; Salatino, P.; Marzocchella, A. Continuous Succinic Acid Production by Immobilized Cells of Actinobacillus succinogenes in a Fluidized Bed Reactor: Entrapment in Alginate Beads. Biochem. Eng. J. 2021, 169, 107968. [Google Scholar] [CrossRef]
- Bradfield, M.F.A.; Mohagheghi, A.; Salvachúa, D.; Smith, H.; Black, B.A.; Dowe, N.; Beckham, G.T.; Nicol, W. Continuous Succinic Acid Production by Actinobacillus succinogenes on Xylose-Enriched Hydrolysate. Biotechnol. Biofuels 2015, 8, 181. [Google Scholar] [CrossRef]
- Bradfield, M.F.A.; Nicol, W. Continuous Succinic Acid Production from Xylose by Actinobacillus succinogenes. Bioprocess Biosyst. Eng. 2016, 39, 233–244. [Google Scholar] [CrossRef]
- Ferone, M.; Raganati, F.; Ercole, A.; Olivieri, G.; Salatino, P.; Marzocchella, A. Continuous Succinic Acid Fermentation by Actinobacillus succinogenes in a Packed-Bed Biofilm Reactor. Biotechnol. Biofuels 2018, 11, 138. [Google Scholar] [CrossRef]
- Ferone, M.; Raganati, F.; Olivieri, G.; Marzocchella, A. Bioreactors for Succinic Acid Production Processes. Crit. Rev. Biotechnol. 2019, 39, 571–586. [Google Scholar] [CrossRef]
- Chen, X.; Zhou, Y.; Zhang, D. Engineering Corynebacterium crenatum for Enhancing Succinic Acid Production. J. Food Biochem. 2018, 42, e12645. [Google Scholar] [CrossRef]
- Ahn, J.H.; Jang, Y.S.; Lee, S.Y. Production of Succinic Acid by Metabolically Engineered Microorganisms. Curr. Opin. Biotechnol. 2016, 42, 54–66. [Google Scholar] [CrossRef] [PubMed]
- Jiang, M.; Ma, J.; Wu, M.; Liu, R.; Liang, L.; Xin, F.; Zhang, W.; Jia, H.; Dong, W. Progress of Succinic Acid Production from Renewable Resources: Metabolic and Fermentative Strategies. Bioresour. Technol. 2017, 245, 1710–1717. [Google Scholar] [CrossRef] [PubMed]
- Yang, Q.; Wu, M.; Dai, Z.; Xin, F.; Zhou, J.; Dong, W.; Ma, J.; Jiang, M.; Zhang, W. Comprehensive Investigation of Succinic Acid Production by Actinobacillus succinogenes: A Promising Native Succinic Acid Producer. Biofuels Bioprod. Biorefining 2019, 14, 950–964. [Google Scholar] [CrossRef]
- Grossmann, I.E.; Harjunkoski, I. Process Systems Engineering: Academic and Industrial Perspectives. Comput. Chem. Eng. 2019, 126, 474–484. [Google Scholar] [CrossRef]
- Solano-Cornejo, M.A.; Vidaurre-Ruiz, J.M. Application of Unstructured Kinetic Models in the Lactic Fermentation Modeling of the Fishery By-Products. Sci. Agropecu. 2017, 8, 367–375. [Google Scholar] [CrossRef][Green Version]
- Almquist, J.; Cvijovic, M.; Hatzimanikatis, V.; Nielsen, J.; Jirstrand, M. Kinetic Models in Industrial Biotechnology—Improving Cell Factory Performance. Metab. Eng. 2014, 24, 38–60. [Google Scholar] [CrossRef]
- Theodoropoulos, C.; Chenhao, S. Bioreactor Models and Modeling Approaches. Eng. Perspect. Biotechnol. Compr. Biotechnol. 2019, 2, 663–680. [Google Scholar]
- Alcón Martín, A. Desarrollo de Modelos Cinéticos para Bioprocesos: Aplicación a la Producción de Xantano; Complutense University: Madrid, Spain, 1999; Available online: https://eprints.ucm.es/id/eprint/3549/ (accessed on 14 January 2022).
- Celler, K.; Picioreanu, C.; van Loosdrecht, M.; van Wezel, G.P. Structured morphological modeling as a framework for rational strain design of Streptomyces species. Antonie Van Leeuwenhoek 2012, 102, 409–423. [Google Scholar] [CrossRef]
- García-Ochoa, F.; Santos, V.E.; Alcón, A. Simulation of Xanthan Gum Production by a Chemically Structured Kinetic Model. Math. Comput. Simul. 1996, 42, 187–195. [Google Scholar] [CrossRef]
- Quirós, C.; Herrero, M.; García, L.A.; Díaz, M. Application of Flow Cytometry to Segregated Kinetic Modeling Based on the Physiological States of Microorganisms. Appl. Environ. Microbiol. 2007, 73, 3993–4000. [Google Scholar] [CrossRef]
- García-Ochoa, F.; Castro, E.G.; Santos, V.E. Oxygen Transfer and Uptake Rates during Xanthan Gum Production. Enzym. Microb. Technol. 2000, 27, 680–690. [Google Scholar] [CrossRef]
- Corona-González, R.I.; Varela-Almanza, K.M.; Arriola-Guevara, E.; de Jesús Martínez-Gómez, Á.; Pelayo-Ortiz, C.; Toriz, G. Bagasse Hydrolyzates from Agave Tequilana as Substrates for Succinic Acid Production by Actinobacillus succinogenes in Batch and Repeated Batch Reactor. Bioresour. Technol. 2016, 205, 15–23. [Google Scholar] [CrossRef]
- Vemuri, G.N.; Eiteman, M.A.; Altman, E. Succinate Production in Dual-Phase Escherichia coli Fermentations Depends on the Time of Transition from Aerobic to Anaerobic Conditions. J. Ind. Microbiol. Biotechnol. 2002, 28, 325–332. [Google Scholar] [CrossRef]
- Litsanov, B.; Brocker, M.; Bott, M. Toward Homosuccinate Fermentation: Metabolic Engineering of Corynebacterium glutamicum for Anaerobic Production of Succinate from Glucose and Formate. Appl. Environ. Microbiol. 2012, 78, 3325–3337. [Google Scholar] [CrossRef]
- Ong, K.L.; Fickers, P.; Lin, C.S.K. Enhancing Succinic Acid Productivity in the Yeast Yarrowia lipolytica with Improved Glycerol Uptake Rate. Sci. Total Environ. 2020, 702, 134911. [Google Scholar] [CrossRef]
- Corona-González, R.I.; Miramontes-Murillo, R.; Arriola-Guevara, E.; Guatemala-Morales, G.; Toriz, G.; Pelayo-Ortiz, C. Immobilization of Actinobacillus succinogenes by Adhesion or Entrapment for the Production of Succinic Acid. Bioresour. Technol. 2014, 164, 113–118. [Google Scholar] [CrossRef]
- Meynial-salles, I.; Dorotyn, S.; Soucaille, P. A New Process for the Continuous Production of Succinic Acid from Glucose at High Yield, Titer, and Productivity. Biotechnol. Bioeng. 2008, 99, 129–135. [Google Scholar] [CrossRef]
- Ito, Y.; Hirasawa, T.; Shimizu, H. Metabolic Engineering of Saccharomyces cerevisiae to Improve Succinic Acid Production Based on Metabolic Profiling. Biosci. Biotechnol. Biochem. 2014, 78, 151–159. [Google Scholar] [CrossRef]
- Kim, D.Y.; Yim, S.C.; Lee, P.C.; Lee, W.G.; Lee, S.Y.; Chang, H.N. Batch and Continuous Fermentation of Succinic Acid from Wood Hydrolysate by Mannheimia succiniciproducens MBEL55E. Enzym. Microb. Technol. 2004, 35, 648–653. [Google Scholar] [CrossRef]
- Dessie, W.; Xin, F.; Zhang, W.; Zhou, J.; Wu, H.; Ma, J.; Jiang, M. Inhibitory Effects of Lignocellulose Pretreatment Degradation Products (Hydroxymethylfurfural and Furfural) on Succinic Acid Producing Actinobacillus succinogenes. Biochem. Eng. J. 2019, 150, 107263. [Google Scholar] [CrossRef]
- Andersson, C.; Helmerius, J.; Hodge, D.; Berglund, K.; Rova, U. Inhibition of Succinic Acid Production in Metabolically Engineered Escherichia coli by Neutralizing Agent, Organic Acids, and Osmolarity. Biotechnol. Prog. 2009, 25, 116–123. [Google Scholar] [CrossRef]
- Kuglarz, M.; Rom, M. Influence of Carbon Dioxide and Nitrogen Source on Sustainable Production of Succinic Acid from Miscanthus Hydrolysates. Int. J. Environ. Sci. Dev. 2019, 10, 362–367. [Google Scholar] [CrossRef]
- Liu, Y.; Wu, H.; Li, Q.; Tang, X.; Li, Z.; Ye, Q. Enzyme and Microbial Technology Process Development of Succinic Acid Production by Escherichia coli NZN111 Using Acetate as an Aerobic Carbon Source. Enzym. Microb. Technol. 2011, 49, 459–464. [Google Scholar] [CrossRef] [PubMed]
- Li, Q.; Wang, D.; Wu, Y.; Yang, M.; Li, W.; Xing, J.; Su, Z. Kinetic Evaluation of Products Inhibition to Succinic Acid Producers Escherichia coli NZN111, AFP111, BL21, and Actinobacillus succinogenes 130ZT. J. Microbiol. 2010, 48, 290–296. [Google Scholar] [CrossRef]
- Corona-González, R.I.; Bories, A.; González-Álvarez, V.; Pelayo-Ortiz, C. Kinetic Study of Succinic Acid Production by Actinobacillus succinogenes ZT-130. Process Biochem. 2008, 43, 1047–1053. [Google Scholar] [CrossRef]
- Purvis, J.E.; Yomano, L.P.; Ingram, L.O. Enhanced Trehalose Production Improves Growth of Escherichia coli under Osmotic Stress. Appl. Environ. Microbiol. 2005, 71, 3761–3769. [Google Scholar] [CrossRef]
- Panikov, N.S. Microbial Growth Kinetics; Springer Science & Business Media: Berlin/Heidelberg, Germany, 1995. [Google Scholar]
- Sadhukhan, S.; Villa, R.; Sarkar, U. Microbial Production of Succinic Acid Using Crude and Purified Glycerol from a Crotalaria juncea Based Biorefinery. Biotechnol. Rep. 2016, 10, 84–93. [Google Scholar] [CrossRef]
- Song, H.; Jang, S.H.; Park, J.M.; Lee, S.Y. Modeling of Batch Fermentation Kinetics for Succinic Acid Production by Mannheimia succiniciproducens. Biochem. Eng. J. 2008, 40, 107–115. [Google Scholar] [CrossRef]
- Luong, J.H.T.; Mulchandani, A. Microbial Inhibition Kinetics Revisited. Enzym. Microb. Technol. 1989, 11, 66–73. [Google Scholar]
- Brink, H.G.; Nicol, W. Succinic Acid Production with Actinobacillus succinogenes: Rate and Yield Analysis of Chemostat and Biofilm Cultures. Microb. Cell Fact. 2014, 13, 111. [Google Scholar] [CrossRef]
- Vlysidis, A.; Binns, M.; Webb, C.; Theodoropoulos, C. Glycerol Utilisation for the Production of Chemicals: Conversion to Succinic Acid, a Combined Experimental and Computational Study. Biochem. Eng. J. 2011, 58–59, 1–11. [Google Scholar] [CrossRef]
- Carvalho, M.; Roca, C.; Reis, M.A.M. Improving Succinic Acid Production by Actinobacillus succinogenes from Raw Industrial Carob Pods. Bioresour. Technol. 2016, 218, 491–497. [Google Scholar] [CrossRef]
- Carvalho, M.; Roca, C.; Reis, M.A.M. Carob Pod Water Extracts as Feedstock for Succinic Acid Production by Actinobacillus succinogenes 130Z. Bioresour. Technol. 2014, 170, 491–498. [Google Scholar] [CrossRef]
- Luthfi, A.A.I.; Jahim, J.M.; Harun, S.; Tan, J.P.; Manaf, S.F.A.; Shah, S.S.M. Kinetics of the Bioproduction of Succinic Acid by Actinobacillus succinogenes from Oil Palm Lignocellulosic Hydrolysate in a Bioreactor. BioResources 2018, 13, 8279–8294. [Google Scholar] [CrossRef]
- Ferone, M.; Raganati, F.; Olivieri, G.; Salatino, P.; Marzocchella, A. Continuous Succinic Acid Fermentation by Actinobacillus succinogenes: Assessment of Growth and Succinic Acid Production Kinetics. Appl. Biochem. Biotechnol. 2019, 187, 782–799. [Google Scholar] [CrossRef]
- Li, C.; Xiao, Y.; Sang, Z.; Yang, Z.; Xu, T.; Yang, X.; Yan, J.; Lin, C.S.K. Inhibition Kinetics of Bio-Based Succinic Acid Production by the Yeast Yarrowia lipolytica. Chem. Eng. J. 2022, 442, 136273. [Google Scholar] [CrossRef]
- Garcia-Ochoa, F.; Gomez, E. Bioreactor Scale-up and Oxygen Transfer Rate in Microbial Processes: An Overview. Biotechnol. Adv. 2009, 27, 153–176. [Google Scholar] [CrossRef]
- Silva, E.M.; Yang, S.T. Kinetics and Stability of a Fibrous-Bed Bioreactor for Continuous Production of Lactic Acid from Unsupplemented Acid Whey. J. Biotechnol. 1995, 41, 59–70. [Google Scholar] [CrossRef]
- Richelle, A. Modelling, Optimization and Control of Yeast Fermentation Processes in Food Industry. Ph.D. Thesis, Université Libre de Bruxelles, Brussels, Belgium, 2014. [Google Scholar] [CrossRef]
- Kumar, A.; Ray, D.K.; Gupta, S.M. Bioprocess Technology. In Biotechnology in Medicine and Agriculture: Principles and Practices; International Publishing House: New York, NY, USA, 2012; pp. 827–857. [Google Scholar]
- Yasin, M.; Jang, N.; Lee, M.; Kang, H.; Aslam, M.; Bazmi, A.A.; Chang, I.S. Bioreactors, Gas Delivery Systems and Supporting Technologies for Microbial Synthesis Gas Conversion Process. Bioresour. Technol. Rep. 2019, 7, 100207. [Google Scholar] [CrossRef]
- Escobar, S.; Rodriguez, A.; Gomez, E.; Alcon, A.; Santos, V.E.; Garcia-Ochoa, F. Influence of Oxygen Transfer on Pseudomonas putida Effects on Growth Rate and Biodesulfurization Capacity. Bioprocess. Biosyst. Eng. 2016, 39, 545–554. [Google Scholar] [CrossRef]
- Xi, Y.; Chen, K.; Li, J.; Fang, X.; Zheng, X.; Sui, S.; Jiang, M.; Wei, P. Optimization of Culture Conditions in CO2 Fixation for Succinic Acid Production Using Actinobacillus succinogenes. J. Ind. Microb. Biotechnol. 2011, 38, 1605. [Google Scholar] [CrossRef] [PubMed]
- Herselman, J.; Bradfield, M.F.A.; Vijayan, U.; Nicol, W. The Effect of Carbon Dioxide Availability on Succinic Acid Production with Biofilms of Actinobacillus succinogenes. Biochem. Eng. J. 2017, 117, 218–225. [Google Scholar] [CrossRef]
- Villadsen, J.; Nielsen, J.; Lidén, G. Bioreaction Engineering Principles; Springer: Berlin/Heidelberg, Germany, 2011; ISBN 9788578110796. [Google Scholar]
- Elhajj, J.; Al-Hindi, M.; Azizi, F. A Review of the Absorption and Desorption Processes of Carbon Dioxide in Water Systems. Ind. Eng. Chem. Res. 2014, 53, 2–22. [Google Scholar] [CrossRef]
- Liu, Y.P.; Zheng, P.; Sun, Z.H.; Ni, Y.; Dong, J.J.; Wei, P. Strategies of PH Control and Glucose-Fed Batch Fermentation for Production of Succinic Acid by Actinobacillus succinogenes. J. Chem. Technol. Biotechnol. 2008, 83, 1163–1169. [Google Scholar] [CrossRef]
- Cao, W.; Wang, Y.; Luo, J.; Yin, J.; Xing, J.; Wan, Y. Effectively Converting Carbon Dioxide into Succinic Acid under Mild Pressure with Actinobacillus succinogenes by an Integrated Fermentation and Membrane Separation Process. Bioresour. Technol. 2018, 266, 26–33. [Google Scholar] [CrossRef]
- Wu, M.; Zhang, W.; Ji, Y.; Yi, X.; Ma, J.; Wu, H.; Jiang, M. Coupled CO2 Fixation from Ethylene Oxide Off-Gas with Bio-Based Succinic Acid Production by Engineered Recombinant Escherichia coli. Biochem. Eng. J. 2017, 117, 1–6. [Google Scholar] [CrossRef]
- Song, H.; Lee, J.W.; Choi, S.; You, J.K.; Hong, W.H.; Lee, S.Y. Effects of Dissolved CO2 Levels on the Growth of Mannheimia succiniciproducens and Succinic Acid Production. Biotechnol. Bioeng. 2007, 98, 1296–1304. [Google Scholar] [CrossRef]
- Zou, W.; Zhu, L.-W.; Li, H.-M.; Tang, Y.-J. Significance of CO2 Donor on the Production of Succinic Acid by Actinobacillus succinogenes ATCC 55618. Microb. Cell Fact. 2011, 10, 87. [Google Scholar] [CrossRef]
- Gunnarsson, I.B.; Alvarado-Morales, M.; Angelidaki, I. Utilization of CO2 Fixating Bacterium Actinobacillus succinogenes 130Z for Simultaneous Biogas Upgrading and Biosuccinic Acid Production. Environ. Sci. Technol. 2014, 48, 12464–12468. [Google Scholar] [CrossRef]
- Amulya, K.; Kopperi, H.; Venkata Mohan, S. Tunable Production of Succinic Acid at Elevated Pressures of CO2 in a High Pressure Gas Fermentation Reactor. Bioresour. Technol. 2020, 309, 123327. [Google Scholar] [CrossRef]
- Schumpe, A.; Deckwer, W.D. Estimation of O2 and CO2 Solubilities in Fermentation Media. Biotechnol. Bioeng. 1979, 21, 298–300. [Google Scholar] [CrossRef]
- Weisenberger, S.; Schumpe, A. Estimation of Gas Solubilities in Salt Solutions at Temperatures from 273 K to 363 K. AIChE J. 1996, 42, 298–300. [Google Scholar] [CrossRef]
- Rischbieter, E.; Schumpe, A.; Wunder, V. Gas Solubilities in Aqueous Solutions of Organic Substances. J. Chem. Eng. Data 1996, 41, 809–812. [Google Scholar] [CrossRef]
- Pitault, I.; Fongarland, P.; Koepke, D.; Mitrovic, M.; Ronze, D.; Forissier, M. Gas–Liquid and Liquid–Solid Mass Transfers in Two Types of Stationary Catalytic Basket Laboratory Reactor. Chem. Eng. Sci. 2005, 60, 6240–6253. [Google Scholar] [CrossRef]
- Royce, P.N. Effect of Changes in the pH and Carbon Dioxide Evolution Rate on the Measured Respiratory Quotient of Fermentations. Biotechnol. Bioeng. 1992, 40, 1129–1138. [Google Scholar] [CrossRef]
- Rigaki, A.; Webb, C.; Theodoropoulos, C. Double Substrate Limitation Model for the Bio-Based Production of Succinic Acid from Glycerol. Biochem. Eng. J. 2020, 153, 107391. [Google Scholar] [CrossRef]
- Hill, G.A. Measurement of Overall Volumetric Mass Transfer Coefficients for Carbon Dioxide in a Well-Mixed Reactor Using a pH Probe. Ind. Eng. Chem. Res. 2006, 45, 5796–5800. [Google Scholar] [CrossRef]
- Kordač, M.; Linek, V. Dynamic Measurement of Carbon Dioxide Volumetric Mass Transfer Coefficient in a Well-Mixed Reactor Using a pH Probe: Analysis of the Salt and Supersaturation Effects. Ind. Eng. Chem. Res. 2008, 47, 1310–1317. [Google Scholar] [CrossRef]
- Longanesi, L.; Frascari, D.; Spagni, C.; DeWever, H.; Pinelli, D. Succinic Acid Production from Cheese Whey by Biofilms of Actinobacillus succinogenes: Packed Bed Bioreactor Tests. J. Chem. Technol. Biotechnol. 2018, 93, 246–256. [Google Scholar] [CrossRef]
- Kim, S.Y.; Park, S.O.; Yeon, J.Y.; Chun, G.T. Development of a Cell-Recycled Continuous Fermentation Process for Enhanced Production of Succinic Acid by High-Yielding Mutants of Actinobacillus succinogenes. Biotechnol. Bioprocess Eng. 2021, 26, 125–136. [Google Scholar] [CrossRef]
- Mokwatlo, S.C.; Nchabeleng, M.E.; Brink, H.G.; Nicol, W. Impact of Metabolite Accumulation on the Structure, Viability and Development of Succinic Acid–Producing Biofilms of Actinobacillus succinogenes. Appl. Microbiol. Biotechnol. 2019, 103, 6205–6215. [Google Scholar] [CrossRef] [PubMed]
- Mokwatlo, S.C.; Brink, H.G.; Nicol, W. Effect of Shear on Morphology, Viability and Metabolic Activity of Succinic Acid-Producing Actinobacillus succinogenes Biofilms. Bioprocess Biosyst. Eng. 2020, 43, 1253–1263. [Google Scholar] [CrossRef] [PubMed]
- Mokwatlo, S.C.; Nicol, W. Structure and Cell Viability Analysis of Actinobacillus succinogenes Biofilms as Biocatalysts for Succinic Acid Production. Biochem. Eng. J. 2017, 128, 134–140. [Google Scholar] [CrossRef]
- Beyenal, H.; Tanyolaç, A.; Lewandowski, Z. Measurement of Local Effective Diffusivity in Heterogeneous Biofilms. Water Sci. Technol. 1998, 38, 171–178. [Google Scholar] [CrossRef]
- Beyenal, H.; Lewandowski, Z. Combined Effect of Substrate Concentration and Flow Velocity on Effective Diffusivity in Biofilms. Water Res. 2000, 34, 528–538. [Google Scholar] [CrossRef]
- Mokwatlo, S.C.; Nicol, W.; Brink, H.G. Internal Mass Transfer Considerations in Biofilms of Succinic Acid Producing Actinobacillus succinogenes. Chem. Eng. J. 2021, 407, 127220. [Google Scholar] [CrossRef]
- Horn, H.; Hempel, D.C. Substrate Utilization and Mass Transfer in an Autotrophic Biofilm System: Experimental Results and Numerical Simulation. Biotechnol. Bioeng. 1997, 53, 363–371. [Google Scholar] [CrossRef]
- Wäsche, S.; Horn, H.; Hempel, D.C. Influence of Growth Conditions on Biofilm Development and Mass Transfer at the Bulk/Biofilm Interface. Water Res. 2002, 36, 4775–4784. [Google Scholar] [CrossRef]
- Galaction, A.-I.; Rotaru, R.; Kloetzer, L.; Vlysidis, A.; Webb, C.; Turnea, M.; Cascaval, D. External and Internal Glucose Mass Transfers in Succinic Acid Fermentation with Stirred Bed of Immobilized Actinobacillus succinogenes under Substrate and Product Inhibitions. J. Microbiol. Biotechnol. 2011, 21, 1257–1263. [Google Scholar] [CrossRef]
- Galaction, A.-I.; Kloetzer, L.; Turnea, M.; Webb, C.; Vlysidis, A.; Caşcaval, D. Succinic Acid Fermentation in a Stationary-Basket Bioreactor with a Packed Bed of Immobilized Actinobacillus succinogenes: 1. Influence of Internal Diffusion on Substrate Mass Transfer and Consumption Rate. J. Ind. Microbiol. Biotechnol. 2012, 39, 877–888. [Google Scholar] [CrossRef]



| Microorganism | Operation Mode | Carbon Source | Species Predicted by the Model | Ref. | |||
|---|---|---|---|---|---|---|---|
| Biomass | Substrate | Product | By-Products | ||||
| A. succinogenes 130Z, E. coli NZN111, AFP111, BL21 | Batch | Glucose | Equations (1), (2) | [78] | |||
| A. succinogenes DSM 22257 | Batch | Glucose, mannose, xylose, arabinose | Equations (1), (4), (8) | [39] | |||
| E. coli ATCC 8739 | Batch | Glycerol | Equations (1), (4)–(10) | [82] | |||
| B. succiniciproducens BPP7 | Fed Batch | Arundo Donax hydrolysate | Equations (1), (14) | [41] | |||
| A. succinogenes 130Z | Batch | Glucose | Combination of Equations (1), (12), (16) | Equation (17) | [79] | ||
| A. succinogenes DSM 22257 | Continuous | Glucose | Combinations of Equations (1), (4), (8), (11), (14)–(16) | Equation (23) | [90] | ||
| A. succinogenes 130Z | Batch | Oil palm frond hydrolysate | Equation (8) | Equation (22) | [89] | ||
| A. succinogenes 130Z | Continuous | Glucose | Empirical | Empirical | [85] | ||
| A. succinogenes 130Z | Batch, Fed Batch | Raw carob pod extracts | Equations (1), (4) | Equation (17) | Equation (20) | [87] | |
| A. succinogenes ATCC 55618 | Batch | Glucose | Combination of Equations (1), (11), (14) | Equation (18) | Equation (20) | Equation (20) | [38] |
| A. succinogenes ATCC 55618 | Batch | Glycerol | Combination of Equations (1), (8), (14) | Equation (19) | Equation (20) | Equation (20) | [86] |
| A. succinogenes 130Z, B. succiniciproducens JF 4016 | Batch | Xylose, galactose, glucose, mannose, arabinose | Combination of Equations (1), (8), (14) | Equation (18) | Equation (20) | Equation (20) | [40] |
| A. succiniciproducens MBEL55E | Batch | Glucose | Combination of Equations (1), (8), (14) | Equation (19) | Equation (20) | Equation (20) | [83] |
| Y. lipolytica PCG0100 | Batch | Glycerol | Combination of Equations (1), (8), (14) | Equation (19) | Equation (20) | Equation (20) | [91] |
| Microorganism | CarbonSource | Eqs. | Parameters | Ref. | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| µm | [S]m | [P]m | KS | KIS | α | β | ||||
| h−1 | g L−1 | g L−1 | g L−1 | g L−1 | ||||||
| A. succinogenes ATCC 55618 | Glucose | (1) (11) (14) | 0.5 | 155 | SA-104.2 ET-42.1 AA-44.2 FA-16.0 PA-74.1 | 2.03 | 0.603 | [38] | ||
| A. succinogenes ATCC 55618 | Glycerol | (1) (8) (14) | 0.12 | 45.6 | 2.896 | 15.36 | 1.074 | [86] | ||
| A. succinogenes 130Z | Xylose galactose glucose mannose arabinose | (1) (8) (14) | 0.394 | AA-38 FA-18 LA-60 SA-55 | 0.698 | 55.484 | AA-2.300 FA-2.300 LA-/ SA-2.300 | [40] | ||
| B. succiniciproducens JF 4016 | 0.932 | AA-38 FA-22 LA-58 SA-55 | 1.556 | 15.173 | AA-2.300 FA-2.299 LA-2.300 SA-2.299 | |||||
| M. succiniciproducens MBEL55E | Glucose | (1) (8) (14) | 1.324 | 17.23 | 1.123 | 88.35 | 1.301 | [83] | ||
| Y. lipolytica PGC0100 | Glycerol | (1) (8) (14) | 0.38 | AA-57.9 SA-243.4 | 0.818 | 223.5 | AA-12.02 SA-12.30 | [91] | ||
| Microorganism | Carbon Source | Substrate | Product and By-Products | Ref. | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Eqs. | Parameters | Eqs. | Parameters | ||||||||
| YXS | YPiS | δ | γ | ms | αi | βi | |||||
| g g−1 | g g−1 h−1 | h−1 | g g−1 | g g−1 h−1 | |||||||
| A. succinogenes ATCC 55618 | Glucose | (18) | 4.35 | 0.308 | (20) | AA-1.430 FA-0.881 PA-0.187 SA-3.600 | AA-0.045 FA-0.013 PA-0.049 SA-0.299 | [38] | |||
| A. succinogenes ATCC 55618 | Glycerol | (19) | 0.130 | 2.790 | 0.001 | (20) | AA-0.753 FA-0.428 SA-9.864 | AA-0.001 FA-0.002 SA-0.001 | [86] | ||
| A. succinogenes 130Z | Xylose galactose glucose mannose arabinose | (18) | 7.575 | 0.051 | (20) | AA-2.258 FA-1.882 LA-/ SA-3.858 | AA-2.136 FA-1.501 LA-0.419 SA-4.080 | [40] | |||
| B. succiniciproducens JF 4016 | 6.685 | 0.034 | AA-0.016 FA-0.006 LA-/ SA-0.040 | AA-0.001 FA-0.001 LA-0.001 SA-0.028 | |||||||
| M. succiniciproducens MBEL55E | Glucose | (19) | 0.765 | AA-0.999 FA-1.532 LA-0.999 SA-1.310 | 0.061 | (20) | AA-0.626 FA-0.665 LA-/ SA-1.619 | AA-0.124 FA-0.105 LA-0.210 SA-0.355 | [83] | ||
| Y. lipolytica PGC0100 | Glycerol | (19) | 0.581 | AA-1.864 SA-1.712 | 0.055 | (20) | AA-0.208 SA-0.386 | AA-0.010 SA-0.013 | [91] | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Escanciano, I.A.; Wojtusik, M.; Esteban, J.; Ladero, M.; Santos, V.E. Modeling the Succinic Acid Bioprocess: A Review. Fermentation 2022, 8, 368. https://doi.org/10.3390/fermentation8080368
Escanciano IA, Wojtusik M, Esteban J, Ladero M, Santos VE. Modeling the Succinic Acid Bioprocess: A Review. Fermentation. 2022; 8(8):368. https://doi.org/10.3390/fermentation8080368
Chicago/Turabian StyleEscanciano, Itziar A., Mateusz Wojtusik, Jesús Esteban, Miguel Ladero, and Victoria E. Santos. 2022. "Modeling the Succinic Acid Bioprocess: A Review" Fermentation 8, no. 8: 368. https://doi.org/10.3390/fermentation8080368
APA StyleEscanciano, I. A., Wojtusik, M., Esteban, J., Ladero, M., & Santos, V. E. (2022). Modeling the Succinic Acid Bioprocess: A Review. Fermentation, 8(8), 368. https://doi.org/10.3390/fermentation8080368








