Effect of a Soil Water Balance Controlled Irrigation on the Cultivation of Acer pseudoplatanus Forest Tree Liners Under Non-Limiting and Limiting Soil Water Conditions
Abstract
1. Introduction
2. Materials and Methods
2.1. Plant Material
2.2. Soil Characteristics
2.3. Soil Moisture Measurements
2.4. Soil Water Balance Model (SWB)
2.5. Irrigation
2.6. Plant Physiological Responses
2.7. Morphological Parameters
2.8. Statistical Analyses
3. Results
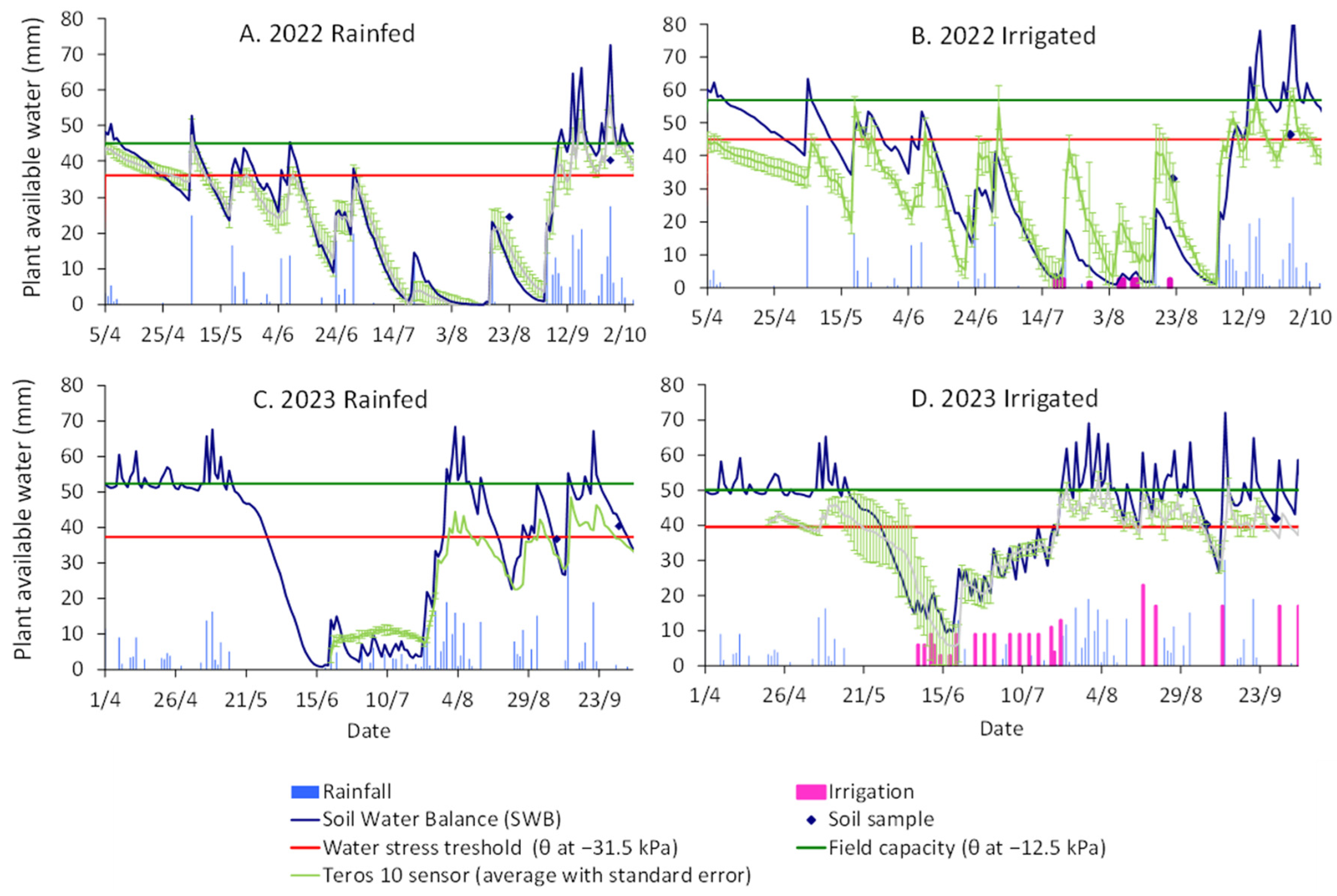
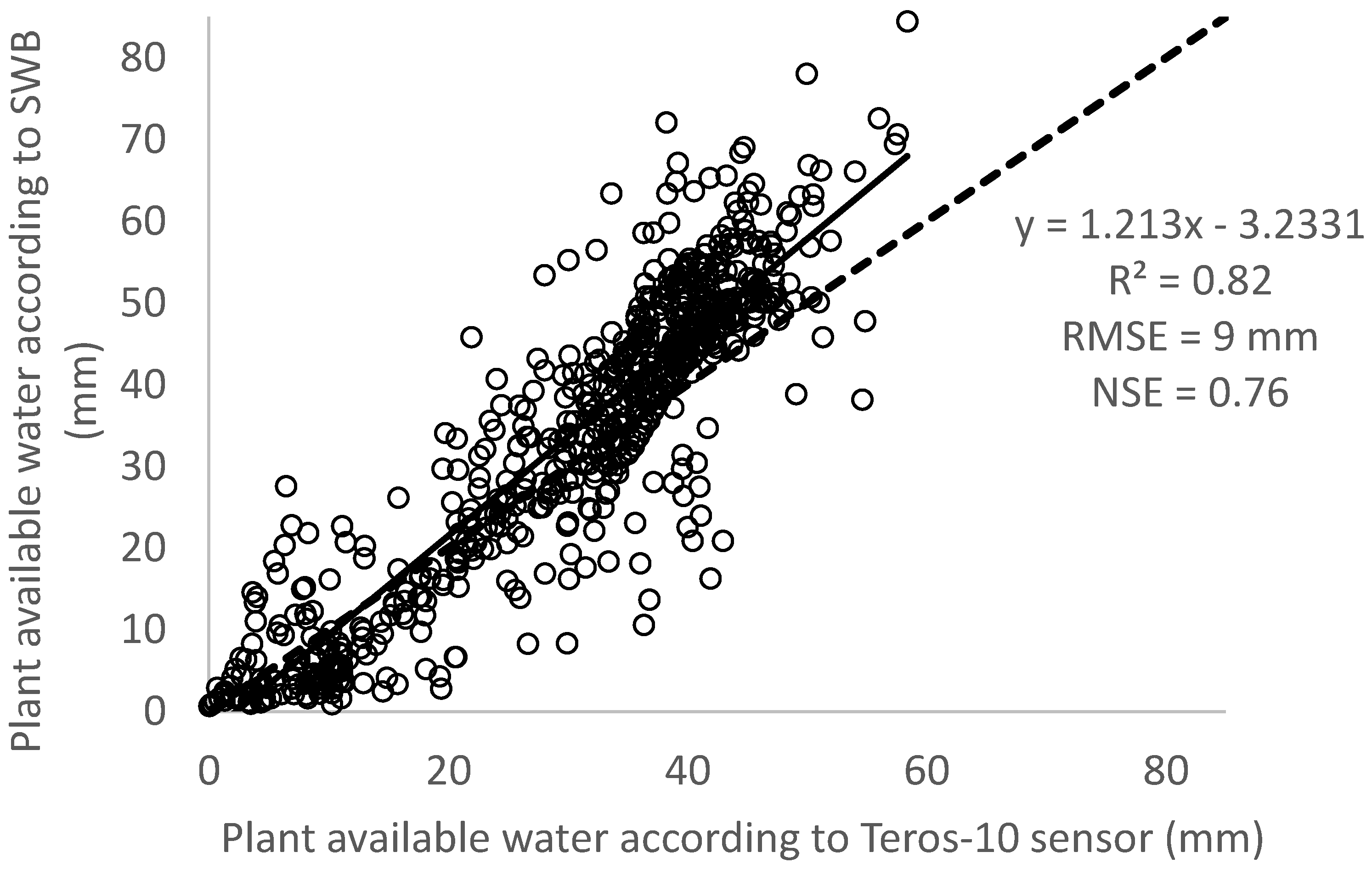
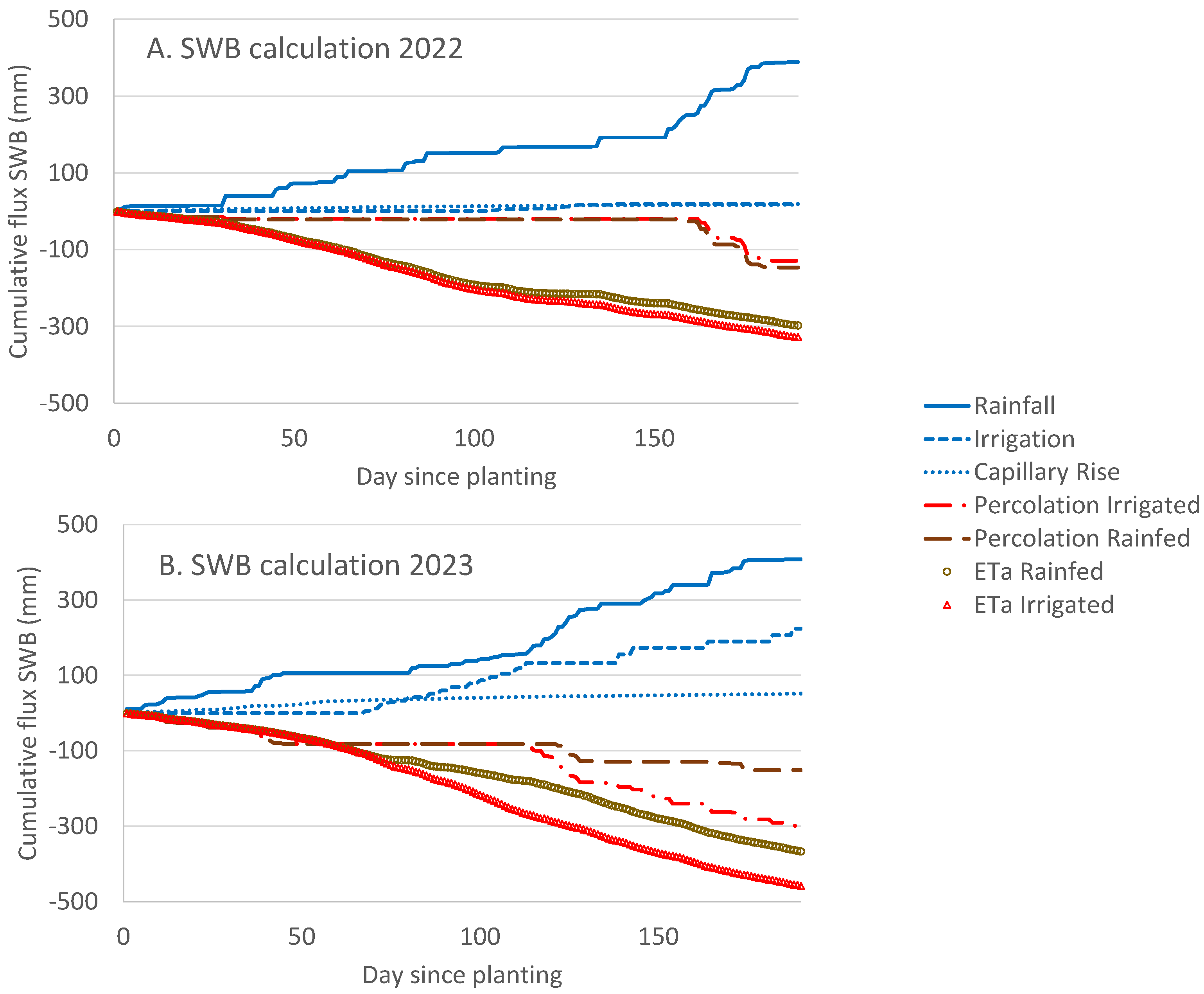
3.1. Soil Water Balance Calculation
3.2. Effect of Irrigation on Midday Stem Water Potential
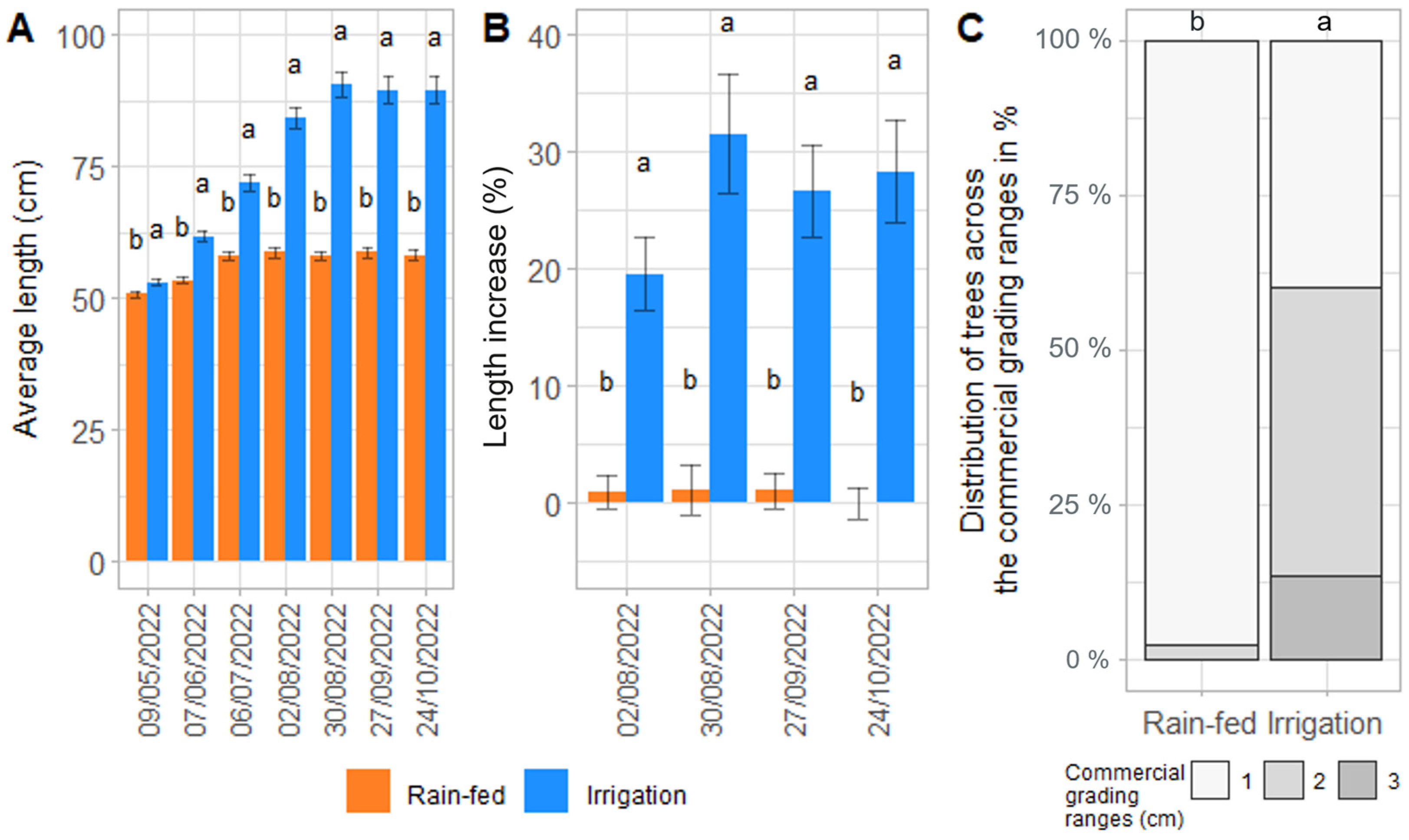
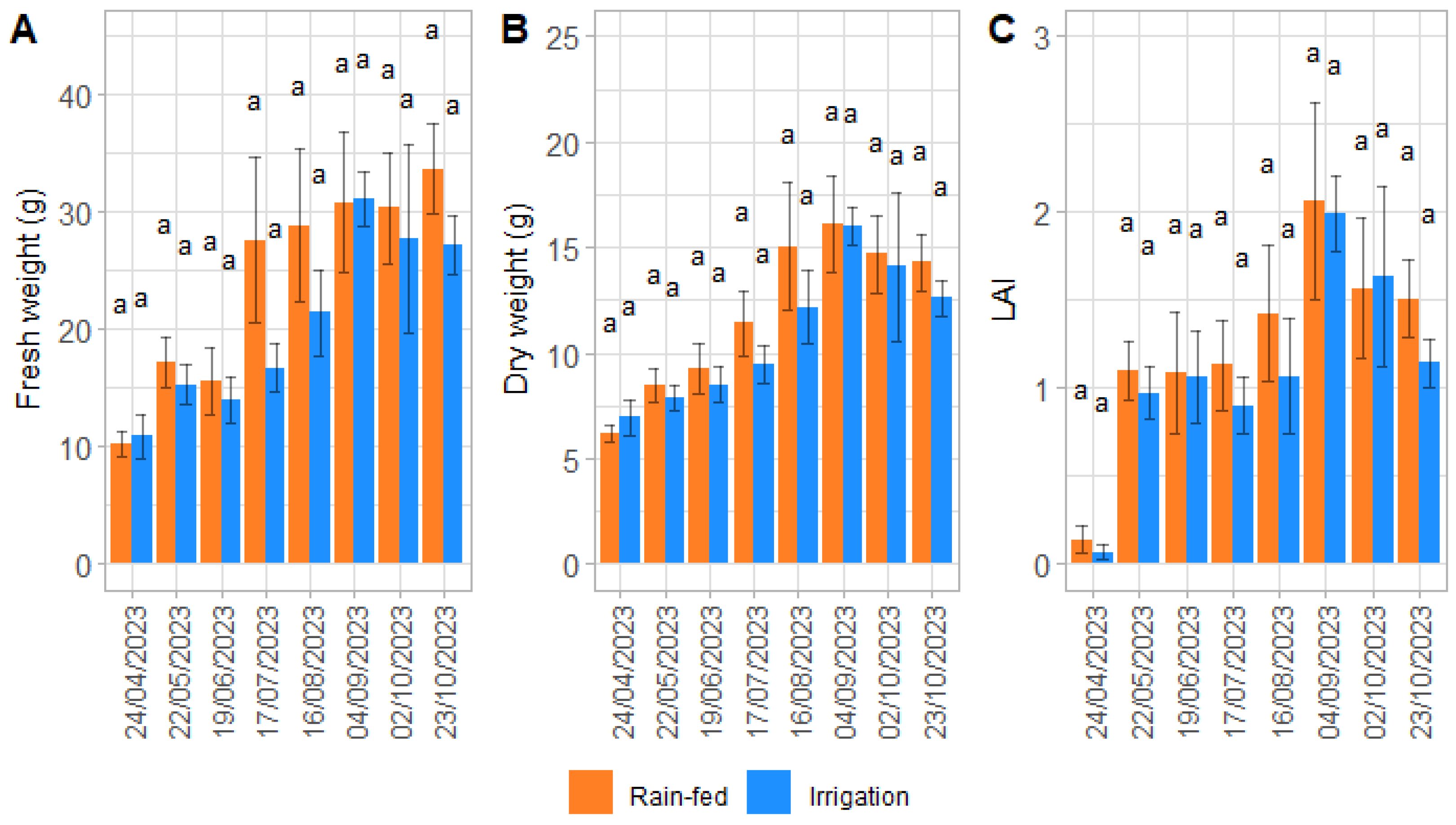
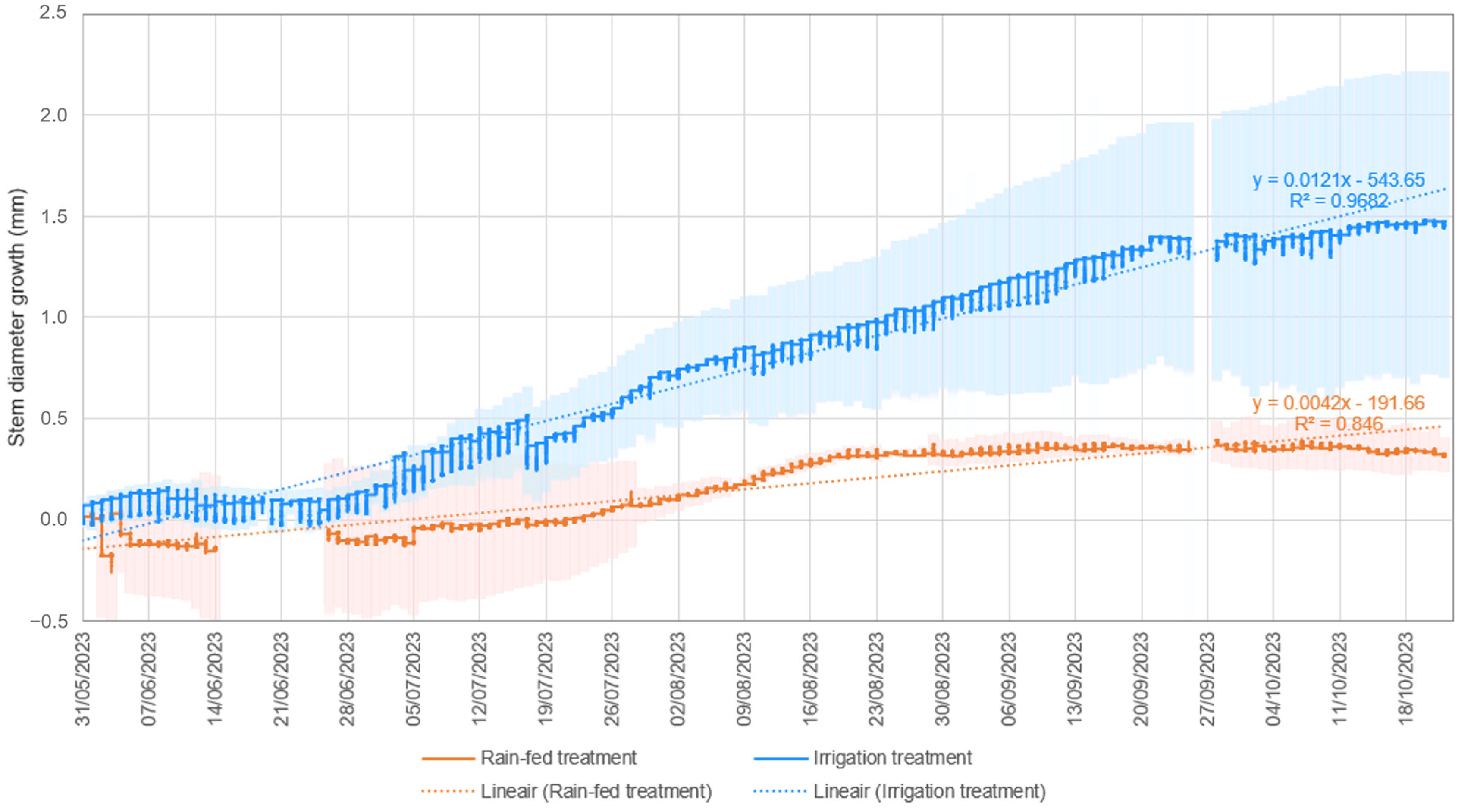
3.3. Effect of Irrigation on Plant Growth and Quality
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Description of the Soil Water Balance Calculation
- Field capacity was set at pF 2 and when soil water content exceeds field capacity, water drains out of the root zone to field capacity the day after. Field capacity was considered at pF 2 because there was a shallow ground water table present in Hoogstraten approximately at 100 cm below the soil surface. In Sint-Truiden, water was retained in the subsoil due to clay accumulation in the Luvisol soil type, which also supports the choice of setting field capacity at pF 2. It has been demonstrated that field capacity differs in function of soil texture, hydraulic conductivity, evapotranspiration, and rooting depth [63,64].
- The soil water balance was for the entire growing season calculated for a single soil layer from 0 to 30 cm.
- In the soil water balance model, capillary rise is calculated with empirical algorithms derived from UPFLOW [65], which calculates the capillary rise as a function of the groundwater table depth, and water retention characteristics. A similar approach was used in the water balance algorithms that underlie AquaCrop [66] (Equation (A2) and Figure A1).
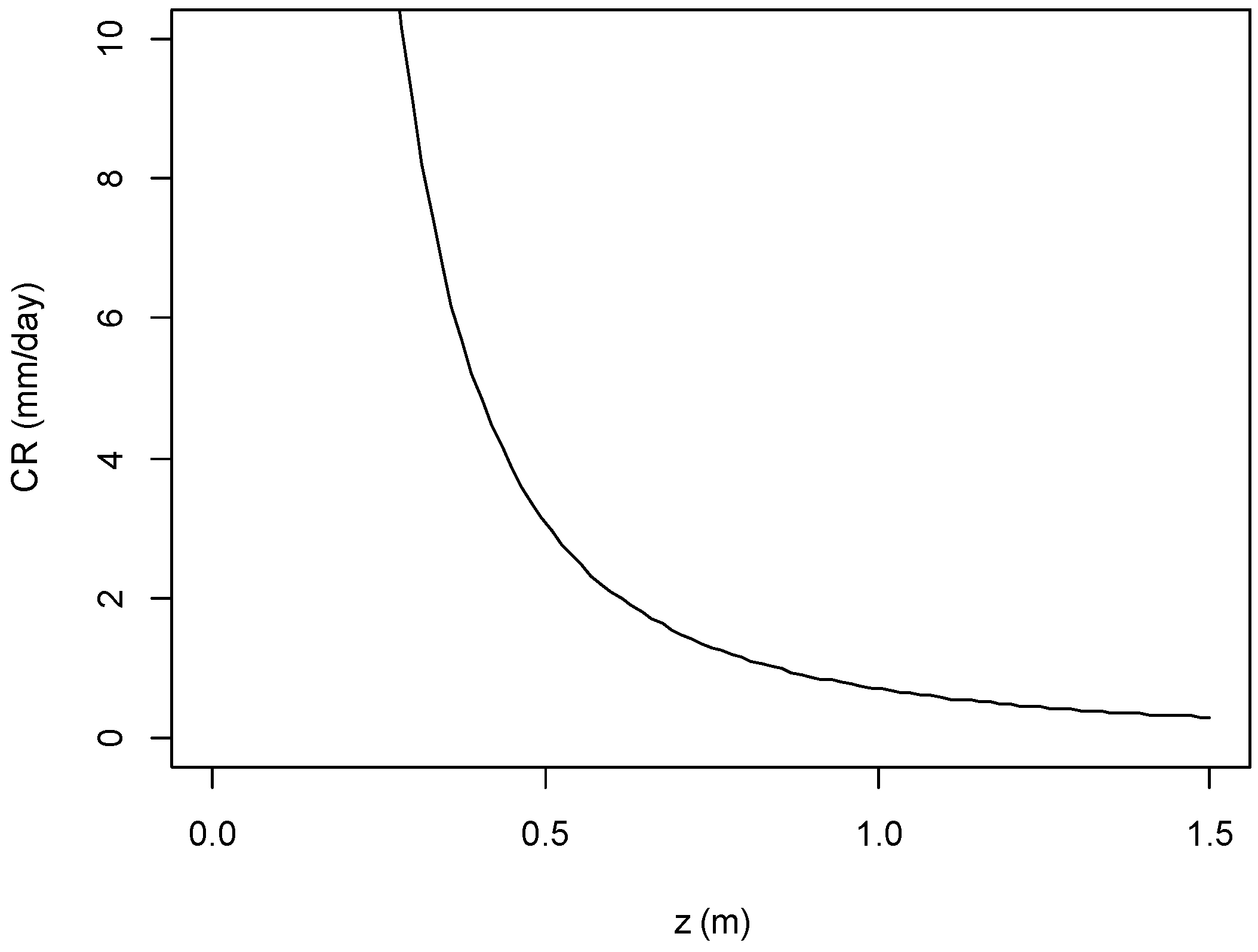
- 4.

- 5.
- After a wetting event, actual evapotranspiration will be dominated by evaporation and is calculated through a Ke factor (Equation (A4)). This Ke factor is related to the time after a wetting event in a curved empirical relationship (Equation (A5) and Figure A3). The first four days after the wetting event, Ke is close to 1, representing the stage I, whereby vaporization is controlled by capillary flow to the vaporization plane at the surface. After four days Ke decreases, representing stage II of vaporization where vapor diffusion is controlled [68].

Appendix B
| Week | Average Temperature (°C) | Radiation Sum (W·m−2) | Relative Humidity (%) | Precipitation (mm) | Irrigation (mm) |
|---|---|---|---|---|---|
| W18 (25/04) | 9.9 | 33,472 | 79.5 | 0.6 | 0 |
| W19 (02/05) | 13.6 | 36,914 | 80.3 | 25 | 0 |
| W20 (09/05) | 16.6 | 42,191 | 70.4 | 0 | 0 |
| W21 (16/05) | 18.0 | 35,063 | 80.1 | 21.8 | 0 |
| W22 (23/05) | 14.5 | 29,659 | 82.2 | 11.4 | 0 |
| W23 (30/05) | 15.1 | 34,701 | 78;6 | 17.2 | 0 |
| W24 (06/06) | 16.8 | 30,755 | 81.2 | 14.4 | 0 |
| W25 (13/06) | 19.6 | 44,760 | 72.6 | 2 | 0 |
| W26 (20/06) | 18.6 | 35,692 | 79.7 | 20.8 | 0 |
| W27 (27/06) | 17.8 | 34,132 | 79.7 | 24.6 | 0 |
| W28 (04/07) | 18.2 | 39,591 | 79.1 | 0.6 | 0 |
| W29 (11/07) | 20.6 | 38,191 | 73.0 | 0 | 0 |
| W30 (18/07) | 21.8 | 34,753 | 77.5 | 14.4 | 5.1 |
| W31 (25/07) | 19.4 | 32,717 | 77.5 | 1.2 | 1.7 |
| W32 (01/08) | 21.2 | 34,135 | 73.8 | 0 | 5.1 |
| W33 (08/08) | 22.9 | 40,933 | 65.5 | 0 | 5.1 |
| W34 (15/08) | 20.5 | 24,952 | 84.6 | 24.2 | 2.5 |
| W35 (22/08) | 21.0 | 28,340 | 80.3 | 0 | 2.5 |
| W36 (29/08) | 19.7 | 26,517 | 80.3 | 0 | 0 |
| W37 (05/09) | 18.2 | 20,759 | 89.3 | 58.2 | 0 |
| W38 (12/09) | 14.6 | 14,999 | 93.8 | 65.6 | 0 |
| W39 (19/09) | 11.9 | 19,453 | 91.7 | 12.4 | 0 |
| W40 (26/09) | 11.6 | 14,155 | 93.0 | 57.8 | 0 |
| W41 (03/10) | 12.2 | 15,258 | 88.8 | 2.2 | 0 |
| W42 (10/10) | 11.5 | 12,214 | 94.1 | 3.4 | 0 |
| W43 (17/10) | 14.7 | 11,548 | 94.8 | 10.4 | 0 |
| W44 (24/10) | 15.4 | 11,725 | 91.6 | 2.4 | 0 |
| Week | Average Temperature (°C) | Radiation Sum (W·m−2) | Relative Humidity (%) | Precipitation (mm) | Irrigation Treatment (mm) |
|---|---|---|---|---|---|
| W18 (24/04) | 9.8 | 28,550 | 67.5 | 6.4 | 0 |
| W19 (01/05) | 14.0 | 33,012 | 66.9 | 21 | 0 |
| W20 (08/05) | 13.8 | 22,901 | 80.1 | 26.8 | 0 |
| W21 (15/05) | 13.0 | 38,675 | 66.4 | 4.2 | 0 |
| W22 (22/05) | 14.8 | 40,198 | 64.0 | 0 | 0 |
| W23 (29/05) | 16.3 | 50,469 | 57.1 | 0 | 0 |
| W24 (05/06) | 21.1 | 48,772 | 55.7 | 0 | 18 |
| W25 (12/06) | 22.5 | 43,780 | 50.5 | 0.6 | 21 |
| W26 (19/06) | 21.7 | 39,262 | 66.4 | 17.8 | 18 |
| W27 (26/06) | 19.0 | 26,008 | 64.6 | 5.8 | 18 |
| W28 (03/07) | 19.9 | 34,068 | 61.7 | 12.6 | 18 |
| W29 (10/07) | 20.4 | 35,065 | 61.3 | 10.6 | 19 |
| W30 (17/07) | 18.0 | 30,327 | 67.9 | 13.2 | 30 |
| W31 (24/07) | 17.9 | 25,584 | 74.2 | 43.4 | 0 |
| W32 (31/07) | 16.3 | 19,845 | 83.4 | 63.8 | 0 |
| W33 (07/08) | 18.5 | 33,279 | 71.2 | 17.2 | 0 |
| W34 (14/08) | 20.6 | 30,832 | 73.6 | 0 | 15 |
| W35 (21/08) | 18.9 | 24,655 | 77.2 | 27.8 | 15 |
| W36 (28/08) | 16.8 | 22,388 | 80.6 | 22.4 | 0 |
| W37 (04/09) | 22.0 | 31,190 | 73.8 | 0.2 | 0 |
| W38 (11/09) | 18.6 | 21,195 | 81.7 | 37.4 | 17 |
| W39 (18/09) | 15.6 | 15,842 | 79.5 | 29.2 | 0 |
| W40 (25/09) | 16.0 | 16,798 | 79.9 | 1.2 | 17 |
| W41 (02/10) | 16.5 | 16,290 | 75.4 | 0.8 | 17 |
| W42 (09/10) | 15.0 | 11,488 | 80.8 | 26.8 | 12 |
| W43 (16/10) | 12.0 | 10,380 | 82.1 | 33 | 0 |
| W44 (23/10) | 10.8 | 10,356 | 89.0 | 28.2 | 0 |
References
- Agentschap Landbouw en Zeevisserij. Productiewaarde Sierteelt. Available online: https://landbouwcijfers.vlaanderen.be/landbouw/sierteelt/productiewaarde-sierteelt (accessed on 10 December 2024).
- VLAM Marketingsdienst. Sierteeltbarometer 2022. Available online: https://www.flandersplants.com/sites/vlamfresh_floriculture/files/publication/file/Sierteeltbarometer%202022.pdf (accessed on 10 December 2024).
- Calvin, K.; Dasgupta, D.; Krinner, G.; Mukherji, A.; Thorne, P.W.; Trisos, C.; Romero, J.; Aldunce, P.; Barrett, K.; Blanco, G.; et al. IPCC, 2023: Climate Change 2023: Synthesis Report. Contribution of Working Groups I, II and III to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; Core Writing Team, Lee, H., Romero, J., Eds.; IPCC: Geneva, Switzerland, 2023. [Google Scholar]
- Carón, M.M.; De Frenne, P.; Brunet, J.; Chabrerie, O.; Cousins, S.A.O.; De Backer, L.; Decocq, G.; Diekmann, M.; Heinken, T.; Kolb, A.; et al. Interacting Effects of Warming and Drought on Regeneration and Early Growth of Acer pseudoplatanus and A. platanoides. Plant Biol. 2015, 17, 52–62. [Google Scholar] [CrossRef] [PubMed]
- Khalil, A.A.M.; Grace, J. Acclimation to Drought in Acer Pseudoplatanus L. (Sycamore) Seedlings. J. Exp. Bot. 1992, 43, 1591–1602. [Google Scholar] [CrossRef]
- Kunz, J.; Räder, A.; Bauhus, J. Effects of Drought and Rewetting on Growth and Gas Exchange of Minor European Broadleaved Tree Species. Forests 2016, 7, 239. [Google Scholar] [CrossRef]
- Koç, İ. Comparison of the Gas Exchange Parameters of Two Maple Species (Acer negundo and Acer pseudoplatanus) Seedlings under Drought Stress. Bartın Orman Fak. Derg. 2022, 24, 65–76. [Google Scholar] [CrossRef]
- Hipps, N.A.; Higgs, K.H.; Collard, L.G. The Effect of Irrigation and Root Pruning on the Growth of Sycamore (Acer pseudoplatanus) Seedlings in Nursery Beds and after Transplantation. J. Hortic. Sci. Biotechnol. 1996, 71, 819–828. [Google Scholar] [CrossRef]
- Fini, A.; Ferrini, F.; Frangi, P.; Amoroso, G. Growth and Physiology of Field-Grown Acer pseudoplatanus L. Trees as Influenced by Irrigation and Fertilization. In SNA Research Conference; Field Production: Columbus, OH, USA, 2007; Volume 52, pp. 51–55. [Google Scholar]
- Fini, A.; Mattii, G.B.; Ferrini, F. Physiological Responses to Different Irrigation Regimes for Shade Trees Grown in Container. Adv. Hortic. Sci. 2008, 22, 13–20. [Google Scholar]
- Bianchi, A.; Masseroni, D.; Thalheimer, M.; de Medici Leonardo, O.; Facchi, A. Field Irrigation Management through Soil Water Potential Measurements: A Review. Ital. J. Agrometeorol. 2017, 22, 25–38. [Google Scholar]
- Thompson, R.; Delcour, I.; Berckmoes, E.; Stavridou, E. The Fertigation Bible Technologies to Optimise Fertigation in Intensive Horticulture. Horizon 2020 grant No 689687. 2018. Available online: https://projectbluearchive.blob.core.windows.net/media/Default/Imported%20Publication%20Docs/The%20Fertigation%20Bible.pdf (accessed on 10 December 2024).
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration. Guidelines for Computing Crop Water Requirements. In FAO Irrigation and Drainage Paper No. 56; FAO: Rome, Italy, 1998. [Google Scholar]
- Campbell, G.S.; Campbell, M.D. Irrigation Scheduling Using Soil Moisture Measurements: Theory and Practice. In Advances in Irrigation; Hillel, D., Ed.; Elsevier: Amsterdam, The Netherlands, 1982; Volume 1, pp. 25–42. [Google Scholar]
- Jones, H.G. Irrigation Scheduling: Advantages and Pitfalls of Plant-Based Methods. J. Exp. Bot. 2004, 55, 2427–2436. [Google Scholar] [CrossRef]
- Jones, H.G. Irrigation Scheduling-Comparison of Soil, Plant and Atmosphere Monitoring Approaches. Acta Hortic. 2008, 792, 391–403. [Google Scholar] [CrossRef]
- Mane, S.; Das, N.; Singh, G.; Cosh, M.; Dong, Y. Advancements in Dielectric Soil Moisture Sensor Calibration: A Comprehensive Review of Methods and Techniques. Comput. Electron. Agric. 2024, 218, 108686. [Google Scholar] [CrossRef]
- Kroes, J.; Supit, I.; Van Dam, J.; Van Walsum, P.; Mulder, M. Impact of Capillary Rise and Recirculation on Simulated Crop Yields. Hydrol. Earth Syst. Sci. 2018, 22, 2937–2952. [Google Scholar] [CrossRef]
- Steppe, K.; De Pauw, D.J.W.; Lemeur, R. A Step towards New Irrigation Scheduling Strategies Using Plant-Based Measurements and Mathematical Modelling. Irrig. Sci. 2008, 26, 505–517. [Google Scholar] [CrossRef]
- McCutchan, H.; Shackel, K.A. Stem-Water Potential as a Sensitive Indicator of Water Stress in Prune Trees (Prunus domestica L. Cv. French). J. Am. Soc. Hortic. Sci. 1992, 117, 607–611. [Google Scholar] [CrossRef]
- Begg, J.E.; Turner, N.C. Water Potential Gradients in Field Tobacco. Plant Physiol. 1970, 46, 343–346. [Google Scholar] [CrossRef]
- Garnier, E.; Berger, A. Testing Water Potential in Peach Trees as an Indicator of Water Stress. J. Hortic. Sci. 1985, 60, 47–56. [Google Scholar] [CrossRef]
- Meyer, W.S.; Green, G.C. Plant Indicators of Wheat and Soybean Crop Water Stress. Irrig. Sci. 1981, 2, 167–176. [Google Scholar] [CrossRef]
- ISO 11274:2019; Soil Quality—Determination of the Water-Retention Characteristic—Laboratory Methods. ISO: Geneva, Switzerland, 2019.
- Raes, D. BUDGET—A Soil Water and Salt Balance Model—Reference Manual Version 5.0; Institute for Land and Water Management: Leuven, Belgium, 2002. [Google Scholar]
- Janssens, P.; Elsen, F.; Elsen, A.; Vandendriessche, H.; Be, P.; Deckers, T. Adapted Soil Water Balance Model for Irrigation Scheduling in ‘Conference’ Pear Orchards. Acta Hortic. 2011, 919, 39–56. [Google Scholar] [CrossRef]
- Janssens, P.; Boonen, M.; Bylemans, D.; Melis, P.; Van Delm, T.; Vendel, I.; Hertog, M.; Elsen, A.; Vandendriessche, H. Limited Irrigation of Field-Grown Strawberry (Fragaria × Ananassa Cv. ‘Elsanta’) in a Temperate Climate: Effects on Yield and Quality. Eur. J. Hortic. Sci. 2024, 89, 1–10. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Core Team: Vienna, Austria, 2021. [Google Scholar]
- Kassambara, A. Ggpubr: “ggplot2” Based Publication Ready Plots. R Package Version 0.6.0. 2023. Available online: https://cran.r-project.org/web/packages/ggpubr/index.html (accessed on 10 December 2024).
- Wickham, H. Ggplot2: Elegant Graphics for Data Analysis; Springer: New York, NY, USA, 2016; ISBN 978-3-319-24277-4. Available online: https://ggplot2.tidyverse.org (accessed on 10 December 2024).
- Wickham, H. Forcats: Tools for Working with Categorical Variables (Factors). R Package Version 1.0.0. 2021. Available online: https://cran.r-project.org/web/packages/forcats/index.html (accessed on 10 December 2024).
- Wickham, H.; Bryan, J. Readxl: Read Excel Files. R Package Version 1.4.2. 2022. Available online: https://cran.r-project.org/web/packages/readxl/index.html (accessed on 23 January 2023).
- Janssens, P.; Diels, J.; Vanderborght, J.; Elsen, F.; Elsen, A.; Deckers, T.; Vandendriessche, H. Numerical calculation of soil water potential in an irrigated ‘conference’ pear orchard. Agric. Water Manag. 2015, 148, 113–122. [Google Scholar] [CrossRef]
- ten Damme, L.; Jing, S.; Montcalm, A.M.; Jepson, M.; Andersen, M.N.; Hansen, E.M. Proper Management of Irrigation and Nitrogen-Application Increases Crop N-Uptake Efficiency and Reduces Nitrate Leaching. Acta Agric. Scand. B Soil Plant Sci. 2022, 72, 913–922. [Google Scholar] [CrossRef]
- Vázquez, N.; Pardo, A.; Suso, M.L.; Quemada, M. Drainage and Nitrate Leaching under Processing Tomato Growth with Drip Irrigation and Plastic Mulching. Agric. Ecosyst. Environ. 2006, 112, 313–323. [Google Scholar] [CrossRef]
- Hack-Ten Broeke, M.J.D. Irrigation Management for Optimizing Crop Production and Nitrate Leaching on Grassland. Agric. Water Manag. 2001, 49, 97–114. [Google Scholar] [CrossRef]
- Naor, A. Irrigation and Crop Load Influence Fruit Size and Water Relations in Field-Grown “Spadona” Pear. J. Am. Soc. Hortic. Sci. 2001, 126, 252–255. [Google Scholar] [CrossRef]
- Intrigliolo, D.S.; Castel, J.R. Performance of Various Water Stress Indicators for Prediction of Fruit Size Response to Deficit Irrigation in Plum. Agric. Water Manag. 2006, 83, 173–180. [Google Scholar] [CrossRef]
- Talluto, G.; Farina, V.; Volpe, G.; Lo Bianco, R. Effects of Partial Rootzone Drying and Rootstock Vigour on Growth and Fruit Quality of ‘Pink Lady’ Apple Trees in Mediterranean Environments. Aust. J. Agric. Res. 2008, 59, 785–794. [Google Scholar] [CrossRef]
- Janssens, P.; Deckers, T.; Elsen, F.; Elsen, A.; Schoofs, H.; Verjans, W.; Vandendriessche, H. Sensitivity of Root Pruned Conference Pear to Water Deficit in a Temperate Climate. Agric. Water Manag. 2011, 99, 58–66. [Google Scholar] [CrossRef]
- Mcdonald, S.E. Irrigation in Forest Tree Nurseries: Monitoring and Effects on Seedling Growth. In Forest Nursery Manual: Production of Bareroot Seedlings; Duryea, M.L., Landis, T.D., Perry, C.R., Eds.; Springer Dordrecht: Dordrecht, The Netherlands, 1984; Volume 11, p. 107121. [Google Scholar]
- Correia, M.J.; Pereira, J.S.; Chaves, M.M.; Rodrigues, M.L.; Pacheco, C.A. ABA Xylem Concentrations Determine Maximum Daily Leaf Conductance of Field-Grown Vitis vinifera L. Plants. Plant Cell Env. 1995, 18, 511–521. [Google Scholar] [CrossRef]
- Löbbe, T.; Schuldt, B.; Leuschner, C. Acclimation of Leaf Water Status and Stem Hydraulics to Drought and Tree Neighbourhood: Alternative Strategies among the Saplings of Five Temperate Deciduous Tree Species. Tree Physiol. 2017, 37, 456–468. [Google Scholar] [CrossRef]
- Keller, S.Q.; McCauley, D.; Sheridan, R.A.; Scagel, C.; Nackley, L. Comparing Drought Responses of Red Oak (Quercus rubra) and Red Maple (Acer rubrum) in Field-Grown Nursery Production. J. Am. Soc. Hortic. Sci. 2024, 149, 302–309. [Google Scholar] [CrossRef]
- De Swaef, T.; Steppe, K.; Lemeur, R. Determining Reference Values for Stem Water Potential and Maximum Daily Trunk Shrinkage in Young Apple Trees Based on Plant Responses to Water Deficit. Agric. Water Manag. 2009, 96, 541–550. [Google Scholar] [CrossRef]
- Naor, A. Relations between Leaf and Stem Water Potentials and Stomatal Conductance in Three Field-Grown Woody Species. J. Hortic. Sci. Biotechnol. 1998, 73, 431–436. [Google Scholar] [CrossRef]
- Naor, A.; Cohen, S. Sensitivity and Variability of Maximum Trunk Shrinkage, Midday Stem Water Potential, and Transpiration Rate in Response to Withholding Irrigation from Field-Grown Apple Trees. HortScience 2003, 38, 547–551. [Google Scholar] [CrossRef]
- Janssens, P. Plant-Soil-Water Relations and Implications for the Management of Irrigation and Fertilization in “Conference” Pear Orchards in a Temperate Climate. Ph.D. Dissertation, Université de Liège, Liège, Belgium, 2015. [Google Scholar]
- Abrisqueta, I.; Conejero, W.; Valdés-Vela, M.; Vera, J.; Ortuño, M.F.; Ruiz-Sánchez, M.C. Stem Water Potential Estimation of Drip-Irrigated Early-Maturing Peach Trees under Mediterranean Conditions. Comput. Electron. Agric. 2015, 114, 7–13. [Google Scholar] [CrossRef]
- Lampinen, B.D.; Shackel, K.A.; Southwick, S.M.; Olson, W.H. Deficit Irrigation Strategies Using Midday Stem Water Potential in Prune. Irrig. Sci. 2001, 20, 47–54. [Google Scholar] [CrossRef]
- Nortes, P.A.; Pérez-Pastor, A.; Egea, G.; Conejero, W.; Domingo, R. Comparison of Changes in Stem Diameter and Water Potential Values for Detecting Water Stress in Young Almond Trees. Agric. Water Manag. 2005, 77, 296–307. [Google Scholar] [CrossRef]
- Shackel, K.A.; Ahmadi, H.; Biasi, W.; Buchner, R.; Goldhamer, D.; Gurusinghe, S.; Hasey, J.; Kester, D.; Krueger, B.; Lampinen, B.; et al. Plant Water Status as an Index of Irrigation Need in Deciduous Fruit Trees. Horttechnology 1997, 7, 23–29. [Google Scholar] [CrossRef]
- Williams, L.E.; Araujo, F.J. Correlations among Predawn Leaf, Midday Leaf, and Midday Stem Water Potential and Their Correlations with Other Measures of Soil and Plant Water Status in Vitis vinifera. J. Am. Soc. Hortic. Sci. 2002, 127, 448–454. [Google Scholar] [CrossRef]
- Percival, D.C.; Proctor, J.T.A.; Privé, J.P. Gas Exchange, Stem Water Potential and Leaf Orientation of Rubus idaeus L. Are Influenced by Drought Stress. J. Hortic. Sci. Biotechnol. 1998, 73, 831–840. [Google Scholar] [CrossRef]
- Fox, L.; Montague, T. Influence of Irrigation Regime on Growth of Select Field-Grown Tree Species in a Semi-Arid Climate. J. Environ. Monit. Restor. 2009, 27, 134–138. [Google Scholar] [CrossRef]
- Montague, D.T.; Bates, A. Montague and Bates: Response of Maple to Reduced Irrigation Response of Two Field-Grown Maple (Acer) Species to Reduced Irrigation in a High Vapor Pressure, Semi-Arid Climate. Arboric. Urban For. 2015, 41, 334–345. [Google Scholar]
- Ponder, H.G.; Gilliam, C.H.; Wilkinson, E.; Eason, J.; Evans, C.E. Influence of Trickle Irrigation and Nitrogen Rates to Acer rubrum L. J. Environ. Hortic. 1984, 2, 40–43. [Google Scholar] [CrossRef]
- Steppe, K.; Sterck, F.; Deslauriers, A. Diel Growth Dynamics in Tree Stems: Linking Anatomy and Ecophysiology. Trends Plant Sci. 2015, 20, 335–343. [Google Scholar] [CrossRef] [PubMed]
- De Swaef, T.; De Schepper, V.; Vandegehuchte, M.W.; Steppe, K. Stem Diameter Variations as a Versatile Research Tool in Ecophysiology. Tree Physiol. 2015, 35, 1047–1061. [Google Scholar] [CrossRef]
- Köcher, P.; Horna, V.; Leuschner, C.; Abrams, M. Environmental Control of Daily Stem Growth Patterns in Five Temperate Broad-Leaved Tree Species. Tree Physiol. 2012, 32, 1021–1032. [Google Scholar] [CrossRef]
- Valdovinos-Ayala, J.; Robles, C.; Fickle, J.C.; Pérez-De-Lis, G.; Pratt, R.B.; Jacobsen, A.L. Seasonal Patterns of Increases in Stem Girth, Vessel Development, and Hydraulic Function in Deciduous Tree Species. Ann. Bot. 2022, 130, 355–365. [Google Scholar] [CrossRef]
- Garnier, E.; Berger, A. Effect of Water Stress on Stem Diameter Changes of Peach Trees Growing in the Field. J. Appl. Ecol. 1986, 23, 193–209. [Google Scholar] [CrossRef]
- de Jong van Lier, Q. Field capacity, a valid upper limit of crop available water? Agric. Water Manag. 2017, 193, 214–220. [Google Scholar] [CrossRef]
- Twarakavi, N.K.C.; Sakai, M.; Šimůnek, J. An objective analysis of the dynamic nature of field capacity. Water Resour. Res. 2009, 45, 1–9. [Google Scholar] [CrossRef]
- Raes, D.; Deproost, P. Model to assess water movement from a shallow water table to the root zone. Agric. Water Manag. 2003, 62, 79–91. [Google Scholar] [CrossRef]
- Raes, D.; Steduto, P.C.; Hsiao, T.; Fereres, E. Reference Manual: AquaCrop Version 6.0-6.1; FAO: Rome, Italy, 2018. [Google Scholar] [CrossRef]
- Camargo, G.G.T.; Kemanian, A.R. Six crop models differ in their simulation of water uptake. Agric. For Meteorol. 2016, 220, 116–129. [Google Scholar] [CrossRef]
- Or, D.; Lehmann, P.; Shahraeeni, E.; Shokri, N. Advances in Soil Evaporation Physics-A Review. Vadose Zo. J. 2013, 12, 1–16. [Google Scholar] [CrossRef]
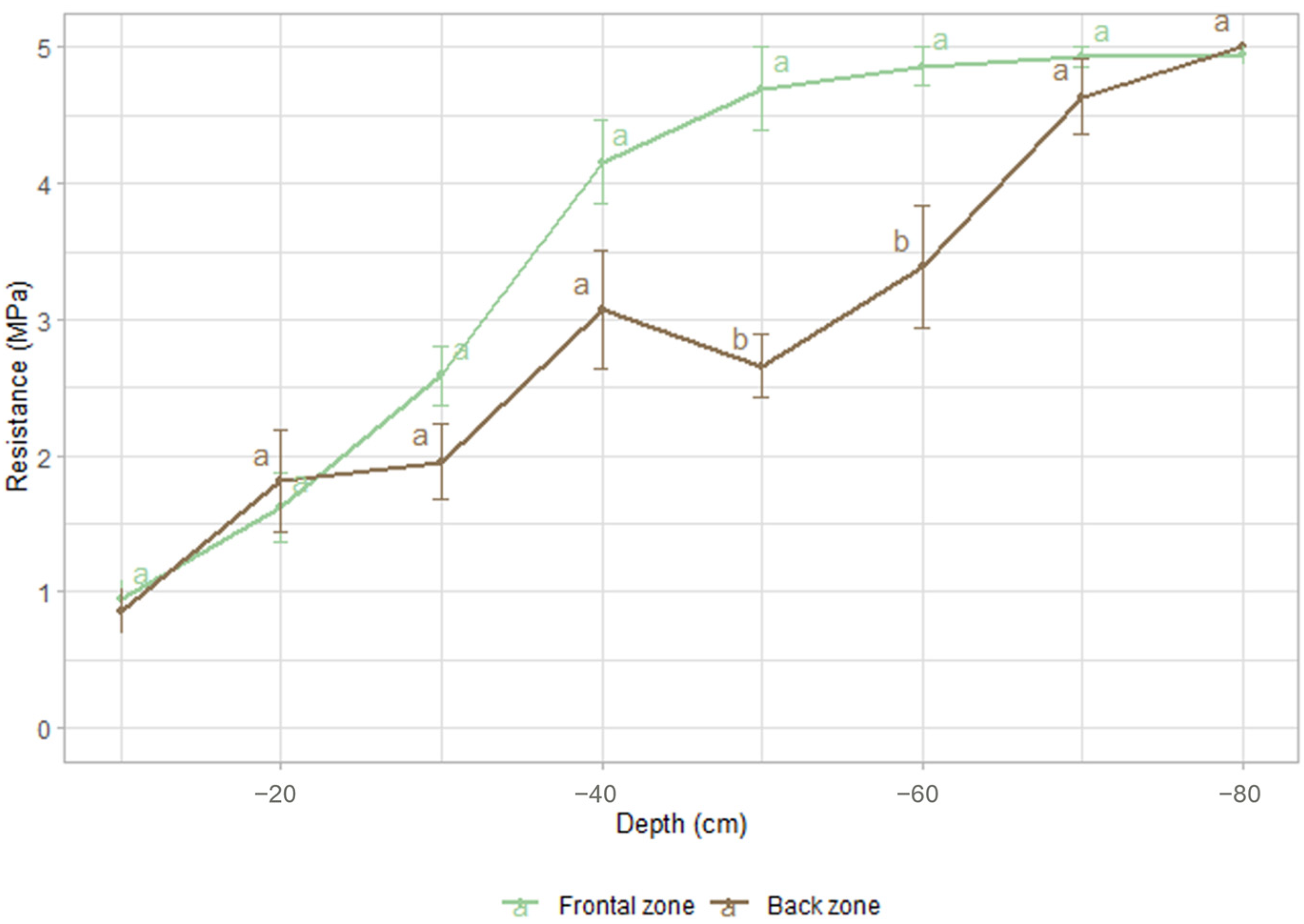




| Location in Field | Soil Texture | pH-KCL | Total Organic Carbon (%) | Magnesium (mg·100 g−1) | Calcium (mg·100 g−1) |
|---|---|---|---|---|---|
| Front zone | Fine sand | 5.0 | 1.61 | 9.0 | 74 |
| Back zone | Coarse sand | 4.3 | 1.53 | 5.0 | 41 |
| Treatment and Year | 2022 | 2023 | |
|---|---|---|---|
| Water retention at pF 0 | Rain-fed | 0.44 ± 0.01 | 0.42 ± 0.01 |
| Irrigation | 0.43 ± 0.00 | 0.42 ± 0.01 | |
| Water retention at pF 2 | Rain-fed | 0.26 ± 0.01 | 0.24 ± 0.01 |
| Irrigation | 0.27 ± 0.00 | 0.23 ± 0.01 | |
| Water retention at pF 2.7 | Rain-fed | 0.15 ± 0.02 | 0.15 ± 0.01 |
| Irrigation | 0.18 ± 0.01 | 0.17 ± 0.02 | |
| Water retention at pF 4.2 | Rain-fed | 0.05 ± 0.01 | 0.05 ± 0.00 |
| Irrigation | 0.05 ± 0.01 | 0.05 ± 0.00 | |
| Input Parameters | ||||
| Experimental Period | 5 April 2022–1 October 2022 | 1 April 2023–5 October 2023 | ||
| Average depth groundwater (m) | 1.9 | 1.4 | ||
| Rainfall (mm) | 376 | 408 | ||
| ETo (mm) | 540 | 509 | ||
| Output Parameters | ||||
| Irrigation Treatment | Rain-Fed | Irrigation | Rain-Fed | Irrigation |
| Irrigation (mm) | 0 | 19 | 0 | 224 |
| Capillary rise (mm) | 16 | 16 | 51 | 48 |
| Water losses due to percolation (mm) | 116 | 105 | 151 | 298 |
| ETC (mm) | 508 | 508 | 470 | 479 |
| ETa (mm) | 286 | 315 | 367 | 458 |
| ETa·ETc−1 | 0.56 | 0.6 | 0.78 | 0.95 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
De Clercq, P.; De Vroe, A.; Janssens, P.; Steppe, K.; Van Haecke, D.; Gobin, B.; Van Labeke, M.-C.; Dhooghe, E. Effect of a Soil Water Balance Controlled Irrigation on the Cultivation of Acer pseudoplatanus Forest Tree Liners Under Non-Limiting and Limiting Soil Water Conditions. Horticulturae 2025, 11, 435. https://doi.org/10.3390/horticulturae11040435
De Clercq P, De Vroe A, Janssens P, Steppe K, Van Haecke D, Gobin B, Van Labeke M-C, Dhooghe E. Effect of a Soil Water Balance Controlled Irrigation on the Cultivation of Acer pseudoplatanus Forest Tree Liners Under Non-Limiting and Limiting Soil Water Conditions. Horticulturae. 2025; 11(4):435. https://doi.org/10.3390/horticulturae11040435
Chicago/Turabian StyleDe Clercq, Paulien, Aster De Vroe, Pieter Janssens, Kathy Steppe, Dominique Van Haecke, Bruno Gobin, Marie-Christine Van Labeke, and Emmy Dhooghe. 2025. "Effect of a Soil Water Balance Controlled Irrigation on the Cultivation of Acer pseudoplatanus Forest Tree Liners Under Non-Limiting and Limiting Soil Water Conditions" Horticulturae 11, no. 4: 435. https://doi.org/10.3390/horticulturae11040435
APA StyleDe Clercq, P., De Vroe, A., Janssens, P., Steppe, K., Van Haecke, D., Gobin, B., Van Labeke, M.-C., & Dhooghe, E. (2025). Effect of a Soil Water Balance Controlled Irrigation on the Cultivation of Acer pseudoplatanus Forest Tree Liners Under Non-Limiting and Limiting Soil Water Conditions. Horticulturae, 11(4), 435. https://doi.org/10.3390/horticulturae11040435







