Next Article in Journal
Design of a 2–4 Decoder Based on All-Spin Logic and Magnetic Tunnel Junction
Next Article in Special Issue
Copper(II)-Promoted Reactions of α-Pyridoin Oxime: A Dodecanuclear Cluster and a 2D Coordination Polymer
Previous Article in Journal
Correction: Atalay et al. Fabrication of a Portable Magnetic Microcantilever Using Fe40Ni38Mo4B18 Amorphous Ribbon and Its Application as a Humidity Sensor by Coating with TiO2 Nanotubes. Magnetochemistry 2024, 10, 98
Previous Article in Special Issue
Exploring the Potential of Oxalyldihydrazide-Derived Schiff Bases as Versatile Ligands: Synthesis, Structural Characterization, and Magnetic Properties
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Magnetochemistry
Volume 11
Issue 2
10.3390/magnetochemistry11020016
magnetochemistry-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Er(III) and Yb(III) Complexes with a Tripodal Nitroxyl Radical: Magnetochemical Study and Ab Initio Calculations

by
Mauro Perfetti
1,
Alexey A. Dmitriev
2 and
Kira E. Vostrikova
3,*
1
Department of Chemistry “U. Schiff”, INSTM-University of Florence Research Unit, Via della Lastruccia 3–13, 50019 Sesto Fiorentino, FI, Italy
2
Voevodsky Institute of Chemical Kinetics and Combustion, Siberian Branch, Russian Academy of Sciences, 630090 Novosibirsk, Russia
3
Nikolaev Institute of Inorganic Chemistry, Siberian Branch, Russian Academy of Sciences, 630090 Novosibirsk, Russia
*
Author to whom correspondence should be addressed.
Magnetochemistry 2025, 11(2), 16; https://doi.org/10.3390/magnetochemistry11020016
Submission received: 26 December 2024 / Revised: 8 February 2025 / Accepted: 12 February 2025 / Published: 14 February 2025
(This article belongs to the Special Issue Latest Research on the Magnetic Properties of Coordination Compounds)
Browse Figures
Versions Notes

Abstract

:
In this paper, we investigate the magnetic exchange interaction and magnetization dynamics of two new members of the [LnRad(NO3)3] family, where Rad is a tripodal nitroxide, and Ln is Er(III) or Yb(III), having the prolate type electron density. Single OK crystal and powder X-ray diffraction studies showed that these complexes are isostructural with their previously investigated Y, Gd, Dy, Tm, Tb, Eu, and Lu congeners. A magnetometric investigation, supported by ab initio calculations, showed the presence of antiferromagnetic coupling between the lanthanide ion and the radical in both compounds with estimated J values of ≈7 and ≈20 cm−1 for Er and Yb, respectively (+J Seff∙ S formalism).

1. Introduction

The primary objective of materials chemists is to modify the electronic structure of a coordination compound so that specific properties are achieved. This can be accomplished by modifying the symmetry and field strength of the ligands that interact with the central atom. The precise regulation of these parameters is facilitated by the employment of ligands that demonstrate a particular tendency to adopt a specific coordination mode. Organic tripodal molecules, which have a donor atom at each of their three “legs”, exhibit predictable coordination, making them an excellent choice for designing chemical complexes with a specific geometry. Additionally, the geometry of these complexes can be easily modified using synthetic organic chemistry techniques. As a result, tripodal ligands are widely used in various fields of applied coordination chemistry, such as the design of molecular gears and motors [1,2], biochemical [3,4,5] and photophysical [6,7,8] applications, catalysis [9,10,11,12,13,14], chemosensing [15,16,17], electroluminescence [6,18,19], and molecular magnetism [8,20,21,22].
The tripodal function of the radical ligand 4,4-dimethyl-2,2-bis(pyridin-2-yl)-1,3-oxazolidine-3-oxyl (Rad, Figure 1a) is provided not only by a set of donor atoms, the oxygen atom of the nitroxyl group and two nitrogen atoms of the 2-pyridyl substituents, but also by the presence of an sp3 carbon acting as a bridgehead. In all previously studied metal complexes involving Rad, only the tripodal mode of its coordination has been found, where the ligand occupies sites on the vertices of a triangle in the coordination sphere of the metal ion [7,20,23,24,25,26,27,28,29,30]. In this particular context, trivalent lanthanide nitrates were identified as suitable precursors. The rationale behind this choice is that the presence of three nitrate anions results in the blocking of six coordination sites, thereby leaving room for only one paramagnetic tripod. This, in turn, leads to the formation of a neutral complex [LnRad(NO3)3], which does not contain any solvent molecules, as illustrated in Figure 1b.
For this paramagnetic tripod, strong magnetic exchange interactions were recorded with 3d metal ions [23,27] and Gd(III) [7] and field-induced slow magnetic relaxation for the Co(II) [25] and Tb(III) [7] complexes. A significant amount of research has focused on lanthanide complexes with paramagnetic ligands, including nitroxyl radicals (NR). However, there is a paucity of studies on the strength of magnetic exchange interactions in NR complexes with lanthanides such as erbium and ytterbium, which exhibit prolate electron density [31] and are Kramers ions (half-integer total spin). It has been observed that Er(III) complexes could be candidates for single-molecule magnets (SMMs), exhibiting a slightly lower level of potential in comparison to Dy(III) [20,32,33,34,35]. The majority of the investigated complexes of NRs encompass two radicals [36,37,38,39,40,41,42,43], while only a few articles describe complexes with one paramagnetic ligand [44,45,46,47,48]. In earlier research, using gadolinium complexes as an example, it was shown that the strength of the magnetic exchange interaction for nitronyl nitroxyl (NN) radicals with Ln3+ was significantly lower than the same parameter for the lanthanide complexes with NRs (TEMPO, DOXYL, etc.) [49]. This is due to the fact that in the former, the spin density is distributed over four centers (O…N….N…O), whereas in the latter, an unpaired electron is shared between two atoms (N…O) [50,51]. Furthermore, the number of papers describing radical complexes of Er(III) and Yb(III) is quite scarce.
In the present work, we described the synthesis and characterization of two new representatives of the [LnRad(NO3)3] series of complexes, where Ln = Er, Yb. The results of the comprehensive magnetochemical and computational studies for these compounds are also presented. Using the calculated crystal field parameters, we were able to fit the experimental magnetic data in order to extract the values of the coupling constants.

2. Materials and Methods

Er(NO3)3·6H2O, Yb(NO3)3·6H2O, and 2,2′-Dipyridyl ketone (99%) were used as received from suppliers (ChemCraft, Kaliningrad, Russia, and Sigma-Aldrich, Saint Louis, MO, USA, correspondingly). The 4,4-dimethyl-2,2-bis(pyridin-2-yl)-1,3-oxazolidine N-oxyl radical was prepared according to a known method [23]. The synthesis of the complexes was performed in an aerobic environment. Elemental (C, H, N) analyses were carried out using standard methods with a Euro-Vector 3000 analyzer (Eurovector, Redavalle, Italy). Powder XRD was carried out using a Shimadzu XRD-7000S diffractometer (Shimadzu, Kyoto, Japan) (CuKα radiation, Ni filter, 2θ angle range from 5° to 30°) using a Dectris MYTHEN2 R 1K detector (λ = 1.54178 Å, Kyoto, Japan). Simulated patterns from the X-ray crystal structure were obtained with Diamond 3.0 (Crystal Impact GbR: Bonn, Germany) from the crystal structures of 1·0.5CH2Cl2·0.5Et2O and 2·CH2Cl2. Fourier transform infrared (FTIR) spectra were measured in ATR mode with a Perkin–Elmer System 2000 FTIR spectrometer (Perkin Elmer, Waltham, MA, USA) in the 4000–500 cm−1 range. A QD MPMS SQUID magnetometer (Quantum Design GmbH, Darmstadt, Germany) was used to study the DC and AC magnetic properties of the compounds in the temperature range 2–300 K with an applied field of 0.1 T for DC measurements, and up to 5 T in the frequency range 1–1000 Hz (for AC characterization). The polycrystalline samples were pressed in a teflon pellet to avoid the preferential orientation of the crystallites. The diamagnetic contributions of the samples were estimated using Pascal’s Constants [52].

2.1. Synthesis of the Compounds

[LnRad(NO3)3] was synthesized according to the procedure used for Er congener.
[ErRad(NO3)3] (1). A solution of the ligand (60 mg, 0.22 mmol) in 0.5 mL of acetonitrile was added to a solution of the nitrate salt, 93 mg (0.2 mmol) of Er(NO3)3·6H2O, in 0.5 mL of CH3CN. The reaction mixture was carefully heated up to 45 C without stirring. When lemon yellow crystals began to form, heating was stopped. The reaction vial was stoppered and allowed to cool slowly on a plate wrapped in heat-insulating material. The next day, the polycrystalline sample was carefully separated from the mother liquor, rinsed with acetone, then with ether, and dried in air. Yield: 60 mg, 80%. Anal. calcd (%) for C15H16ErN6O11: C, 28.94; H, 2.6; N, 13.51. Found: C, 29.3; H, 2.3; N, 13.55. IR (KBr): ν (cm−1) 3127 (w), 2984 (w), 2934 (w), 2892 (w), 1599 (m), 1507 (s), 1491 (s), 1472 (s), 1437 (s), 1379 (m), 1368 (sh), 1287 (sh), 1264 (s), 1192 (w), 1163 (m), 1148 (m), 1103 (w), 1074 (m), 1063 (m), 1022 (s), 1003 (m), 980 (w), 960 (w), 941 (sh), 930 (w), 912 (w), 903 (w), 876 (w), 833 (w), 814 (m), 772 (s), 758 (w), 743 (s), 708 (w), 679 (sh), 664 (m), 638 (m), 621 (m), 567 (m), 513 (w), 419 (w).
[YbRad(NO3)3] (2). Yb(NO3)3·6H2O—96 mg, 0.22 mmol, Rad—63 mg, 0.23 mmol. Yield: 70%. Anal. calcd (%) for C15H16YbN6O11: C, 28.57; H, 2.6; N, 13.34. Found: C, 28.6; H, 2.2; N, 13.41. IR (KBr): ν (cm−1) 3134 (w), 2986 (w), 2941 (w), 2897(w), 1621 (sh), 1605 (s), 1570 (w), 1536 (s), 1518 (s), 1504 (s), 1491 (s), 1476 (sh), 1464 (sh), 1441 (s), 1385 (s), 1300 (s), 1288 (sh), 1277 (s), 1260 (sh), 1227 (w), 1194 (w), 1150 (w), 1103 (w), 1078 (m), 1063 (m), 1028 (s), 1020 (sh), 1005 (m), 982 (w), 958 (w), 939 (sh), 932 (w), 912 (w), 902 (w), 837 (sh), 814 (m), 772 (s), 748 (m), 708 (m), 664 (m), 643 (m), 638 (m), 621 (w), 569 (w), 515 (m), 424 (w), 415 (sh).

2.2. X-Ray Structure Determination

Single-crystal XRD data for 1 were collected with a Bruker D8 Venture diffractometer (Karlsruhe, Germany) equipped with a CMOS PHOTON III detector and IμS 3.0 source (MoKα, λ = 0.71073 Å, graphite monochromator, φ- and ω-scans with a step of 0.5°) at 100 K, respectively (Table S1). The φ- and ω-scan techniques were employed to measure intensities. Absorption corrections were applied with the use of the SADABS program_ENREF_50 [53]. The crystal structure was solved and refined using the SHELXL-2019/3 [54,55] program with OLEX2 GUI [56]. Atomic displacement parameters for non-hydrogen atoms were refined anisotropically.

2.3. Computational Details

The computational study of the electronic structures of [LnRad(NO3)3] complexes was performed at DFT and ab initio levels [57,58]. The XRD geometry at 100 K was used in all calculations for the complex [YbRad(NO3)3] (2). In all performed calculations for the complex [ErRad(NO3)3] (1), the ytterbium atom was substituted by the erbium one. The DFT calculation with the following NPA [59] analysis was performed at B3LYP [60] using Gaussian 16 and NBO 7.0 [61] program packages. The natural charge distributions (Figure S1) and spin density (Figure S2 and S3) were calculated at the B3LYP/def2–TZVP level with the SARC2–DKH–QZVP basis set for Er and Yb. These distributions for the lowest quintet and triplet states of the Er complex and the lowest triplet and singlet states of the Yb complex were taken into account. The electronic structure calculations for [ErRad(NO3)3] (1) at ab initio SA-CASSCF/NEVPT2/QDPT level [62,63,64,65] were performed using the ORCA 5.0.3 [66,67,68] program package, and [YbRad(NO3)3] (2) at ab initio RASSCF/XMS-CASPT2/SO-RASSI/Single-Aniso level [62,63,64,65] were performed using the OpenMOLCAS program package [69,70] (version 21.06).
Relativistic effects were taken into account with the use of DKH2 Hamiltonian [71,72]. The SARC2-DKH-QZVP [73] basis set for Er and DKH-def2-TZVP(-f) [74,75] basis set for other atoms were used for calculations and JK auxiliary basis sets for RI-JK approximation to the Coulomb and exchange integrals [76,77]. In the case of 2, ANO-RCC-VDZ was used for C and H atoms and ANO-RCC-VTZP for the other atoms [78]. Spin–orbit coupling effects in 1 were included using quasi-degenerate perturbation theory (QDPT) with mixing CASSCF states in the spin–orbit mean field [79]. The spin–orbit coupling in 2 was treated non-perturbatively within the mean-field theory in the restricted active space state interaction (SO-RASSI) method [80,81]. The temperature and field dependences of magnetic susceptibility for 1 were calculated by differentiating the QDPT Hamiltonian with respect to the magnetic field. To calculate the static magnetic properties of 2, the SINGLE_ANISO program [82,83] was used.

3. Results and Discussion

3.1. Characterization

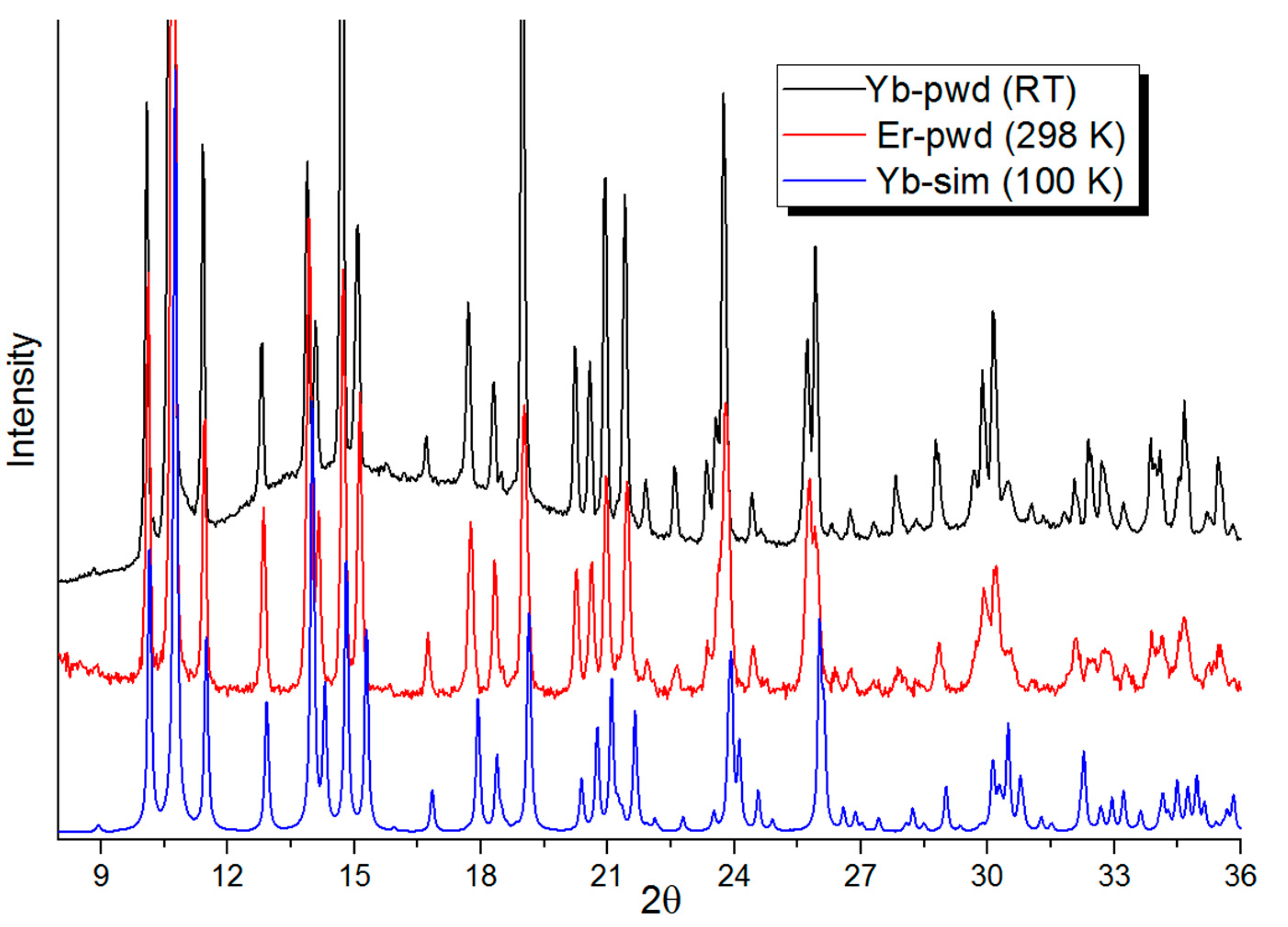
3.1.1. Crystal and Molecular Structure

As established in previous studies of single-crystal and powder RXD of the series complexes [LnRad(NO3)3] (Ln = Gd, Dy, Tb, Tm, Y, Eu, and Lu), all complexes in this series are isostructural [7]. Powder diffractograms indicate that complexes 1 and 2 are isostructural with their congeners (Figure 2). The crystal cell parameters for 1 and 2, along with the SCXRD experimental details, are delineated in Table S1.
According to the stereochemical analysis [84], the LnO7N2 polyhedron for the series [7] is best defined as a spherical tricapped trigonal prism geometry belonging to D3h point group symmetry. In the neutral complexes, the paramagnetic ligand is coordinated to the central atom in a tridentate tripodal manner through two nitrogen atoms of the two pyridyl substituents and one oxygen of the NO group (Figure 2) and three [NO3]− moieties acting as bidentate anionic ligands compensating the tri-positive charge of the Ln atom. The three donor atoms (N,N,O) of Rad form a triangular face of the prism. The Yb–ORad bond distances are 2.3451 (16) Å. N–O bond length of the nitroxide group is 1.281 (2) Å. Notably, both these bond lengths and the angles are within the anticipated range. The packing of molecules and distances between lanthanide ions correspond to those for the previously published complexes [7].

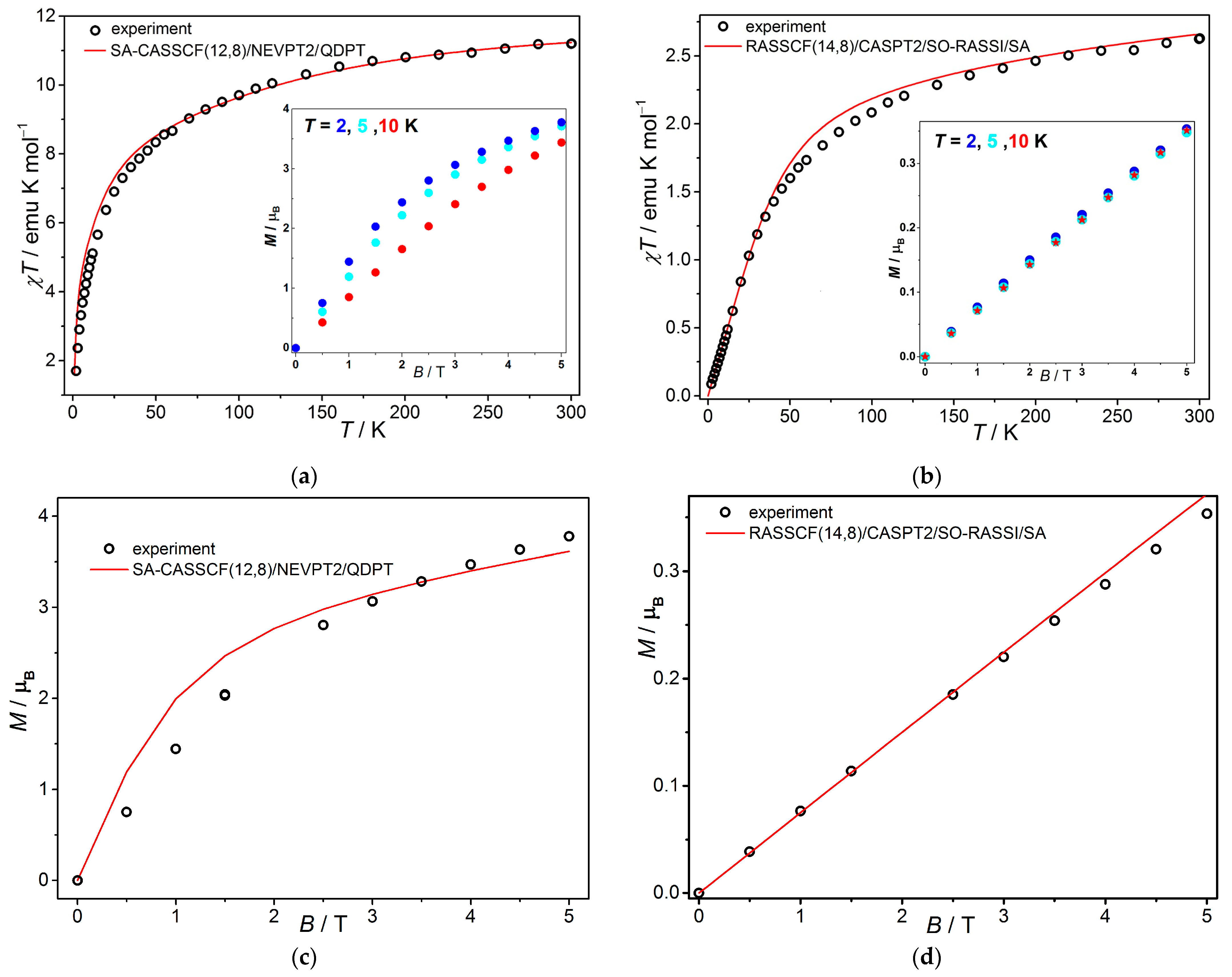
3.1.2. SQUID Magnetometry

The temperature dependence of susceptibility for randomly oriented pressed polycrystalline samples of 1 and 2 is presented in Figure 3a,b as a χT(T) plot. The χT at 300 K reaches the value of 11.20 and 2.60 emu K mol−1 for 1 and 2, respectively. In both cases, the value is lower than the sum of the contributions expected from a radical and Er3+ or Yb3+ (0.375 and 11.48/2.57 emu K mol−1). Upon lowering the temperature, the value decreases, reaching ca. 1.5 and 0 emu K mol−1 at 2 K for 1 and 2, respectively. Such behavior suggests strong antiferromagnetic (AFM) coupling between the lanthanide and the radical, as previously observed for other isostructural complexes containing other lanthanide ions [7,85]. The M vs. B plots of 1 (inset in Figure 3a) are not linear, but they never saturate and their value is far from the one expected for an axial environment of the Er3+ ion and a radical (4.5 + 1 = 5.5 µB) [86]. This observation indicates that the metal ion does not exhibit a highly axial ground state and that the AFM interaction between the radical and the Er3+ is relatively strong. The M vs. B plots of 2 (inset in Figure 3b) are instead linear, superimposable, and reach an extremely low value (0.36 µB) at 5 T and 2 K, suggesting a very strong AFM coupling between Yb3+ and the radical generating a diamagnetic spin ground state (GS). Coherently, no ac signal was observed at any temperature for 1 and 2.

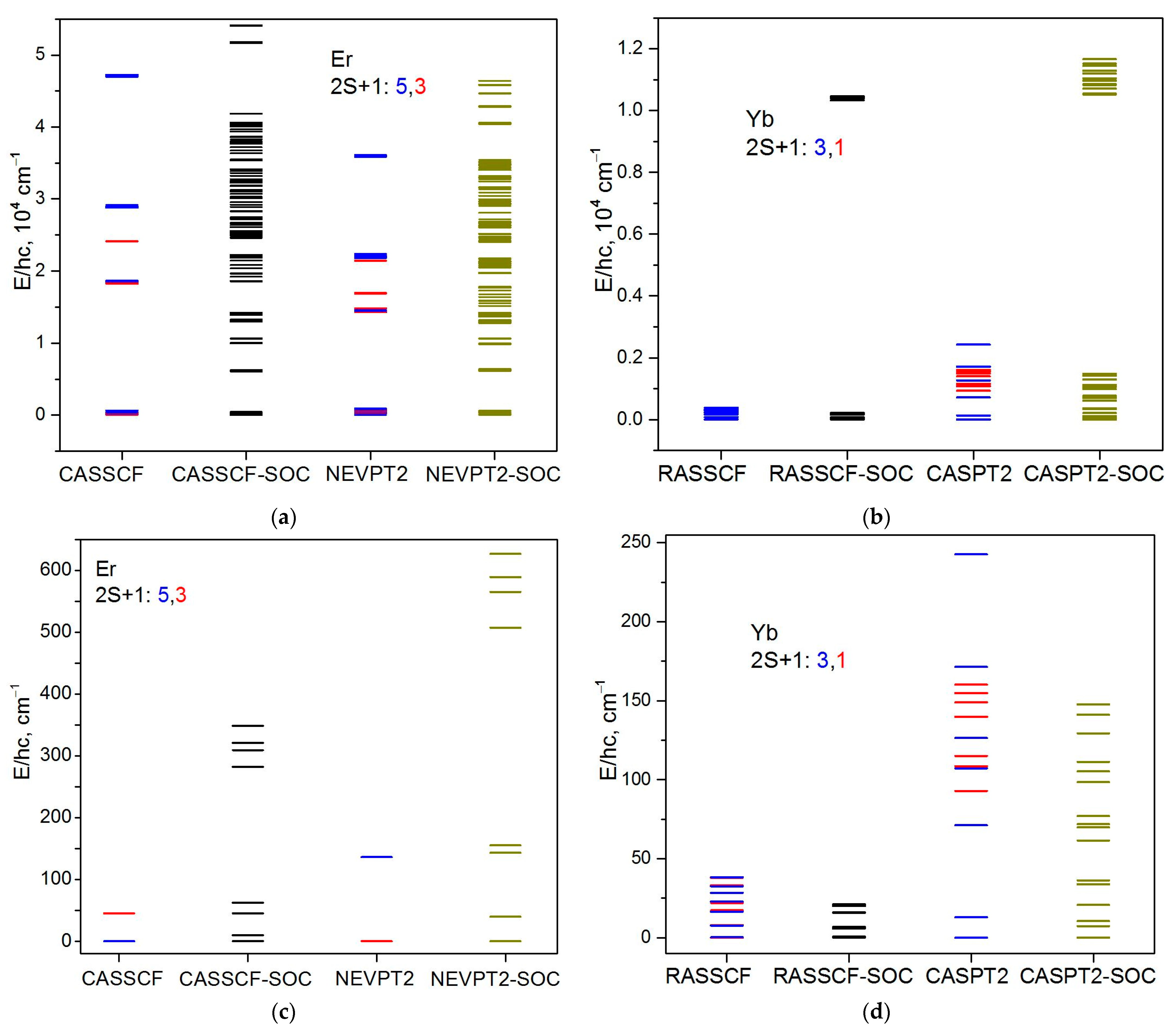
3.2. Theoretical Calculations and Magnetic Behavior Modeling

Active space was constructed with seven 4f orbitals of Er or Yb and one SOMO of radical ligand with dominant orbital density on the nitroxyl (NO) group coordinated by the metal ion (Figure 4); 12 and 14 electrons were taken into account for Er and Yb, correspondingly. Based on the result of interaction between erbium 4I or ytterbium 2F terms and the radical 2S term, 35 quintets and triplets for 1, as well as 7 triplet and singlet states for 2, were taken into consideration.
The natural charge distributions (NCDs) of the ground triplet and ground singlet states of 1 and 2 (see Figures S1 and S2) are nearly identical for both complexes. The charges on the Er and Yb ions are 1.5 and 1.7, which is consistent with the DFT calculation results for Ln(III) complexes in general. The charge distribution on the donor atoms exhibits a negative character, with values approaching −0.5 on nitrate oxygens and −0.45 on pyridyl nitrogens. Notably, lower values are observed on the oxygen atom of the nitroxyl moiety of the radical, with estimates of −0.37 and −0.31 for 1 and 2, respectively. This distribution leads to the formation of a relatively strong crystal field.
For the tripod, the lower negative charge density in the oxygen donor compared to the pyridyl nitrogens may be attributed to the stronger interaction with the lanthanide cation, accompanied by the partial charge transfer to the 5d and 6s orbitals of the lanthanide from the oxygen orbitals. This was shown in thorough NBO and ETS-NOCV calculations for the isostructural Eu complex in our recent paper [7], and we suppose that the mechanism of coordination is the same in the current case. The spin density calculations for the triplet ground state of 1 (Figure S2) and the first excited state of 2 (Figure S3) yielded the anticipated results. As the DFT method is incapable of reproducing the SD of the diamagnetic GS, the calculation of the first excited triplet state of 2 was performed to define the SD distribution in a molecule of the complex. The SD values of Er and Yb ions were found to be close to 3 and 1, respectively. Additionally, the SD distribution on the O and N atoms of the nitroxyl group exhibited a nearly equal distribution, with a positive SD for Er and a negative SD for Yb.
The complete electronic structures of complexes 1 and 2 after the calculations at different levels of theory are shown in Figure 5a,b. The account of the dynamic correlation leads to the inversion of the lowest spin-specific roots, which is shown in Figure 5c,d. Tables S2 and S3 show the wavefunction composition of the lowest roots according to the CASSCF calculations. All of them represent a strongly multireference character with the electronic configurations differing by the population of 4f orbitals with one electron always on the radical ligand SOMO.
The account of spin–orbit coupling (SOC) leads to the splitting into the groups of four states (see Figure 5, SOC) that can be regarded as the consequence of the interaction between the Kramers doublets (KDs) of the lanthanide cation subsequent to the consideration of the crystal field (CF) and Kramers doublet of the radical ligand.
The calculated temperature dependences (red lines in Figure 3a,c) of the magnetic molecular susceptibility show reliable coincidence with the experiment data for both complexes. In the case of 2, the calculated magnetization curve reproduces well the experimental one (Figure 3d). The magnetization of 1 displays a slight divergence between the theoretical and experimental plots, with the calculated curve exhibiting a quicker saturation exit. This discrepancy can be attributed to the disparity in the methodologies employed for the dynamic correlation account, namely NEVPT2 for the Er complex and XMS–CASPT2 for the Yb one. The NEVPT2 procedure addresses exclusively the contributions to the energy of the considered states, whereas XMS–CASPT2 additionally considers the interaction between the states of specific multiplicity and the perturbation of the initial RASSCF wavefunctions, yielding a novel set of state energies and corresponding wavefunctions (See Supplementary Materials). Therefore, in the case of ytterbium, there are more hidden correlations considered within the XMS–CASPT2 framework, leading to the better reproduction of the experimental data. In the case of complex 1, the XMS-CASPT2 approach was not employed due to the substantial computational demands associated with the extensive number of states. The NEVPT2 calculations were deemed the more reliable approach. More details about all calculations employed in the case of erbium and ytterbium complexes can be found at the end of Supplementary Materials.
In order to extract the exchange coupling directly from the experimental magnetic data in a fitting procedure, we performed the ab initio calculations for the anion and cation forms of both complexes. Our goal was to take the energies of the lowest corresponding to the splitting of the lanthanide ion states with J = 15/2 (Er) and J = 7/2 (Yb). As it is difficult to assess the influence of the crystal field on the lanthanides in the neutral complex with the radical part, this scheme was applied. The decomposition of the wavefunctions corresponding to the lowest metal ion multiplets in wavefunctions with definite projections of the total moment on the quantization axis for both complexes are presented in Table 1 and Table 2. According to these results, the wavefunctions of all states have a rather multireference nature.
Finally, to estimate the coupling between a lanthanide and a radical in 1 and 2, we have used the two sets of crystal field parameters obtained by ab initio calculations for the anionic and cationic derivatives of the (Er/Yb)Rad(NO3)3; i.e., the species with a formal absence of an unpaired electron on the tripodal ligand (see Tables S4 and S5 in Supplementary Materials). The resulting values of the ground state g tensor are reported in Table 3. Subsequently, the following Hamiltonian, acting on the radical spin (S = 1/2) and a lanthanide effective spin (Seff = 1/2), was employed to simulate the low-temperature magnetization plot:
H = μ B g f r e e B · S ^ r a d + μ B B · g e f f · S ^ e f f , L n + J S ^ r a d · S ^ e f f , L n
In Equation (1), gfree is the g value of the radical (taken as 2.0023), geff is the g tensor obtained from the ab initio calculations, and J is an isotropic coupling constant. The results of this simulation are reported in Table 3 and Figure 6. Their excellent agreement with the experiments shows that the coupling between the radical and the lanthanide is strong and antiferromagnetic, the values obtained for 1 starting from the cationic and the anionic structures being extremely similar. It is worth noting that the fits obtained for 2 vary more, even though they remain of the same order of magnitude. This finding indicates that the minor alterations to the structure, resulting from the in-silico removal or addition of one electron, can, under certain conditions, exert a substantial influence on the resultant magnetic properties. It is noteworthy that the value of JEr-Rad is approximately 7 cm−1, which is substantially larger than the value of +0.12 cm−1 [45] found for [(NIT-2-Pm)Er(hfac)3] but lower than +15 cm−1 [47] obtained for the [(NN)Er(hfac)3] radical complexes. The only value of JYb-Rad that was found in the literature for the complex [(NN)Yb(hfac)3] is +3 cm−1 [47], which is considerably lower than the corresponding values from Table 3.

4. Conclusions

In this paper, we have analyzed the magnetic behavior of two new complexes of generic formula [LnRad(NO3)3] (Ln = Er, Yb). Single crystal and powder X-ray diffraction studies showed that these two compounds are isostructural to their congeners [LnRad(NO3)3], where Ln = Y, Gd, Dy, Tm, Tb, Eu, and Lu. The field dependencies of magnetization, obtained using DC magnetometry, allowed us to estimate the magnetic coupling between the radical and the lanthanide. The values of about 7 and 20 cm−1 estimated for JLn-Rad for Er and Yb, respectively, are remarkably large. Furthermore, the magnetization temperature and field dependencies obtained from ab initio calculations demonstrate excellent agreement with the experiments.

Supplementary Materials

The following supporting information can be downloaded at https://www.mdpi.com/article/10.3390/magnetochemistry11020016/s1; Table S1: SCXRD experimental details; Figure S1: Natural charge distribution calculated at UB3LYP/def2-TZVP level with SARC2-DKH-QZVP basis set for Er and relativistic DKH2 Hamiltonian: for the ground triplet state of [ErRad(NO3)3] (left) and for the ground singlet state of [YbRad(NO3)3]; Figure S2: Spin density map for [ErRad(NO3)3] calculated for the ground triplet state at UB3LYP/def2-TZVP level with SARC2-DKH-QZVP basis set for Er and relativistic DKH2 Hamiltonian; Figure S3: Spin density map for [YbRad(NO3)3] calculated for the first excited triplet state at UB3LYP/def2-TZVP level with SARC2-DKH-QZVP basis set for Yb and relativistic DKH2 Hamiltonian; Table S2: Lowest 13 quintets and triplets after SA-CASSCF (12,8) calculations (total 35 quintets and triplets) of 1 with their energies and contributions (>0.1) of different electronic configurations to the wavefunction of each root; Table S3: Lowest 7 triplets and singlets after SA-CASSCF(14,8) calculations (total 7 triplets and singlets) of 2 with their energies and contributions (>0.1) of different electronic configurations to the wavefunction of each root; Table S4: The crystal field parameters B k q calculated for the ground state of the anion and cation forms of 1 (J = 15/2); Table S5: The crystal field parameters calculated for the ground state of the anion and cation forms of 2 (J = 7/2); Figure S4: The results of the computation at different levels of theory for 2: (a) RASSCF/XMS-CASPT2/SO-RASSI (A) and SA-CASSCF/NEVPT2/QDPT (B); (b) SA-CASSCF(14,8)/QD-NEVPT2; (c) state-averaged version of NEVPT2.

Author Contributions

Conceptualization, All; methodology, K.E.V.; formal analysis, M.P. and A.A.D.; investigation, K.E.V.; resources, K.E.V.; data curation, M.P. and K.E.V.; writing—original draft preparation, All; writing—review and editing, All; visualization, K.E.V.; funding acquisition, K.E.V. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the Russian Science Foundation, grant number 23-23-00437.

Data Availability Statement

Crystallographic data have been deposited at the CCDC under CCDC number 2412095 and can be obtained directly from https://www.ccdc.cam.ac.uk/structures. Accessed on 20 December 2024.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Kammerer, C.; Rapenne, G. Scorpionate Hydrotris(Indazolyl)Borate Ligands as Tripodal Platforms for Surface-Mounted Molecular Gears and Motors. Eur. J. Inorg. Chem. 2016, 2016, 2214–2226. [Google Scholar] [CrossRef]
  2. Chen, K.-Y.; Ivashenko, O.; Carroll, G.T.; Robertus, J.; Kistemaker, J.C.M.; London, G.; Browne, W.R.; Rudolf, P.; Feringa, B.L. Control of Surface Wettability Using Tripodal Light-Activated Molecular Motors. J. Am. Chem. Soc. 2014, 136, 3219–3224. [Google Scholar] [CrossRef]
  3. Rabinovich, D. Synthetic Bioinorganic Chemistry: Scorpionates Turn 50 BT—50 Years of Structure and Bonding—The Anniversary Volume; Mingos, D.M.P., Ed.; Springer International Publishing: Cham, Switzerland, 2017; pp. 139–157. ISBN 978-3-319-35138-4. [Google Scholar]
  4. Eliseeva, S.V.; Bünzli, J.-C.G. Lanthanide Luminescence for Functional Materials and Bio-Sciences. Chem. Soc. Rev. 2010, 39, 189–227. [Google Scholar] [CrossRef] [PubMed]
  5. Kurşunlu, A.N.; Özmen, M.; Güler, E. A Fluorescent Sensor-Based Tripodal-Bodipy for Cu (II) Ions: Bio-Imaging on Cells. Turkish J. Chem. 2021, 45, 31. [Google Scholar] [CrossRef]
  6. Yu, T.; Zhao, Y.; Fan, D.; Hong, Z.; Su, W. Preparation, Photo- and Electro-Luminescent Properties of a Novel Complex of Tb (III) with a Tripod Ligand. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2008, 69, 654–658. [Google Scholar] [CrossRef] [PubMed]
  7. Perfetti, M.; Caneschi, A.; Sukhikh, T.S.; Vostrikova, K.E. Lanthanide Complexes with a Tripodal Nitroxyl Radical Showing Strong Magnetic Coupling. Inorg. Chem. 2020, 59, 16591–16598. [Google Scholar] [CrossRef]
  8. Lyubov, D.M.; Mahrova, T.V.; Cherkasov, A.V.; Fukin, G.K.; Fedorov, Y.V.; Trifonov, A.A. Synthesis, Structures, and Luminescent Properties of Chloride and Nitrate LnIII Complexes Coordinated by Tris(pyrazolyl)methane. Eur. J. Inorg. Chem. 2023, 26, e202300292. [Google Scholar] [CrossRef]
  9. Szczepura, L.F.; Witham, L.M.; Takeuchi, K.J. Tris(2-Pyridyl) Tripod Ligands. Coord. Chem. Rev. 1998, 174, 5–32. [Google Scholar] [CrossRef]
  10. Natrajan, L.; Pécaut, J.; Mazzanti, M.; LeBrun, C. Controlled Hydrolysis of Lanthanide Complexes of the N-Donor Tripod Tris(2-pyridylmethyl)amine versus Bisligand Complex Formation. Inorg. Chem. 2005, 44, 4756–4765. [Google Scholar] [CrossRef] [PubMed]
  11. Bellemin-Laponnaz, S.; Gade, L.H. A Modular Approach to C1 and C3 Chiral N-Tripodal Ligands for Asymmetric Catalysis. Angew. Chem. Int. Ed. 2002, 41, 3473–3475. [Google Scholar] [CrossRef]
  12. Chen, Y.-J.; Chen, H.-H. 1,1,1-Tris(hydroxymethyl)ethane as a New, Efficient, and Versatile Tripod Ligand for Copper-Catalyzed Cross-Coupling Reactions of Aryl Iodides with Amides, Thiols, and Phenols. Org. Lett. 2006, 8, 5609–5612. [Google Scholar] [CrossRef] [PubMed]
  13. Eckert, M.; Brethon, A.; Li, Y.-X.; Sheldon, R.A.; Arends, I.W.C.E. Study of the Efficiency of Amino-Functionalized Ruthenium and Ruthenacycle Complexes as Racemization Catalysts in the Dynamic Kinetic Resolution of 1-Phenylethanol. Adv. Synth. Catal. 2007, 349, 2603–2609. [Google Scholar] [CrossRef]
  14. Andrez, J.; Bozoklu, G.; Nocton, G.; Pécaut, J.; Scopelliti, R.; Dubois, L.; Mazzanti, M. Lanthanide(II) Complexes Supported by N,O-donor Tripodal Ligands: Synthesis, Structure, and Ligand-dependent Redox Behavior. Chem.—Eur. J. 2015, 21, 15188–15200. [Google Scholar] [CrossRef] [PubMed]
  15. Wietzke, R.; Mazzanti, M.; Latour, J.-M.; Pécaut, J.; Cordier, P.-Y.; Madic, C. Lanthanide(III) Complexes of Tripodal N-donor Ligands: Structural Models for the Species Involved in Solvent Extraction of Actinides(III). Inorg. Chem. 1998, 37, 6690–6697. [Google Scholar] [CrossRef]
  16. Dai, Z.; Canary, J.W. Tailoring Tripodal Ligands for Zinc Sensing. New J. Chem. 2007, 31, 1708–1718. [Google Scholar] [CrossRef]
  17. Kuswandi, B.; N/a, N.; Verboom, W.; Reinhoudt, D.N. Tripodal Receptors for Cation and Anion Sensors. Sensors 2006, 6, 978–1017. [Google Scholar] [CrossRef]
  18. Zhu, L.; Tang, H.; Harima, Y.; Yamashita, K.; Hirayama, D.; Aso, Y.; Otsubo, T. Electrochemical Properties of Self-assembled Monolayers of Tripod-Shaped Molecules and Their Applications to Organic Light-emitting Diodes. Chem. Commun. 2001, 18, 1830–1831. [Google Scholar] [CrossRef] [PubMed]
  19. Zheng, X.-L.; Liu, Y.; Pan, M.; Lü, X.-Q.; Zhang, J.-Y.; Zhao, C.-Y.; Tong, Y.-X.; Su, C.-Y. Bright Blue-Emitting Ce3+ Complexes with Encapsulating Polybenzimidazole Tripodal Ligands as Potential Electroluminescent Devices. Angew. Chem. Int. Ed. 2007, 46, 7399–7403. [Google Scholar] [CrossRef] [PubMed]
  20. Vostrikova, K.E. The Tripodal Ligand’s 4f Complexes: Use in Molecular Magnetism. Inorganics 2023, 11, 307. [Google Scholar] [CrossRef]
  21. Hay, M.A.; Boskovic, C. Lanthanoid Complexes as Molecular Materials: The Redox Approach. Chem. Eur. J. 2021, 27, 3608–3637. [Google Scholar] [CrossRef] [PubMed]
  22. Vostrikova, K.E.; Sukhikh, T.S.; Lavrov, A.N. The Synthesis, Crystal Structure, and Magnetic Properties of Mono-scorpionate Eu(III) Complexes. Inorganics 2023, 11, 418. [Google Scholar] [CrossRef]
  23. Ito, A.; Nakano, Y.; Urabe, M.; Tanaka, K.; Shiro, M. Structural and Magnetic Studies of Copper(II) and Zinc(II) Coordination Complexes Containing Nitroxide Radicals as Chelating Ligands. Eur. J. Inorg. Chem. 2006, 2006, 3359–3368. [Google Scholar] [CrossRef]
  24. Gass, I.A.; Lu, J.; Ojha, R.; Asadi, M.; Lupton, D.W.; Geoghegan, B.L.; Moubaraki, B.; Martin, L.L.; Bond, A.M.; Murray, K.S. [FeII(L•)2][TCNQF4•−]2: A Redox-active Double Radical Salt. Aust. J. Chem. 2019, 72, 769–777. [Google Scholar] [CrossRef]
  25. Gass, I.A.; Tewary, S.; Nafady, A.; Chilton, N.F.; Gartshore, C.J.; Asadi, M.; Lupton, D.W.; Moubaraki, B.; Bond, A.M.; Boas, J.F.; et al. Observation of Ferromagnetic Exchange, Spin Crossover, Reductively Induced Oxidation, and Field-induced Slow Magnetic Relaxation in Monomeric Cobalt Nitroxides. Inorg. Chem. 2013, 52, 7557–7572. [Google Scholar] [CrossRef] [PubMed]
  26. Gass, I.A.; Tewary, S.; Rajaraman, G.; Asadi, M.; Lupton, D.W.; Moubaraki, B.; Chastanet, G.; Létard, J.-F.; Murray, K.S. Solvate-Dependent Spin Crossover and Exchange in Cobalt(II) Oxazolidine Nitroxide Chelates. Inorg. Chem. 2014, 53, 5055–5066. [Google Scholar] [CrossRef] [PubMed]
  27. Gass, I.A.; Asadi, M.; Lupton, D.W.; Moubaraki, B.; Bond, A.M.; Guo, S.-X.; Murray, K.S. Manganese(II) Oxazolidine Nitroxide Chelates: Structure, Magnetism, and Redox Properties. Aust. J. Chem. 2014, 67, 1618. [Google Scholar] [CrossRef]
  28. Pedersen, A.H.; Geoghegan, B.L.; Nichol, G.S.; Lupton, D.W.; Murray, K.S.; Martínez-Lillo, J.; Gass, I.A.; Brechin, E.K. Hexahalorhenate(IV) Salts of Metal Oxazolidine Nitroxides. Dalt. Trans. 2017, 46, 5250–5259. [Google Scholar] [CrossRef]
  29. Gass, I.A.; Lu, J.; Asadi, M.; Lupton, D.W.; Forsyth, C.M.; Geoghegan, B.L.; Moubaraki, B.; Cashion, J.D.; Martin, L.L.; Bond, A.M.; et al. Use of the (TCNQF4)2− Dianion in the Spontaneous Redox Formation of [FeIII(L−)2][TCNQF4−]. Chempluschem 2018, 83, 658–668. [Google Scholar] [CrossRef] [PubMed]
  30. Rey, P.; Caneschi, A.; Sukhikh, T.S.; Vostrikova, K.E. Tripodal Oxazolidine-N-oxyl Diradical Complexes of Dy3+ and Eu3+. Inorganics 2021, 9, 91. [Google Scholar] [CrossRef]
  31. Vogel, R.; Müntener, T.; Häussinger, D. Intrinsic Anisotropy Parameters of a Series of Lanthanoid Complexes Deliver New Insights into the Structure-Magnetism Relationship. Chem 2021, 7, 3144–3156. [Google Scholar] [CrossRef]
  32. Brzozowska, M.; Handzlik, G.; Kurpiewska, K.; Zychowicz, M.; Pinkowicz, D. Pseudo-tetrahedral vs. Pseudo-octahedral Er(III) Single Molecule Magnets and the Disruptive Role of Coordinated TEMPO Radical. Inorg. Chem. Front. 2021, 8, 2817–2828. [Google Scholar] [CrossRef]
  33. Zhang, P.; Zhang, L.; Wang, C.; Xue, S.; Lin, S.-Y.; Tang, J. Equatorially Coordinated Lanthanide Single Ion Magnets. J. Am. Chem. Soc. 2014, 136, 4484–4487. [Google Scholar] [CrossRef] [PubMed]
  34. Brown, A.J.; Pinkowicz, D.; Saber, M.R.; Dunbar, K.R. A Trigonal-Pyramidal Erbium(III) Single-Molecule Magnet. Angew. Chem. Int. Ed. 2015, 54, 5864–5868. [Google Scholar] [CrossRef]
  35. Zhang, H.; Nakanishi, R.; Katoh, K.; Breedlove, B.K.; Kitagawa, Y.; Yamashita, M. Low Coordinated Mononuclear Erbium(III) Single-Molecule Magnets with C3v Symmetry: A Method for Altering Single-Molecule Magnet Properties by Incorporating Hard and Soft Donors. Dalt. Trans. 2018, 47, 302–305. [Google Scholar] [CrossRef] [PubMed]
  36. Wang, J.-M.; Wen, L.-M.; Liu, F.-F.; Wang, S.-P.; Zhang, J.-J.; Liu, Z.-Y. Magnetic Slow Relaxation of Pseudo-Binuclear Ln(III)-Nitronyl Nitroxide Radical Complexes Involving Non-Covalent O⋯O Interactions. J. Mol. Struct. 2020, 1207, 127735. [Google Scholar] [CrossRef]
  37. Wang, Y.; Fan, Z.; Yin, X.; Wang, S.; Yang, S.; Zhang, J.; Geng, L.; Shi, S. Structure and Magnetic Investigation of a Series of Rare Earth Heterospin Monometallic Compounds of Nitronyl Nitroxide Radical. Z. Für Anorg. Und Allg. Chem. 2016, 642, 148–154. [Google Scholar] [CrossRef]
  38. Zhao, Q.-H.; Ma, Y.-P.; Du, L.; Fang, R.-B. Three Novel Rare-Earth Complexes with Nitronyl Nitroxide Radical [RE(Hfac)3 (NITPhOCH3)2] (RE = GdIII, YIII and ErIII): Syntheses, Crystal Structures and Magnetic Properties. Transit. Met. Chem. 2006, 31, 593–597. [Google Scholar] [CrossRef]
  39. Xiao, Z.-X.; Miao, H.; Shao, D.; Wei, H.-Y.; Zhang, Y.-Q.; Wang, X.-Y. A Family of Lanthanide Compounds with Reduced Nitronyl Nitroxide Diradical: Syntheses, Structures and Magnetic Properties. Dalt. Trans. 2018, 47, 7925–7933. [Google Scholar] [CrossRef] [PubMed]
  40. Wang, X.-L. Four Tri-Spin Lanthanide–Nitronyl Nitroxide (LnIII = GdIII, DyIII, ErIII, and HoIII) Complexes: Syntheses, Structures, and Magnetic Properties. J. Coord. Chem. 2011, 64, 4334–4343. [Google Scholar] [CrossRef]
  41. Lv, X.-H.; Yang, S.-L.; Li, Y.-X.; Zhang, C.-X.; Wang, Q.-L. A Family of Lanthanide Compounds Based on Nitronyl Nitroxide Radicals: Synthesis, Structure, Magnetic and Fluorescence Properties. RSC Adv. 2017, 7, 38179–38186. [Google Scholar] [CrossRef]
  42. Wang, X.-L. Five New Tri-spin Lanthanide–Nitronyl Nitroxide (LnIII= GdIII, TbIII, DyIII, HoIII, ErIII) Complexes: Structures and Magnetic Properties. Inorganica Chim. Acta 2012, 387, 20–24. [Google Scholar] [CrossRef]
  43. Xie, J.; Li, C.; Sun, G.; Yang, M.; Li, L.-C. New 2p-3d-4f Chain Compounds [LnZn(Hfac)5(NIT-Pyrim)2] Constructed from Pyrimidine Based Nitronyl Nitroxides. Z. Für Anorg. Und Allg. Chem. 2018, 644, 827–832. [Google Scholar] [CrossRef]
  44. Dong, H.; Ma, S.; Zhong, Q.; Zhu, M. Crystal Structure, Magnetic Properties and Luminescent Behavior of Four Mononuclear Lanthanide-Radical Complexes. J. Mol. Struct. 2022, 1252, 132195. [Google Scholar] [CrossRef]
  45. Wang, J.; Miao, H.; Xiao, Z.-X.; Zhou, Y.; Deng, L.-D.; Zhang, Y.-Q.; Wang, X.-Y. Syntheses, Structures and Magnetic Properties of the Lanthanide Complexes of the Pyrimidyl-Substituted Nitronyl Nitroxide Radical. Dalt. Trans. 2017, 46, 10452–10461. [Google Scholar] [CrossRef]
  46. Wang, X.; Zhu, M.; Wang, J.; Li, L. Unusual Gd—Nitronyl Nitroxide Antiferromagnetic Coupling and Slow Magnetic Relaxation in the Corresponding Tb Analogue. Dalt. Trans. 2015, 44, 13890–13896. [Google Scholar] [CrossRef] [PubMed]
  47. Miao, H.; Li, H.-Q.; Shen, F.-X.; Wei, H.-Y.; Wang, B.-L.; Wang, X.-Y. A Family of Lanthanide Complexes with a Bis-Tridentate Nitronyl Nitroxide Radical: Syntheses, Structures and Magnetic Properties. Dalt. Trans. 2019, 48, 10337–10345. [Google Scholar] [CrossRef] [PubMed]
  48. Bai, F.; Yao, B.; Wang, R.; Wang, W.; Wang, Q.; Ma, Y.; Li, L. Structures and Magnetic Properties of Five Lanthanide-Radical Complexes Constructed by 8-Methoxyquinoline Substituted Tridentate Chelating Nitronyl Nitroxide Radical. J. Solid State Chem. 2021, 298, 122115. [Google Scholar] [CrossRef]
  49. Huang, G.; Daiguebonne, C.; Calvez, G.; Suffren, Y.; Guillou, O.; Guizouarn, T.; Le Guennic, B.; Cador, O.; Bernot, K. Strong Magnetic Coupling and Single-Molecule-Magnet Behavior in Lanthanide-TEMPO Radical Chains. Inorg. Chem. 2018, 57, 11044–11057. [Google Scholar] [CrossRef] [PubMed]
  50. Zheludev, A.; Barone, V.; Bonnet, M.; Delley, B.; Grand, A.; Ressouche, E.; Rey, P.; Subra, R.; Schweizer, J. Spin Density in a Nitronyl Nitroxide Free Radical. Polarized Neutron Diffraction Investigation and ab initio Calculations. J. Am. Chem. Soc. 1994, 116, 2019–2027. [Google Scholar] [CrossRef]
  51. Schweizer, J.; Ressouche, E. Neutron Scattering and Spin Densities in Free Radicals. In Magnetism: Molecules to Materials I; Miller, J.S., Drillon, M., Eds.; Wiley-VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 2001; pp. 325–355. ISBN 9783527600847. [Google Scholar]
  52. Bain, G.A.; Berry, J.F. Diamagnetic Corrections and Pascal’s Constants. J. Chem. Educ. 2008, 85, 532. [Google Scholar] [CrossRef]
  53. Apex3 Software Suite: Apex3, SADABS-2016/2 and SAINT 8.40a; Bruker AXS Inc.: Madison, WI, USA, 2017.
  54. Sheldrick, G.M. SHELXT—Integrated Space-Group and Crystal Structure Determination. Acta Crystallogr. Sect. A Found. Adv. 2015, 71, 3–8. [Google Scholar] [CrossRef] [PubMed]
  55. Sheldrick, G.M. Crystal Structure Refinement with SHELXL. Acta Crystallogr. Sect. C Struct. Chem. 2015, 71, 3–8. [Google Scholar] [CrossRef] [PubMed]
  56. Dolomanov, O.V.; Bourhis, L.J.; Gildea, R.J.; Howard, J.A.K.; Puschmann, H. OLEX2: A Complete Structure Solution, Refinement and Analysis Program. J. Appl. Crystallogr. 2009, 42, 339–341. [Google Scholar] [CrossRef]
  57. Wu, X.; Li, J.-F.; Yin, B. The Interpretation and Prediction of Lanthanide Single-Ion Magnets from ab initio Electronic Structure Calculation: The Capability and Limit. Dalt. Trans. 2022, 51, 14793–14816. [Google Scholar] [CrossRef] [PubMed]
  58. Chibotaru, L.F. Ab Initio Investigation of Anisotropic Magnetism and Magnetization Blocking in Metal Complexes BT—Computational Modelling of Molecular Nanomagnets; Rajaraman, G., Ed.; Springer International Publishing: Cham, Switzerland, 2023; pp. 1–62. ISBN 978-3-031-31038-6. [Google Scholar]
  59. Glendening, E.D.; Landis, C.R.; Weinhold, F. Natural Bond Orbital Methods. WIREs Comput. Mol. Sci. 2012, 2, 1–42. [Google Scholar] [CrossRef]
  60. Becke, A.D. Density-Functional Thermochemistry. III. The Role of Exact Exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef]
  61. Glendening, E.D.; Landis, C.R.; Weinhold, F. NBO 7.0: New Vistas in Localized and Delocalized Chemical Bonding Theory. J. Comput. Chem. 2019, 40, 2234–2241. [Google Scholar] [CrossRef]
  62. Roos, B.O.; Taylor, P.R.; Sigbahn, P.E.M. A Complete Active Space SCF Method (CASSCF) Using a Density Matrix Formulated Super-CI Approach. Chem. Phys. 1980, 48, 157–173. [Google Scholar] [CrossRef]
  63. Angeli, C.; Bories, B.; Cavallini, A.; Cimiraglia, R. Third-order Multireference Perturbation Theory: The n-Electron Valence State Perturbation-Theory Approach. J. Chem. Phys. 2006, 124, 054108. [Google Scholar] [CrossRef] [PubMed]
  64. Angeli, C.; Cimiraglia, R.; Evangelisti, S.; Leininger, T.; Malrieu, J.-P. Introduction of n-Electron Valence States for Multireference Perturbation Theory. J. Chem. Phys. 2001, 114, 10252–10264. [Google Scholar] [CrossRef]
  65. Angeli, C.; Cimiraglia, R.; Malrieu, J.-P. n-Electron Valence State Perturbation Theory: A Fast Implementation of the Strongly Contracted Variant. Chem. Phys. Lett. 2001, 350, 297–305. [Google Scholar] [CrossRef]
  66. Neese, F. Software Update: The ORCA Program System—Version 5.0. WIREs Comput. Mol. Sci. 2022, 12, e1606. [Google Scholar] [CrossRef]
  67. Neese, F.; Wennmohs, F.; Becker, U.; Riplinger, C. The ORCA Quantum Chemistry Program Package. J. Chem. Phys. 2020, 152, 224108. [Google Scholar] [CrossRef]
  68. Neese, F. The ORCA Program System. WIREs Comput. Mol. Sci. 2012, 2, 73–78. [Google Scholar] [CrossRef]
  69. Li Manni, G.; Fdez. Galván, I.; Alavi, A.; Aleotti, F.; Aquilante, F.; Autschbach, J.; Avagliano, D.; Baiardi, A.; Bao, J.J.; Battaglia, S.; et al. The OpenMolcas Web: A Community-driven Approach to Advancing Computational Chemistry. J. Chem. Theory Comput. 2023, 19, 6933–6991. [Google Scholar] [CrossRef] [PubMed]
  70. Aquilante, F.; Autschbach, J.; Baiardi, A.; Battaglia, S.; Borin, V.A.; Chibotaru, L.F.; Conti, I.; De Vico, L.; Delcey, M.; Fdez.Galván, I.; et al. Modern Quantum Chemistry with [Open]Molcas. J. Chem. Phys. 2020, 152, 214117. [Google Scholar] [CrossRef]
  71. Hess, B.A. Relativistic Electronic-Structure Calculations Employing a Two-component No-pair Formalism with External-Field Projection Operators. Phys. Rev. A 1986, 33, 3742–3748. [Google Scholar] [CrossRef]
  72. Wolf, A.; Reiher, M.; Hess, B.A. The Generalized Douglas–Kroll Transformation. J. Chem. Phys. 2002, 117, 9215–9226. [Google Scholar] [CrossRef]
  73. Aravena, D.; Neese, F.; Pantazis, D.A. Improved Segmented All-electron Relativistically Contracted Basis Sets for the Lanthanides. J. Chem. Theory Comput. 2016, 12, 1148–1156. [Google Scholar] [CrossRef]
  74. Weigend, F.; Ahlrichs, R. Balanced Basis Sets of Split Valence, Triple Zeta Valence and Quadruple Zeta Valence Quality for H to Rn: Design and Assessment of Accuracy. Phys. Chem. Chem. Phys. 2005, 7, 3297. [Google Scholar] [CrossRef]
  75. Pantazis, D.A.; Chen, X.-Y.; Landis, C.R.; Neese, F. All-electron Scalar Relativistic Basis Sets for Third-Row Transition Metal Atoms. J. Chem. Theory Comput. 2008, 4, 908–919. [Google Scholar] [CrossRef] [PubMed]
  76. Weigend, F. A Fully Direct RI-HF Algorithm: Implementation, Optimised Auxiliary Basis Sets, Demonstration of Accuracy and Efficiency. Phys. Chem. Chem. Phys. 2002, 4, 4285–4291. [Google Scholar] [CrossRef]
  77. Weigend, F. Hartree–Fock Exchange Fitting Basis Sets for H to Rn. J. Comput. Chem. 2008, 29, 167–175. [Google Scholar] [CrossRef] [PubMed]
  78. Roos, B.O.; Lindh, R.; Malmqvist, P.-Å.; Veryazov, V.; Widmark, P.-O. Main Group Atoms and Dimers Studied with a New Relativistic ANO Basis Set. J. Phys. Chem. A 2004, 108, 2851–2858. [Google Scholar] [CrossRef]
  79. Neese, F. Efficient and Accurate Approximations to the Molecular Spin-orbit Coupling Operator and Their Use in Molecular g-Tensor Calculations. J. Chem. Phys. 2005, 122, 034107. [Google Scholar] [CrossRef] [PubMed]
  80. Malmqvist, P.Å.; Roos, B.O.; Schimmelpfennig, B. The Restricted Active Space (RAS) State Interaction Approach with Spin–Orbit Coupling. Chem. Phys. Lett. 2002, 357, 230–240. [Google Scholar] [CrossRef]
  81. Roos, B.O.; Malmqvist, P.-Å. Relativistic Quantum Chemistry: The Multiconfigurational Approach. Phys. Chem. Chem. Phys. 2004, 6, 2919. [Google Scholar] [CrossRef]
  82. Chibotaru, L.F.; Ungur, L. Ab initio Calculation of Anisotropic Magnetic Properties of Complexes. I. Unique Definition of Pseudospin Hamiltonians and Their Derivation. J. Chem. Phys. 2012, 137, 064112. [Google Scholar] [CrossRef] [PubMed]
  83. Ungur, L.; Chibotaru, L.F. Computational Modelling of the Magnetic Properties of Lanthanide Compounds. In Lanthanides and Actinides in Molecular Magnetism; Wiley: Hoboken, NJ, USA, 2015; pp. 153–184. [Google Scholar]
  84. Llunell, M.; Casanova, D.; Cirera, J.; Alemany, P.; Alvarez, S. SHAPE, Version 2.1, Program for the Stereochemical Analysis of Molecular Fragments by Means of Continuous Shape Measures and Associated Tools; University of Barcelona: Barcelona, Spain, 2013. [Google Scholar]
  85. Sorace, L.; Dmitriev, A.A.; Perfetti, M.; Vostrikova, K.E. Slow Magnetic Relaxation and Strong Magnetic Coupling in the Nitroxyl Radical Complexes of Lanthanide(III) with Diamagnetic Ground State (Ln = Lu, Eu). Chem. Sci. 2025, 16, 218–232. [Google Scholar] [CrossRef] [PubMed]
  86. Briganti, M.; Lucaccini, E.; Chelazzi, L.; Ciattini, S.; Sorace, L.; Sessoli, R.; Totti, F.; Perfetti, M. Magnetic Anisotropy Trends along a Full 4f-Series: The f(n+7) Effect. J. Am. Chem. Soc. 2021, 143, 8108–8115. [Google Scholar] [CrossRef]
Magnetochemistry 11 00016 g001
Figure 1. (a) Tridentate oxazolidine radical, (Rad): 4,4-dimethyl-2,2-bis(pyridin-2-yl)-1,3-oxazolidine-3-oxyl.; (b) molecular structure of [LnRad(NO3)3], hydrogen atoms are omitted for clarity.
Figure 1. (a) Tridentate oxazolidine radical, (Rad): 4,4-dimethyl-2,2-bis(pyridin-2-yl)-1,3-oxazolidine-3-oxyl.; (b) molecular structure of [LnRad(NO3)3], hydrogen atoms are omitted for clarity.
Magnetochemistry 11 00016 g001
Magnetochemistry 11 00016 g002
Figure 2. Simulated (blue) and experimental powder patterns of the compounds [LnRad(NO3)3].
Figure 2. Simulated (blue) and experimental powder patterns of the compounds [LnRad(NO3)3].
Magnetochemistry 11 00016 g002
Magnetochemistry 11 00016 g003
Figure 3. Experimental (circles) and theoretical (red solid lines) magnetic data: (a) dependence of χT vs. T and magnetization plots M vs. B for 1 at three different temperatures (insert); (b) dependence of χT vs. T and magnetization plots M vs. B at three different temperatures (insert) for 2; (c) magnetization plot M vs. B for 1 at 2 K; (d) magnetization plot M vs. B for 2 at 2 K. See text for details.
Figure 3. Experimental (circles) and theoretical (red solid lines) magnetic data: (a) dependence of χT vs. T and magnetization plots M vs. B for 1 at three different temperatures (insert); (b) dependence of χT vs. T and magnetization plots M vs. B at three different temperatures (insert) for 2; (c) magnetization plot M vs. B for 1 at 2 K; (d) magnetization plot M vs. B for 2 at 2 K. See text for details.
Magnetochemistry 11 00016 g003
Magnetochemistry 11 00016 g004
Figure 4. MOs involved in the active space of the CASSCF (nel,8) (nel = 12 for Er, 14 for Yb) calculations for complexes 1 and 2.
Figure 4. MOs involved in the active space of the CASSCF (nel,8) (nel = 12 for Er, 14 for Yb) calculations for complexes 1 and 2.
Magnetochemistry 11 00016 g004
Magnetochemistry 11 00016 g005
Figure 5. (a) The 35 quintets and triplets for 1 found at SA–CASSCF(12,8) (CASSCF) and SA–CASSCF(12,8)/NEVPT2 (NEVPT2) levels and SO multiplets after the accounting of SOC at QDPT level (CASSCF–SOC and NEVPT2–SOC). (b) The 7 triplets and singlets for 2 obtained at SA–CASSCF(12,8) (CASSCF) and SA–CASSCF(12,8)/NEVPT2 (NEVPT2) levels and SO–multiplets after the accounting of SOC at QDPT level (CASSCF–SOC and NEVPT2–SOC). The energy structure under 3000 cm−1 for (c) 1 and (d) 2. See, also, Tables S2 and S3 in Supplementary Materials.
Figure 5. (a) The 35 quintets and triplets for 1 found at SA–CASSCF(12,8) (CASSCF) and SA–CASSCF(12,8)/NEVPT2 (NEVPT2) levels and SO multiplets after the accounting of SOC at QDPT level (CASSCF–SOC and NEVPT2–SOC). (b) The 7 triplets and singlets for 2 obtained at SA–CASSCF(12,8) (CASSCF) and SA–CASSCF(12,8)/NEVPT2 (NEVPT2) levels and SO–multiplets after the accounting of SOC at QDPT level (CASSCF–SOC and NEVPT2–SOC). The energy structure under 3000 cm−1 for (c) 1 and (d) 2. See, also, Tables S2 and S3 in Supplementary Materials.
Magnetochemistry 11 00016 g005
Magnetochemistry 11 00016 g006
Figure 6. M vs. B plot of 1 (a) and 2 (b). The symbols are the experimental points, while the blue and red solid lines represent the best simulation using the g and J parameters reported in Table 3.
Figure 6. M vs. B plot of 1 (a) and 2 (b). The symbols are the experimental points, while the blue and red solid lines represent the best simulation using the g and J parameters reported in Table 3.
Magnetochemistry 11 00016 g006
Table 1. Decomposition of the wavefunctions corresponding to the lowest atomic multiplet J = 15/2 in wavefunctions with a definite projection of the total moment on the quantization axis at SA-CASSCF/NEVPT2 level of calculations for the anion and cation derivatives of the complex 1. The predominant contributions for each KD are indicated in bold.
Table 1. Decomposition of the wavefunctions corresponding to the lowest atomic multiplet J = 15/2 in wavefunctions with a definite projection of the total moment on the quantization axis at SA-CASSCF/NEVPT2 level of calculations for the anion and cation derivatives of the complex 1. The predominant contributions for each KD are indicated in bold.
AnionCation
KDΔE, cm−1|Jz| (Contribution, %)KDΔE, cm−1|Jz| (Contribution, %)
1013/2 (54.7), 11/2 (12.1)1013/2 (60.6), 11/2 (16.5)
266.911/2 (32.2), 1/2 (19.8), 3/2 (14.1), 13/2 (11.6)2108.61/2 (34.3), 11/2 (34.1), 9/2 (9.7)
3209.43/2 (23.4), 13/2 (19.3), 1/2 (15.3), 9/2 (13.7), 5/2 (11.3)3286.715/2 (40.4), 9/2 (18.0), 13/2 (17.1), 1/2 (9.6)
4268.61/2 (38.9), 11/2 (18.9), 3/2 (11.3)4353.73/2 (30.5), 11/2 (18.2), 5/2 (14.9), 15/2 (12.3), 9/2 (10.6)
5381.315/2 (33.4), 9/2 (23.4), 7/2 (16.8), 5/2 (14.4)5402.53/2 (33.7), 11/2 (19.7), 1/2 (13.5), 5/2 (11.5)
6467.53/2 (26.4), 9/2 (22.6), 1/2 (19.5), 5/2 (13.3)6521.67/2 (36.0), 5/2 (23.4), 15/2 (13.5)
7513.615/2 (35.7), 7/2 (21.2), 11/2 (12.8), 5/2 (10.8), 3/2 (10.2)7574.31/2 (21.0), 5/2 (20.6), 9/2 (19.9), 7/2 (15.0), 11/2 (14.7)
8636.57/2 (30.3), 5/2 (27.5), 9/2 (16.5), 15/2 (13.9)8691.27/2 (27.1), 9/2 (24.8), 5/2 (16.7), 3/2 (15.5)
Table 2. Decomposition of the wavefunctions corresponding to the lowest atomic multiplet J = 7/2 in wave functions with a definite projection of the total moment on the quantization axis at RASSCF/XMS-CASPT2 level of calculations for the anion and cation derivatives of the complex 2. The predominant contributions for each KD are indicated in bold.
Table 2. Decomposition of the wavefunctions corresponding to the lowest atomic multiplet J = 7/2 in wave functions with a definite projection of the total moment on the quantization axis at RASSCF/XMS-CASPT2 level of calculations for the anion and cation derivatives of the complex 2. The predominant contributions for each KD are indicated in bold.
AnionCation
KDΔE, cm−1|Jz| (Contribution, %)KDΔE, cm−1|Jz| (Contribution, %)
107/2 (65.6), 3/2 (20.2), 1/2 (10.8)107/2 (89.8)
2169.35/2 (49.8), 1/2 (25.6), 3/2 (17.6)2224.75/2 (65.5), 3/2 (24.8)
3385.75/2 (36), 3/2 (25.8), 7/2 (20.7), 5/2 (17.3)3438.81/2 (64.5), 3/2 (18.8), 5/2 (13.2)
4537.91/2 (46.2), 3/2 (36.5), 5/2 (10.8)4565.73/2 (52.9), 1/2 (29.9), 5/2 (15.3)
Table 3. The g-tensors obtained from the ab initio calculations on the anionic and cationic structures and value of the coupling.
Table 3. The g-tensors obtained from the ab initio calculations on the anionic and cationic structures and value of the coupling.
1 Anion1 Cation2 Anion2 Cation
g(0.79, 0.54, 13.4)(0.30, 0.61, 14.2)(1.07, 3.05, 5.55)(1.18, 1.66, 6.90)
J, cm−1671626
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Perfetti, M.; Dmitriev, A.A.; Vostrikova, K.E. Er(III) and Yb(III) Complexes with a Tripodal Nitroxyl Radical: Magnetochemical Study and Ab Initio Calculations. Magnetochemistry 2025, 11, 16. https://doi.org/10.3390/magnetochemistry11020016

AMA Style

Perfetti M, Dmitriev AA, Vostrikova KE. Er(III) and Yb(III) Complexes with a Tripodal Nitroxyl Radical: Magnetochemical Study and Ab Initio Calculations. Magnetochemistry. 2025; 11(2):16. https://doi.org/10.3390/magnetochemistry11020016

Chicago/Turabian Style

Perfetti, Mauro, Alexey A. Dmitriev, and Kira E. Vostrikova. 2025. "Er(III) and Yb(III) Complexes with a Tripodal Nitroxyl Radical: Magnetochemical Study and Ab Initio Calculations" Magnetochemistry 11, no. 2: 16. https://doi.org/10.3390/magnetochemistry11020016

APA Style

Perfetti, M., Dmitriev, A. A., & Vostrikova, K. E. (2025). Er(III) and Yb(III) Complexes with a Tripodal Nitroxyl Radical: Magnetochemical Study and Ab Initio Calculations. Magnetochemistry, 11(2), 16. https://doi.org/10.3390/magnetochemistry11020016

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop