Comparison between XY Spin Chains with Spin 1/2 or 1 Interacting with Quantized Electromagnetic Field by One and Two Photon Jaynes-Cummings Model
Abstract
:1. Introduction
2. Results
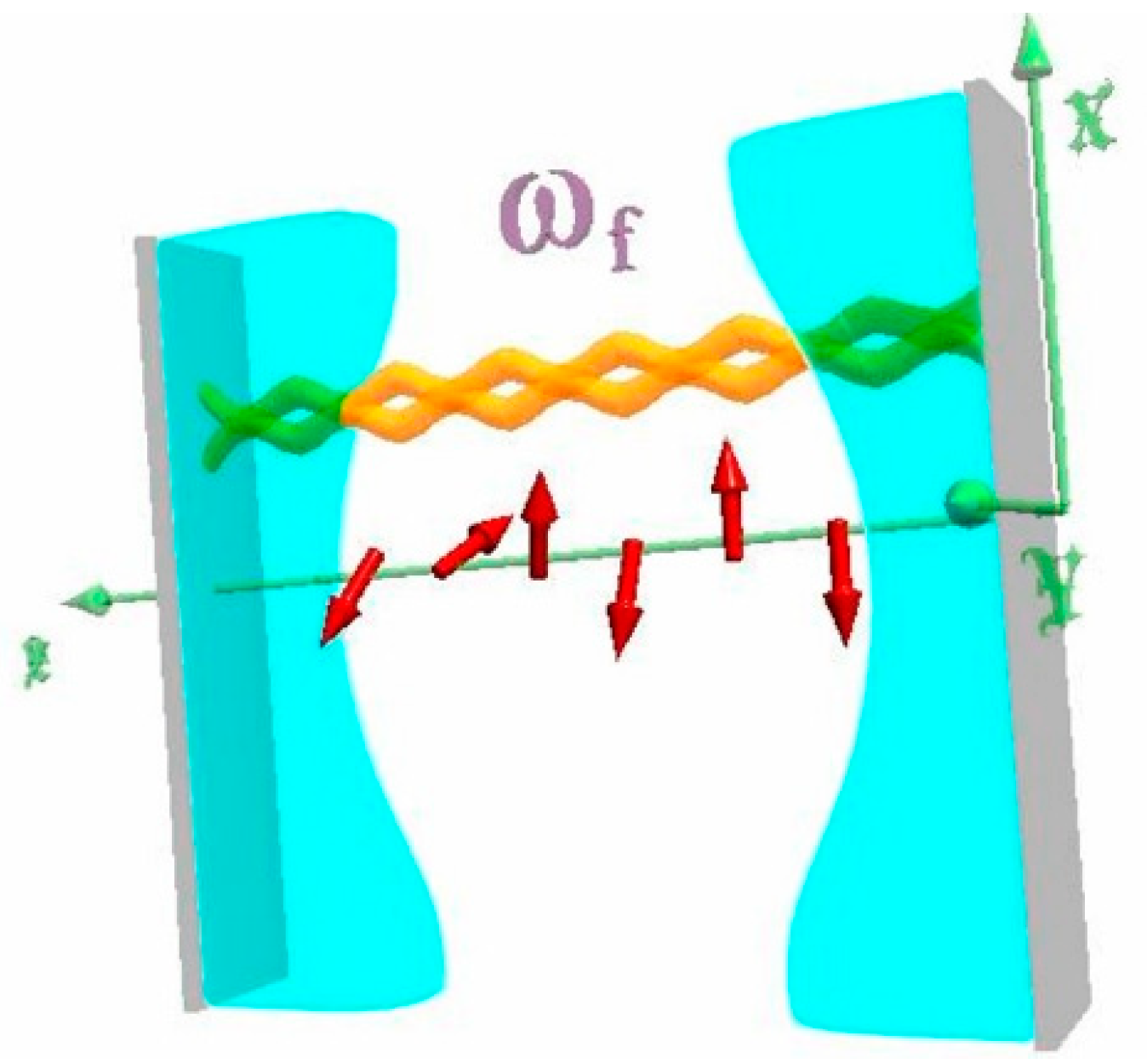
2.1. Spin Chain with Spin 1/2 Interacting with the Electromagnetic Field
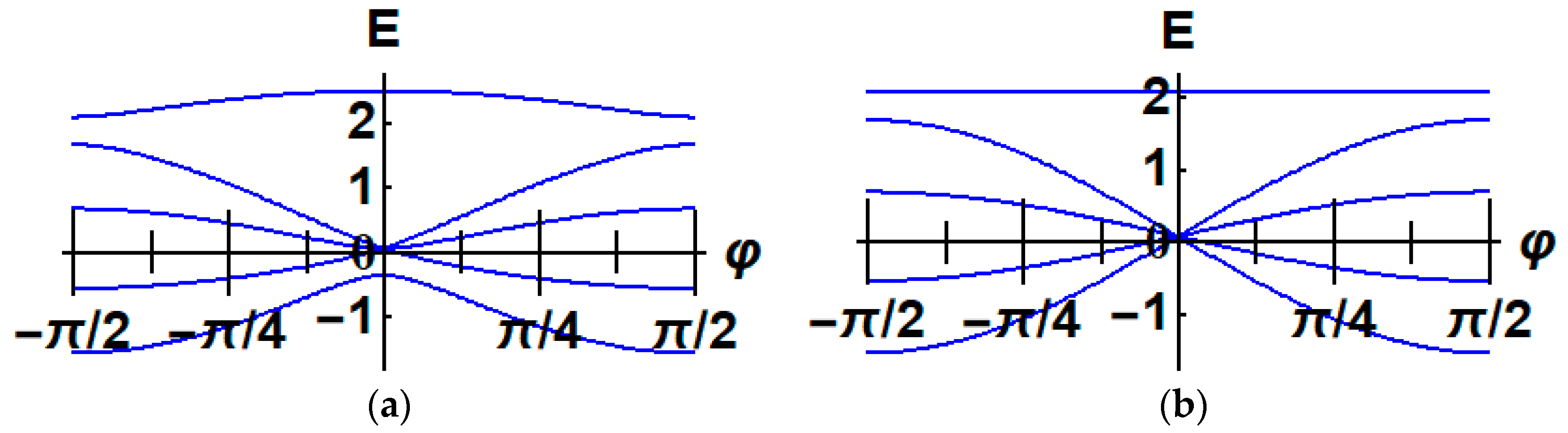
2.1.1. Hamiltonian, Invariant, and Block Structure of the Hamiltonian
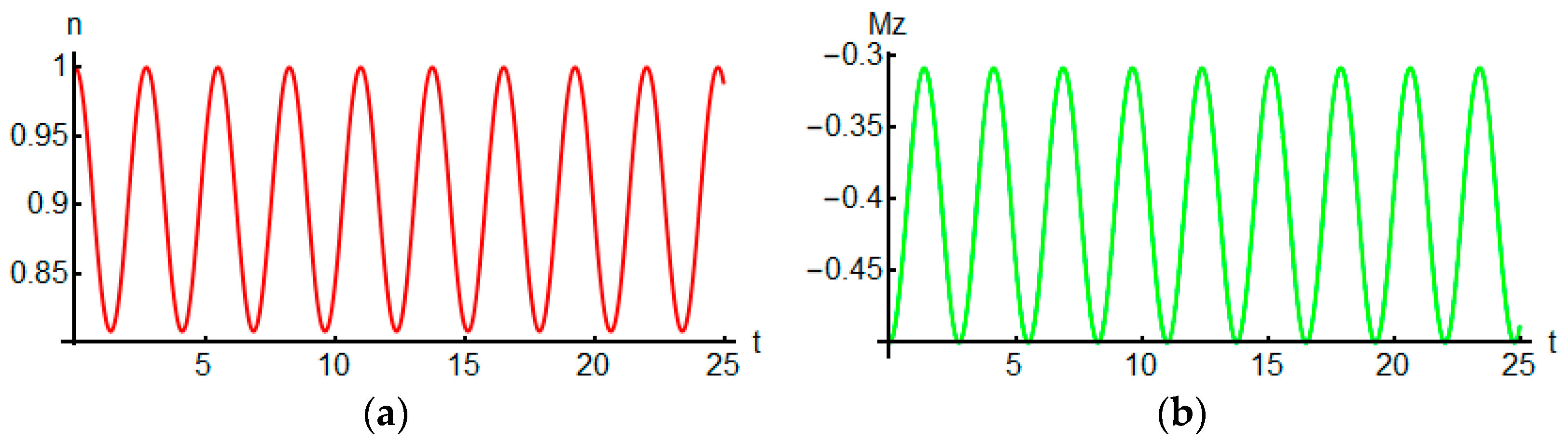
2.1.2. Evolution of Magnetic Moment and Number of Photons
2.2. Spin Chain with Spin 1 Interacting with the Electromagnetic Field
2.2.1. Hamiltonian
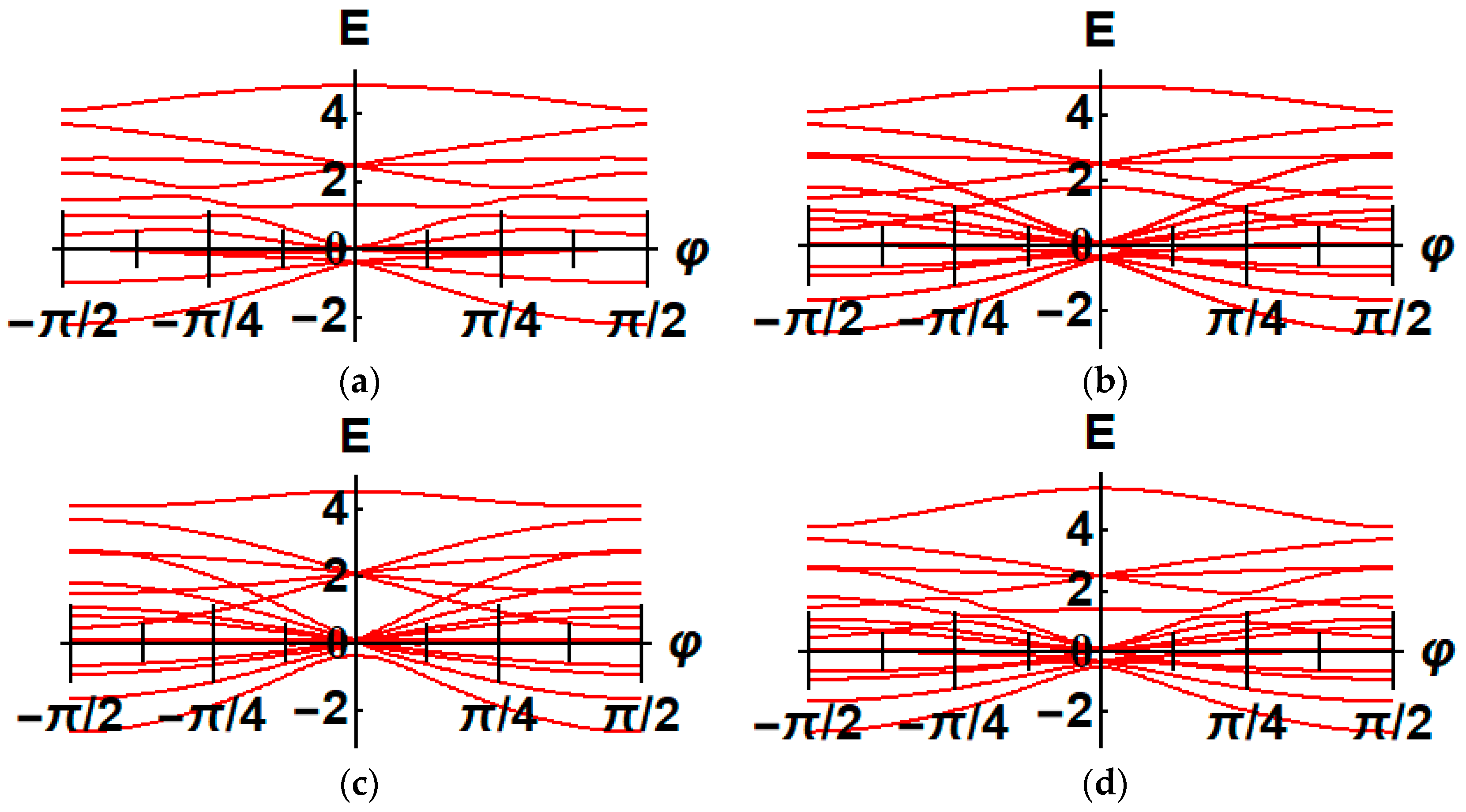
2.2.2. Invariant and Block Structure
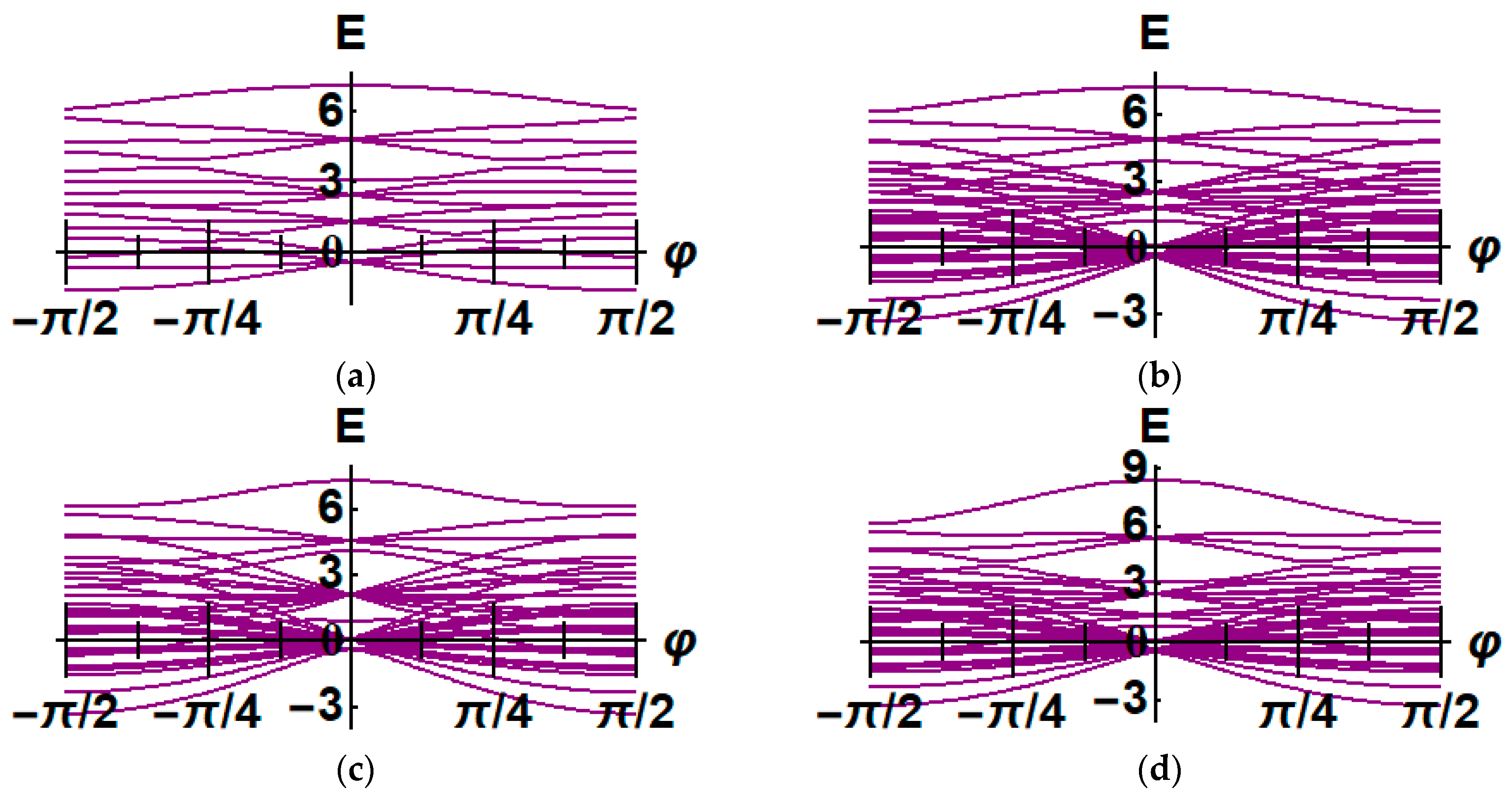
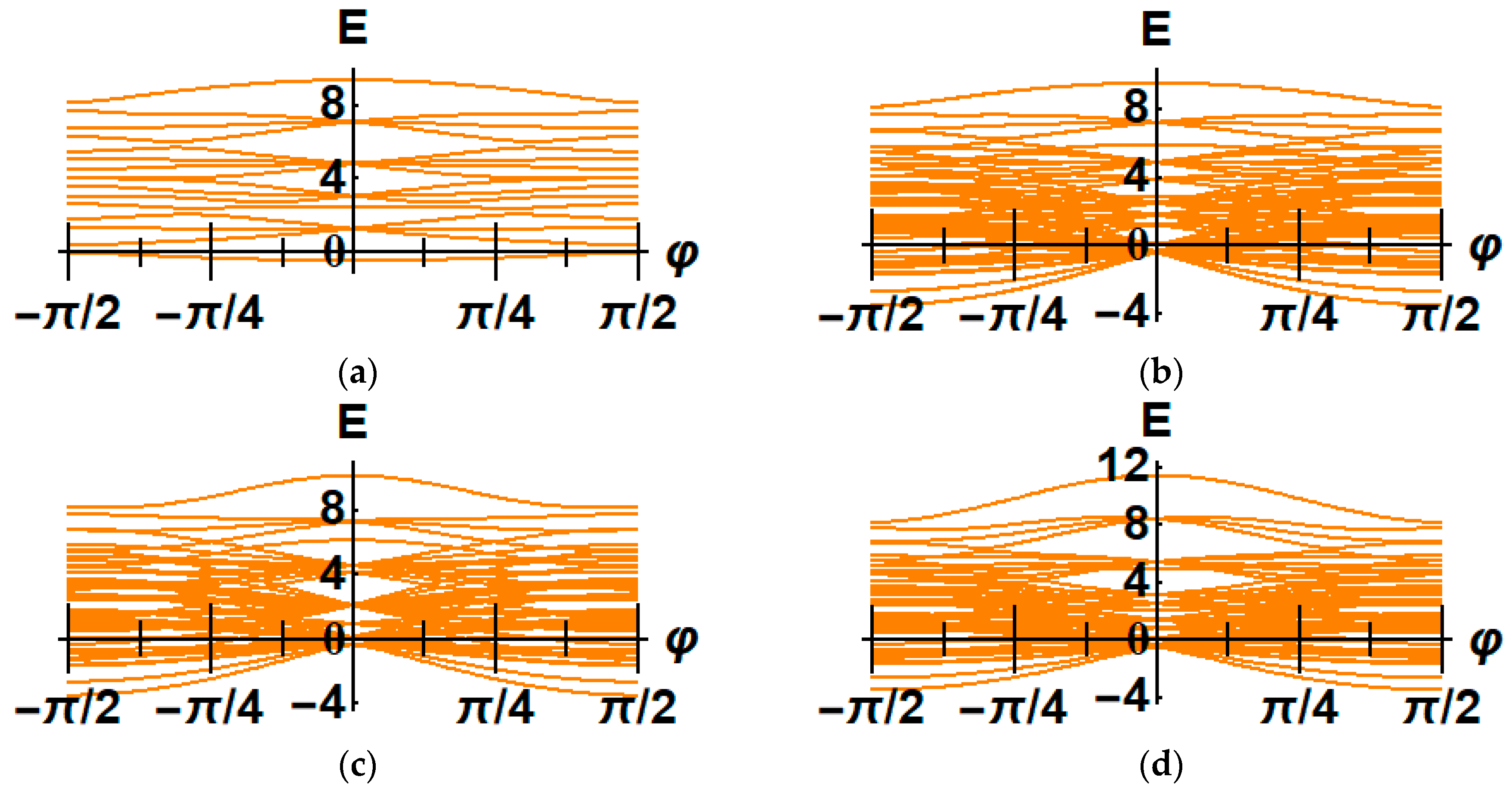
2.2.3. Numerical Simulation for Energy Spectrum
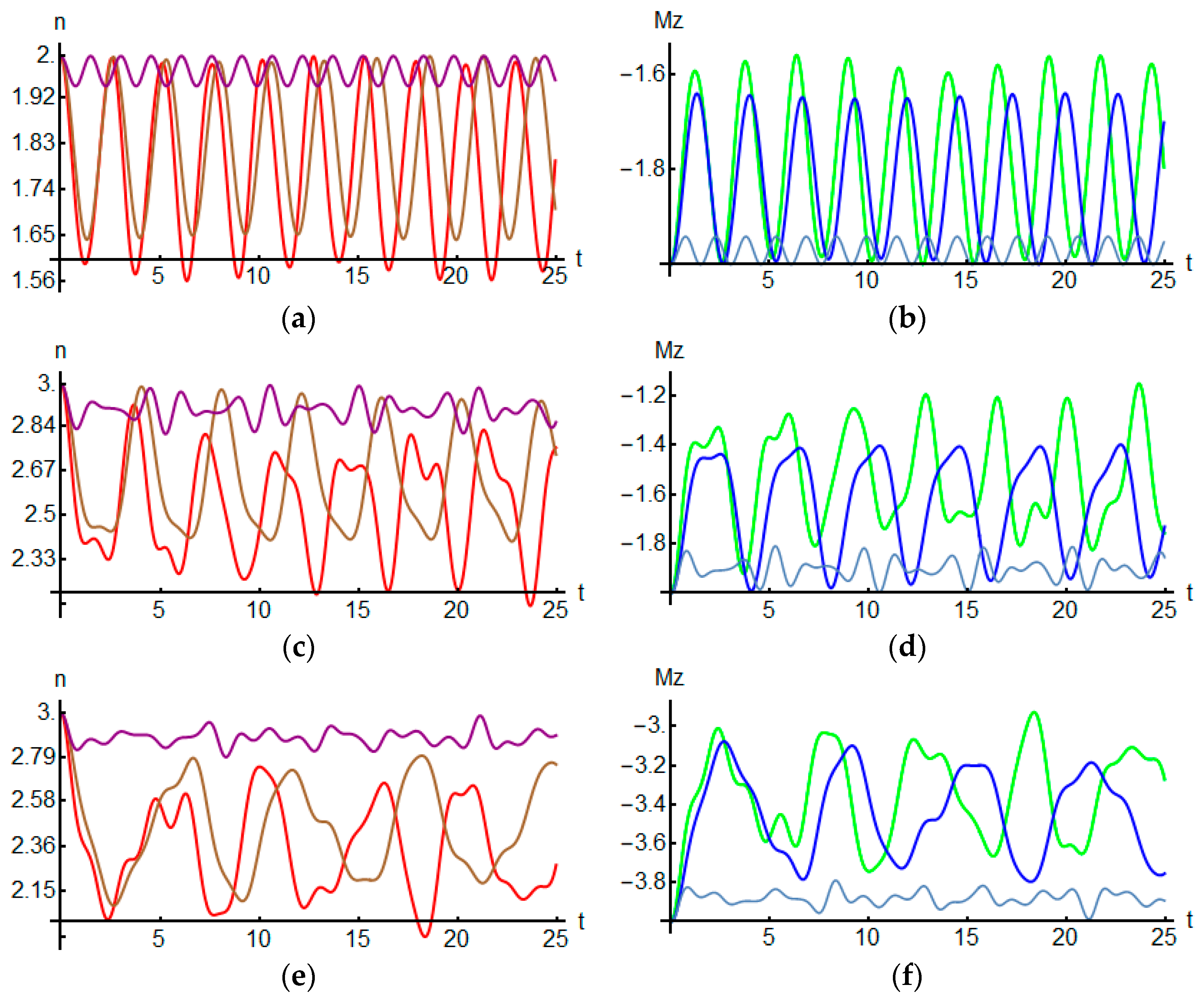
2.2.4. Numerical Simulation of Magnetic Moment and the Number of Photons
3. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Gerry, C.C.; Knight, P. Introductory Quantum Optics; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar] [CrossRef]
- Scully, M.O.; Zubairy, M.S. Quantum Optics; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar] [CrossRef]
- Jaynes, E.T.; Cummings, F.W. Comparison of quantum and semiclassical radiation theories with application to the beam maser. Proc. IEEE 1963, 51, 89–109. [Google Scholar] [CrossRef] [Green Version]
- Vogel, W.; Filho, R.L.D.M. Nonlinear Jaynes-Cummings dynamics of a trapped ion. Phys. Rev. A 1995, 52, 4214–4217. [Google Scholar] [CrossRef] [PubMed]
- Moya-Cessa, H.; Jonathan, D.; Knight, P.L. A family of exact eigenstates for a single trapped ion interacting with a laser field. J. Mod. Opt. 2009, 50, 265–273. [Google Scholar] [CrossRef]
- Wu, Y.; Yang, X. Jaynes-Cummings Model for a Trapped Ion in Any Position of a Standing Wave. Phys. Rev. Lett. 1997, 78, 3086–3088. [Google Scholar] [CrossRef]
- You, J.Q.; Nori, F. Quantum information processing with superconducting qubits in a microwave field. Phys. Rev. B 2003, 68, 064509. [Google Scholar] [CrossRef] [Green Version]
- Madsen, K.H.; Ates, S.; Lund-Hansen, T.; Loffler, A.; Reitzenstein, S.; Forchel, A.; Lodahl, P. Observation of Non-Markovian Dynamics of a Single Quantum Dot in a Micropillar Cavity. Phys. Rev. Lett. 2011, 106, 233601. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, J.-M.; Fang, H.-H.; Xu, X.-X. Two-photon Jaynes–Cummings model interacting with the squeezed vacuum state solved by dressed-state method. Optik 2018, 169, 180–189. [Google Scholar] [CrossRef]
- Alsing, P.; Guo, D.-S.; Carmichael, H.J. Dynamic Stark effect for the Jaynes-Cummings system. Phys. Rev. A 1992, 45, 5135–5143. [Google Scholar] [CrossRef]
- Rempe, G.; Walther, H.; Klein, N. Observation of quantum collapse and revival in a one-atom maser. Phys. Rev. Lett. 1987, 58, 353–356. [Google Scholar] [CrossRef]
- Dodonov, A.V.V.; Mizrahi, S.S. Engineering quantum jump superoperators for single-photon detectors. Phys. Rev. A 2006, 74, 033823. [Google Scholar] [CrossRef] [Green Version]
- Ludlow, A.D.; Boyd, M.M.; Ye, J.; Peik, E.; Schmidt, P.O. Optical atomic clocks. Rev. Mod. Phys. 2015, 87, 637–701. [Google Scholar] [CrossRef]
- Mølmer, K. Jaynes-Cummings Dynamics with a Matter Wave Oscillator. Phys. Rev. Lett. 2003, 90, 110403. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mischuck, B.; Mølmer, K. Qudit quantum computation in the Jaynes-Cummings model. Phys. Rev. A 2013, 87, 022341. [Google Scholar] [CrossRef] [Green Version]
- Ionicioiu, R.; Spiller, T.P.; Munro, W.J. Generalized Toffoli gates using qudit catalysis. Phys. Rev. A 2009, 80, 012312. [Google Scholar] [CrossRef] [Green Version]
- Singh, S. Field statistics in some generalized Jaynes-Cummings models. Phys. Rev. A 1982, 25, 3206–3216. [Google Scholar] [CrossRef]
- Huang, H.-B.; Fan, H.-Y. Jaynes-Cummings model for double m-photon lasers. Phys. Lett. A 1991, 159, 323–327. [Google Scholar] [CrossRef]
- Puri, R.R.; Bullough, R.K. Quantum electrodynamics of an atom making two-photon transitions in an ideal cavity. J. Opt. Soc. Am. B 1988, 5, 2021–2028. [Google Scholar] [CrossRef]
- Bergmann, K.; Theuer, H.; Shore, B.W. Coherent population transfer among quantum states of atoms and molecules. Rev. Mod. Phys. 1998, 70, 1003–1025. [Google Scholar] [CrossRef]
- Vitanov, N.V.; Rangelov, A.A.; Shore, B.W.; Bergmann, K. Stimulated Raman adiabatic passage in physics, chemistry, and beyond. Rev. Mod. Phys. 2017, 89, 015006. [Google Scholar] [CrossRef]
- Zhu, C.; Dong, L.; Pu, H. Effects of spin-orbit coupling on Jaynes-Cummings and Tavis-Cummings models. Phys. Rev. A 2016, 94, 053621. [Google Scholar] [CrossRef] [Green Version]
- Dong, L.; Zhu, C.; Pu, H. Photon-Induced Spin-Orbit Coupling in Ultracold Atoms inside Optical Cavity. Atoms 2015, 3, 182–194. [Google Scholar] [CrossRef] [Green Version]
- Dziarmaga, J. Dynamics of a Quantum Phase Transition: Exact Solution of the Quantum Ising Model. Phys. Rev. Lett. 2005, 95, 245701. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Arnesen, M.C.; Bose, S.; Vedral, V. Natural Thermal and Magnetic Entanglement in the 1D Heisenberg Model. Phys. Rev. Lett. 2001, 87, 017901. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Batle, J.; Casas, M. Nonlocality and entanglement in theXYmodel. Phys. Rev. A 2010, 82, 062101. [Google Scholar] [CrossRef] [Green Version]
- Maucourt, J.; Grempel, D.R. Lower Critical Dimension of theXYSpin-Glass Model. Phys. Rev. Lett. 1998, 80, 770–773. [Google Scholar] [CrossRef] [Green Version]
- Jongen, G.; Bollé, D.; Coolen, A.C.C. TheXYspin glass with slow dynamic couplings. J. Phys. A Math. Gen. 1998, 31, L737–L742. [Google Scholar] [CrossRef]
- Gu, S.-J.; Tian, G.-S.; Lin, H.-Q. Local entanglement and quantum phase transition in spin models. New J. Phys. 2006, 8, 61. [Google Scholar] [CrossRef]
- Wang, X.; Li, H.-B.; Sun, Z.; Li, Y.-Q. Entanglement in spin-1 Heisenberg chains. J. Phys. A Math. Gen. 2005, 38, 8703–8713. [Google Scholar] [CrossRef] [Green Version]
- Ren, J.; Wang, Y.; You, W.-L. Quantum phase transitions in spin-1 XXZ chains with rhombic single-ion anisotropy. Phys. Rev. A 2018, 97, 042318. [Google Scholar] [CrossRef] [Green Version]
- Richter, J.; Casper, N.; Brenig, W.; Steinigeweg, R. Magnetization dynamics in clean and disordered spin-1 XXZ chains. Phys. Rev. B 2019, 100, 144423. [Google Scholar] [CrossRef] [Green Version]
- Medenjak, M.; De Nardis, J. Domain wall melting in spin-1 XXZ chains. Phys. Rev. B 2020, 101, 081411. [Google Scholar] [CrossRef] [Green Version]
- Bravyi, S.; Caha, L.; Movassagh, R.; Nagaj, D.; Shor, P.W. Criticality without Frustration for Quantum Spin-1 Chains. Phys. Rev. Lett. 2012, 109, 207202. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pixley, J.H.; Shashi, A.; Nevidomskyy, A.H. Frustration and multicriticality in the antiferromagnetic spin-1 chain. Phys. Rev. B 2014, 90, 214426. [Google Scholar] [CrossRef] [Green Version]
- Messikh, A.; Ficek, Z.; Wahiddin, M.R.B. Entanglement and spin squeezing in the two-atom Dicke model. J. Opt. B Quantum Semiclassical Opt. 2003, 5, L1–L4. [Google Scholar] [CrossRef] [Green Version]
- Vidal, J.; Dusuel, S. Finite-size scaling exponents in the Dicke model. EPL 2006, 74, 817–822. [Google Scholar] [CrossRef] [Green Version]
- Kirton, P.; Roses, M.M.; Keeling, J.; Torre, E.G.D. Introduction to the Dicke Model: From Equilibrium to Nonequilibrium, and Vice Versa. Adv. Quantum Technol. 2019, 2, 1800043. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.K.; Hioe, F.T. Phase Transition in the Dicke Model of Superradiance. Phys. Rev. A 1973, 7, 831–836. [Google Scholar] [CrossRef]
- Lambert, N.; Emary, C.; Brandes, T. Entanglement and the Phase Transition in Single-Mode Superradiance. Phys. Rev. Lett. 2004, 92, 073602. [Google Scholar] [CrossRef] [Green Version]
- Scully, M.O. Collective Lamb Shift in Single Photon Dicke Superradiance. Phys. Rev. Lett. 2009, 102, 143601. [Google Scholar] [CrossRef]
- Wu, N. Determinant representations of spin-operator matrix elements in the XX spin chain and their applications. Phys. Rev. B 2018, 97, 014301. [Google Scholar] [CrossRef] [Green Version]
- Tonchev, H.; Donkov, A.A.; Chamati, H. Energy spectra of a spin-½ XY spin molecule interacting with a single mode field cavity. J. Phys. Conf. Ser. 2019, 1186, 012021. [Google Scholar] [CrossRef]
- Pandit, M.; Das, S.; Roy, S.S.; Dhar, H.S.; Sen, U. Effects of cavity–cavity interaction on the entanglement dynamics of a generalized double Jaynes–Cummings model. J. Phys. B At. Mol. Opt. Phys. 2018, 51, 045501. [Google Scholar] [CrossRef] [Green Version]
- Zhiqiang, Z.; Lee, C.H.; Kumar, R.; Arnold, K.J.; Masson, S.J.; Parkins, A.S.; Barrett, M.D. Nonequilibrium phase transition in a spin-1 Dicke model. Optica 2017, 4, 424–429. [Google Scholar] [CrossRef]
- Vorrath, T.; Brandes, T.; Kramer, B. Dynamics of a large spin with weak dissipation. Chem. Phys. 2004, 296, 295–300. [Google Scholar] [CrossRef] [Green Version]
- Wang, X. Entanglement in the quantum HeisenbergXYmodel. Phys. Rev. A 2001, 64, 012313. [Google Scholar] [CrossRef] [Green Version]
- Bian, M.-M.; Chen, M.-F.; Yang, Z.-B.; Wu, H. Implementation of three-qubit Toffoli gates via the HeisenbergXYmodel in coupled cavities. J. Mod. Opt. 2015, 62, 1283–1290. [Google Scholar] [CrossRef]
- Klimov, A.B.; Guzmán, R.; Retamal, J.C.; Saavedra, C. Qutrit quantum computer with trapped ions. Phys. Rev. A 2003, 67, 062313. [Google Scholar] [CrossRef]
- Ivanov, S.S.; Tonchev, H.S.; Vitanov, N.V. Time-efficient implementation of quantum search with qudits. Phys. Rev. A 2012, 85, 062321. [Google Scholar] [CrossRef] [Green Version]
- Tonchev, H.S.; Vitanov, N.V. Quantum phase estimation and quantum counting with qudits. Phys. Rev. A 2016, 94, 042307. [Google Scholar] [CrossRef]
- Mc Hugh, D.; Twamley, J. Trapped-ion qutrit spin molecule quantum computer. New J. Phys. 2005, 7, 174. [Google Scholar] [CrossRef] [Green Version]
- Imamog¯lu, A.; Awschalom, D.D.; Burkard, G.; DiVincenzo, D.P.; Loss, D.; Sherwin, M.; Small, A. Quantum Information Processing Using Quantum Dot Spins and Cavity QED. Phys. Rev. Lett. 1999, 83, 4204–4207. [Google Scholar] [CrossRef] [Green Version]
- Tonchev, H.; Donkov, A.A.; Chamati, H. Energy spectra of a spin-½ XY spin molecule interacting with a single mode field cavity: Numerical study. J. Phys. Conf. Ser. 2016, 764, 012017. [Google Scholar] [CrossRef] [Green Version]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tonchev, H. Comparison between XY Spin Chains with Spin 1/2 or 1 Interacting with Quantized Electromagnetic Field by One and Two Photon Jaynes-Cummings Model. Magnetochemistry 2021, 7, 4. https://doi.org/10.3390/magnetochemistry7010004
Tonchev H. Comparison between XY Spin Chains with Spin 1/2 or 1 Interacting with Quantized Electromagnetic Field by One and Two Photon Jaynes-Cummings Model. Magnetochemistry. 2021; 7(1):4. https://doi.org/10.3390/magnetochemistry7010004
Chicago/Turabian StyleTonchev, Hristo. 2021. "Comparison between XY Spin Chains with Spin 1/2 or 1 Interacting with Quantized Electromagnetic Field by One and Two Photon Jaynes-Cummings Model" Magnetochemistry 7, no. 1: 4. https://doi.org/10.3390/magnetochemistry7010004
APA StyleTonchev, H. (2021). Comparison between XY Spin Chains with Spin 1/2 or 1 Interacting with Quantized Electromagnetic Field by One and Two Photon Jaynes-Cummings Model. Magnetochemistry, 7(1), 4. https://doi.org/10.3390/magnetochemistry7010004



