1. Introduction
In many cases, encountered in natural conditions or in engineering, the main mechanism of heat transfer is natural convection. The regularities of thermal convection in liquids have been intensively studied, both experimentally and theoretically, for many years. One interesting direction in these studies is the influence of an external magnetic field on thermal convection in a liquid. The basic statement of the problem, in this case, is to consider the establishment of the thermal instability of a flat horizontal layer of a liquid heated from below. The influence of the imposed external magnetic field, in the case of a layer of electrically conducting liquid, was first considered theoretically in [
1] and experimentally in [
2]. The principal result of these studies was to establish that the critical Rayleigh number at which the instability sets in depends on the strength of the magnetic field. Particularly, the critical Rayleigh number grows when the field is oriented perpendicularly to the heat flux. Further development of these studies for problems with different materials and spatial geometries was presented in a number of works (e.g., [
3,
4,
5,
6,
7]). Another way to achieve the effect of the magnetic field on the parameters of thermal convection is to use electrically non-conductive weakly magnetic (para- and diamagnetic) fluids. Various manifestations of thermomagnetic convection phenomena of weakly magnetic fluids have been investigated in detail, experimentally, theoretically, and computationally, in a number of works (e.g., [
8,
9,
10,
11,
12]).
The disadvantage of using conducting fluids, as well as weakly magnetic fluids for the purpose of regulating thermal convection, is the need to use strong magnetic fields, the creation of which in an extended area of space can be problematic. In this regard, the attention of researchers is drawn to the use of composite nanofluids demonstrating interesting properties that are not typical of classical liquid media [
13,
14,
15,
16,
17]. This applies in particular to magnetic nanofluids. Magnetic nanofluid is an artificial material that is a colloidal dispersion of ultra-fine ferro- or ferrimagnetic nanoparticles with an average size of about 10 nm. Magnetic nanoparticles are stabilized by surfactants to prevent their aggregation. Magnetic nanofluids can maintain stability for a long time and are used in various technological processes (magnetic fluid gas and dust sealings, linear vibration motor, ore separation, speaker and hearing devises, targeted drug delivery, magnetic hyperthermia, etc.) [
18]. In the context of heat transfer and hydrodynamics problems, the key feature of magnetic nanofluids is the presence of an additional volume force determined by local magnetization and magnetic field gradient. This creates attractive prospects for the use of magnetic nanofluids in cooling devices and heat exchangers.
It was established that the magnetic field affects the critical parameters of the thermal convection initiation in magnetic nanofluids. In addition, the magnetic field leads to a change in the convective flow patterns in magnetic nanofluids. Classical results on thermomagnetic convection in magnetic nanofluids are summarized in [
19,
20]. Current research in this area focuses mainly on various system geometries, nanofluid compositions, and configurations of the applied magnetic field (see, e.g., [
21,
22,
23,
24,
25,
26,
27]). In particular, it was established that the magnetic field gradient plays a key role in the mechanism of thermomagnetic convection. The magnetic field gradient may be associated with nonuniformity of applied external magnetic field. The external uniform magnetic field can become nonuniform in the cavity filled with magnetic nanofluid due to the refraction of the magnetic field lines at the sample boundary. The magnetic field gradient can also be created as a result of the inhomogeneity of the magnetic properties of nonuniformly heated magnetic nanofluid. In a significant number of practical cases, we have to deal with homogeneous external magnetic fields, so this study will consider just such a case. Most of the existing studies report augmentation of heat transfer resulting from the magnetic field action. Fewer studies discuss the inhibition of heat transfer in magnetic nanofluids in the presence of the magnetic field [
27,
28]. The current study will also focus on the possibilities of depreciation of heat transfer by a magnetic field.
Among the variety of possible geometries of the system, the basic case of a flat quasi-two-dimensional rectangular layer of a magnetic nanofluid attracts attention. The influence of an external uniform magnetic field on convection in a vertical quasi-two-dimensional rectangular layer of magnetic nanofluid heated from below was considered in [
29,
30,
31,
32]. Only the case of a magnetic field parallel to the temperature gradient was considered. The stimulation of convection by a magnetic field in this case has been demonstrated. In this paper, we will also consider a flat vertical quasi-two-dimensional rectangular layer of magnetic nanofluid heated from below, which allows us to visualize the flow pattern in the sample. However, in contrast to [
29,
30,
31,
32], here we consider the case of a magnetic field directed perpendicular to the temperature gradient.
It should be noted that in existing studies, prevalent attention was paid to the stationary regimes of convective heat transfer and much less to the dynamics of convection development and damping in magnetic nanofluids in the presence of a magnetic field [
33]. In contrast to previous studies, we focus on the processes of convection development when heating is initiated and the subsequent convection damping when heating is turned off. In particular, the dynamics of heating and cooling of metal plates in a magnetic nanofluid without and under the influence of an external magnetic field is considered.
2. Materials and Methods
In our experiments, we used a water based electrostatically stabilized magnetic nanofluid with dispersed magnetite nanoparticles of about 10 nm in size. The measured properties of the magnetic nanofluid are: density is 1100 kg/m
3, dynamic viscosity is 1.3 mPa⋅s, initial static magnetic susceptibility is 0.22, saturation magnetization is 3.9 kA/m, thermal conductivity is 0.6 W/(m⋅K), and electrical conductivity is 1.1·10
−2 S/m. The density was measured with a vibrating density meter (Termex, Tomsk, Russia), the viscosity with a Rheotest RN 4.1 rotational viscometer (RHEOTEST Medingen GmbH, Ottendorf-Okrilla, Germany), the thermal conductivity with a DTC-300 Thermal Conductivity Meter (TA Instruments, New Castle, DE, USA), and electrical conductivity with a Impedance Analyzer 6510B (Wayne Kerr, Bognor Regis, UK). The size of nanoparticles was determined using a Photocor Complex dynamic and static light scattering spectrometer (Photocor, Moscow, Russia). The magnetization curve of the ferrofluid measured with vibrating sample magnetometer 7410 VSM (Lake Shore Cryotronics, Westerville, OH, USA) is presented in
Figure 1.
To study convective heat transfer in a magnetic nanofluid, we used the experimental setup shown in
Figure 2. The magnetic nanofluid formed a layer with a horizontal length of 8 cm, a vertical length of 1 cm, and a thickness of 2 mm. Below and above the layer was bounded by aluminum plates. At the back, the layer was bounded by a plexiglass plate that fixed the entire structure of the measuring cell. At the front, the magnetic nanofluid layer was bounded by a thin film transparent to infrared radiation. The magnetic nanofluid layer under study can be considered as quasi-two-dimensional. Resistors in a ceramic frame were tightly pressed to the bottom aluminum plate. The bottom aluminum plate was heated by passing an electric current through resistors. In the described experiments, a fixed value of the current strength creating a heating power of 55 W was used. The lower end of the top aluminum plate was in contact with the magnetic nanofluid, while the rest of this plate was in contact with the surrounding air and was not additionally thermostated. Thus, it works as a passive radiator.
We analyzed the process of heat transfer from the bottom plate to the top plate when the bottom plate heating was turned on, as well as the process of cooling the bottom plate when the heating was turned off. The study of the thermal regime and the temperature distribution measurements in the cell were carried out using an infrared imager Flir E8 (FLIR Systems, Wilsonville, OR, USA) To study the influence of an external magnetic field, the measuring cell was placed between the poles of the electromagnet. The electromagnet powered by a dc source provided a uniform static magnetic field in the direction perpendicular to the heat flux in the cell and parallel to the magnetic nanofluid layer.
Figure 3a demonstrates the dependencies of the magnetic field strength components on the horizontal coordinate between the electromagnet poles. The dependencies shown on
Figure 3a were measured along the centerline of the magnetizing system, where the magnetic nanofluid has been located, and along the line connecting the edges of the poles.
Figure 3b shows the magnetic field strength vector field in the central vertical plane between the poles of the electromagnet. The magnetic field strength has been measured with a Model 425 gauss meter (Lake Shore Cryotronics, Westerville, OH, USA). The relative deviation of the magnetic field from the homogeneous one in the region of the magnetic nanofluid location did not exceed 2%.
3. Results
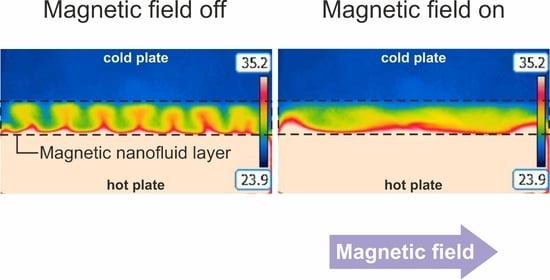
It was observed that when the bottom plate is heated by an electric current of a strength higher than a certain critical value, the development of convective flows is taking place in the magnetic nanofluid. Further studies were carried out at a fixed value of the current strength exceeding this critical value. The bottom plate was gradually heated over time by the current in the resistors, and when a certain temperature difference was reached between the bottom and top plates, a convective flow occurred. It was found that applying a magnetic field perpendicular to the temperature gradient in the cell suppresses convection. Thus, if a magnetic field is applied to a magnetic nanofluid in which thermal convection has developed, this will lead to blurring of convective flows, disintegration of the convective pattern and the formation of a more uniform distribution of the thermal field in the cell. The illustration of this is shown in
Figure 4.
The dependences of temperature of the bottom (
Tb) and top (
Tt) aluminum plates of the cell on time during heating of the bottom plate were measured. Initially, studies were carried out in the absence of a magnetic field.
Figure 5 shows the time dependence of the temperature of bottom plate measured after heating is turned on. It is seen that the temperature reaches a certain stationary value. It was observed that the increase in the temperature of the top plate accelerates significantly when thermal convection develops in the system. Under experimental conditions, this occurred approximately 2 min after the start of heating (
Figure 6). The temperature difference between the bottom and top plates increases until convection develops. This is due to the fact that the bottom plate is heated by electric current much faster than the outflow of heat due to thermal conductivity. After the development of convection, the temperature difference between the bottom and top plates begins to decrease until a stationary temperature difference between the plates is established (
Figure 7).
The experiments have shown that the presence of the magnetic field delays the onset of convection. Convection develops after a longer time interval in comparison with the analogous case in the absence of a magnetic field. At sufficiently high magnetic field strengths (
H), complete inhibition of the development of convection can occur. As a result of magnetic field inhibition of convection, heat transfer from the heated bottom plate to the passive top plate of the cell slows down. This leads to the fact that the temperature of the bottom plate is higher (
Figure 5), and the temperature of the top plate is lower (
Figure 6) than the corresponding values in the absence of a field. Due to the suppression of convection by the magnetic field, the decreasing section of the dependence in
Figure 7 disappears. The temperature difference between the bottom and top plates of the cell reaches a stationary value (much higher than that in the absence of magnetic field) when the heat inflow from the bottom plate heaters is balanced by the heat outflow due to thermal conductivity.
The cooling process of the bottom plate of the cell was studied depending on the influence of the external magnetic field. To do this, the bottom plate was first heated in the absence of a magnetic field to the state of stable thermal convection in the magnetic nanofluid. After that, the heating was turned off and the magnetic field was simultaneously turned on. In the absence of a magnetic field, after the heating was turned off, thermal convection persisted for some time, providing more intense cooling of the bottom plate. Suppression of convection by the magnetic field slowed down the cooling process. The temperature difference between the bottom and top plates of the cell was measured as a function of time to demonstrate this effect (
Figure 8). The difference in the cooling rate of a heated plate in a magnetic field and in the absence of a field is also demonstrated in
Figure 9, which shows the time dependence of the rate of change in the temperature difference between the bottom and top plates of the cell. To obtain the dependencies shown in
Figure 9, the data shown in
Figure 8 were approximated by polynomial functions and then the derivative of these functions was numerically found.
It should be noted that no effect of a magnetic field has been observed on the thermal convection in pure water under our experimental conditions.
4. Discussion and Conclusions
The studied quasi-two-dimensional convective flow of a magnetic nanofluid can also be considered as a Hele-Shaw flow. Natural convection of magnetic nanofluid in a rectangular Hele-Shaw cell is governed by the following equations [
29,
30,
31,
32]:
where η is the viscosity, ρ the density, α the volumetric expansion coefficient, μ
0 the magnetic constant, C the specific heat, λ the thermal conductivity,
M the magnetization, and
h the thickness of the cell. These equations differ from the equations describing the convection of an ordinary liquid by the presence of terms that characterize the magnetic field and magnetization of the medium. The influence of these magnetic terms on the resulting behavior of the liquid medium was considered in detail, for example, in [
19]. In particular, it was shown that in the case when the magnetic field gradient is opposite to the temperature gradient in the medium, this leads to the suppression of convection. In the case under study, the magnetic field gradient is created by the inhomogeneity of the magnetization of the magnetic nanofluid, which occurs due to the inhomogeneous temperature distribution in the medium. The lower, more heated layers of the magnetic nanofluid have, under experimental conditions, a lower magnetization than the upper layers. As a result, the magnetic field gradient is directed opposite to the temperature gradient.
The absolute error of the experimental measurements presented in this paper is characterized by the value of the scatter of points on the corresponding dependencies. To control the accuracy of the results obtained, all the dependencies presented in the work were measured three times. As a result, the reproducibility of the experimental data was established within the relative error of 5%. It should be noted that the interpretation of the obtained results is complicated by the fact that in the conditions of the described experiments, a perceptible part of the heat flow from hot bodies goes into the surrounding space and structural elements of the measuring cell, and not only into the magnetic nanofluid. However, the heat flow through the magnetic nanofluid is still predominant, and the obtained qualitative regularities and principal results can be considered correct.
Regarding the results obtained on the cooling of a heated plate in a magnetic field in a magnetic nanofluid, it should be noted that to a certain extent similar studies were presented in [
34]. However, in contrast to the current work, in [
34], the change in the cooling rate of a heated object was associated with a change in the thermal conductivity of a magnetic nanofluid in a magnetic field due to the formation of a microstructure of aggregates in it. Visual observations using an optical microscope did not reveal the formation of a noticeable microstructure in the magnetic nanofluid used in the experiments described above. To further exclude the possibility of the effect of changes of thermal conductivity of magnetic nanofluid on the results and conclusions obtained in this study, we conducted direct measurements of thermal conductivity of magnetic nanofluid using a DTC-300 Thermal Conductivity Meter (TA Instruments). The measurement did not reveal noticeable changes of thermal conductivity under magnetic field for our sample of magnetic nanofluid. It can be concluded that the effects described in the current paper are related precisely to the suppression of convection in a magnetic nanofluid by a magnetic field.
The development of thermal convection has a threshold character and occurs when the critical value of the temperature gradient is exceeded. It is also well known that the magnetic field acting perpendicular to the temperature gradient in the magnetic nanofluid layer increases the threshold level of convection initiation [
19,
20], which is qualitatively consistent with the effects observed in the current work. However, all of this applies to the conditions of loss of stability and the stationary mode of convection in a layer of magnetic nanofluid. The dynamics of the development and damping of convection considered in this paper cannot be explained at the qualitative level in terms and concepts used in previous studies. This requires a full consideration of the dynamic problem, which is an incentive and motivation for further research in this direction.
The main results of this study are to establish the fact that the magnetic field not only affects the critical conditions for the convection onset, but can also slow down its development. The inhibition of convection leads to the fact that the heat transfer through the magnetic nanofluid in the magnetic field is reduced in comparison with the heat transfer in the absence of the field. This is reflected both in the dynamics of heating initially cold objects, and in the dynamics of cooling initially hot objects in magnetic nanofluid. The possibility to control with a magnetic field heat transfer in fluid systems can be very useful in many technological applications, such as cooling devices for electronics, heat exchangers, and zero gravity engineering. In addition to the direct interest in the subject area of magnetic nanofluids, the results obtained in this work can be considered as models for understanding the processes occurring in other systems in which convective transfer takes place, complicated by the influence of external magnetic fields [
35].