?SR-Study of a 3% CoFe2O4 Nanoparticle Concentration Ferrofluid
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Muon Spin Rotation (μSR) Method
3. Results and Discussion
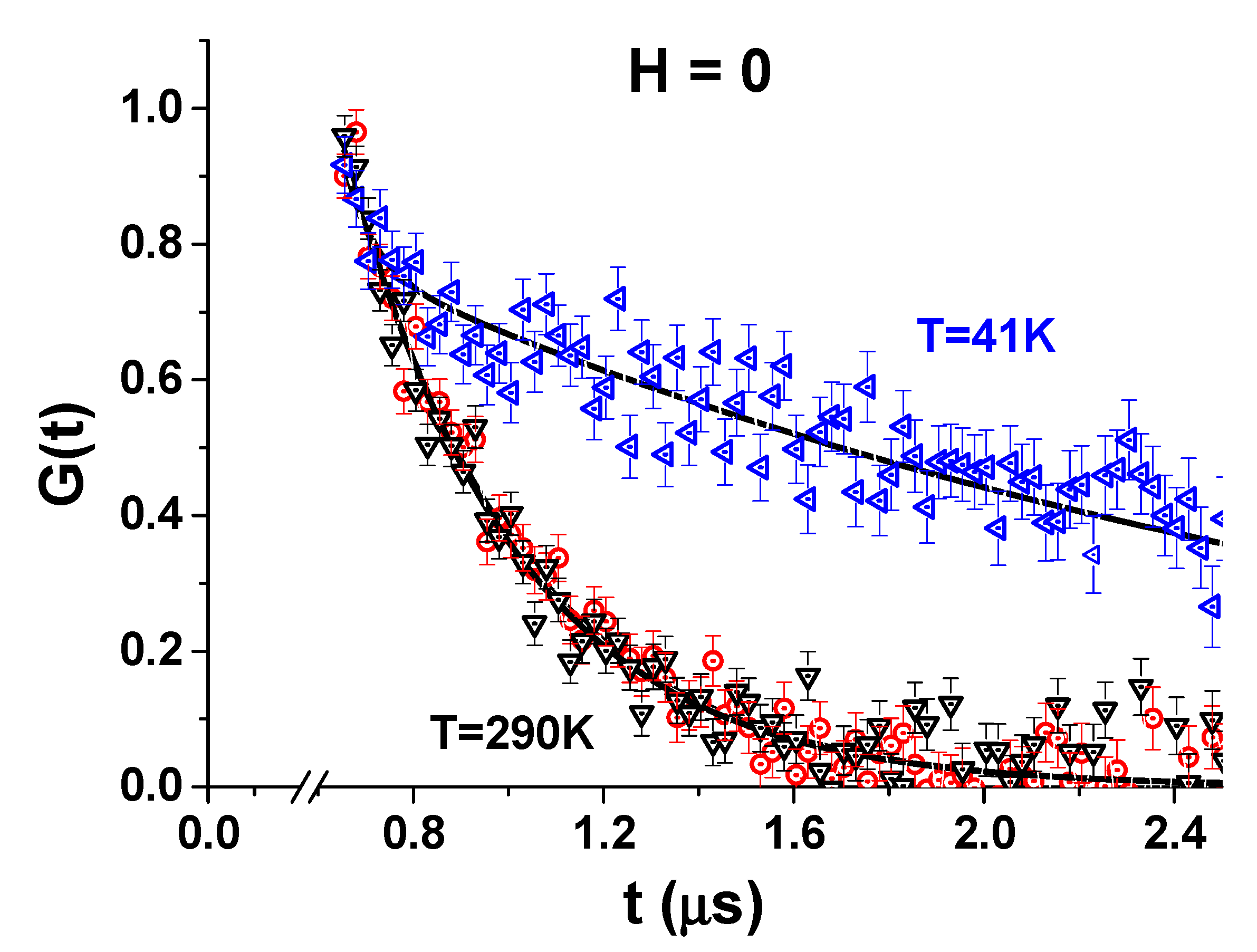
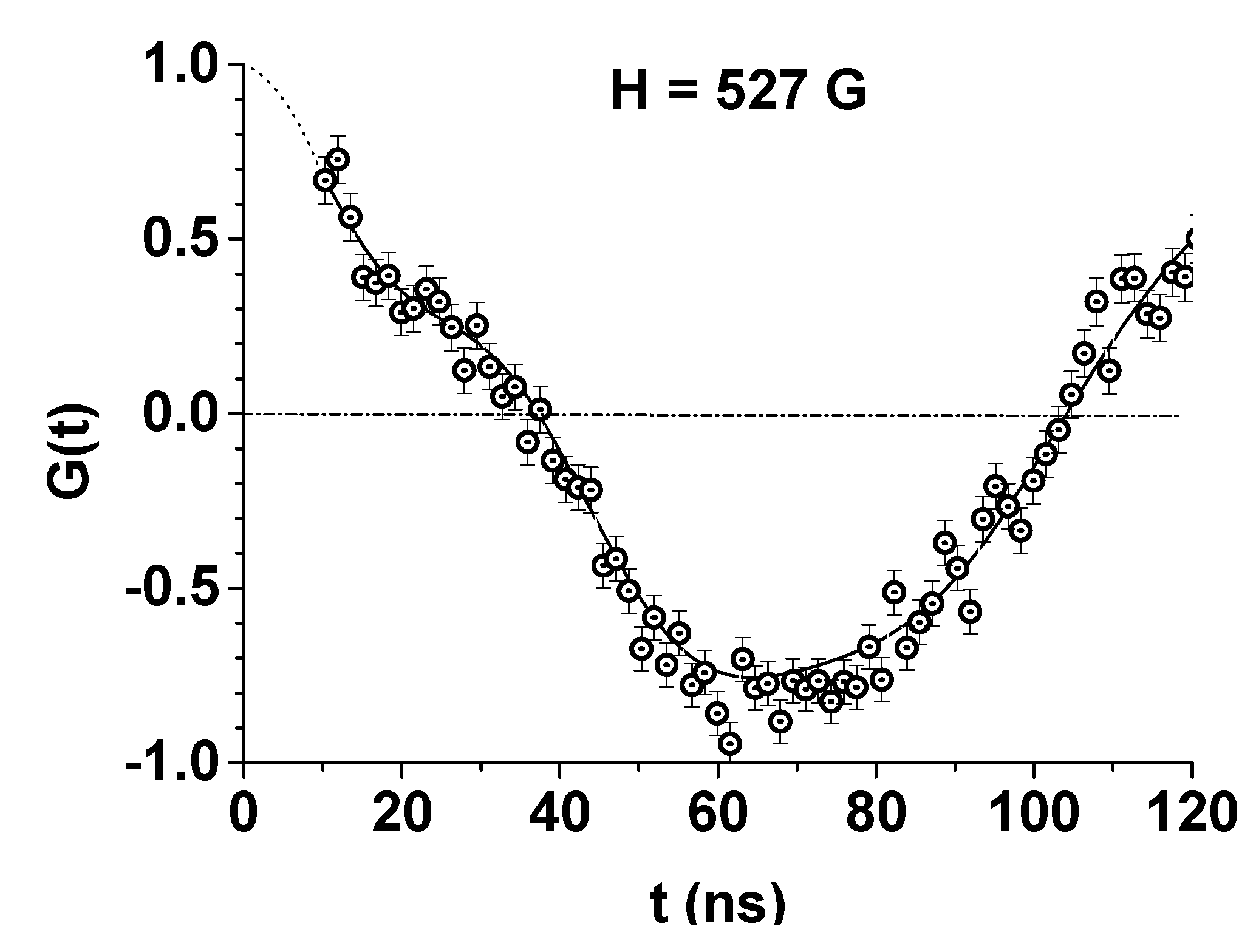
3.1. Zero Field Measurements
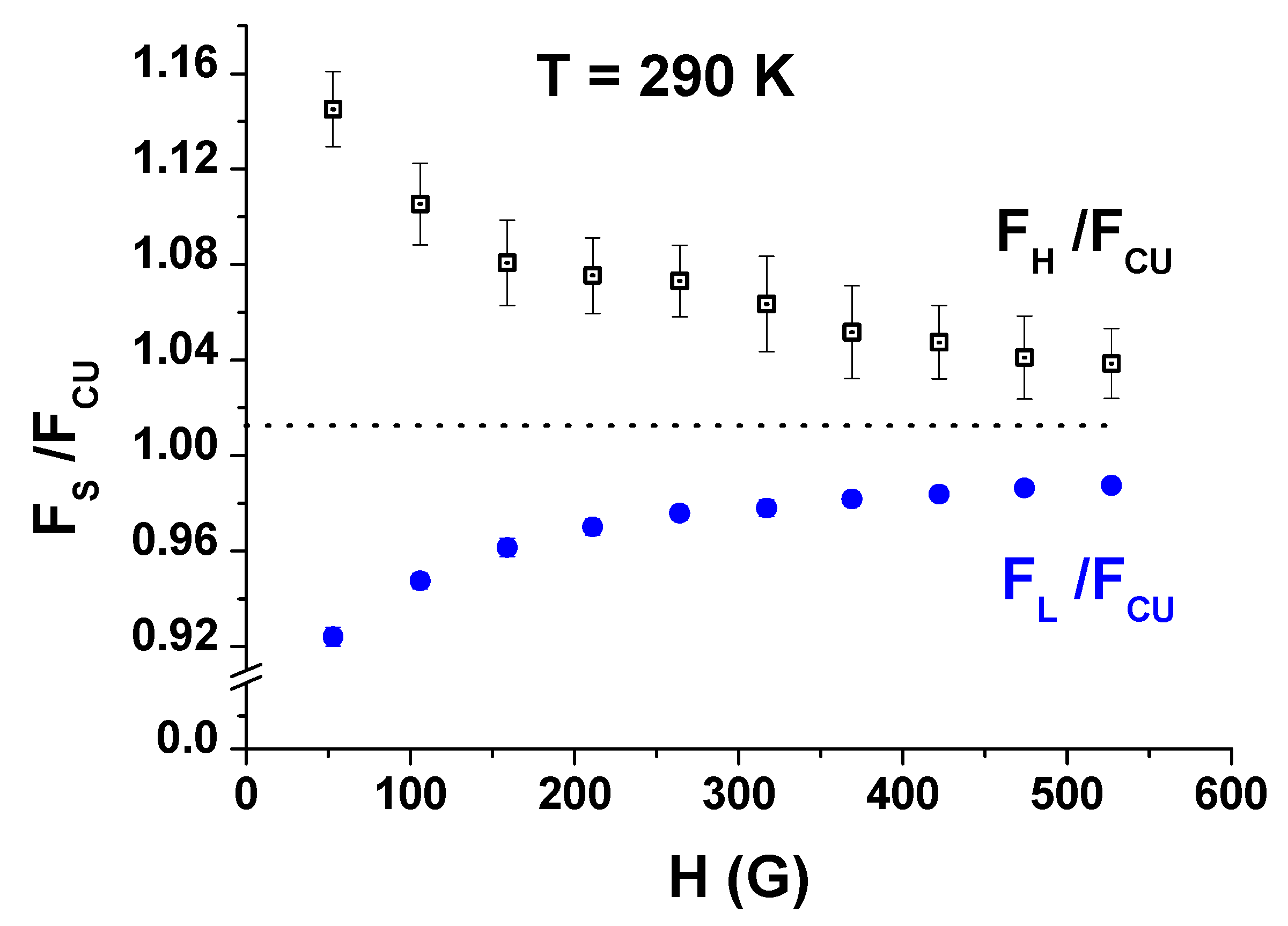
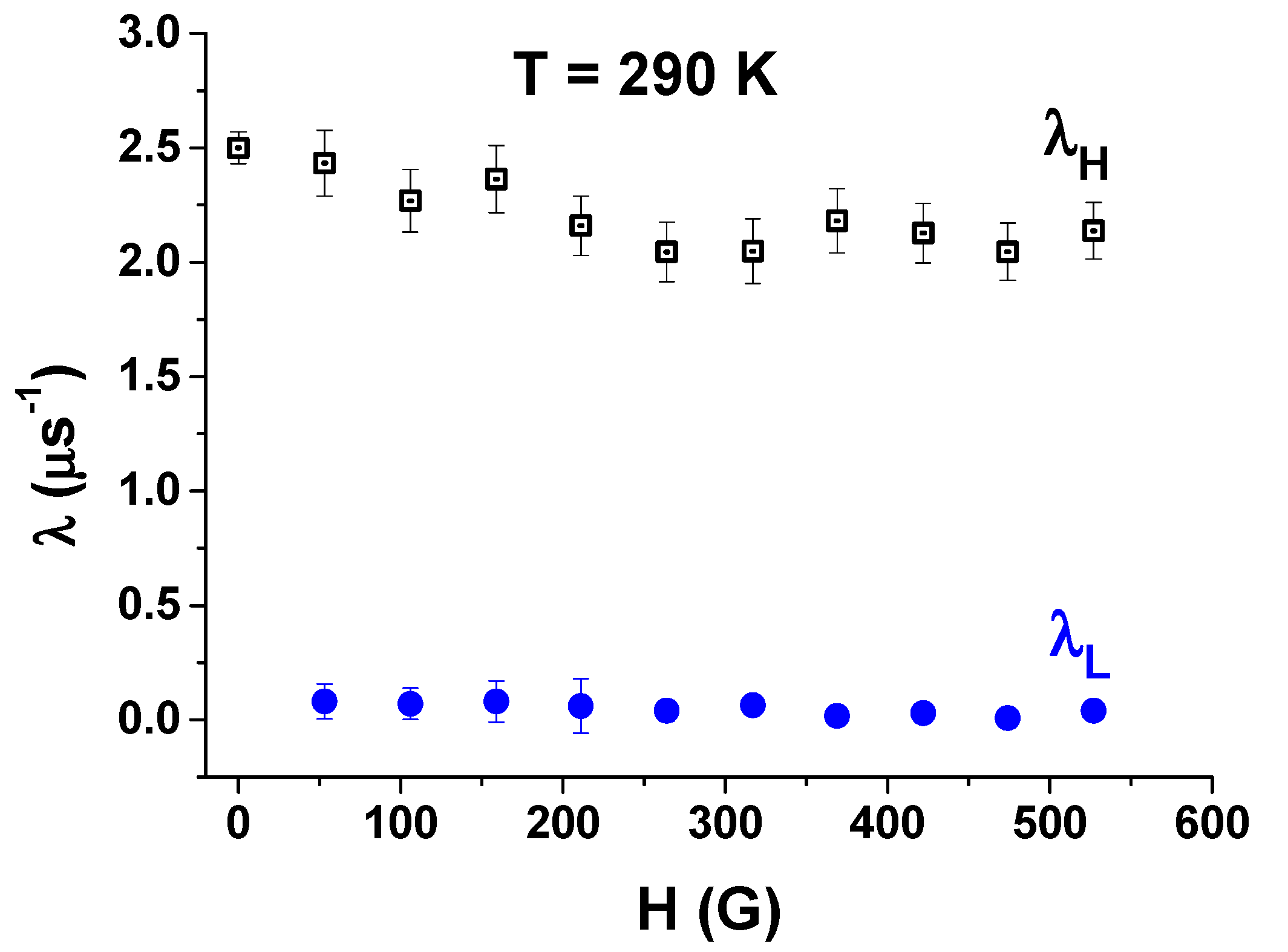
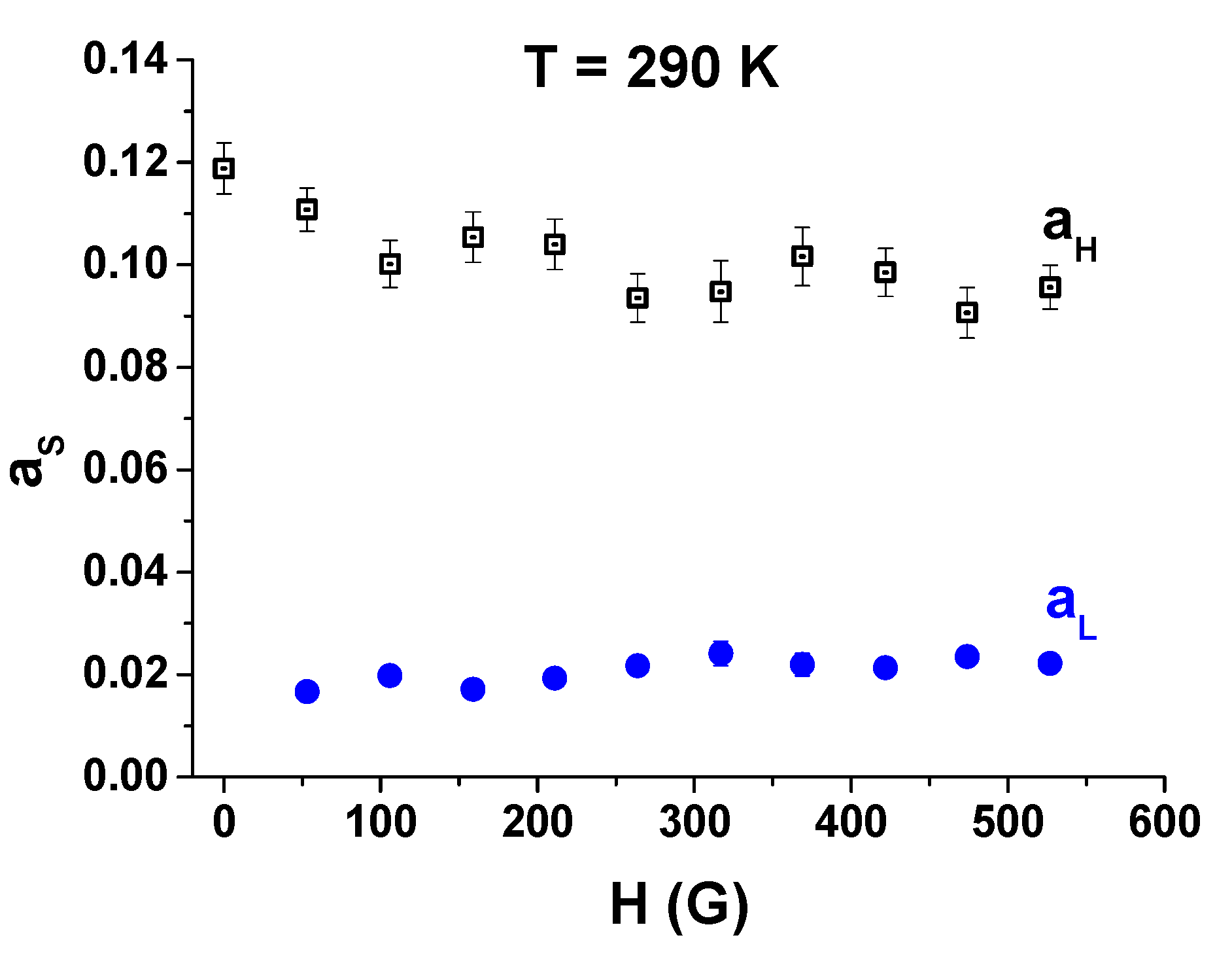
3.2. The Field Scan at the Room Temperature
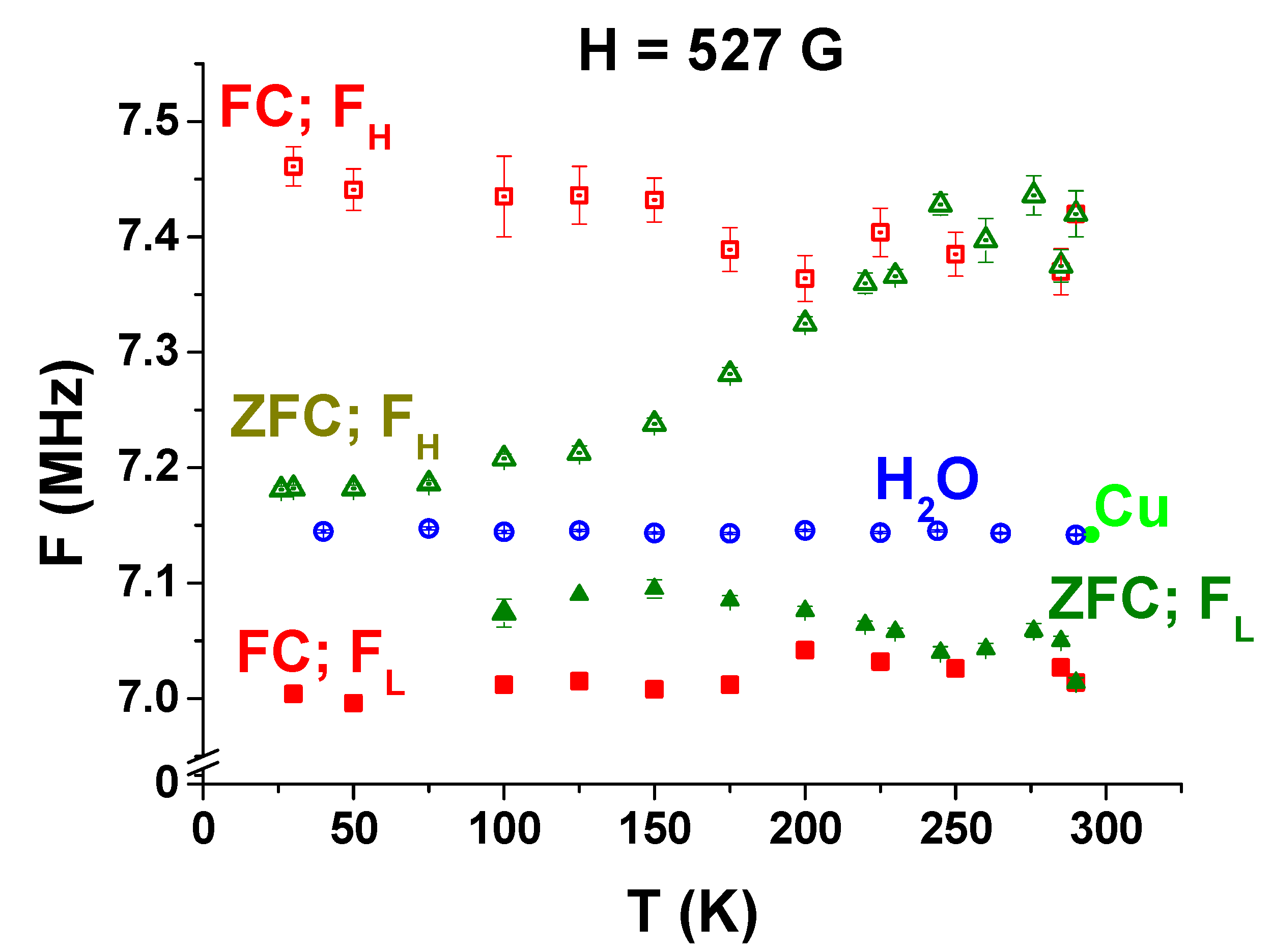
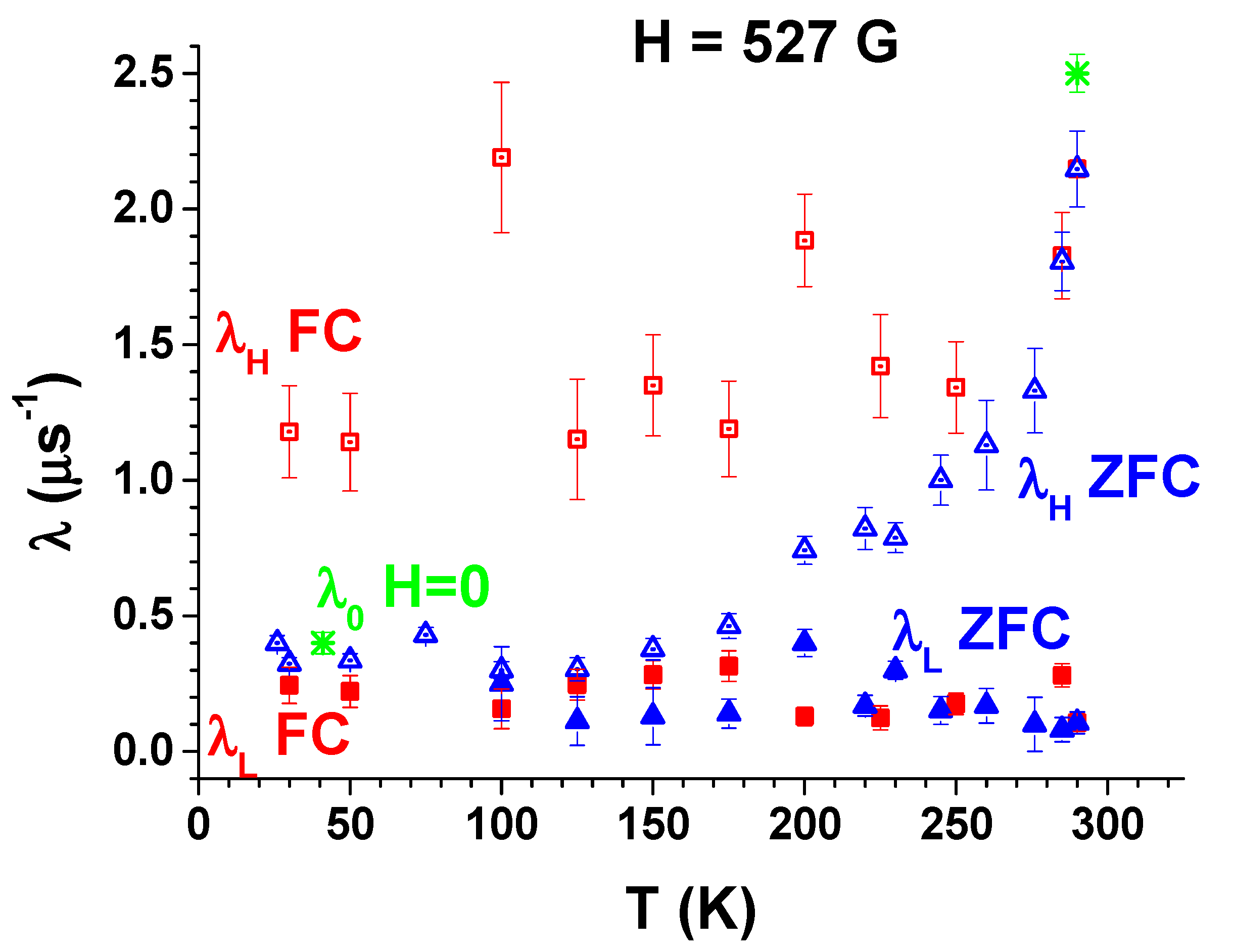
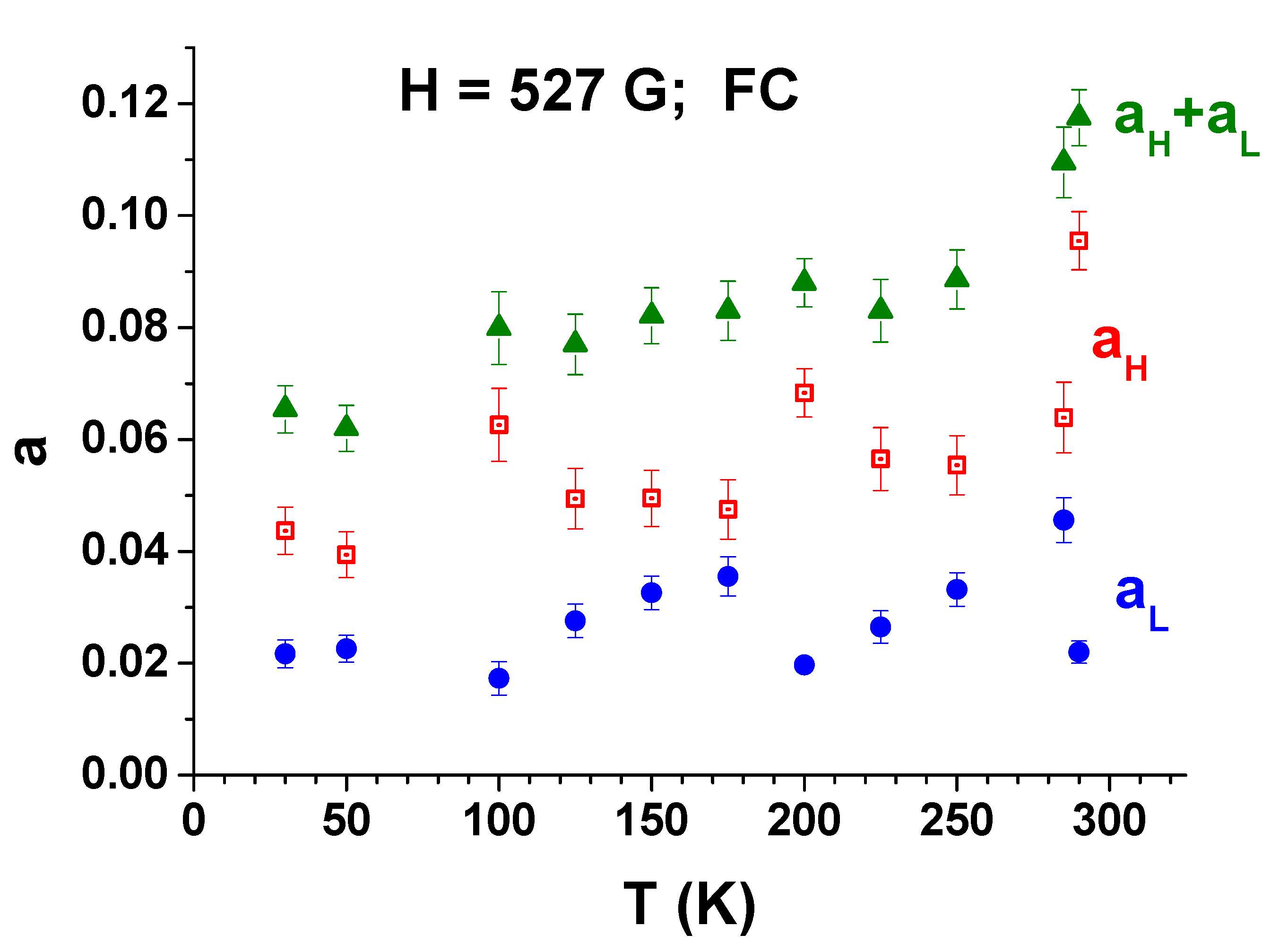
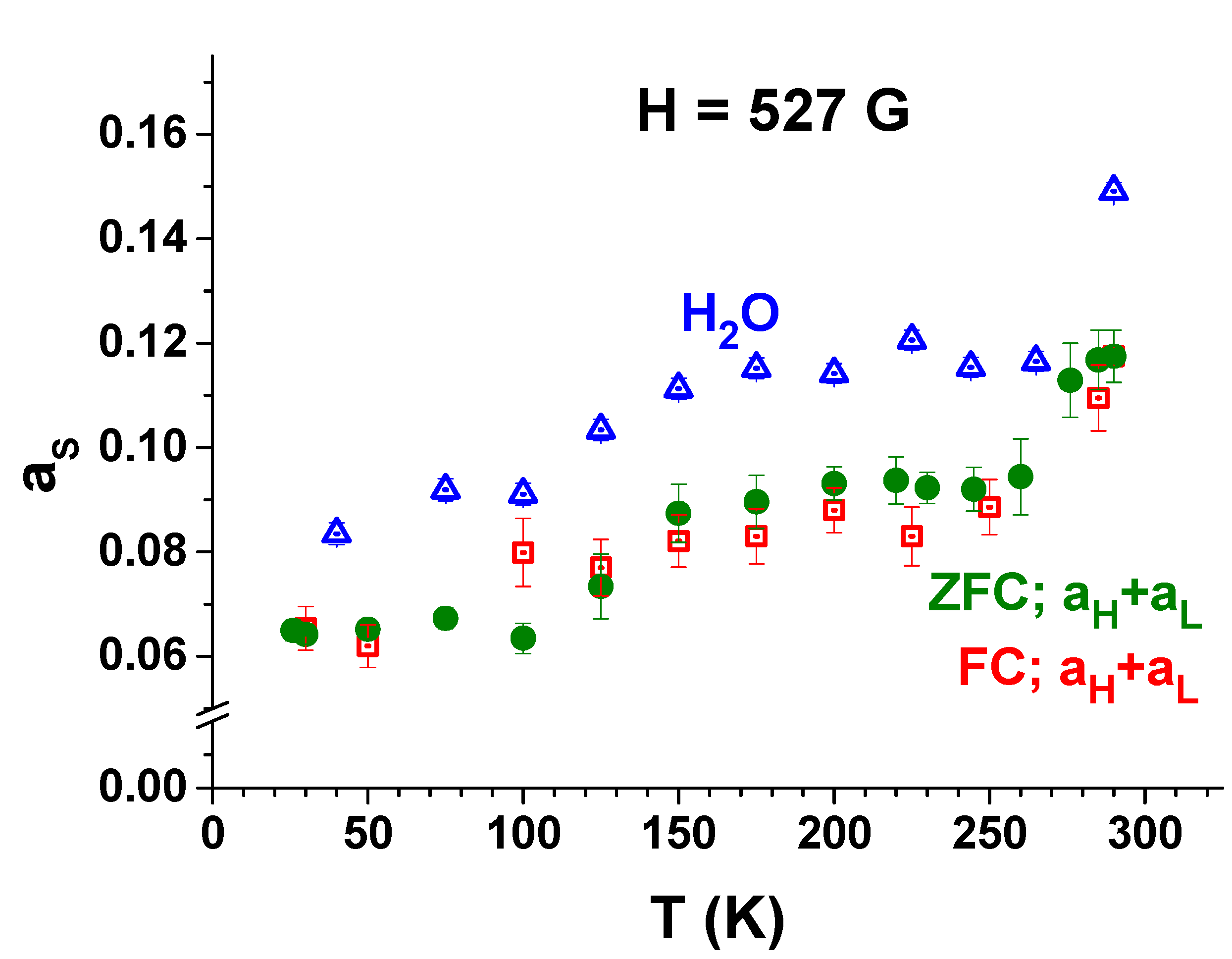
3.3. FC and ZFC Measurements
3.4. The Estimation of the Magnitude of the Magnetic Field Near the Nanoparticle
4. Conclusions
- (i)
- The structure and value of the magnetization of a ferrofluid with CoFe2O4 nanoparticles depend on the viscosity of the liquid itself.
- (ii)
- At room temperature (~290 K), when the sample was a superparamagnetic system, from the experimentally determined magnetization an average magnetic field of 20 G was obtained.
- (iii)
- A small fraction of the sample with negative magnetization, characteristic for diamagnetic systems, was also determined.
- (iv)
- At low temperatures (~30 K), the sample exhibits paramagnetic behavior in a magnetic field.
- (v)
- The magnetic field inside and in the immediate vicinity of the CoFe2O4 nanoparticles was first measured by the μSR method, and its value was B = 1.96 ± 0.44 kG.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gubin, S.P.; Koksharov, Y.A.; Khomutov, G.B.; Yurkov, G.Y. Magnetic nanoparticles: Preparation, structure and properties. Russ. Chem. Rev. 2005, 74, 489–520. [Google Scholar] [CrossRef]
- Joseph, S.A.; Mathew, S. Ferrofluids: Synthetic Strategies, Stabilization, Physicochemical Features, Characterization, and Applications. ChemPlusChem 2014, 79, 13821420. [Google Scholar]
- Torres-Diaz, I.; Rinaldi, C. Recent progress in ferrofluids research: Novel applications of magnetically controllable and tunable fluids. Soft Matter 2014, 10, 8584–8602. [Google Scholar] [CrossRef]
- Vestal, C.R.; Zhang, Z.J. Magnetic spinel ferrite nanoparticles from microemulsions. Int. J. Nanotechnol. 2004, 1, 240–263. [Google Scholar] [CrossRef]
- Odenbach, S. (Ed.) Colloidal Magnetic Fluids: Basics, Development and Application of Ferrofluids; Springer: Berlin/Heidelberg, Germany, 2009; p. 763. [Google Scholar]
- Socoliuc, V.; Peddis, D.; Petrenko, V.I.; Avdeev, M.V.; Susan-Resiga, D.; Szabó, T.; Turcu, R.; Tombácz, E.; Vékás, L. Magnetic Nanoparticle Systems for Nanomedicine—A Materials Science Perspective. Magnetochemistry 2019, 6, 2. [Google Scholar] [CrossRef] [Green Version]
- Popescu, R.C.; Andronescu, E.; Vasile, B.S. Recent Advances in Magnetite Nanoparticle Functionalization for Nanomedicine. Nanomaterials 2019, 9, 1791. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hosu, O.; Tertis, M.; Cristea, C. Implication of Magnetic Nanoparticles in Cancer Detection, Screening and Treatment. Magnetochemistry 2019, 5, 55. [Google Scholar] [CrossRef] [Green Version]
- Bilal, M.; Mehmood, S.; Rasheed, T.; Iqbal, H.M.N. Bio-Catalysis and Biomedical Perspectives of Magnetic Nanoparticles as Versatile Carriers. Magnetochemistry 2019, 5, 42. [Google Scholar] [CrossRef] [Green Version]
- Katz, E. Magnetic Nanoparticles. Magnetochemistry 2020, 6, 6. [Google Scholar] [CrossRef] [Green Version]
- Larkin, T.I.; Bol’ginov, V.V.; Stolyarov, V.S.; Ryazanov, V.V.; Vernik, I.V.; Tolpygo, S.K.; Mukhanov, O.A. Ferromagnetic Josephson switching device with high characteristic voltage. Appl. Phys. Lett. 2012, 100, 222601. [Google Scholar] [CrossRef] [Green Version]
- Bergeret, F.S.; Verso, A.; Volkov, A.F. Electronic transport through ferromagnetic and superconducting junctions with spin-filter tunneling barriers. Phys. Rev. B 2012, 86, 214516. [Google Scholar] [CrossRef] [Green Version]
- Richardson, C.L.; Devine-Stoneman, J.M.; Divitini, G.; Vickers, M.E.; Chang, C.-Z.; Amado, M.; Moodera, J.S.; Robinson, J.W.A. Structural properties of thin-film ferromagnetic topological insulators. Sci. Rep. 2017, 7, 12061. [Google Scholar] [CrossRef] [Green Version]
- Parlato, L.; Caruso, R.; Vettoliere, A.; Satariano, R.; Ahmad, H.G.; Miano, A.; Montemurro, D.; Salvoni, D.; Ausanio, G.; Tafuri, F.; et al. Characterization of scalable Josephson memory element containing a strong ferromagnet. J. Appl. Phys. 2020, 127, 193901. [Google Scholar] [CrossRef]
- Felicia, L.J.; Vinod, S.; Philip, J. Recent Advances in Magnetorheology of Ferrofluids (Magnetic Nanofluids)—A Critical Review. J. Nanofluids 2016, 5, 1–22. [Google Scholar] [CrossRef]
- Kole, M.; Khandekar, S. Engineering applications of ferrofluids: A review. J. Magn. Magn. Mater. 2021, 537, 168222. [Google Scholar] [CrossRef]
- Krasia-Christoforou, T.; Socoliuc, V.; Knudsen, K.D.; Tombácz, E.; Turcu, R.; Vékás, L. From Single-Core Nanoparticles in Ferrofluids to Multi-Core Magnetic Nanocomposites: Assembly Strategies, Structure, and Magnetic Behavior. Nanomaterials 2020, 10, 2178. [Google Scholar] [CrossRef] [PubMed]
- Lysenko, S.N.; Lebedev, A.V.; Astaf’eva, S.A.; Yakusheva, D.E.; Balasoiu, M.; Kuklin, A.I.; Kovalev, Y.S.; Turchenko, V.A. Preparation and magneto-optical behavior of ferrofluids with anisometric particles. Phys. Scr. 2020, 95, 044007. [Google Scholar] [CrossRef]
- Bica, D.; Vekas, L.; Avdeev, M.V.; Marinica, O.; Socoliuc, V.; Balasoiu, M.; Garamus, V.M. Sterically stabilized water based magnetic fluids: Synthesis, structure and properties. J. Magn. Magn. Mater. 2007, 311, 17–21. [Google Scholar] [CrossRef]
- Lebedev, A.V.; Lysenko, S.N. A multifunctional stabilizer of magnetic fluids. Appl. Phys. Lett. 2009, 95, 013508. [Google Scholar] [CrossRef]
- Lysenko, S.N.; Yakushev, R.M.; Strel’nikov, V.N.; Gabdrakhimova, Y.I.; Borisova, I.A. Steric stabilization and functionalization of magnetite particles and preparation of colloid magnetite dispersions in oligomeric media. Russ. J. Appl. Chem. 2010, 83, 1399–1402. [Google Scholar] [CrossRef]
- Vekas, L.; Rasa, M.; Bica, D. Physical properties of magnetic fluids and nanoparticles from magnetic and magneto-rheological measurements. J. Colloid Interface Sci. 2000, 231, 247–254. [Google Scholar] [CrossRef]
- Socoliuc, V.; Bica, D.; Vekas, L. Estimation of magnetic particle clustering in magnetic fluids from static magnetization experiments. J. Colloid Interface Sci. 2003, 264, 141–147. [Google Scholar] [CrossRef]
- Lebedev, A.V. Temperature dependence of magnetic moments of nnoparticles and their dipole interaction in magnetic fluids. J. Magn. Magn. Mater. 2015, 374, 120–124. [Google Scholar] [CrossRef]
- Sergeenkov, S.; Stan, C.; Cristescu, C.P.; Balasoiu, M.; Perov, N.S.; Furtado, C. Evidence forfield induced proximity type behavior in based ferromagnetic nanofluid. Philos. Mag. Lett. 2017, 97, 287–293. [Google Scholar] [CrossRef] [Green Version]
- Gamarra, L.F.; Pontuschka, W.M.; Mamani, J.B.; Cornejo, D.R.; Oliveira, T.R.; Vieira, E.D.; Costa-Filho, A.J.; Amaro, E., Jr. Magnetic characterization by SQUID and FMR of a biocompatible ferrofluid based on Fe3O4. J. Phys. Condens. Matter 2009, 21, 115104. [Google Scholar] [CrossRef]
- Granata, C.; Vettoliere, A. Nano superconducting quantum interface device: A powerful tool for nanoscale investigations. Phys. Rep. 2016, 614, 1–69. [Google Scholar] [CrossRef] [Green Version]
- Kuncser, V.; Schinteie, G.; Sahoo, B.; Keune, W.; Bica, D.; Vekas, L.; Filoti, G. Magnetic interactions in water based ferrofluids studied by Mössbauer spectroscopy. J. Phys. Condens. Matter 2006, 19, 016205. [Google Scholar] [CrossRef]
- Spanu, V.; Filoti, G.; Bica, D.; Balasoiu, M.; Crisan, O. Mossbauer Spectroscopy Studies of Fine Fe3O4 Particles Contained in Magnetic Fluids. Rom. Rep. Phys. 1995, 47, 299–307. [Google Scholar]
- Grabcev, B.; Balasoiu, M.; Tarziu, A.; Kuklin, A.I.; Bica, D. Application of contrast variation method in SANS experiments with ferrofluids. J. Magn. Magn. Mater. 1999, 201, 140–143. [Google Scholar] [CrossRef]
- Avdeev, M.V.; Balasoiu, M.; Aksenov, V.L.; Garamus, V.M.; Kohlbrecher, J.; Bica, D.; Vekas, L. On the magnetic structure of magnetite/oleic acid/benzene ferrofluids by small-angle neutron scattering. J. Magn. Magn. Mater. 2004, 270, 371–379. [Google Scholar] [CrossRef]
- Balasoiu, M.; Kuklin, A.I. Magnetic scattering determination from SANS contrast variation experiments at IBR-2 reactor. Rom. J. Phys. 2016, 61, 473–482. [Google Scholar]
- Muehlbauer, S.; Honecher, D.; Perigo, E.A.; Bergner, F.; Disch, S.; Heinemann, A.; Erokhin, S.; Berkov, D.; Leighton, C.; Eskiidsen, M.; et al. Magnetic small-angle neutron scattering. Rev. Mod. Phys. 2019, 91, 015004. [Google Scholar] [CrossRef] [Green Version]
- Schenck, A. Muon Spin Rotation Spectroscopy; Adam Hilger, Ltd.: Bristol, UK, 1985. [Google Scholar]
- Jackson, T.J.; Binns, C.; Forgan, E.M.; Morenzoni, E.; Niedermayer, C.; Gluckler, H.; Hofer, A.; Luetkens, H.; Prokscha, T.; Riseman, T.M.; et al. Superparamagnetic relaxation in iron nanoclusters measured by low energy muon spin rotation. J. Phys. Condens. Matter 2000, 12, 1399–1411. [Google Scholar] [CrossRef]
- Boekema, C.; Lichti, R.L.; Brabers, V.A.M.; Denison, A.B.; Cooke, D.W.; Heffner, R.H.; Hutson, R.L.; Leon, M.; Schillaci, M.E. Magnetic interactions, bonding, and motion of positive muons in magnetite. Phys. Rev. B 1985, 31, 1233. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Boekema, C.; Lichti, R.L.; Chan, K.C.B.; Brabers, V.A.M.; Denison, A.B.; Cooke, D.W.; Heffner, R.H.; Hutson, R.L.; Schillaci, M.E. Experimental evidence for a Mott-Wigner glass phase of magnetite above the Verwey temperature. Phys. Rev. B 1986, 33, 210. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.; Zhao, F.; Wu, W.; Cao, S.-H.; Zhao, G. Magnetic properties in silica-coated CoFe2O4 nanoparticles: Quantitative test for a theory of single-domain particles with cubic anisotropy. Phys. Lett. A 2012, 376, 547–549. [Google Scholar] [CrossRef]
- Balasoiu, M.; Barsov, S.G.; Bica, D.; Vekas, L.; Vorob’ev, S.I.; Gritsaj, K.I.; Duginov, V.N.; Zhukov, V.A.; Komarov, E.N.; Koptev, V.P.; et al. muSR Study of the Properties of Fe3O4-Based Nanostructured Magnetic Systems. JETP Lett. 2008, 88, 210–213. [Google Scholar] [CrossRef]
- Lebedev, A.V.; Lysenko, S.N. Magnetic fluids stabilized by polypropylene glycol. J. Magn. Magn. Mater. 2011, 323, 1198–1202. [Google Scholar] [CrossRef]
- Yakushev, R.M.; Lysenko, S.N.; Tiunova, T.G.; Borisova, I.A.; Lebedev, A.V. Rheology of magnetite dispersions in oligo(propylene glycol) and the structure of the stabilizing layer on dispersed phase particles. Colloid J. 2013, 75, 226–230. [Google Scholar] [CrossRef]
- Barsov, S.G.; Vorob’ev, S.I.; Koptev, V.P.; Kotov, S.A.; Mikirtych’yants, S.M.; Shcherbakov, G.V. The μSR setup on the muon beam of the synchrocyclotron at the Konstantinov Institute of Nuclear Physics. Instrum. Exp. Tech. 2007, 50, 750–756. [Google Scholar] [CrossRef]
- Smilga, V.P.; Belousov, Y.M. The Muon Method in Science; Nova Science Publishers: New York, NY, USA, 1992. [Google Scholar]
- Percival, P.W. Muonium formation in water and aqueous solutions. Hyperfine Interact. 1981, 8, 315–324. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vorob’ev, S.I.; Balasoiu, M.; Buzatu, D.; Duginov, V.N.; Getalov, A.L.; Gritsaj, K.I.; Komarov, E.N.; Kotov, S.A.; Stan, C.; Scherbakov, G.V. ?SR-Study of a 3% CoFe2O4 Nanoparticle Concentration Ferrofluid. Magnetochemistry 2021, 7, 104. https://doi.org/10.3390/magnetochemistry7070104
Vorob’ev SI, Balasoiu M, Buzatu D, Duginov VN, Getalov AL, Gritsaj KI, Komarov EN, Kotov SA, Stan C, Scherbakov GV. ?SR-Study of a 3% CoFe2O4 Nanoparticle Concentration Ferrofluid. Magnetochemistry. 2021; 7(7):104. https://doi.org/10.3390/magnetochemistry7070104
Chicago/Turabian StyleVorob’ev, S. I., M. Balasoiu, D. Buzatu, V. N. Duginov, A. L. Getalov, K. I. Gritsaj, E. N. Komarov, S. A. Kotov, C. Stan, and G. V. Scherbakov. 2021. "?SR-Study of a 3% CoFe2O4 Nanoparticle Concentration Ferrofluid" Magnetochemistry 7, no. 7: 104. https://doi.org/10.3390/magnetochemistry7070104
APA StyleVorob’ev, S. I., Balasoiu, M., Buzatu, D., Duginov, V. N., Getalov, A. L., Gritsaj, K. I., Komarov, E. N., Kotov, S. A., Stan, C., & Scherbakov, G. V. (2021). ?SR-Study of a 3% CoFe2O4 Nanoparticle Concentration Ferrofluid. Magnetochemistry, 7(7), 104. https://doi.org/10.3390/magnetochemistry7070104





