Hyperfine Decoupling of ESR Spectra Using Wavelet Transform
Abstract
:1. Introduction
2. Materials
2.1. Spin-Systems
2.2. Choice of Microwave Frequency
2.3. Simulation of ESR Spectra
3. Methods
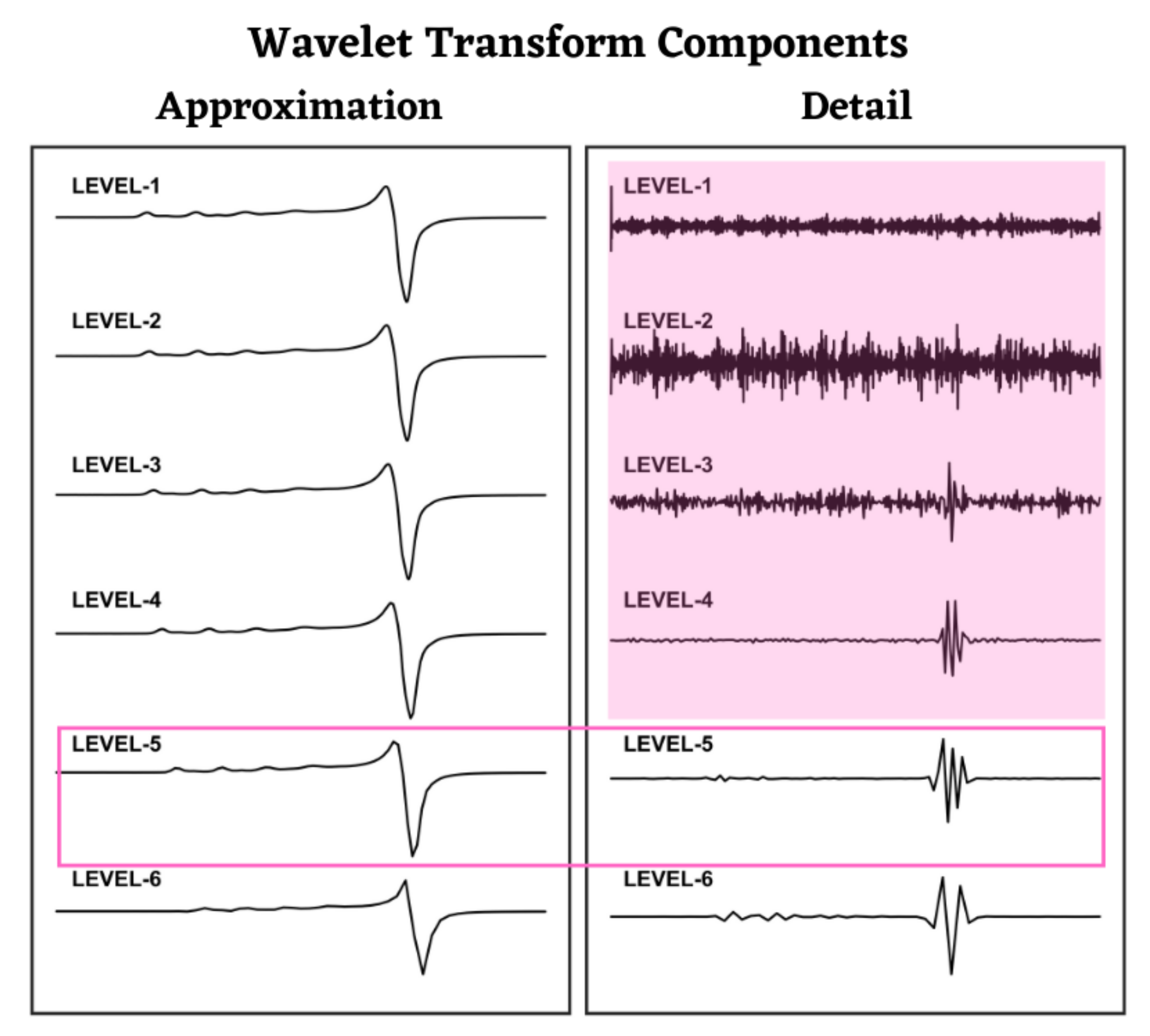
3.1. Wavelet Transforms
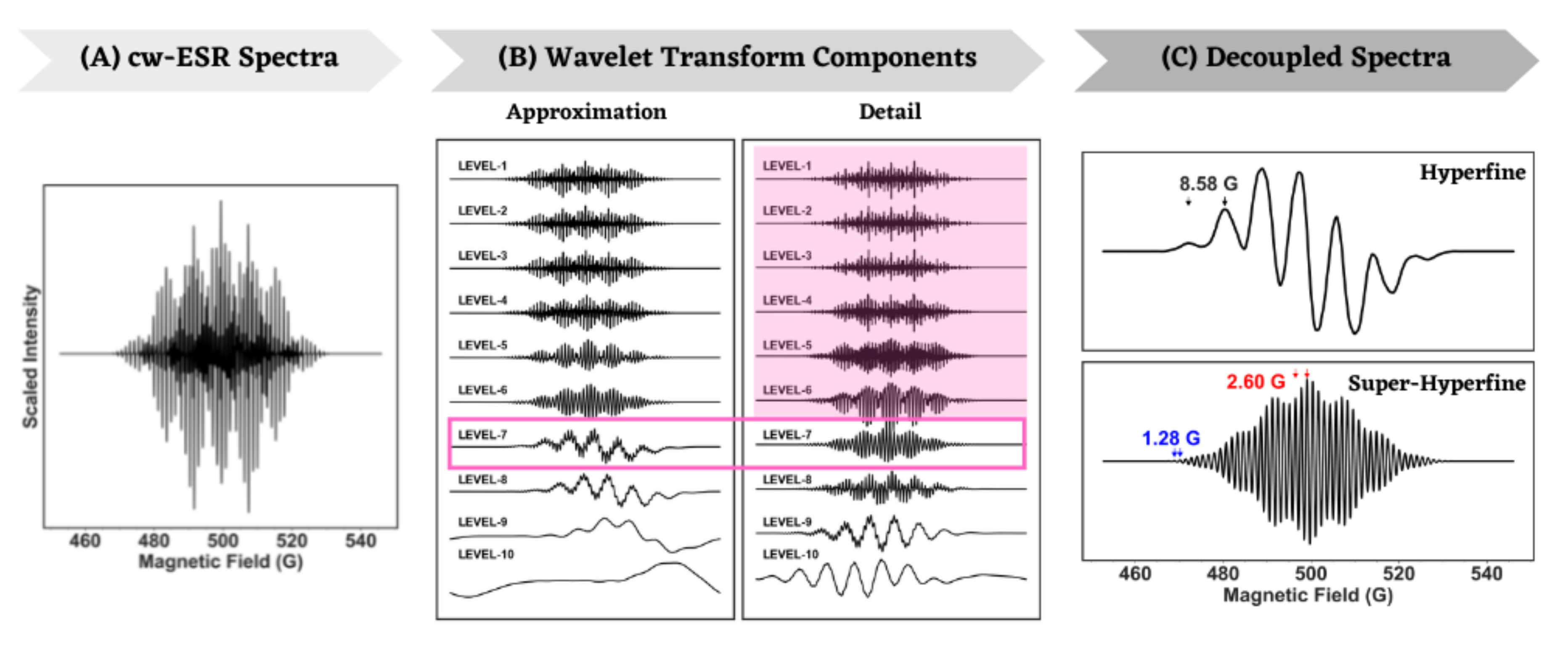
3.2. NERD Method
- (a)
- Wavelet Selection: There are many standard wavelet families that can be used for the UDWT. We use the Daubechies family wavelet “db6”. The Daubechies family provides the best sensitivity and selectivity for adjacent frequency values, as it maximizes the vanishing moments. Better frequency resolution is essential for distinguishing and separating features from the overlapped spectra. db6 wavelet is selected for its appropriate length. A smaller length may not capture all the necessary information, whereas a larger length would yield redundant information.
- (b)
- Undecimated Discrete Wavelet Transform: In NERD, we use the undecimated discrete wavelet transform [39] to achieve the maximum signal resolution in the Detail and Approximation components. This means that each Detail and Approximation component has the same length as that of the input signal. For instance, a signal with data length of 1024 will have 10 Detail and Approximation components (from 10 decomposition levels), each having a length of 1024 data points. The maximum number of decomposition levels, N, is defined as (p being the input signal length) [40]. The UDWT improves the resolution in the wavelet domain by preserving the input data length at all decomposition levels. In the decimated version, the Detail and Approximation components are downsampled by 2 at each level, and hence reduces the resolution essential for extracting the hyperfine lines.
- (c)
- Detail Component Selection: This step is adapted in the NERD method for the feature extraction purpose. For denoising, this step is associated with identifying noisy Detail components and applying noise thresholds to remove it [18,38,41,42]. For feature extraction, we retain the Detail components that contain hyperfine and/or super-hyperfine spectra, while removing all other Detail components, including the Approximation component. This step is repeated for each feature.
| Algorithm 1 Adapted NERD Algorithm for pseudo-decoupling |
|
4. Results and Discussion
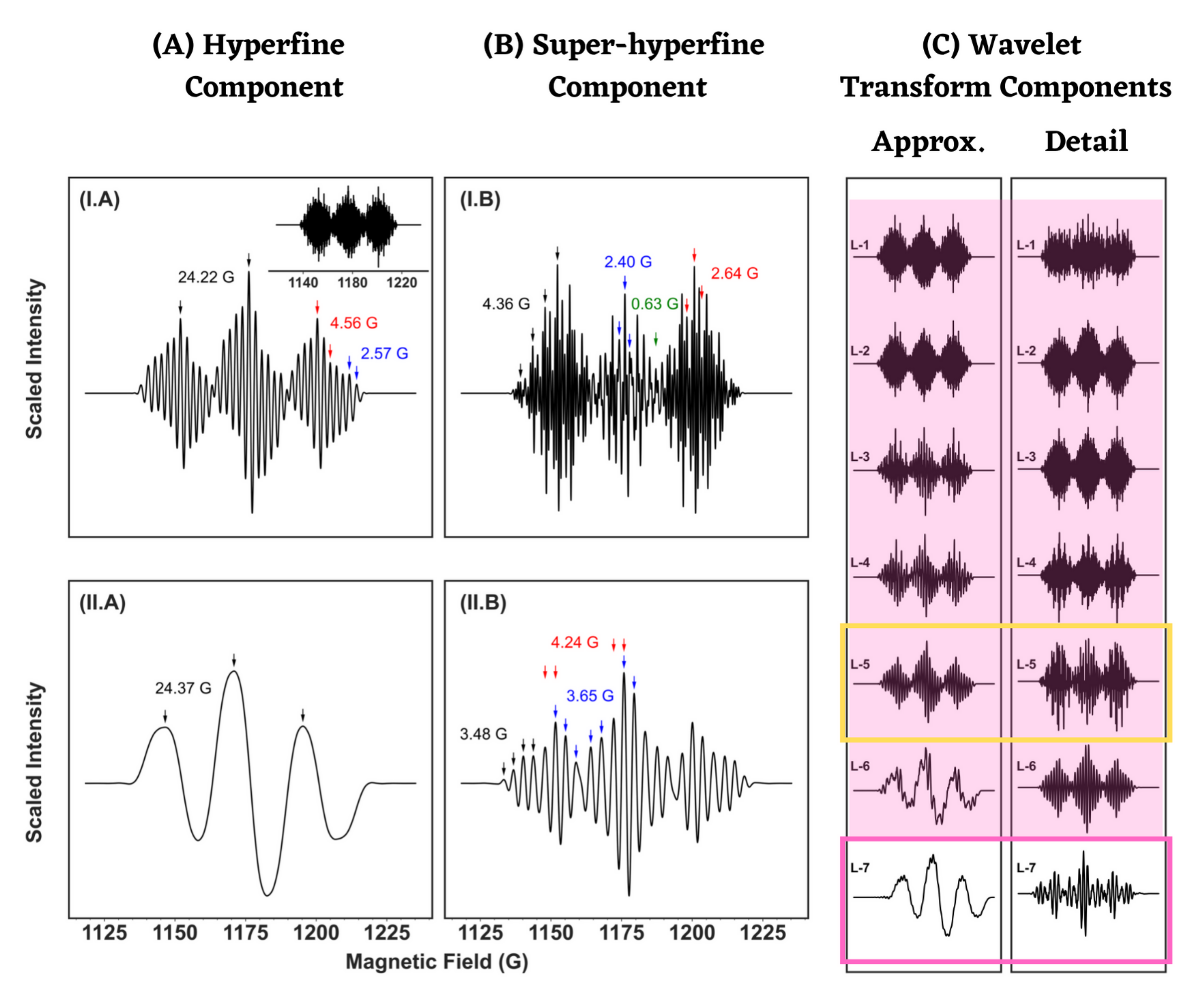
4.1. Analysis of Isotropic ESR Spectra
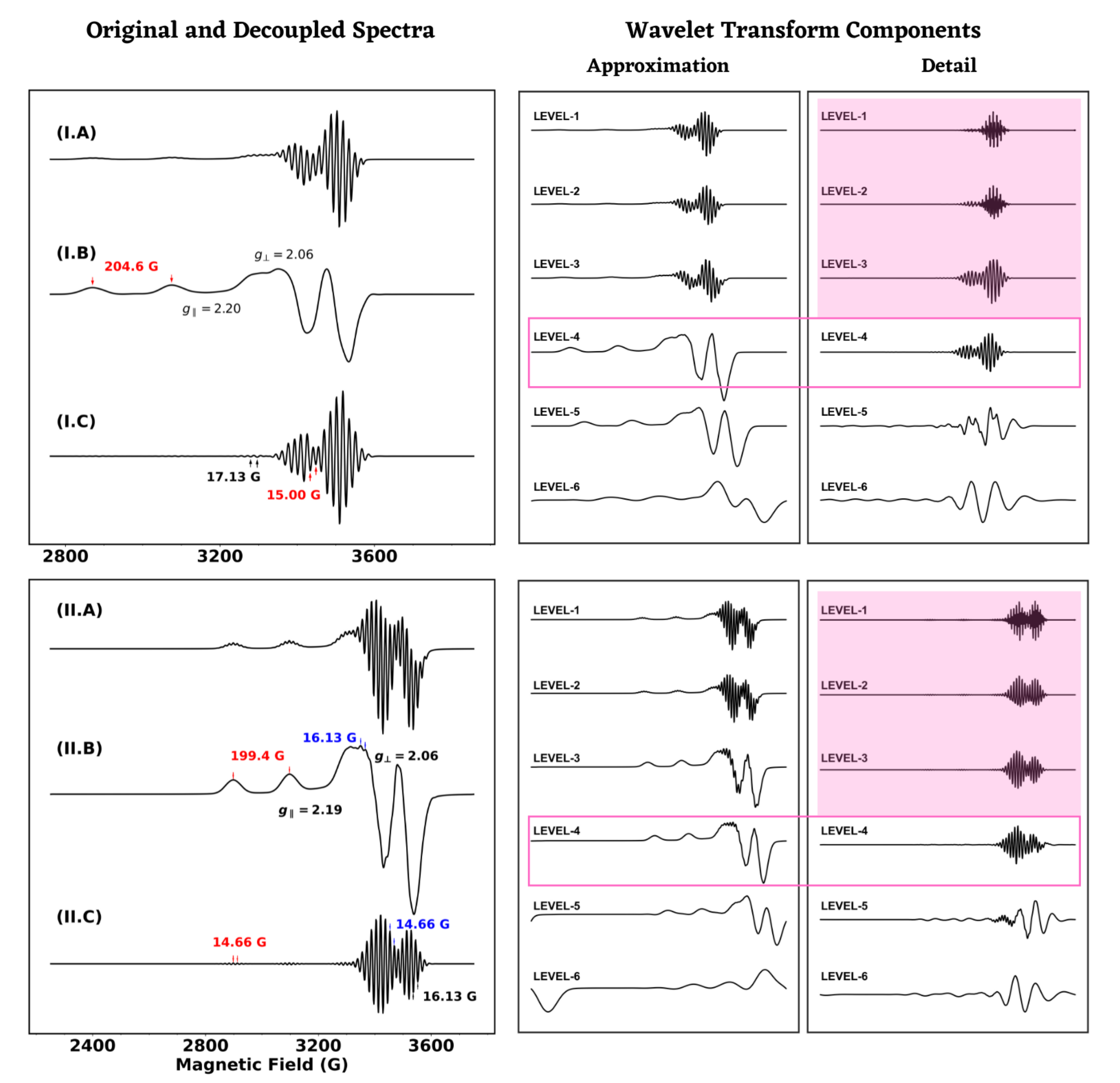
4.2. Analysis of Anisotropic ESR Spectra
4.3. Spectral Analysis of Experimental Data
5. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ESR | Electron spin resonance |
| PDS | Pulsed dipolar spectroscopy |
| NERD | Noise Elimination and Reduction via Denoising |
Appendix A. EasySpin Codes
Appendix A.1. Simulation Code for R-I ESR Spectra
A = mt2mhz([0.791, −0.249, −0.120], gfree) % conversion to MHz
Sys = struct(’g’, gfree, ’Nucs’ ’1H,1H,1H’ ’n’, [6, 4, 4],
’A’, A, ’lw’, 0.02);
Params = struct(’mwFreq’, 9.8, ’nPoints’, 8192);
% Simulation of isotropic spectra %
[B,spec] = garlic(Sys, Params);
Appendix A.2. Simulation Code for R-II ESR Spectra
A_Gauss = [4.34, −2.39, −0.65, −2.81, −0.23, 24.24]; % in Gauss
A_MHz = mt2mhz(A_Gauss/10, gfree); % Gauss to MHz
Sys = struct(’g’ 2.00316, ’Nucs’ ’14N,1H,1H,1H,1H,1H’,
’n’, [2, 2, 2, 2, 2], ’A’, A_MHz, ’lwpp’, [0 0.006]);
Params = struct(’mwFreq’ 9.878, ’CenterSweep’, [352 24],
’nPoints’, 4096);
% Simulation of isotropic spectra %
[B, spec] = garlic(Sys, Params);
Appendix A.3. Simulation Code for M-I ESR Spectra
A_MHz = [−54 −54 −608; 52 42 42]; % in MHz
Sys = struct(’g’, [2.0525 2.1994], ’Nucs’, ’63Cu,14N’,
’n’, [1, 4], ’A’, A_MHz, ’tcorr’ 10^−7.5,
’lw’, 0.3);
Params = struct(’mwFreq’, 9.8); % GHz
% Following setting is for treating the 14N nuclei
% perturbationally using post-convolution.
Opt.PostConvNucs = 2;
Opt.LLKM = [16 0 0 4]; % axial symmetry of 63Cu+e system
% Simulation of slow-motional spectra %
[x,y] = chili(Sys, Params, Opt);
Appendix A.4. Simulation Code for M-II ESR Spectra
A_Cu = [0.0019 0.0203]; % in cm^−1
A_N = [0.00145 0.0017]; % in cm^−1
A_Frame = [0 0 0; 0 −1 0; −1 −1 0; −2 −1 0; −3 −1 0]∗pi/2;
A_MHz = [A_Cu;A_N;A_N;A_N;A_N]∗30e3; cm^−1 to MHz
Sys = struct(’g’, [2.05 2.19], ’Nucs’, ’63Cu,14N,14N,14N,14N’,
’A’, A_MHz, ’AFrame’, A_Frame, ’lwpp’, [0 0.65]);
Params = struct(’mwFreq’, 9.8, ’Range’, [225 375]);
Opt.Method = ’perturb’;
Opt.nKnots = [181 0];
% Simulation of frozen spectra %
[x,y] = pepper(Sys, Params, Opt);
References
- Murphy, D.M.; Farley, R.D. Principles and applications of ENDOR spectroscopy for structure determination in solution and disordered matrices. Chem. Soc. Rev. 2006, 35, 249–268. [Google Scholar] [CrossRef] [PubMed]
- Cutsail, G.E. Applications of electron paramagnetic resonance spectroscopy to heavy main-group radicals. Dalton Trans. 2020, 49, 12128–12135. [Google Scholar] [CrossRef] [PubMed]
- Nagashima, H.; Mino, H. Highly resolved proton matrix ENDOR of oriented photosystem II membranes in the S2 state. Biochim. Biophys. Acta (BBA)-Bioenerg. 2013, 1827, 1165–1173. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Misra, S.K.; Andronenko, S.I.; Earle, K.A.; Freed, J.H. Single-crystal EPR studies of transition-metal ions in inorganic crystals at very high frequency. Appl. Magn. Reson. 2001, 21, 549–561. [Google Scholar] [CrossRef]
- Burghaus, O.P.M.; Rohrer, M.; Möbius, K.; MacMillan, F.; Lubitz, W. 3-mm High-field EPR on semiquinone radical anions Q.cntdot.-related to photosynthesis and on the primary donor P.cntdot.+ and acceptor QA.cntdot.-in reaction centers of Rhodobacter sphaeroides R-26. J. Phys. Chem. 1993, 97, 7639–7647. [Google Scholar] [CrossRef]
- Lakshmi, K.V.; Reifler, M.J.; Brudvig, G.W.; Poluektov, O.G.; Wagner, A.M.; Thurnauer, M.C. High-field EPR study of carotenoid and chlorophyll cation radicals in photosystem II. J. Phys. Chem. B 2000, 104, 10445–10448. [Google Scholar] [CrossRef]
- Bennati, M. EPR interactions—Hyperfine couplings. In EPR Spectroscopy: Fundamentals and Methods; John Wiley & Sons: Chichester, UK, 2018; p. 81. [Google Scholar]
- Hyde, J.S.; Bennett, B.; Kittell, A.W.; Kowalski, J.M.; Sidabras, J.W. Moving difference (MDIFF) non-adiabatic rapid sweep (NARS) EPR of copper (II). J. Magn. Reson. 2013, 236, 15–25. [Google Scholar] [CrossRef] [Green Version]
- Golombek, A.P.; Hendrich, M.P. Quantitative analysis of dinuclear manganese (II) EPR spectra. J. Magn. Reson. 2003, 165, 33–48. [Google Scholar] [CrossRef]
- Dzikovski, B.; Tipikin, D.; Livshits, V.; Earle, K.; Freed, J. Multifrequency ESR study of spin-labeled molecules in inclusion compounds with cyclodextrins. Phys. Chem. Chem. Phys. 2009, 11, 6676–6688. [Google Scholar] [CrossRef]
- Dzikovski, B.; Earle, K.; Pachtchenko, S.; Freed, J. High-field ESR on aligned membranes: A simple method to record spectra from different membrane orientations in the magnetic field. J. Magn. Reson. 2006, 179, 273–279. [Google Scholar] [CrossRef]
- Feher, G. Observation of nuclear magnetic resonances via the electron spin resonance line. Phys. Rev. 1956, 103, 834. [Google Scholar] [CrossRef]
- Gemperle, C.; Schweiger, A. Pulsed electron-nuclear double resonance methodology. Chem. Rev. 1991, 91, 1481–1505. [Google Scholar] [CrossRef]
- Deligiannakis, Y.; Louloudi, M.; Hadjiliadis, N. Electron spin echo envelope modulation (ESEEM) spectroscopy as a tool to investigate the coordination environment of metal centers. Coord. Chem. Rev. 2000, 204, 1–112. [Google Scholar] [CrossRef]
- Mims, W.B. Envelope modulation in spin-echo experiments. Phys. Rev. B 1972, 5, 2409. [Google Scholar] [CrossRef]
- Levanon, H.; Möbius, K. Advanced EPR spectroscopy on electron transfer processes in photosynthesis and biomimetic model systems. Annu. Rev. Biophys. Biomol. Struct. 1997, 26, 495–540. [Google Scholar] [CrossRef]
- Prisner, T.; Rohrer, M.; MacMillan, F. Pulsed EPR spectroscopy: Biological applications. Annu. Rev. Phys. Chem. 2001, 52, 279–313. [Google Scholar] [CrossRef] [Green Version]
- Srivastava, M.; Anderson, C.L.; Freed, J.H. A New Wavelet Denoising Method for Selecting Decomposition Levels and Noise Thresholds. IEEE Access 2016, 4, 3862–3877. [Google Scholar] [CrossRef]
- Drzewiecki, A.; Sczaniecki, P. Wavelet analysis in EPR spectroscopy. Acta Phys. Pol.-Ser. Gen. Phys. 2005, 108, 73–80. [Google Scholar] [CrossRef]
- Buchanan, S.K.; Dismukes, G.C. Substitution of copper (2+) in the reaction center diquinone electron acceptor complex of Rhodobacter sphaeroides: Determination of the metal–ligand coordination. Biochemistry 1987, 26, 5049–5055. [Google Scholar] [CrossRef]
- Ali, A.; Prakash, D.; Majumder, P.; Ghosh, S.; Dutta, A. Flexible Ligand in a Molecular Cu Electrocatalyst Unfurls Bidirectional O2/H2O Conversion in Water. ACS Catal. 2021, 11, 5934–5941. [Google Scholar] [CrossRef]
- Carter, E.; Sharples, K.M.; Platts, J.A.; Murphy, D.M. Structure determination of bound nitrogen-based adducts with copper (II) acetylacetonato; an EPR, ENDOR and DFT study. Phys. Chem. Chem. Phys. 2015, 17, 11445–11454. [Google Scholar] [CrossRef]
- Bolton, J.R.; Carrington, A.; McLachlan, A.D. Electron spin resonance studies of hyperconjugation in aromatic ions. Mol. Phys. 1962, 5, 31–41. [Google Scholar] [CrossRef]
- Valenzuela, J.A.; Bard, A.J. Electron spin resonance studies of hyperconjugation in 2,3-, 2,6-, and 2,7-dimethylanthracene cation and anion radicals. J. Phys. Chem. 1969, 73, 779–788. [Google Scholar] [CrossRef]
- Di Mauro, E.; Guedes, C.L.B.; Nascimento, O.R. Multifrequency (X-band to W-band) CW EPR of the organic free radical in petroleum asphaltene. Appl. Magn. Reson. 2005, 29, 569. [Google Scholar] [CrossRef]
- Sullivan, P.D.; Fong, J.Y.; Williams, M.L.; Parker, V.D. Electron paramagnetic resonance studies of bridged biaryl cation radicals. J. Phys. Chem. 1978, 82, 1181–1185. [Google Scholar] [CrossRef]
- Karlin, K.D.; Tyeklár, Z. Bioinorganic Chemistry of Copper; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Festa, R.A.; Thiele, D.J. Copper: An essential metal in biology. Curr. Biol. 2011, 21, R877–R883. [Google Scholar] [CrossRef] [Green Version]
- Dudzik, C.G.; Walter, E.D.; Millhauser, G.L. Coordination features and affinity of the Cu2+ site in the α-synuclein protein of Parkinson’s disease. Biochemistry 2011, 50, 1771–1777. [Google Scholar] [CrossRef] [Green Version]
- Jun, S.; Saxena, S. The aggregated state of amyloid-β peptide in vitro depends on Cu2+ ion concentration. Angew. Chem. 2007, 119, 4033–4035. [Google Scholar] [CrossRef]
- Schneider, D.J.; Freed, J.H. Calculating slow motional magnetic resonance spectra. In Spin Labeling; Springer: Berlin/Heidelberg, Germany, 1989; pp. 1–76. [Google Scholar]
- Budil, D.E.; Lee, S.; Saxena, S.; Freed, J.H. Nonlinear-least-squares analysis of slow-motion EPR spectra in one and two dimensions using a modified Levenberg–Marquardt algorithm. J. Magn. Reson. Ser. A 1996, 120, 155–189. [Google Scholar] [CrossRef] [Green Version]
- Stoll, S.; Schweiger, A. EasySpin, a comprehensive software package for spectral simulation and analysis in EPR. J. Magn. Reson. 2006, 178, 42–55. [Google Scholar] [CrossRef]
- Hogben, H.J.; Krzystyniak, M.; Charnock, G.T.P.; Hore, P.J.; Kuprov, I. Spinach- A software library for simulation of spin dynamics in large spin systems. J. Magn. Reson. 2011, 208, 179–194. [Google Scholar] [CrossRef]
- Lehner, J.; Stoll, S. Modeling of motional EPR spectra using hindered Brownian rotational diffusion and the stochastic Liouville equation. J. Chem. Phys. 2020, 152, 094103. [Google Scholar] [CrossRef] [PubMed]
- Addison, P. The Illustrated Wavelet Transform Handbook: Introductory Theory and Applications in Science, Engineering, Medicine and Finance, 2nd ed.; CRC Press: London, UK, 2016. [Google Scholar]
- Srivastava, M. Improving Signal Resolution and Reducing Experiment Time in Electron Spin Resonance Spectroscopy via Data Processing Methods. Ph.D. Thesis, Cornell University, Ithaca, NY, USA, 2018. [Google Scholar]
- Srivastava, M.; Dzikovski, B.; Freed, J.H. Extraction of Weak Spectroscopic Signals with High Fidelity: Examples from ESR. J. Phys. Chem. A 2021, 125, 4480–4487. [Google Scholar] [CrossRef] [PubMed]
- Starck, J.; Fadili, J.; Murtagh, F. The Undecimated Wavelet Decomposition and its Reconstruction. IEEE Trans. Image Process. 2007, 16, 297–309. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Antoniadis, A.; Oppenheim, G. Wavelets and Statistics; Springer: New York, NY, USA, 1995. [Google Scholar]
- Srivastava, M.; Freed, J.H.; Anderson, C.L. Systems, Methods and Programs for Denoising Signals Using Wavelets. U.S. Patent 10,891,719, 12 January 2021. [Google Scholar]
- Bekerman, W.; Srivastava, M. Determining Decomposition Levels for Wavelet Denoising Using Sparsity Plot. IEEE Access 2021, 9, 110582–110591. [Google Scholar] [CrossRef]
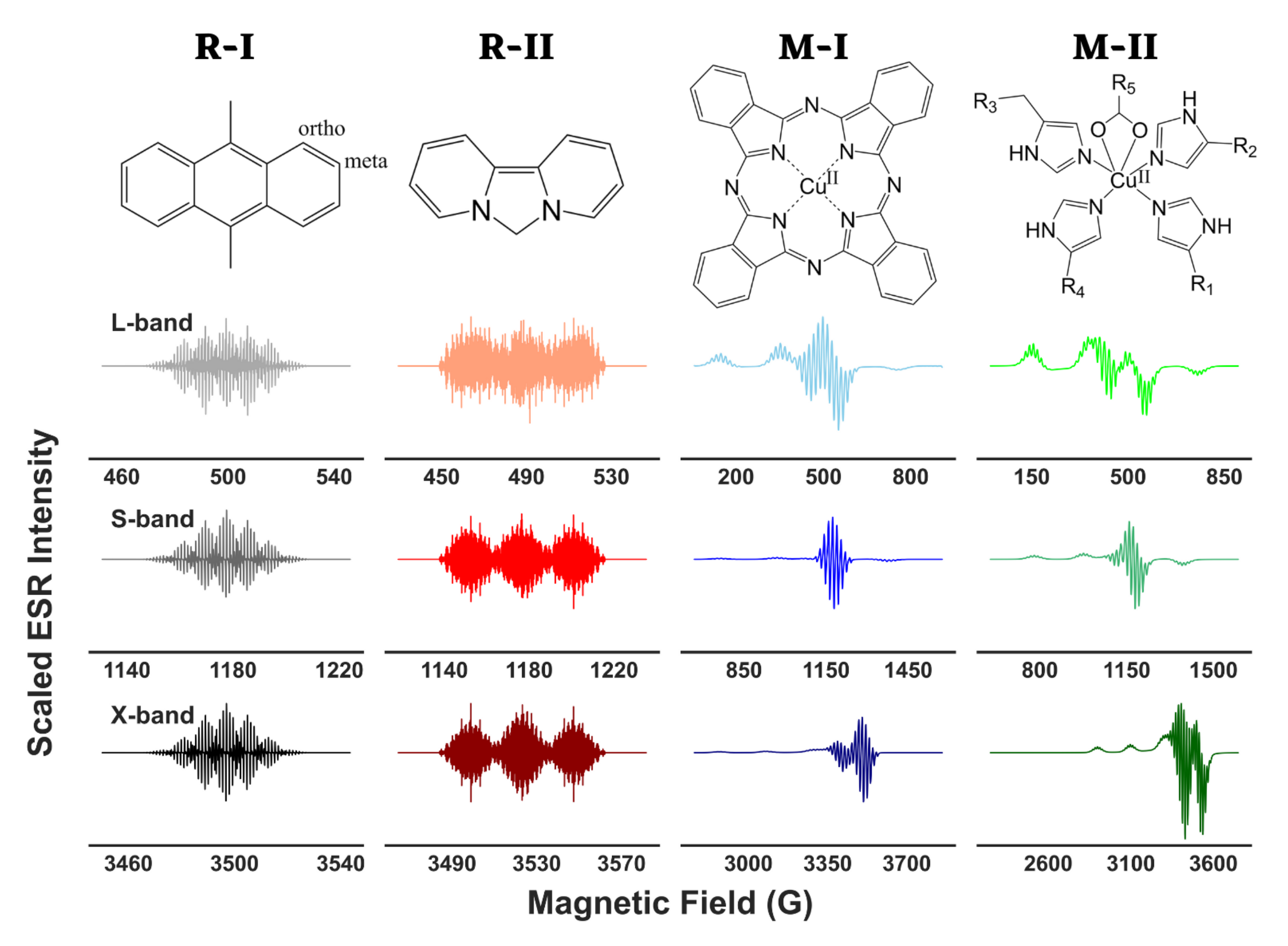

| Molecule | Simulation Type | g Value | A (Gauss) |
|---|---|---|---|
| R-I | Isotropic | 2.0316 | Amethyl = 7.91 Aortho−H = −2.49, Ameta−H = −1.20 |
| R-II | Isotropic | 2.0316 | ACH2 = 24.24, AN = 4.34, AH3 = −2.81 AH4 = −2.39, AH5 = −0.65, AH6 = −0.23 |
| M-I | Slow-motional | (2.05, 2.20) | ACu = (−18.82, −18.82, −197.46) AN = (14.64, 14.64, 16.89) |
| M-II | Frozen | (2.05, 2.19) | ACu = (18.60, 18.60, 198.68) AN = (14.99, 14.99, 17.78) |
| Molecule | ESR Frequency | ||
|---|---|---|---|
| L-Band | S-Band | X-Band | |
| R-I | Amethyl = 8.58 = 2.60 = 1.28 | 8.52 2.59 1.28 | 8.20 2.59 1.28 |
| R-II | ACH2 = 24.26 = 4.34 = 2.63, 2.46, 0.83 | 24.22 4.36 2.64, 2.40, 0.63 | 24.22 4.37 2.66, 2.51, 0.66 |
| M-I | = 2.20, = ± 0.02 = 207.3 = 14.98, 16.65 | 2.20, 2.02 207.4 15.07, 15.96 | 2.20, 2.06 204.6 15.00, 17.13 |
| M-II | = 2.14, = ± 0.02 = 212.0 = 14.96, 15.84 | 2.19, 2.01 200.4 14.66, 16 | 2.19, 2.06 199.4 14.66, 16. |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Roy, A.S.; Srivastava, M. Hyperfine Decoupling of ESR Spectra Using Wavelet Transform. Magnetochemistry 2022, 8, 32. https://doi.org/10.3390/magnetochemistry8030032
Roy AS, Srivastava M. Hyperfine Decoupling of ESR Spectra Using Wavelet Transform. Magnetochemistry. 2022; 8(3):32. https://doi.org/10.3390/magnetochemistry8030032
Chicago/Turabian StyleRoy, Aritro Sinha, and Madhur Srivastava. 2022. "Hyperfine Decoupling of ESR Spectra Using Wavelet Transform" Magnetochemistry 8, no. 3: 32. https://doi.org/10.3390/magnetochemistry8030032
APA StyleRoy, A. S., & Srivastava, M. (2022). Hyperfine Decoupling of ESR Spectra Using Wavelet Transform. Magnetochemistry, 8(3), 32. https://doi.org/10.3390/magnetochemistry8030032






