Simulating Evaluation Method on Heating Performances of Magnetic Nanoparticles with Temperature-Dependent Heating Efficiencies in Tumor Hyperthermia
Abstract
:1. Introduction
2. Materials and Methods
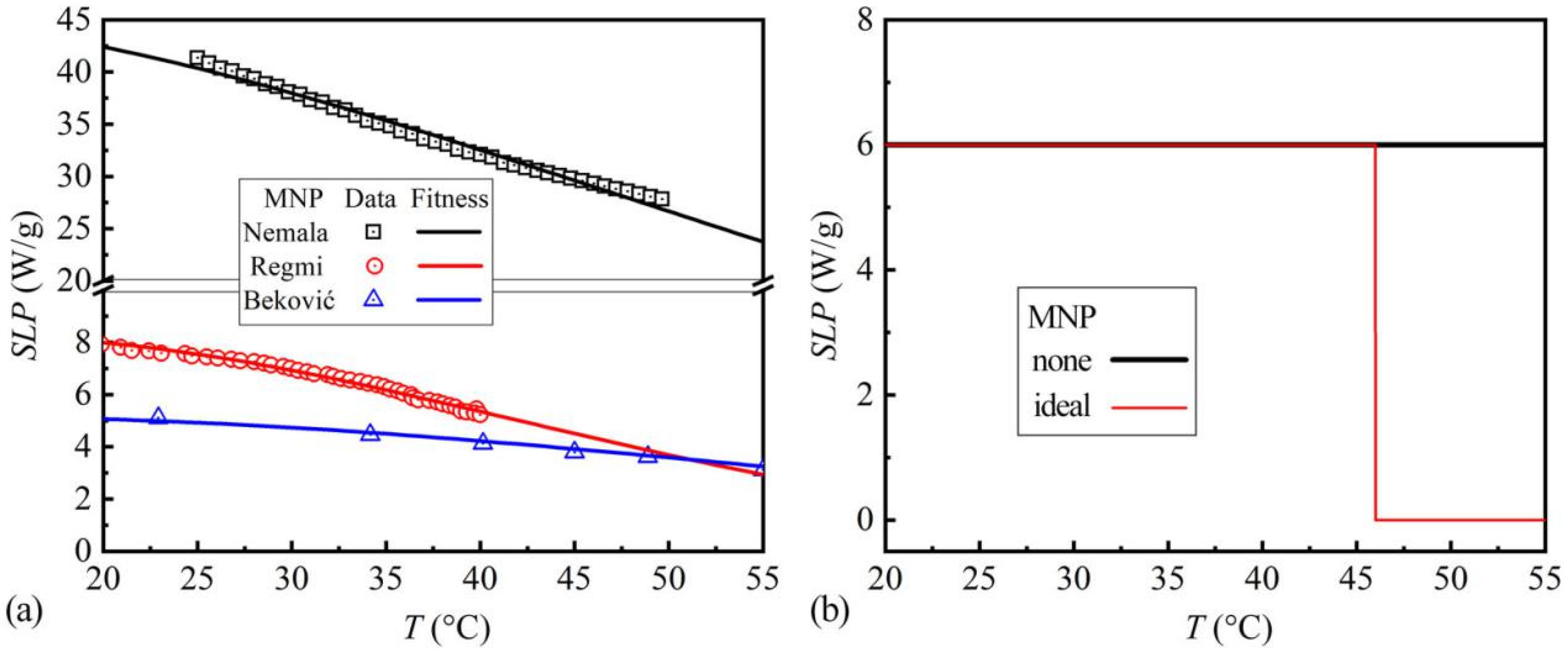
2.1. Temperature-Dependent SLP Measurements
2.2. Heating Performance Simulations
3. Results and Discussion
3.1. SLP-T Relationships
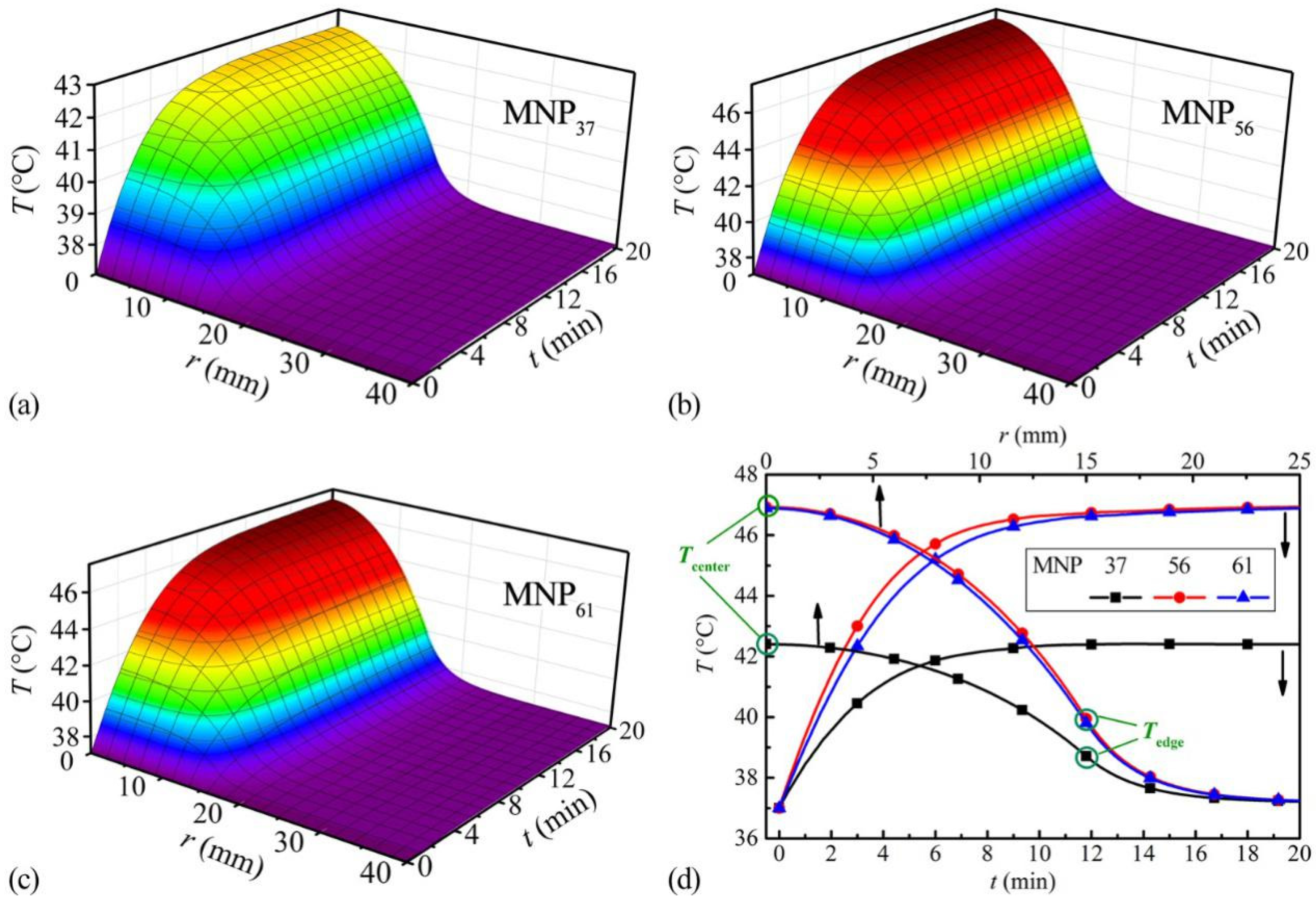
3.2. Heating Performances
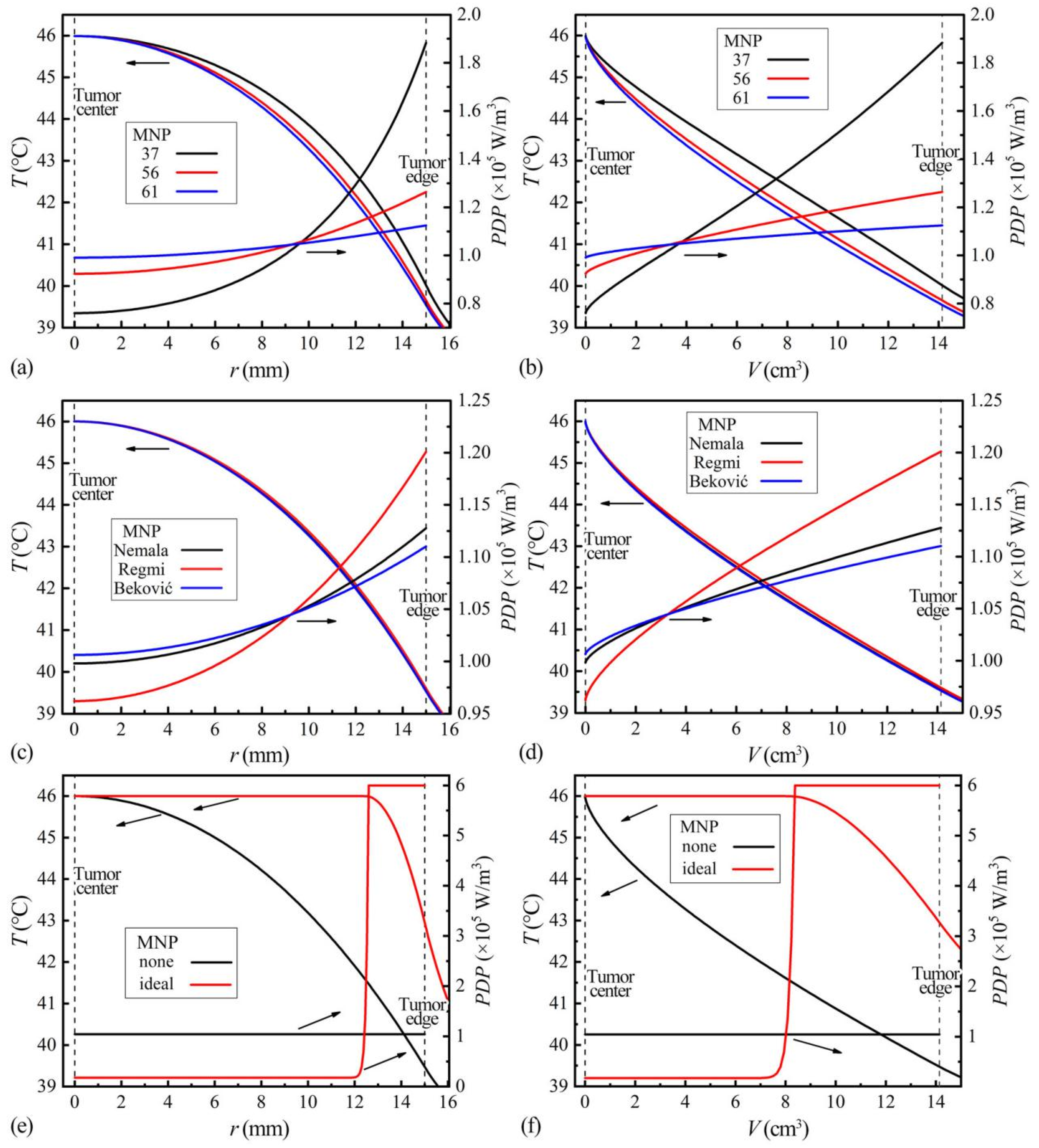
3.2.1. Temperature Rises and Distributions
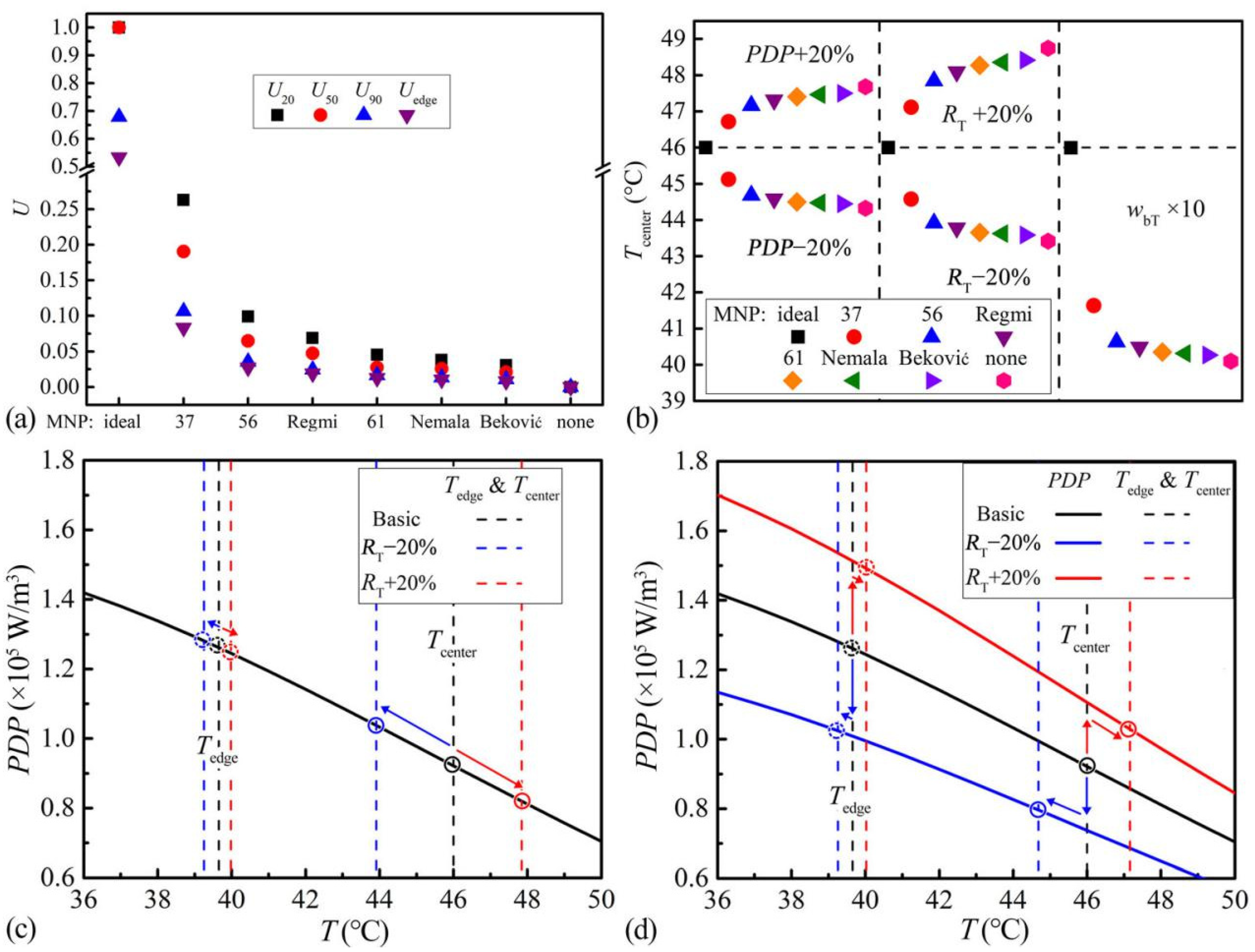
3.2.2. Capacities
3.2.3. Uniformities
3.2.4. Stabilities
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| AMF | alternating magnetic field |
| TC | Curie temperature (°C) |
| MHG | magnetic hydrogel |
| MNP | magnetic nanoparticles |
| MNP37, MNP56, MNP61 | ZnCoCrFeO MNPs with TC of 37.5 °C, 56.0 °C and 61.0 °C |
| MNPNemala | MNPs by Nemala et al. |
| MNPRegmi | MNPs by Regmi et al. |
| MNPBeković | MNPs by Beković et al. |
| MNPideal | assumed ideal MNPs with TC of 46 °C (heating efficiency is constant below TC and zero above TC) |
| MNPnone | assumed MNPs without TC (heating efficiency does not change with temperature) |
| b (subscript) | of blood |
| L (subscript) | of healthy liver tissue |
| MHG (subscript) | of MHG |
| MNP (subscript) | of MNPs |
| T (subscript) | of tumor |
| TP (subscript) | of tumor and MNPs |
| T (°C) | temperature |
| t (s) | time |
| Tcenter (°C) | temperature at the center of the tumor |
| T20, T50, T90 (°C) | temperatures exceeded in 20%, 50% or 90% volume of the tumor |
| Tedge (°C) | temperature at the edge between tumor and healthy tissue |
| Tα (°C) | the temperature of arterial blood (37 °C) |
| U20, U50, U90, Uedge (dimensionless) | uniformities within 20%, 50%, 90% or 100% volume of the tumor |
| SLP (W/g) | specific loss power |
| PDP (W/m3) | power dissipation of MNPs per unit of tumor volume |
| c (J/(kg·°C)) | specific heat capacity |
| C (kg/m3 or mg/mL) | MNP concentration in tumor region (MNP mass/tumor volume) |
| RT, RL (mm) | radiuses of tumor region and overall healthy liver region |
| r (mm) | radius from the tumor center |
| ρ (kg/m3) | density |
| k (W/(m·°C)) | thermal conductivity |
| Qm (W/m3) | power density of metabolic heat generation |
| Qm0 (W/m3) | power density of metabolic heat generation at body temperature (37 °C) |
| Qb (W/m3) | power density of heat dissipation by blood perfusion effect |
| wb (1/s) | blood perfusion rate |
| ϕ | volume fraction of MNPs in the tumor |
References
- Johannsen, M.; Gneveckow, U.; Eckelt, L.; Feussner, A.; Waldöfner, N.; Scholz, R.; Deger, S.; Wust, P.; Loening, S.A.; Jordan, A. Clinical hyperthermia of prostate cancer using magnetic nanoparticles: Presentation of a new interstitial technique. Int. J. Hyperth. 2005, 21, 637–647. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wust, P.; Gneveckow, U.; Johannsen, M.; Böhmer, D.; Henkel, T.; Kahmann, F.; Sehouli, J.; Felix, R.; Ricke, J.; Jordan, A. Magnetic nanoparticles for interstitial thermotherapy-feasibility, tolerance and achieved temperatures. Int. J. Hyperth. 2006, 22, 673–685. [Google Scholar] [CrossRef] [PubMed]
- Maier-Hauff, K.; Ulrich, F.; Nestler, D.; Niehoff, H.; Wust, P.; Thiesen, B.; Orawa, H.; Budach, V.; Jordan, A. Efficacy and safety of intratumoral thermotherapy using magnetic iron-oxide nanoparticles combined with external beam radiotherapy on patients with recurrent glioblastoma multiforme. J. Neuro-Oncol. 2011, 103, 317–324. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Grauer, O.; Jaber, M.; Hess, K.; Weckesser, M.; Schwindt, W.; Maring, S.; Wölfer, J.; Stummer, W. Combined intracavitary thermotherapy with iron oxide nanoparticles and radiotherapy as local treatment modality in recurrent glioblastoma patients. J. Neuro-Oncol. 2019, 141, 83–94. [Google Scholar] [CrossRef] [Green Version]
- Yu, X.; Ding, S.; Yang, R.; Wu, C.; Zhang, W. Research progress on magnetic nanoparticles for magnetic induction hyperthermia of malignant tumor. Ceram. Int. 2021, 47, 5909–5917. [Google Scholar] [CrossRef]
- Astefanoaei, I.; Dumitru, I.; Chiriac, H.; Stancu, A. Controlling temperature in magnetic hyperthermia with low Curie temperature particles. J. Appl. Phys. 2014, 115, 17B531. [Google Scholar] [CrossRef]
- Tang, Y.-D.; Flesch, R.; Jin, T. Numerical analysis of temperature field improvement with nanoparticles designed to achieve critical power dissipation in magnetic hyperthermia. J. Appl. Phys. 2017, 122, 034702. [Google Scholar] [CrossRef]
- Prasad, N.K.; Rathinasamy, K.; Panda, D.; Bahadur, D. TC-tuned biocompatible suspension of La0.73Sr0.27MnO3 for magnetic hyperthermia. J. Biomed. Mater. Res. B 2008, 85B, 409–416. [Google Scholar] [CrossRef]
- Hanini, A.; Lartigue, L.; Gavard, J.; Kacem, K.; Wilhelm, C.; Gazeau, F.; Chau, F.; Ammar, S. Zinc substituted ferrite nanoparticles with Zn0.9Fe2.1O4 formula used as heating agents for in vitro hyperthermia assay on glioma cells. J. Magn. Magn. Mater. 2016, 416, 315–320. [Google Scholar] [CrossRef]
- Yu, X.; Yang, R.; Wu, C.; Zhang, W. Effect of chromium ion substitution of ZnCo ferrites on magnetic induction heating. J. Alloys Compd. 2020, 830, 154724. [Google Scholar] [CrossRef]
- Tang, Q.; Zhang, D.; Cong, X.; Wan, M.; Jin, L. Using thermal energy produced by irradiation of Mn-Zn ferrite magnetic nanoparticles (MZF-NPs) for heat-inducible gene expression. Biomaterials 2008, 29, 2673–2679. [Google Scholar] [CrossRef]
- Saito, H.; Mitobe, K.; Ito, A.; Sugawara, Y.; Maruyama, K.; Minamiya, Y.; Motoyama, S.; Yoshimura, N.; Ogawa, J. Self-regulating hyperthermia induced using thermosensitive ferromagnetic material with a low Curie temperature. Cancer Sci. 2008, 99, 805–809. [Google Scholar] [CrossRef] [PubMed]
- Ito, A.; Saito, H.; Mitobe, K.; Minamiya, Y.; Takahashi, N.; Maruyama, K.; Motoyama, S.; Katayose, Y.; Ogawa, J.-I. Inhibition of heat shock protein 90 sensitizes melanoma cells to thermosensitive ferromagnetic particle-mediated hyperthermia with low Curie temperature. Cancer Sci. 2009, 100, 558–564. [Google Scholar] [CrossRef] [PubMed]
- Ding, S.; Wu, C.-W.; Yu, X.-G.; Li, H.; Yu, L.; Zhang, Y.-X.; Yang, R.-P.; Zhang, W. Magnetic hydrogel with long in situ retention time for self-regulating temperature hyperthermia. Int. J. Hyperth. 2021, 38, 13–21. [Google Scholar] [CrossRef] [PubMed]
- Nemala, H.; Thakur, J.S.; Naik, V.M.; Vaishnava, P.P.; Lawes, G.; Naik, R. Investigation of magnetic properties of Fe3O4 nanoparticles using temperature dependent magnetic hyperthermia in ferrofluids. J. Appl. Phys. 2014, 116, 034309. [Google Scholar] [CrossRef] [Green Version]
- Regmi, R.; Naik, A.; Thakur, J.S.; Vaishnava, P.P.; Lawes, G. Temperature dependent dissipation in magnetic nanoparticles. J. Appl. Phys. 2014, 115, 17B301. [Google Scholar] [CrossRef]
- Beković, M.; Trlep, M.; Jesenik, M.; Goričan, V.; Hamler, A. An experimental study of magnetic-field and temperature dependence on magnetic fluid’s heating power. J. Magn. Magn. Mater. 2013, 331, 264–268. [Google Scholar] [CrossRef]
- Hilger, I.; Frühauf, K.; Andrä, W.; Hiergeist, R.; Hergt, R.; Kaiser, W.A. Heating potential of iron oxides for therapeutic purposes in interventional radiology. Acad. Radiol. 2002, 9, 198–202. [Google Scholar] [CrossRef]
- Bordelon, D.E.; Cornejo, C.; Grüttner, C.; Westphal, F.; DeWeese, T.L.; Ivkov, R. Magnetic nanoparticle heating efficiency reveals magneto-structural differences when characterized with wide ranging and high amplitude alternating magnetic fields. J. Appl. Phys. 2011, 109, 124904. [Google Scholar] [CrossRef]
- Wildeboer, R.R.; Southern, P.; Pankhurst, Q.A. On the reliable measurement of specific absorption rates and intrinsic loss parameters in magnetic hyperthermia materials. J. Phys. D Appl. Phys. 2014, 47, 495003. [Google Scholar] [CrossRef]
- Ebrahimi, M. On the temperature control in self-controlling hyperthermia therapy. J. Magn. Magn. Mater. 2016, 416, 134–140. [Google Scholar] [CrossRef]
- Astefanoaei, I.; Dumitru, I.; Chiriac, H.; Stancu, A. Thermo-fluid analysis in magnetic hyperthermia using low Curie temperature particles. IEEE Trans. Magn. 2016, 52, 1–5. [Google Scholar] [CrossRef]
- Wang, Q.; Deng, Z.S.; Liu, J. Theoretical evaluations of magnetic nanoparticle-enhanced heating on tumor embedded with large blood vessels during hyperthermia. J. Nanopart Res. 2012, 14, 974. [Google Scholar] [CrossRef]
- Gupta, P.K.; Singh, J.; Rai, K.N. Numerical simulation for heat transfer in tissues during thermal therapy. J. Therm. Biol. 2010, 35, 295–301. [Google Scholar] [CrossRef]
- Pennes, H.H. Analysis of tissue and arterial blood temperatures in the resting human forearm. J. Appl. Physiol. 1948, 1, 93–122. [Google Scholar] [CrossRef]
- Hasgall, P.A.; Di Gennaro, F.; Baumgartner, C.; Neufeld, E.; Lloyd, B.; Gosselin, M.C.; Payne, D.; Klingenböck, A.; Kuster, N. IT’IS Database for Thermal and Electromagnetic Parameters of Biological Tissues, Version 4.0; IT’IS Foundation: Zurich, Switzerland, 2018. [Google Scholar]
- Raouf, I.; Khalid, S.; Khan, A.; Lee, J.; Kim, H.S.; Kim, M.-H. A review on numerical modeling for magnetic nanoparticle hyperthermia: Progress and challenges. J. Therm. Biol. 2020, 91, 102644. [Google Scholar] [CrossRef]
- Hergt, R.; Dutz, S. Magnetic particle hyperthermia-biophysical limitations of a visionary tumour therapy. J. Magn. Magn. Mater. 2007, 311, 187–192. [Google Scholar] [CrossRef]
- Johannsen, M.; Gneveckow, U.; Thiesen, B.; Taymoorian, K.; Cho, C.H.; Waldöfner, N.; Scholz, R.; Jordan, A.; Loening, S.A.; Wust, P. Thermotherapy of prostate cancer using magnetic nanoparticles: Feasibility, imaging, and three-dimensional temperature distribution. Eur. Urol. 2006, 52, 1653–1662. [Google Scholar] [CrossRef]
- Rosensweig, R.E. Heating magnetic fluid with alternating magnetic field. J. Magn. Magn. Mater. 2002, 252, 370–374. [Google Scholar] [CrossRef]
- Thrall, D.E.; Rosner, G.L.; Azuma, C.; LaRue, S.M.; Case, B.C.; Samulski, T.; Dewhirst, M.W. Using units of CEM 43 °C T90, local hyperthermia thermal dose can be delivered as prescribed. Int. J. Hyperth. 2000, 16, 415–428. [Google Scholar] [CrossRef]
- Bagaria, H.G.; Johnson, D.T. Transient solution to the bioheat equation and optimization for magnetic fluid hyperthermia treatment. Int. J. Hyperth. 2005, 21, 57–75. [Google Scholar] [CrossRef] [PubMed]
- Liangruksa, M.; Ganguly, R.; Puri, I.K. Parametric investigation of heating due to magnetic fluid hyperthermia in a tumor with blood perfusion. J. Magn. Magn. Mater. 2011, 323, 708–716. [Google Scholar] [CrossRef]
- Zhang, C.; Johnson, D.T.; Brazel, C.S. Numerical study on the multi-region bio-heat equation to model magnetic fluid hyperthermia (MFH) using low Curie temperature nanoparticles. IEEE Trans. Nanobiosci. 2008, 7, 267–275. [Google Scholar] [CrossRef]
- Richter, H.; Kettering, M.; Wiekhorst, F.; Steinhoff, U.; Hilger, I.; Trahms, L. Magnetorelaxometry for localization and quantification of magnetic nanoparticles for thermal ablation studies. Phys. Med. Biol. 2010, 55, 623–633. [Google Scholar] [CrossRef] [PubMed]
- Rast, L.; Harrison, J.G. Computational modeling of electromagnetically induced heating of magnetic nanoparticle materials for hyperthermic cancer treatment. PIERS Online 2010, 6, 5. [Google Scholar] [CrossRef] [Green Version]



| ρ | c | k | wb | Qm0 | |
|---|---|---|---|---|---|
| kg/m3 | J/(kg·°C) | W/(m·°C) | 1/s | W/m3 | |
| Tumor [7] | 1060 | 3540 | 0.52 | 0.000833 | 5790 |
| Blood [26] | 1050 | 3617 | N/A | N/A | N/A |
| Liver [26] | 1079 | 3540 | 0.52 | 0.0155 | 10,682 |
| MNPs [7] | 5180 | 670 | 40 | N/A | N/A |
| a | b | c | |
|---|---|---|---|
| MNP37 | 7.369 | 20.210 | 17.330 |
| MNP56 | 5.196 | 28.500 | 24.070 |
| MNP61 | 3.892 | 30.200 | 35.770 |
| a | b | c | |
|---|---|---|---|
| MNPNemala | 46.350 | 0 | 67.240 |
| MNPRegmi | 8.257 | 12.480 | 41.810 |
| MNPBeković | 5.158 | 11.240 | 64.400 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ding, S.-W.; Wu, C.-W.; Yu, X.-G.; Dai, C.; Zhang, W.; Gong, J.-P. Simulating Evaluation Method on Heating Performances of Magnetic Nanoparticles with Temperature-Dependent Heating Efficiencies in Tumor Hyperthermia. Magnetochemistry 2022, 8, 63. https://doi.org/10.3390/magnetochemistry8060063
Ding S-W, Wu C-W, Yu X-G, Dai C, Zhang W, Gong J-P. Simulating Evaluation Method on Heating Performances of Magnetic Nanoparticles with Temperature-Dependent Heating Efficiencies in Tumor Hyperthermia. Magnetochemistry. 2022; 8(6):63. https://doi.org/10.3390/magnetochemistry8060063
Chicago/Turabian StyleDing, Shuai-Wen, Cheng-Wei Wu, Xiao-Gang Yu, Chao Dai, Wei Zhang, and Jian-Po Gong. 2022. "Simulating Evaluation Method on Heating Performances of Magnetic Nanoparticles with Temperature-Dependent Heating Efficiencies in Tumor Hyperthermia" Magnetochemistry 8, no. 6: 63. https://doi.org/10.3390/magnetochemistry8060063
APA StyleDing, S.-W., Wu, C.-W., Yu, X.-G., Dai, C., Zhang, W., & Gong, J.-P. (2022). Simulating Evaluation Method on Heating Performances of Magnetic Nanoparticles with Temperature-Dependent Heating Efficiencies in Tumor Hyperthermia. Magnetochemistry, 8(6), 63. https://doi.org/10.3390/magnetochemistry8060063







