Pulse Reverse Plating of Copper Micro-Structures in Magnetic Gradient Fields
Abstract
:1. Introduction
2. Methods
2.1. Experimental
2.2. Numerical
3. Results and Discussion
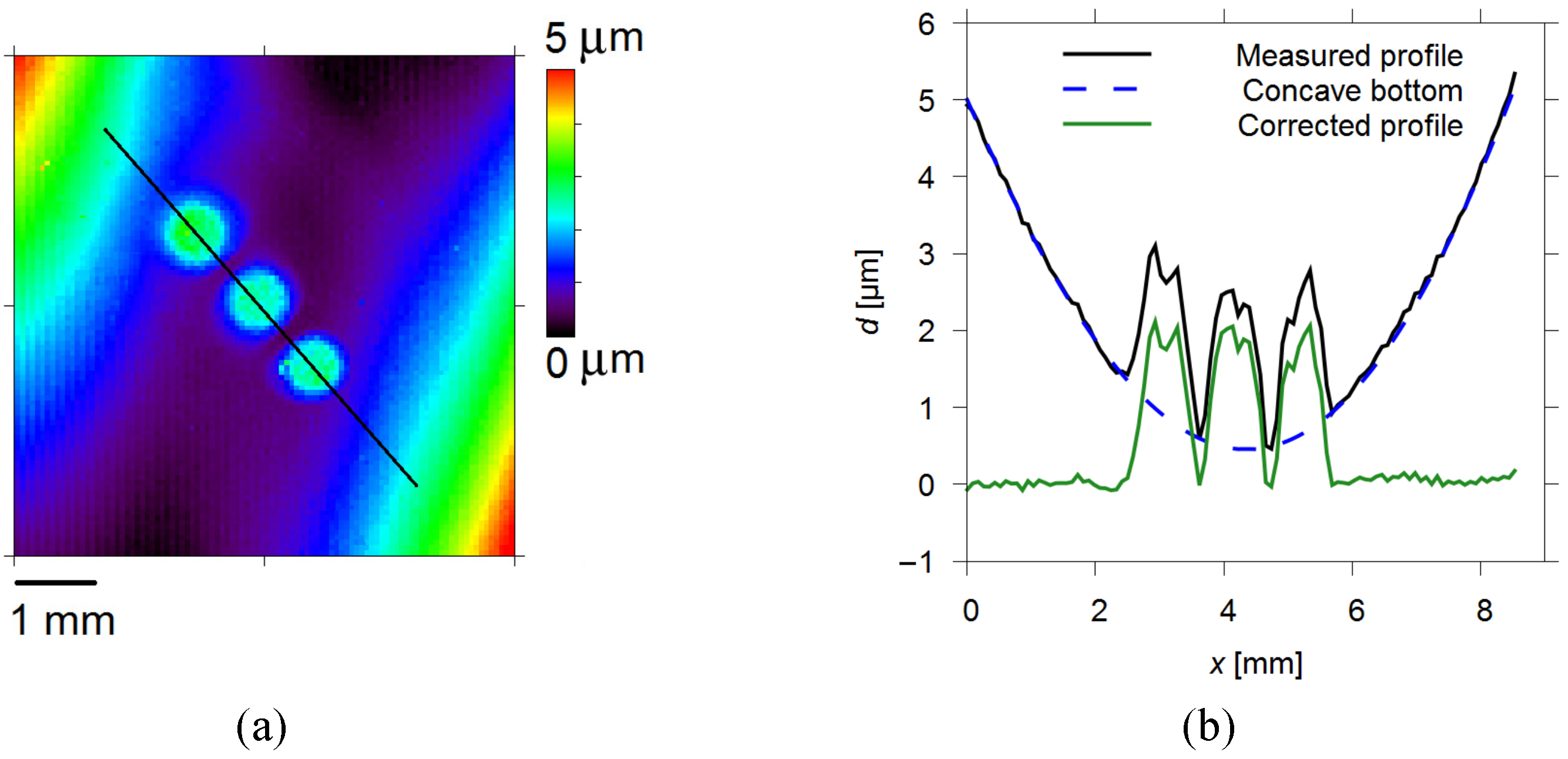
3.1. Electrode Kinetics Related to the Cu Layer Distribution on the WE
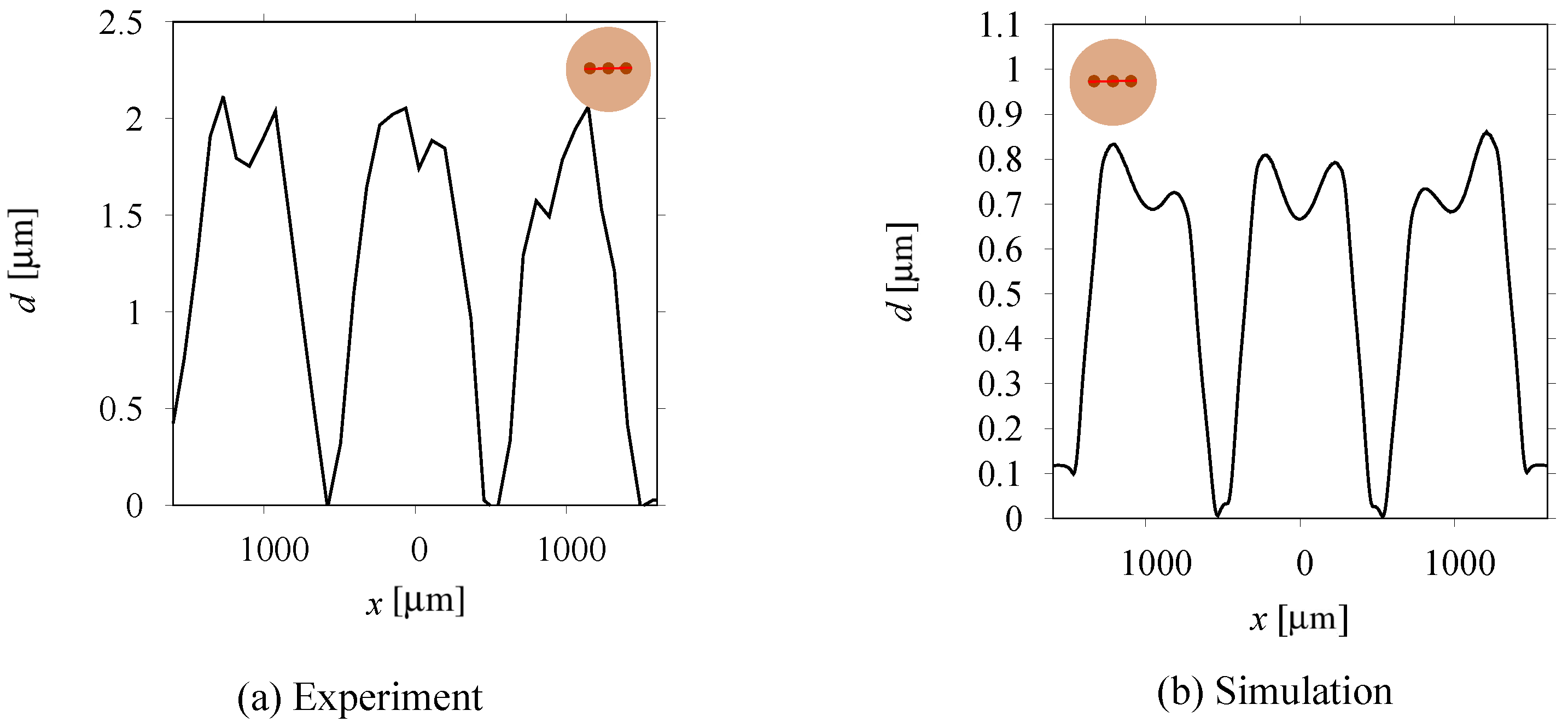
3.2. Structured Deposit Growth
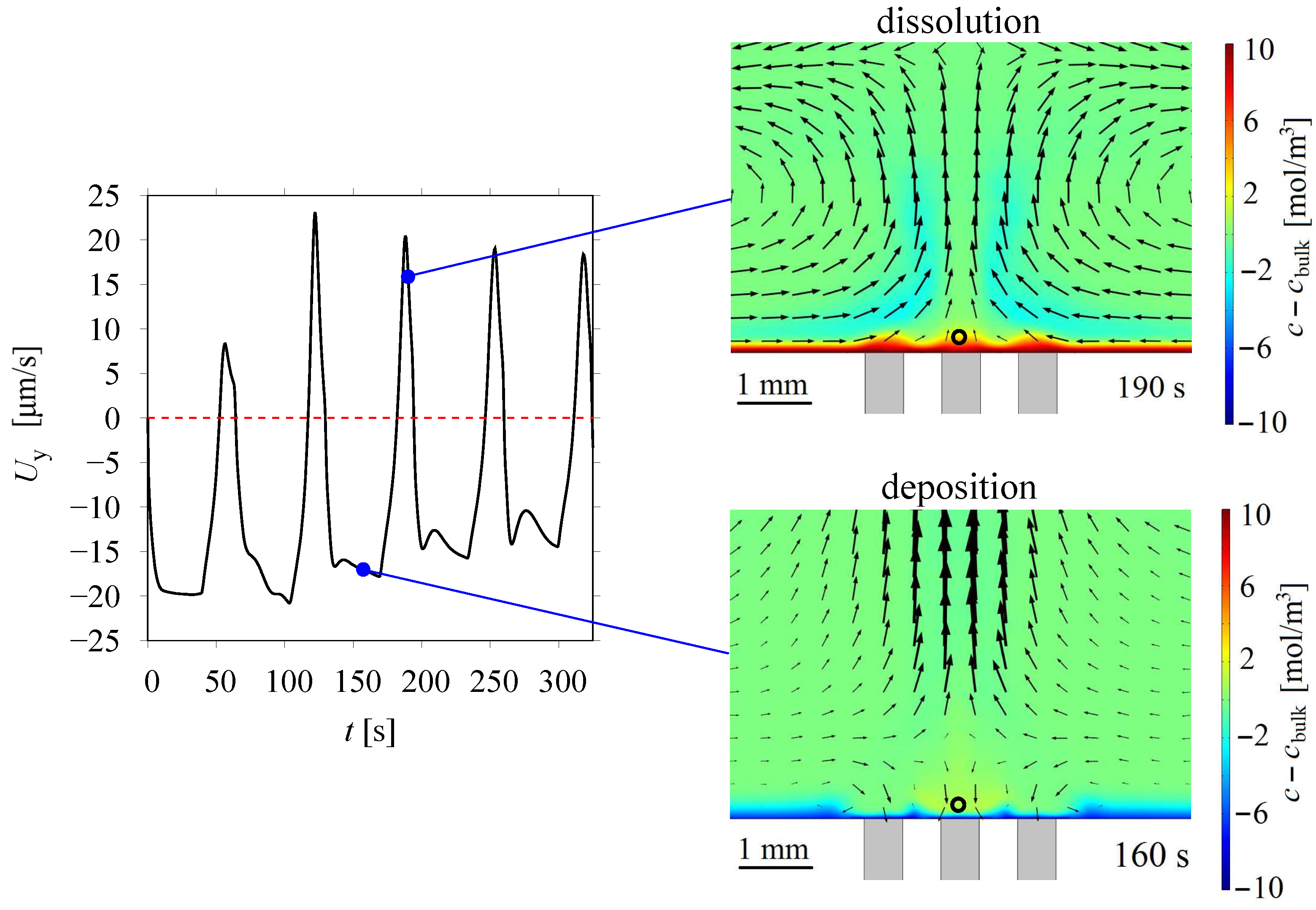
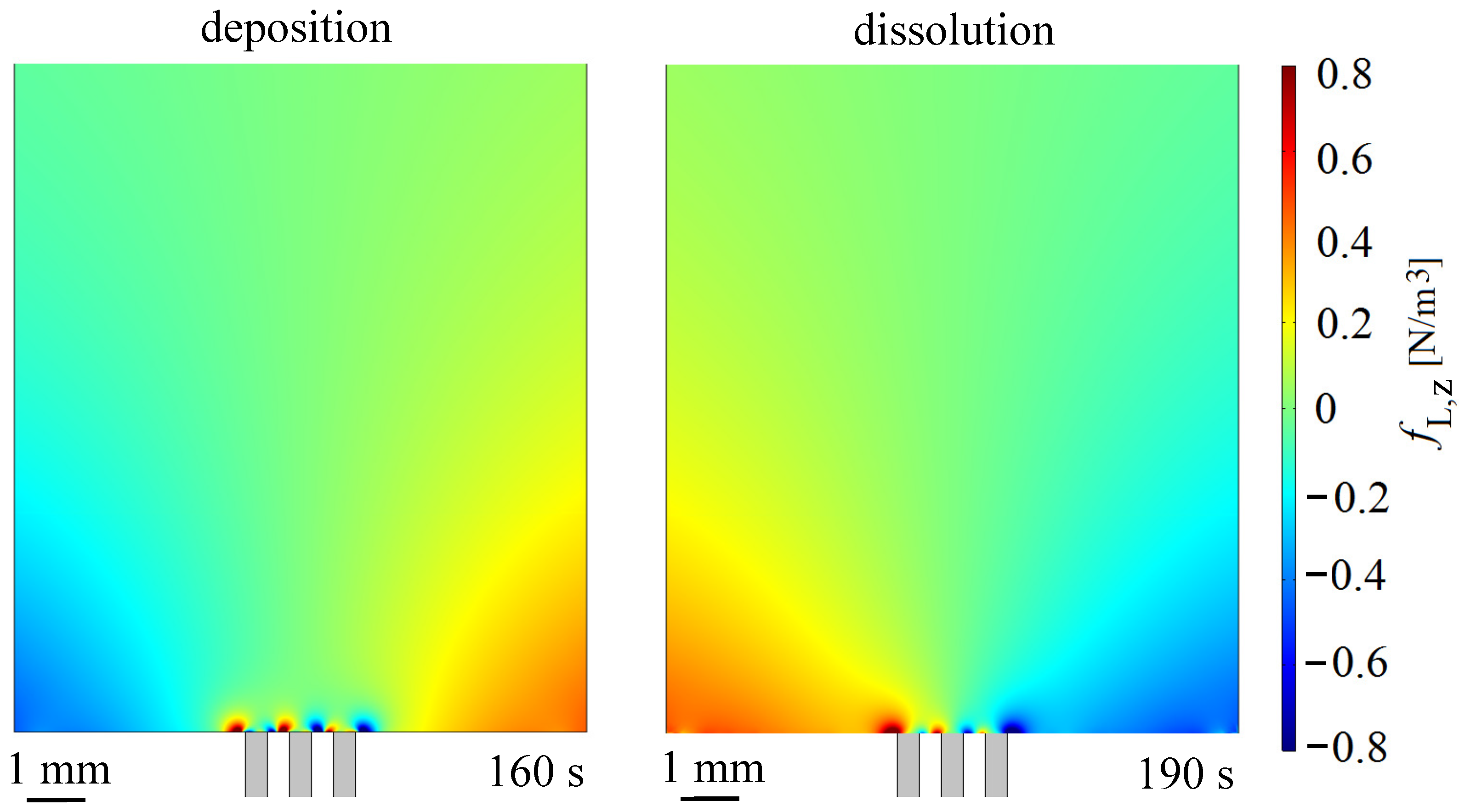
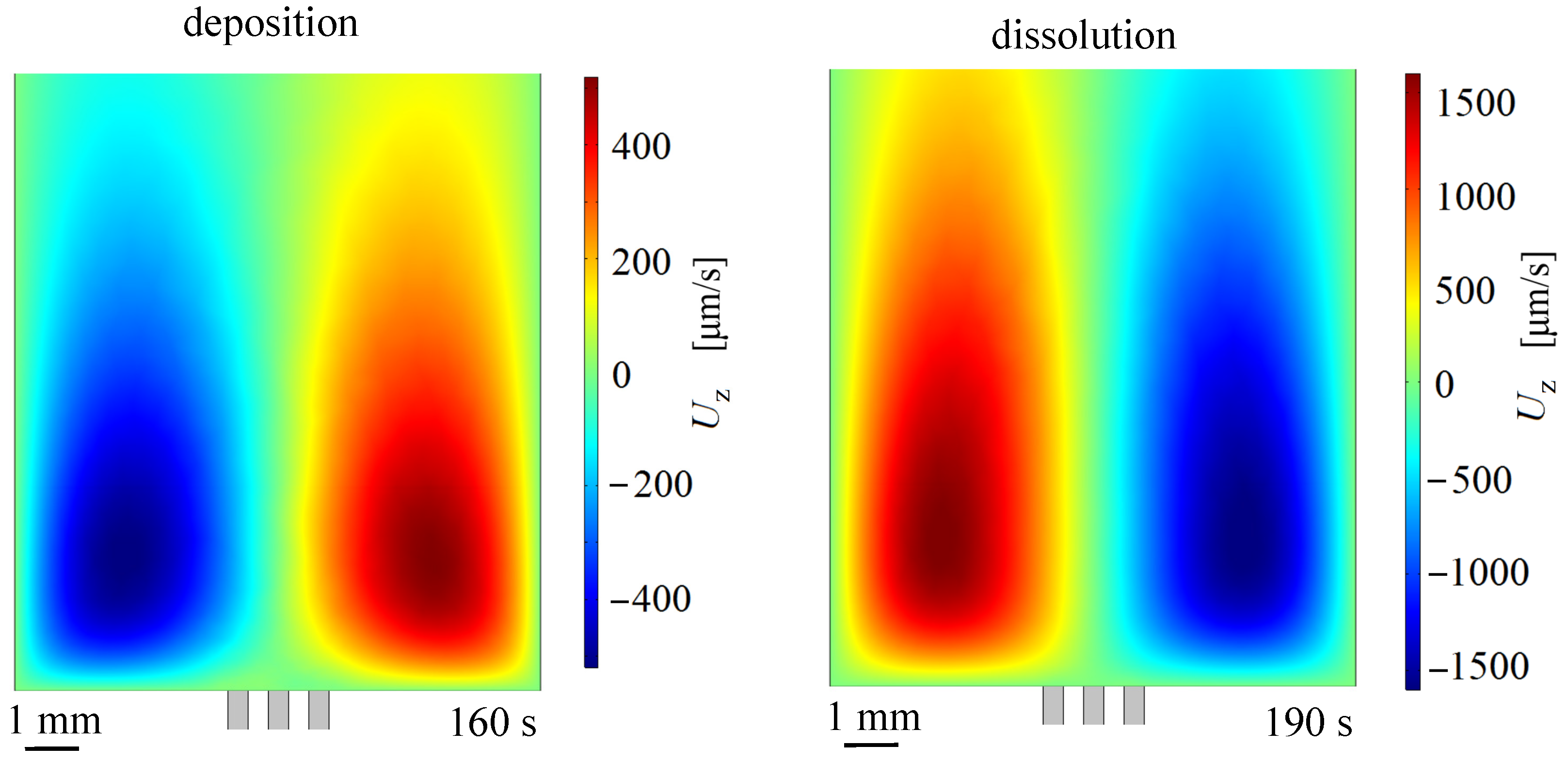
3.3. Lorentz Force Effect
4. Conclusions and Outlook
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zoski, C.G.; Liu, B.; Bard, A.J. Scanning electrochemical microscopy: Theory and characterization of electrodes of finite conical geometry. Anal. Chem. 2004, 76, 3646–3654. [Google Scholar] [CrossRef] [PubMed]
- Fujimura, T.; Kunimoto, M.; Fukunaka, Y.; Homma, T. Analysis of the hydrogen evolution reaction at Ni micro-patterned electrodes. Electrochim. Acta 2021, 368, 137678. [Google Scholar] [CrossRef]
- Arai, S.; Ozawa, M.; Shimizu, M. Communication Micro-Scale Columnar Architecture Composed of Copper Nano Sheets by Electrodeposition Technique. J. Electrochem. Soc. 2016, 164, D72–D74. [Google Scholar] [CrossRef]
- Skibińska, K.; Kołczyk-Siedlecka, K.; Kutyła, D.; Gajewska, M.; Żabiński, P. Synthesis of Co–Fe 1D Nanocone Array Electrodes Using Aluminum Oxide Template. Materials 2021, 14, 1717. [Google Scholar] [CrossRef]
- Gorobets, O.Y.; Gorobets, V.Y.; Derecha, D.O.; Brukva, O.M. Nickel electrodeposition under influence of constant homogeneous and high-gradient magnetic field. J. Phys. Chem. C 2008, 112, 3373–3375. [Google Scholar] [CrossRef]
- Mutschke, G.; Tschulik, K.; Uhlemann, M.; Bund, A.; Fröhlich, J. Comment on magnetic structuring of electrodeposits. Phys. Rev. Lett. 2012, 109, 229401. [Google Scholar] [CrossRef]
- Dunne, P.; Mazza, L.; Coey, J. Magnetic structuring of electrodeposits. Phys. Rev. Lett. 2011, 107, 024501. [Google Scholar] [CrossRef]
- Tschulik, K.; Sueptitz, R.; Koza, J.; Uhlemann, M.; Mutschke, G.; Weier, T.; Gebert, A.; Schultz, L. Studies on the patterning effect of copper deposits in magnetic gradient fields. Electrochim. Acta 2010, 56, 297–304. [Google Scholar] [CrossRef]
- Uhlemann, M.; Tschulik, K.; Gebert, A.; Mutschke, G.; Fröhlich, J.; Bund, A.; Yang, X.; Eckert, K. Structured electrodeposition in magnetic gradient fields. Eur. Phys. J. Spec. Top. 2013, 220, 287–302. [Google Scholar] [CrossRef]
- Karnbach, F.; Uhlemann, M.; Gebert, A.; Eckert, J.; Tschulik, K. Magnetic field templated patterning of the soft magnetic alloy CoFe. Electrochim. Acta 2014, 123, 477–484. [Google Scholar] [CrossRef]
- Tschulik, K.; Yang, X.; Mutschke, G.; Uhlemann, M.; Eckert, K.; Sueptitz, R.; Schultz, L.; Gebert, A. How to obtain structured metal deposits from diamagnetic ions in magnetic gradient fields? Electrochem. Commun. 2011, 13, 946–950. [Google Scholar] [CrossRef]
- Tschulik, K.; Cierpka, C.; Mutschke, G.; Gebert, A.; Schultz, L.; Uhlemann, M. Clarifying the mechanism of reverse structuring during electrodeposition in magnetic gradient fields. Anal. Chem. 2012, 84, 2328–2334. [Google Scholar] [CrossRef] [PubMed]
- Mutschke, G.; Tschulik, K.; Weier, T.; Uhlemann, M.; Bund, A.; Fröhlich, J. On the action of magnetic gradient forces in micro-structured copper deposition. Electrochim. Acta 2010, 55, 9060–9066. [Google Scholar] [CrossRef]
- Mutschke, G.; Hess, A.; Bund, A.; Fröhlich, J. On the origin of horizontal counter-rotating electrolyte flow during copper magnetoelectrolysis. Electrochim. Acta 2010, 55, 1543–1547. [Google Scholar] [CrossRef]
- Chen, Z.; Zhu, C.; Cai, M.; Yi, X.; Li, J. Growth and morphology tuning of ordered nickel nanocones routed by one-step pulse electrodeposition. Appl. Surf. Sci. 2020, 508, 145291. [Google Scholar] [CrossRef]
- Tschulik, K.; Sueptitz, R.; Uhlemann, M.; Schultz, L.; Gebert, A. Electrodeposition of separated 3D metallic structures by pulse-reverse plating in magnetic gradient fields. Electrochim. Acta 2011, 56, 5174–5177. [Google Scholar] [CrossRef]
- Huang, M.; Skibinska, K.; Zabinski, P.; Wojnicki, M.; Włoch, G.; Eckert, K.; Mutschke, G. On the prospects of magnetic-field-assisted electrodeposition of nano-structured ferromagnetic layers. Electrochim. Acta 2022, 420, 140422. [Google Scholar] [CrossRef]
- COMSOL Inc. COMSOL Multiphysics Documentation Suite V 5.6; COMSOL Inc.: Burlington, MA, USA, 2018. [Google Scholar]
- Newman, J.; Thomas-Alyea, K.E. Electrochemical Systems, 3rd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Coey, J.; Rhen, F.; Dunne, P.; McMurry, S. The magnetic concentration gradient force—Is it real? J. Solid State Electrochem. 2007, 11, 711–717. [Google Scholar] [CrossRef]
- Lide, D.R. CRC Handbook of Chemistry and Physics; CRC Press: Boca Raton, FL, USA, 2004. [Google Scholar]
- Koschichow, D.; Mutschke, G.; Yang, X.; Bund, A.; Fröhlich, J. Numerical simulation of the onset of mass transfer and convection in copper electrolysis subjected to a magnetic field. Russ. J. Electrochem. 2012, 48, 682–691. [Google Scholar] [CrossRef]
- Van Den Bossche, B.; Bortels, L.; Deconinck, J.; Vandeputte, S.; Hubin, A. Numerical steady state analysis of current density distributions in axisymmetrical systems for multi-ion electrolytes: Application to the rotating disc electrode. J. Electroanal. Chem. 1996, 411, 129–143. [Google Scholar] [CrossRef]
- Georgiadou, M. Finite-Difference Simulation of Multi-Ion Electrochemical Systems Governed by Diffusion, Migration, and Convection: Implementation in Parallel-Plate Electrochemical Reactor and Backward-Facing Step Geometries. J. Electrochem. Soc. 1997, 144, 2732. [Google Scholar] [CrossRef]
- Tschulik, K.; Kozä, J.A.; Uhlemann, M.; Gebert, A.; Schultz, L. Effects of well-defined magnetic field gradients on the electrodeposition of copper and bismuth. Electrochem. Commun. 2009, 11, 2241–2244. [Google Scholar] [CrossRef]
- Tschulik, K.; Cierpka, C.; Gebert, A.; Schultz, L.; Kahler, C.J.; Uhlemann, M. In situ analysis of three-dimensional electrolyte convection evolving during the electrodeposition of copper in magnetic gradient fields. Anal. Chem. 2011, 83, 3275–3281. [Google Scholar] [CrossRef] [PubMed]
- Huang, M.; Eckert, K.; Mutschke, G. Magnetic-field-assisted electrodeposition of metal to obtain conically structured ferromagnetic layers. Electrochim. Acta 2020, 365, 137374. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, M.; Uhlemann, M.; Eckert, K.; Mutschke, G. Pulse Reverse Plating of Copper Micro-Structures in Magnetic Gradient Fields. Magnetochemistry 2022, 8, 66. https://doi.org/10.3390/magnetochemistry8070066
Huang M, Uhlemann M, Eckert K, Mutschke G. Pulse Reverse Plating of Copper Micro-Structures in Magnetic Gradient Fields. Magnetochemistry. 2022; 8(7):66. https://doi.org/10.3390/magnetochemistry8070066
Chicago/Turabian StyleHuang, Mengyuan, Margitta Uhlemann, Kerstin Eckert, and Gerd Mutschke. 2022. "Pulse Reverse Plating of Copper Micro-Structures in Magnetic Gradient Fields" Magnetochemistry 8, no. 7: 66. https://doi.org/10.3390/magnetochemistry8070066
APA StyleHuang, M., Uhlemann, M., Eckert, K., & Mutschke, G. (2022). Pulse Reverse Plating of Copper Micro-Structures in Magnetic Gradient Fields. Magnetochemistry, 8(7), 66. https://doi.org/10.3390/magnetochemistry8070066






