Spin Symmetry in Polynuclear Exchange-Coupled Clusters
Abstract
:1. Introduction
- Spherical-tensor matrices:
- Shift-operator matrices:
- Cartesian matrices:
- Isotropic exchange constants are uniformly defined through the form .
- The angular momentum operators yield eigenvalues in units of the reduced Planck constant, , when operating on the corresponding wave function (ket).
- The Condon–Shortley phase convention is used together with the pseudo-standard phase system for irreducible tensor operators.
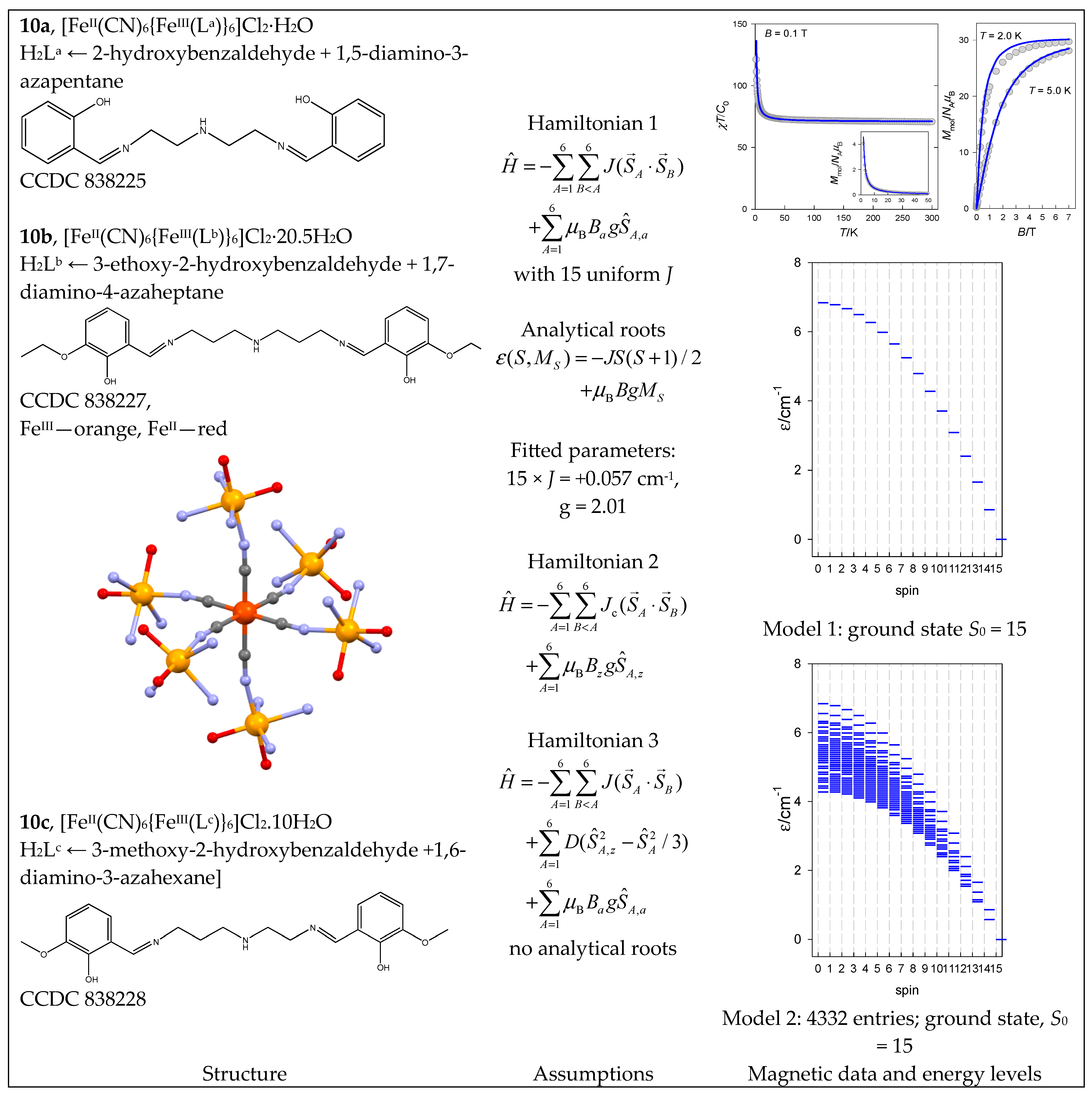
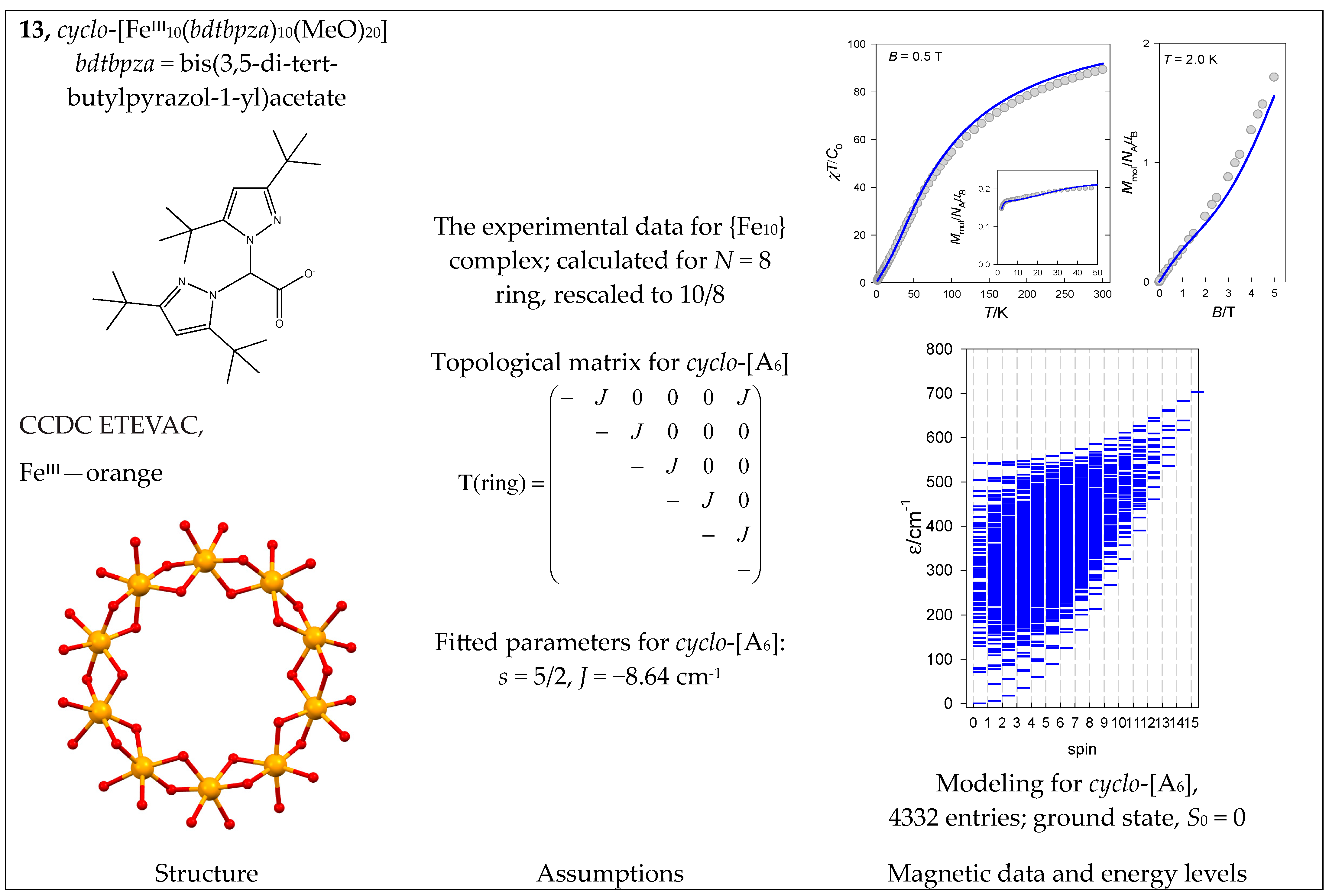
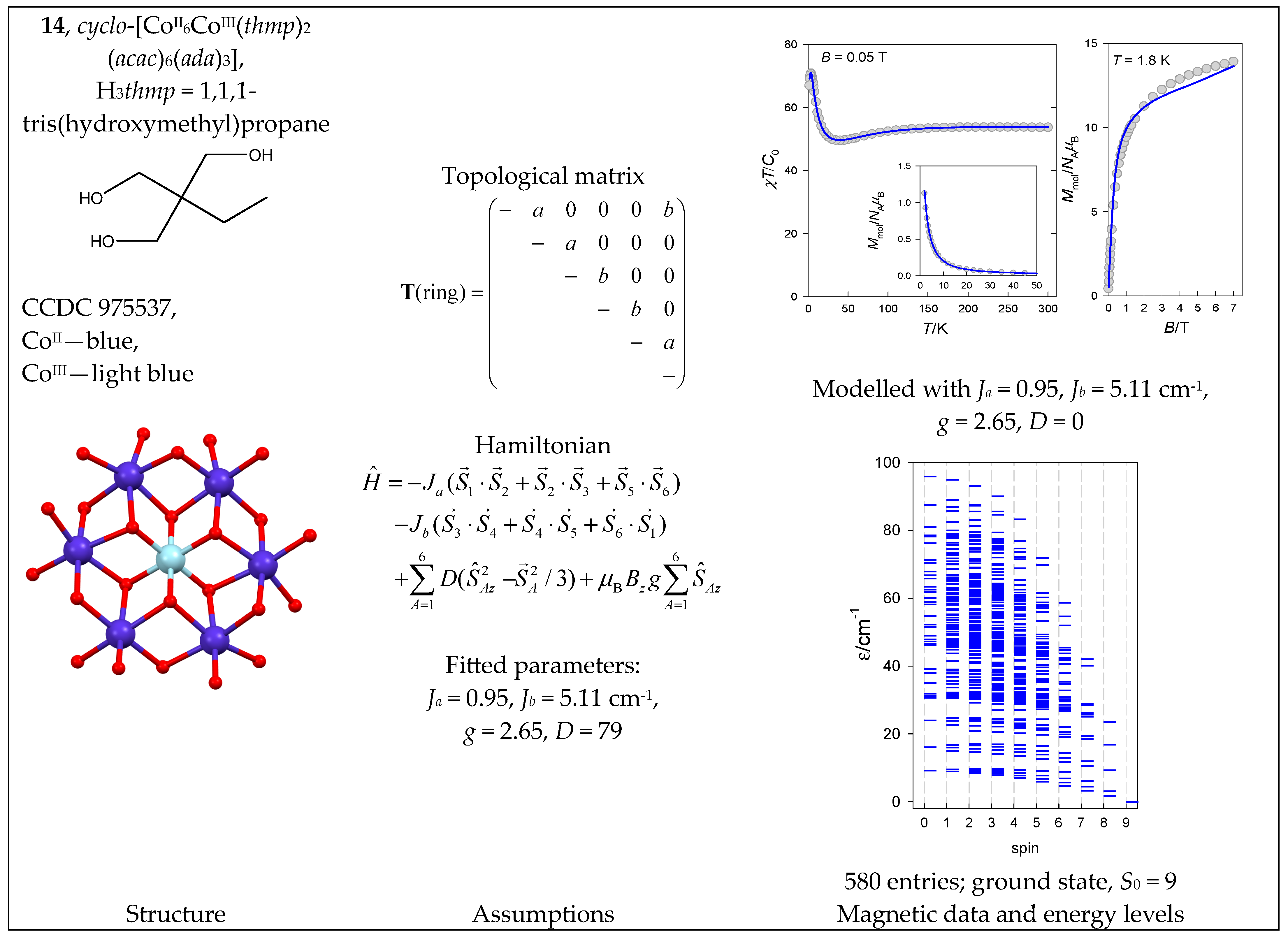
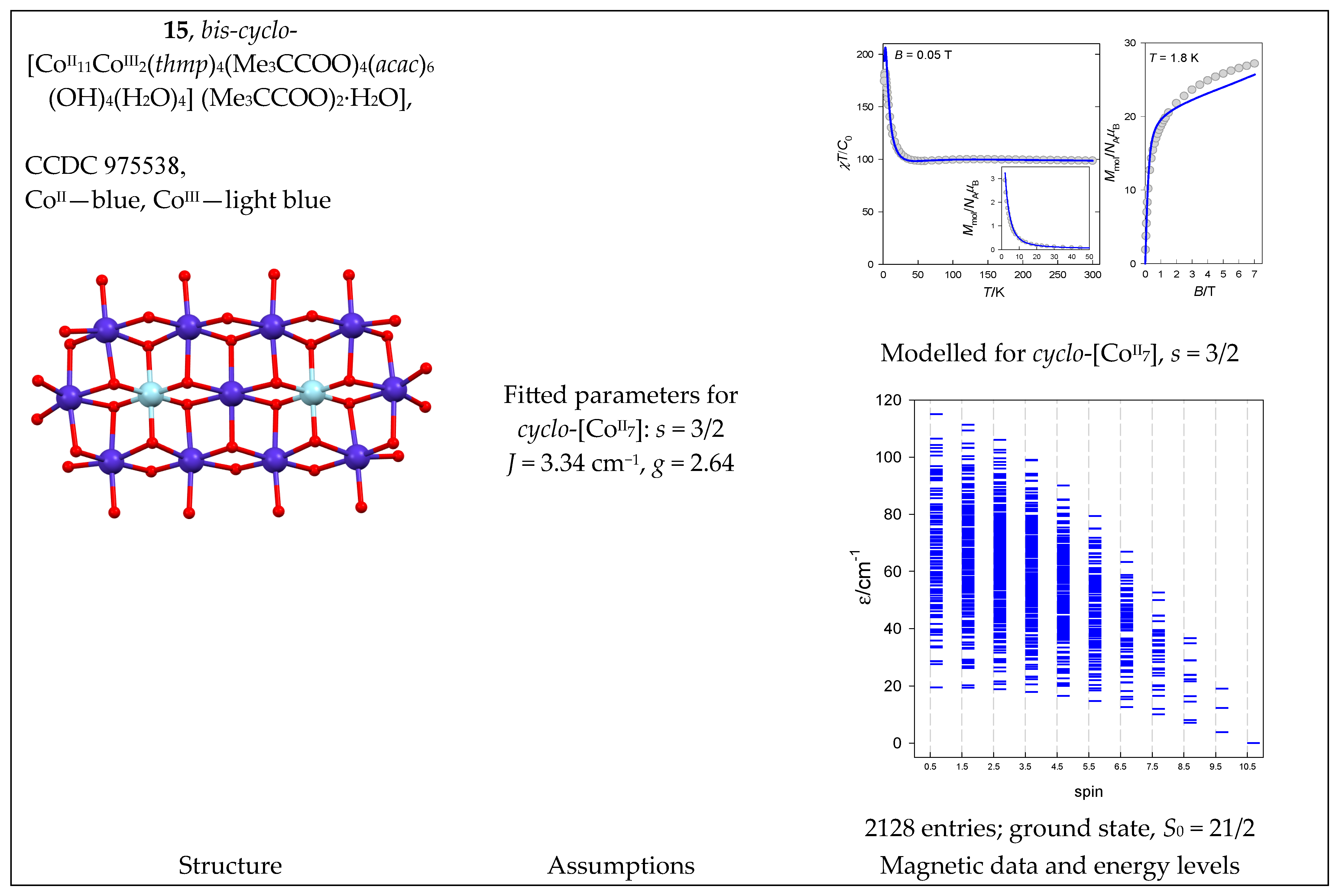
- It is assumed that the energy quantities, E (like ε, J, D), are in the form of the corresponding wavenumber; i.e., E/hc are provided in units of cm−1.
- SI units are used consistently through the paper; χmol [SI] = 4π × 10−6 χmol [cgs&emu].
- Fundamental physical constants (μ0, NA, kB, μB, ) adopt their usual meaning. The reduced Curie constant = 4.7141997 × 10−6 K m3 mol−1 is met in the contribution.
- The temperature evolution of the magnetic susceptibility is often displayed through the product function, χT, given in units of cgs&emu [cm3 K mol−1]. This old-fashioned representation can be equivalently expressed as χT/C0. This dimensionless product function has some advantages as its values for Curie paramagnets (χ = C0g2S(S + 1)/3T with g = 2) are 1, 8/3, 5, 8, 35/3, 16, and 21 for S = 1/2 to 7/2. This quantity is additive unlike the effective magnetic moment, so it is more suitable for polynuclear systems. Conversion to non-SI units: χT[cgs&emu] = C0/(4π × 10−6) × (χT/C0) = 0.3751 × χT/C0. The conversion of the effective magnetic moment to a dimensionless product function is χT/C0 = (μeff2)/3 when μeff is given in the unit of the Bohr magneton, μB.
2. Methodology
2.1. Spin Symmetry
2.2. Matrix Elements
- (a)
- Bilinear isotropic exchange:
- (b)
- Zeeman operator:
2.3. Density of State Function
2.4. Implementation
- Define the topological matrix, T(A,B).
- Determine the total number of zero-field states, M; limit Smin and Smax and the size of the matrices with the same spin dim(S).
- For the final spin states, S, prepare the coupling history matrix: CHM = {D1, D12, D123,…., D1…N = 2S}.
- For pairs of centers, prepare operator ranks, OR = {k1,…, kN}, and intermediate operator ranks, IOR = {, …, }.
- Open a loop over the molecular spins, S = Smin to Smax, and fill matrix elements of the blocks for the same spin and all intermediate spins, , for each relevant pair, {A,B}. The row and column indices of such a matrix use the set of intermediate spins contained in the CHM.
- The final block, , is the sum of all relevant matrices, , multiplied by a non-zero topological matrix, T(A,B), containing the current value of J(A,B).
- The final block is diagonalized (only eigenvalues are searched). The zero-field eigenvalues are enriched with a Zeeman term in the form of , where uniform geff-factors occur. (This approximation is either a weakness or a strength of the whole procedure.)
- Magnetic energy levels, , enter the statistical partition function, Z(B,T), from which the magnetization and susceptibility are calculated using Equations (33)–(37).
- The calculated susceptibility, χc(B,T), and magnetization, Mc(B,T), together with the experimental points enter the error functional, F(B,T), which is processed by advanced minimization procedures such as simulated annealing or genetic algorithms to obtain an optimized set of magnetic parameters, JAB and geff.
2.5. Utilization of Symmetry
- Spatial symmetry of atomic coordinates within the point group, G;
- Angular momentum symmetry within the fully rotational group in three dimensions, R3, and the special unitary group, SU2j+1 in (2j + 1), dimensions, which contains 4j(j + 1) tensor operators for and ;
- Permutation symmetry, which corresponds to permutations of individual particles (spins) within the symmetry group, SN.
- The basis set consists of uncoupled kets, i.e., ; this approach is applicable to the general case, which includes other interactions besides isotropic exchange, such as asymmetric exchange, etc.
- The basis set is represented by coupled kets, ; this is appropriate for isotropic exchange alone with a uniform Zeeman term (all g-factors are equivalent.
| D2 (h = 4) | ||||
|---|---|---|---|---|
| A | +1 | +1 | +1 | +1 |
| B1 | +1 | +1 | –1 | –1 |
| B3 | +1 | –1 | –1 | +1 |
| B2 | +1 | –1 | +1 | –1 |
3. Modeling of Finite Chains
4. Modeling of Finite Rings
5. Modeling of Convex Polyhedra
6. Exchange Interaction in Real Clusters
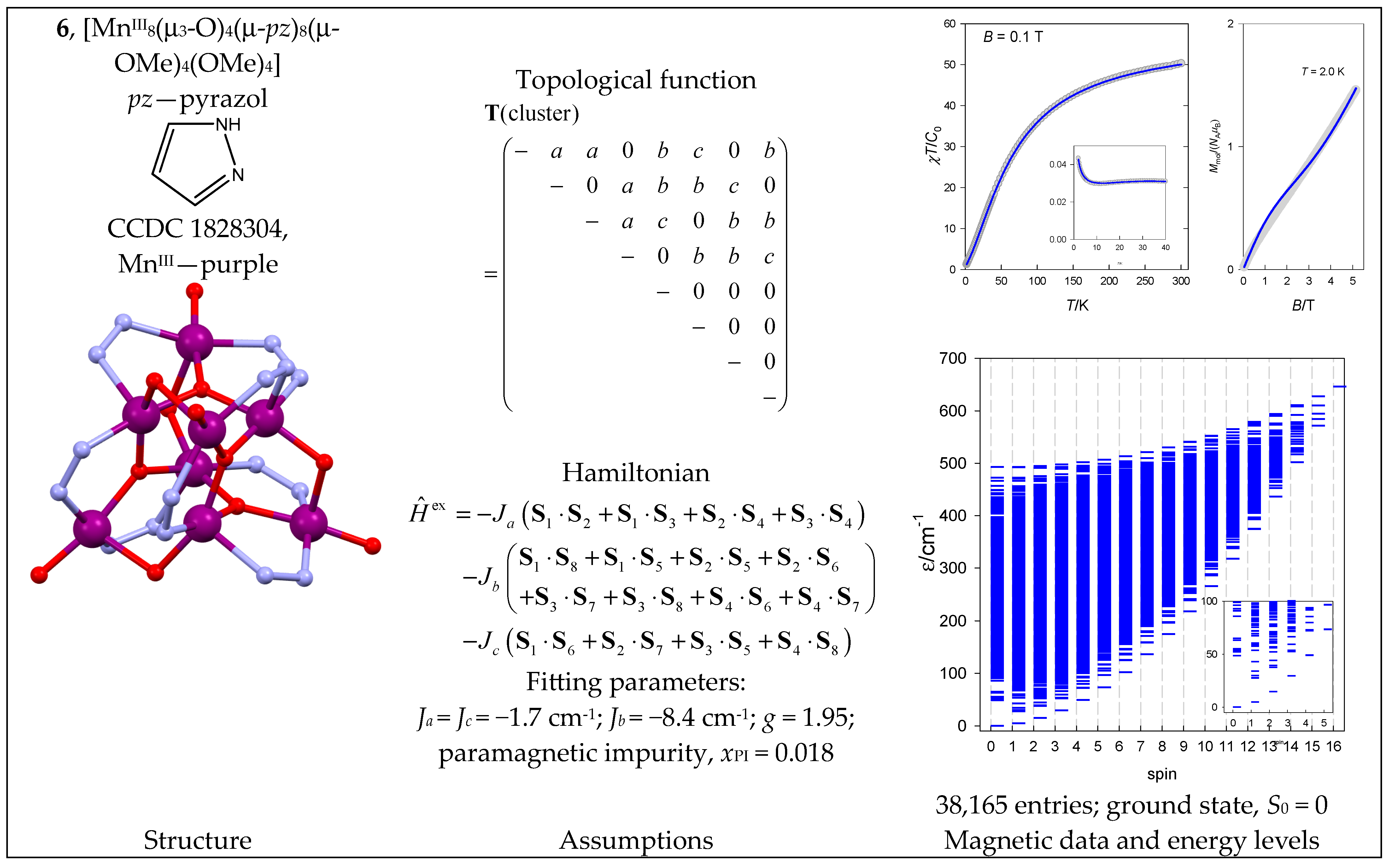
6.1. Mn Complexes
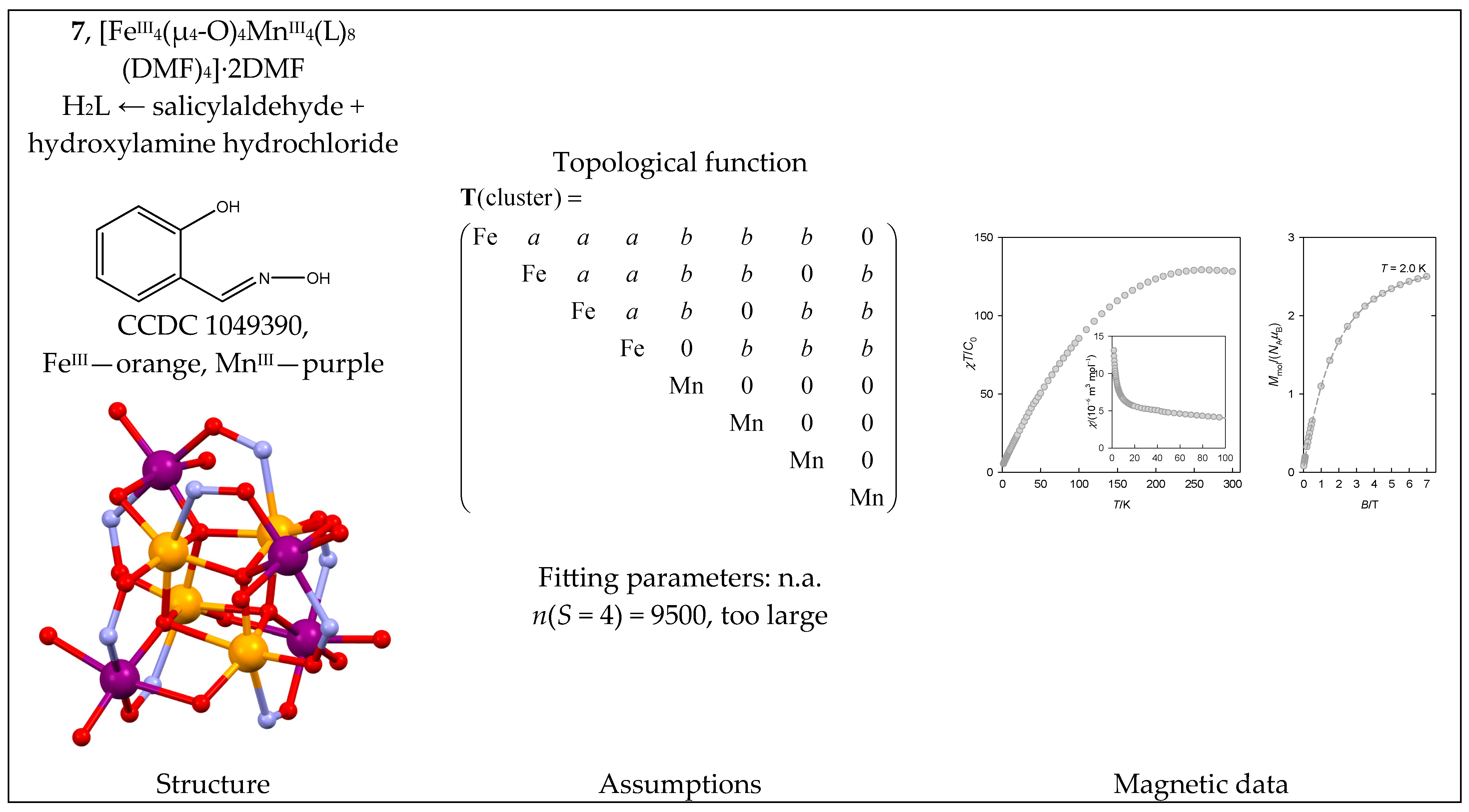
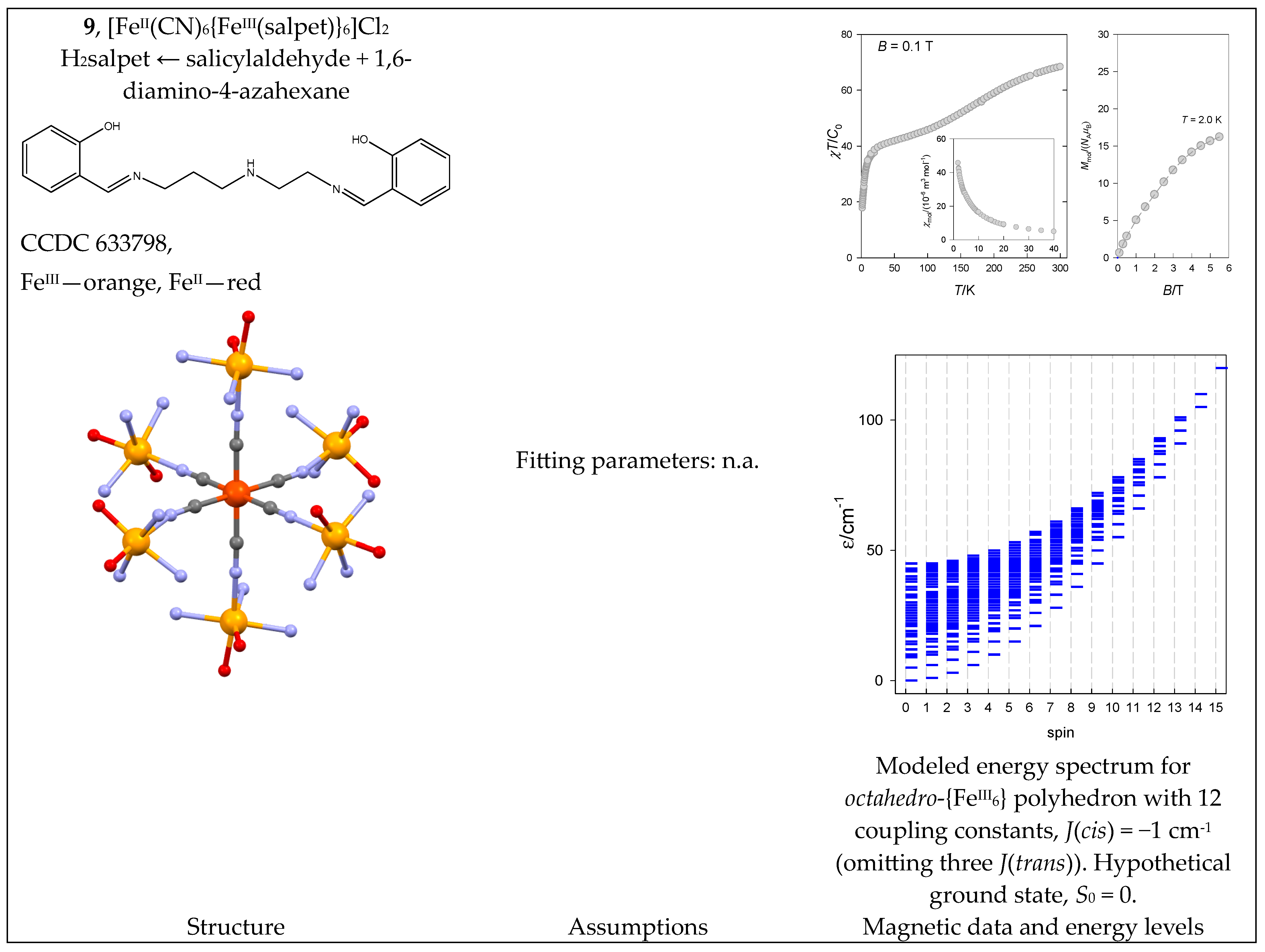
6.2. Fe(III) Complexes
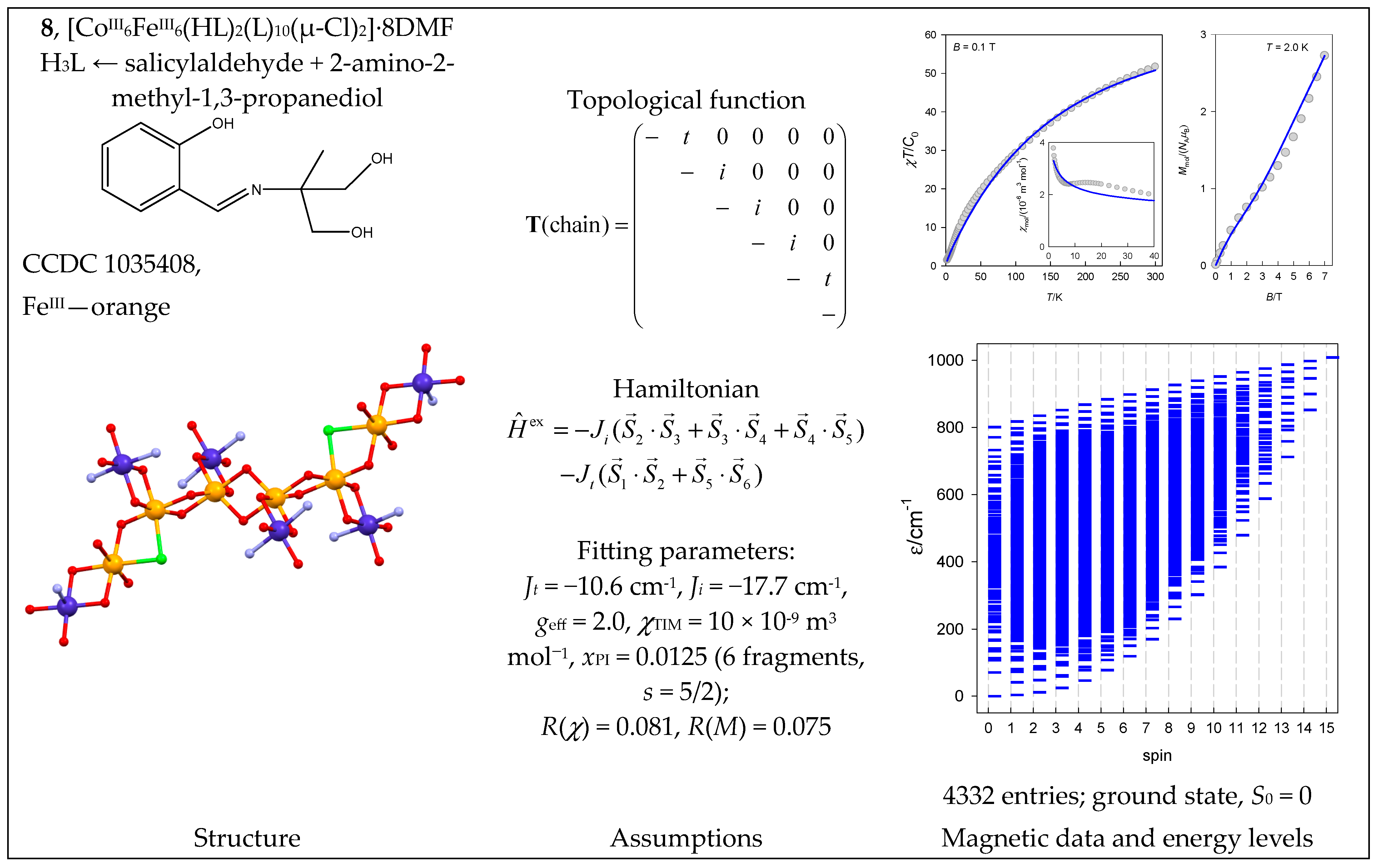
6.3. Co(II) Complexes
6.4. Ln(III) Complexes
7. Conclusions
- A number of magnetic centers, N, and spins, SA, on individual centers in any order and size;
- The topological matrix T(A,B), which defines the coupling path; this contains a trial set of exchange-coupling constants, J(A,B), that will be optimized; their number is less or equal to N(N—1)/2;
- The value of the g-factor, which must be uniform (geff), to correctly exploit the blocking of the Hamiltonian matrix according to molecular spin.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kambe, K. On the Paramagnetic Susceptibilities of Some Polynuclear Complex Salts. J. Phys. Soc. Jpn. 1950, 5, 48–51. [Google Scholar] [CrossRef]
- Kahn, O. Molecular Magnetism; VCH: Weinheim, Germany, 1993; ISBN 9780471188384. [Google Scholar]
- Rose, M.E. Elementary Theory of Angular Momentum; Wiley: New York, NY, USA, 1957; ISBN 9780471735243. [Google Scholar]
- Fano, U.; Racah, G. Irreducible Tensorial Sets; Academic Press: New York, NY, USA, 1959; ISBN 9781483230597. [Google Scholar]
- Griffith, J.S. The Irreducible Tensor Method for Molecular Symmetry Group; Courier Dover Publications: Mineola, NY, USA; Prentice-Hall: London, UK, 1962. [Google Scholar]
- Brink, D.M.; Satchler, G.R. Angular Momentum; Claredon Press: Oxford, UK, 1962. [Google Scholar]
- Judd, B.R. Operator Techniques in Atomic Spectroscopy; McGraw–Hill: New York, NY, USA, 1963; ISBN 9781114630574. [Google Scholar]
- Wybourne, B.G. Spectroscopic Properties of Rare Earths; Wiley: New York, NY, USA, 1965; ISBN 9780470965078. [Google Scholar]
- Jucys, A.P.; Savukynas, A.V. Mathematical Foundations of the Atomic Theory; Mintis: Viljnus, Lithuania, 1972. (In Russian) [Google Scholar]
- Varshalovich, D.A.; Moskalev, A.N.; Chersonskii, V.K. Quantum Theory of Angular Momentum; Nauka: Saint Petersburg, Russia, 1975. (In Russian) [Google Scholar]
- Silver, B.L. Irreducible Tensor Method; Academic Press: New York, NY, USA, 1976. [Google Scholar]
- Sobelman, I.I. Atomic Spectra and Radiative Transitions; Springer: Berlin/Heidelberg, Germany, 1979; ISBN 9783662059050. [Google Scholar] [CrossRef]
- Zare, R.N. Angular Momentum: Understanding Spatial Aspects in Chemistry and Physics; Wiley: New York, NY, USA, 1988; ISBN 9780471858928. [Google Scholar]
- Tsukerblat, B.S. Group Theory in Chemistry and Spectroscopy; Academic Press: London, UK, 1994; ISBN 9780127022857. [Google Scholar]
- Lueken, H. Magnetochemie; Teubner: Stuttgart, Germany, 1999; ISBN 9783519035305. (In German) [Google Scholar]
- Bencini, A.; Gatteschi, D. Electron Paramagnetic Resonance of Exchange Coupled Systems; Springer: Berlin/Heidelberg, Germany, 1990; ISBN 9783642746017. [Google Scholar]
- Borras-Almenar, J.; Clemente-Juan, J.; Coronado, E.; Palii, A.; Tsukerblat, B. Magnetic Exchange between Orbitally Degenerate Ions: A New Development for the Effective Hamiltonian. J. Phys. Chem. A 1998, 102, 200–213. [Google Scholar] [CrossRef]
- Ceulemans, A.; Chibotaru, L.; Heylen, G.; Pierloot, K.; Vanquickenborne, L. Theoretical Models of Exchange Interactions in Dimeric Transition-Metal Complexes. Chem. Rev. 2000, 100, 787–806. [Google Scholar] [CrossRef] [PubMed]
- Palii, A.; Tsukerblat, B.; Coronado, E.; Clemente-Juan, J.; Borras-Almenar, J. Orbitally dependent magnetic coupling between cobalt(II) ions: The problem of the magnetic anisotropy. J. Chem. Phys. 2003, 118, 5566–5581. [Google Scholar] [CrossRef]
- Mironov, V.; Chibotaru, L.; Ceulemans, A. Mechanism of a Strongly Anisotropic MoIII–CN–MnII Spin–Spin Coupling in Molecular Magnets Based on the [Mo(CN)7]4- Heptacyanometalate: A New Strategy for Single-Molecule Magnets with High Blocking Temperatures. J. Am. Chem. Soc. 2003, 125, 9750–9760. [Google Scholar] [CrossRef] [PubMed]
- Palii, A.; Tsukerblat, B.; Clemente-Juan, J.M.; Coronado, E. Magnetic exchange between metal ions with unquenched orbital angular momenta: Basic concepts and relevance to molecular magnetism. Int. Rev. Phys. Chem. 2010, 29, 135–230. [Google Scholar] [CrossRef]
- Schnale, R.; Schnack, J. Calculating the energy spectra of magnetic molecules: Application of real- and spin-space symmetries. Int. Rev. Phys. Chem. 2010, 29, 403–452. [Google Scholar] [CrossRef]
- Borras-Almenar, J.J.; Clemente-Juan, J.M.; Coronado, E.; Tsukerblat, B.S. High-Nuclearity Magnetic Clusters: Generalized Spin Hamiltonian and Its Use for the Calculation of the Energy Levels, Bulk Magnetic Properties, and Inelastic Neutron Scattering Spectra. Inorg. Chem. 1999, 38, 6081–6088. [Google Scholar] [CrossRef]
- Tsukerblat, B. Group-theoretical approaches in molecular magnetism: Metal clusters. Inorg. Chim. Acta 2008, 361, 3746–3760. [Google Scholar] [CrossRef]
- Boyarchenkov, A.S.; Bostrem, I.G.; Ovchinnikov, A.S. Quantum magnetization plateau and sign change of the magnetocaloric effect in a ferrimagnetic spin chain. Phys. Rev. B 2007, 76, 224410. [Google Scholar] [CrossRef]
- Borras-Almenar, J.J.; Clemente-Juan, J.M.; Coronado, E.; Tsukerblat, B.S. MAGPACK1 A package to calculate the energy levels, bulk magnetic properties, and inelastic neutron scattering spectra of high nuclearity spin clusters. J. Comp. Chem. 2001, 22, 985–991. [Google Scholar] [CrossRef]
- Schnack, J.; Luban, M. Rotational modes in molecular magnets with antiferromagnetic Heisenberg exchange. Phys. Rev. B 2000, 63, 014418. [Google Scholar] [CrossRef]
- Waldmann, O. Spin dynamics of finite antiferromagnetic Heisenberg spin rings. Phys. Rev. B 2001, 65, 024424. [Google Scholar] [CrossRef]
- Waldmann, O. E-band excitations in the magnetic Keplerate molecule Fe30. Phys. Rev. B 2007, 75, 012415. [Google Scholar] [CrossRef]
- Waldmann, O.; Stamatatos, T.C.; Christou, G.; Güdel, H.U.; Sheikin, I.; Mutka, H. Quantum Phase Interference and Néel-Vector Tunneling in Antiferromagnetic Molecular Wheels. Phys. Rev. Lett. 2009, 102, 157202. [Google Scholar] [CrossRef]
- Boča, R. Zero-field splitting in metal complexes. Coord. Chem. Rev. 2004, 248, 757–815. [Google Scholar] [CrossRef]
- Boča, R.; Herchel, R. Antisymmetric exchange in polynuclear metal complexes. Coord. Chem. Rev. 2010, 254, 2973–3025. [Google Scholar] [CrossRef]
- Bärwinkel, K.; Schmidt, H.-J.; Schnack, J. Structure and relevant dimension of the Heisenberg model and applications to spin rings. J. Magn. Magn. Mater. 2000, 212, 240–250. [Google Scholar] [CrossRef]
- Uhrecký, R.; Moncoľ, J.; Koman, M.; Titiš, J.; Boča, R. Structure and magnetism of a Mn(III)–Mn(II)–Mn(II)–Mn(III) chain complex. Dalton Trans. 2013, 42, 9490–9494. [Google Scholar] [CrossRef] [PubMed]
- Reis Conceição, N.; Nesterova, O.V.; Rajnák, C.; Boča, R.; Pombeiro, A.J.L.; Guedes da Silva, M.F.C.; Nesterov, D.S. New members of the polynuclear manganese family: MnII2MnIII2 single-molecule magnets and Mn II3Mn III8 antiferromagnetic complexes. Synthesis and magnetostructural correlations. Dalton Trans. 2020, 49, 13970–13985. [Google Scholar] [CrossRef]
- Meng, Z.-S.; Yun, L.; Zhang, W.-X.; Hong, C.-G.; Herchel, R.; Ou, Y.-C.; Leng, J.-D.; Peng, M.-X.; Lin, Z.-J.; Tong, M.-L. Reactivity of 4-amino-3,5-bis(pyridin-2-yl)-1,2,4-triazole, structures and magnetic properties of polynuclear and polymeric Mn(II), Cu(II) and Cd(II) complexes. Dalton Trans. 2009, 10284–10295. [Google Scholar] [CrossRef] [PubMed]
- Semenaka, V.V.; Nesterova, O.V.; Kokozay, V.N.; Zybatyuk, R.I.; Shishkin, O.V.; Boča, R.; Shevchenkod, D.V.; Huang, P.; Styring, S. Direct synthesis of an heterometallic {MnII3CrIII4} wheel by decomposition of Reineckes salt. Dalton Trans. 2010, 39, 2344–2349. [Google Scholar] [CrossRef] [PubMed]
- Herchel, R.; Boča, R.; Gembický, M.; Falk, K.; Fuess, H.; Haase, W.; Svoboda, I. Magnetic Properties of a Manganese(II) Trinuclear Complex Involving a Tridentate Schiff-Base Ligand. Inorg. Chem. 2007, 46, 1544–1546. [Google Scholar] [CrossRef] [PubMed]
- Babic-Samardzija, K.; Baran, P.; Boča, R.; Herchel, R.; Raptis, R.G.; Velez, C.L. Structural and magnetic susceptibility study of an octanuclear MnIII-oxo-pyrazolido complex. Polyhedron 2018, 149, 142–147. [Google Scholar] [CrossRef]
- Nesterova, O.V.; Chygorin, E.N.; Kokozay, V.N.; Omelchenko, I.V.; Shishkin, O.V.; Boča, R.; Pombeiro, A.J.L. A self-assembled octanuclear complex bearing the uncommon close-packed {Fe4Mn4(μ4-O)4(μ-O)4} molecular core. Dalton Trans. 2015, 44, 14918–14924. [Google Scholar] [CrossRef]
- Chygorin, E.N.; Kokozay, V.N.; Omelchenko, I.V.; Shishkin, O.V.; Titiš, J.; Boča, R.; Nesterov, D.S. Direct synthesis of a {Co III6Fe III6} dodecanuclear complex, revealing an unprecedented molecular structure type. Dalton Trans. 2015, 44, 10918–10922. [Google Scholar] [CrossRef]
- Boča, R.; Šalitroš, I.; Kožíšek, J.; Linares, J.; Moncoľ, J.; Renz, F. Spin crossover in a heptanuclear mixed-valence iron complex. Dalton Trans. 2010, 39, 2198–2200. [Google Scholar] [CrossRef]
- Šalitroš, I.; Boča, R.; Herchel, R.; Moncoľ, J.; Nemec, I.; Ruben, M.; Renz, F. Mixed-Valence Heptanuclear Iron Complexes with Ferromagnetic Interaction. Inorg. Chem. 2012, 51, 12755–12767. [Google Scholar] [CrossRef]
- Hale, A.R.; Lott, M.E.; Peralta, J.E.; Foguet-Albiol, D.; Abboud, K.A.; Christou, G. Magnetic Properties of High-Nuclearity Fex-oxo (x = 7, 22, 24) Clusters Analyzed by a Multipronged Experimental, Computational, and Magnetostructural Correlation Approach. Inorg. Chem. 2022, 61, 11261–11276. [Google Scholar] [CrossRef]
- Baran, P.; Boča, R.; Chakraborty, I.; Giapintzakis, J.; Herchel, R.; Huang, Q.; McGrady, J.E.; Raptis, R.G.; Sanakis, Y.; Simopoulos, A. Synthesis, Characterization, and Study of Octanuclear Iron-Oxo Clusters Containing a Redox-Active Fe4O4-Cubane Core. Inorg. Chem. 2008, 47, 645–655. [Google Scholar] [CrossRef]
- Gajewska, M.J.; Bieńko, A.; Herchel, R.; Haukka, M.; Jerzykiewicz, M.; Ożarowski, A.; Drabent, K.; Hung, C.-H. Iron(III) bis(pyrazol-1-yl)acetate based decanuclear metallacycles: Synthesis, structure, magnetic properties and DFT calculations. Dalton Trans. 2016, 45, 15089–15096. [Google Scholar] [CrossRef]
- Leng, J.-D.; Xing, S.-K.; Herchel, R.; Liu, J.-L.; Tong, M.-L. Disklike Hepta- and Tridecanuclear Cobalt Clusters. Synthesis, Structures, Magnetic Properties, and DFT Calculations. Inorg. Chem. 2014, 53, 5458–5466. [Google Scholar] [CrossRef] [PubMed]
- Zheng, L.-L.; Leng, J.-D.; Herchel, R.; Lan, Y.-H.; Powell, A.K.; Tong, M.-L. Anion-Dependent Facile Route to Magnetic Dinuclear and Dodecanuclear Cobalt Clusters. Eur. J. Inorg. Chem. 2010, 2010, 2229–2234. [Google Scholar] [CrossRef]
- Gebrezgiabher, M.; Schlittenhardt, S.; Rajnák, C.; Kuchár, J.; Sergawie, A.; Černák, J.; Ruben, M.; Thomas, M.; Boča, R. Triangulo-{ErIII3} complex showing field supported slow magnetic relaxation. RSC Adv. 2022, 12, 21674–21680. [Google Scholar] [CrossRef] [PubMed]
- Gebrezgiabher, M.; Schlittenhardt, S.; Rajnák, C.; Sergawie, A.; Ruben, M.; Thomas, M.; Boča, R. A Tetranuclear Dysprosium Schiff Base Complex Showing Slow Relaxation of Magnetization. Inorganics 2022, 10, 66. [Google Scholar] [CrossRef]
- Gusev, A.; Herchel, R.; Nemec, I.; Shuľgin, V.; Eremenko, I.L.; Lyssenko, K.; Linert, W.; Trávníček, Z. Tetranuclear Lanthanide Complexes Containing a Hydrazone-type Ligand. Dysprosium [2 × 2] Gridlike Single-Molecule Magnet and Toroic. Inorg. Chem. 2016, 55, 12470–12476. [Google Scholar] [CrossRef]
- Mičová, R.; Rajnák, C.; Titiš, J.; Moncoľ, J.; Nováčiková, J.; Bieńko, A.; Renz, F.; Boča, R. to be published.
- Delfs, C.; Gatteschi, D.; Pardi, L.; Sessoli, R.; Weighardt, K.; Hanke, D. Magnetic properties of an octanuclear iron(III) cation. Inorg. Chem. 1993, 32, 3099–3103. [Google Scholar] [CrossRef]
- Waldmann, O. Symmetry and energy spectrum of high-nuclearity spin clusters. Phys. Rev. 2000, B61, 6138–6144. [Google Scholar] [CrossRef]
- Schnack, J. Exact diagonalization techniques for quantum spin systems. Chall. Adv. Comput. Chem. Phys. 2023, 34, 155–177. [Google Scholar] [CrossRef]
- Boča, R. A Handbook of Magnetochemical Formulae; Elsevier: Amsterdam, The Netherlands, 2012; ISBN 9780124160149. [Google Scholar]
- Kunitsky, S.V.; Palii, A.V.; Tsukerblat, B.S.; Clemente-Juan, J.M.; Coronado, E. MVPROG: A program to calculate energy levels and magnetic properties of high nuclearity mixed valence clusters. Moldav. J. Phys. Sci. 2004, 3, 325–328. [Google Scholar]
- Wang, F.; Wang, B.; Wang, M.; Chen, Z. Irreducible tensor operator method study on molecular magnetism: A practical approach and its use for high-nuclearity magnetic cluster. Chem. Phys. Lett. 2008, 454, 177–183. [Google Scholar] [CrossRef]
- Borrás-Almenar, J.; Cardona-Serra, S.; Clemente-Juan, J.; Coronado, E.; Palii, A.; Tsukerblat, B. MVPACK: A Package to Calculate Energy Levels and Magnetic Properties of High Nuclearity Mixed Valence Clusters. J. Comput. Chem. 2009, 31, 1321–1332. [Google Scholar] [CrossRef] [PubMed]
- Chilton, N.F.; Anderson, R.P.; Turner, L.D.; Soncini, A.; Murray, K.S. PHI: A powerful new program for the analysis of anisotropic monomeric and exchange-coupled polynuclear d- and f-block complexes. J. Comput. Chem. 2013, 34, 1164–1175. [Google Scholar] [CrossRef] [PubMed]
- Boča, R. A General Program for Magnetism of Polynuclear Complexes; University of SS Cyril and Methodius: Trnava, Slovakia, 2023. [Google Scholar]
- Schnack, J.; Wendland, O. Properties of highly frustrated magnetic molecules studied by the finite-temperature Lanczos method. Eur. Phys. J. 2010, B78, 535–541. [Google Scholar] [CrossRef]
- Schnack, J.; Ummethum, J. Advanced quantum methods for the largest magnetic molecules. Polyhedron 2013, 66, 28–33. [Google Scholar] [CrossRef]






| AN System | Magnetic States, K | Zero-Field States, M | Dimension n(S) from the Lowest Spin, Smin = 0 or 1/2, to the Highest Spin, Smax = N·SA |
|---|---|---|---|
| SA = ½ | |||
| A3 | 8 | 3 | 2, 1 |
| A4 | 16 | 6 | 2, 3, 1 |
| A5 | 32 | 10 | 5, 4, 1 |
| A6 | 64 | 20 | 5, 9, 5, 1 |
| A7 | 128 | 35 | 14, 14, 6, 1 |
| A8 | 256 | 70 | 14, 28, 20, 7, 1 |
| A9 | 512 | 126 | 42, 48, 27, 8, 1 |
| A10 | 1024 | 252 | 42, 90, 75, 35, 9, 1 |
| A11 | 2048 | 462 | 132, 165, 110, 44, 10, 1 |
| A12 | 4096 | 924 | 132, 297, 275, 154, 54, 11,1 |
| A13 | 8192 | 1716 | 429, 572, 429, 208, 65, 12, 1 |
| A14 | 16,384 | 3432 | 429, 1001, 1001, 637, 273, 77, 13, 1 |
| A15 | 32,768 | 6435 | 1430, 2002, 1638, 910, 350, 90, 14 1 |
| SA = 1 | |||
| A3 | 27 | 7 | 1, 3, 2, 1 |
| A4 | 81 | 19 | 3, 6, 6, 3, 1 |
| A5 | 243 | 51 | 6, 15, 15, 10, 4, 1 |
| A6 | 729 | 141 | 15, 36, 40, 29, 15, 5, 1 |
| A7 | 2187 | 393 | 36, 91, 105, 84, 49, 21, 6, 1 |
| A8 | 6561 | 1107 | 91, 232, 280, 238, 154, 76, 28, 7, 1 |
| A9 | 19,683 | 3139 | 232, 603, 750, 672, 468, 258, 111, 36, 8, 1 |
| A10 | 59,049 | 8954 | 603, 1585, 2025, 1890, 1398, 837, 405, 155, 45, 9, 1 |
| SA = 3/2 | |||
| A3 | 64 | 12 | 2, 4, 3, 2, 1 |
| A4 | 256 | 44 | 4, 9, 11, 10, 6, 3, 1 |
| A5 | 1024 | 155 | 20, 34, 36, 30, 20, 10, 4, 1 |
| A6 | 4096 | 580 | 34, 90, 120, 120, 96, 64, 35, 15, 5, 1 |
| A7 | 16,384 | 2128 | 210, 364, 426, 400, 315, 210, 119, 56, 21, 6, 1 |
| A8 | 65,536 | 8092 | 364, 1000, 1400, 1505, 1351, 1044, 700, 406, 202, 84, 28, 7, 1 |
| A9 | 262,144 | 30,276 | 2400, 4269, 5256, 5300, 4600, 3501, 2352, 1392, 720, 321, 120, 36, 8, 1 |
| A10 | 1,048,576 | 116,304 | 4269, 11,925, 17,225, 19,425, 18,657, 15,753, 11,845, 7965, 4785, 2553, 1197, 485, 165, 45, 9, 1 |
| SA = 2 | |||
| A3 | 125 | 19 | 1, 3, 5, 4, 3, 2, 1 |
| A4 | 625 | 85 | 5, 12, 16, 17, 15, 10, 6, 3, 1 |
| A5 | 3125 | 381 | 16, 45, 65, 70, 64, 51, 35, 20, 10, 4, 1 |
| A6 | 15,625 | 1751 | 65, 180, 260, 295, 285, 240, 180, 120, 79, 35, 15, 5, 1 |
| A7 | 78,125 | 8135 | 260, 735, 1085, 1260, 1260, 1120, 895, 645, 420, 245, 126, 56, 21, 6, 1 |
| A8 | 390,625 | 38,165 | 1085, 3080, 4600, 5460, 5620, 5180, 4340, 3325, 2331, 1492, 868, 454, 210, 84, 28, 7, 1 |
| A9 | 1,953,125 | 180,325 | 4600, 13,140, 19,845, 23,940, 25,200, 23,925, 20,796, 16,668, 12,356. 8470, 5355, 3108, 1644, 783, 330, 120, 36, 8, 1 |
| A10 | 9,765,625 | 856,945 | 19,845, 56,925, 86,725, 106,050, 113,706, 110,529, 98,945, 82,215, 63,645, 45,957, 30,933, 19,360, 11,220, 5985, 2913, 1277, 495, 165, 45, 9, 1 |
| SA = 5/2 | |||
| A3 | 216 | 27 | 2, 4, 6, 5, 4, 3, 2, 1 |
| A4 | 1296 | 146 | 6, 15, 21, 24, 24, 21, 15, 10, 6, 3, 1 |
| A5 | 7776 | 780 | 45, 84, 111, 120, 115, 100, 79, 56, 35, 20, 10, 4, 1 |
| A6 | 46,656 | 4332 | 111, 315, 475, 575, 609, 581, 505, 405, 300, 204, 126, 70, 35, 15, 5, 1 |
| A7 | 279,936 | 24,017 | 1050, 1974, 2666, 3060, 3150, 2975, 2604, 2121, 1610, 1140, 750, 455, 252, 126, 56, 21, 6, 1 |
| A8 | 1,679,616 | 135,954 | 2666, 7700, 11,900, 14,875, 16,429, 16,576, 15,520, 13,600, 11,200, 8680, 6328, 4333, 2779, 1660, 916, 462, 210, 84, 28, 7, 1 |
| A9 | 10,077,696 | 767,394 | 26,775, 50,904, 70,146, 83,000, 88,900, 88,200, 82,005, 71,904, 59,661, 46,920, 34,980, 24,696, 16,478, 10,360, 6111, 3360, 1707, 792, 330, 120, 36, 8, 1 |
| A10 | 60,466,176 | 4,395,456 | 70,146, 204,050, 319,725, 407,925, 463,155, 484,155, 473,670, 437,590, 383,670, 320,166, 254,639, 193,095, 139,545, 95,985, 62,712, 38,808, 22,660, 12,420, 6345, 2993, 1287, 495, 165, 45, 9, 1 |
| Coupling Scheme 1 | Coupling Scheme 2 | |||||||
|---|---|---|---|---|---|---|---|---|
| DA | 2 | 2 | 1 | 1 | 1 | 2 | 2 | 1 |
| State | D1 | D12 | D123 | D1234 = 2S | D1 | D12 | D123 | D1234 = 2S |
| 1 | 2 | 0 | 1 | 0 | 1 | 1 | 1 | 0 |
| 2 | 2 | 0 | 1 | 2 | 1 | 1 | 1 | 2 |
| 3 | 2 | 2 | 1 | 0 | 1 | 1 | 3 | 2 |
| 4 | 2 | 2 | 1 | 2 | 1 | 1 | 3 | 4 |
| 5 | 2 | 2 | 3 | 2 | 1 | 3 | 1 | 0 |
| 6 | 2 | 2 | 3 | 4 | 1 | 3 | 1 | 2 |
| 7 | 2 | 4 | 3 | 2 | 1 | 3 | 3 | 2 |
| 8 | 2 | 4 | 3 | 4 | 1 | 3 | 3 | 4 |
| 9 | 2 | 4 | 5 | 4 | 1 | 3 | 5 | 4 |
| 10 | 2 | 4 | 5 | 6 | 1 | 3 | 5 | 6 |
| Operator Ranks, OR | Intermediate Operator Ranks, IOR | ||||||
|---|---|---|---|---|---|---|---|
| Pair A, B | k1 | k2 | k3 | k4 | |||
| 1, 2 | 1 | 1 | 0 | 0 | 0 | 0 | 0 |
| 1, 3 | 1 | 0 | 1 | 0 | 1 | 0 | 0 |
| 2, 3 | 0 | 1 | 1 | 0 | 1 | 0 | 0 |
| 1, 4 | 1 | 0 | 0 | 1 | 1 | 1 | 0 |
| 2, 4 | 0 | 1 | 0 | 1 | 1 | 1 | 0 |
| 3, 4 | 0 | 0 | 1 | 1 | 0 | 1 | 0 |
| Partition | Young Diagram | IR a Гλ(d) | Dimension n × d | Spin, S, in R3 b 0–8 | Dimension of Blocks | Reduced Blocks Free of Projections c | IR Td |
|---|---|---|---|---|---|---|---|
| [4000] = [4] |  | Г1(1) | 70 × 1 = 70 | 0, 22, 42, 5, 6, 8 | 1, 10, 18, 11, 13, 17 = 70 | 1, 2, 2, 1, 1, 1 | A1 |
| [1111] = [14] |  | Г2(1) | 5 × 1 | 2 | 5 | 1 | A2 |
| [2200] = [22] |  | Г3(2) | 50 × 2 = 100 | 02, 22, 3, 42, 6 | (2, 10, 7, 18, 13) = 50 × 2 | (2, 2, 1, 2, 1) × 2 | E |
| [3100] |  | Г4(3) | 105 × 3 = 315 | 12, 22, 33, 42, 52, 6, 7 | (6, 10, 21, 18, 22, 13, 15) = 105 × 3 | (2, 2, 3, 2, 2, 1, 1) × 3 | T2 |
| [2110] = [212] |  | Г5(3) | 45 × 3 = 135 | 12, 2, 32, 4, 5 | (6, 5, 14, 9, 11) = 45 × 3 | (2, 1, 2, 1, 1) × 3 | T1 |
| sum | K = 625 magnetic states | 119 | K = 625 magnetic states | 85 zero-field states |
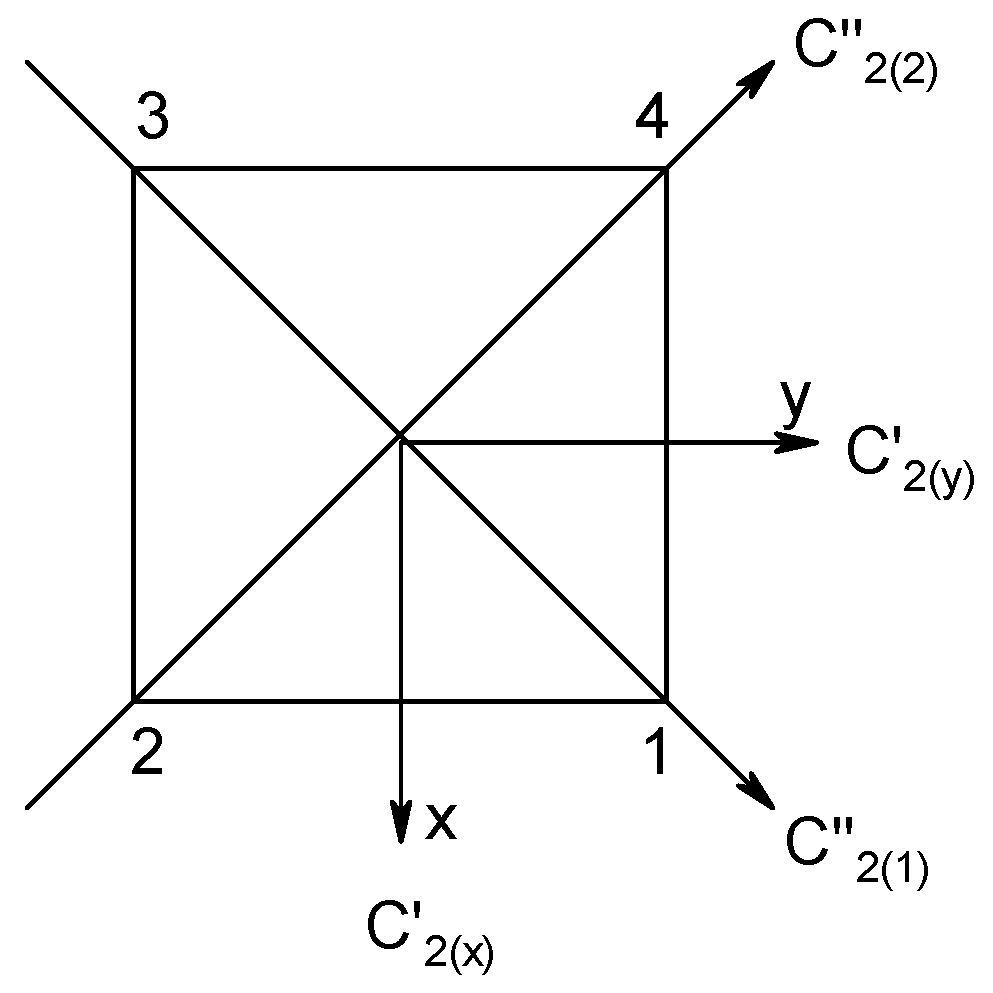
| Symmetry Operation | E | C2(z) | C2(x) | C2(y) |
|---|---|---|---|---|
| Permutation | O(12345678) | O(21436587) | O(34128765) | O(43217856) |
| Coupling of centers | <1,2,12> | <2,1,12> | <3,4,34> | <4,3,34> |
| <3,4,34> | <4,3,34> | <1,2,12> | <2,1,12> | |
| <5,6,56> | <6,5,56> | <8,7,78> | <7,8,78> | |
| <7,8,78> | <8,7,78> | <6,5,56> | <5,6,56> | |
| Coupling of diads | <12,34,1234> | <12,34,1234> | <34,12,1234> | <34,12,1234> |
| <56,78,5678> | <56,78,5678> | <78,56,5678> | <78,56,5678> | |
| Coupling of tetrads | <1234,5678,S> | <1234,5678,S> | <1234,5678,S> | <1234,5678,S> |
| S | A1 | B1 | B2 | B3 | Total Number |
|---|---|---|---|---|---|
| 0 | 776 | 630 | 630 | 630 | 2666 |
| 1 | 1820 | 1960 | 1960 | 1960 | 7700 |
| 2 | 3080 | 2940 | 2940 | 2940 | 11,900 |
| 3 | 3625 | 3750 | 3750 | 3750 | 14,875 |
| 4 | 4201 | 4076 | 4076 | 4076 | 16,429 |
| 5 | 4066 | 4170 | 4170 | 4170 | 16,576 |
| 6 | 3958 | 3854 | 3854 | 3854 | 15,520 |
| 7 | 3340 | 3420 | 3420 | 3420 | 13,600 |
| 8 | 2860 | 2780 | 2780 | 2780 | 11,200 |
| 9 | 2128 | 2184 | 2184 | 2184 | 8680 |
| 10 | 1624 | 1568 | 1568 | 1568 | 6328 |
| 11 | 1057 | 1092 | 1092 | 1092 | 4333 |
| 12 | 721 | 686 | 686 | 686 | 2779 |
| 13 | 400 | 420 | 420 | 420 | 1660 |
| 14 | 244 | 224 | 224 | 224 | 916 |
| 15 | 108 | 118 | 118 | 118 | 462 |
| 16 | 60 | 50 | 50 | 50 | 210 |
| 17 | 18 | 22 | 22 | 22 | 84 |
| 18 | 10 | 6 | 6 | 6 | 28 |
| 19 | 1 | 2 | 2 | 2 | 7 |
| 20 | 1 | 0 | 0 | 0 | 1 |
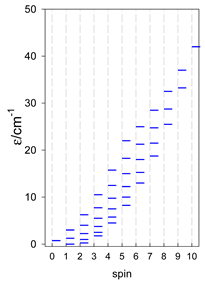
| catena-[A4], Jn(3×) | catena-[A5], Jn(4×) | catena-[A6], Jn(5×) |
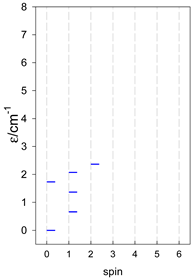 | 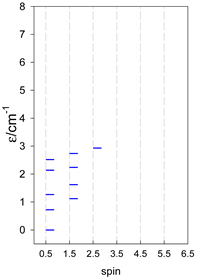 | 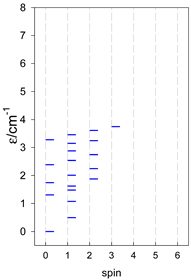 |
| catena-[A7], Jn(6×) | catena-[A8], Jn(7×) | catena-[A9], Jn(8×) |
 | 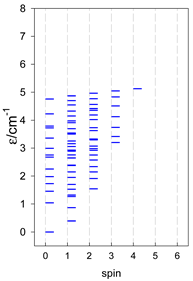 | 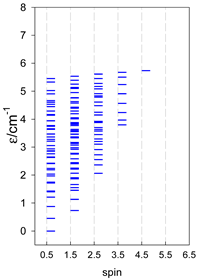 |
| catena-[A10], Jn(9×) | catena-[A11], Jn(10×) | catena-[A12], Jn(11×) |
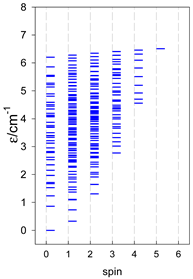 | 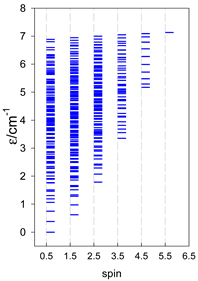 | 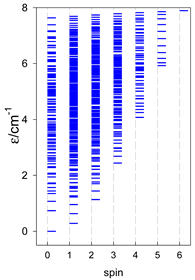 |
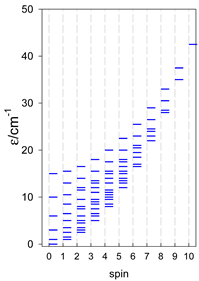
| catena-[A4], Jn(3×) | catena-[A5], Jn(4×) | catena-[A6], Jn(5×) |
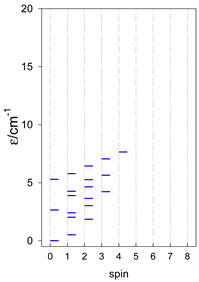 | 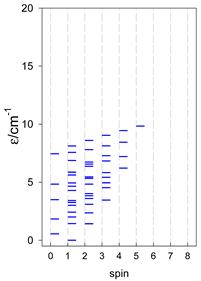 | 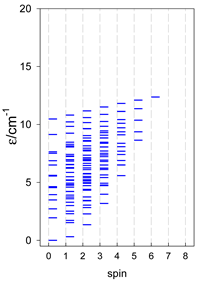 |
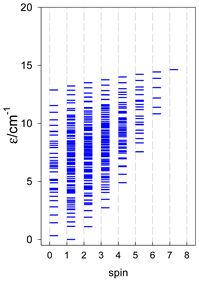
| catena-[A7], Jn(6×) | catena-[A8], Jn(7×) | catena-[A9], Jn(8×) |
 | 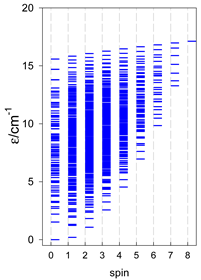 | 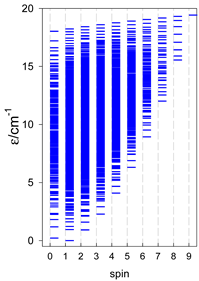 |
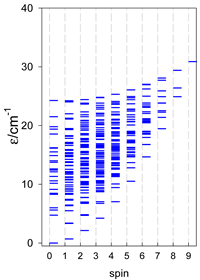
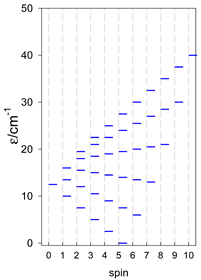
| catena-[A4], s = 3/2, Jn(3×) | catena-[A4], s = 2, Jn(3×) | catena-[A4], s = 5/2, Jn(3×) |
 |  | 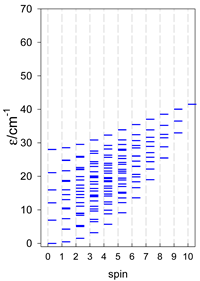 |
| catena-[A5], s = 3/2, Jn(4×) | catena-[A5], s = 2, Jn(4×) | catena-[A5], s = 5/2, Jn(4×) |
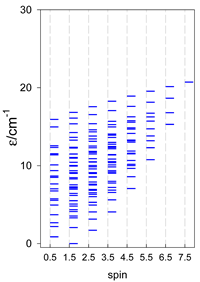 |  | 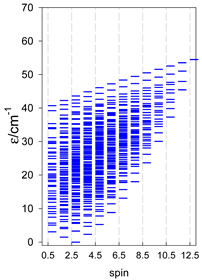 |
| catena-[A6], s = 3/2, Jn(5×) | catena-[A6], s = 2, Jn(5×) | catena-[A6], s = 5/2, Jn(5×) |
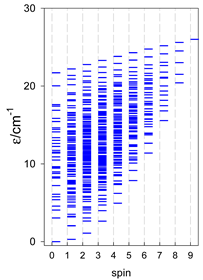 | 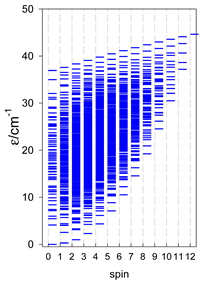 | 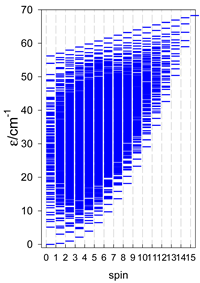 |
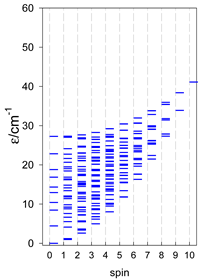
| cyclo-[A4] | cyclo-[A5] | cyclo-[A6] |
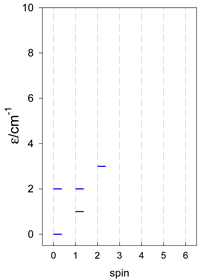 | 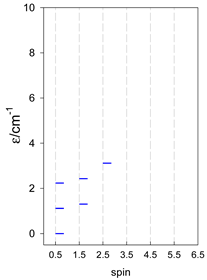 | 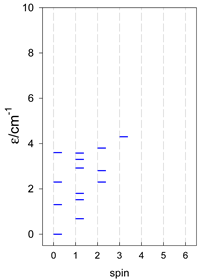 |
| cyclo-[A7] | cyclo-[A8] | cyclo-[A9] |
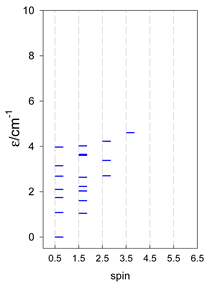 | 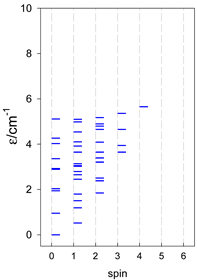 | 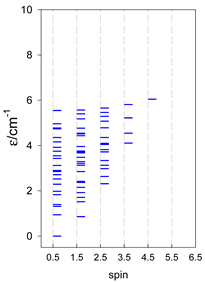 |
| cyclo-[A10] | cyclo-[A11] | cyclo-[A12] |
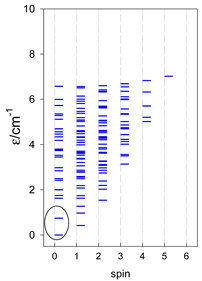 |  | 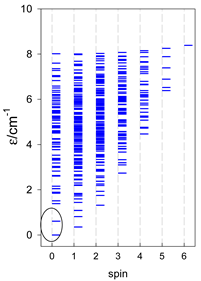 |
| cyclo-[A4] | cyclo-[A5] | cyclo-[A6] |
 | 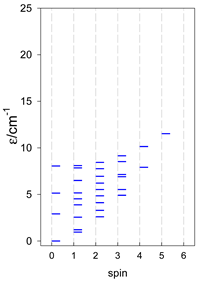 | 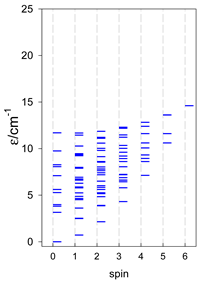 |
| cyclo-[A7] | cyclo-[A8] | cyclo-[A9] |
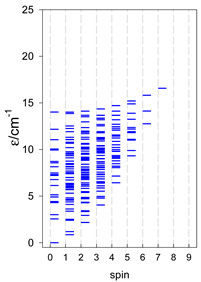 | 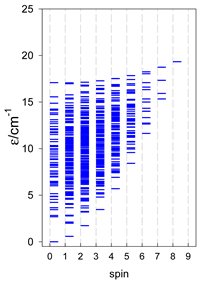 | 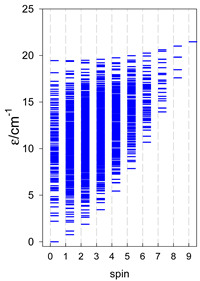 |
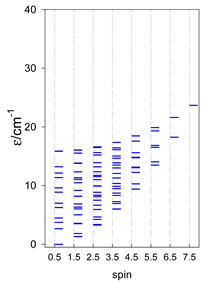
| cyclo-[A4], s = 3/2 | cyclo-[A4], s = 2 | cyclo-[A4], s = 5/2 |
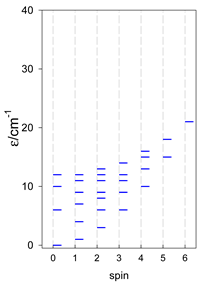 | 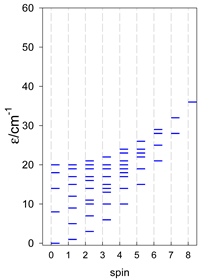 | 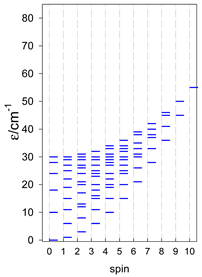 |
| cyclo-[A5], s = 3/2 | cyclo-[A5], s = 2 | cyclo-[A5], s = 5/2 |
 |  |  |
| cyclo-[A6], s = 3/2 | cyclo-[A6], s = 2 | cyclo-[A6], s = 5/2 |
 |  |  |
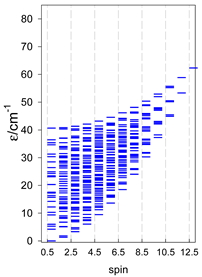
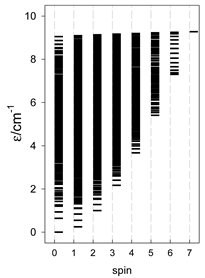
| Catena-[A13], S0 = 1/2 (1×) | n(S) = 429, 572, 429, 208, 65, 12, 1 a | cyclo-[A13], S0 = 1/2 (2×) |
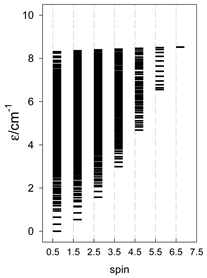 |  |  |
| catena-[A14], S0 = 0 (1×) | n(S) = 429, 1001, 1001, 637, 273, 77, 13, 1 | cyclo-[A14], S0 = 0 (1×) |
 | 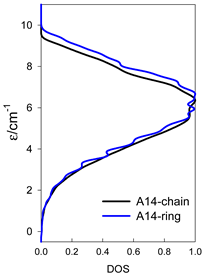 | 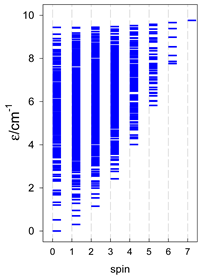 |
| catena-[A15], S0 = 1/2 (1×) | n(S) = 1430, 2002, 1638, 910, 350, 90, 14, 1 | cyclo-[A15], S0 = 1/2 (2×) |
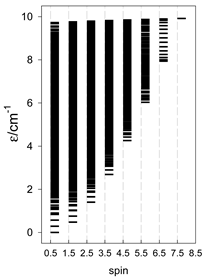 | 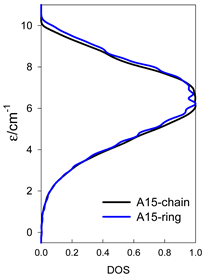 | 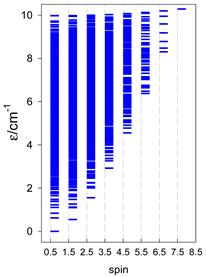 |
| Catena-[A9], S0 = 1 (1×) | n(S) = 603, 750, 672, 468, 258, 111, 36, 8, 1 | cyclo-[A9], S0 = 0 (1×) |
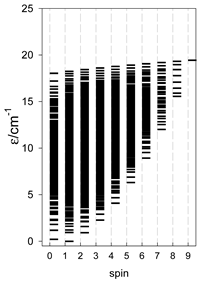 |  | 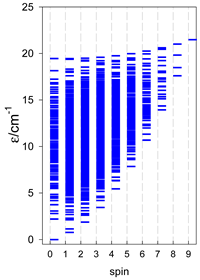 |
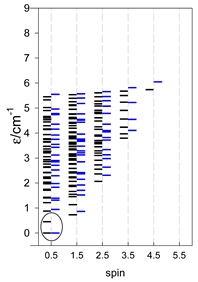
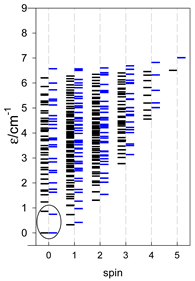
| catena-[A10], S0 = 0 (1×) | n(S) = 603, 1585, 2025, 1890, 1398, 837, 405, 155, 45, 9, 1 | cyclo-[A10], S0 = 0 (1×) |
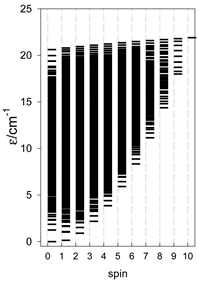 |  |  |
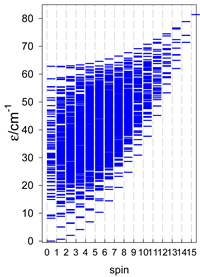
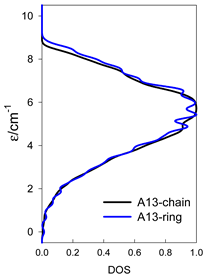
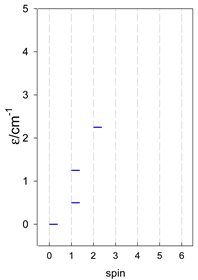
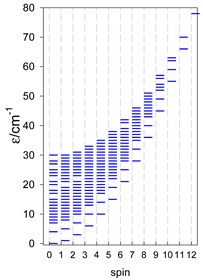
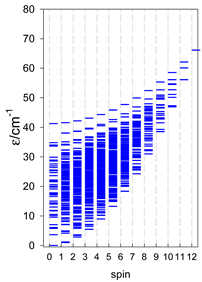
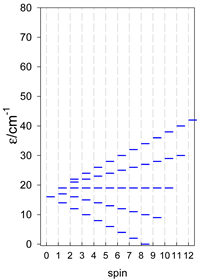
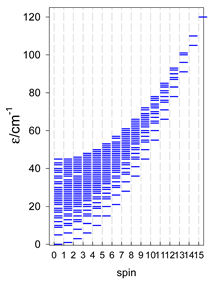
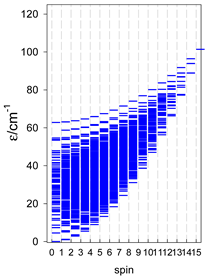
| A9 | A10 | A11 | A12 | A13 |
|---|---|---|---|---|
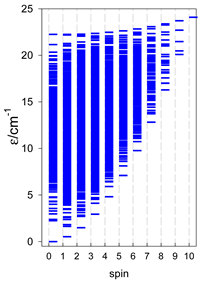
| Energy spectrum for a chain—aligned left (black); for a ring—aligned right (blue) a | ||||
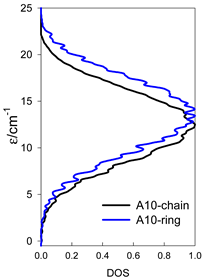
 |  | 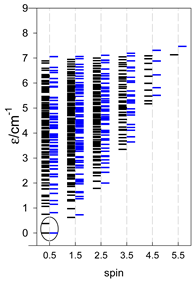 | 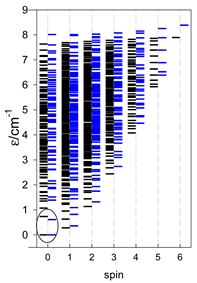 | 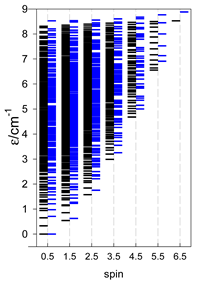 |
| Normalized density of states: for a chain—black; for a ring—blue | ||||
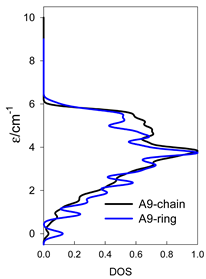 |  | 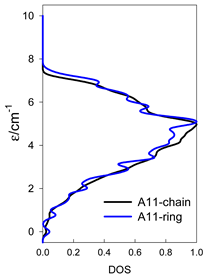 | 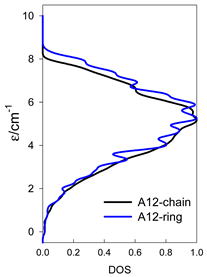 | 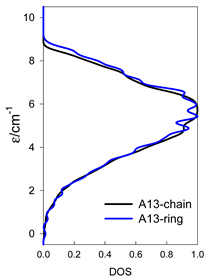 |
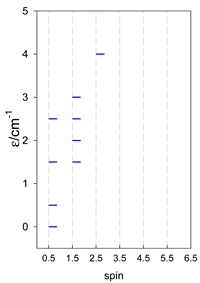
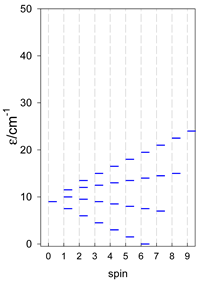
| [A3B], trigonal pyramid, s = 1/2Jb(3×), Ja(3×) = Jb/2, T1 | [A2B2], bisphenoid, s = 1/2Ja(2×), Jc(4×) = Ja/2, T2 | [A3B], star, s = 1/2, Jc(5×), s = 1/2 T3 |
 | 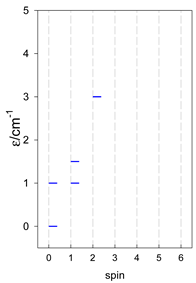 | 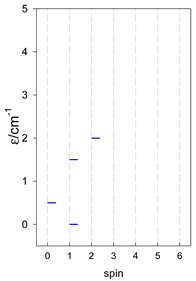 |
| [A3B], trigonal pyramid, s = 1 | [A2B2], bisphenoid, s = 1 | [A3B], star, s = 1 |
 | 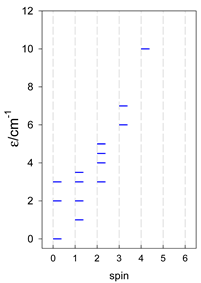 | 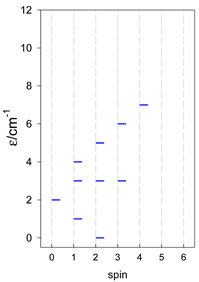 |
| [A3B], trigonal pyramid, s = 3/2 | [A2B2], bisphenoid, s = 3/2 | [A3B], star, s = 3/2 |
 |  |  |
| [A3B], trigonal pyramid, s = 2 | [A2B2], bisphenoid, s = 2 | [A3B], star, s = 2 |
 |  |  |
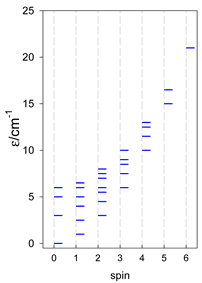
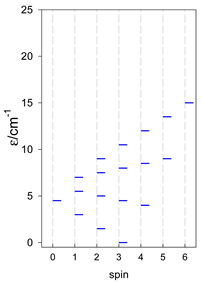
| [A3B], trigonal pyramid, s = 5/2 | [A2B2], bisphenoid, s = 5/2 | [A3B], star, s = 5/2 |
 |  |  |
| Topological matrices that define pair interactions of the centers: | ||
| [A4B], tetragonal pyramid, s = 1/2 Jb(4×), Ja(4×), Jt(2×) = 0, T1 | [A3B2], trigonal bipyramid, s = 1/2 Jb(3×), Ja(6×), Jt(1×) = 0, T2 | [A4B], star, s = 1/2 Jc(4×), T3 |
 |  | 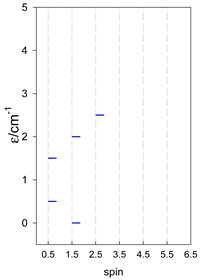 |
| [A4B], tetragonal pyramid, s = 1 | [A3B2], trigonal bipyramid, s = 1 | [A4B], star, s = 1 |
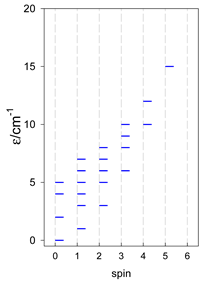 | 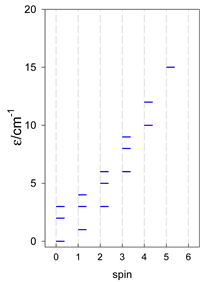 | 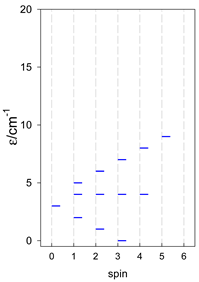 |
| [A4B], tetragonal pyramid, s = 3/2 | [A3B2], trigonal bipyramid, s = 3/2 | [A4B], star, s = 3/2 |
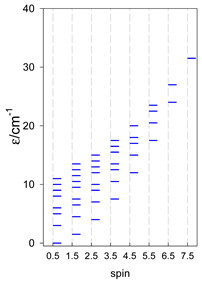 | 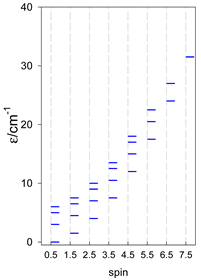 | 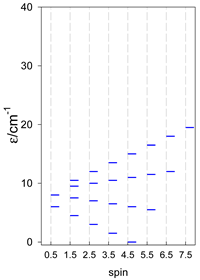 |
| [A4B], tetragonal pyramid, s = 2 | [A3B2], trigonal bipyramid, s = 2 | [A4B], star, s = 2 |
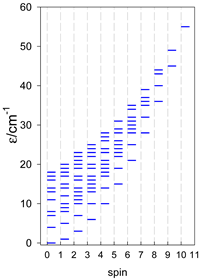 | 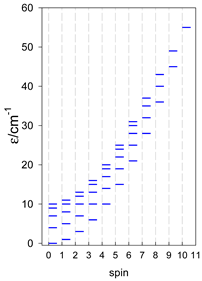 | 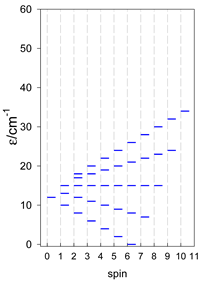 |
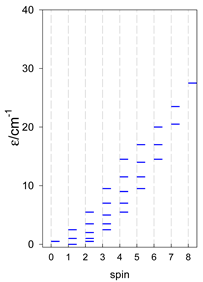
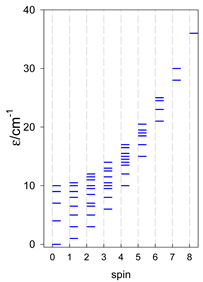
| [A4B], tetragonal pyramid, s = 5/2 | [A3B2], trigonal bipyramid, s = 5/2 | [A4B], star, s = 5/2 |
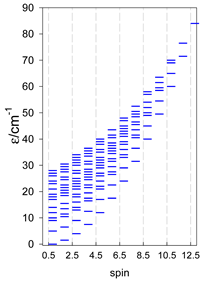 |  | 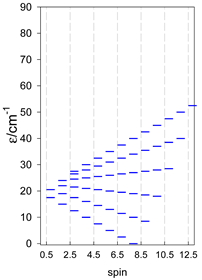 |
| Topological matrices that define pair interactions of the centers: | ||
| [A6] octahedron, s = 1/2 Jc(12×), Jt(3×) = 0, T1 | A6, trigonal prism, s = 1/2 Jb(6×) = Ja(3×), Ja2(6×) = 0, T2 | A5B, star, s = 1/2, Jc(5×), T3 |
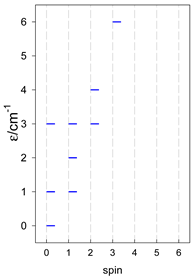 | 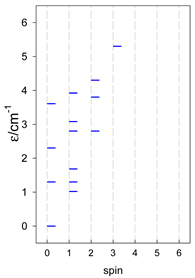 |  |
| [A6] octahedron, s = 1 | A6, trigonal prism, s = 1 | A5B, star, s = 1 |
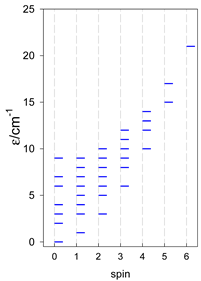 |  | 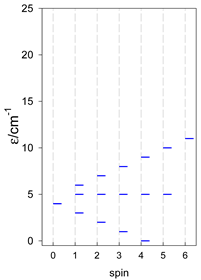 |
| [A6] octahedron, s = 3/2 | A6, trigonal prism, s = 3/2 | A5B, star, s = 3/2 |
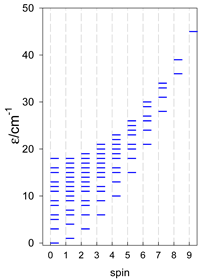 | 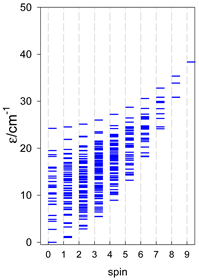 |  |
| [A6] octahedron, s = 2 | A6, trigonal prism, s = 2 | A5B, star, s = 2 |
 |  |  |
| [A6] octahedron, s = 5/2 | A6, trigonal prism, s = 5/2 | A5B, star, s = 5/2 |
 |  |  |
| Topological matrices that define pair interactions of the centers: | ||
Trigonal antiprism T1a is equivalent to T1 when Jb(6×) = Je(6×), Jt(3×) = 0 | ||
| No | Core | K | M | Size of Blocks {Smin through Smax} a |
|---|---|---|---|---|
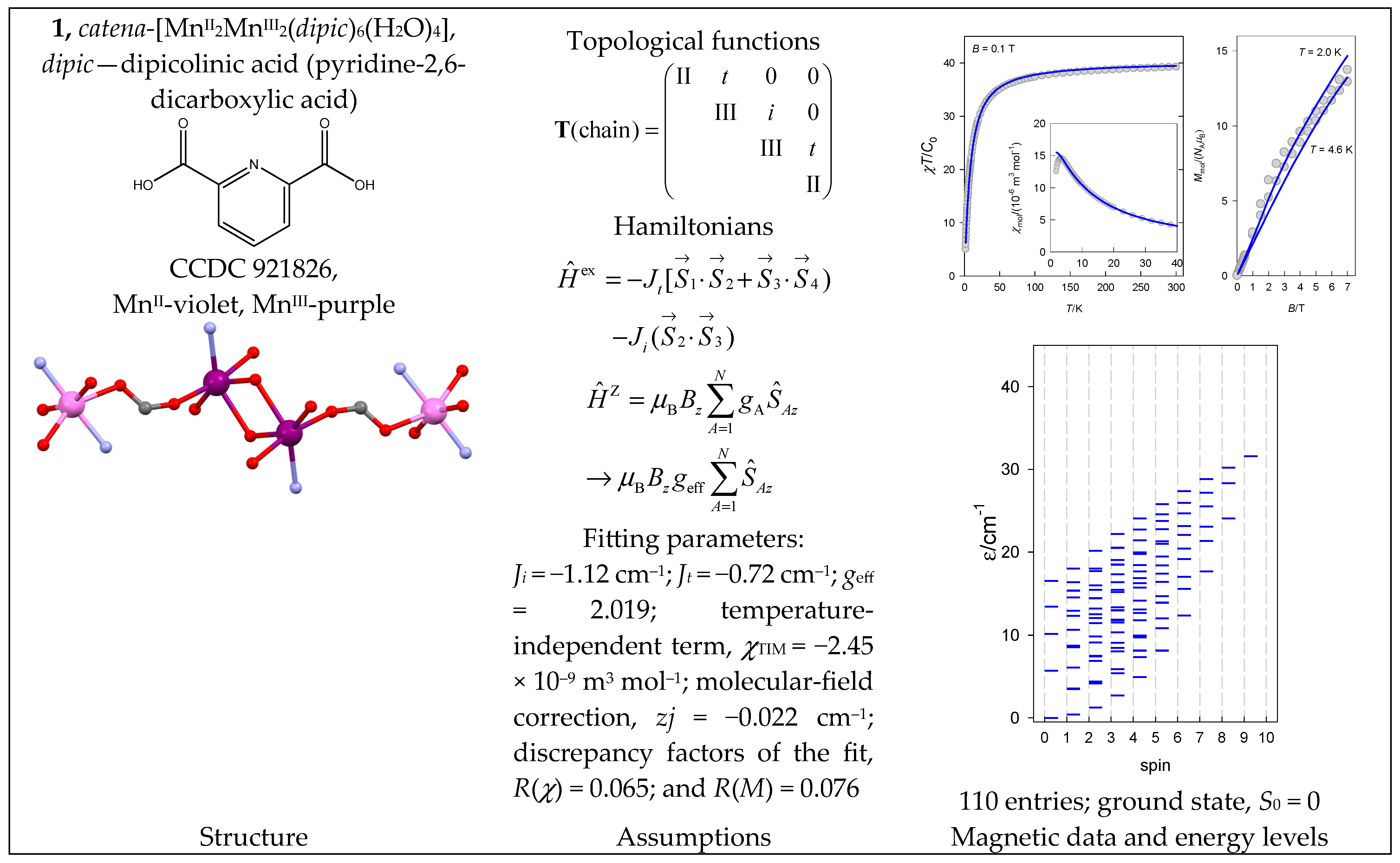
| 1, 2 | {MnII2MnIII2} | 62·52 = 900 | 110 | {S = 0–9}: 5, 13, 18, 29, 19, 15, 10, 6, 3, 1 |
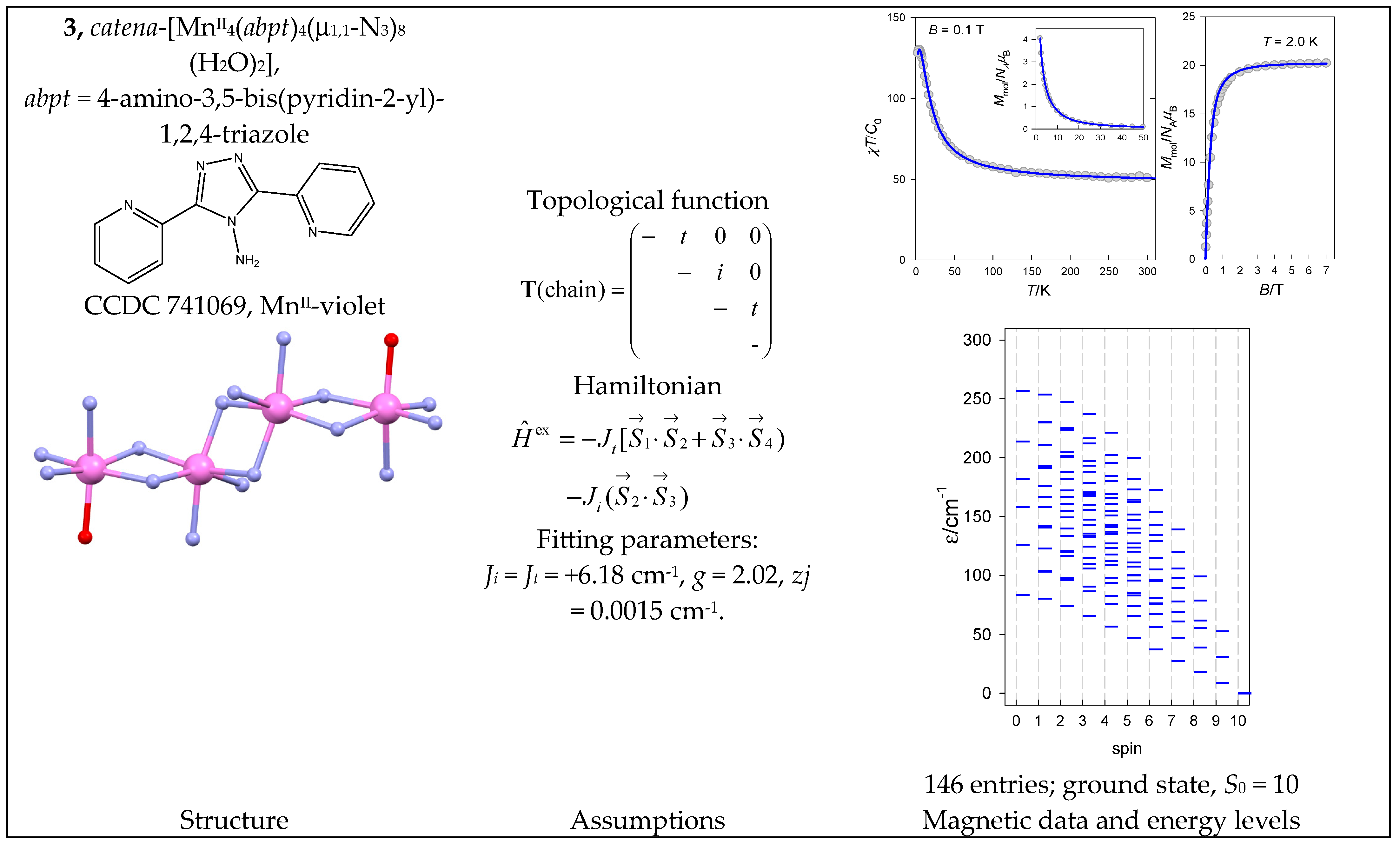
| 3 | {MnII4} | 64 = 1296 | 146 | {S = 0–10}: 6, 15, 21, 24, 24, 21, 15, 10, 6, 3, 1 |
| 4 | {MnII3CrIII4} | 6344 = 55,296 | 5737 | {S =1/2–27/2}: 326, 661, 852, 915, 862, 726, 550, 375, 228, 122, 56, 21, 6, 1 |
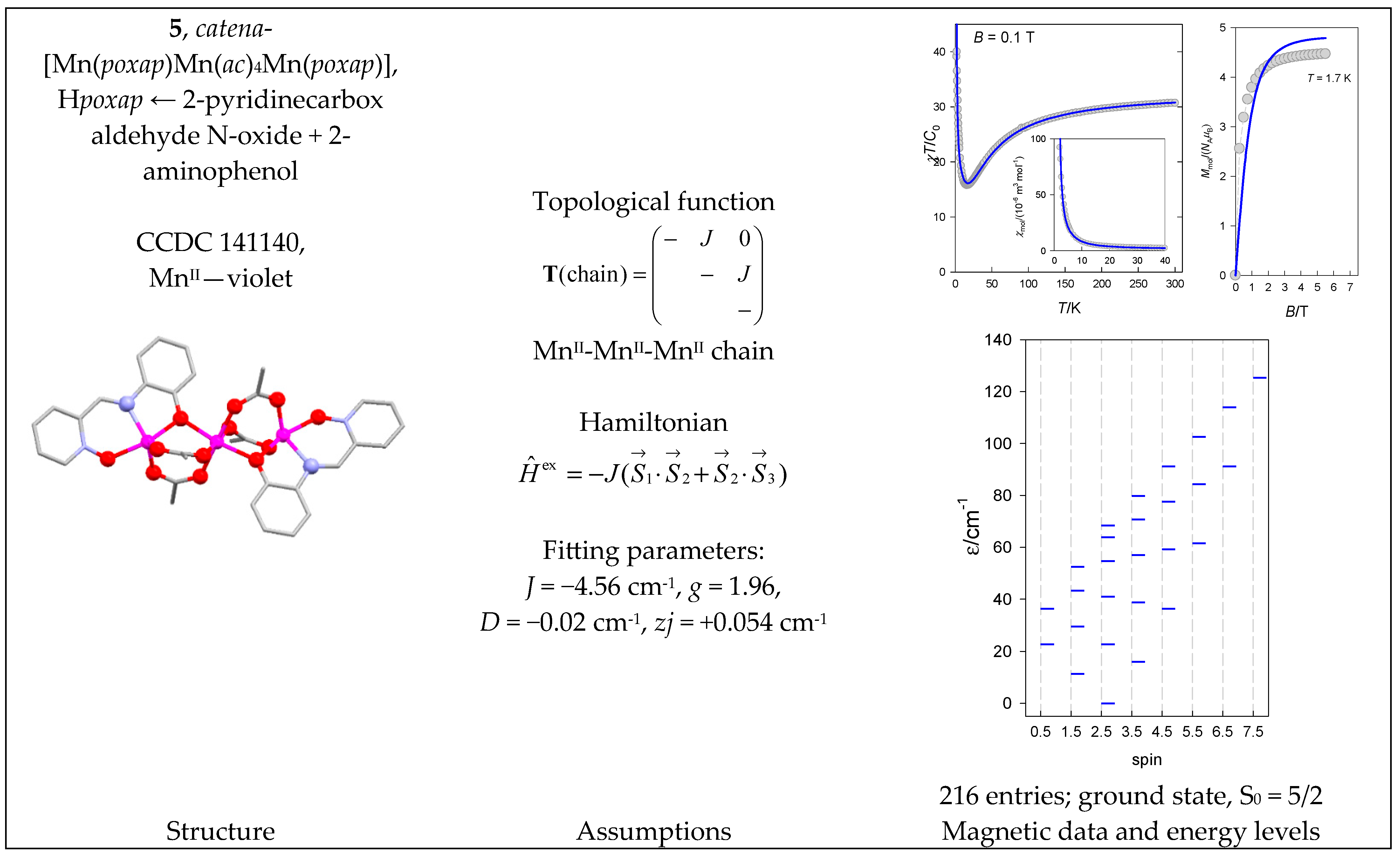
| 5 | {MnII3} | 63 = 216 | 216 | {S =1/2–15/2}: 2, 4, 6, 5, 4, 3, 2, 1 |
| 6 | {MnIII8} | 58 = 390,625 | 38,165 | {S = 0–16}: 1085, 3080, 4600, 5460, 5620, 5180, 4340, 3325, 1492, 868, 454, 210, 84, 28, 7, 1 |
| 7 | {FeIII4MnIII4} | 64·54 = 810,000 | 71,346 | {S = 0–18}: 1650, 4735, 7221, 8844, 9500, 9250, 8290, 6890, 5326, 3829, 2555, 1576, 892, 458, 210, 84, 28, 7, 1 |
| 8 | {FeIII6CoIII6} | 66 = 46,656 | 4332 | {S = 0–15}: 111, 315, 475, 575, 609, 581, 505, 405, 300, 204, 126, 70, 35, 15, 5, 1 |
| 9, 10 | {FeIII6FeII} | 66 = 46,656 | 4332 | {S = 0–15}: 111, 315, 475, 575, 609, 581, 505, 405, 300, 204, 126, 70, 35, 15, 5, 1 |
| 11 | {FeIII7} | 67 = 279,936 | 24,017 | {S = 1/2–35/2} 1050, 1974, 2666, 3060, 3150, 2975, 2604, 2121, 1610, 1140, 750, 455, 252, 126, 56, 21, 6, 1 |
| 12, 13 | {FeIII8}, {FeIII10} → {FeIII8} | 68 = 1,679,616 | 135,954 | {S = 0–20}: 2666, 7700, 11,900, 14,875, 16,429, 16,576, 15,520, 13,600, 11,200, 8680, 6328, 4333, 2779, 1660, 916, 462, 210, 84, 28, 7, 1 |
| 14 | {CoII6CoIII} | 46 = 4096 | 580 | {S = 0–9}: 34, 90, 120, 120, 96, 64, 35, 15, 5, 1 |
| 15 | {CoII11CoIII2} → {CoII7} | 47 = 16,384 | 2128 | {S = 1/2–21/2}: 210, 364, 426, 400, 315, 210, 119, 56, 21, 6, 1 |
| 16 | {CoII9CoIII3} | 49 = 262,144 | 30,276 | {S = 1/2–27/2}: 2400, 4269, 5256, 5300, 4600, 3501, 2352, 1392, 720, 321, 120, 36, 8, 1 |
| 17 | {ErIII3} | 163 = 4096 | 192 | {J = 1/2–45/2}: 2, 4, 6, 8, 10, 12, 14, 16, 15, 14, 13, 12, 11, 10, 9, 8, 7, 6, 5, 4, 3, 2, 1 |
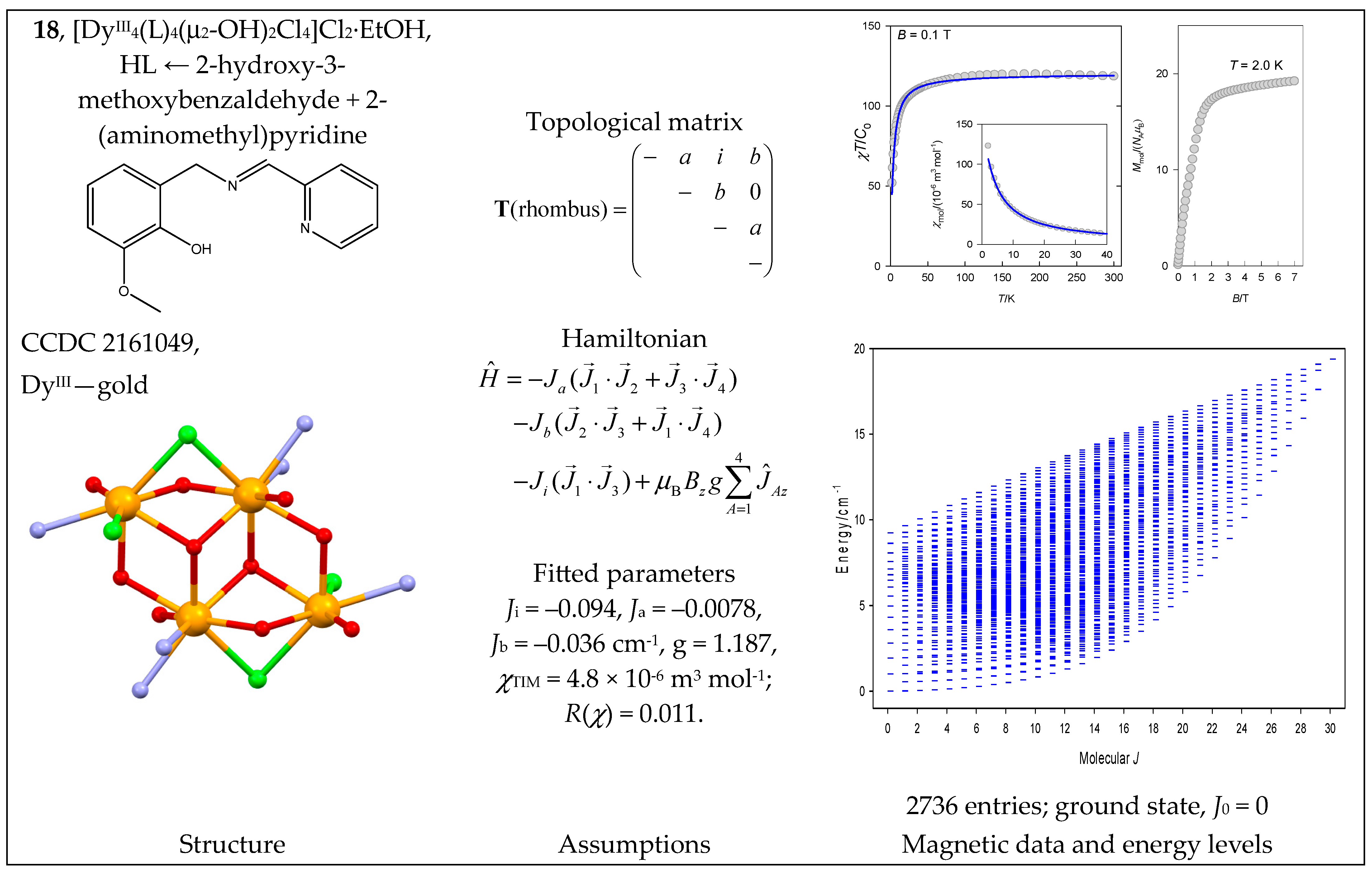
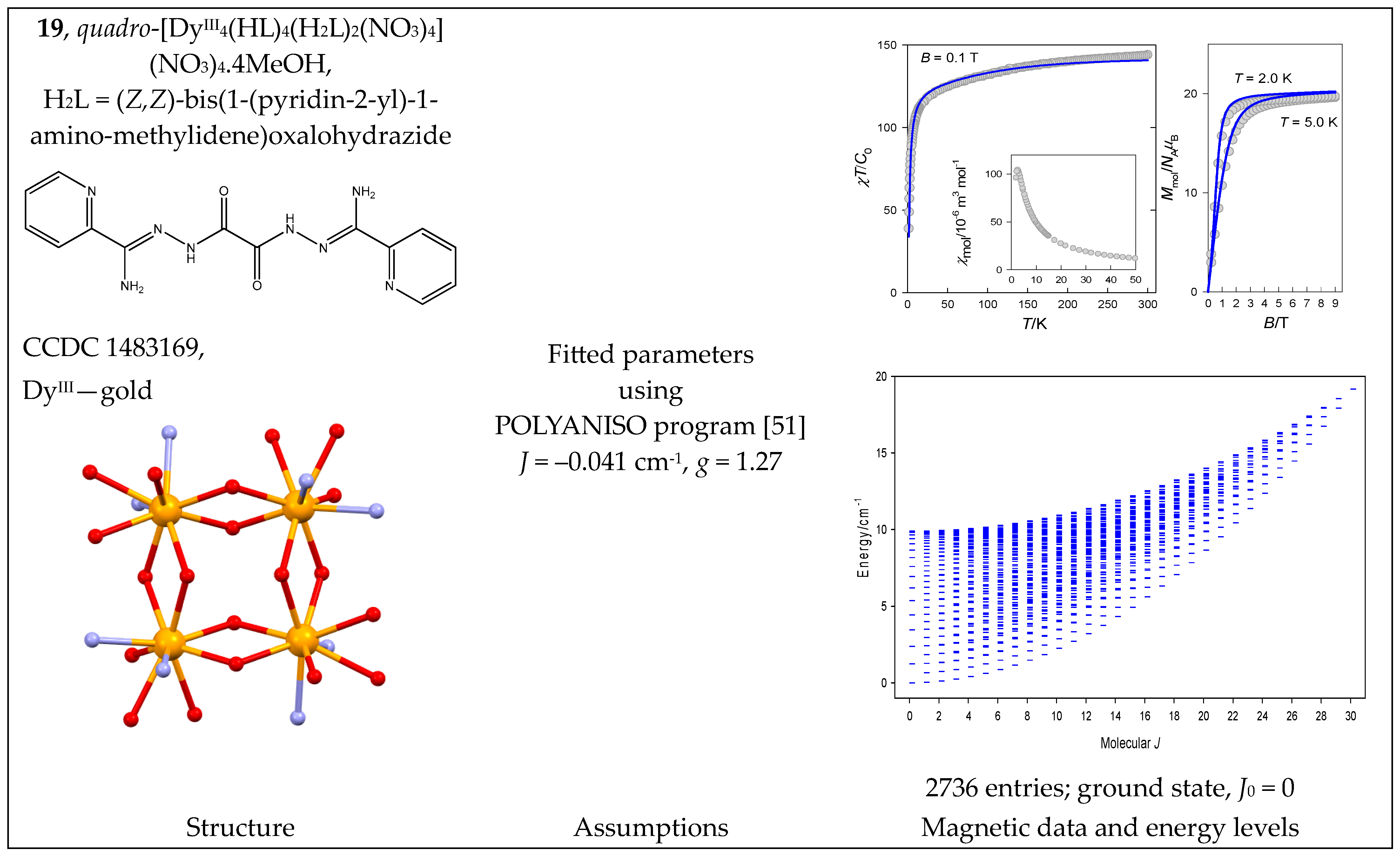
| 18, 19 | {DyIII4} | 164 = 65,536 | 2736 | {J = 0–30}: 16, 45, 71, 94, 114, 131, 145, 156, 164, 169, 171, 170, 166, 159, 149, 136, 120, 105, 91, 78, 66, 55, 45, 36, 28, 21, 15, 10, 6, 3, 1 |
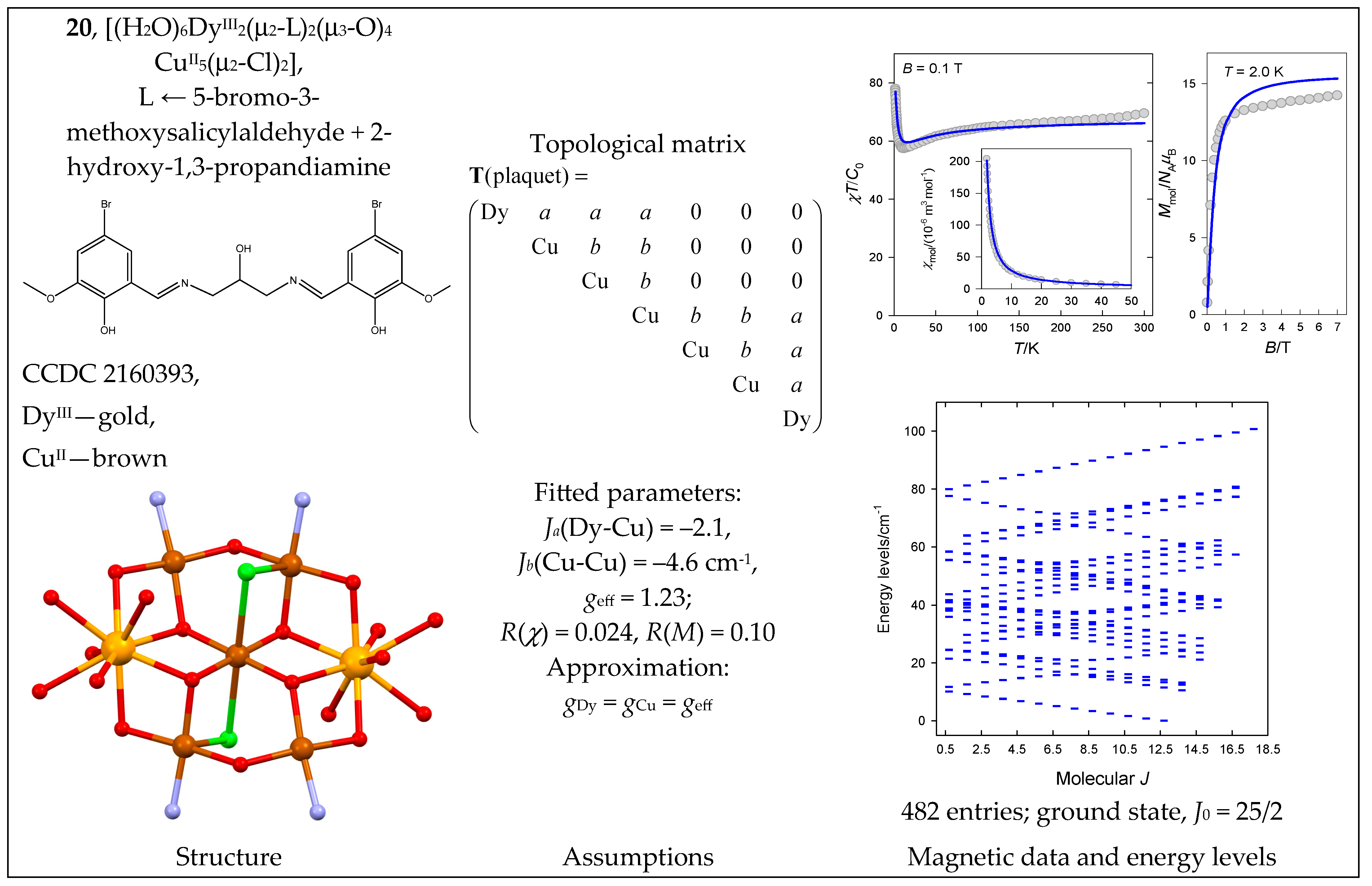
| 20 | {DyIII2CuII5} | 162·25 = 8192 | 482 | {J = 1/2–35/2}: 0, 30, 32, 32, 32, 32, 32, 32, 32, 32, 32, 32, 32, 31, 26, 16, 6, 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Boča, R.; Rajnák, C.; Titiš, J. Spin Symmetry in Polynuclear Exchange-Coupled Clusters. Magnetochemistry 2023, 9, 226. https://doi.org/10.3390/magnetochemistry9110226
Boča R, Rajnák C, Titiš J. Spin Symmetry in Polynuclear Exchange-Coupled Clusters. Magnetochemistry. 2023; 9(11):226. https://doi.org/10.3390/magnetochemistry9110226
Chicago/Turabian StyleBoča, Roman, Cyril Rajnák, and Ján Titiš. 2023. "Spin Symmetry in Polynuclear Exchange-Coupled Clusters" Magnetochemistry 9, no. 11: 226. https://doi.org/10.3390/magnetochemistry9110226
APA StyleBoča, R., Rajnák, C., & Titiš, J. (2023). Spin Symmetry in Polynuclear Exchange-Coupled Clusters. Magnetochemistry, 9(11), 226. https://doi.org/10.3390/magnetochemistry9110226








