Heat Pipe Embedded Battery Cooling System for Future Electric Vehicle
Abstract
1. Introduction
2. Experiments
2.1. System Description
2.2. Material Properties of Experimental Components
2.3. Experimental Setup
2.4. Assessment of Thermal Characteristics on the Experiment
2.4.1. Filling Ratio of the Working Fluid
2.4.2. Thermal Resistance
2.4.3. Wick Porosity Estimation
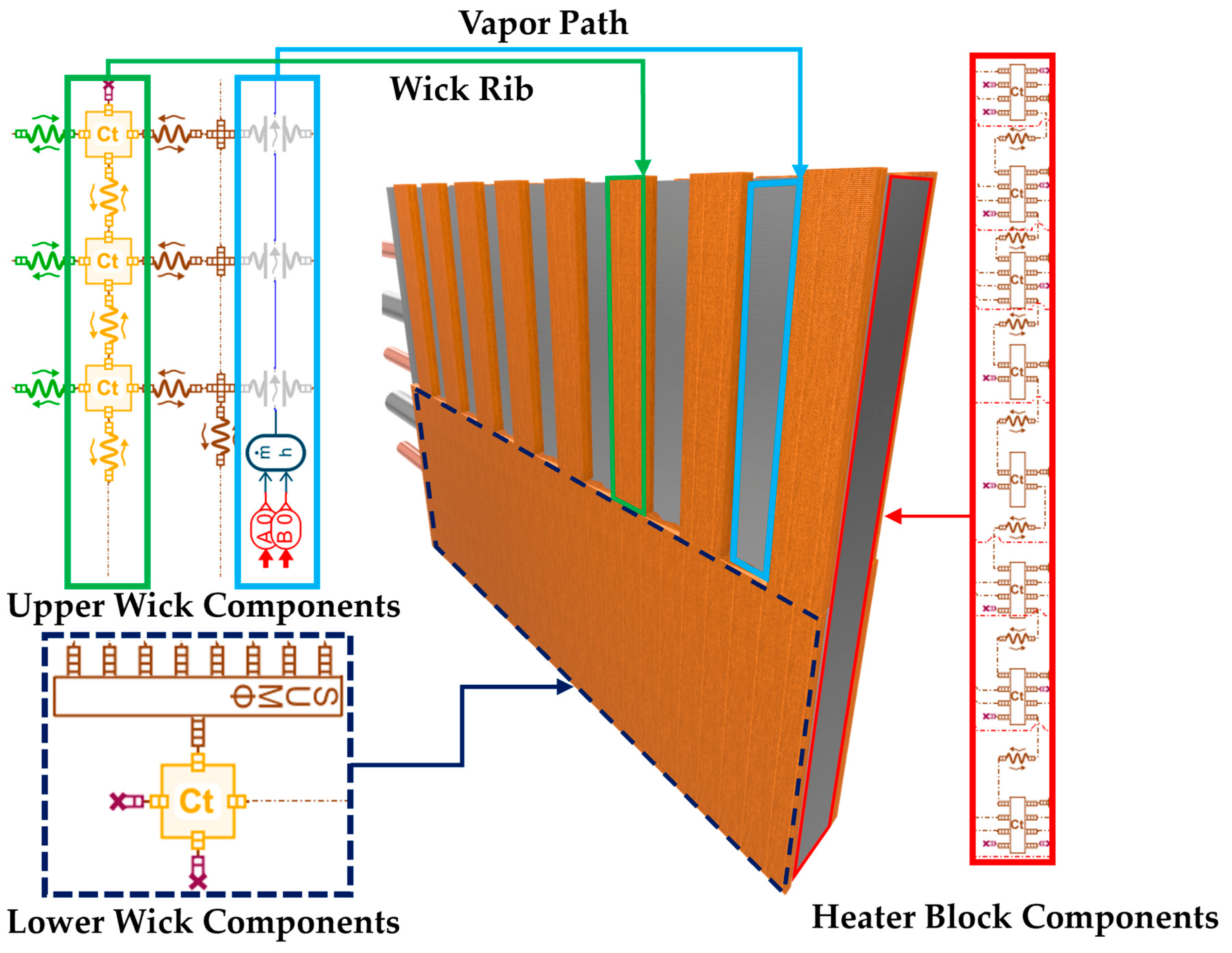
2.5. Numerical Analysis Strategy with 1-D Modeling Method
2.5.1. Saturation Level of the Wick
2.5.2. Effective Equations for the Wick Structure Saturated with Working Fluid
2.5.3. The 1-D Simulation Model for the Experiment
3. Result and Discussion
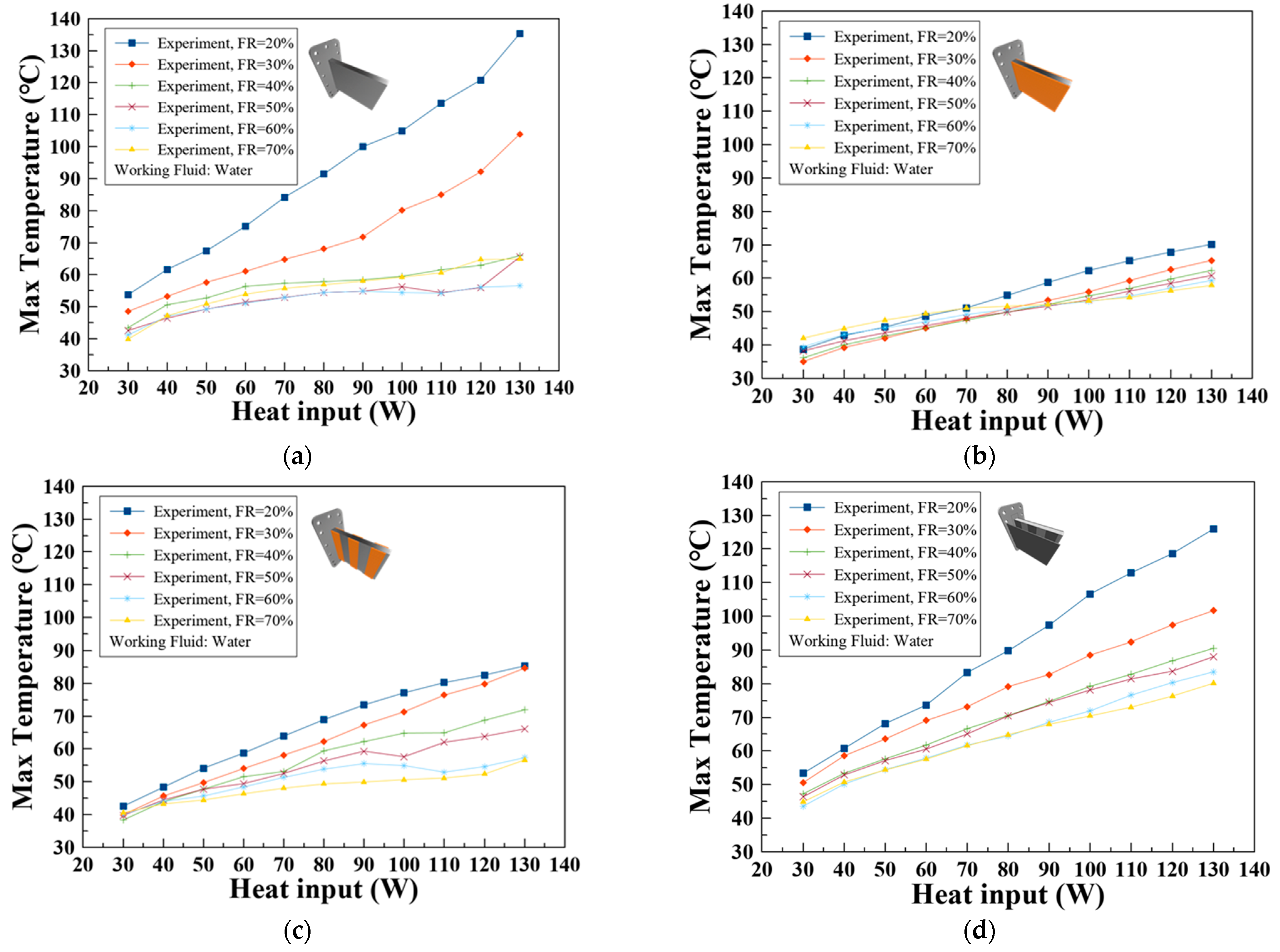
3.1. Effect of Various Wick Structures
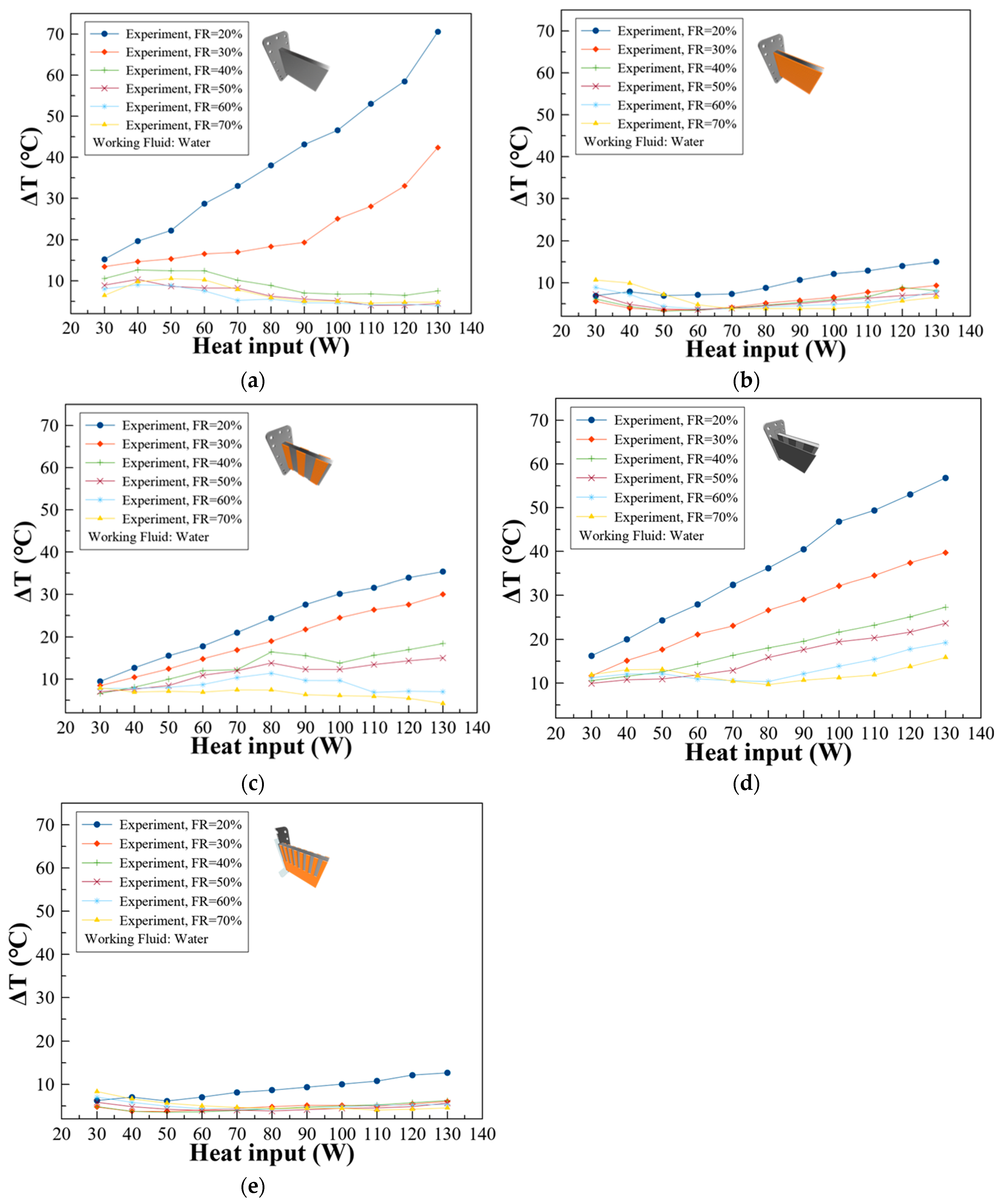
3.2. Temperature Difference of the Battery Surface with Various Types of Wicks
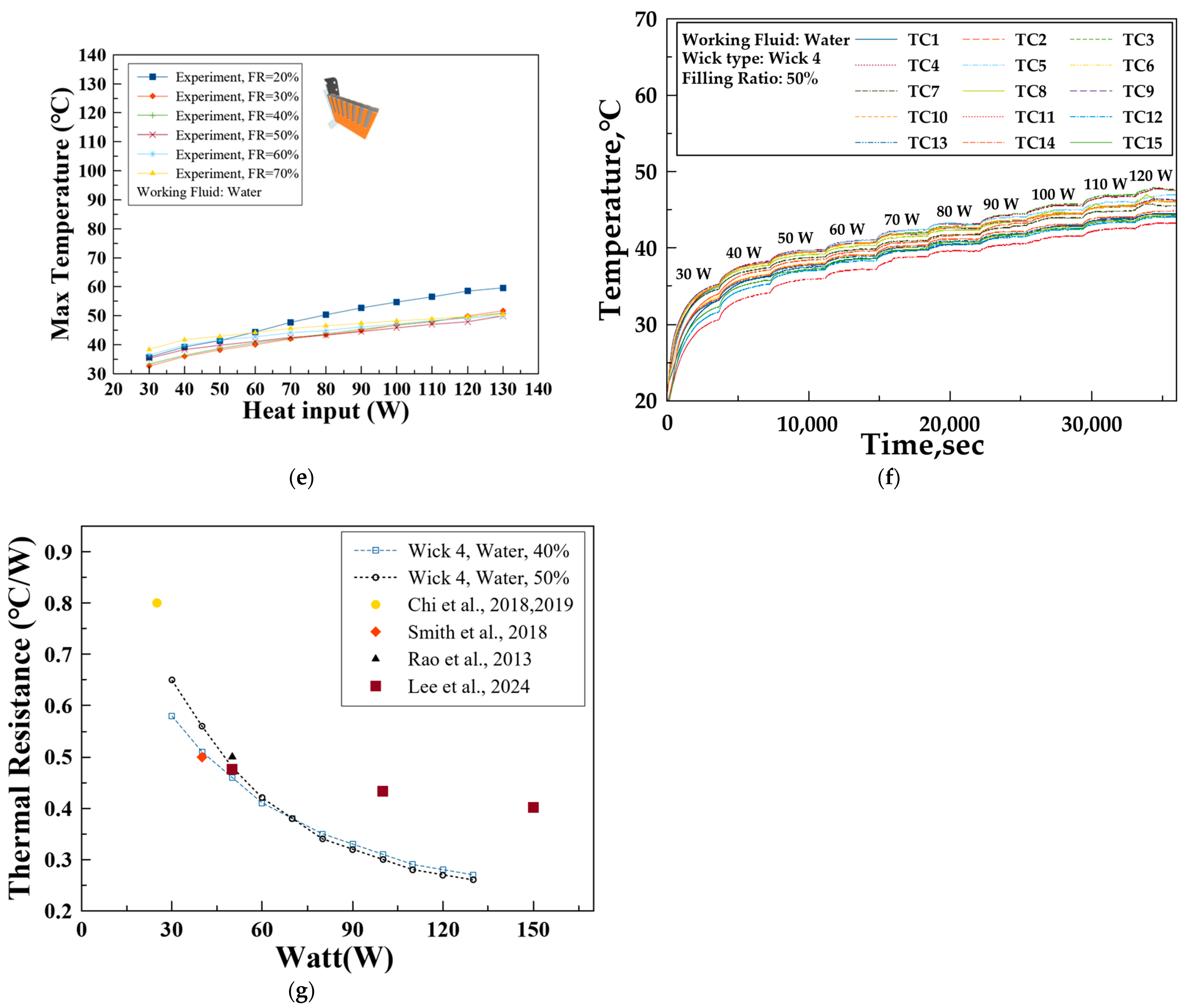
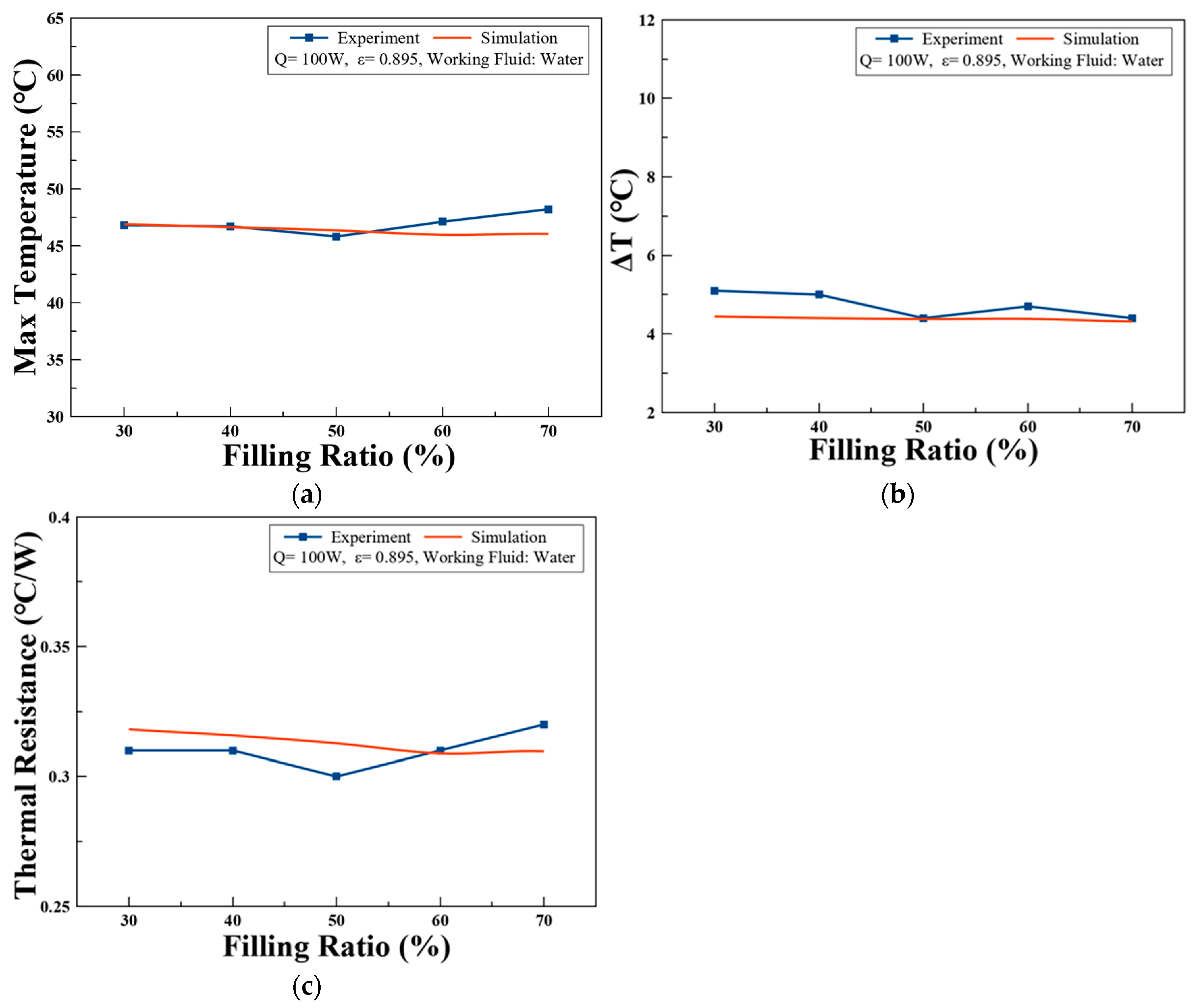
3.3. Simulation Model Validation
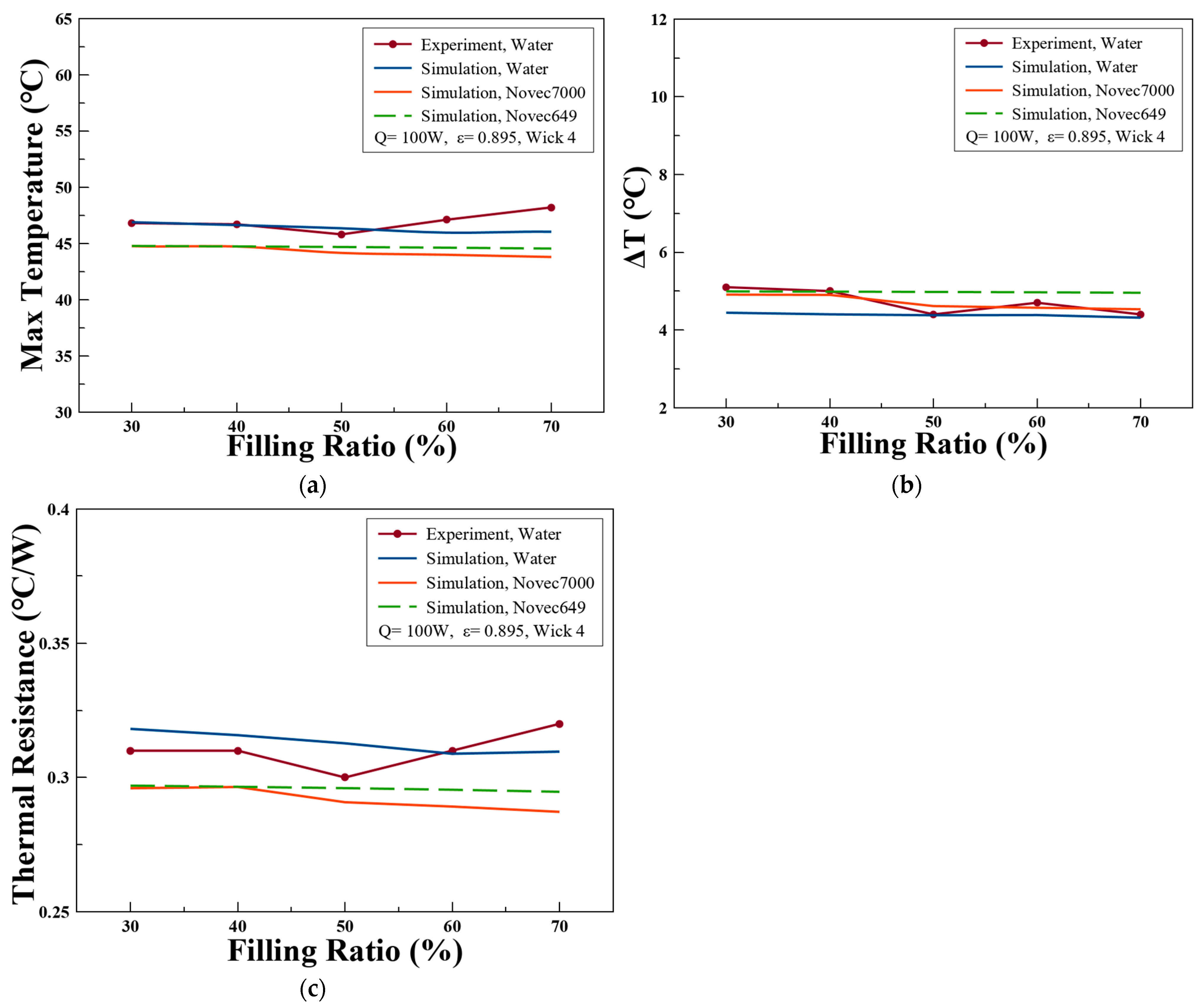
3.4. Simulated Predictions with Different Wick Porosities
3.5. Simulated Predictions with Different Working Fluids
4. Conclusions
- -
- At a 20% filling ratio with a heat input of 130 W, Wick 4 maintained a maximum temperature of 59.6 °C, demonstrating its capability to manage high thermal loads with minimal working fluid while keeping temperatures below the critical threshold of 60 °C.
- -
- The optimal thermal performance was observed at a 50% filling ratio, where the maximum temperature was 49.9 °C and the highest recorded temperature difference was 5.8 °C at a 130 W heat input, with all other temperature differences remaining below 5 °C, ensuring conditions favorable for LIB health.
- -
- As the best performance was observed at a 50% filling ratio, there is an advantage in the weight of the battery pack.
- -
- The effect of the wick in dissipating heat from the battery is demonstrated by the results, whose performance may vary with the types and shapes of the wicks. Wick 4 showed considerable effectiveness in promoting the heat exchange.
- -
- A 1-D multiphysics-based simulation model closely aligned with the experimental results for Wick 4, confirming the model’s reliability for further predictive studies.
- -
- This validation highlights the potential of the simulation model as a robust tool for investigating additional variables such as wick porosity and working fluid types.
- -
- Extended simulations provided valuable insights into the suitability of dielectric fluids as working fluids for the cooling system.
- -
- Recommendations for the selection of optimal material properties to enhance thermal performance were also derived from these analyses.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Abbreviations | |
| EV | Electric Vehicle |
| TR | Thermal Runaway |
| LIB | Li-ion Battery |
| SOC | State of Charge |
| DLC | Direct Liquid Cooling |
| CPCM | Composite Phase Change Material |
| TC | Thermocouple |
| FR | Filling Ratio |
| SL | Saturation Level |
| BMS | Battery Management System |
| SEI | Solid Electrolyte Interphase |
| LFP | Lithium Iron Phosphate |
| NMC | Nickel Manganese Cobalt |
| XPS | Extruded Polystyrene |
| STR | System Thermal Resistance |
| AMESim | Advanced Modeling Environment for Simulation |
| Nomenclature | |
| Vt | Internal total volume of device, m3 |
| Vf | Volume of fluid, m3 |
| Thermal resistance, W/m2 | |
| T | Static temperature, °C |
| Q | Total heat generation of the battery, W |
| V | Voltage, V |
| I | Current, A |
| UR | Uncertainty in thermal resistance, °C/W |
| UT | Uncertainty in thermocouple, °C |
| UQ | Uncertainty in heat input, W |
| S | Saturation level |
| Vfluid | Volume of fluid injected, m3 |
| VWick Saturated | Volume of fluid that wick can absorb, m3 |
| mfluid | Mass of working fluid, kg |
| mcompensation | Mass of fluid compensation, kg |
| k | Thermal conductivity, W/m·K |
| Cp | Specific heat capacity, J/kg·K |
| x | Quality |
| h | Convective heat transfer coefficient, W/m2·K |
| A | Area, m2 |
| f | Friction coefficient |
| Mass flow rate, kg/s | |
| Nu | Nusselt number, dimensionless |
| Pr | Prandtl number, dimensionless |
| Ra | Rayleigh number, dimensionless |
| Re | Reynolds number, dimensionless |
| Gr | Grashof number, dimensionless |
| Lc | Characteristic length, m |
| Vs | Average flow velocity, m/s |
| hv | Specific enthalpy of vapor, J/kg |
| hl | Specific enthalpy of liquid, J/kg |
| g | Gravitational acceleration, m/s2 |
| lv | Latent heat of fluid, J/kg |
| P | Static pressure, N/m2 |
| F | Correction factor, dimensionless |
| Greek | |
| Porosity | |
| Density of wick, kg/m3 | |
| Density of cellulose material, kg/m3 | |
| Density of working fluid, kg/m3 | |
| Density of liquid phase, kg/m3 | |
| Density of solid, kg/m3 | |
| Thermal expansion | |
| Dynamic viscosity, kg/m·s | |
| l | Liquid |
| v | Vapor |
| Subscripts | |
| HP | Heat pipe |
| e | Evaporator |
| c | Condenser |
| eff | Effective |
| s | Solid |
| l | Liquid |
| LO | Liquid only |
| VO | Vapor only |
| NcB | Nucleate boiling |
| Amb | Ambient |
| Wall | Wall |
| Surf | Surface |
| Red | Reduced |
| TP | Two-phase |
Appendix A
Library Components Used in the Simulation Model

References
- Dalkic-Melek, G.; Saltik, E.C.; Tuydes-Yaman, H. Electric Vehicle (EV) Market Penetration in Countries with Rising Motorization Rates. Int. J. Civ. Eng. 2025, 23, 461–480. [Google Scholar] [CrossRef]
- Ma, J.; Gong, Y.; Xu, W. Predicting User Preference for Innovative Features in Intelligent Connected Vehicles from a Cultural Perspective. World Electr. Veh. J. 2024, 15, 130. [Google Scholar] [CrossRef]
- Faizal, M.; Feng, S.Y.; Zureel, M.F.; Sinidol, B.E.; Wong, D.; Jian, G.K. A review on challenges and opportunities of electric vehicles (EVS). J. Mech. Eng. Res. Dev. 2019, 42, 130–137. [Google Scholar] [CrossRef]
- Funke, S.Á.; Sprei, F.; Gnann, T.; Plötz, P. How Much Charging Infrastructure Do Electric Vehicles Need? A Review of the Evidence and International Comparison. Transp. Res. Part Transp. Environ. 2019, 77, 224–242. [Google Scholar] [CrossRef]
- BYD Blade Battery|BYD Europe. Available online: https://www.byd.com/eu/technology/byd-blade-battery (accessed on 22 January 2025).
- Brand, M.; Gläser, S.; Geder, J.; Menacher, S.; Obpacher, S.; Jossen, A.; Quinger, D. Electrical Safety of Commercial Li-Ion Cells Based on NMC and NCA Technology Compared to LFP Technology. World Electr. Veh. J. 2013, 6, 572–580. [Google Scholar] [CrossRef]
- Sang, V.T.D.; Duong, Q.H.; Zhou, L.; Arranz, C.F.A. Electric Vehicle Battery Technologies and Capacity Prediction: A Comprehensive Literature Review of Trends and Influencing Factors. Batteries 2024, 10, 451. [Google Scholar] [CrossRef]
- Buidin, T.I.C.; Mariasiu, F. Battery Thermal Management Systems: Current Status and Design Approach of Cooling Technologies. Energies 2021, 14, 4879. [Google Scholar] [CrossRef]
- Wang, C.; Zhang, G.; Meng, L.; Li, X.; Situ, W.; Lv, Y.; Rao, M. Liquid Cooling Based on Thermal Silica Plate for Battery Thermal Management System. Int. J. Energy Res. 2017, 41, 2468–2479. [Google Scholar] [CrossRef]
- Li, A.; Weng, J.; Yuen, A.C.Y.; Wang, W.; Liu, H.; Lee, E.W.M.; Wang, J.; Kook, S.; Yeoh, G.H. Machine Learning Assisted Advanced Battery Thermal Management System: A State-of-the-Art Review. J. Energy Storage 2023, 60, 106688. [Google Scholar] [CrossRef]
- Shi, Y.; Ahmad, S.; Liu, H.; Lau, K.T.; Zhao, J. Optimization of Air-Cooling Technology for LiFePO4 Battery Pack Based on Deep Learning. J. Power Sources 2021, 497, 229894. [Google Scholar] [CrossRef]
- E, J.; Han, D.; Qiu, A.; Zhu, H.; Deng, Y.; Chen, J.; Zhao, X.; Zuo, W.; Wang, H.; Chen, J.; et al. Orthogonal Experimental Design of Liquid-Cooling Structure on the Cooling Effect of a Liquid-Cooled Battery Thermal Management System. Appl. Therm. Eng. 2018, 132, 508–520. [Google Scholar] [CrossRef]
- Mousavi, S.; Zadehkabir, A.; Siavashi, M.; Yang, X. An Improved Hybrid Thermal Management System for Prismatic Li-Ion Batteries Integrated with Mini-Channel and Phase Change Materials. Appl. Energy 2023, 334, 120643. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhao, R.; Zhao, S.; Zou, H.; Liu, Z.; Luo, X.; Liu, W. Performance Characteristics of a Two-Phase Pump-Assisted Loop Heat Pipe with Dual-Evaporators in Parallel. Therm. Sci. Eng. Prog. 2023, 38, 101657. [Google Scholar] [CrossRef]
- Lander, L.; Kallitsis, E.; Hales, A.; Edge, J.S.; Korre, A.; Offer, G. Cost and Carbon Footprint Reduction of Electric Vehicle Lithium-Ion Batteries through Efficient Thermal Management. Appl. Energy 2021, 289, 116737. [Google Scholar] [CrossRef]
- Chi, R.-G.; Chung, W.-S.; Rhi, S.-H. Thermal Characteristics of an Oscillating Heat Pipe Cooling System for Electric Vehicle Li-Ion Batteries. Energies 2018, 11, 655. [Google Scholar] [CrossRef]
- Chi, R.-G.; Rhi, S.-H. Oscillating Heat Pipe Cooling System of Electric Vehicle’s Li-Ion Batteries with Direct Contact Bottom Cooling Mode. Energies 2019, 12, 1698. [Google Scholar] [CrossRef]
- Wu, X.; Du, J.; Guo, H.; Qi, M.; Hu, F.; Shchurov, N.I. Boundary Conditions for Onboard Thermal-Management System of a Battery Pack under Ultrafast Charging. Energy 2022, 243, 123075. [Google Scholar] [CrossRef]
- Giammichele, L.; D’Alessandro, V.; Ricci, R.; Falone, M. Experimental Study of a Direct Immersion Liquid Cooling of a Li-Ion Battery for Electric Vehicles Applications. Int. J. Heat Technol. 2022, 40, 1–8. [Google Scholar] [CrossRef]
- Tan, X.; Lyu, P.; Fan, Y.; Rao, J.; Ouyang, K. Numerical investigation of the direct liquid cooling of a fast-charging lithium-ion battery pack in hydrofluoroether. Appl. Therm. Eng. 2021, 196, 117279. [Google Scholar] [CrossRef]
- Sun, P.; Bisschop, R.; Niu, H.; Huang, X. A Review of Battery Fires in Electric Vehicles. Fire Technol. 2020, 56, 1361–1410. [Google Scholar] [CrossRef]
- Chi, S.W. Heat Pipe Theory and Practice: A Sourcebook; McGraw-Hill Inc.: New York, NY, USA, 1976. [Google Scholar]
- Nishikawara, M.; Nagano, H. Optimization of Wick Shape in a Loop Heat Pipe for High Heat Transfer. Int. J. Heat Mass Transf. 2017, 104, 1083–1089. [Google Scholar] [CrossRef]
- Smith, J.; Singh, R.; Hinterberger, M.; Mochizuki, M. Battery Thermal Management System for Electric Vehicle Using Heat Pipes. Int. J. Therm. Sci. 2018, 134, 517–529. [Google Scholar] [CrossRef]
- Rao, Z. Experimental Investigation on Thermal Management of Electric Vehicle Battery with Heat Pipe. Energy Convers. Manag. 2013, 65, 92–97. [Google Scholar] [CrossRef]
- Burkitbayev, A.; Weragoda, D.M.; Ciampa, F.; Lo, K.H.; Tian, G. A Numerical and Experimental Investigation on a Gravity-Assisted Heat-Pipe-Based Battery Thermal Management System for a Cylindrical Battery. Batteries 2023, 9, 456. [Google Scholar] [CrossRef]
- Oh, I.-T.; Lee, J.-S.; Han, J.-S.; Lee, S.-W.; Kim, S.-J.; Rhi, S.-H. Li-Ion Battery Immersed Heat Pipe Cooling Technology for Electric Vehicles. Electronics 2023, 12, 4931. [Google Scholar] [CrossRef]
- Uetani, K.; Hatori, K. Thermal Conductivity Analysis and Applications of Nanocellulose Materials. Sci. Technol. Adv. Mater. 2017, 18, 877–892. [Google Scholar] [CrossRef]
- Mun, S.Y.; Lim, H.M.; Lee, D.J. Preparation and Thermal Properties of Polyacrylonitrile-Based Carbon Fiber–Silicon Carbide Core–Shell Hybrid. Thermochim. Acta 2015, 600, 62–66. [Google Scholar] [CrossRef]
- Flame retardant non-woven fabric NT PREOX 200. Available online: https://texfire.net/en/flame-retardant-fabrics/flame-retardant-nonwoven-fabric/non-woven-flame-retardant-nt-preox-200.html (accessed on 4 February 2025).
- Qi, C.; Hou, S.; Lu, J.; Xue, W.; Sun, K. Thermal Characteristics of Birch and Its Cellulose and Hemicelluloses Isolated by Alkaline Solution. Holzforschung 2020, 74, 1099–1112. [Google Scholar] [CrossRef]
- Abdulshaheed, A.A.; Wang, P.; Huang, G.; Zhao, Y.; Li, C. Filling Ratio Optimization for High-Performance Nanoengineered Copper-Water Heat Pipes. J. Therm. Sci. Eng. Appl. 2021, 13, 1–28. [Google Scholar] [CrossRef]
- Reay, D.; Kew, P.; Mcglen, R. Heat Pipes: Theory, Design and Applications, 6th ed.; Butterworth-Heinemann: Oxford, UK, 2013; pp. 1–251. [Google Scholar]
- Lee, J.-S.; Kim, S.-J.; Han, W.-S.; Rhi, S.-H. Anti-Gravity 3D Pulsating Heat Pipe for Cooling Electric Vehicle Batteries. Energies 2024, 17, 2283. [Google Scholar] [CrossRef]
- Ha, J.; Kim, J.; Jung, Y.; Yun, G.; Kim, D.-N.; Kim, H.-Y. Poro-Elasto-Capillary Wicking of Cellulose Sponges. Sci. Adv. 2018, 4, eaao7051. [Google Scholar] [CrossRef] [PubMed]
- Antlauf, M.; Boulanger, N.; Berglund, L.; Oksman, K.; Andersson, O. Thermal Conductivity of Cellulose Fibers in Different Size Scales and Densities. Biomacromolecules 2021, 22, 3800–3809. [Google Scholar] [CrossRef]
- Kantzas, A.; Bryan, J.; Taheri, S. Fundamentals of Fluid Flow in Porous Media; Special Core Analysis (SCAL) & Enhanced Oil Recovery (EOR) Laboratory: Calgary, AB, Canada, 2012. [Google Scholar]
- Siemens. Simcenter AMESim User Manual, SIMATIC Motion Control Library; Siemens: Munich, Germany, 2023; Available online: https://www.hmkdirect.com/downloads/simatic_-_all_about_motion_control_-_guide.pdf (accessed on 31 January 2025).
- Kapekov, A. Development of an Innovative Cooling Concept for Turbofan Engines. Master’s Thesis, KTH School of Industrial Engineering and Management, Stockholm, Switzerland, 2018. [Google Scholar]
- Holman, J.P. Heat Transfer, 10th ed.; McGraw-Hill Education: New York, NY, USA, 2010; ISBN 978-0-07-352936-3. [Google Scholar]
- Bibin, C.; Vijayaram, M.; Suriya, V.; Sai Ganesh, R.; Soundarraj, S. A Review on Thermal Issues in Li-Ion Battery and Recent Advancements in Battery Thermal Management System. Mater. Today Proc. 2020, 33, 116–128. [Google Scholar] [CrossRef]
- Kong, L.; Li, Y.; Feng, W. Strategies to Solve Lithium Battery Thermal Runaway: From Mechanism to Modification. Electrochem. Energy Rev. 2021, 4, 633–679. [Google Scholar] [CrossRef]
- Troxler, Y.; Wu, B.; Marinescu, M.; Yufit, V.; Patel, Y.; Marquis, A.J.; Brandon, N.P.; Offer, G.J. The Effect of Thermal Gradients on the Performance of Lithium-Ion Batteries. J. Power Sources 2014, 247, 1018–1025. [Google Scholar] [CrossRef]
- Galatro, D.; Al-Zareer, M. Thermal behavior of lithium-ion batteries: Aging, heat generation, thermal management and failure. Front. Heat Mass Transf. 2020, 14, 1–18. [Google Scholar] [CrossRef]
- Chen, J.-S.; Chou, J.-H. Cooling Performance of Flat Plate Heat Pipes with Different Liquid Filling Ratios. Int. J. Heat Mass Transf. 2014, 77, 874–882. [Google Scholar] [CrossRef]
- Lips, S.; Lefèvre, F.; Bonjour, J. Combined Effects of the Filling Ratio and the Vapour Space Thickness on the Performance of a Flat Plate Heat Pipe. Int. J. Heat Mass Transf. 2010, 53, 694–702. [Google Scholar] [CrossRef]
- Borkar, R.S.; Pachghare, P.R. Effect of working fluid, filling ratio and number of turns on pulsating heat pipe thermal performance. Front. Heat Pipes 2015, 6, 1–4. [Google Scholar] [CrossRef]
- Hwang, G.S.; Kaviany, M.; Anderson, W.G.; Zuo, J. Modulated Wick Heat Pipe. Int. J. Heat Mass Transf. 2007, 50, 1420–1434. [Google Scholar] [CrossRef]
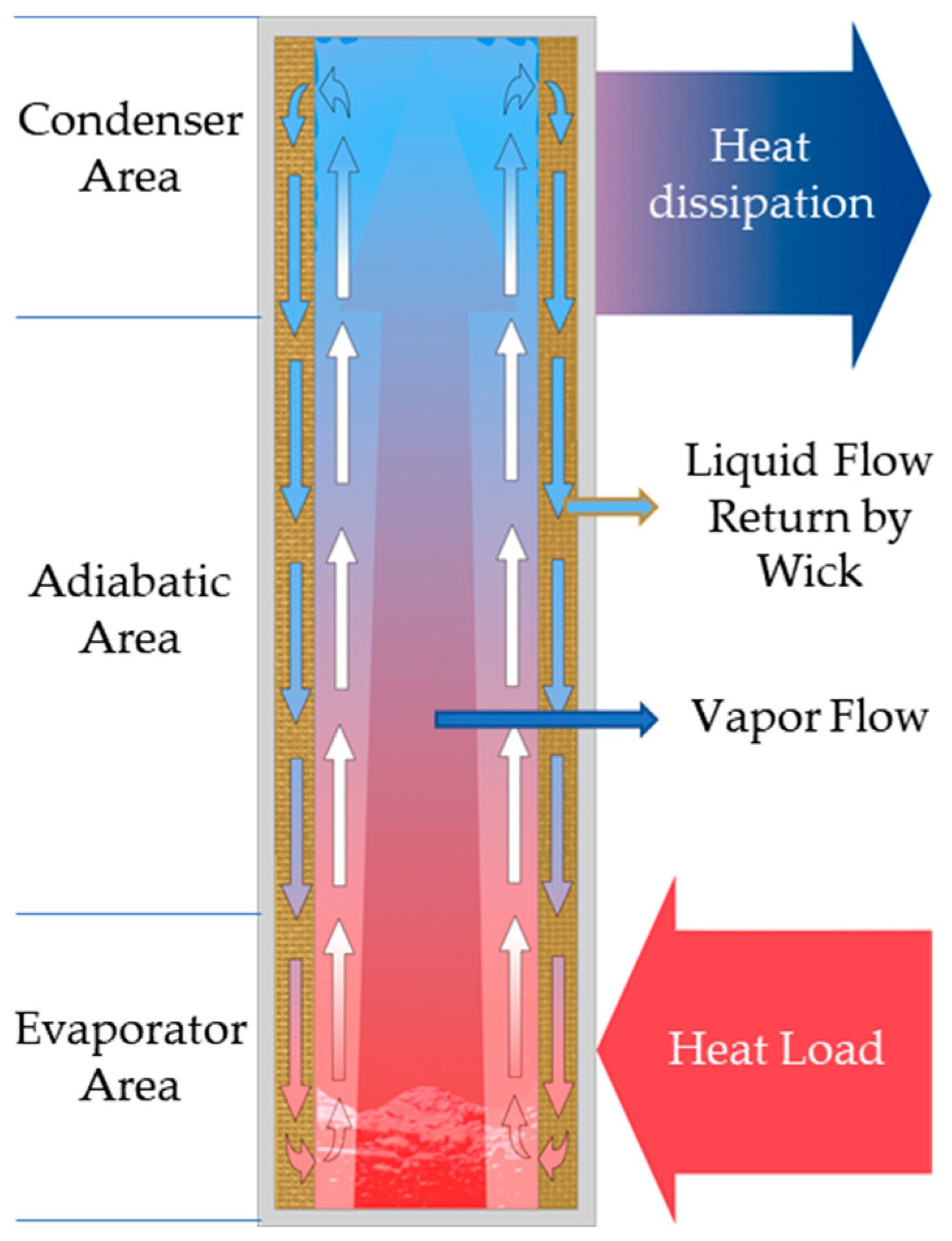
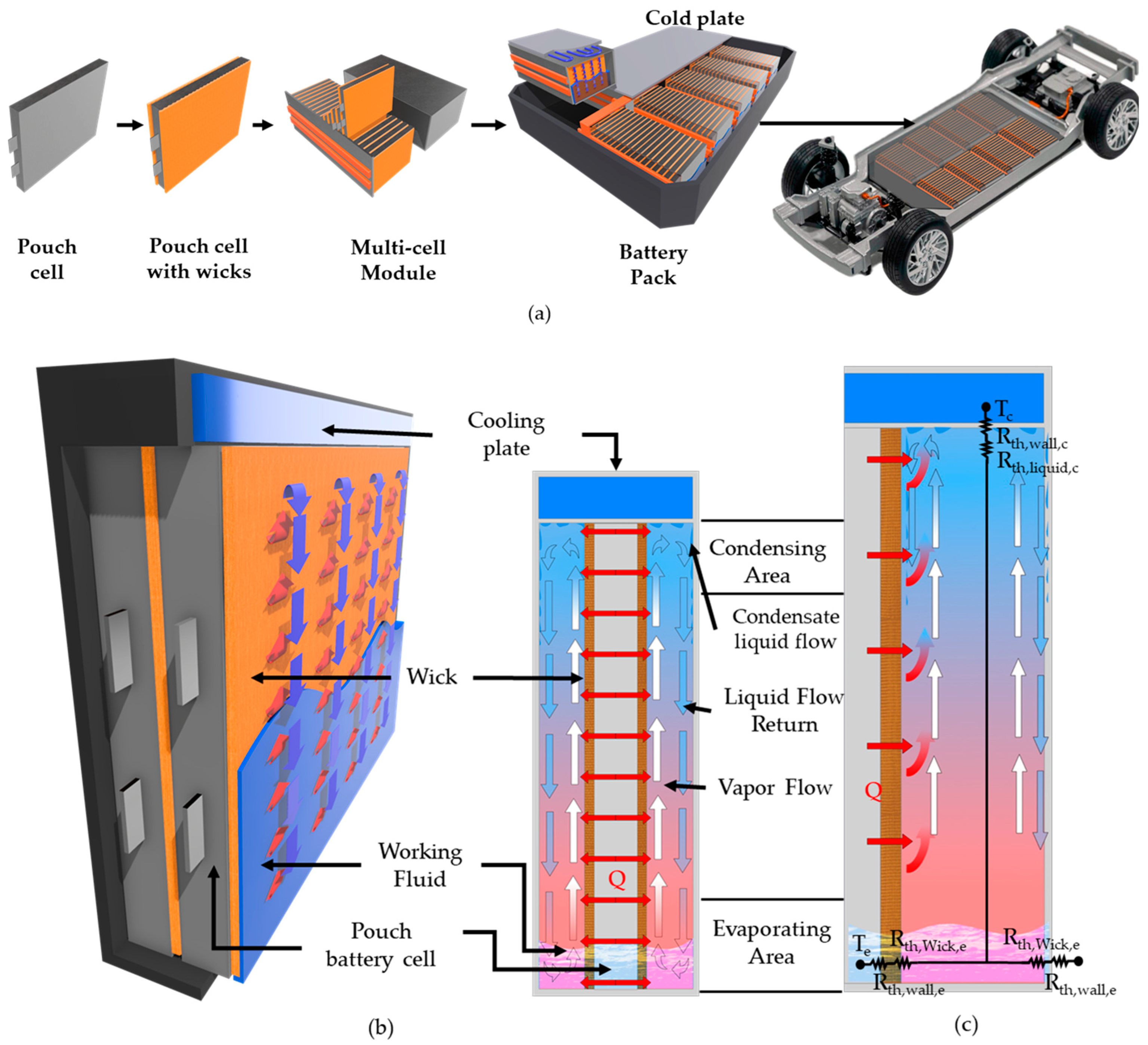



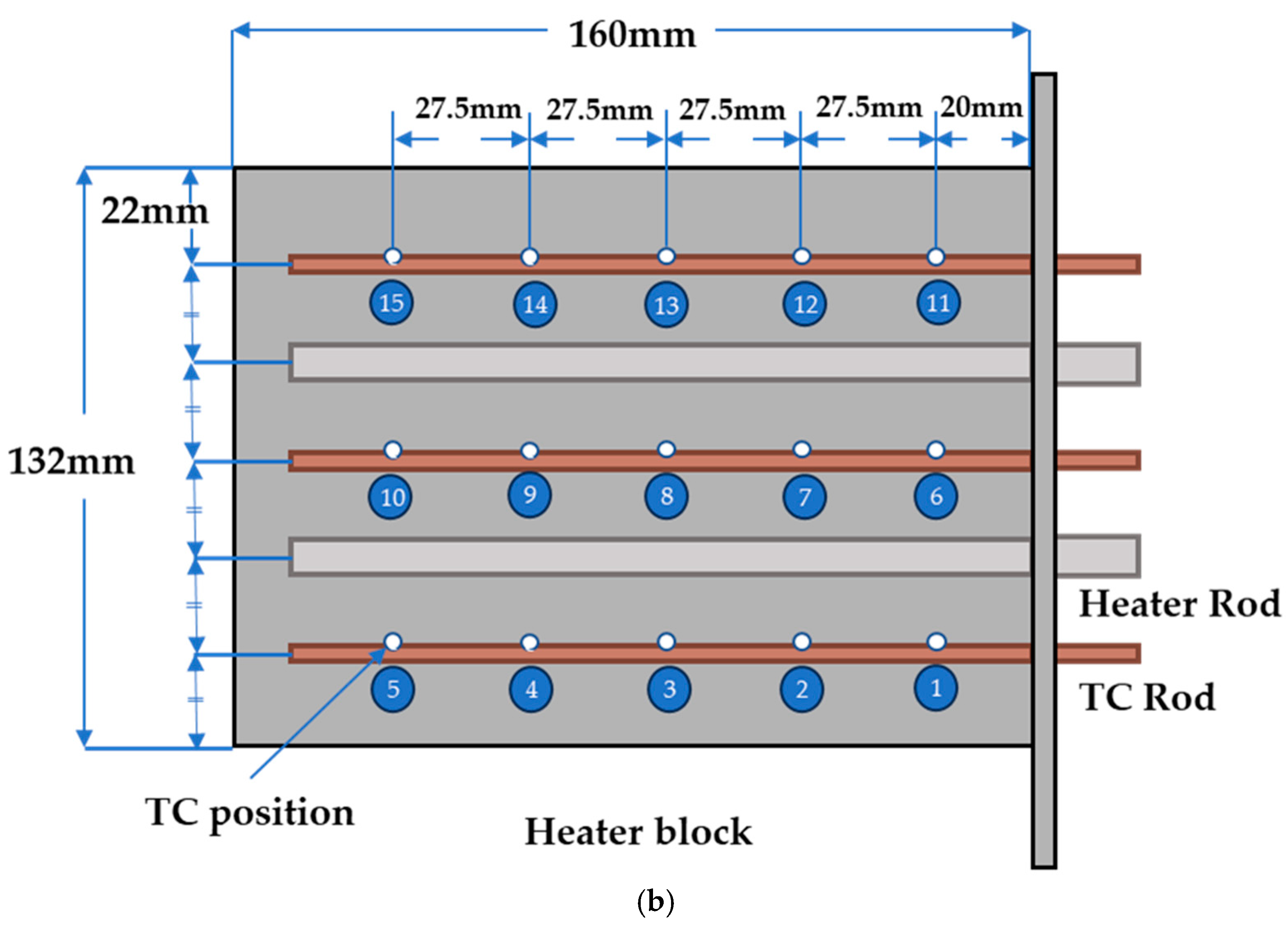
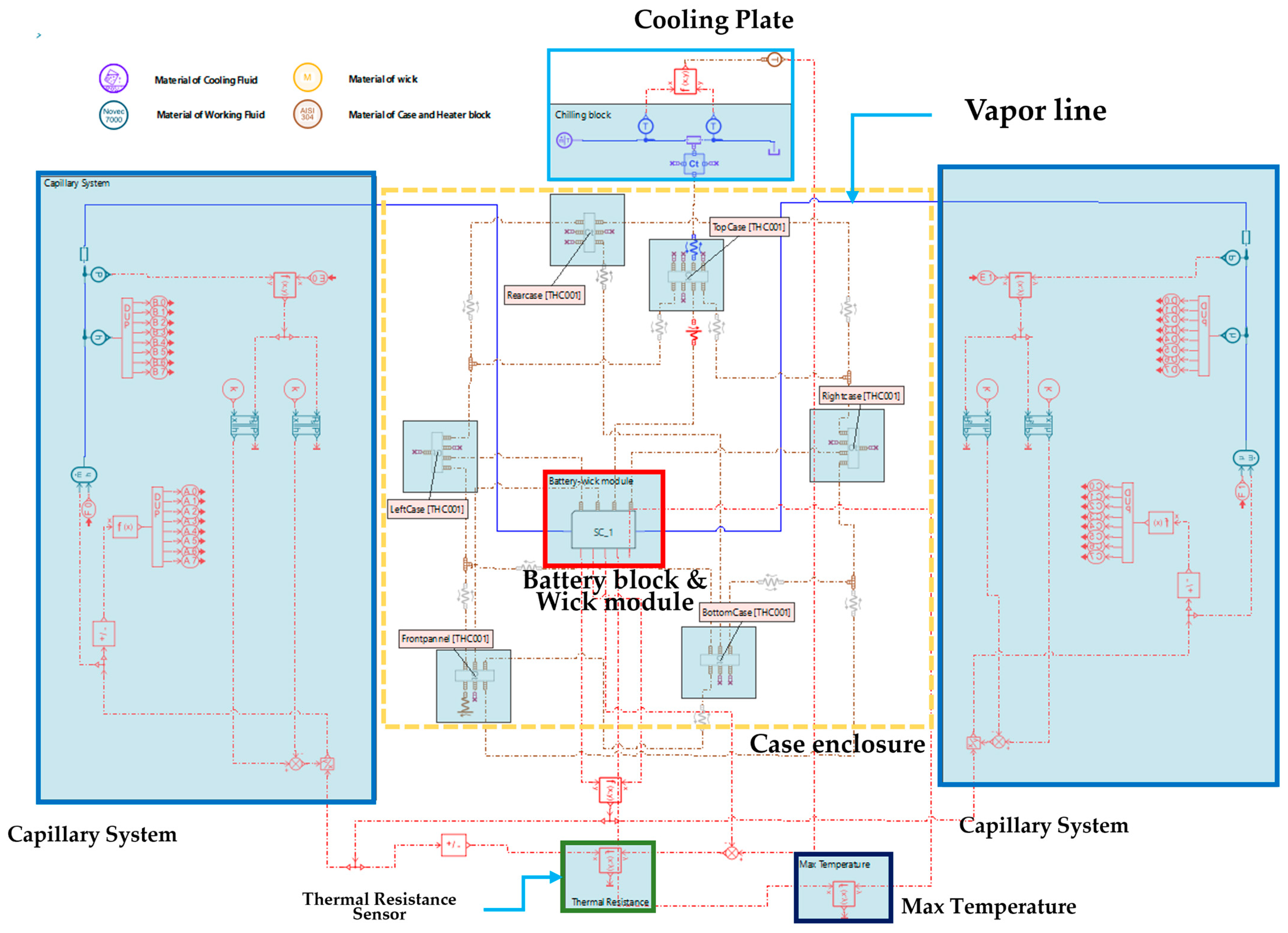

| Unit (mm) | Case | Heater Block |
|---|---|---|
| Length | 200 | 160 |
| Width | 21 | 15 |
| Height | 134 | 132 |
| Material | Density [kg/m3] | Thermal Conductivity [W/m·K] | Specific Heat [J/kg·K] |
|---|---|---|---|
| SUS 304 | 8000 | 16.3 | 530 |
| Cellulose Fiber | 1500 | 0.57 | 1209 |
| Pre-carbonized Polyacrylonitrile (PAN-CF) | 1168 | 0.216 | 1341 |
| Filling Ratio [%] | Mass of Working Fluid [kg] | Saturation Level [S] |
|---|---|---|
| 20 | 0.032 | 0.311 |
| 30 | 0.049 | 0.467 |
| 40 | 0.065 | 0.622 |
| 50 | 0.082 | 0.778 |
| 60 | 0.098 | 0.933 |
| 70 | 0.1149 | 1 |
| Variables | Values |
|---|---|
| ε | 0.895 |
| ks | 0.57 |
| kl | 0.6 |
| s [kg/m3] | 1500 |
| l [kg/m3] | 980.62 |
| Cp,s [J/kg·K] | 1209 |
| Cp,l [J/kg·K] | 4195.03 |
| Category | Condition |
|---|---|
| Material of heater block | SUS 304 |
| Material of wick | Cellulose fiber |
| Working fluid | Distilled water |
| Coolant fluid | Water |
| Initial temperature of heater block (°C) | 22 |
| Temperature of coolant (°C) | 15.4 |
| Mass flow rate of coolant (L/min) | 0.9 |
| Thickness of wick (mm) | 3 |
| Porosity (%) | 0.895 |
| Heat input (W) | 30–130 with interval in 10 W |
| Variables | Distilled Water | Novec 649 | Novec 7000 |
|---|---|---|---|
| Porosity (ε) | 0.7, 0.8, 0.895 | 0.895 | 0.895 |
| Thermal conductivity of cellulose (ks) [W/m·K] | 0.57 | 0.57 | 0.57 |
| Thermal conductivity of working fluid (kl) [W/m·K] | 0.6 | 0.054 | 0.063 |
| s) [kg/m3] | 1500 | 1500 | 1500 |
| l) [kg/m3] | 980.6 | 1528.2 | 1380.1 |
| Specific Heat of cellulose (Cp,s) [J/kg·K] | 1209 | 1209 | 1209 |
| Specific Heat of working fluid Cp,l [J/kg·K] | 4195.0 | 1121.3 | 1257.8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, S.-J.; Lee, J.-S.; Rhi, S.-H. Heat Pipe Embedded Battery Cooling System for Future Electric Vehicle. Batteries 2025, 11, 164. https://doi.org/10.3390/batteries11040164
Kim S-J, Lee J-S, Rhi S-H. Heat Pipe Embedded Battery Cooling System for Future Electric Vehicle. Batteries. 2025; 11(4):164. https://doi.org/10.3390/batteries11040164
Chicago/Turabian StyleKim, Su-Jong, Ji-Su Lee, and Seok-Ho Rhi. 2025. "Heat Pipe Embedded Battery Cooling System for Future Electric Vehicle" Batteries 11, no. 4: 164. https://doi.org/10.3390/batteries11040164
APA StyleKim, S.-J., Lee, J.-S., & Rhi, S.-H. (2025). Heat Pipe Embedded Battery Cooling System for Future Electric Vehicle. Batteries, 11(4), 164. https://doi.org/10.3390/batteries11040164







