Exploring the Flow and Mass Transfer Characteristics of an All-Iron Semi-Solid Redox Flow Battery
Abstract
:1. Introduction
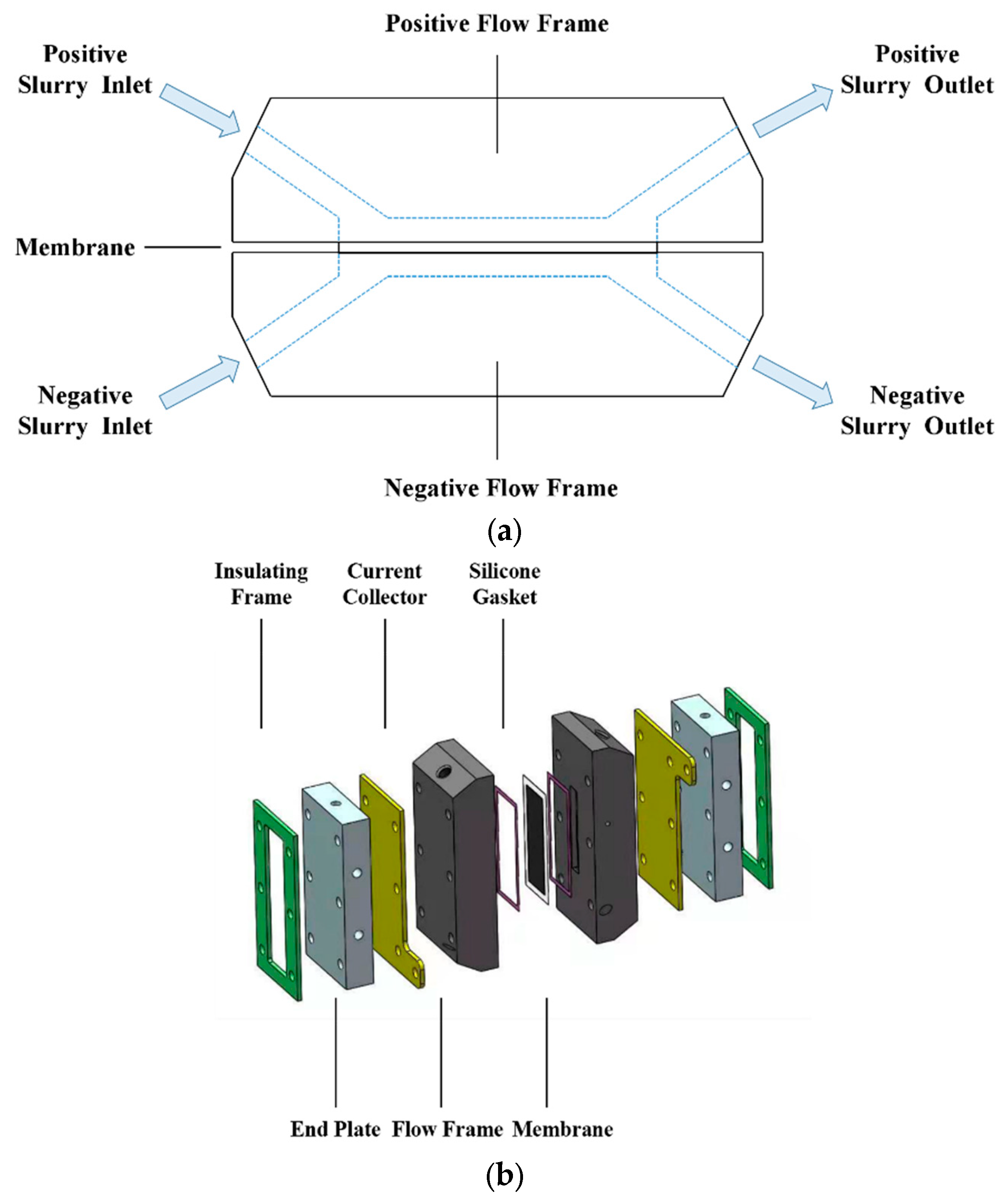
2. Experimental Set-Up
2.1. Preparation
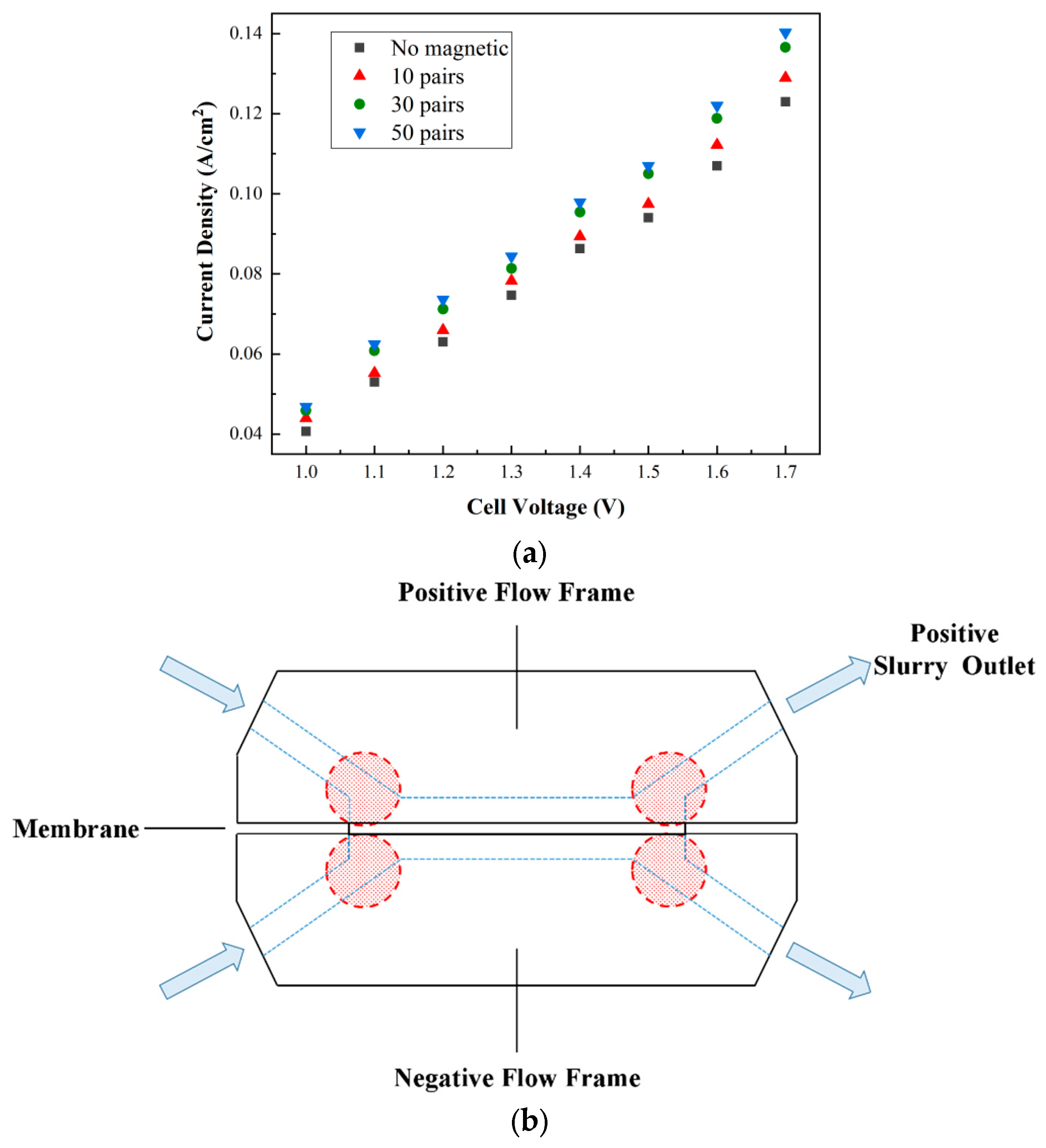
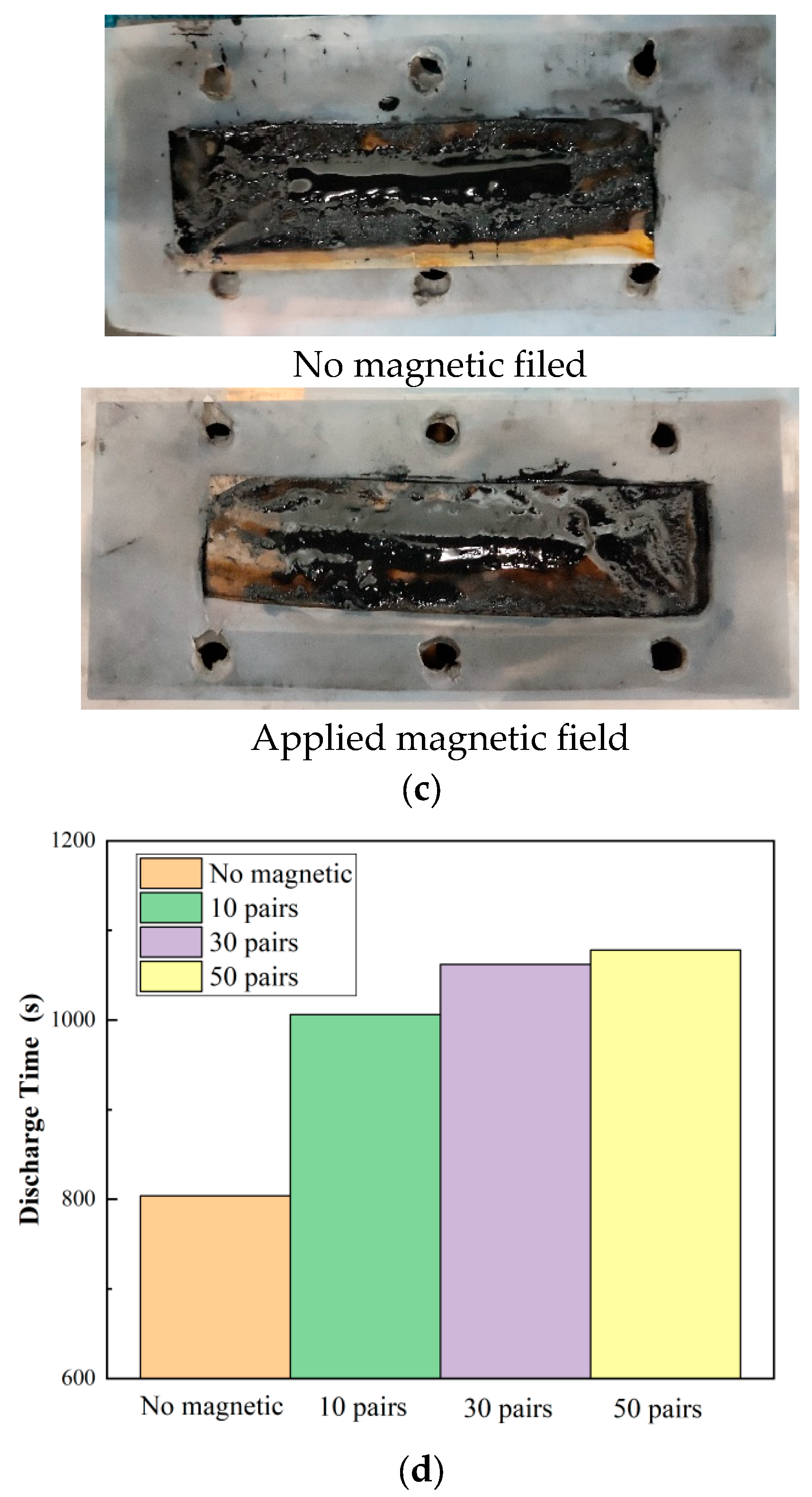
2.2. Measurements
2.3. Results and Discussion
3. Simulations
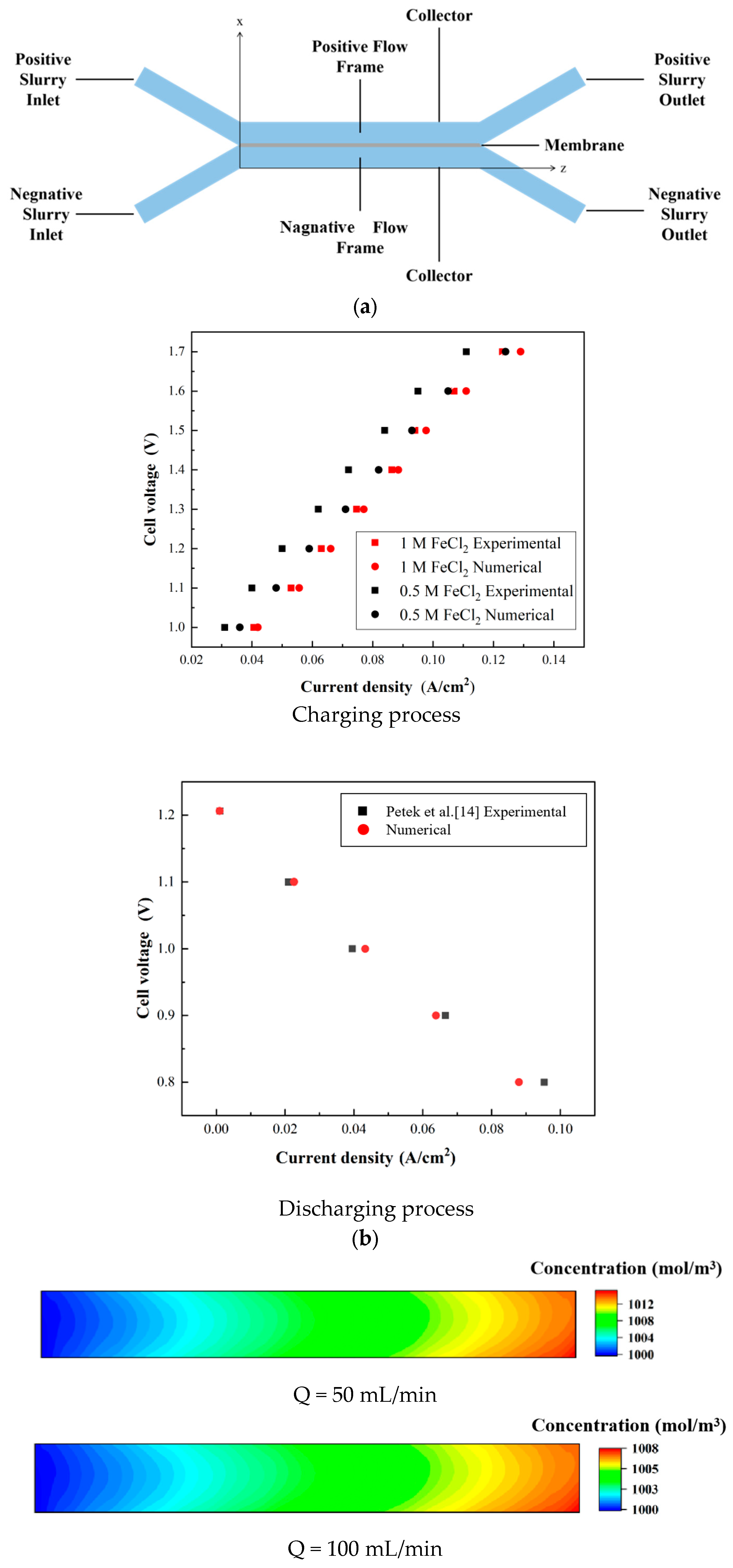
3.1. Model Description
3.2. Validation of Model
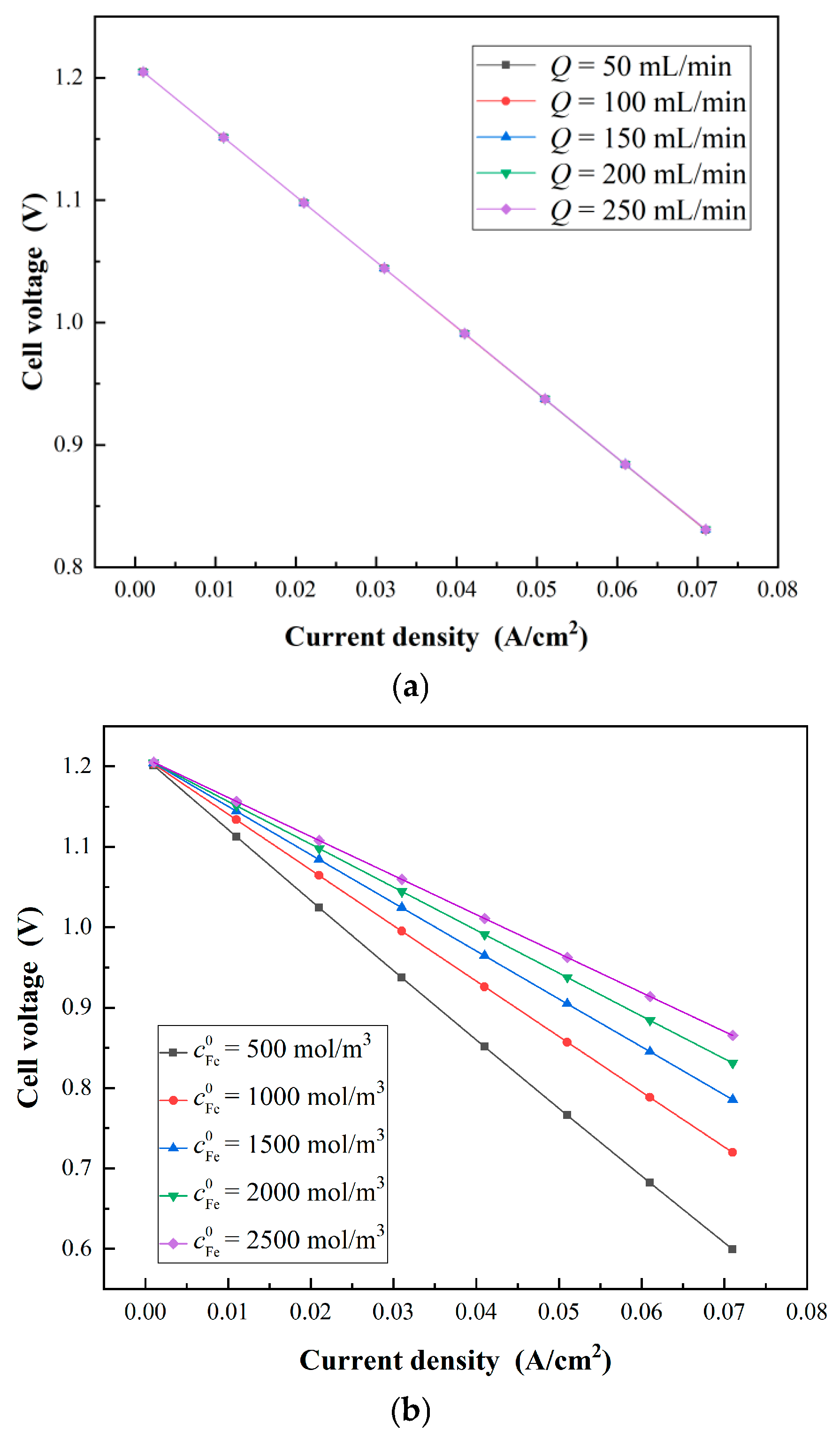
3.3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| B | Magnetic field strength (Gs) |
| SOC | State of charge |
| CE | Coulombic efficiency |
| VE | Voltage efficiency |
| EE | Energy efficiency |
| tdis | Discharge time (s) |
| tch | Charging time (s) |
| Average discharge voltage (V) | |
| Average charging voltage (V) | |
| Porosity of the slurry electrode (0.63) | |
| ji | Pore wall flux (mol/m2s) |
| Flux of the substance i caused by migration, convection, and diffusion (mol/m2s) | |
| av | Ratio of the surface area to the volume of the electrode (m−1) |
| Anion and cation flux (mol/m2s) | |
| Effective diffusion coefficient in the electrolyte (m2/s) | |
| D0 | Diffusion coefficient of the electrolyte salt outside any porous structure (m2/s) (Fe2+: 7.2 × 10−10, Fe3+: 6.1 × 10−10, Fe0: 5 × 10−13, Cl−: 2 × 10−9) |
| The number of cation or anion transfers | |
| il | Ionic current density in the electrolyte phase (A/m2) |
| F | Faraday constant (C/mol) (96,485) |
| Average flow rate (m/s) | |
| Interfacial flux of anions and cations between the solid active particles and the electrolyte solution (mol/m2·s) | |
| c | Molar concentration (mol/L) |
| Chemical potential of the substance (J/mol) | |
| R | Ideal gas constant (8.314 J/mol·k) |
| T | Temperature (K) |
| ion velocities of substances (m/s) | |
| ct | Total molar concentration in the electrolyte (mol/L) |
| Dij | Stefan–Maxwell binary diffusion coefficient for multi-component diffusion (m2/s) (6.1 × 10−10) |
| Concentration of intercalation substance i in the solid active particle (mol/L) | |
| Ds,j | Solid-state diffusion coefficient of substance i in the solid active particle (m2/s) |
| r | Radial coordinate (m) |
| Rp | Radius of the solid active particle (μm) (5) |
| is | Current density due to electron conduction in the solid active particle phase (A/m2) |
| Solid phase potential (V) | |
| Electrolyte phase potential (V) | |
| Electronic conductivity of the slurry electrode (S/m) (0.16) | |
| Effective electronic conductivity (S/m) | |
| Electrolyte conductivity (S/m) (0.16) | |
| Average molar activity of the electrolyte salt (mol/L) | |
| A | Specific surface area of the electrode (m2/g) (20) |
| positive and negative ion exchange coefficient | |
| Positive and negative electrode overpotential (V) | |
| Positive and negative electrode exchange current density (A/m2) |
References
- Fu, Y.; Howard, A.; Zeng, C.; Chen, Y.; Gao, P.; Stinis, P. Physics-guided continual learning for predicting emerging aqueous organic redox flow bat-tery material performance. ACS Energy Lett. 2024, 9, 2767–2774. [Google Scholar] [CrossRef]
- Hatzell, K.B.; Beidaghi, M.; Campos, J.W.; Dennison, C.R.; Kumbur, E.C.; Gogotsi, Y. A high performance pseudocapacitive sus-pension electrode for the electrochemical flow capacitor. Electrochim. Acta 2013, 111, 888–897. [Google Scholar] [CrossRef]
- Cai, Y.; Zhao, X.; Wang, Y.; Ma, D.; Xu, S. Enhanced desalination performance utilizing sulfonated carbon nanotube in the flow-electrode capacitive deionization process. Sep. Purif. Technol. 2019, 237, 116381. [Google Scholar] [CrossRef]
- Dahiya, S.; Mishra, B.K. Enhancing understandability and performance of flow electrode capacitive deionisation by optimizing configurational and operational parameters: A review on recent progress. Sep. Purif. Technol. 2020, 240, 116660. [Google Scholar] [CrossRef]
- Boota, M.; Hatzell, K.; Alhabeb, M.; Kumbur, E.; Gogotsi, Y. Graphene-containing flowable electrodes for capacitive energy storage. Carbon 2015, 92, 142–149. [Google Scholar] [CrossRef]
- Zhang, C.; Hatzell, K.B.; Boota, M.; Dyatkin, B.; Beidaghi, M.; Long, D.; Qiao, W.; Kumbur, E.C.; Gogotsi, Y. Highly porous carbon spheres for electrochemical capacitors and capacitive flowable suspension electrodes. Carbon 2014, 77, 155–164. [Google Scholar] [CrossRef]
- Campos, J.W.; Beidaghi, M.; Hatzell, K.B.; Dennison, C.R.; Musci, B.; Presser, V.; Kumbur, E.C.; Gogotsi, Y. Investigation of carbon materials for use as a flowable electrode in electrochemical flow capacitors. Electrochim. Acta 2013, 98, 123–130. [Google Scholar] [CrossRef]
- Cho, Y.; Yoo, C.-Y.; Lee, S.W.; Yoon, H.; Lee, K.S.; Yang, S.; Kim, D.K. Flow-electrode capacitive deionization with highly enhanced salt removal performance utilizing high-aspect ratio functionalized carbon nanotubes. Water Res. 2019, 151, 252–259. [Google Scholar] [CrossRef] [PubMed]
- Dennison, C.; Beidaghi, M.; Hatzell, K.; Campos, J.; Gogotsi, Y.; Kumbur, E. Effects of flow cell design on charge percolation and storage in the carbon slurry electrodes of electrochemical flow capacitors. J. Power Sources 2014, 247, 489–496. [Google Scholar] [CrossRef]
- Lohaus, J.; Rall, D.; Kruse, M.; Steinberger, V.; Wessling, M. On charge percolation in slurry electrodes used in vanadium redox flow batteries. Electrochem. Commun. 2019, 101, 104–108. [Google Scholar] [CrossRef]
- Brunini, V.E.; Chiang, Y.-M.; Carter, W.C. Modeling the hydrodynamic and electrochemical efficiency of semi-solid flow batteries. Electrochim. Acta 2012, 69, 301–307. [Google Scholar] [CrossRef]
- Hoyt, N.C.; Wainright, J.S.; Savinell, R.F. Mathematical Modeling of Electrochemical Flow Capacitors. J. Electrochem. Soc. 2015, 162, A652–A657. [Google Scholar] [CrossRef]
- Chayambuka, K.; Fransaer, J.; Dominguez-Benetton, X. Modeling and design of semi-solid flow batteries. J. Power Sources 2019, 434, 226740. [Google Scholar] [CrossRef]
- Petek, T.J.; Hoyt, N.C.; Savinell, R.F.; Wainright, J.S. Slurry electrodes for iron plating in an all-iron flow battery. J. Power Sources 2015, 294, 620–626. [Google Scholar] [CrossRef]
- Petek, T.J.; Hoyt, N.C.; Savinell, R.F.; Wainright, J.S. Characterizing Slurry Electrodes Using Electrochemical Impedance Spec-troscopy. J. Electrochem. Soc. 2016, 163, A5001–A5009. [Google Scholar] [CrossRef]
- Yang, K.; Xiong, S.; Zhang, H. A comprehensive 3D multi-physics coupled simulation model of slurry redox flow batteries. J. Power Sources 2022, 531, 231315. [Google Scholar] [CrossRef]
- Fang, W.; Pan, S.; Zhang, F.; Zhao, Y.; Zhang, H.; Zhang, S. A three-dimensional flow-electrochemistry coupling model for optimizing the channel config-uration of lithium slurry redox flow battery. Chem. Eng. J. 2024, 485, 149572. [Google Scholar] [CrossRef]
- Devi, N.; Singh, P.; Arpornwichanop, A.; Chen, Y.-S. Study on the treatment of carbon black for slurry electrodes of all-iron redox flow batteries. Electrochim. Acta 2025, 511, 145393. [Google Scholar] [CrossRef]
- Xiong, B.; Zhao, J.; Li, J. Modeling of an all-vanadium redox flow battery and optimization of flow rates. In Proceedings of the 2013 IEEE Power & Energy Society General Meeting, Vancouver, BC, Canada, 21–25 July 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 1–5. [Google Scholar]






| FeCl3 (M) | FeCl2 (M) | NH4Cl (M) | Conductivity (mS/cm) | |
|---|---|---|---|---|
| Positive | 1 | 1 | 1 | 180 |
| Negative | / | 1 | 1 | 150 |
| Parameter | Symbol | Value | Unit |
|---|---|---|---|
| Flow channel width | W_channel | 0.01 | m |
| Flow channel depth | D_channel | 0.004 | m |
| Middle section channel length | L_ch_mid | 0.06 | m |
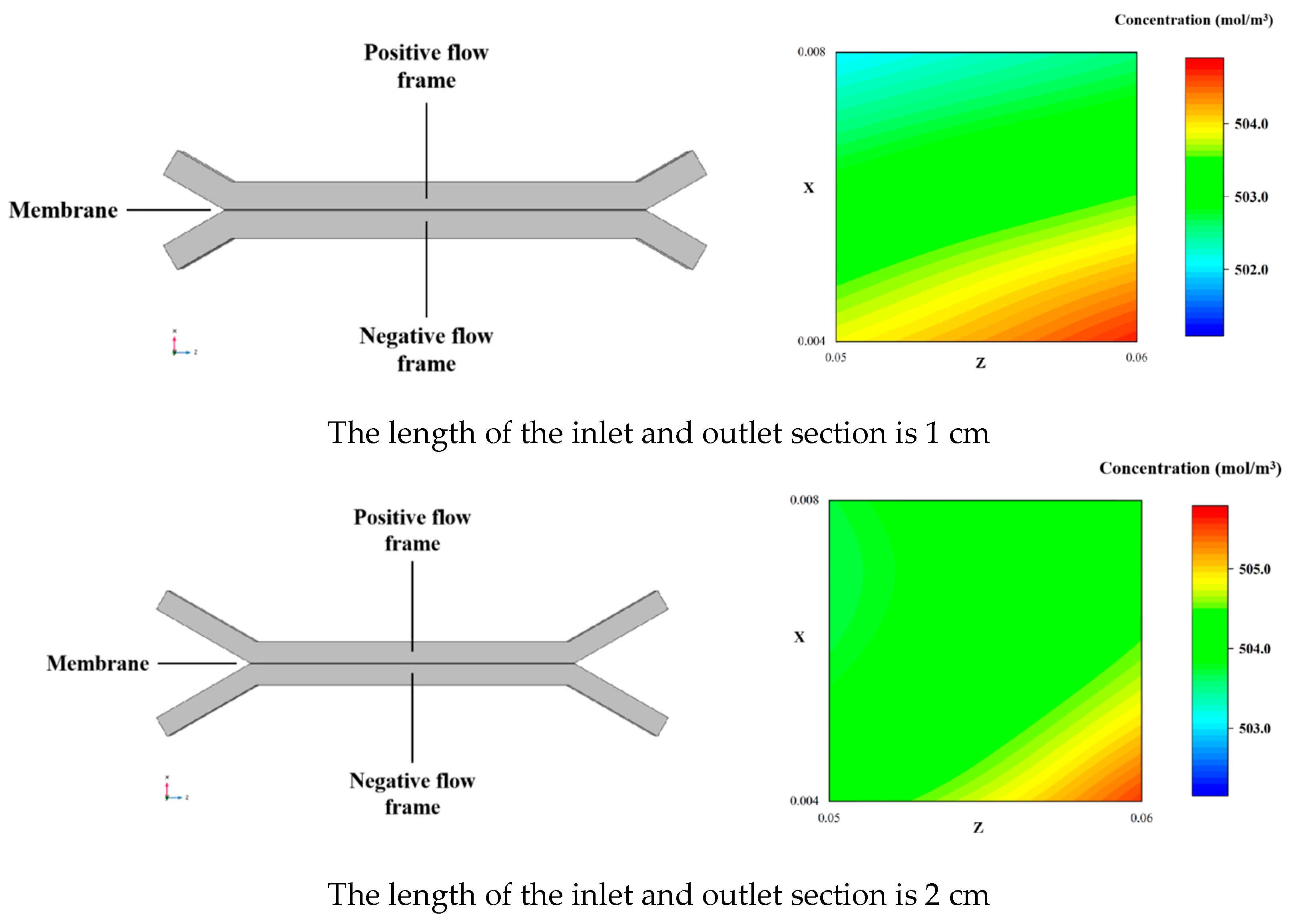
| Length of inlet and outlet channel | L_ch_let | 0.03 | m |
| Membrane thickness | L_m | 0.00022 | m |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, H.; Zhang, Z.; Zhang, H.; Zhou, Y. Exploring the Flow and Mass Transfer Characteristics of an All-Iron Semi-Solid Redox Flow Battery. Batteries 2025, 11, 166. https://doi.org/10.3390/batteries11040166
Li H, Zhang Z, Zhang H, Zhou Y. Exploring the Flow and Mass Transfer Characteristics of an All-Iron Semi-Solid Redox Flow Battery. Batteries. 2025; 11(4):166. https://doi.org/10.3390/batteries11040166
Chicago/Turabian StyleLi, Heyao, Zhuqian Zhang, Haojie Zhang, and Yuchen Zhou. 2025. "Exploring the Flow and Mass Transfer Characteristics of an All-Iron Semi-Solid Redox Flow Battery" Batteries 11, no. 4: 166. https://doi.org/10.3390/batteries11040166
APA StyleLi, H., Zhang, Z., Zhang, H., & Zhou, Y. (2025). Exploring the Flow and Mass Transfer Characteristics of an All-Iron Semi-Solid Redox Flow Battery. Batteries, 11(4), 166. https://doi.org/10.3390/batteries11040166






