Determination of the Distribution of Relaxation Times by Means of Pulse Evaluation for Offline and Online Diagnosis of Lithium-Ion Batteries
Abstract
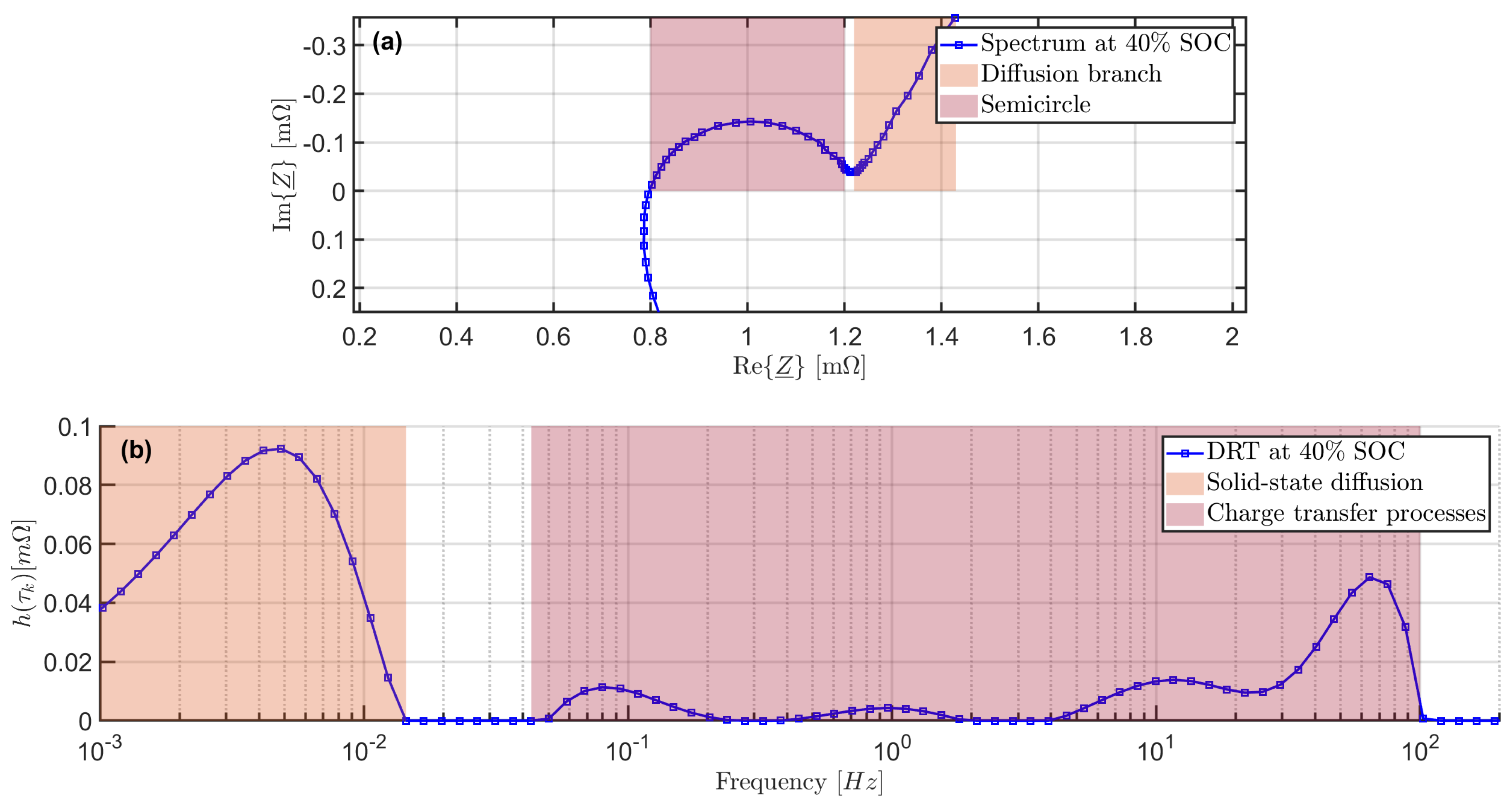
:1. Introduction
2. Methods
2.1. DRT of Frequency Domain Data
2.2. DRT of Time Domain Data
2.2.1. General Approach
2.2.2. Predefinition of Time Constants
2.2.3. Pre-Processing of Measurement Data
2.2.4. Calculation of the DRT
3. Experimental
3.1. Experimental Validation
3.2. Aging Study
4. Results
4.1. Experimental Validation
4.2. Aging Study
4.2.1. EIS Measurement Evaluation
- An increase of the internal cell resistance during aging (Shifting of the zero crossing of the imaginary axis to higher real parts)
- Disappearance of the second semicircle at 20% SOC during the first 1050 cycles of the long-term test
4.2.2. Pulse Test Evaluation
4.2.3. Comparison of DRT by Time and Frequency Domain Data
- Processes with characteristic time constants that do not meet Equation (12) cannot be identified with the set sampling rate using the time domain data alone.
- Already with a maximum sampling rate of 10 , which is realistic for online applications, the DRT by time domain data can be used to identify charge transfer processes and to provide a qualitative description. However, the change in process parameters during aging can only be traced to a limited extent.
- Quantitative statements for charge transfer processes, even if higher sampling rates are used, differ between the two methods due to the Butler–Volmer kinetics. In fact, due to the strongly non-linear excitations in real applications, the better transferability of the results obtained from frequency domain data is questionable.
- The DRT based on time domain data is more sensitive for processes with large characteristic time constants such as solid state diffusion.
- When using frequency domain data, either longer measuring periods are required or the measuring range is limited to higher frequencies, since different frequencies have to be excited successively during EIS.
4.2.4. Correlation of the Capacity and the Identified Process Parameters
5. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| DRT | Distribution of relaxation times |
| LIB | Lithium-ion battery |
| EIS | Electrochemical impedance spectroscopy |
| EV | Electric vehicle |
| OCV | Open circuit voltage |
| SEI | Solid electrolyte interface |
| FFT | Fast Fourier transform |
| ECM | Equivalent circuit model |
| SOC | State of charge |
| NMC | Nickel-manganese-cobalt-oxide |
| CCCV | constant-current-constant-voltage |
| DOD | Depth of discharge |
| LAMAn | Loss of active material at the anode |
| LLI | Loss of lithium inventory |
References
- Pastor-Fernández, C.; Uddin, K.; Chouchelamane, G.H.; Widanage, W.D.; Marco, J. A Comparison between Electrochemical Impedance Spectroscopy and Incremental Capacity-Differential Voltage as Li-ion Diagnostic Techniques to Identify and Quantify the Effects of Degradation Modes within Battery Management Systems. J. Power Sources 2017, 360, 301–318. [Google Scholar] [CrossRef]
- Pastor-Fernández, C.; Yu, T.F.; Widanage, W.D.; Marco, J. Critical review of non-invasive diagnosis techniques for quantification of degradation modes in lithium-ion batteries. Renew. Sustain. Energy Rev. 2019, 109, 138–159. [Google Scholar] [CrossRef]
- Schindler, S.; Bauer, M.; Petzl, M.; Danzer, M.A. Voltage relaxation and impedance spectroscopy as in-operando methods for the detection of lithium plating on graphitic anodes in commercial lithium-ion cells. J. Power Sources 2016, 304, 170–180. [Google Scholar] [CrossRef]
- Steinhauer, M.; Risse, S.; Wagner, N.; Friedrich, K.A. Investigation of the Solid Electrolyte Interphase Formation at Graphite Anodes in Lithium-Ion Batteries with Electrochemical Impedance Spectroscopy. Electrochim. Acta 2017, 228, 652–658. [Google Scholar] [CrossRef]
- Shafiei Sabet, P.; Warnecke, A.J.; Meier, F.; Witzenhausen, H.; Martinez-Laserna, E.; Sauer, D.U. Non-invasive yet separate investigation of anode/cathode degradation of lithium-ion batteries (nickel–cobalt–manganese vs. graphite) due to accelerated aging. J. Power Sources 2020, 449, 227369. [Google Scholar] [CrossRef]
- Schmitt, J.; Maheshwari, A.; Heck, M.; Lux, S.; Vetter, M. Impedance change and capacity fade of lithium nickel manganese cobalt oxide-based batteries during calendar aging. J. Power Sources 2017, 353, 183–194. [Google Scholar] [CrossRef]
- Andre, D.; Meiler, M.; Steiner, K.; Wimmer, C.; Soczka-Guth, T.; Sauer, D.U. Characterization of high-power lithium-ion batteries by electrochemical impedance spectroscopy. I. Experimental investigation. J. Power Sources 2011, 196, 5334–5341. [Google Scholar] [CrossRef]
- Tröltzsch, U.; Kanoun, O.; Tränkler, H.R. Characterizing aging effects of lithium ion batteries by impedance spectroscopy. Electrochim. Acta 2006, 51, 1664–1672. [Google Scholar] [CrossRef]
- Jossen, A. Fundamentals of battery dynamics. J. Power Sources 2006, 154, 530–538. [Google Scholar] [CrossRef]
- Tuncer, E.; Macdonald, J.R. Comparison of methods for estimating continuous distributions of relaxation times. J. Appl. Phys. 2006, 99, 074106. [Google Scholar] [CrossRef] [Green Version]
- Saccoccio, M.; Wan, T.H.; Chen, C.; Ciucci, F. Optimal Regularization in Distribution of Relaxation Times applied to Electrochemical Impedance Spectroscopy: Ridge and Lasso Regression Methods - A Theoretical and Experimental Study. Electrochim. Acta 2014, 147, 470–482. [Google Scholar] [CrossRef]
- Wan, T.H.; Saccoccio, M.; Chen, C.; Ciucci, F. Influence of the Discretization Methods on the Distribution of Relaxation Times Deconvolution: Implementing Radial Basis Functions with DRTtools. Electrochim. Acta 2015, 184, 483–499. [Google Scholar] [CrossRef]
- Boukamp, B.A.; Rolle, A. Analysis and Application of Distribution of Relaxation Times in Solid State Ionics. Solid State Ion. 2017, 302, 12–18. [Google Scholar] [CrossRef]
- Danzer, M.A. Generalized Distribution of Relaxation Times Analysis for the Characterization of Impedance Spectra. Batteries 2019, 5, 53. [Google Scholar] [CrossRef] [Green Version]
- Hahn, M.; Schindler, S.; Triebs, L.C.; Danzer, M.A. Optimized Process Parameters for a Reproducible Distribution of Relaxation Times Analysis of Electrochemical Systems. Batteries 2019, 5, 43. [Google Scholar] [CrossRef] [Green Version]
- Ivers-Tiffée, E.; Weber, A. Evaluation of electrochemical impedance spectra by the distribution of relaxation times. J. Ceram. Soc. Jpn. 2017, 125, 193–201. [Google Scholar] [CrossRef] [Green Version]
- Manikandan, B.; Ramar, V.; Yap, C.; Balaya, P. Investigation of physico-chemical processes in lithium-ion batteries by deconvolution of electrochemical impedance spectra. J. Power Sources 2017, 361, 300–309. [Google Scholar] [CrossRef]
- Alavi, S.; Birkl, C.R.; Howey, D.A. Time-domain fitting of battery electrochemical impedance models. J. Power Sources 2015, 288, 345–352. [Google Scholar] [CrossRef]
- Klotz, D.; Schönleber, M.; Schmidt, J.P.; Ivers-Tiffée, E. New approach for the calculation of impedance spectra out of time domain data. Electrochim. Acta 2011, 56, 8763–8769. [Google Scholar] [CrossRef]
- Karger, A.; Wildfeuer, L.; Maheshwari, A.; Wassiliadis, N.; Lienkamp, M. Novel method for the on-line estimation of low-frequency impedance of lithium-ion batteries. J. Energy Storage 2020, 32, 101818. [Google Scholar] [CrossRef]
- Schröer, P.; Khoshbakht, E.; Nemeth, T.; Kuipers, M.; Zappen, H.; Sauer, D.U. Adaptive modeling in the frequency and time domain of high-power lithium titanate oxide cells in battery management systems. J. Energy Storage 2020, 32, 101966. [Google Scholar] [CrossRef]
- Zou, C.; Zhang, L.; Hu, X.; Wang, Z.; Wik, T.; Pecht, M. A review of fractional-order techniques applied to lithium-ion batteries, lead-acid batteries, and supercapacitors. J. Power Sources 2018, 390, 286–296. [Google Scholar] [CrossRef] [Green Version]
- Schmidt, J.P.; Berg, P.; Schönleber, M.; Weber, A.; Ivers-Tiffée, E. The distribution of relaxation times as basis for generalized time-domain models for Li-ion batteries. J. Power Sources 2013, 221, 70–77. [Google Scholar] [CrossRef]
- Zhu, J.; Dewi Darma, M.S.; Knapp, M.; Sørensen, D.R.; Heere, M.; Fang, Q.; Wang, X.; Dai, H.; Mereacre, L.; Senyshyn, A.; et al. Investigation of lithium-ion battery degradation mechanisms by combining differential voltage analysis and alternating current impedance. J. Power Sources 2020, 448, 227575. [Google Scholar] [CrossRef]
- Hentunen, A.; Lehmuspelto, T.; Suomela, J. Time-Domain Parameter Extraction Method for Thévenin-Equivalent Circuit Battery Models. IEEE Trans. Energy Convers. 2014, 29, 558–566. [Google Scholar] [CrossRef]
- Xiaosong, H.; Fengchun, S.; Yuan, Z.; Huei, P. Online estimation of an electric vehicle Lithium-Ion battery using recursive least squares with forgetting. In Proceedings of the 2011 American Control Conference, San Francisco, CA, USA, 29 June–1 July 2011; pp. 935–940. [Google Scholar] [CrossRef]
- Goldammer, M.S.E.; Kowal, J. Investigation of degradation mechanisms in lithium-ion batteries by incremental open-circuit-voltage characterization and impedance spectra. In Proceedings of the 2020 IEEE Vehicle Power and Propulsion Conference (VPPC), Gijon, Spain, 18 November–16 December 2020; pp. 1–8. [Google Scholar] [CrossRef]
- Tikhonov, A.N.; Goncharsky, A.V.; Hazewinkel, M. Numerical Methods for the Solution of Ill-Posed Problems; Springer: Dordrecht, The Netherlands, 2010. [Google Scholar]
- Schindler, S. Diskrete Elektrochemische Modellierung und Experimentelle Identifikation von Lithium-Ionen-Zellen Basierend auf Halbzellpotentialen; Universität Bayreuth: Bayreuth, Germany, 2018. [Google Scholar]
- Barai, A.; Widanage, W.D.; Marco, J.; McGordon, A.; Jennings, P. A study of the open circuit voltage characterization technique and hysteresis assessment of lithium-ion cells. J. Power Sources 2015, 295, 99–107. [Google Scholar] [CrossRef]
- Gantenbein, S.; Schönleber, M.; Weiss, M.; Ivers-Tiffée, E. Capacity Fade in Lithium-Ion Batteries and Cyclic Aging over Various State-of-Charge Ranges. Sustainability 2019, 11, 6697. [Google Scholar] [CrossRef] [Green Version]
- Kindermann, F.M.; Noel, A.; Erhard, S.V.; Jossen, A. Long-term equalization effects in Li-ion batteries due to local state of charge inhomogeneities and their impact on impedance measurements. Electrochim. Acta 2015, 185, 107–116. [Google Scholar] [CrossRef]
- Shafiei Sabet, P.; Sauer, D.U. Separation of predominant processes in electrochemical impedance spectra of lithium-ion batteries with nickel-manganese-cobalt cathodes. J. Power Sources 2019, 425, 121–129. [Google Scholar] [CrossRef]
- Illig, J.; Ender, M.; Weber, A.; Ivers-Tiffée, E. Modeling graphite anodes with serial and transmission line models. J. Power Sources 2015, 282, 335–347. [Google Scholar] [CrossRef]
- Dubarry, M.; Baure, G.; Devie, A. Durability and Reliability of EV Batteries under Electric Utility Grid Operations: Path Dependence of Battery Degradation. J. Electrochem. Soc. 2018, 165, A773–A783. [Google Scholar] [CrossRef]
- Anseán, D.; Dubarry, M.; Devie, A.; Liaw, B.Y.; García, V.M.; Viera, J.C.; González, M. Operando lithium plating quantification and early detection of a commercial LiFePO4 cell cycled under dynamic driving schedule. J. Power Sources 2017, 356, 36–46. [Google Scholar] [CrossRef] [Green Version]
- Schindler, S.; Danzer, M.A. A novel mechanistic modeling framework for analysis of electrode balancing and degradation modes in commercial lithium-ion cells. J. Power Sources 2017, 343, 226–236. [Google Scholar] [CrossRef]
- Fermín-Cueto, P.; McTurk, E.; Allerhand, M.; Medina-Lopez, E.; Anjos, M.F.; Sylvester, J.; dos Reis, G. Identification and machine learning prediction of knee-point and knee-onset in capacity degradation curves of lithium-ion cells. Energy AI 2020, 1, 100006. [Google Scholar] [CrossRef]









| Parameter | Calculated Value | Model Value | Relative Error |
|---|---|---|---|
| 30 | 5% | ||
| 9.2% | |||
| 39 | 3.8% | ||
| 4.9% | |||
| 117 | <0.1% | ||
| 1.5% |
| Cycling Scenario | [%] | [A] |
|---|---|---|
| 60 | 37.5 | |
| 20 | 37.5 | |
| 80 | 18.75 |
| Cycling Scenario | [%] | [%] |
|---|---|---|
| 60 | 99.1 | |
| 20 | 92.8 | |
| 80 | 98.0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Goldammer, E.; Kowal, J. Determination of the Distribution of Relaxation Times by Means of Pulse Evaluation for Offline and Online Diagnosis of Lithium-Ion Batteries. Batteries 2021, 7, 36. https://doi.org/10.3390/batteries7020036
Goldammer E, Kowal J. Determination of the Distribution of Relaxation Times by Means of Pulse Evaluation for Offline and Online Diagnosis of Lithium-Ion Batteries. Batteries. 2021; 7(2):36. https://doi.org/10.3390/batteries7020036
Chicago/Turabian StyleGoldammer, Erik, and Julia Kowal. 2021. "Determination of the Distribution of Relaxation Times by Means of Pulse Evaluation for Offline and Online Diagnosis of Lithium-Ion Batteries" Batteries 7, no. 2: 36. https://doi.org/10.3390/batteries7020036
APA StyleGoldammer, E., & Kowal, J. (2021). Determination of the Distribution of Relaxation Times by Means of Pulse Evaluation for Offline and Online Diagnosis of Lithium-Ion Batteries. Batteries, 7(2), 36. https://doi.org/10.3390/batteries7020036







