Methodology for the Optimisation of Battery Hybrid Energy Storage Systems for Mass and Volume Using a Power-To-Energy Ratio Analysis

Abstract

Increasingly stringent emission regulations and environmental concerns have propelled the development of electrification technology in the transport industry. Yet, the greatest hurdle to developing fully electric vehicles is electrochemical energy storage, which struggles to achieve profitable specific power, specific energy and cost targets. Hybrid energy storage systems (HESSs), which combine energy- and power-optimised sources, seem to be the most promising solution for improving the overall performance of energy storage. The potential for gravimetric and volumetric reduction is strictly dependent on the overall power-to-energy ratio (PE ratio) of the application, packaging factors, the minimum and maximum PE ratio achievable for the system’s energy- and power-optimised sources and the performance of power electronics. This paper presents a simple optimisation methodology that considers these factors and identifies the optimal HESS requirements that may present new opportunities for a variety of vehicles where low weight and volume are of high importance. The simplicity of the method means that decisions relating to a HESS can be made earlier in the system design process. This method of analysis showed that a battery HESS has the potential to reduce cell mass and volume by over 30% for applications that are well suited to optimal HESS characteristics.

1. Introduction

The choice of which energy storage technologies to use can be made on the basis of many factors, including efficiency, system integration, energy and power densities, durability and cost. A range of energy storage technologies are available based on different principles [1]:

• Mechanical, such as flywheels or compressed fluid;
• Thermal, such as latent heat or cryogenic systems;
• Electrical, such as capacitors and supercapacitors;
• Electrochemical, such as batteries or conversion to fluids, such as hydrogen or ammonia.

Each approach will have its own benefits and drawbacks, and in many cases, these will need to be traded off against each other, with no single technology offering the highest performance across all factors. Using multiple technologies in conjunction with each other offers a way of mitigating these trade-offs. The scope of this work was to consider the energy density and power density trade-off within a hybrid energy storage system (HESS). The approach is intended for mobile applications, such as road vehicles or aircraft, where weight and volume take on the highest importance, and the focus will be on a HESS consisting of different lithium-ion cells.

Lithium-ion battery technology has been improving rapidly since the first commercial breakthrough by Sony in 1991 [2]. The energy density has increased by almost 240%, increasing from 80 Wh/kg to over 270 Wh/kg in some of today’s cell technologies [3]. Moreover, from 2010 to 2018, the volume-weighted average price of battery packs was found to have decreased by 85% [4].

Nevertheless, lithium-ion technology still needs to make large strides to enable electric vehicles to achieve a similar range to vehicles based on the internal combustion engine without having to design overly large and heavy battery packs. Roadmaps indicate that by 2035, battery energy and power density will need to approximately double to meet the required driving range and electric drive power [5]. Yet, achieving both these criteria from a single battery technology is extremely difficult, as lithium-ion batteries are predisposed to a trade-off between their energy and power capability [6]. One of the most promising solutions is to develop a hybrid energy storage system (HESS), combining power- and energy-optimised sources to achieve the desired overall power and energy requirements [7].

HESSs have been used primarily for microgrid applications and involve combining two or more renewable energy sources and storage technologies, such as wind turbines, solar power, hydro power, fuel cells and battery storage systems [1,8,9,10]. The focus of these systems is to achieve prolonged operating life while meeting the demands of the power grid despite large fluctuations in power from renewable sources. Much research has gone into these systems, with a focus on control and sizing techniques to increase battery life [11,12,13,14,15]. As these systems are stationary, the optimisation of their mass and volume has not been the primary objective. When sizing for the optimisation of the lifetime cost of a HESS, a detailed system model is required in order to capture the current drawn from the system, which is strongly linked to degradation. Consequently, significant effort is required in specifying the duty cycle, particularly if this comes from randomly varying sources, such as wind power, used for the grid [12,13].

Conversely, a HESS that is designed for a vehicle is significantly more dependent on mass and volume and is critical for both packaging and performance. In general, HESSs in vehicles can include electrical, chemical and mechanical storage systems, including batteries, fuel cells, flywheels and ultracapacitors [16,17,18,19,20,21,22,23,24]. Recently, more research has been focused on their implementation in vehicles, covering a variety of applications, such as city buses, tramways, passenger cars and construction machinery. However, most research has also been focused on the improvement of battery degradation by complementing battery storage with optimally controlled and sized ultracapacitors managing the high-frequency power demands to reduce the micro-cycling of the battery [11,25,26]. Research improving the driving range and energy consumption has also been carried out using control strategies that improve the overall efficiency of the HESS [25,27]; these studies do not consider the sizing of the HESS, but instead, only consider the energy management for a HESS that has already been specified.

Despite the importance of size and weight in electric vehicles, there is little published research focusing on the sizing of a HESS that is optimised for weight and volume. Furthermore, most investigations implement ultracapacitors as power-optimised devices. This simplifies the sizing problem due to the very low energy density of the supercapacitors: the energy requirement needs to come solely from the battery and therefore its sizing is straightforward based on the total energy requirement. The ultracapacitor sizing is therefore the only sizing variable that requires optimisation: this is achieved by considering the power fluctuations during the cycle based on a target, which is usually the overall energy consumption or lifetime. Ultracapacitors may not always have enough energy for applications requiring peak load for longer periods, and their voltage drop with capacity also limits their integration into certain HESS topologies [28]. When a mix of Li-ion technologies are considered, both parts may make significant contributions to the energy and power ratings of the HESS and the sizing problem becomes less trivial with two variables to consider.

A study published by the University of Aachen implemented power- and energy-optimised lithium-ion technology for HESS optimisation [29]. The study presented a dimensioning and optimisation approach for HESS using an evolutionary optimisation algorithm and a detailed MATLAB–Simulink model for both the powertrain and vehicle. It concluded that weight and volume savings of up to 20% and 31%, respectively, could be achieved. However, the presented approach was based on a complete battery simulation cost function, incorporating cell, thermal and battery management system models and runtime for the optimisation is significant. The complex simulation requires a larger number of parameters relating to a specific design, and the longer runtime means that it is not feasible to evaluate a large number of design options. This also limits the number of different cell types that can reasonably be studied; the authors considered five within their work.

The aim of this paper was to present a methodology for the initial assessment of the potential weight and volume savings of implementing a HESS for a wide variety of applications without requiring detailed simulations. This approach creates a tool that requires few parameters that are linked to a specific design, meaning it can be applied at the early stages of the design process. Equally, the fast runtime means many evaluations or architectures can be considered, making it beneficial for informing key early design decisions in conjunction with a wider vehicle simulation. The approach will focus specifically on minimising the weight and volume, without consideration for other optimisation targets, such as cost, efficiency or lifecycle. The starting point for this methodology was the Ragone chart [30], which is a graphical method that is used to compare energy sources on the basis of energy and power densities. Ragone charts can be made to compare different types of energy storage, such as liquid or gaseous fuels, batteries and supercapacitors. This work focused on different Li-ion battery types and a Ragone chart illustrating the range of available power and energy densities is provided in Figure 1.

In Section 2, the opportunities for HESSs are introduced based on data collected about current state-of-the-art battery technology. Section 3 summarises the main HESS topologies and their main advantages and disadvantages. Section 4 describes a method of how to optimise the sizing of a HESS, as well as how this is affected by the application power-to-energy ratio, battery performance and DC/DC converter technology. Section 5 introduces a second methodology that enables comparing a HESS to a single energy storage system (SESS) over a wide range of power-to-energy ratios. Finally, Section 6 introduces additional HESS design constraints that are also demonstrated using the methodology from Section 5. Within this study, the proposed method was applied exclusively to different Li-ion cell types; however, the method could easily be extended to cover other types of energy storage systems that can be quantified in terms of scalable specific energy and specific power.

2. Opportunity for Hybrid Lithium-Ion Energy Storage

Lithium-ion batteries display a trade-off between their power and energy capabilities. This is due to the characteristics of the chemistries, as well as the percentage of active material contained in the cell design [6]. It is therefore very difficult to develop a single energy storage system (SESS) based on a battery that achieves both high power and energy performance.

Most lithium-ion cells are optimised for energy density but depending on the chemistry and the percentage of active material, they also achieve variations in cost and lifespan. Their applications range from smartphones, laptops and power tools to electric vehicles. Some chemistries, such as lithium iron phosphate (LFP) and variants of nickel manganese cobalt (NMC) are optimised for power density, also achieving better lifecycle performance and are usually developed for hybrid vehicles or motorsport applications [31]. Lithium-ion cells displaying well-rounded power and energy performance do also exist; however, they have significantly lower power densities than the most power-optimised cell and lower energy density than energy-optimised cell designs.

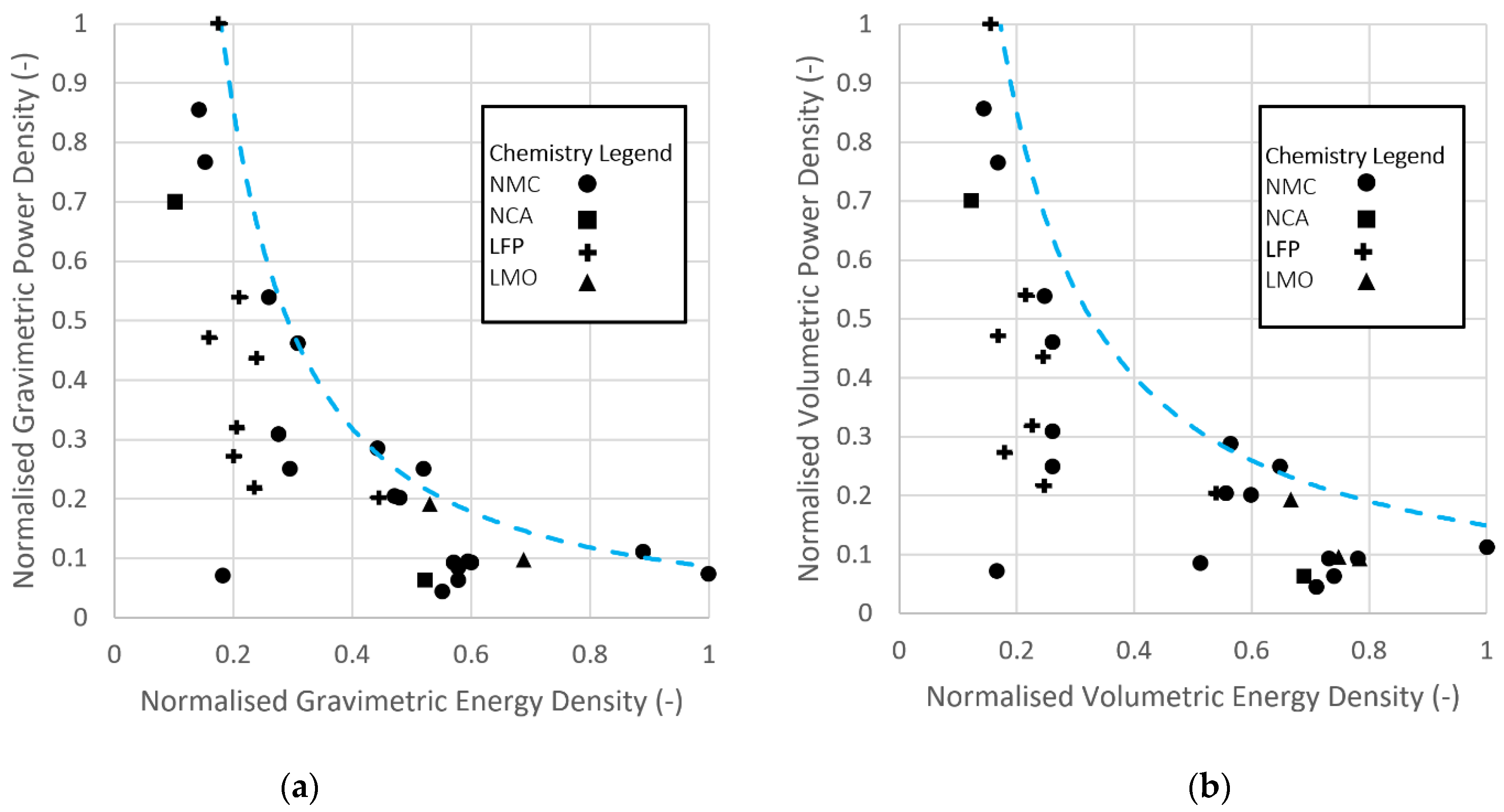
To demonstrate the trade-off between power and energy density, data were collected for various commercially accessible lithium-ion cells. This included chemistries such as lithium cobalt oxide (LCO), nickel manganese cobalt oxide (NMC), lithium manganese oxide (LMO), lithium iron phosphate (LFP) and lithium cobalt aluminium oxide (NCA).

The calculated gravimetric and volumetric power and energy densities for the collected cells were plotted in Figure 1. Different cell chemistries were categorised by marker type, as shown in the legend. A Pareto front curve was also added in the Ragone plot to emphasise the trade-off between the power and energy density. This was added by fitting an exponential curve trendline to the cell with the highest power and the cell with the highest energy, as well as the cell with the best energy and power compromise.

The plot highlights that no lithium-ion cells currently exist that achieve both the highest possible specific power and specific energy. If a higher energy density is required, the power density will be reduced, and vice versa for achieving more power density. In other words, the power-to-energy (PE) ratio will be low for energy-focused cells, and high for power-dense cells.

The definition of the PE ratio that was used in this study is expressed in Equation (1). Peak power is used to represent the highest power capability of the battery, and maximum energy represents the highest energy storage capability. This is not necessarily the energy the cell achieves at the peak power level. This is the most suitable definition for applications that are designed to run at fluctuating power duty cycles and not continuously at maximum power. The maximum C-rate of a cell is also a very important aspect for a HESS and will be discussed in Section 6.1.

$$PE Ratio (h{r}^{-1})=\frac{Peak Power \left(kW\right)}{Maximum Energy \left(kWh\right)}$$

(1)

An application can also be categorised by a PE ratio based on its highest power demand and its overall energy requirement. Examples of PE ratios for different applications include a low-power EV, such as a Renault Zoe (~3) [32], an EVTOL, such as the Lilium (~5) [33], a premium EV, such as the Tesla Model S (~6) [34], a battery in a hybrid sports, car such as the BMW i8 (~9) [35] and KERS systems in F1 cars (~500) [36].

The cell technologies presented have been developed over several years. State-of-the-art battery development is very competitive and not much information is readily available to the public. Batteries used in Formula 1 KERS systems are in fact quoted to achieve between 15–20 kW/kg and 60–120 Wh/kg, but specifications for the cells are also not available [37]. It must also be noted that cell performance is heavily dependent on the temperature control of the cell and its cooling method. Moreover, suppliers quote power and energy density in different ways; therefore, for more accuracy, rigorous testing must be performed to understand the true cell performance. This will of course also influence the performance on the Ragone chart.

Hybrid energy storage systems combine power-dense cells and energy-dense cells to better meet the energy and power requirements of a specific application. HESSs have the advantage that they can achieve an overall energy and power density that can be significantly higher than that of a single energy source. This can be achieved using different hybrid energy storage architectures and will be covered in Section 3. The optimisation of the proportion of power cell to energy cell mass allows for the overall HESS performance to be tailored to any application requirements and will be discussed in Section 4. A high-level evaluation method using the Ragone plot is then presented in Section 5. Further design constraints due to the duty cycle and packaging is considered in Section 6.

3. Hybrid Energy Storage Topologies

There is significant literature describing the different topologies that can be used to achieve a hybrid energy storage system. Across all the different architectures, there are two primary categories: passive systems, which do not incorporate any power electronics in the architecture, and active systems, which use power electronics to enhance the capability of the system [38,39,40,41,42].

The primary advantage of a passive HESS system (shown in Figure 2) is that it adds no power electronics weight and costs. However, the split in discharge and charge is only determined by the overall difference in internal resistance between the two packs and therefore enables limited control. The energy storage performance of one pack may also limit the performance of the other pack, such as the maximum usable degree of discharge, as well as the maximum power during discharging or charging. Furthermore, for a passive system, both packs must have the same nominal voltage. Pack sizing is therefore strictly constrained by the operating voltage range and the passive power split.

An active HESS offers significantly more control and design flexibility compared to a passive system. A DC-DC converter can be used to decouple one of the energy storage systems from the main bus or a DC-DC converter may also be used on both packs to decouple the entire system. Both types of active topologies enable independently controlling the power drawn from the packs and allow each pack to be designed for different voltages. The advantage of the single-DC-DC-converter topology is that it adds less weight, has a lower cost and incurs lower power losses. However, the double-DC-DC-converter architecture offers full control over the DC bus voltage at the inverter and can be helpful for pack voltage design, as well as the inverter and motor performance.

In summary, including one or two DC/DC converters to create an active system will improve the control of the link voltage, allow for better control of the power split and ultimately allow for downsizing of the pack. These benefits will need to be traded off against the additional weight and cost of the DC/DC converter.

4. Challenges and Trade-Offs of Hybrid Energy Storage Sizing

To achieve the desired power and energy targets, a HESS needs to be designed with the appropriate power-to-energy ratio. A simple optimisation tool was developed to optimise this ratio by assuming that the HESS was designed mainly to achieve peak power and energy requirements, such as a vehicle’s attributes of peak power and range. The methodology only focussed on weight and volume, explicitly ignoring cost, temperature or lifetime. However, the inclusion of a packaging factor did indirectly account for control, monitoring and thermal management, which would impact these factors.

The HESS analysis for this was be based on an ‘active’ topology using a single DC/DC converter, which enabled supplying maximum power simultaneously from both the energy and power source. In this way, the work focussed only on the mass of the cells. Subsequently, with a small level of added complexity, the sensitivity of the total mass to the power electronics power density and efficiency was included; this provided an insight into the realistic total HESS mass and volume.

Based on this principle, the total weight of the HESS and optimal split between the mass of energy and power cells could be calculated using Equations (2)–(4):

$$Energy Target=Eden{s}_{ECell}\times m_{ECellET}+Eden{s}_{PCell}\times m_{PCellET}$$

(2)

$$Power Target=Pden{s}_{ECell}\times m_{ECellPT}+Pden{s}_{PCell}\times m_{PCellPT}$$

(3)

$$Total Mass=\max (m_{ECellET}+m_{PCellET}, m_{ECellPT}+m_{PCellPT })$$

(4)

where $m_{ECellET}$ and $m_{ECellPT}$ correspond to the energy cell mass for the energy and power target and $m_{PCellET}$ and $m_{PCellPT}$ correspond to the power cell mass for the energy and power target. $Eden{s}_{PCell}$ and $Eden{s}_{ECell}$ correspond to the specific energy of the energy- and power-optimised cell and $Pden{s}_{Pcell}$ and $Pden{s}_{ECell}$ correspond to the specific power of the energy- and power-optimised cell. The total mass is the overall mass of energy and power cells, which satisfies both the power and energy target (whichever is greatest). The results of this were plotted for different ratios of power cell mass to total cell mass to work out which ratio achieved the lowest overall mass.

4.1. Impact of Application’s PE Ratio Requirement on HESS Sizing

The following sections illustrate using the tool for optimising the overall mass of a HESS for two different PE ratio applications. As a starting point, the cells with the highest power and energy density must be selected for the HESS to increase the weight-saving potential. For example, two specific power and energy cells that could have been selected from the available cell options presented in Figure 1 are as follows:

• The power cell has an approximate power and energy density of 8000 W/kg and 80 Wh/kg, respectively (PE ratio 100);
• The energy cell has an approximate power and energy density of 800 W/kg and 400 Wh/kg, respectively (PE ratio 2).

Figure 3a,b shows the results of using the hybrid cell mass for the two applications, where the x-axis represents the proportion of the total HESS mass that is dedicated to power-dense cells and the y-axis represents the normalised total cell mass. The mass of the system at the extremities of the x-axis represents a SESS using either only the energy cell or power cell.

The first application represents a relatively low PE ratio of 5 and the second application represents a higher PE ratio of 20. It is evident for both cases that there is an optimum ratio of power to total cell mass that achieves the lowest overall mass. This ratio represents the point where the system achieves exactly the required energy and power targets. Below this ratio, the system will have excess energy to achieve the power target, and above this ratio, the system will have excess power to achieve the energy target.

The main difference between both applications is that the one with a lower PE ratio required a lower optimal proportion of power cell mass (~12%), whereas the high PE ratio application required a higher overall optimal proportion of power cell mass (~60%). This was because the higher the system’s relative power target to its energy target, the more it became useful to increase the proportion of power cells with respect to energy cells.

It is also evident that if a single energy storage system was developed using either only the energy cell or only the power cell (the extremities of the graph), both would result in a significantly heavier system.

It can also be noted that by varying the proportion of the power pack relative to the whole pack, this enables any overall energy or any power density of the HESS to be achieved if it is between the values of the power and energy cell used for the system. In other words, the HESS’s overall PE ratio can be designed to be almost any value between that of the high power and high energy cell PE ratios. This same concept also applies to optimising the system for volume.

4.2. Impact of Energy Storage Technology Performance on HESS Sizing

The cell mass optimisation tool can also be used to demonstrate the effects of changing the performance of the two energy storage technologies used for the HESS. Figure 4a,b demonstrates how the mass optimisation curves’ changes when changing the power density of the power-optimised source and the energy density of the energy-optimised source. Both figures demonstrate this impact for the previous applications requiring PE ratios of 5 and 20. In both figures, the x-axis represents the proportion of the total HESS mass that is dedicated to power-dense cells and the y-axis shows the total mass of all cells, which were normalised such that 100% relates to the mass of using energy or power cells only (whichever was highest).

As expected, increasing the power density in Figure 4a resulted in a lower overall cell mass; however, it also caused the optimal power to total cell mass proportion to decrease. This was because a smaller power pack could be used to achieve the overall power target, but this also required a slightly larger energy pack for the system to still have the same overall energy; therefore, both these factors contributed to the decrease in the proportion of power cell mass. Interestingly, the weight savings were more noticeable for application 2 since it had a higher PE ratio and therefore a higher proportion of power cell mass.

In Figure 4b, increasing the energy density of the energy-optimised source also achieved an overall mass reduction of the system, shifting the optimal point to a larger proportion of power cell mass. This occurred because the energy target could be achieved with a smaller energy pack, but this required a slightly larger power pack for the system to still achieve the same peak power level. In this case, the mass reduction was more pronounced in the low PE application as it had a larger total energy cell mass.

4.3. Impact of Power Electronics Performance on HESS Sizing

As discussed in Section 3, to allow for significant control over the hybrid energy storage system, power electronics need to be implemented in the architecture. An analysis of the impact of using DC/DC converters on either the power or energy pack was considered for the two previous application cases investigated.

The first impact of the DC/DC converter was that it added a new path of losses for the energy storage system. This means that whichever pack was connected to a DC/DC converter experienced a reduction of the pack’s total useful energy, as well as its maximum power output. In other words, the cell’s power and energy density were reduced by the DC/DC converter efficiency. This effect was added to the HESS optimisation curves for a DC/DC converter with an efficiency of 100%, 90% and 80%. The results are shown in Figure 5a for the case of the DC/DC converter on the energy pack and in Figure 5b for the DC/DC converter on the power pack.

The DC/DC converter losses on both the energy and power pack clearly increased the overall cell mass required to achieve the same power and energy targets compared to an ideal DC/DC converter with no losses. This occurred because the pack size connected to the DC/DC converter needed to be increased to deliver the same performance without DC/DC converter losses. Consequently, this changed the ideal proportions of power and energy cell masses. Placing the DC/DC converter on the energy pack increased the optimal proportion of energy cell mass, whilst placing the DC/DC converter on the power pack decreased the optimal proportion for the energy cell mass.

For the energy pack DC/DC converter, this had more of an impact on the low PE application as it had a larger proportion of energy pack mass. Conversely, for the DC/DC converter on the power pack, the impact was greater on the higher PE application. Comparing the two architectures, it can be noted that for efficiency purposes, a DC/DC converter on the power pack was more effective on an application with a low PE ratio, whereas a DC/DC converter on the energy pack was more effective for a high PE ratio application. These findings will however also depend on the PE ratio on the individual energy- and power-optimised cells.

The second impact the DC/DC converter had on the HESS performance was the added weight and volume of the device to the system. The DC/DC converter weight also decreased the energy storage system’s overall energy and power densities. This could be accounted for by considering the added DC/DC converter’s mass or volume that was added to the system based on the DC/DC converter’s power density. For example, a 10 kW/kg DC/DC converter on a 1 kW/kg battery means that 0.1 kg of DC/DC converter mass is added for each kW of battery power, resulting in a system power density reduction to 0.909 kW/kg. If the battery was originally rated for 100 Wh/kg, then this also reduces to 90.9 Wh/kg. This will be the same case for the volumetric power and energy density, which will however instead depend on the DC/DC converter’s volumetric power density.

Figure 6a,b shows the effect of a single 5 kW/kg or 10 kW/kg DC/DC converter on the system, positioned either on the energy or the power pack. The figures show both the resultant sum of the cell and the DC/DC converter’s mass. In the case of the DC/DC converter on the energy pack (Figure 6a), increasing the proportion of the power pack decreased the DC/DC converter’s weight as it reduced the power required to go through the DC/DC converter. Instead, for the DC/DC converter on the power pack (Figure 6b), reducing the power pack proportion clearly reduced the DC/DC converter’s mass as it required a smaller amount of power to pass through the device.

Evidently, using a DC/DC converter with a lower power density rating always added more weight to the systems for all the cases shown. Yet, for the two different PE ratio applications investigated, the DC/DC converter’s mass had a significantly lower impact on the high-PE-ratio system when used on the energy pack. These results will vary depending on the PE ratio chosen for the high-energy and high-power sources.

5. High-Level Sizing Method for Hybrid Energy Storage System

5.1. Theoretical Pareto-Front-Based Gravimetric and Volumetric Saving

The high-level weight and volumetric saving of an active topology HESS for different powertrain applications can be evaluated based on an alteration to the Ragone plot shown in Figure 1.

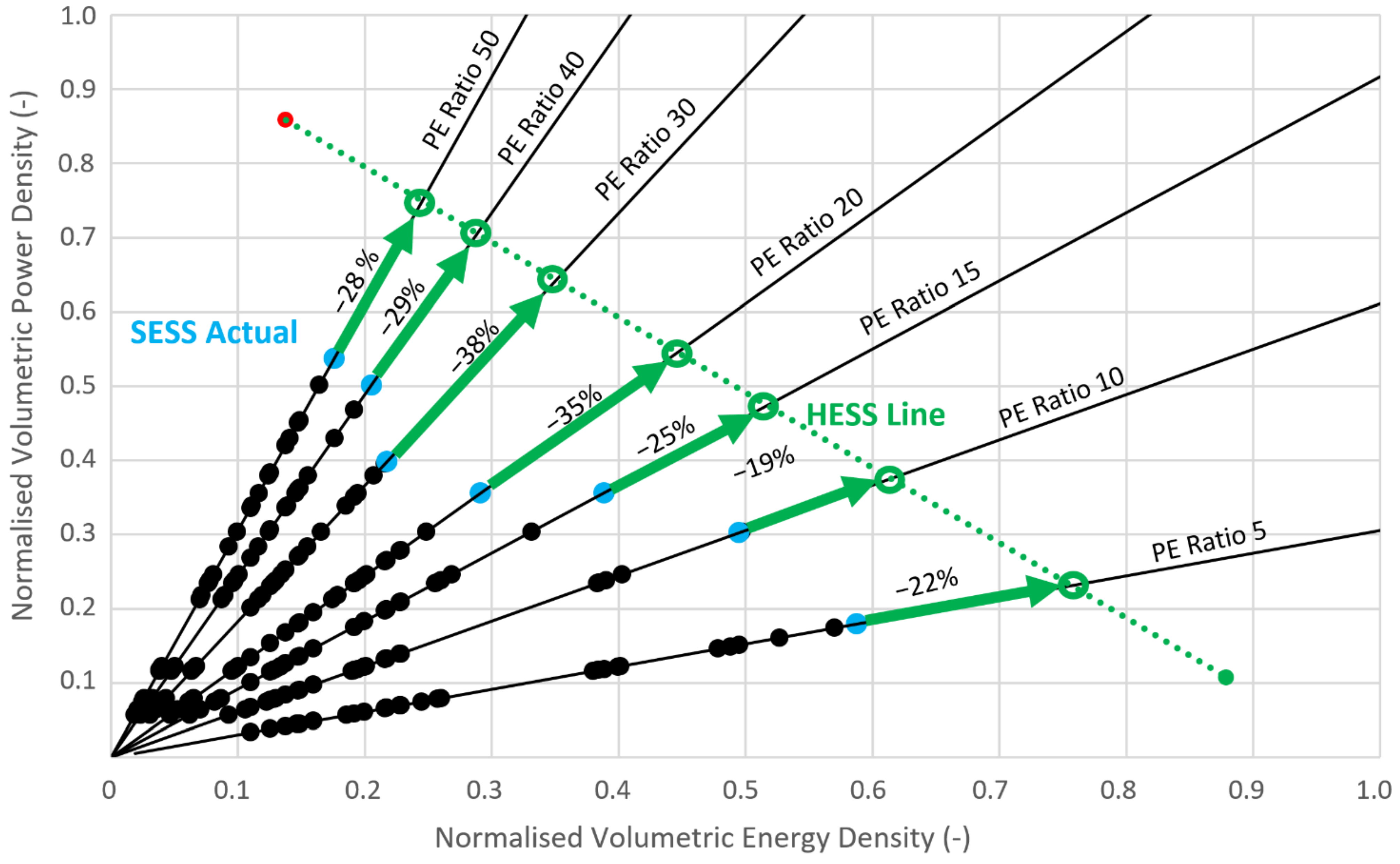
Using the gravimetric and volumetric Pareto front found for current electrochemical energy storage technology, various constant PE ratio lines were added to represent the target PE ratio that would be required for a certain application. For example, low-performance applications with high-energy (or high-range) targets would inherently have a very low PE ratio requirement, whilst high-performance applications with relatively low-energy (or low-range) targets would result in a high PE ratio.

Where the PE ratio line crosses the Pareto front line represents the theoretical best-case single energy storage system for that application. This is a theoretical best-case scenario because there might not be cell technology available with that exact PE ratio along the Pareto front, even if it were designed by the cell manufacturer as a bespoke product.

The best possible HESS performance was represented by a line that connects the most power-dense and energy-dense technologies. This summarised all the possible HESS combinations with a PE ratio in between that of a single power and energy cell. Each of these combinations had the optimal split of power-cell-to-energy-cell mass ratio for a specific PE ratio (as shown in Section 4.1 with the previous analysis tool).

Moving along the HESS line, the closer the HESS PE ratio was to that of the single power or energy cell, the greater the proportion of the power or energy cell mass. This is also indicated in Figure 7 and Figure 8 for each HESS that coincided with the illustrated PE lines. This ranged from an 82% power-cell-to-total-cell mass ratio for a PE ratio of 50 to a 13% power-cell-to-total-cell mass ratio for a PE ratio of 5. Both figures were obtained by assuming an active parallel topology with a single DC/DC converter but ignoring the mass of the DC/DC converter itself.

The final weight- or volume-saving percentage between a HESS and SESS could therefore be calculated for each PE line based on either the energy or power density differences of the two systems. The values calculated for each PE ratio were also added to the figures.

It is evident from this comparison that the PE ratio of the application would have a large impact on the effectiveness of a HESS. For the cells presented, a PE ratio between 20 to 10 demonstrated the greatest mass saving potential of over 33%; however, applications with a PE ratio closer to that of the energy cell or power cell enabled smaller weight savings.

Similar results were also seen when using this same graphical HESS analysis for the volumetric density. Figure 8 was created in a similar fashion to the gravimetric analysis; however, it used the highest volumetric power and energy-dense sources as the HESS building blocks. These resulted in the same cells used for the gravimetric plot. This figure indicates that based on these technologies, the greatest volumetric saving was over 30% for an application with a PE ratio between 20 and 10. However, for lower and higher PE-ratio applications, the volumetric savings were less noticeable.

If cost data were available for each of these cells, a cell cost per unit mass analysis could also be achieved using this same method; however, this was outside the scope of this study.

5.2. Practical HESS Gravimetric and Volumetric Savings

The theoretical Pareto front analysis is very effective at identifying the potential savings of a HESS compared to a theoretical SESS. However, in practice, there can be even greater savings because there are only a finite number of cells that exist near the SESS Pareto front. This section presents an additional technique that enables comparing a HESS against a finite number of SESS cell technologies.

To compare a finite number of cells, their effective power or energy density must be adjusted for the targeted PE line in the Ragone plot; this way they all show their performance along the same PE line. Cells with a higher PE ratio can be assessed with a de-rated usable power density, and the cells with a lower PE ratio can be assessed with a lower usable energy density, as shown in Equations (5) and (6). This effectively means that cells with an excessive PE ratio will need to be sized for energy, and cells with lower PE ratios will be sized for power.

$$Cell PE ratio>P{E}_{target}\to PDen{s}_{usable}=P{E}_{target}\ast Edens$$

(5)

$$Cell PE ratio<P{E}_{target}\to EDen{s}_{usable}=\frac{PDens}{P{E}_{target}}$$

(6)

Figure 9 and Figure 10 show the results for this analysis using the available commercial cells in Figure 1. The best-performing SESS for each PE ratio was highlighted and compared to the achievable performance of a HESS. This placed all cell technologies on the same PE ratio line (represented by black circles) and enabled a clear comparison of which SESS was best for a specific application PE ratio.

Figure 9 shows all the cells fitted to the individual PE lines, as well as the original HESS performance line. Interestingly, even greater weight savings could be seen for most PE ratios, with the greatest being over 40% at a PE ratio of 15. This was due to comparing only limited cell options, considering the case that the ideal or desirable single cell might not exist.

This highlights one of the other advantages of a HESS, namely, the ability to be tailored to meet any PE ratio of an application whilst making the most of the available cell technology. A SESS, on the other hand, may need to be compromised or the application may need to be forced to use a different and possibly less desirable PE ratio.

Similar analysis can also be carried out for volumetric performance, as shown in Figure 10. In this case, for certain PE ratios, the performance savings were also higher compared to the theoretical Pareto front. However, for certain PE ratios, this analysis showed slightly lower volumetric savings. This was because some cell technologies did not fit the original theoretical Pareto front curve and exceeded the Pareto front line. As explained earlier, this was most likely due to the Pareto front attempting to fit cell technologies that were developed in different periods.

6. Further Design Constraints and Duty Cycle Considerations

6.1. Maximum and Minimum PE Ratio

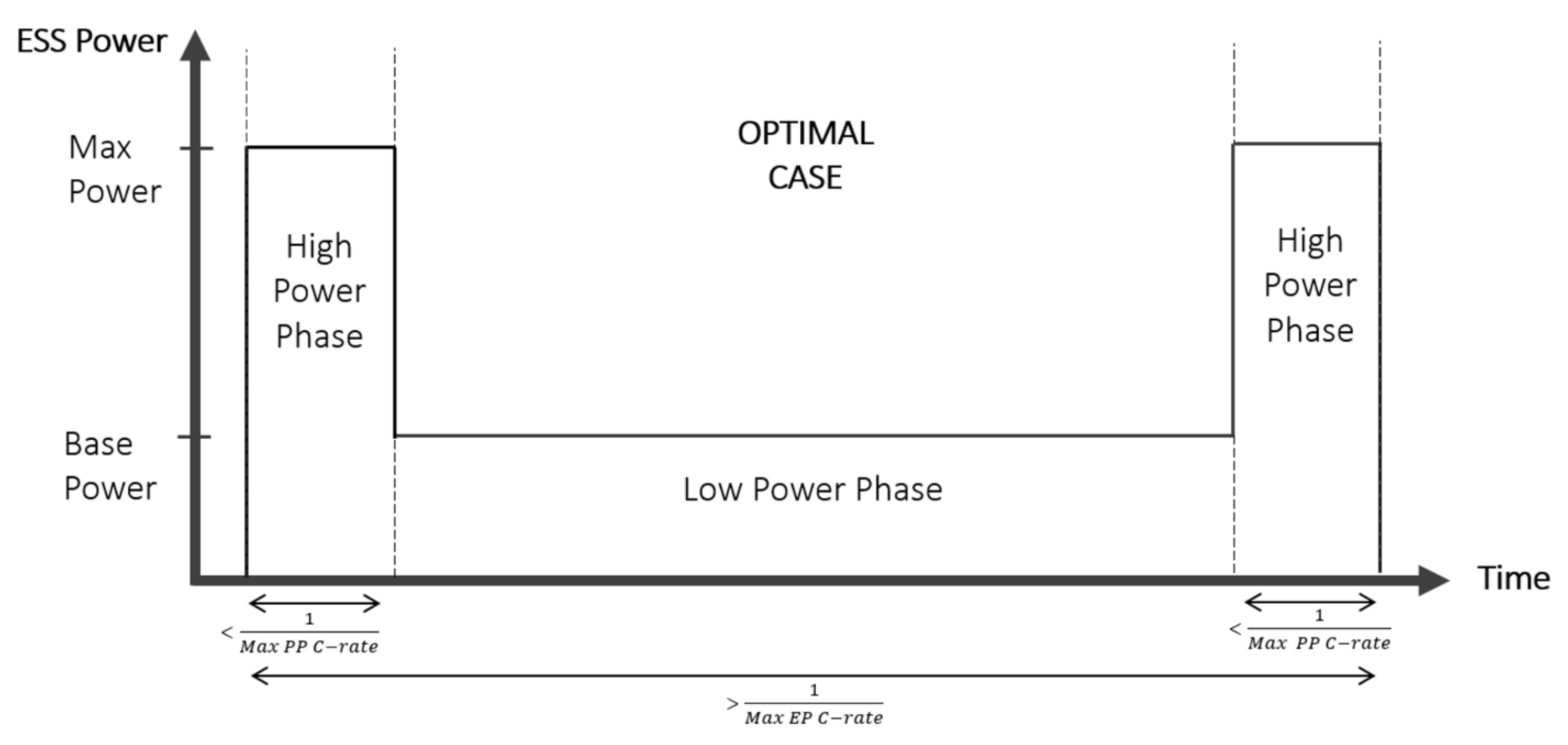
An important design consideration for a HESS is the maximum allowable PE ratio (or maximum C-rate) for the power source and the minimum allowable PE ratio (or minimum C-rate) for the energy source. These two criteria are defined using the most aggressive duty cycle requirements of the application.

The maximum PE ratio is determined by the longest duration of peak discharge. The power source should not operate above the maximum cycle PE ratio and may need to be de-rated for the application or it would risk running out of energy. On the other hand, the minimum PE ratio limit is set by the overall duty cycle duration. If the energy source operates at a PE ratio below the minimum requirement, it will not deploy all its energy within the duty cycle duration. The net effect of both these limits is a cap on the ‘useful’ power and energy density of the power and energy cells.

A simplified optimal duty cycle that would not impose maximum or minimum PE ratio limits for a HESS is shown in Figure 11. As shown, the peak power duration must not exceed the power cell discharge time at maximum C-rate, and the overall cycle duration must not be below the energy cell discharge time at its maximum C-rate.

This duty cycle does not consider the impact of energy recuperation. If the energy pack also experiences periods of charging, this will increase the minimum PE ratio requirement of the energy cell as it will need to run at even higher C-rates to discharge the total energy in time. Dynamic modelling may enable a better assessment of this.

If the duty cycle does impose maximum and minimum PE ratio limits, the impact on the performance can also be considered using the Ragone plot analysis method. An example of the impact of minimum and maximum PE ratios was added to the HESS graphs in Figure 12 and Figure 13. Figure 12 represents a design that required maximum peak power for just over 50 s. This means the maximum PE ratio was reduced from the original power cell value of 100 down to 70. The lower HESS line in Figure 13 represents a design limit set by the duty cycle duration completing within 20 min. This means the minimum PE ratio of the energy cell was therefore increased from the original values of 2 to a value of 3.

The maximum PE ratio limit clearly shows how the maximum power density of the power cell was limited and therefore was reduced, which shifted the HESS line closer to the performance of the SESS. This had less of an impact at low PE ratios, as at a PE ratio of 5, the weight saving only dropped from 33 to 31%, but had more of an impact for high PE ratios, where the PE 50 case dropped from 35 to only 5%.

The minimum PE ratio increased to 3 instead shows that the useful energy density of the energy cell was reduced, which moved the HESS performance line closer to the performance of a SESS. In this case, the high PE ratio cases were less impacted, with the PE 50 case dropping from 35 to 30%, but for the low PE ratio cases, such as PE 5, this dropped the savings from 33 to 2%.

6.2. Sensitivity to Packaging Weight and Volume

The packaging factor is another important aspect to consider when comparing energy and power packs used for a HESS. The packaging factor for a battery pack is defined as the ratio of cell mass to the overall pack mass. This ratio depends on numerous factors and is difficult to estimate. Packaging density may worsen for power-optimised packs that require more cooling or are of smaller size, but very little data is available from manufacturers.

Currently, the best packaging factor for commercial vehicles is approximately 70% found on the Tesla Model 3, which uses an 18,650-cylindrical-cell format from Panasonic [43]. This pack is large and a more energy-optimised pack with a maximum PE ratio of approximately 3.5 based on the vehicle’s attributes (258 kW/74 kWh). Various sources estimate the cell density to be approximately 265 Wh/kg [44]. This would indicate the cell is used at a power density of approximately 1000 W/kg.

To understand the HESS sensitivity to packaging factor variations, a worst-case scenario of packaging effectiveness was set as 50% at the highest power pack power density, and 75% at zero power density. This was also assessed against a scenario assuming a constant packaging factor of 70%. The results are shown in Figure 14a,b.

Comparing the two cases, it is evident that the scenario considering a packaging factor variation between 50 to 75% enabled lower weight saving compared to the constant packaging ratio case for all pack power densities. However, the impact was greater for a higher PE ratio (−35% vs. −28%), where a large power pack is needed. Conversely, the impact on a low PE ratio system was much smaller (−33% vs. −31%) since the power pack mass was a smaller proportion of the overall mass.

7. Limitations of the Proposed Methodology

The proposed methodology enables a time-efficient analysis of different cell technologies and their effectiveness for a HESS. The evaluation is generated with negligible computing power as long as power and energy density specifications for the candidate cell technologies are available. This makes the approach ideal for use at the early stages of the design process to make key technology and topology choices. Nevertheless, battery performance is sensitive to numerous factors and will vary based on the assessment conditions. For this reason, the Ragone-based approach may present limitations when used for the later stages of a detailed design.

The main limitation is capturing peak power and energy variations with time, temperature and state of charge (SoC). In theory, each cell could be more accurately represented by a curve to describe the cell’s variation in energy retention and power at different C-rates. Multiple curves would also be required to capture variations due to the SoC and temperature. For illustration purposes and the overall objective of this tool, the cell was represented as a single point using the most appropriate power and energy density.

For this analysis, the peak power density was only based on a generic 10 s value and at 50% SoC. This can be adjusted to better reflect the requirement for the duty cycle; however, it will not capture the impact of the dynamic power variations across the full duty cycle.

Consideration of a duty cycle requiring both varying degrees of pack discharging and charging can also be substantially more complex. The sizing will become strictly linked to the control strategy. In extreme cases, sizing can also be focused on to meet the maximum cycle charging power requirement rather than discharge power requirement. For more complex duty cycles, dynamic simulations need to be conducted to make an accurate assessment.

The final drawback of the proposed methodology is that it ignores the packaging limitations of cells and modules for the appropriate electrical configuration. This will primarily impact the combinations of energy and power pack sizes that can be implemented for the HESS, and therefore only allows for a discrete number of solutions along the HESS line for different PE ratios. If a specific PE ratio cannot be achieved, the HESS sizing would need to be compromised.

The proposed work presented here could be used in conjunction with the more detailed optimisation-based analysis presented in [29], where the Ragone-based approach can pre-select the most interesting cell technology combinations prior to constructing a detailed electrochemical model that will overcome the limitations discussed above.

8. Conclusions

This paper presents a novel method to understand the trade-offs when designing a HESS and conduct a swift evaluation of many variants of HESS systems for numerous applications without using in-depth simulation or optimisation algorithms. The work focussed on mixing different types of Li-ion batteries with a range of power-dense and energy-dense battery chemistries. The approach is based on a Ragone plot and does not require the use of a detailed electrochemical model and thus allows for an effective evaluation of different energy storage technologies at an early stage of the design process.

Through using the tool, it was shown that the largest theoretical weight savings from a HESS occurred at a PE ratio between 10 and 30. These savings were above 30% compared to a single energy storage system. However, even at PE ratios of 5 and 50, there were still potential savings of 26% and 22%, respectively. The actual weight savings are higher as only a finite set of real battery chemistries are available on the market, meaning the compromise for a single energy storage system is worse than in an ideal case. When this factor is considered, the weight savings could be over 40%.

In addition to the cell chemistry, five other factors are important and underpin the effectiveness of a HESS: the DC/DC converter topology, the performance of power electronics, the application duty cycle and PE ratio, the minimum/maximum PE limits and the system integration of the cells characterised by a packaging factor.

The DC/DC converter topology, efficiency and power density have an impact on the overall weight, partly because of the physical addition of power electronics, but also because the DC/DC converter will introduce a loss that is dependent on the power passing through it. This impacts the optimal split of cell types and must be considered simultaneously with the cell selection. For example, it was illustrated that the overall HESS mass was particularly sensitive to the power electronics power density if the DC/DC converter was located on the power cells and used in a high PE ratio application.

The duty cycle and the time-varying nature of the power demand of the HESS create additional constraints on the system that are not captured simply through an overall PE ratio. In particular, the maximum C-rate applied to the power cells might have to be reduced at certain periods of the duty cycle to avoid the power cells running out of energy. This effectively means that more power cells are required, which reduces the achievable power density. High-PE-ratio applications are more strongly affected by the required power cells C-rate limit: for an application PE ratio of 50, if the duty cycle required an in-cycle limit PE ratio of 70, then the saving in overall weight from the HESS over the SESS reduced from 35 to just 5%.

The packaging factor is a real constraint for battery design and is expected to be worse for hybrid packs, reducing the expected benefit in weight saving from 40 to 35% for a PE ratio of 20. The effect was smaller for lower PE ratios. This is also dependent on the relative packaging factors of the HESS power and energy pack.

The work presented within this paper will underpin the development of future energy storage systems and allow for an effective assessment of HESS at an early stage in the design process, thus facilitating their adoption in future products. Although the framework was applied exclusively to Li-ion cell technologies within this work, it can also be used to encompass other energy storage forms, provided their characteristics can be expressed in terms of power and energy density.