Durable Fast Charging of Lithium-Ion Batteries Based on Simulations with an Electrode Equivalent Circuit Model
Abstract
:1. Introduction
2. Material and Methods
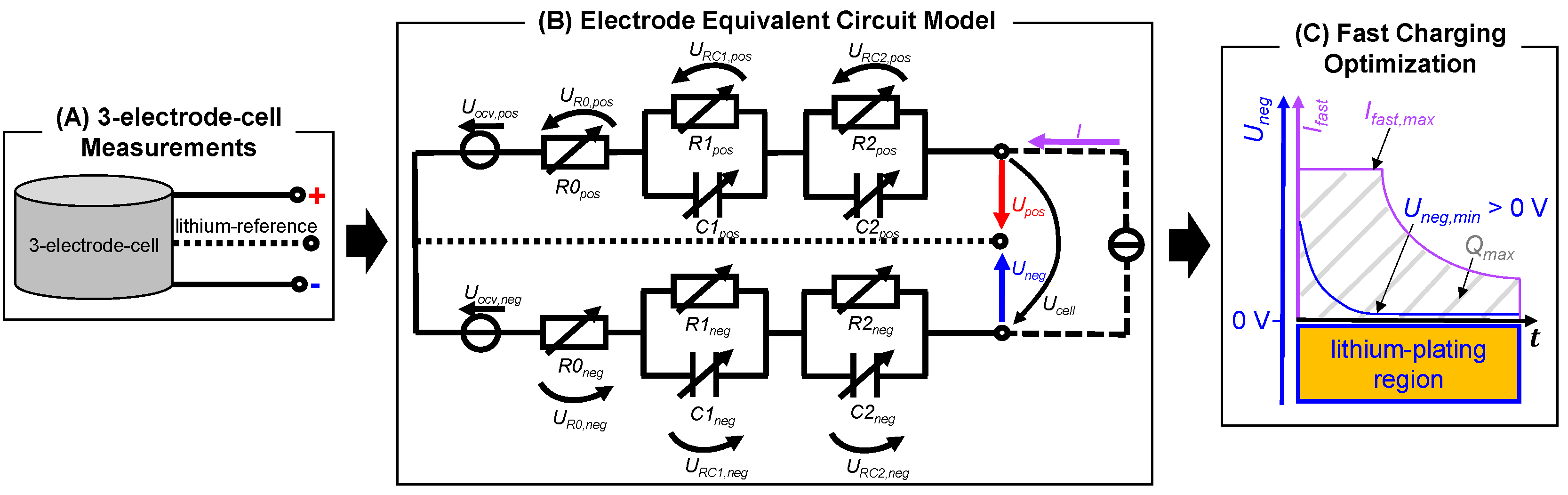
2.1. Advanced Electrode Equivalent Circuit Model
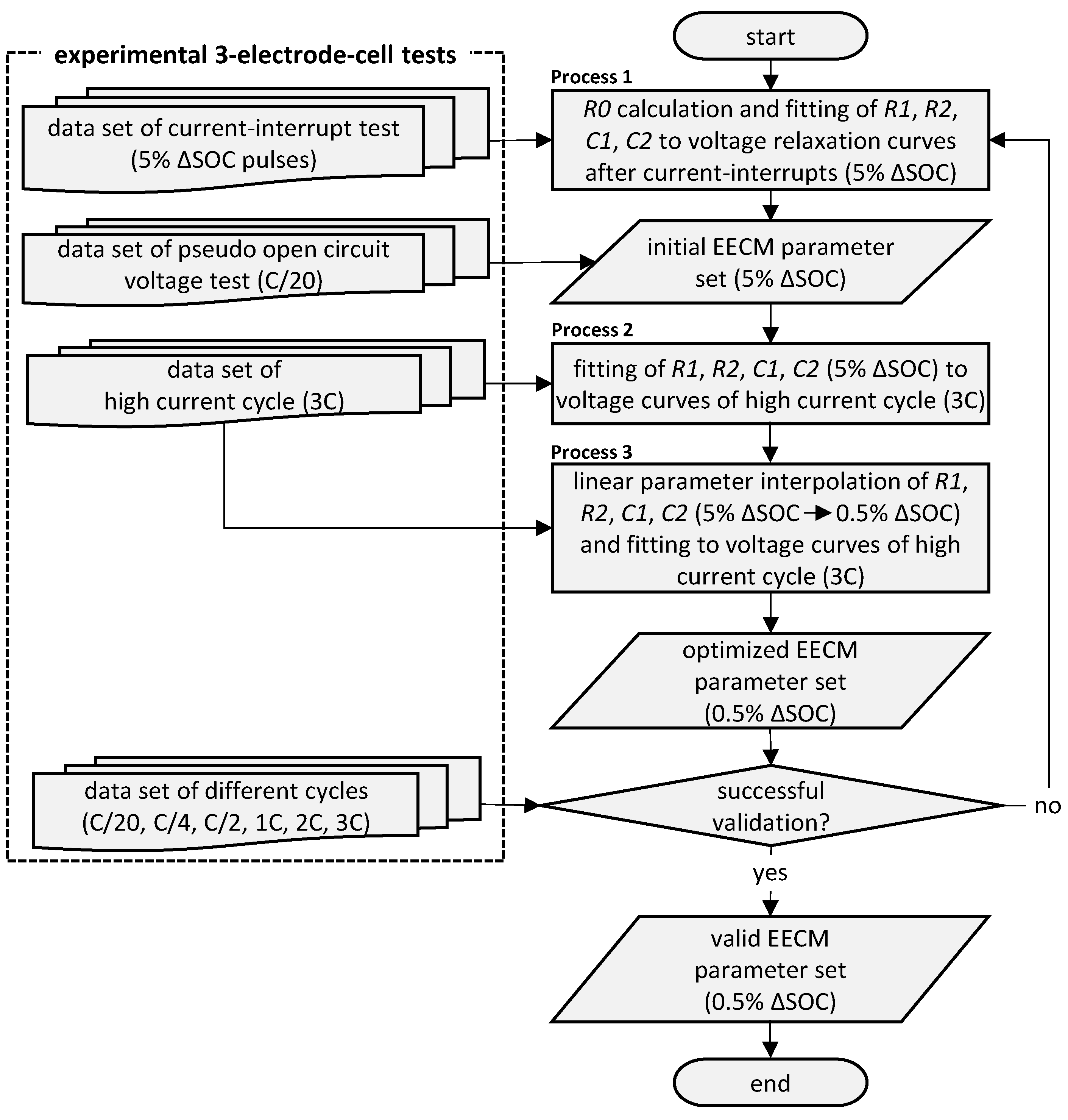
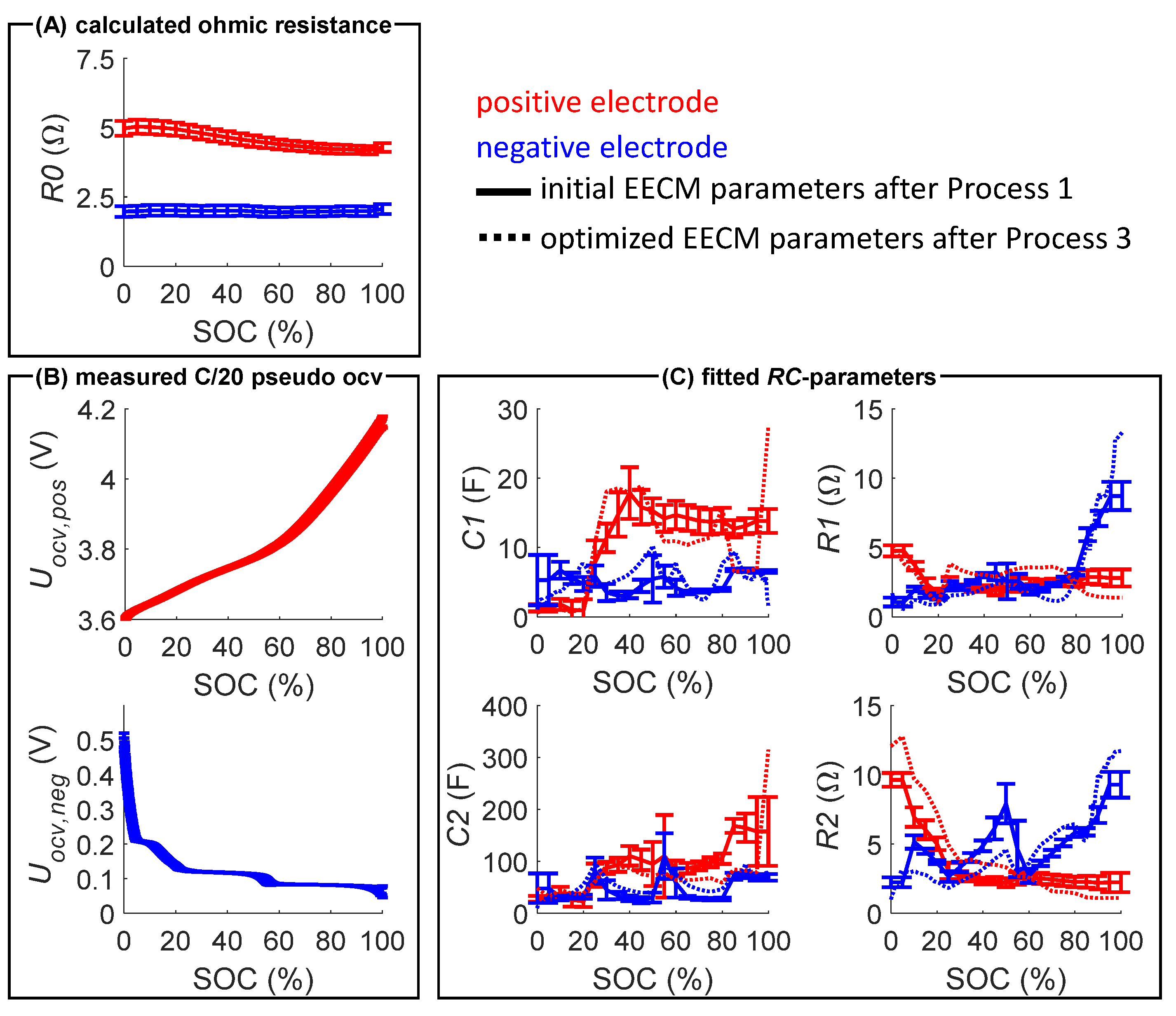
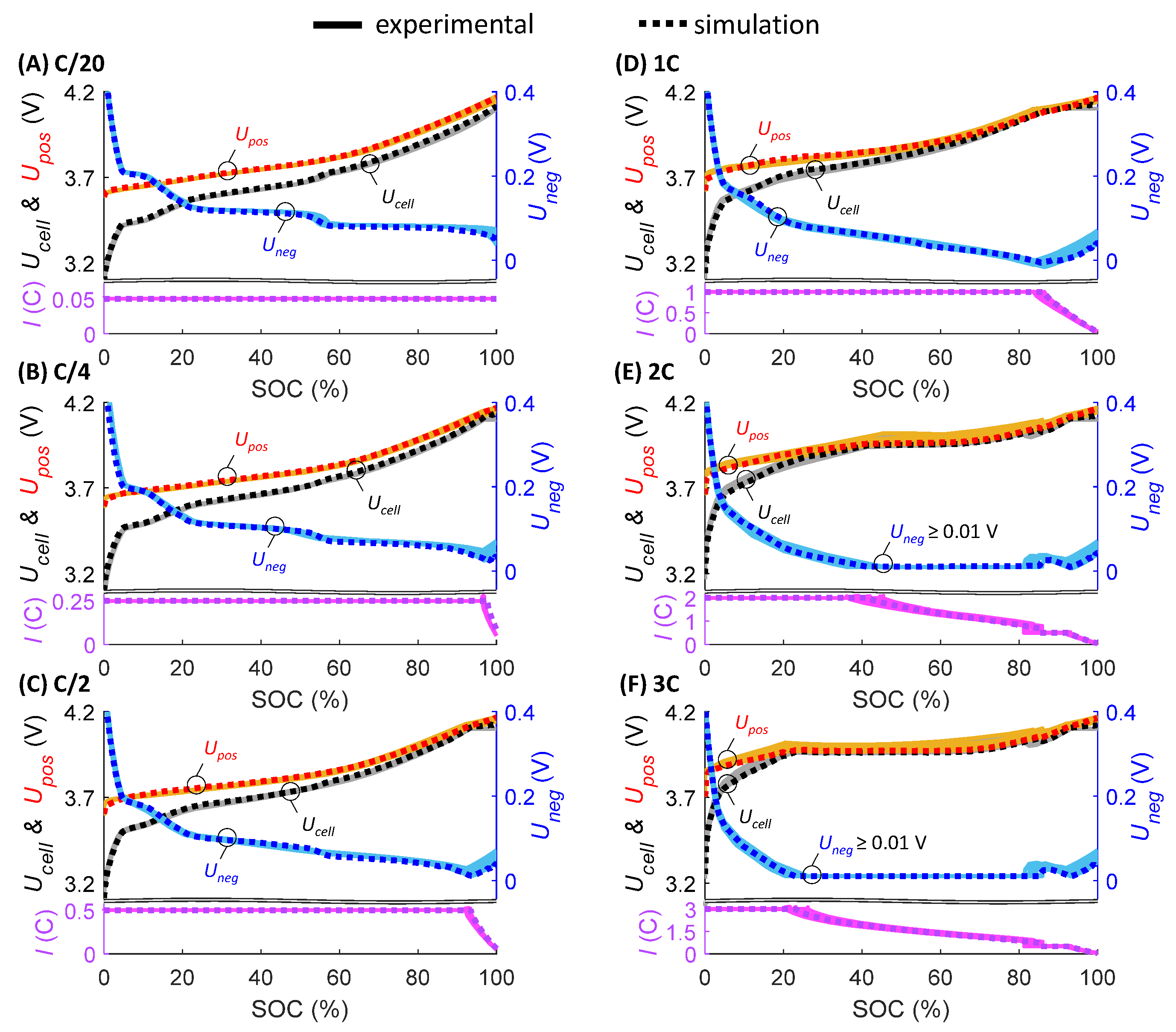
2.2. Model Parameterization and Validation
3. Results
3.1. Model-Based Design of Different Fast-Charging Strategies
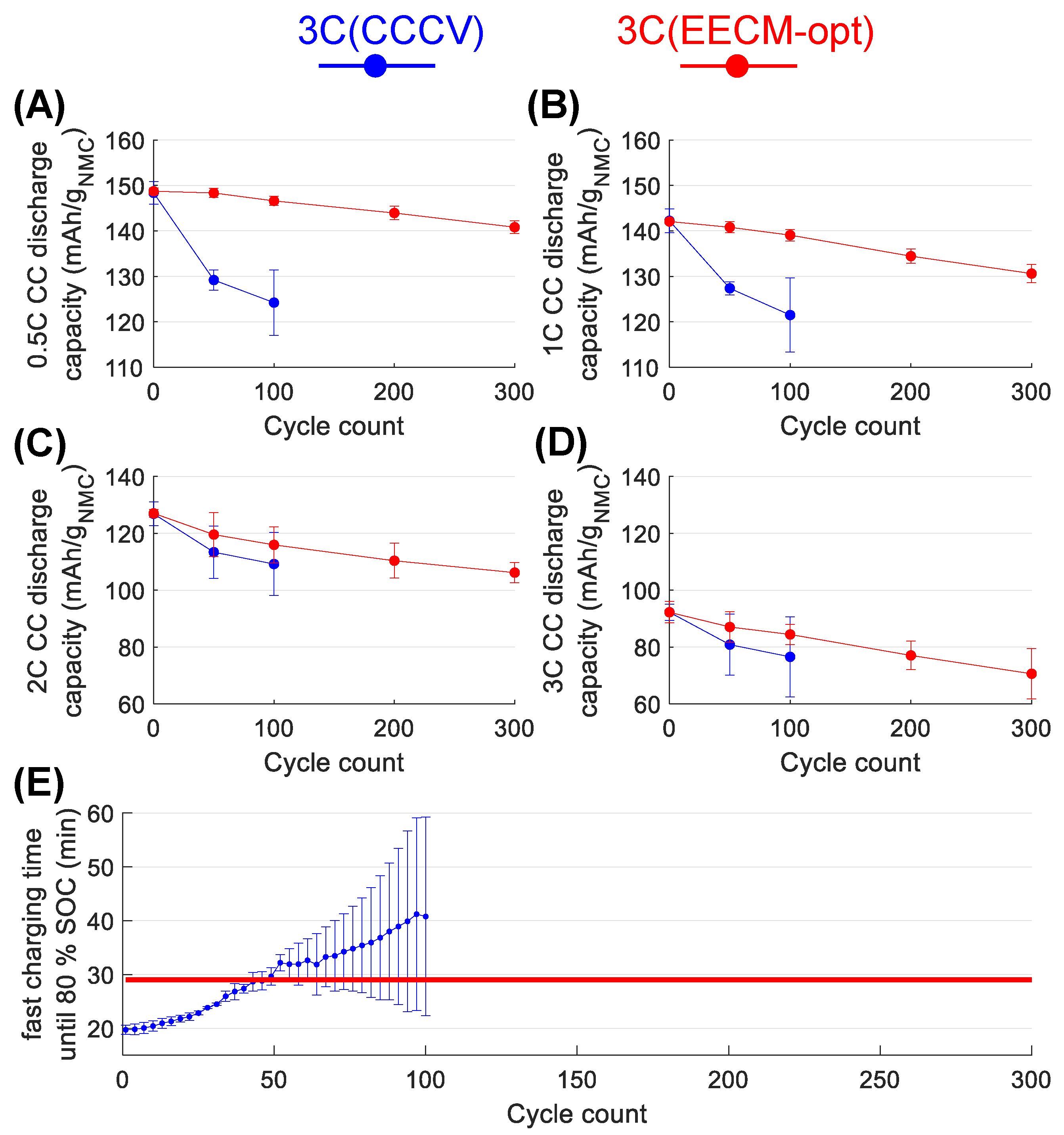
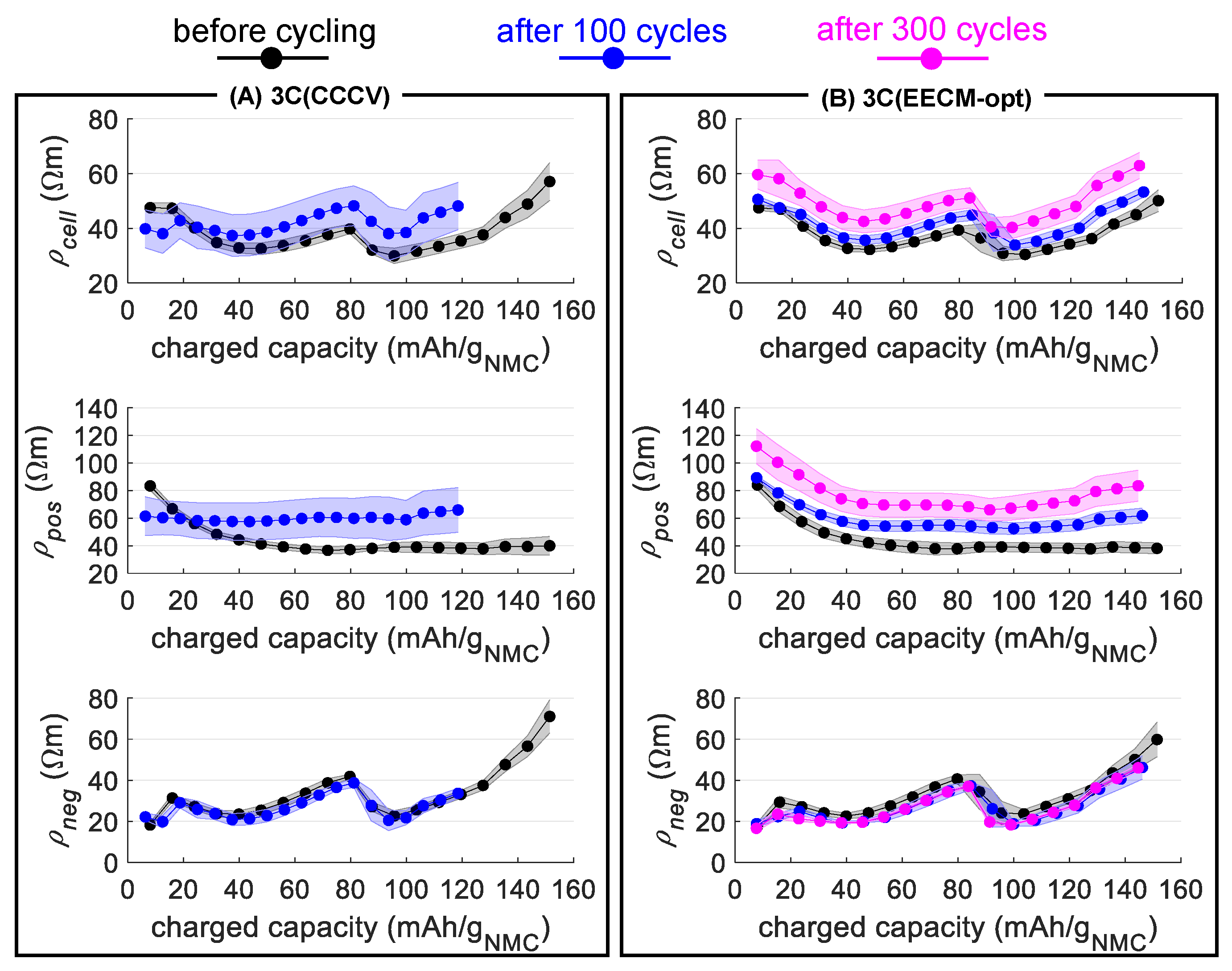
3.2. Experimental Fast-Charging Cycling and Assessment
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hwang, S.; Kim, D.-H.; Shin, J.H.; Jang, J.E.; Ahn, K.H.; Lee, C.; Lee, H. Ionic Conduction and Solution Structure in LiPF 6 and LiBF 4 Propylene Carbonate Electrolytes. J. Phys. Chem. C 2018, 122, 19438–19446. [Google Scholar] [CrossRef]
- Lain, M.J.; Brandon, J.; Kendrick, E. Design Strategies for High Power vs. High Energy Lithium Ion Cells. Batteries 2019, 5, 64. [Google Scholar] [CrossRef] [Green Version]
- Tomaszewska, A.; Chu, Z.; Feng, X.; O’Kane, S.; Liu, X.; Chen, J.; Ji, C.; Endler, E.; Li, R.; Liu, L.; et al. Lithium-ion battery fast charging: A review. eTransportation 2019, 1, 100011. [Google Scholar] [CrossRef]
- Botsford, C.; Szczepanek, A. Fast Charging vs. Slow Charging: Pros and cons for the New Age of Electric Vehicles. In Proceedings of the EVS24 International Battery, Hybrid and Fuel Cell Electric Vehicle Symposium, Stavanger, Norway, 13–16 May 2009. [Google Scholar]
- U.S. Advanced Battery Consortium. USABC Electric Vehicle Battery Test Procedures Manual: Revision 2. 1996. Available online: https://www.osti.gov/biblio/214312-usabc-electric-vehicle-battery-test-procedures-manual-revision (accessed on 22 July 2021).
- Zhu, G.-L.; Zhao, C.-Z.; Huang, J.-Q.; He, C.; Zhang, J.; Chen, S.; Xu, L.; Yuan, H.; Zhang, Q. Fast Charging Lithium Batteries: Recent Progress and Future Prospects. Small 2019, 15, e1805389. [Google Scholar] [CrossRef]
- Yang, X.-G.; Liu, T.; Gao, Y.; Ge, S.; Leng, Y.; Wang, D.; Wang, C.-Y. Asymmetric Temperature Modulation for Extreme Fast Charging of Lithium-Ion Batteries. Joule 2019, 3, 3002–3019. [Google Scholar] [CrossRef]
- Chen, S.; Bao, N.; Garg, A.; Peng, X.; Gao, L. A Fast Charging–Cooling Coupled Scheduling Method for a Liquid Cooling-Based Thermal Management System for Lithium-Ion Batteries. Engineering 2021, 7, 1165–1176. [Google Scholar] [CrossRef]
- Zhang, S.S.; Xu, K.; Jow, T.R. Study of the charging process of a LiCoO2-based Li-ion battery. J. Power Sources 2006, 160, 1349–1354. [Google Scholar] [CrossRef]
- Edge, J.S.; O’Kane, S.; Prosser, R.; Kirkaldy, N.D.; Patel, A.N.; Hales, A.; Ghosh, A.; Ai, W.; Chen, J.; Yang, J.; et al. Lithium ion battery degradation: What you need to know. Phys. Chem. Chem. Phys. 2021, 23, 8200–8221. [Google Scholar] [CrossRef]
- Broussely, M.; Herreyre, S.; Biensan, P.; Kasztejna, P.; Nechev, K.; Staniewicz, R. Aging mechanism in Li ion cells and calendar life predictions. J. Power Sources 2001, 97–98, 13–21. [Google Scholar] [CrossRef]
- Vetter, J.; Novák, P.; Wagner, M.R.; Veit, C.; Möller, K.-C.; Besenhard, J.O.; Winter, M.; Wohlfahrt-Mehrens, M.; Vogler, C.; Hammouche, A. Ageing mechanisms in lithium-ion batteries. J. Power Sources 2005, 147, 269–281. [Google Scholar] [CrossRef]
- Tang, M.; Albertus, P.; Newman, J. Two-Dimensional Modeling of Lithium Deposition during Cell Charging. J. Electrochem. Soc. 2009, 156, A390. [Google Scholar] [CrossRef]
- Cannarella, J.; Arnold, C.B. The Effects of Defects on Localized Plating in Lithium-Ion Batteries. J. Electrochem. Soc. 2015, 162, A1365–A1373. [Google Scholar] [CrossRef] [Green Version]
- Liu, Q.; Du, C.; Shen, B.; Zuo, P.; Cheng, X.; Ma, Y.; Yin, G.; Gao, Y. Understanding undesirable anode lithium plating issues in lithium-ion batteries. RSC Adv. 2016, 6, 88683–88700. [Google Scholar] [CrossRef]
- Uhlmann, C.; Illig, J.; Ender, M.; Schuster, R.; Ivers-Tiffée, E. In situ detection of lithium metal plating on graphite in experimental cells. J. Power Sources 2015, 279, 428–438. [Google Scholar] [CrossRef]
- Qian, Y.; Shang, J.; Liu, D.; Yang, G.; Wang, X.; Chen, C.; Kou, L.; Lei, W. Enhanced Ion Sieving of Graphene Oxide Membranes via Surface Amine Functionalization. J. Am. Chem. Soc. 2021, 143, 5080–5090. [Google Scholar] [CrossRef] [PubMed]
- Zhou, S.; Xie, L.; Zhang, L.; Wen, L.; Tang, J.; Zeng, J.; Liu, T.; Peng, D.; Yan, M.; Qiu, B.; et al. Interfacial Super-Assembly of Ordered Mesoporous Silica-Alumina Heterostructure Membranes with pH-Sensitive Properties for Osmotic Energy Harvesting. ACS Appl. Mater. Interfaces 2021, 13, 8782–8793. [Google Scholar] [CrossRef] [PubMed]
- Xu, R.; Kang, Y.; Zhang, W.; Zhang, X.; Pan, B. Oriented UiO-67 Metal-Organic Framework Membrane with Fast and Selective Lithium-Ion Transport. Angew. Chem. Int. Ed. Engl. 2022, 61, e202115443. [Google Scholar] [CrossRef] [PubMed]
- Zhou, S.; Xie, L.; Yan, M.; Zeng, H.; Zhang, X.; Zeng, J.; Liang, Q.; Liu, T.; Chen, P.; Jiang, L.; et al. Super-assembly of freestanding graphene oxide-aramid fiber membrane with T-mode subnanochannels for sensitive ion transport. Analyst 2022, 147, 652–660. [Google Scholar] [CrossRef]
- Waldmann, T.; Iturrondobeitia, A.; Kasper, M.; Ghanbari, N.; Aguesse, F.; Bekaert, E.; Daniel, L.; Genies, S.; Gordon, I.J.; Löble, M.W.; et al. Review—Post-Mortem Analysis of Aged Lithium-Ion Batteries: Disassembly Methodology and Physico-Chemical Analysis Techniques. J. Electrochem. Soc. 2016, 163, A2149–A2164. [Google Scholar] [CrossRef]
- Burns, J.C.; Stevens, D.A.; Dahn, J.R. In-Situ Detection of Lithium Plating Using High Precision Coulometry. J. Electrochem. Soc. 2015, 162, A959–A964. [Google Scholar] [CrossRef]
- Waldmann, T.; Hogg, B.-I.; Wohlfahrt-Mehrens, M. Li plating as unwanted side reaction in commercial Li-ion cells–A review. J. Power Sources 2018, 384, 107–124. [Google Scholar] [CrossRef]
- Petzl, M.; Danzer, M.A. Nondestructive detection, characterization, and quantification of lithium plating in commercial lithium-ion batteries. J. Power Sources 2014, 254, 80–87. [Google Scholar] [CrossRef]
- Schindler, S.; Bauer, M.; Petzl, M.; Danzer, M.A. Voltage relaxation and impedance spectroscopy as in-operando methods for the detection of lithium plating on graphitic anodes in commercial lithium-ion cells. J. Power Sources 2016, 304, 170–180. [Google Scholar] [CrossRef]
- Waldmann, T.; Quinn, J.B.; Richter, K.; Kasper, M.; Tost, A.; Klein, A.; Wohlfahrt-Mehrens, M. Electrochemical, Post-Mortem, and ARC Analysis of Li-Ion Cell Safety in Second-Life Applications. J. Electrochem. Soc. 2017, 164, A3154–A3162. [Google Scholar] [CrossRef] [Green Version]
- Dotoli, M.; Milo, E.; Giuliano, M.; Rocca, R.; Nervi, C.; Baricco, M.; Ercole, M.; Sgroi, M.F. Detection of Lithium Plating in Li-Ion Cell Anodes Using Realistic Automotive Fast-Charge Profiles. Batteries 2021, 7, 46. [Google Scholar] [CrossRef]
- Rangarajan, S.P.; Sarkar, S.; Barsukov, Y.; Mukherjee, P.P. 3ε-A Versatile Operando Analytics Toolbox in Energy Storage. ACS Omega 2021, 6, 33284–33292. [Google Scholar] [CrossRef]
- Perumaram Rangarajan, S.; Barsukov, Y.; Mukherjee, P.P. Plating energy as a universal descriptor to classify accelerated cell failure under operational extremes. Cell Rep. Phys. Sci. 2022, 3, 100720. [Google Scholar] [CrossRef]
- Xie, W.; Liu, X.; He, R.; Li, Y.; Gao, X.; Li, X.; Peng, Z.; Feng, S.; Feng, X.; Yang, S. Challenges and opportunities toward fast-charging of lithium-ion batteries. J. Energy Storage 2020, 32, 101837. [Google Scholar] [CrossRef]
- Doyle, M.; Fuller, T.F.; Newman, J. Modeling of galvanostatic charge and discharge of the lithium/polymer/insertion cell. J. Electrochem. Soc. 1993, 140, 1526–1533. [Google Scholar] [CrossRef]
- Daigle, M.; Kulkarni, C.S. Electrochemistry-based Battery Modeling for Prognostics. In Proceedings of the Annual Conference of the Prognostics and Health Management Society, New Orleans, LA, USA, 14–17 October 2013. [Google Scholar] [CrossRef]
- Daigle, M.; Kulkarni, C.S. End-of-Discharge and End-of-Life Prediction in Lithium-Ion Batteries with Electrochemistry-Based Aging Models; AIAA Infotech @ Aerospace, American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2016. [Google Scholar] [CrossRef] [Green Version]
- Arora, P.; Doyle, M.; White, R.E. Mathematical Modeling of the Lithium Deposition Overcharge Reaction in Lithium-Ion Batteries Using Carbon-Based Negative Electrodes. J. Electrochem. Soc. 1999, 146, 3543–3553. [Google Scholar] [CrossRef] [Green Version]
- Klein, R.; Chaturvedi, N.A.; Christensen, J.; Ahmed, J.; Findeisen, R.; Kojic, A. Optimal Charging Strategies in Lithium-Ion Battery. In Proceedings of the 2011 American Control Conference, San Francisco, CA, USA, 29 June–1 July 2011; Available online: http://ieeexplore.ieee.org/servlet/opac?punumber=5975310 (accessed on 22 March 2022).
- Klein, R.; Chaturvedi, N.A.; Christensen, J.; Ahmed, J.; Findeisen, R.; Kojic, A. Electrochemical Model Based Observer Design for a Lithium-Ion Battery. IEEE Trans. Contr. Syst. Technol. 2013, 21, 289–301. [Google Scholar] [CrossRef]
- Chu, Z.; Feng, X.; Lu, L.; Li, J.; Han, X.; Ouyang, M. Non-destructive fast charging algorithm of lithium-ion batteries based on the control-oriented electrochemical model. Appl. Energy 2017, 204, 1240–1250. [Google Scholar] [CrossRef]
- Rangarajan, S.P.; Barsukov, Y.; Mukherjee, P.P. Anode potential controlled charging prevents lithium plating. J. Mater. Chem. A 2020, 8, 13077–13085. [Google Scholar] [CrossRef]
- Epding, B.; Rumberg, B.; Mense, M.; Jahnke, H.; Kwade, A. Aging-Optimized Fast Charging of Lithium Ion Cells Based on Three-Electrode Cell Measurements. Energy Technol. 2020, 8, 2000457. [Google Scholar] [CrossRef]
- Koleti, U.R.; Zhang, C.; Malik, R.; Dinh, T.Q.; Marco, J. The development of optimal charging strategies for lithium-ion batteries to prevent the onset of lithium plating at low ambient temperatures. J. Energy Storage 2019, 24, 100798. [Google Scholar] [CrossRef]
- Lu, B.; Zhao, Y.; Song, Y.; Zhang, J. Stress-limited fast charging methods with time-varying current in lithium-ion batteries. Electrochim. Acta 2018, 288, 144–152. [Google Scholar] [CrossRef]
- Xu, M.; Wang, R.; Zhao, P.; Wang, X. Fast charging optimization for lithium-ion batteries based on dynamic programming algorithm and electrochemical-thermal-capacity fade coupled model. J. Electrochem. Soc. 2019, 438, 227015. [Google Scholar] [CrossRef]
- Laue, V.; Röder, F.; Krewer, U. Practical identifiability of electrochemical P2D models for lithium-ion batteries. J. Appl Electrochem 2021, 51, 1253–1265. [Google Scholar] [CrossRef]
- Parvini, Y.; Vahidi, A. Maximizing charging efficiency of lithium-ion and lead-acid batteries using optimal control theory. In Proceedings of the American Control Conference (ACC), Chicago, IL, USA, 1–3 July 2015; pp. 317–322. [Google Scholar] [CrossRef]
- Wang, J. Charging strategy studies for phev batteries based on power loss model. In Proceedings of the SAE 2010 World Congress and Exhibition, Detroit, MO, USA, 13–15 April 2010. [Google Scholar] [CrossRef]
- Chen, Z.; Xia, B.; Mi, C.C.; Xiong, R. Loss-Minimization-Based Charging Strategy for Lithium-Ion Battery. IEEE Trans. Ind. Applicat. 2015, 51, 4121–4129. [Google Scholar] [CrossRef]
- Khamar, M.; Askari, J. A Charging Method for Lithium-Ion Battery Using Min-Max Optimal Control. In Proceedings of the 2014 22nd Iranian Conference on Electrical Engineering (ICEE), Tehran, Iran, 20–22 May 2014. [Google Scholar] [CrossRef]
- Zhang, C.; Jiang, J.; Gao, Y.; Zhang, W.; Liu, Q.; Hu, X. Charging optimization in lithium-ion batteries based on temperature rise and charge time. Appl. Energy 2017, 194, 569–577. [Google Scholar] [CrossRef]
- von Srbik, M.-T.; Marinescu, M.; Martinez-Botas, R.F.; Offer, G.J. A physically meaningful equivalent circuit network model of a lithium-ion battery accounting for local electrochemical and thermal behaviour, variable double layer capacitance and degradation. J. Power Sources 2016, 325, 171–184. [Google Scholar] [CrossRef] [Green Version]
- Gantenbein, S.; Weiss, M.; Ivers-Tiffée, E. Impedance based time-domain modeling of lithium-ion batteries: Part I. J. Power Sources 2018, 379, 317–327. [Google Scholar] [CrossRef]
- Merla, Y.; Wu, B.; Yufit, V.; Martinez-Botas, R.F.; Offer, G.J. An easy-to-parameterise physics-informed battery model and its application towards lithium-ion battery cell design, diagnosis, and degradation. J. Power Sources 2018, 384, 66–79. [Google Scholar] [CrossRef]
- Drees, R.; Lienesch, F.; Kurrat, M. Fast charging lithium-ion battery formation based on simulations with an electrode equivalent circuit model. J. Energy Storage 2021, 36, 102345. [Google Scholar] [CrossRef]
- Westerhoff, U.; Kurbach, K.; Lienesch, F.; Kurrat, M. Analysis of Lithium-Ion Battery Models Based on Electrochemical Impedance Spectroscopy. Energy Technol. 2016, 4, 1620–1630. [Google Scholar] [CrossRef] [Green Version]
- The MathWorks. Curve Fitting Toolbox. Available online: https://de.mathworks.com/products/curvefitting.html (accessed on 2 July 2021).
- The MathWorks. Parameter Estimation. Available online: https://de.mathworks.com/discovery/parameter-estimation.html (accessed on 2 July 2021).
- The MathWorks. 1-D Data Interpolation-Function: Interp1. Available online: https://de.mathworks.com/help/matlab/ref/interp1.html (accessed on 2 July 2021).
- Lewerenz, M. Dissection and Quantitative Description of Aging of Lithium-Ion Batteries Using Non-Destructive Methods Validated by Post-Mortem-Analyses; RWTH Aachen University: Aachen, Germany, 2018. [Google Scholar]
- Ruess, R.; Schweidler, S.; Hemmelmann, H.; Conforto, G.; Bielefeld, A.; Weber, D.A.; Sann, J.; Elm, M.T.; Janek, J. Influence of NCM Particle Cracking on Kinetics of Lithium-Ion Batteries with Liquid or Solid Electrolyte. J. Electrochem. Soc. 2020, 167, 100532. [Google Scholar] [CrossRef]
- An, S.J.; Li, J.; Daniel, C.; Mohanty, D.; Nagpure, S.; Wood, D.L. The state of understanding of the lithium-ion-battery graphite solid electrolyte interphase (SEI) and its relationship to formation cycling. Carbon 2016, 105, 52–76. [Google Scholar] [CrossRef] [Green Version]


| Positive Electrode | Negative Electrode | |
|---|---|---|
| active material | NMC622 | SMG-A5 |
| current collector | 20 μm aluminum | 10 μm copper |
| coating thickness | 68 μm | 82 μm |
| calendered coating density | 3 g/cm3 | 1.3 g/cm3 |
| cross-sectional area | 2.54 cm2 | 2.54 cm2 |
| active material percentage | 95.5% | 93.0% |
| theoretical areal capacity | 3.41 mAh/cm2 | 3.60 mAh/cm2 |
| electrolyte | 100 μL 1.0M LiPF6 in EC:EMC (3:7) + 2% VC | |
| separator | 260 μm Whatman GF/A with lithium reference ring | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Drees, R.; Lienesch, F.; Kurrat, M. Durable Fast Charging of Lithium-Ion Batteries Based on Simulations with an Electrode Equivalent Circuit Model. Batteries 2022, 8, 30. https://doi.org/10.3390/batteries8040030
Drees R, Lienesch F, Kurrat M. Durable Fast Charging of Lithium-Ion Batteries Based on Simulations with an Electrode Equivalent Circuit Model. Batteries. 2022; 8(4):30. https://doi.org/10.3390/batteries8040030
Chicago/Turabian StyleDrees, Robin, Frank Lienesch, and Michael Kurrat. 2022. "Durable Fast Charging of Lithium-Ion Batteries Based on Simulations with an Electrode Equivalent Circuit Model" Batteries 8, no. 4: 30. https://doi.org/10.3390/batteries8040030
APA StyleDrees, R., Lienesch, F., & Kurrat, M. (2022). Durable Fast Charging of Lithium-Ion Batteries Based on Simulations with an Electrode Equivalent Circuit Model. Batteries, 8(4), 30. https://doi.org/10.3390/batteries8040030






