Co-Estimation of State-of-Charge and State-of-Health for High-Capacity Lithium-Ion Batteries
Abstract
:1. Introduction
2. Materials and Methods
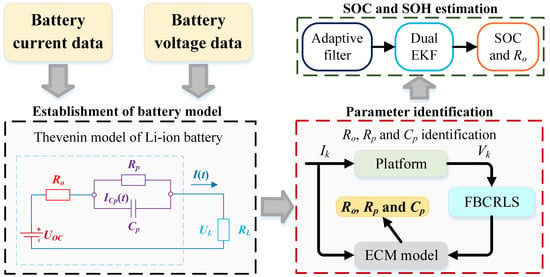
2.1. Modeling of Battery Equivalent Circuit
2.2. FFBCRLS Parameter Identification
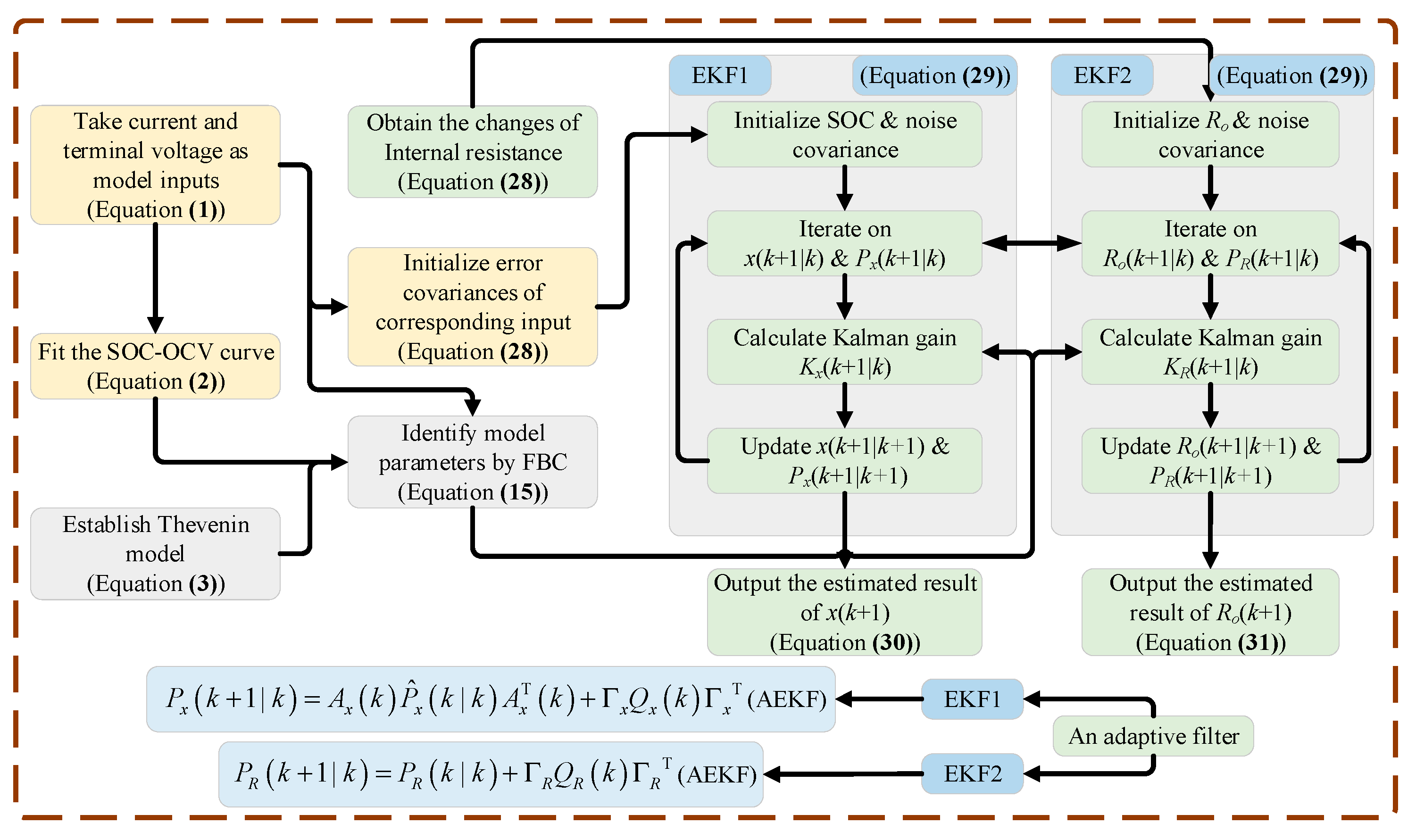
2.3. Principle of the DAEKF Approach
2.4. Calculation Process of the DAEKF Approach
3. Results
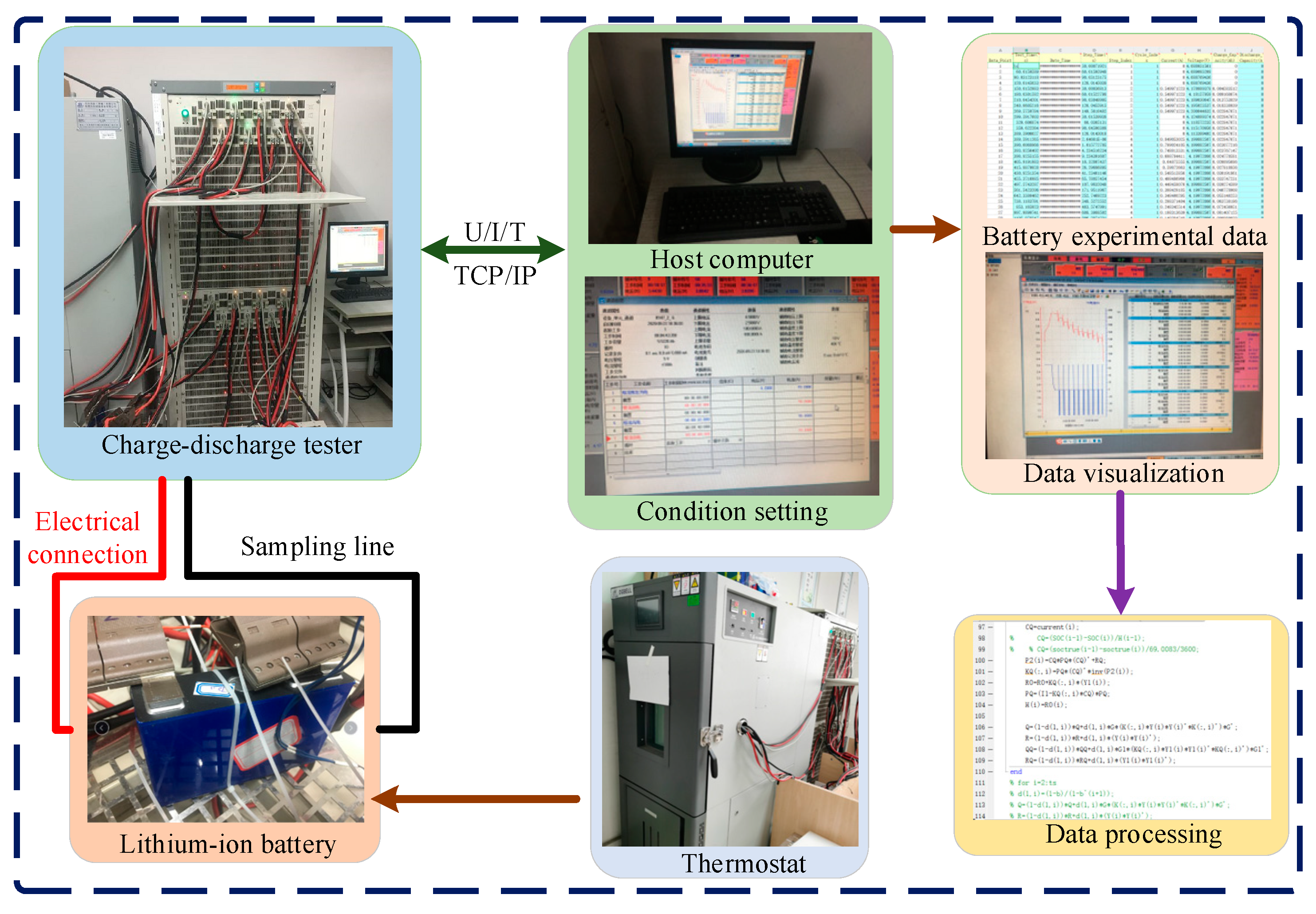
3.1. Experimental Platform and Corresponding Setup
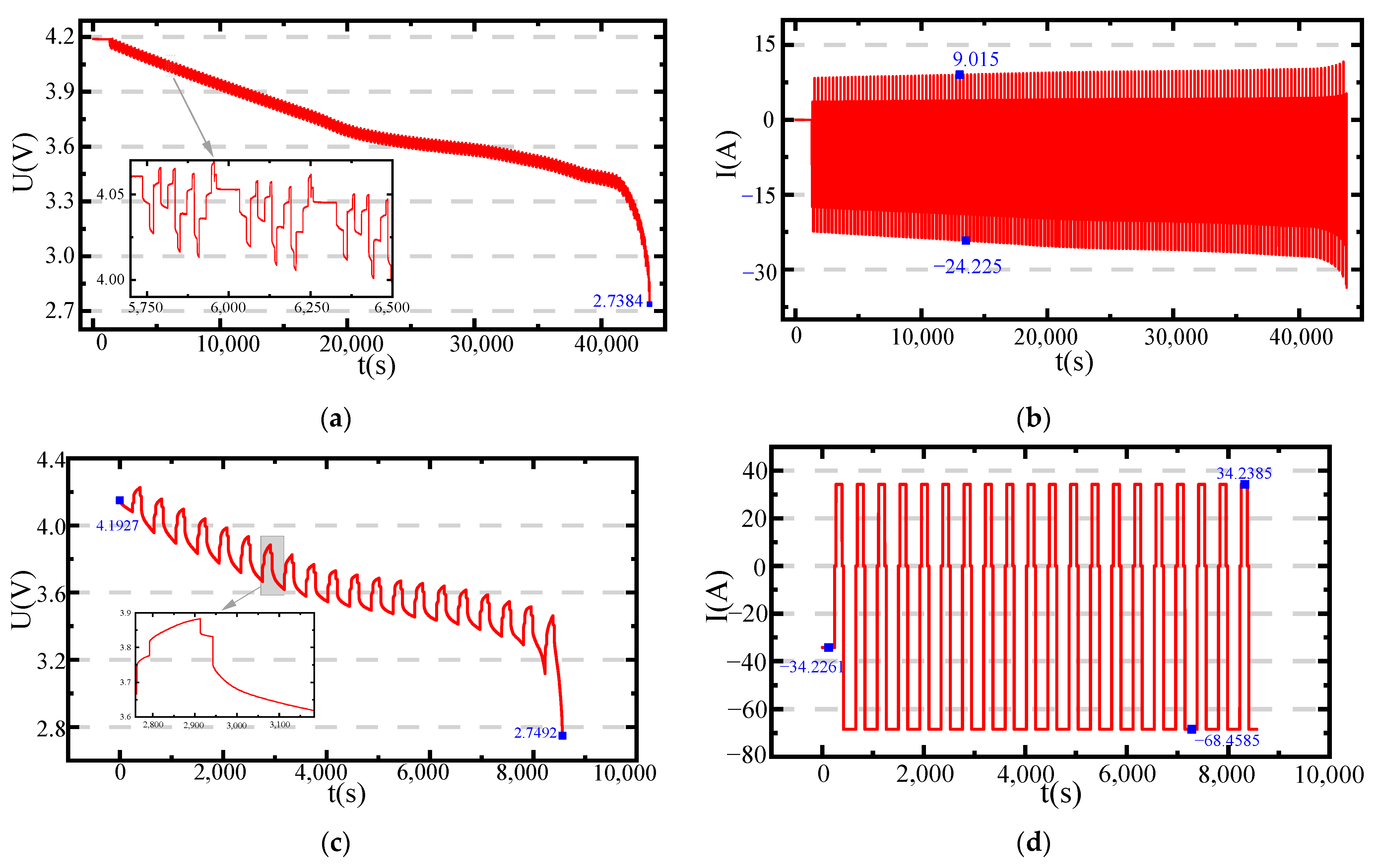
3.2. Identification Results and Model Verification
3.3. Estimation Analysis under Complicated Conditions
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chen, Y.; Huang, D.; Zhu, Q.; Liu, W.; Liu, C.; Xiong, N. A new state of charge estimation algorithm for lithium-ion batteries based on the fractional unscented Kalman filter. Energies 2017, 10, 1313. [Google Scholar] [CrossRef]
- Sun, F. Green Energy and Intelligent Transportation—promoting green and intelligent mobility. Green Energy Intell. Transp. 2022, 1, 100017. [Google Scholar] [CrossRef]
- Li, X.; Huang, Z.; Tian, J.; Tian, Y. State-of-charge estimation tolerant of battery aging based on a physics-based model and an adaptive cubature Kalman filter. Energy 2021, 220, 119767. [Google Scholar] [CrossRef]
- Mawonou, K.S.R.; Eddahech, A.; Dumur, D.; Beauvois, D.; Godoy, E. Improved state of charge estimation for Li-ion batteries using fractional order extended Kalman filter. J. Power Sources 2019, 435, 226710. [Google Scholar] [CrossRef]
- Jia, Y.; Luo, G.; Zhang, Y. Development of optimal speed trajectory control strategy for electric vehicles to suppress battery aging. Green Energy Intell. Transp. 2022, 1, 100030. [Google Scholar] [CrossRef]
- Xiong, R.; Kim, J.; Shen, W.; Lv, C.; Li, H.; Zhu, X.; Zhao, W.; Gao, B.; Guo, H.; Zhang, C.; et al. Key technologies for electric vehicles. Green Energy Intell. Transp. 2022, 1, 100041. [Google Scholar] [CrossRef]
- Farzin, H.; Fotuhi-Firuzabad, M.; Moeini-Aghtaie, M. A practical scheme to involve degradation cost of lithium-ion batteries in vehicle-to-grid applications. IEEE Trans. Sustain. Energy 2016, 7, 1730–1738. [Google Scholar] [CrossRef]
- Feng, F.; Yang, R.; Meng, J.; Xie, Y.; Zhang, Z.; Chai, Y.; Mou, L. Electrochemical impedance characteristics at various conditions for commercial solid–liquid electrolyte lithium-ion batteries: Part 1. experiment investigation and regression analysis. Energy 2022, 242, 122880. [Google Scholar] [CrossRef]
- Ling, L.; Wei, Y. State-of-charge and state-of-health estimation for lithium-ion batteries based on dual fractional-order extended Kalman filter and online parameter identification. IEEE Access 2021, 9, 47588–47602. [Google Scholar] [CrossRef]
- Zhang, Y.; Feng, F.; Wang, S.; Meng, J.; Xie, J.; Ling, R.; Yin, H.; Zhang, K.; Chai, Y. Joint nonlinear-drift-driven Wiener process-Markov chain degradation switching model for adaptive online predicting lithium-ion battery remaining useful life. Appl. Energy 2023, 341, 121043. [Google Scholar] [CrossRef]
- Zhu, X.; Macía, L.F.; Jaguemont, J.; de Hoog, J.; Nikolian, A.; Omar, N.; Hubin, A. Electrochemical impedance study of commercial LiNi0.80Co0.15Al0.05O2 electrodes as a function of state of charge and aging. Electrochim. Acta 2018, 287, 10–20. [Google Scholar] [CrossRef]
- Jin, G.; Li, L.; Xu, Y.; Hu, M.; Fu, C.; Qin, D. Comparison of SOC estimation between the integer-order model and fractional-order model under different operating conditions. Energies 2020, 13, 1785. [Google Scholar] [CrossRef]
- Chen, Z.; Yang, L.; Zhao, X.; Wang, Y.; He, Z. Online state of charge estimation of Li-ion battery based on an improved unscented Kalman filter approach. Appl. Math. Model. 2019, 70, 532–544. [Google Scholar] [CrossRef]
- Muhammad, N.P.A.; Artono, D.S.; Hendri, W. Design a battery management system (BMS) with an automatic cut off system on LFP (LiFePO4) battery type for powerbank application. J. Phys. Conf. Ser. 2021, 1825, 012038. [Google Scholar]
- Ran, X.; Shunli, W.; Carlos, F.; Chunmei, Y.; Yongcun, F.; Wen, C.; Cong, J. A novel joint estimation method of state of charge and state of health based on the strong tracking-dual adaptive extended Kalman filter algorithm for the electric vehicle lithium-ion batteries. Int. J. Electrochem. Sci. 2021, 16, 211114. [Google Scholar]
- Cai, M.; Chen, W.; Tan, X. Battery state-of-charge estimation based on a dual unscented Kalman filter and fractional variable-order model. Energies 2017, 10, 1577. [Google Scholar] [CrossRef]
- Li, J.; Lai, Q.; Wang, L.; Lyu, C.; Wang, H. A method for SOC estimation based on simplified mechanistic model for LiFePO4 battery. Energy 2016, 114, 1266–1276. [Google Scholar] [CrossRef]
- Luo, Y.; Qi, P.; Kan, Y.; Huang, J.; Huang, H.; Luo, J.; Wang, J.; Wei, Y.; Xiao, R.; Zhao, S. State of charge estimation method based on the extended Kalman filter algorithm with consideration of time-varying battery parameters. Int. J. Energy Res. 2020, 44, 10538–10550. [Google Scholar] [CrossRef]
- Liu, K.; Hu, X.; Yang, Z.; Xie, Y.; Feng, S. Lithium-ion battery charging management considering economic costs of electrical energy loss and battery degradation. Energy Convers. Manag. 2019, 195, 167–179. [Google Scholar] [CrossRef]
- Xiaosong, H.; Kai, Z.; Kailong, L. Advanced fault diagnosis for lithium-ion battery systems: A review of fault mechanisms, fault features, and diagnosis procedures. IEEE Ind. Electron. Mag. 2020, 14, 65–91. [Google Scholar]
- Fan, Y.; Bao, Y.; Ling, C.; Chu, Y.; Tan, X.; Yang, S. Experimental study on the thermal management performance of air cooling for high energy density cylindrical lithium-ion batteries. Appl. Therm. Eng. 2019, 155, 96–109. [Google Scholar] [CrossRef]
- Feng, F.; Hu, X.; Hu, L.; Hu, F.; Li, Y.; Zhang, L. Propagation mechanisms and diagnosis of parameter inconsistency within Li-Ion battery packs. Renew. Sustain. Energy Rev. 2019, 112, 102–113. [Google Scholar] [CrossRef]
- Xu, J.; Sun, C.; Ni, Y.; Lyu, C.; Wu, C.; Zhang, H.; Yang, Q.; Feng, F. Fast identification of micro-health parameters for retired batteries based on a simplified P2D model by using padé approximation. Batteries 2023, 9, 64. [Google Scholar] [CrossRef]
- Ren, H.; Zhao, Y.; Chen, S.; Wang, T. Design and implementation of a battery management system with active charge balance based on the SOC and SOH online estimation. Energy 2019, 166, 908–917. [Google Scholar] [CrossRef]
- Feng, F.; Song, B.; Xu, J.; Na, W.; Zhang, K.; Chai, Y. Multiple time scale state-of-charge and capacity-based equalisation strategy for lithium-ion battery pack with passive equaliser. J. Energy Storage 2022, 53, 105196. [Google Scholar] [CrossRef]
- Park, J.; Lee, M.; Kim, G.; Park, S.; Kim, J. Integrated approach based on dual extended Kalman filter and multivariate autoregressive model for predicting battery capacity using health indicator and SOC/SOH. Energies 2020, 13, 2138. [Google Scholar] [CrossRef]
- Chang, C.; Zheng, Y.; Yu, Y. Estimation for battery state of charge based on temperature effect and fractional extended Kalman filter. Energies 2020, 13, 5947. [Google Scholar] [CrossRef]
- Lashway, C.R.; Mohammed, O.A. Adaptive battery management and parameter estimation through physics-based modeling and experimental verification. IEEE Trans. Transp. Electrif. 2016, 2, 454–464. [Google Scholar] [CrossRef]
- Ahmad, A.B.; Ooi, C.A.; Ishak, D.; Teh, J. State-of-charge balancing control for on/off-line internal cells using hybrid modular multi-level converter and parallel modular dual L-bridge in a grid-scale battery energy storage system. IEEE Access 2019, 7, 131–147. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, P.; Liu, Y.; Cheng, Z. Variable-order equivalent circuit modeling and state of charge estimation of lithium-ion battery based on electrochemical impedance spectroscopy. Energies 2021, 14, 769. [Google Scholar] [CrossRef]
- Stroe, D.-I.; Swierczynski, M.; Stroe, A.-I.; Kaer, S.K.; Teodorescu, R. Lithium-ion battery power degradation modelling by electrochemical impedance spectroscopy. IET Renew. Power Gener. 2017, 11, 1136–1141. [Google Scholar] [CrossRef]
- Westerhoff, U.; Kroker, T.; Kurbach, K.; Kurrat, M. Electrochemical impedance spectroscopy based estimation of the state of charge of lithium-ion batteries. J. Energy Storage 2016, 8, 244–256. [Google Scholar] [CrossRef]
- Feng, F.; Yang, R.; Meng, J.; Xie, Y.; Zhang, Z.; Chai, Y.; Mou, L. Electrochemical impedance characteristics at various conditions for commercial solid–liquid electrolyte lithium-ion batteries: Part. 2. Modeling and prediction. Energy 2022, 243, 123091. [Google Scholar] [CrossRef]
- Chen, C.; Xiong, R.; Yang, R.; Li, H. A novel data-driven method for mining battery open-circuit voltage characterization. Green Energy Intell. Transp. 2022, 1, 100001. [Google Scholar] [CrossRef]
- Sheng, H.; Xiao, J. Electric vehicle state of charge estimation: Nonlinear correlation and fuzzy support vector machine. J. Power Sources 2015, 281, 131–137. [Google Scholar] [CrossRef]
- Sun, X.; Zhong, K.; Han, M. A hybrid prognostic strategy with unscented particle filter and optimized multiple kernel relevance vector machine for lithium-ion battery. Measurement 2021, 170, 108679. [Google Scholar] [CrossRef]
- Xiaojun, T.; Di, Z.; Pengxiang, L.; Jun, R.; Yuqian, F. Online state-of-health estimation of lithium-ion battery based on dynamic parameter identification at multi timescale and support vector regression. J. Power Sources 2021, 484, 229233. [Google Scholar] [CrossRef]
- Bin, X.; Bing, X.; Luoshi, L. Rapid measurement method for lithium-ion battery state of health estimation based on least squares support vector regression. Int. J. Energy Res. 2020, 45, 5695–5709. [Google Scholar]
- Ruhatiya, C.; Gandra, R.; Kondaiah, P.; Manivas, K.; Samhith, A.; Gao, L.; Lam, J.S.L.; Garg, A. Intelligent optimization of bioleaching process for waste lithium-ion batteries: An application of support vector regression approach. Int. J. Energy Res. 2020, 45, 6152–6162. [Google Scholar] [CrossRef]
- Jia, J.; Liang, J.; Shi, Y.; Wen, J.; Pang, X.; Zeng, J. SOH and RUL prediction of lithium-ion batteries based on Gaussian process regression with indirect health indicators. Energies 2020, 13, 375. [Google Scholar] [CrossRef]
- Tian, Y.; Lai, R.; Li, X.; Xiang, L.; Tian, J. A combined method for state-of-charge estimation for lithium-ion batteries using a long short-term memory network and an adaptive cubature Kalman filter. Appl. Energy 2020, 265, 114789. [Google Scholar] [CrossRef]
- Xia, B.; Cui, D.; Sun, Z.; Lao, Z.; Zhang, R.; Wang, W.; Sun, W.; Lai, Y.; Wang, M. State of charge estimation of lithium-ion batteries using optimized Levenberg-Marquardt wavelet neural network. Energy 2018, 153, 694–705. [Google Scholar] [CrossRef]
- Jiménez-Bermejo, D.; Fraile-Ardanuy, J.; Castaño-Solis, S.; Merino, J.; Álvaro-Hermana, R. Using dynamic neural networks for battery state of charge estimation in electric vehicles. Procedia Comput. Sci. 2018, 130, 533–540. [Google Scholar] [CrossRef]
- Jiao, M.; Wang, D.; Qiu, J. A GRU-RNN based momentum optimized algorithm for SOC estimation. J. Power Sources 2020, 459, 228051. [Google Scholar] [CrossRef]
- Hicham, C.; Christopher, I.E.C. State of charge and state of health estimation for lithium batteries using recurrent neural networks. IEEE Trans. Veh. Technol. 2017, 66, 8773–8783. [Google Scholar]
- Chemali, E.; Kollmeyer, P.J.; Preindl, M.; Emadi, A. State-of-charge estimation of Li-ion batteries using deep neural networks: A machine learning approach. J. Power Sources 2018, 400, 242–255. [Google Scholar] [CrossRef]
- Li, C.; Xiao, F.; Fan, Y. An approach to state of charge estimation of lithium-ion batteries based on recurrent neural networks with gated recurrent unit. Energies 2019, 12, 1592. [Google Scholar] [CrossRef]
- Zhou, Z.; Liu, Y.; You, M.; Xiong, R.; Zhou, X. Two-stage aging trajectory prediction of LFP lithium-ion battery based on transfer learning with the cycle life prediction. Green Energy Intell. Transp. 2022, 1, 100008. [Google Scholar] [CrossRef]
- Dai, H.; Zhao, G.; Lin, M.; Wu, J.; Zheng, G. A novel estimation method for the state of health of lithium-ion battery using prior knowledge-based neural network and Markov chain. IEEE Trans. Ind. Electron. 2019, 66, 7706–7716. [Google Scholar] [CrossRef]
- Zhang, R.; Li, X.; Sun, C.; Yang, S.; Tian, Y.; Tian, J. State of charge and temperature joint estimation based on ultrasonic reflection waves for lithium-ion battery applications. Batteries 2023, 9, 335. [Google Scholar] [CrossRef]
- Li, J.; Ye, M.; Gao, K.; Xu, X.; Wei, M.; Jiao, S. Joint estimation of state of charge and state of health for lithium-ion battery based on dual adaptive extended Kalman filter. Int. J. Energy Res. 2021, 45, 13307–13322. [Google Scholar] [CrossRef]
- Zhu, Q.; Xu, M.; Liu, W.; Zheng, M. A state of charge estimation method for lithium-ion batteries based on fractional order adaptive extended kalman filter. Energy 2019, 187, 115880. [Google Scholar] [CrossRef]
- Li, Y.; Chen, J.; Lan, F. Enhanced online model identification and state of charge estimation for lithium-ion battery under noise corrupted measurements by bias compensation recursive least squares. J. Power Sources 2020, 456, 227984. [Google Scholar] [CrossRef]
- Ouyang, T.; Xu, P.; Chen, J.; Lu, J.; Chen, N. Improved parameters identification and state of charge estimation for lithium-ion battery with real-time optimal forgetting factor. Electrochim. Acta 2020, 353, 136576. [Google Scholar] [CrossRef]
- Lin, Q.; Li, X.; Tu, B.; Cao, J.; Zhang, M.; Xiang, J. Stable and accurate estimation of SOC using eXogenous Kalman filter for lithium-ion batteries. Sensors 2023, 23, 467. [Google Scholar] [CrossRef] [PubMed]
- Yi, S.; Zorzi, M. Robust Kalman filtering under model uncertainty: The case of degenerate densities. IEEE Trans. Autom. Control 2022, 67, 3458–3471. [Google Scholar] [CrossRef]
- Sahri, Y.; Belkhier, Y.; Tamalouzt, S.; Ullah, N.; Shaw, R.N.; Chowdhury, M.S.; Techato, K. Energy management system for hybrid PV/wind/battery/fuel cell in microgrid-based hydrogen and economical hybrid battery/super capacitor energy storage. Energies 2021, 14, 5722. [Google Scholar] [CrossRef]
- Yi, S.; Zorzi, M. Robust fixed-lag smoothing under model perturbations. J. Frankl. Inst. 2023, 360, 458–483. [Google Scholar] [CrossRef]
- Tang, A.; Jiang, Y.; Yu, Q.; Zhang, Z. A hybrid neural network model with attention mechanism for state of health estimation of lithium-ion batteries. J. Energy Storage 2023, 68, 107734. [Google Scholar] [CrossRef]
- Yang, Y.; Zhao, L.; Yu, Q.; Liu, S.; Zhou, G.; Shen, W. State of charge estimation for lithium-ion batteries based on cross-domain transfer learning with a feedback mechanism. J. Energy Storage 2023, 70, 108037. [Google Scholar] [CrossRef]
- Yu, Q.; Liu, Y.; Long, S.; Jin, X.; Li, J.; Shen, W. A branch current estimation and correction method for a parallel connected battery system based on dual BP neural networks. Green Energy Intell. Transp. 2022, 1, 100029. [Google Scholar] [CrossRef]
- Jialu, Q.; Shunli, W.; Chunmei, Y.; Weihao, S.; Carlos, F. A novel bias compensation recursive least square-multiple weighted dual extended Kalman filtering method for accurate state-of-charge and state-of-health co-estimation of lithium-ion batteries. Int. J. Circuit Theory Appl. 2021, 49, 3879–3893. [Google Scholar]
- Gholizadeh, M.; Yazdizadeh, A. Systematic mixed adaptive observer and EKF approach to estimate SOC and SOH of lithium–ion battery. IET Electr. Syst. Transp. 2020, 10, 135–143. [Google Scholar] [CrossRef]
- Wassiliadis, N.; Adermann, J.; Frericks, A.; Pak, M.; Reiter, C.; Lohmann, B.; Lienkamp, M. Revisiting the dual extended Kalman filter for battery state-of-charge and state-of-health estimation: A use-case life cycle analysis. J. Energy Storage 2018, 19, 73–87. [Google Scholar] [CrossRef]






| Algorithm Type | Beijing Bus DST Condition | DST Condition |
|---|---|---|
| Ah | RMSE: 5.38% MAE: 5.37% convergence time: ∞ | RMSE: 4.97% MAE: 4.99% convergence time: ∞ |
| RLS-EKF | RMSE: 1.89% MAE: 1.16% convergence time: 4 s | RMSE: 0.94% MAE: 0.76% convergence time: 8 s |
| FBC-DEKF | RMSE: 1.04% MAE: 0.82% convergence time: 4 s | RMSE: 0.88% MAE: 0.68% convergence time: 8 s |
| FBC-DAEKF | RMSE: 0.19% MAE: 0.17% convergence time: 4 s | RMSE: 0.07% MAE: 0.05% convergence time: 5 s |
| Algorithm Type | Beijing Bus DST Condition | DST Condition |
|---|---|---|
| FBC-DEKF | RMSE: 0.078% MAE: 0.017% convergence time: 23 s | RMSE: 0.043% MAE: 0.022% convergence time: 240 s |
| FBC-DAEKF | RMSE: 0.075% MAE: 0.018% convergence time: 23 s | RMSE: 0.043% MAE: 0.014% convergence time: 240 s |
| Temperature | Estimation Type | Beijing Bus DST Condition |
|---|---|---|
| 15 °C | SOC | RMSE: 1.31% MAE: 1.32% convergence time: 1 s |
| Ro | RMSE: 0.011% MAE: 0.016% convergence time: 13 s | |
| 25 °C | SOC | RMSE: 0.19% MAE: 0.17% convergence time: 4 s |
| Ro | RMSE: 0.075% MAE: 0.018% convergence time: 23 s | |
| 35 °C | SOC | RMSE: 0.182% MAE: 0.324% convergence time: 1 s |
| Ro | RMSE: 0.044% MAE: 0.045% convergence time: 13 s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiong, R.; Wang, S.; Feng, F.; Yu, C.; Fan, Y.; Cao, W.; Fernandez, C. Co-Estimation of State-of-Charge and State-of-Health for High-Capacity Lithium-Ion Batteries. Batteries 2023, 9, 509. https://doi.org/10.3390/batteries9100509
Xiong R, Wang S, Feng F, Yu C, Fan Y, Cao W, Fernandez C. Co-Estimation of State-of-Charge and State-of-Health for High-Capacity Lithium-Ion Batteries. Batteries. 2023; 9(10):509. https://doi.org/10.3390/batteries9100509
Chicago/Turabian StyleXiong, Ran, Shunli Wang, Fei Feng, Chunmei Yu, Yongcun Fan, Wen Cao, and Carlos Fernandez. 2023. "Co-Estimation of State-of-Charge and State-of-Health for High-Capacity Lithium-Ion Batteries" Batteries 9, no. 10: 509. https://doi.org/10.3390/batteries9100509
APA StyleXiong, R., Wang, S., Feng, F., Yu, C., Fan, Y., Cao, W., & Fernandez, C. (2023). Co-Estimation of State-of-Charge and State-of-Health for High-Capacity Lithium-Ion Batteries. Batteries, 9(10), 509. https://doi.org/10.3390/batteries9100509