Physics-Based Electrochemical Model of Vanadium Redox Flow Battery for Low-Temperature Applications
Abstract
1. Introduction
- Positive electrode:
- Negative electrode:
- Overall reaction:
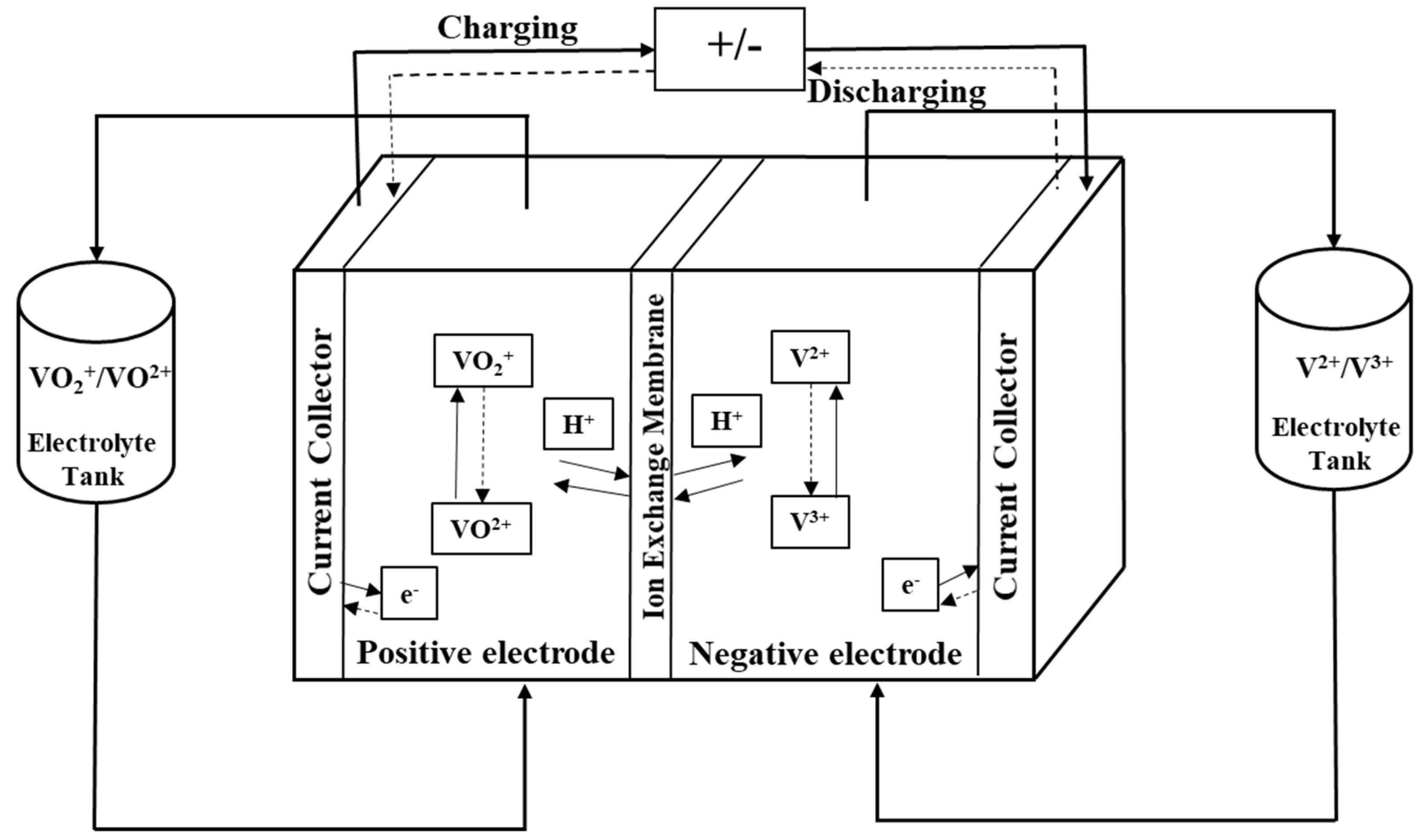
2. Description of the Model
- Electrolyte flow rate is uniform, and concentration variations over the cell are small and can be neglected.
- The electrolyte is uniformly mixed, and the concentration of vanadium species is the same throughout.
- Since vanadium ion cross-over and self-discharge of the battery are slow processes, these are neglected in the present study, and the membrane is assumed to be impermeable to vanadium ions.
- Oxygen and hydrogen evolution is negligible, and no side reactions occur other than those listed in Equations (1)–(3).
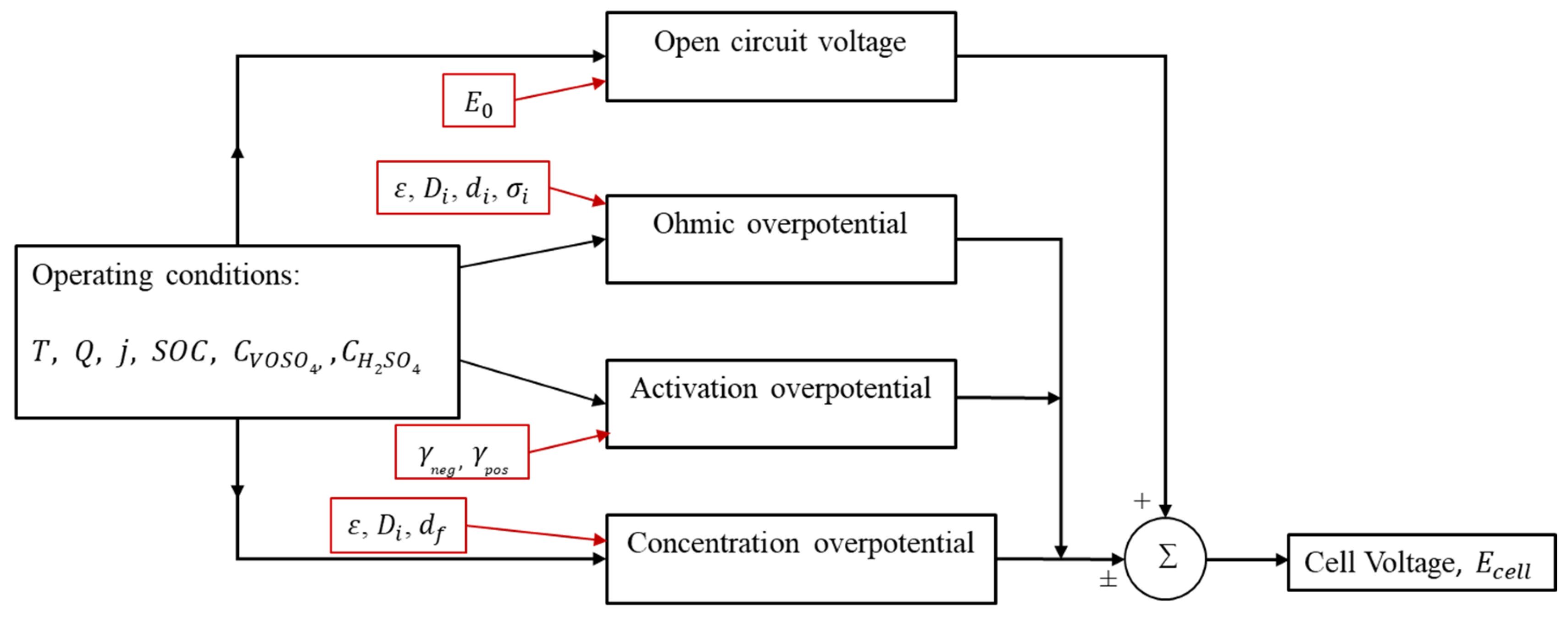
2.1. Open Circuit Voltage (V)
2.2. Ohmic Overpotential
2.3. Activation Overpotential
2.4. Concentration Overpotential
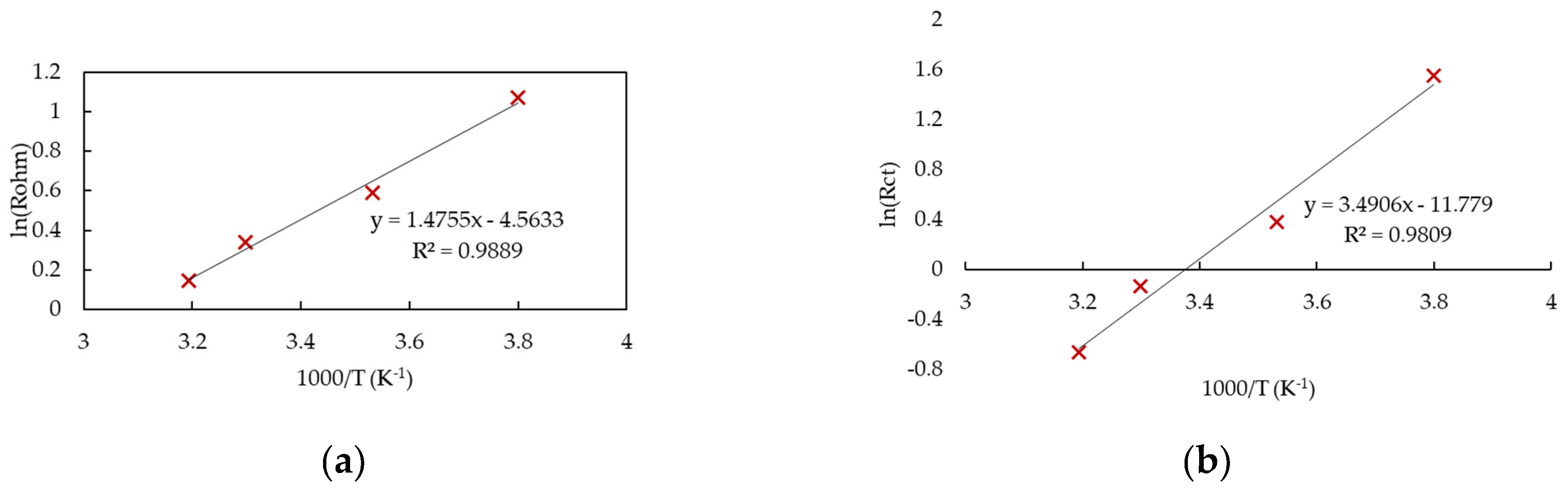
3. Temperature Sensitivity of the Model Parameters
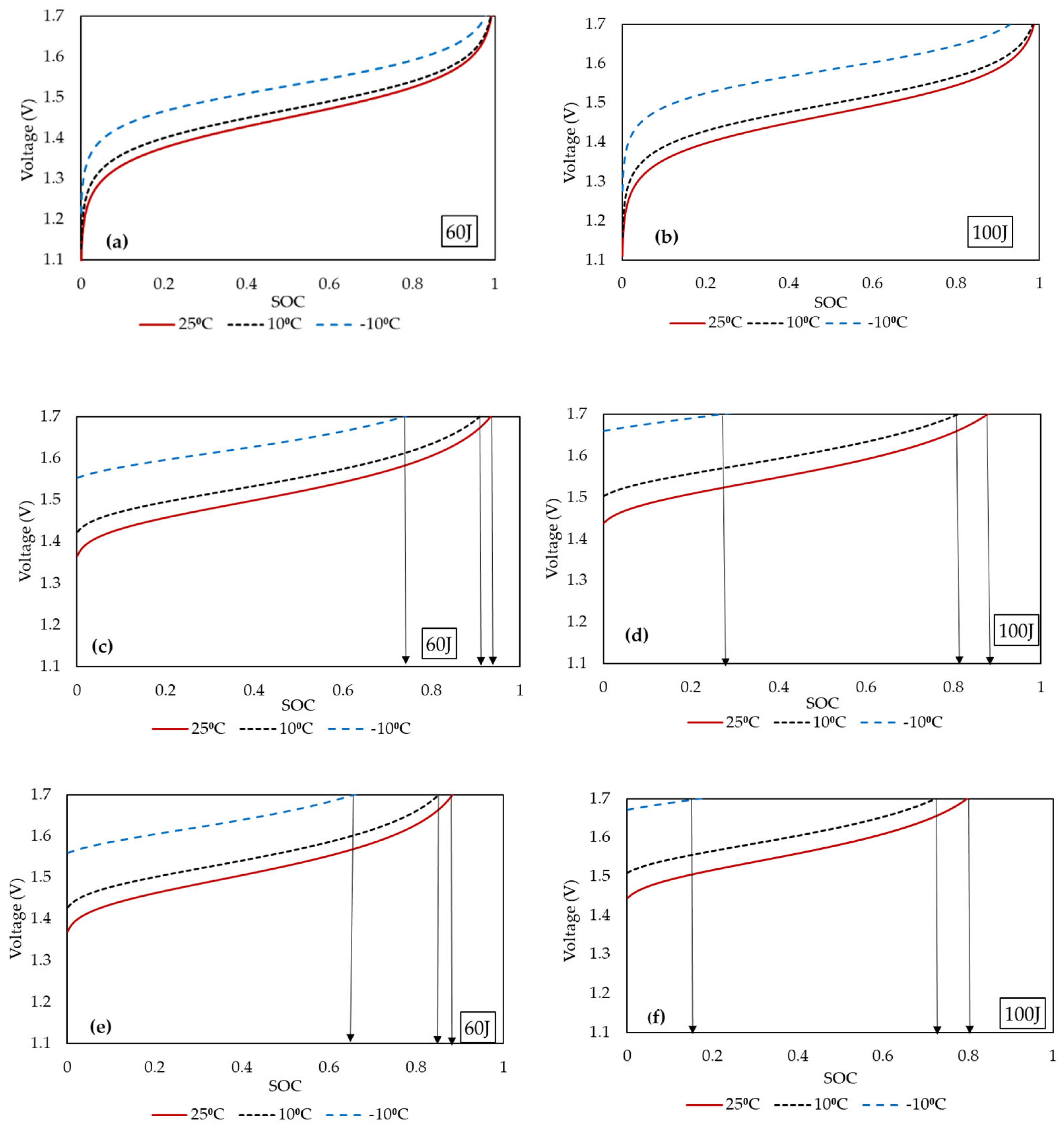
4. Results and Discussion
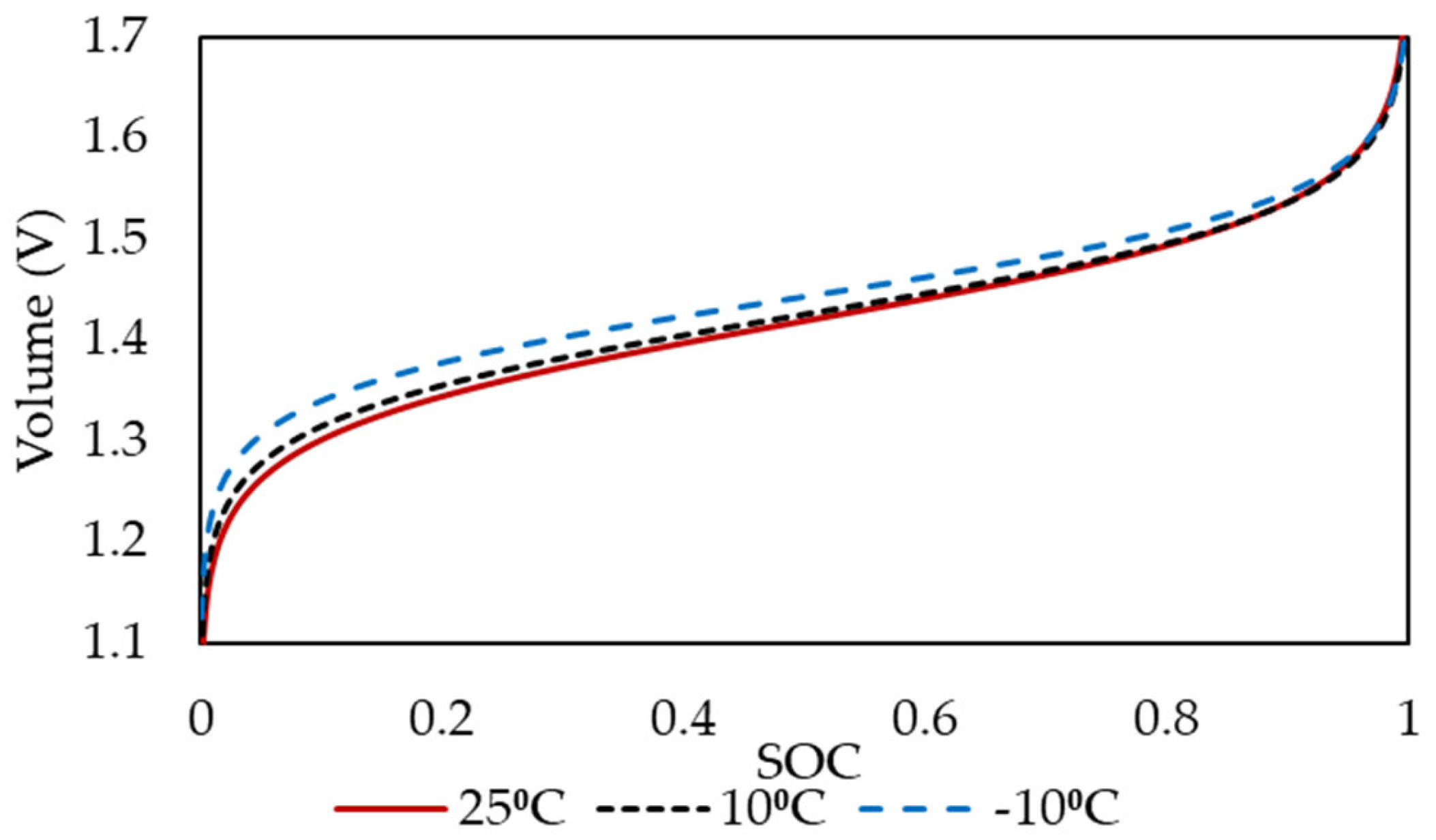
4.1. Open-Circuit Voltage and Overpotentials
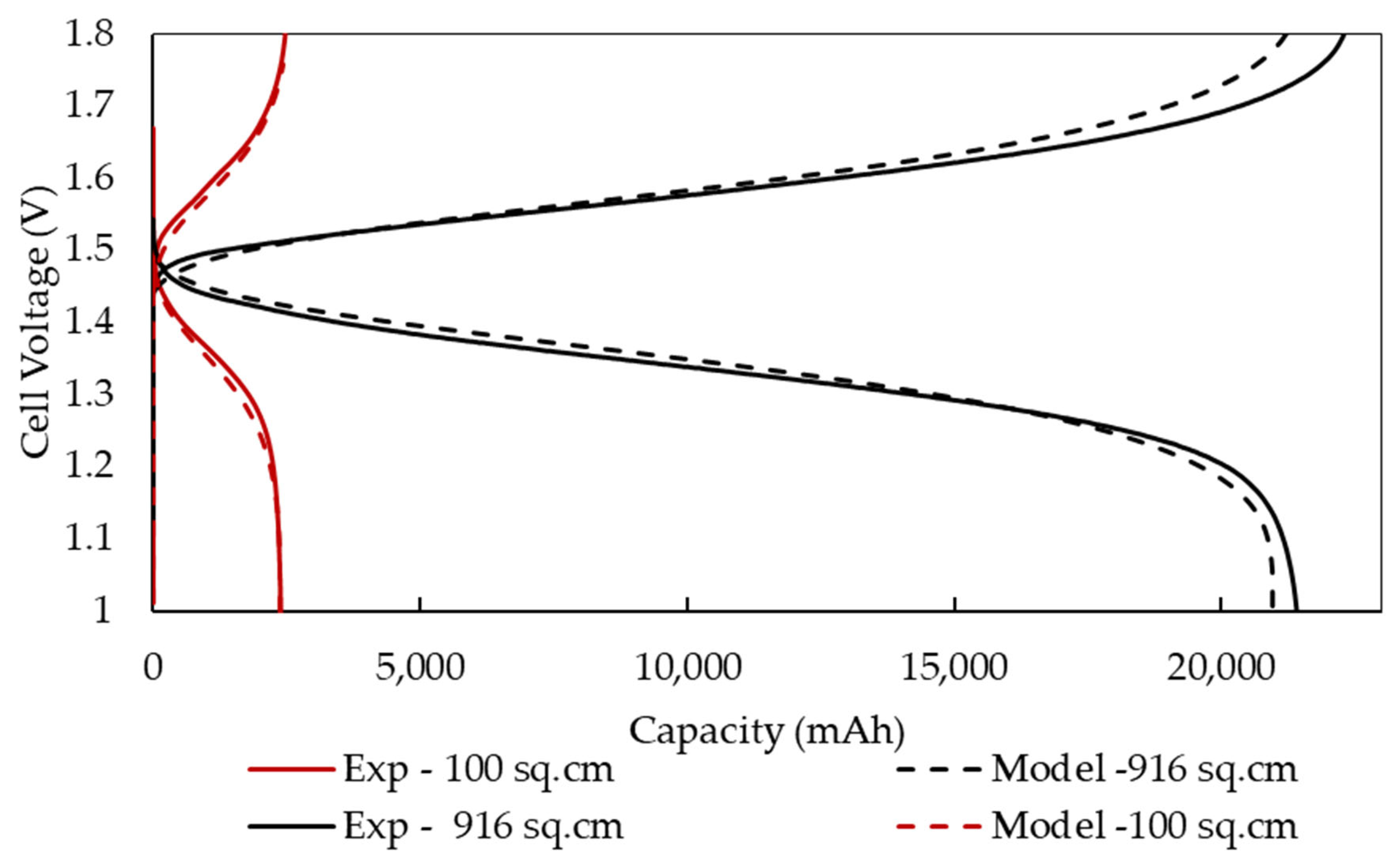
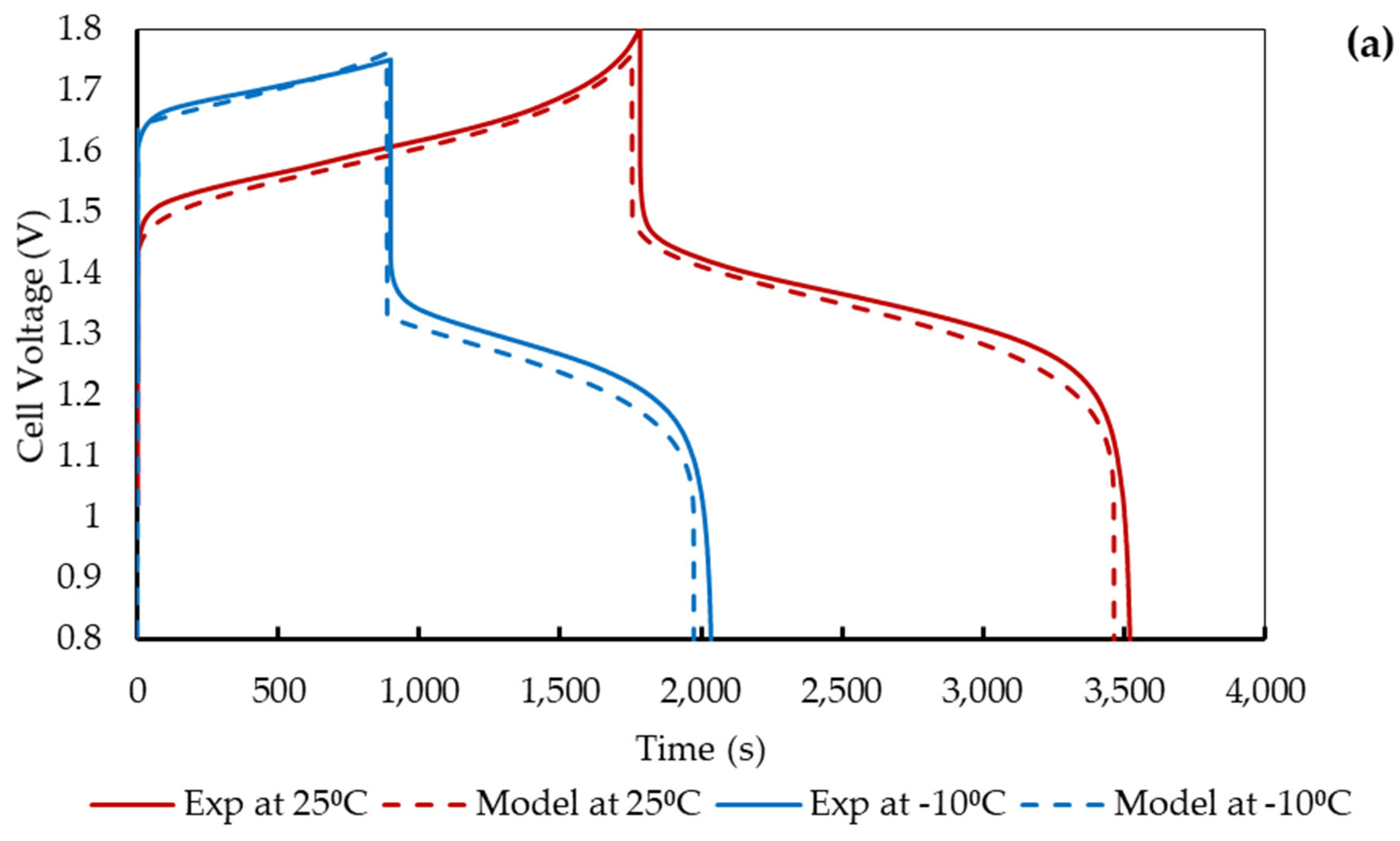
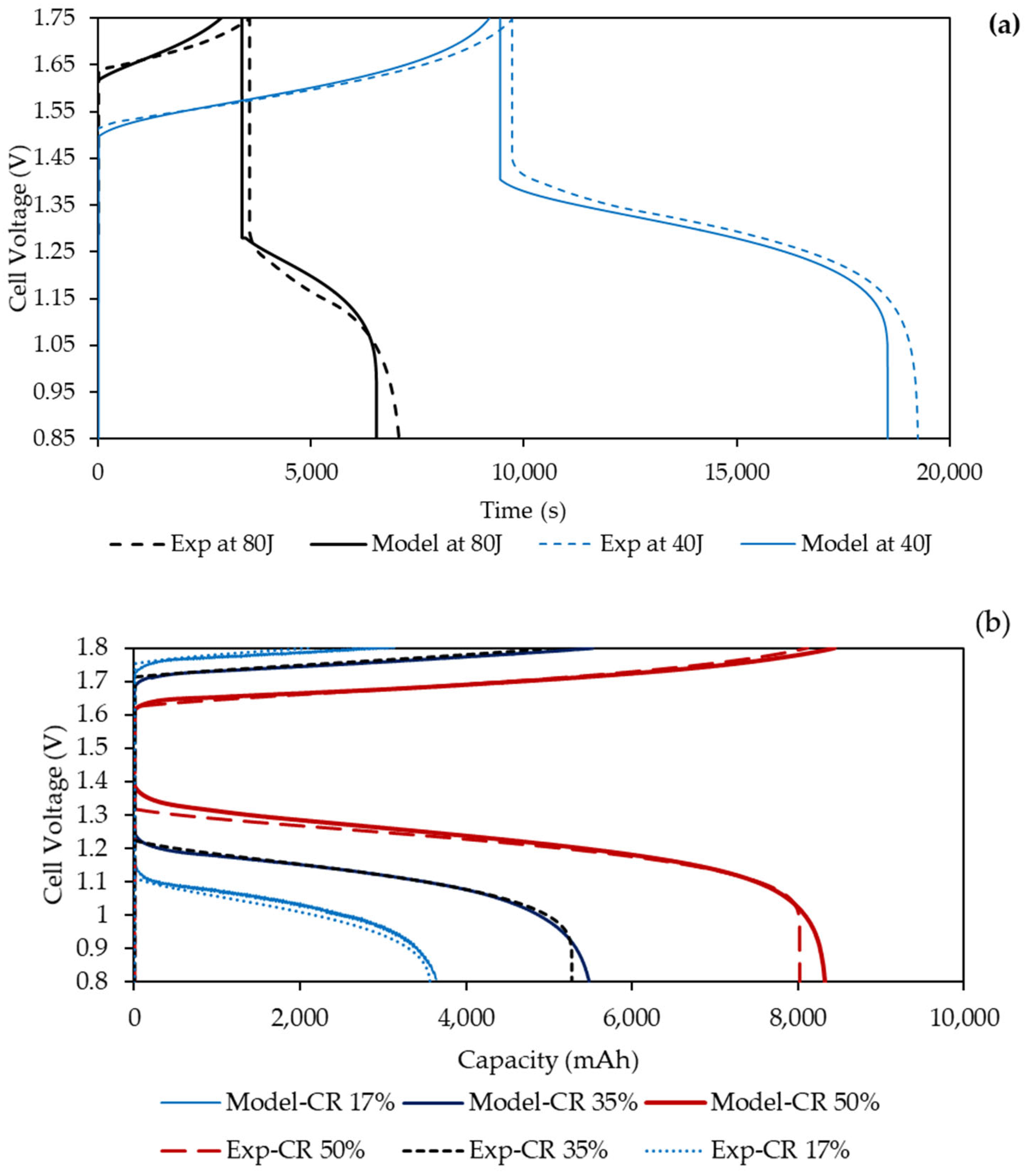
4.2. Comparison with Experimental Data
4.3. Contributors to Overpotentials
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Skyllas-Kazacos, M.; Rychcik, M.; Robins, R.G.; Fane, A.G.; Green, M.A. New all vanadium redox flow cell. J. Electrochem. Soc. 1986, 133, 1057–1058. [Google Scholar] [CrossRef]
- You, D.; Zhang, H.; Chen, J. A simple model for the vanadium redox battery. Electrochim. Acta 2009, 54, 6827–6836. [Google Scholar] [CrossRef]
- Shah, A.A.; Tangirala, R.; Singh, R.; Wills, R.G.A.; Walsh, F.C. A Dynamic Unit Cell Model for the All-Vanadium Flow Battery. J. Electrochem. Soc. 2011, 158, A671–A677. [Google Scholar] [CrossRef]
- Sun, C.; Negro, E.; Vezzù, K.; Pagot, G.; Cavinato, G.; Nale, A.; Bang, Y.H.; Di Noto, V. Hybrid inorganic-organic proton-conducting membranes based on SPEEK doped with WO3 nanoparticles for application in vanadium redox flow batteries. Electrochim. Acta 2019, 309, 311–325. [Google Scholar] [CrossRef]
- Gundlapalli, R.; Jayanti, S. Effective splitting of serpentine flow field for applications in large-scale flow batteries. J. Power Sources 2021, 487, 229409. [Google Scholar] [CrossRef]
- Rao, P.; Gundlapalli, R.; Jayanti, S. Assessment of hydrodynamic performance of vanadium redox flow batteries at low temperatures. J. Energy Storage 2022, 55, 105746. [Google Scholar] [CrossRef]
- Mongird, K.; Viswanathan, V.; Alam, J.; Vartanian, C.; Sprenkle, V.; Baxter, R. 2020 grid energy storage technology cost and performance assessment. Energy 2020, 2020, 6–15. [Google Scholar]
- Zhang, C.; Zhao, T.; Xu, Q.; An, L.; Zhao, G. Effects of operating temperature on the performance of vanadium redox flow batteries. Appl. Energy 2015, 155, 349–353. [Google Scholar] [CrossRef]
- Xiao, S.; Yu, L.; Wu, L.; Liu, L.; Qiu, X.; Xi, J. Broad temperature adaptability of vanadium redox flow battery—Part 1: Electrolyte research. Electrochim. Acta 2016, 18, 525–534. [Google Scholar] [CrossRef]
- Yin, S.; Zhou, L.; Du, X.; Yang, Y. Influence of temperature on performance of all vanadium redox flow battery: Analysis of ionic mass transfer. Ionics 2018, 25, 593–606. [Google Scholar] [CrossRef]
- Rao, P.; Jayanti, S. Influence of electrode design parameters on the performance of vanadium redox flow battery cells at low temperatures. J. Power Sources 2020, 482, 228988. [Google Scholar] [CrossRef]
- Shah, A.; Watt-Smith, M.; Walsh, F. A dynamic performance model for redox-flow batteries involving soluble species. Electrochim. Acta 2008, 53, 8087–8100. [Google Scholar] [CrossRef]
- Sathisha, H.M.; Dalal, A. Two-Dimensional Unsteady Simulation of All-Vanadium Redox Flow Battery. J. Therm. Sci. Eng. Appl. 2015, 8, 011019-1–011019-14. [Google Scholar] [CrossRef]
- Tang, A.; Bao, J.; Skyllas-Kazacos, M. Studies on pressure losses and flow rate optimization in vanadium redox flow battery. J. Power Sources 2014, 248, 154–162. [Google Scholar] [CrossRef]
- Khazaeli, A.; Vatani, A.; Tahouni, N.; Panjeshahi, M.H. Numerical investigation and thermodynamic analysis of the effect of electrolyte flow rate on performance of all vanadium redox flow batteries. J. Power Sources 2015, 293, 599–612. [Google Scholar] [CrossRef]
- Wang, T.; Fu, J.; Zheng, M.; Yu, Z. Dynamic control strategy for the electrolyte flow rate of vanadium redox flow batteries. Appl. Energy 2018, 227, 613–623. [Google Scholar] [CrossRef]
- Murthy, S.K.; Sharma, A.K.; Choo, C.; Birgersson, E. Analysis of Concentration Overpotential in an All-Vanadium Redox Flow Battery. J. Electrochem. Soc. 2018, 165, A1746–A1752. [Google Scholar] [CrossRef]
- Noto, V.D.; Vezzù, K.; Crivellaro, G.; Pagot, G.; Sun, C.; Meda, L.; Rutkowska, I.A.; Kulesza, P.J.; Zawodzinski, T.A. A general electrochemical formalism for vanadium redox flow batteries. Electrochim. Acta 2022, 408, 139937. [Google Scholar] [CrossRef]
- Tang, A.; Ting, S.; Bao, J.; Skyllas-Kazacos, M. Thermal modelling and simulation of the all-vanadium redox flow battery. J. Power Sources 2012, 203, 165–176. [Google Scholar] [CrossRef]
- Zhang, B.W.; Lei, Y.; Bai, B.F.; Xu, A.; Zhao, T.S. A two-dimensional mathematical model for vanadium redox flow battery stacks incorporating non uniform electrolyte distribution in the flow fram. Appl. Therm. Eng. 2019, 151, 495–505. [Google Scholar] [CrossRef]
- Knehr, K.; Kumbur, E. Open circuit voltage of vanadium redox flow batteries: Discrepancy between models and experiments. Electrochem. Commun. 2011, 13, 342–345. [Google Scholar] [CrossRef]
- O’Hayre, R.; Cha, S.W.; Colella, W.; Prinz, F.B. Fuel Cell Fundamentals, 3rd ed.; Wiley Publications: Hoboken, NJ, USA, 1991. [Google Scholar]
- Blanc, C. Modeling of a Vanadium Redox Flow Battery Electricity Storage System. Ph.D. Thesis, EPF, Lausanne, Switzerland, 2009. [Google Scholar]
- Kumar, S.; Jayanti, S. Effect of electrode intrusion on pressure drop and electrochemical performance of an all-vanadium redox flow battery. J. Power Sources 2017, 360, 548–558. [Google Scholar] [CrossRef]
- Alipour, M.; Ziebert, C.; Conte, F.V.; Kizilel, R. A Review on Temperature-Dependent Electrochemical Properties, Aging, and Performance of Lithium-Ion Cells. Batteries 2020, 6, 35. [Google Scholar] [CrossRef]
- Schmal, D.; Van Erkel, J.; Van Buin, P.J. Mass transfer at carbon fibre electrodes. J. Appl. Electrochem. 1986, 16, 422–430. [Google Scholar] [CrossRef]
- Epan, D.E.; Choudhary, S.R.; Rengaswamy, R. Low grade heat recovery for power generation through electrochemical route: Vanadium Redox Flow Battery, a case study. Appl. Surf. Sci. 2019, 474, 262–268. [Google Scholar]
- Praphulla. Experimental and Modelling Studies on Low Temperature Performance of Vanadium Redox Flow Batteries. Ph.D. Thesis, IIT Madras, Chennai, India, 2021. Available online: https://shodhganga.inflibnet.ac.in:8443/jspui/handle/10603/463182 (accessed on 27 June 2023).
- Gundlapalli, R. Optimal Performance Conditions and Scale-Up Criteria for VANADIUM redox Flow Batteries. Ph.D. Thesis, IIT Madras, Chennai, India, 2019. [Google Scholar]
- Ghimire, P.C.; Bhattarai, A.; Schweiss, R.; Scherer, G.G.; Wai, N.; Yan, Q. A comprehensive study of electrode compression effects in all vanadium redox flow batteries including locally resolved measurements. Appl. Energy 2018, 230, 974–982. [Google Scholar] [CrossRef]
- Gundlapalli, R.; Jayanti, S. Effect of electrode compression and operating parameters on the performance of large vanadium redox flow battery cells. J. Power Sources 2019, 427, 231–242. [Google Scholar] [CrossRef]
- Wang, C.; Li, N.; Shin, D.W.; Lee, S.Y.; Kang, N.R.; Lee, Y.W.; Guiver, M.D. Fluorene-Based Poly(arylene ether sulfone)s Containing Clustered Flexible Pendant Sulfonic Acids as Proton Exchange Membranes. Macromolecules 2011, 44, 7296–7306. [Google Scholar] [CrossRef]
- Sun, C.; Zlotorowicz, A.; Nawn, G.; Negro, E.; Bertasi, F.; Pagot, G.; Vezzù, K.; Pace, G.; Guarnieri, M.; Di Noto, V. [Nafion/(WO3)x] hybrid membranes for vanadium redox flow batteries. Solid State Ion. 2018, 319, 110–116. [Google Scholar] [CrossRef]
- Xi, J.; Jiang, B.; Yu, L.; Liu, L. Membrane evaluation for vanadium flow batteries in a temperature, range of 20–50 °C. J. Membr. Sci. 2017, 522, 45–55. [Google Scholar] [CrossRef]
- Li, L.; Kim, S.; Wang, W.; Vijayakumar, M.; Nie, Z.; Chen, B.; Zhang, J.; Xia, G.; Hu, J.; Graff, G.; et al. A Stable Vanadium Redox-Flow Battery with High Energy Density for Large-Scale Energy Storage. Adv. Energy Mater. 2011, 1, 394–400. [Google Scholar] [CrossRef]
- Du, J.; Liu, J.; Liu, S.; Wang, L.; Chou, K.-C. Research progress of vanadium battery with mixed acid system: A review. J. Energy Storage 2023, 70, 107961. [Google Scholar] [CrossRef]

| Symbol | Description | Quantity |
|---|---|---|
| Conductivity of electrode with thickness 4.6 mm | 130.1 S/m (SGL datasheet) | |
| Conductivity of membrane with thickness of 18.3 μm | 8 S/m | |
| Conductivity of graphite plate with thickness of 10 mm | 71,428 S/m (SGL datasheet) | |
| Conductivity of copper plate with thickness of 3 mm | 90,000 S/m | |
| Porosity in carbon felt, uncompressed | 0.94 (SGL datasheet) | |
| Fiber diameter of electrode | 10 μm [12] | |
| diffusivity in electrolyte at 298 K | 2.4 × 10−10 m2/s [15] | |
| diffusivity in electrolyte at 298 K | 2.4 × 10−10 m2/s [15] | |
| diffusivity in electrolyte at 298 K | 3.9 × 10−10 m2/s [15] | |
| diffusivity in electrolyte at 298 K | 3.9 × 10−10 m2/s [15] | |
| in electrolyte at 298 K | 9.3 × 10−9 m2/s [15] | |
| diffusivity in electrolyte at 298 K | 1.23 × 10−9 m2/s [15] | |
| Rate constant of reaction (1) at 298 K | 3 × 10−5 m/s (fitted) | |
| Rate constant of reaction (2) at 298 K | 2.6 × 10−6 m/s [15] |
| Ions | Diffusivities at 10 °C (m2/s) | Diffusivities at −10 °C (m2/s) |
|---|---|---|
| 1.44 × 10−10 | 3.72 × 10−11 | |
| 1.44 × 10−10 | 3.72 × 10−11 | |
| 2.34 × 10−10 | 6.04 × 10−11 | |
| 2.34 × 10−10 | 6.04 × 10−11 | |
| 5.58 × 10−9 | 1.44 × 10−9 | |
| 7.38 × 10−9 | 1.91 × 10−9 |
| Temperature | Current Density (mA/cm2) | Overpotential (mV) | |||
|---|---|---|---|---|---|
| (oC) | Ohmic | Activation-Negative | Activation-Positive | Concentration | |
| 25 | 20 | 10.4 | 25.4 | 2.2 | 2.8 |
| 40 | 20.9 | 46.4 | 4.5 | 5.7 | |
| 60 | 31.3 | 62.8 | 6.7 | 8.9 | |
| 80 | 41.7 | 75.7 | 8.9 | 12.2 | |
| 100 | 52.1 | 86.3 | 11.1 | 15.8 | |
| 10 | 20 | 14.5 | 37.7 | 3.5 | 3.1 |
| 40 | 29.1 | 63.6 | 7.0 | 6.4 | |
| 60 | 43.6 | 81.4 | 10.5 | 9.9 | |
| 80 | 58.2 | 94.7 | 13.9 | 13.8 | |
| 100 | 72.7 | 105.2 | 17.2 | 18.1 | |
| −10 | 20 | 28.5 | 54.3 | 5.7 | 4.7 |
| 40 | 57.0 | 82.6 | 11.4 | 10.0 | |
| 60 | 85.5 | 100.3 | 16.9 | 16.0 | |
| 80 | 114.0 | 113.1 | 22.1 | 23.1 | |
| 100 | 142.6 | 123.1 | 27.1 | 31.8 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rao, P.; Jayanti, S. Physics-Based Electrochemical Model of Vanadium Redox Flow Battery for Low-Temperature Applications. Batteries 2023, 9, 374. https://doi.org/10.3390/batteries9070374
Rao P, Jayanti S. Physics-Based Electrochemical Model of Vanadium Redox Flow Battery for Low-Temperature Applications. Batteries. 2023; 9(7):374. https://doi.org/10.3390/batteries9070374
Chicago/Turabian StyleRao, Praphulla, and Sreenivas Jayanti. 2023. "Physics-Based Electrochemical Model of Vanadium Redox Flow Battery for Low-Temperature Applications" Batteries 9, no. 7: 374. https://doi.org/10.3390/batteries9070374
APA StyleRao, P., & Jayanti, S. (2023). Physics-Based Electrochemical Model of Vanadium Redox Flow Battery for Low-Temperature Applications. Batteries, 9(7), 374. https://doi.org/10.3390/batteries9070374