Kinetic and Thermodynamic Analysis of Fried Tilapia Fish Waste Pyrolysis for Biofuel Production
Abstract
:1. Introduction
2. Materials and Method
2.1. Sample Preparation
2.2. Thermogravimetric Experiment
3. Kinetic Analysis
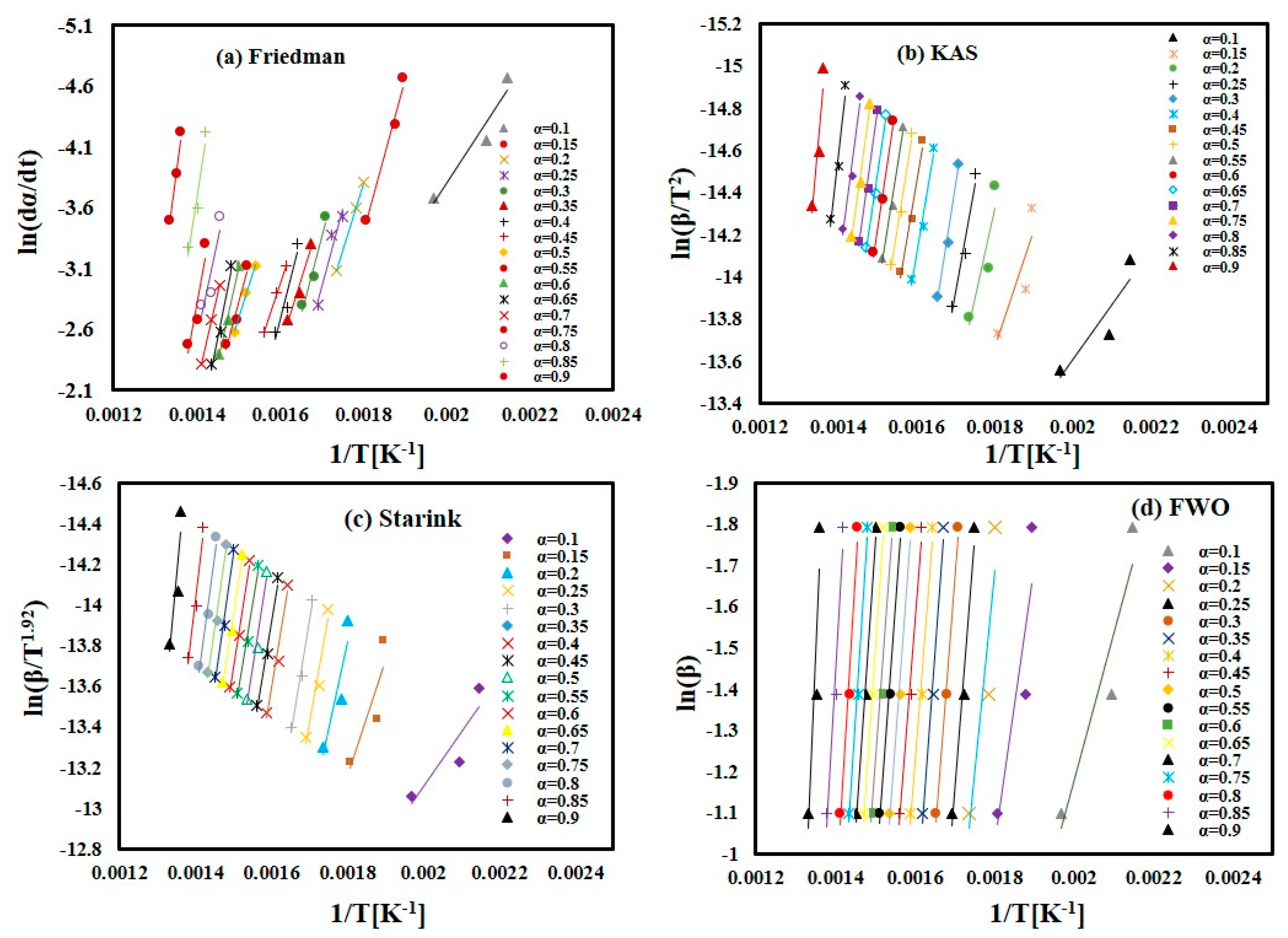
3.1. Determination of the Activation Energy
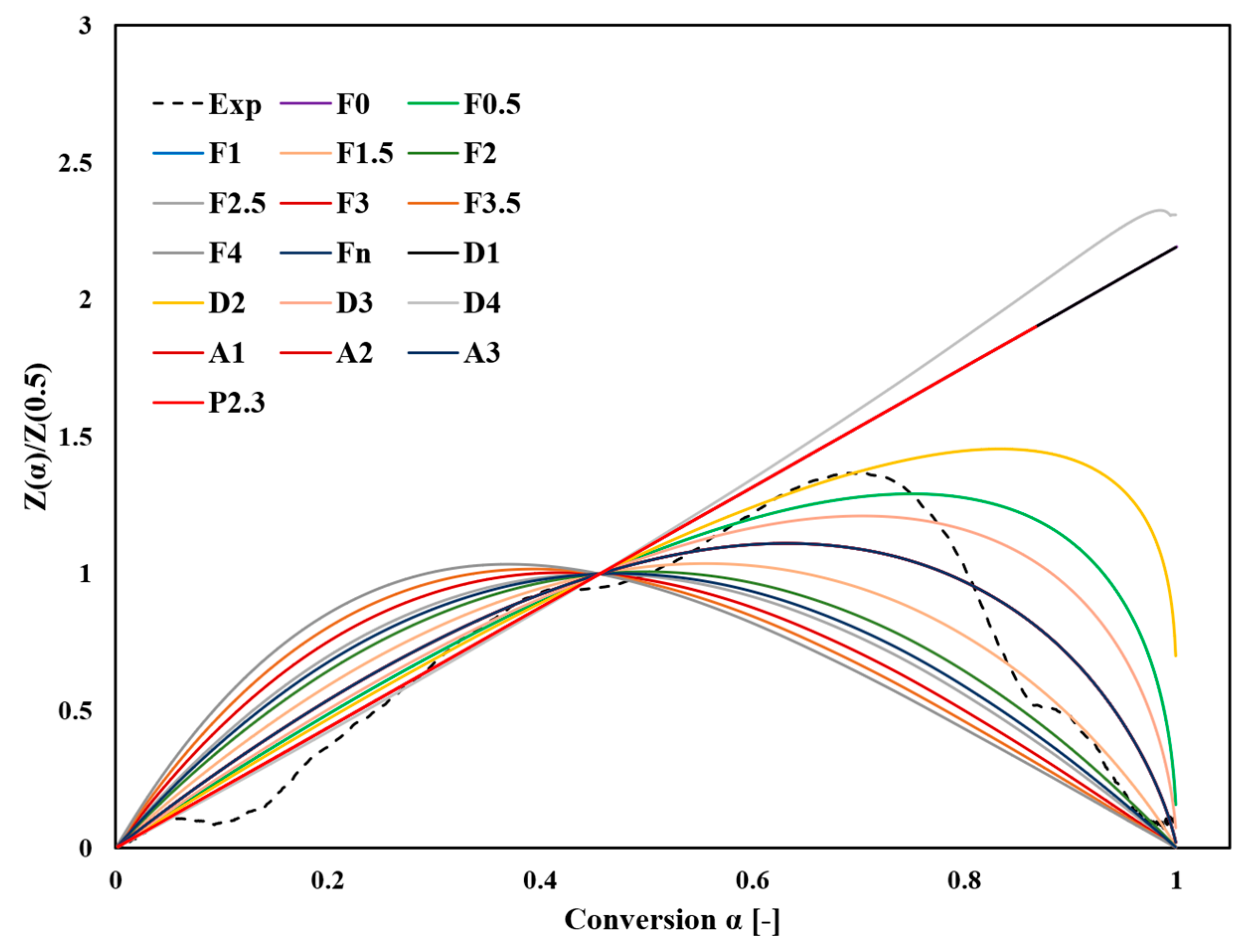
3.2. Determination of the Reaction Mechanism
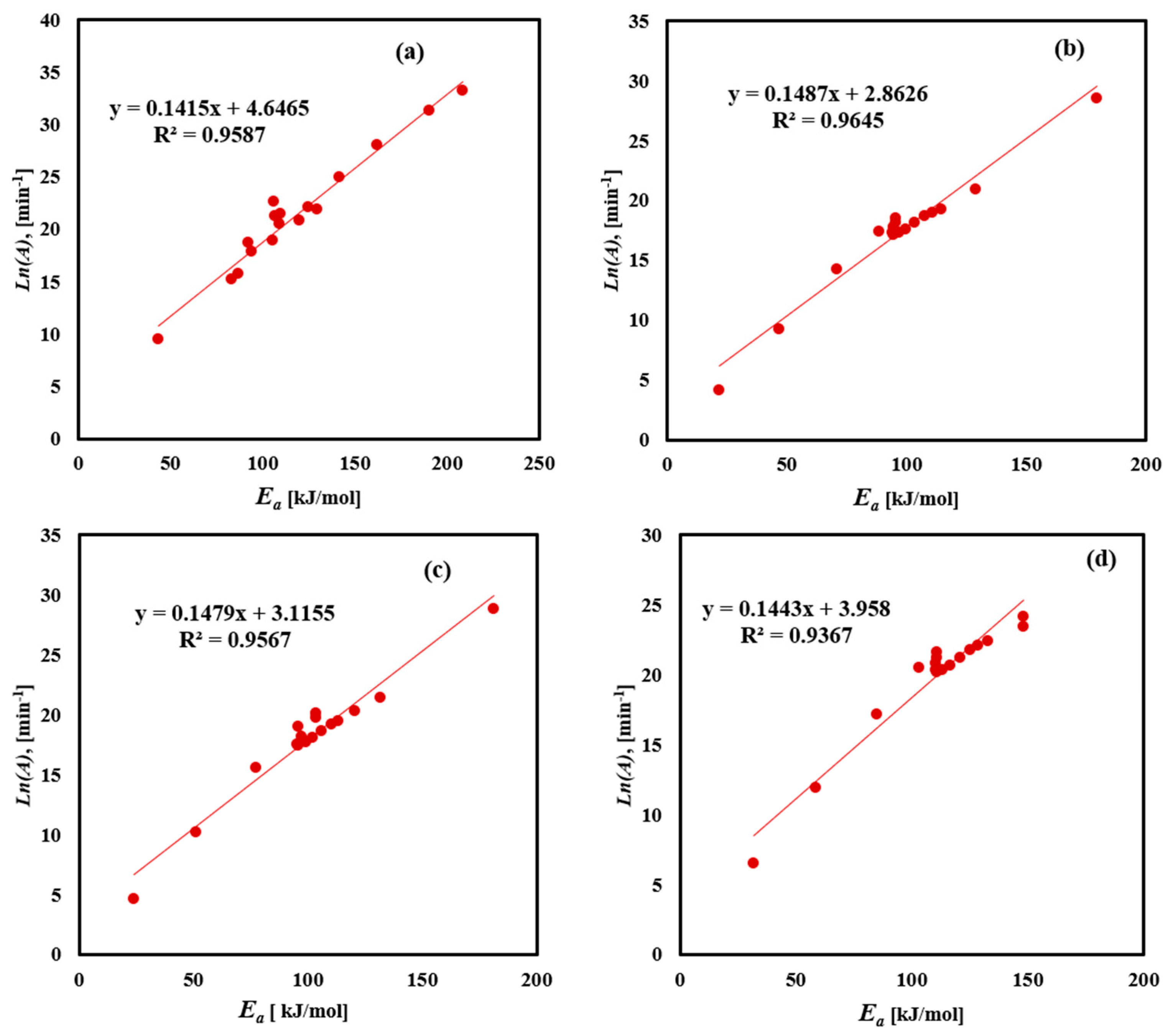
3.3. Pre-Exponential Factor Estimation
3.4. Thermodynamic Parameters
4. Results and Discussions
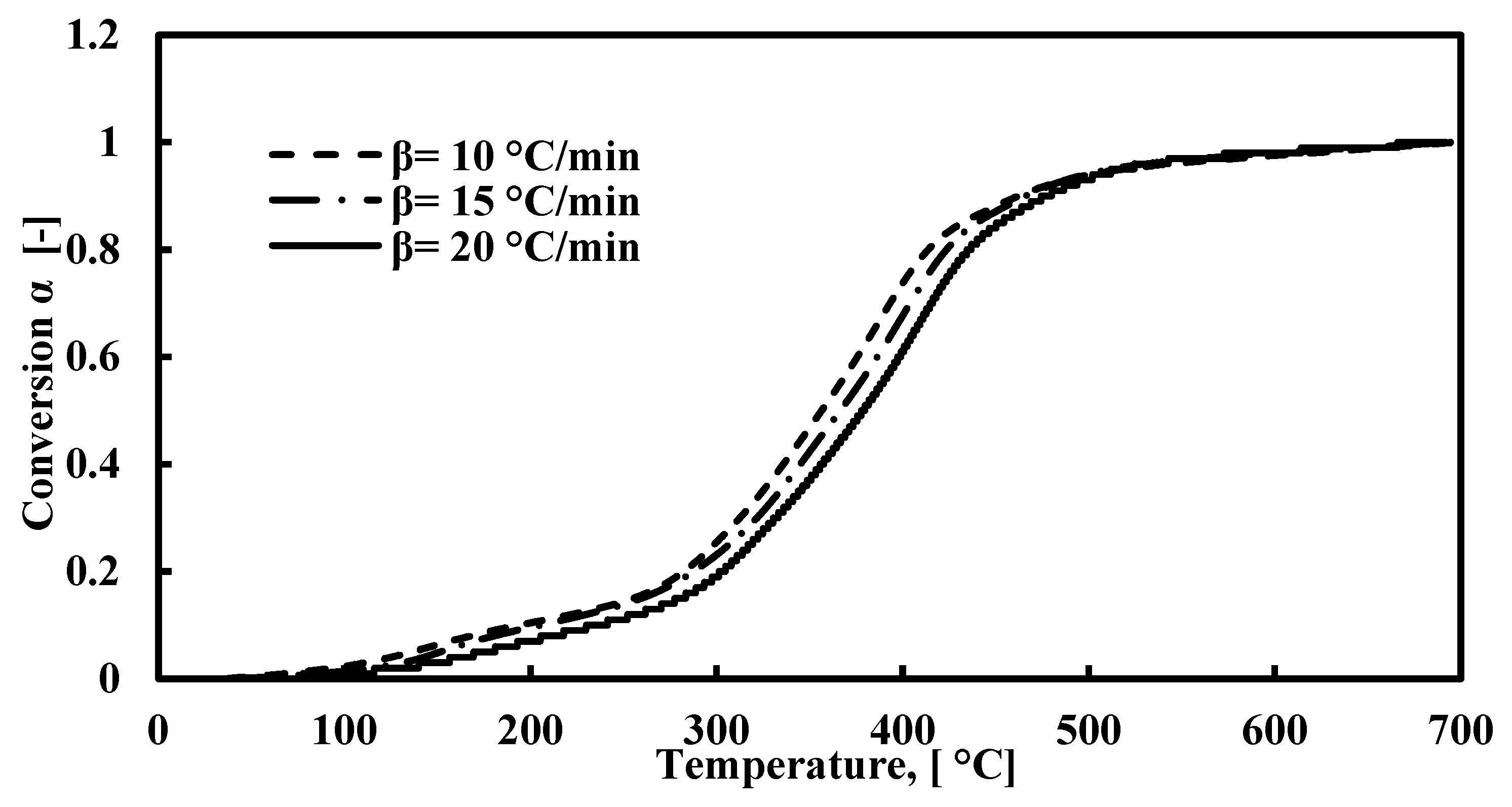
4.1. TGA and DTG Results Discussions
4.2. Kinetic Triplet Parameters Calculations
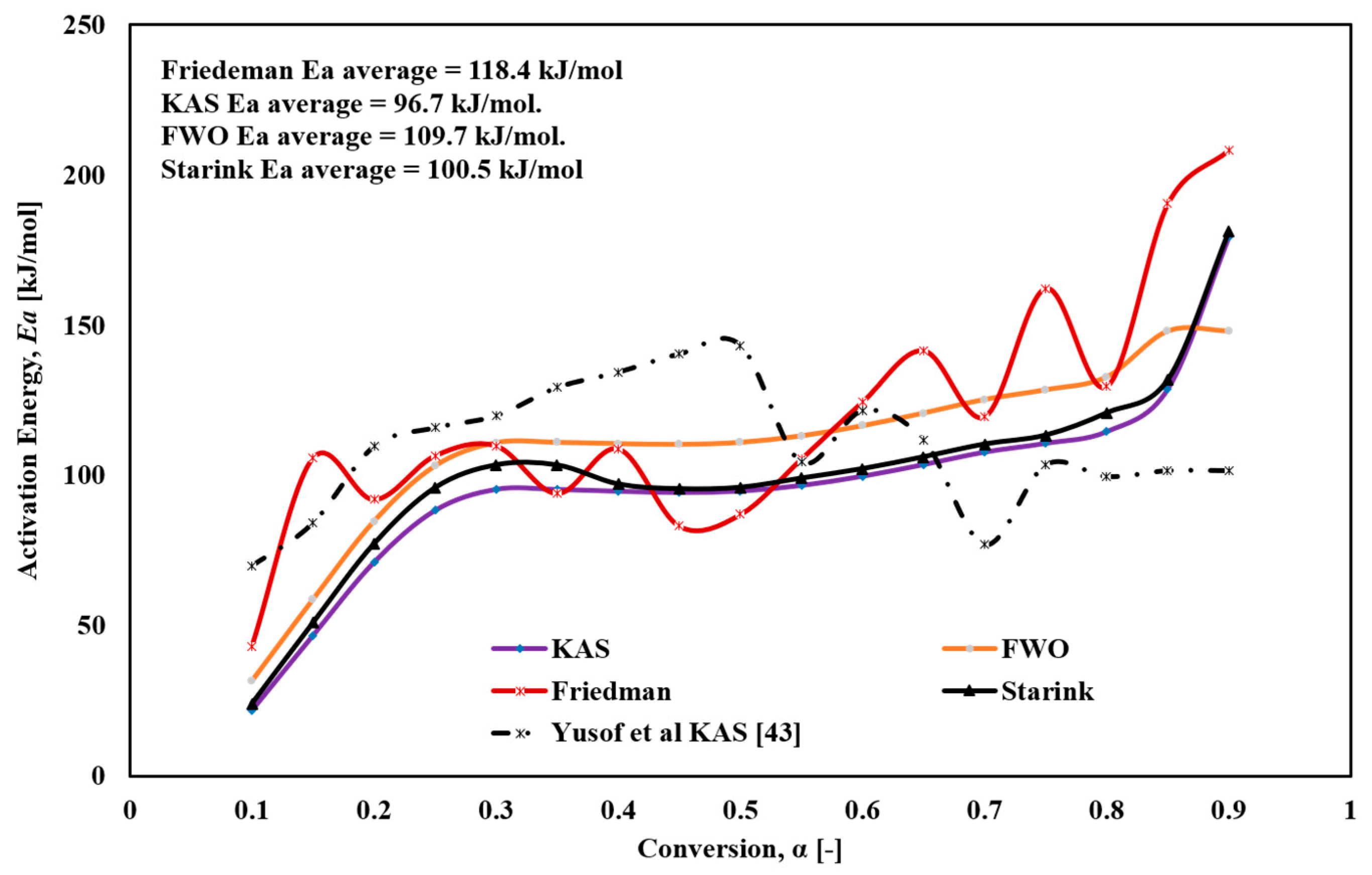
4.2.1. Activation Energy (Ea)
4.2.2. Reaction Mechanism F(α)
4.2.3. Pre-Exponential Factor
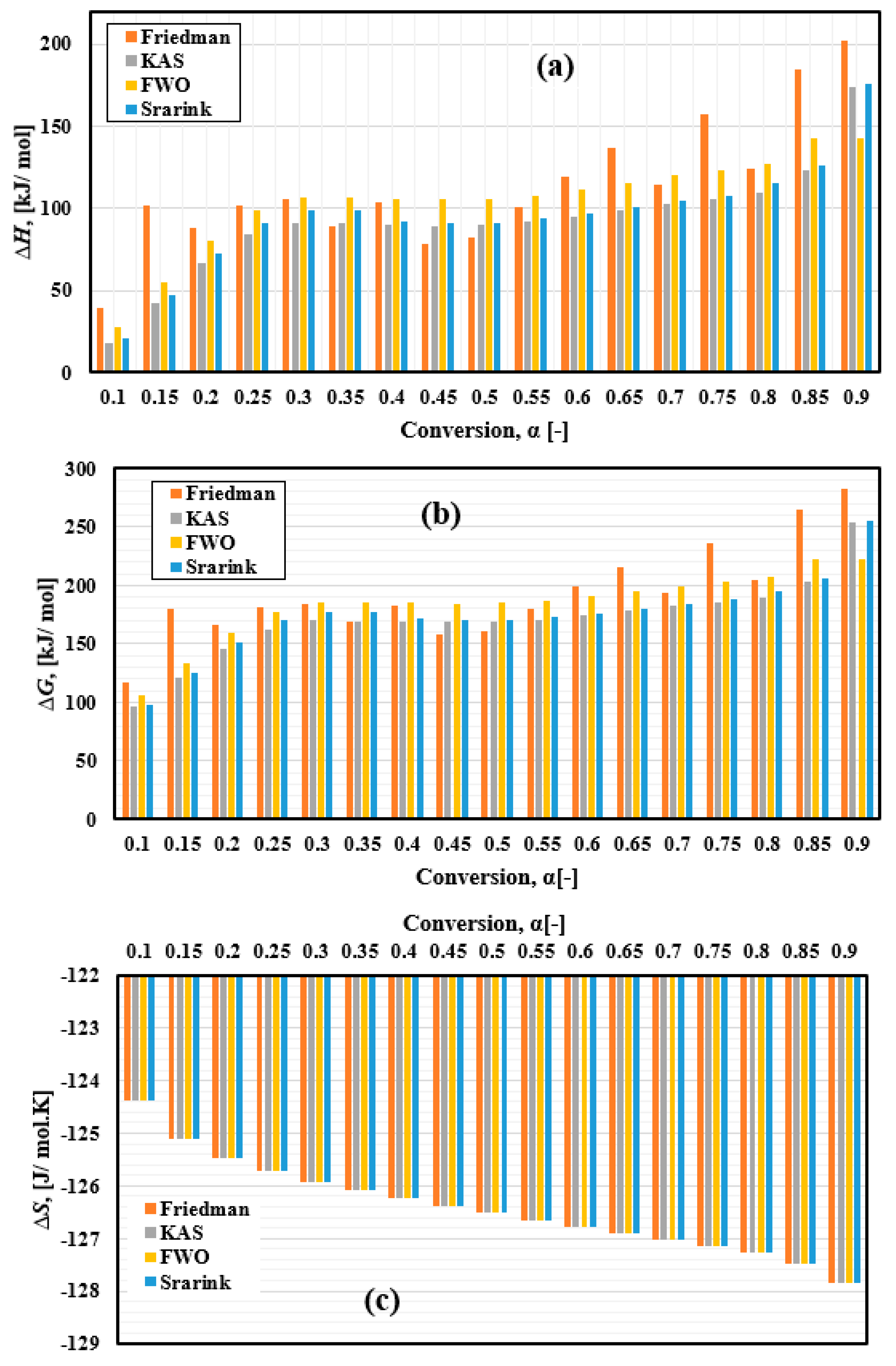
4.3. Thermodynamic Analysis Results
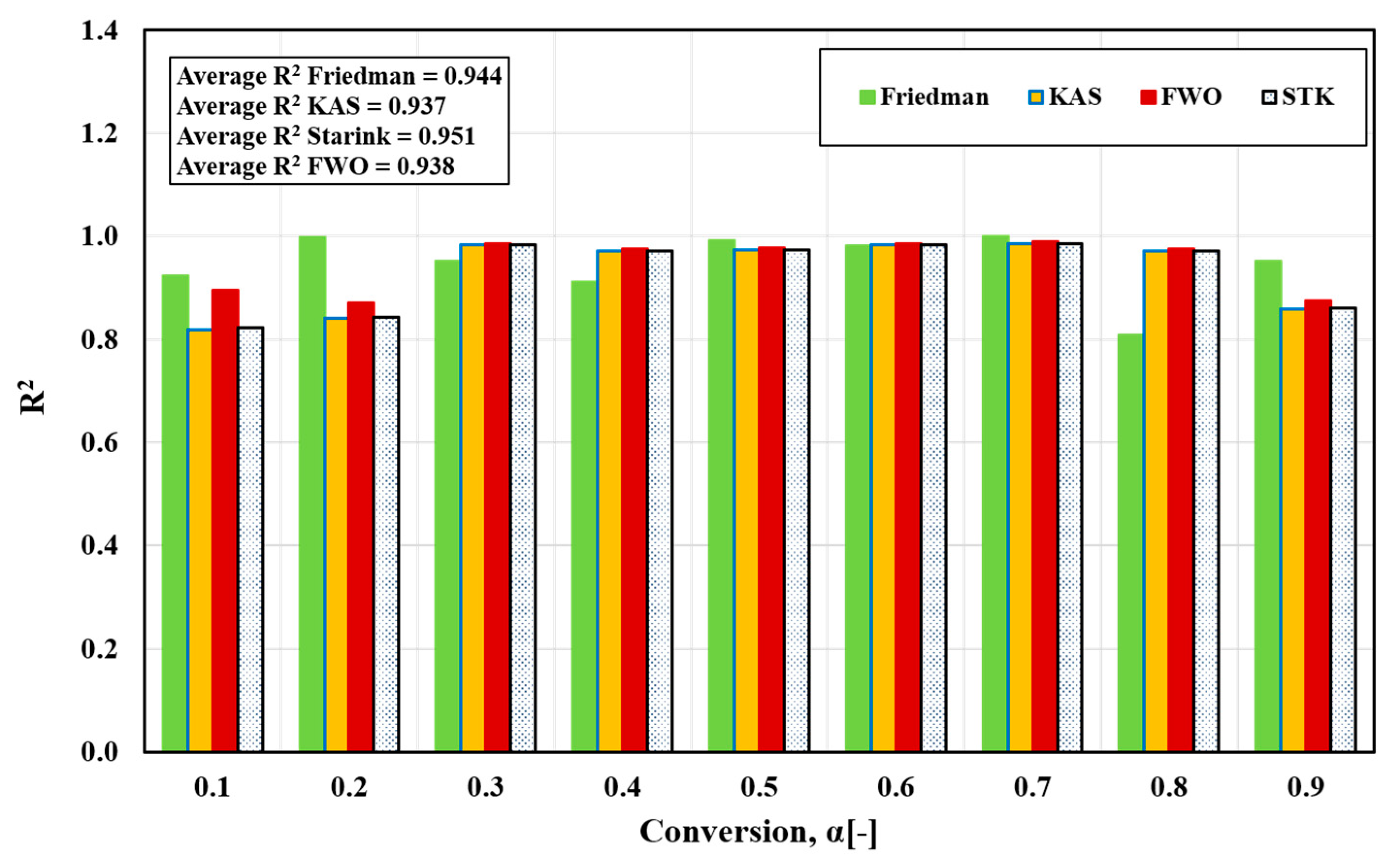
5. Error Analysis
- ▪
- Assumption of a single reaction mechanism while the FTFW pyrolysis consists of multiple overlapping reactions (degradation of lipids, proteins, and residual carbohydrates).
- ▪
- Uncertainties in TGA experiments, including heating rate changes, mass loss fluctuations, and instrumental sensitivity.
- ▪
- The linear regression model’s limitation, which supposes an ideal reaction pathway without considering the impact of heat and mass transfer.
6. Economic or Feasibility Study
7. Conclusions
- ▪
- The average activation energy values calculated by the Friedman, KAS, Starink, and FWO methods were 118.4, 96.7, 109.7, and 100.5 kJ/mol, respectively.
- ▪
- The low activation energy of FTFW, compared to other feedstocks, highlights its potential as a promising candidate for the pyrolysis process.
- ▪
- The pre-exponential factor values obtained by the Friedman, KAS, Starink, and FWO methods were 1.78 × 1013, 1.4 × 1011, 3.95 × 109, and 1.92 × 109 min⁻1, respectively.
- ▪
- The average enthalpy changes estimated using the Friedman, FWO, KAS, and Starink methods were 113.45, 91.78, 95.58, and 104.73 kJ/mol, respectively.
- ▪
- The average Gibbs free energy values for the Friedman, KAS, Starink, and FWO methods were 192.71, 171.04, 183.99, and 174.83 kJ/mol, respectively.
- ▪
- The results of this study offer essential information needed in the efficient design of pyrolysis reactors, indicating the need for optimizing pyrolysis conditions. The results guide the design of efficient pyrolysis reactors, which are useful for waste-to-energy applications, and thus will enhance sustainable biofuel production and improve the valorization strategies for waste.
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Cabrera-Jiménez, R.; Mateo-Sanz, J.M.; Gavaldà, J.; Jiménez, L.; Pozo, C. Comparing biofuels through the lens of sustainability: A data envelopment analysis approach. Appl. Energy 2022, 307, 118201. [Google Scholar] [CrossRef]
- Amigun, B.; Musango, J.K.; Stafford, W. Biofuels and sustainability in Africa. Renew. Sustain. Energy Rev. 2011, 15, 1360–1372. [Google Scholar] [CrossRef]
- Brennan, L.; Langley, S.; Verghese, K.; Lockrey, S.; Ryder, M.; Francis, C.; Phan-Le, N.T.; Hill, A. The role of packaging in fighting food waste: A systematised review of consumer perceptions of packaging. J. Clean. Prod. 2021, 281, 125276. [Google Scholar] [CrossRef]
- Gustafsson, U.; Wills, W.; Draper, A. Food and Public Health: Contemporary Issues and Future Directions; Routledge: London, UK, 2015; pp. 1–9. [Google Scholar] [CrossRef]
- Lorenz, B.A.S.; Hartmann, M.; Langen, N. What makes people leave their food? The interaction of personal and situational factors leading to plate leftovers in canteens. Appetite 2017, 116, 45–56. [Google Scholar] [CrossRef]
- Xu, Z.; Zhang, Z.; Liu, H.; Zhong, F.; Bai, J.; Cheng, S. Food-away-from-home plate waste in China: Preference for variety and quantity. Food Policy 2020, 97, 101918. [Google Scholar] [CrossRef]
- Yin, Y.; Liu, Y.J.; Meng, S.J.; Kiran, E.U.; Liu, Y. Enzymatic pretreatment of activated sludge, food waste and their mixture for enhanced bioenergy recovery and waste volume reduction via anaerobic digestion. Appl. Energy 2016, 179, 1131–1137. [Google Scholar] [CrossRef]
- Yong, Z.; Dong, Y.; Zhang, X.; Tan, T. Anaerobic co-digestion of food waste and straw for biogas production. Renew. Energy 2015, 78, 527–530. [Google Scholar] [CrossRef]
- Su, G.; Ong, H.C.; Fattah, I.M.R.; Ok, Y.S.; Jang, J.H.; Wang, C.T. State-of-the-art of the pyrolysis and co-pyrolysis of food waste: Progress and challenges. Sci. Total Environ. 2022, 809, 151170. [Google Scholar] [CrossRef]
- Koraiem Handawy, M.; Yu Snegirev, A.; Stepanov, V.V.; Talalov, V.A. Energy recovery strategies as a sustainable solutions for municipal solid waste in Egypt. IOP Conf. Ser.: Mater. Sci. Eng. 2021, 1100, 012052. [Google Scholar] [CrossRef]
- FAO. The State of World Fisheries and Aquaculture. Towards Blue Transformation; FAO: Rome, Italy, 2022. [Google Scholar]
- Alfio, V.G.; Manzo, C.; Micillo, R. From Fish Waste to Value: An Overview of the Sustainable Recovery of Omega-3 for Food Supplements. Molecules 2021, 26, 1002. [Google Scholar] [CrossRef]
- Ferraz De Arruda, L.; Borghesi, R.; Oetterer, M. Use of fish waste as silage: A review. Braz. Arch. Biol. Technol. 2007, 50, 879–886. [Google Scholar] [CrossRef]
- Salah, S.I.; Eltaweel, M.; Abeykoon, C. Towards a sustainable energy future for Egypt: A systematic review of renewable energy sources, technologies, challenges, and recommendations. Clean. Eng. Technol. 2022, 8, 100497. [Google Scholar] [CrossRef]
- Bu, Q.; Chen, K.; Morgan, H.M.; Liang, J.; Zhang, X.; Yan, L.; Mao, H. Thermal Behavior and Kinetic Study of the Effects of Zinc-Modified Biochar Catalyst on Lignin and Low-Density Polyethylene (LDPE) Co-Pyrolysis. Trans. ASABE 2018, 61, 1783–1793. [Google Scholar] [CrossRef]
- Qiu, L.; Li, C.; Zhang, S.; Wang, S.; Li, B.; Cui, Z.; Tang, Y.; Hu, X. Distinct property of biochar from pyrolysis of poplar wood, bark, and leaves of the same origin. Ind. Crops Prod. 2023, 202, 117001. [Google Scholar] [CrossRef]
- Jing, Y.; Zhang, Y.; Han, I.; Wang, P.; Mei, Q.; Huang, Y. Effects of different straw biochars on soil organic carbon, nitrogen, available phosphorus, and enzyme activity in paddy soil. Sci. Rep. 2020, 10, 8837. [Google Scholar] [CrossRef]
- Park, Y.K.; Lee, B.; Lee, H.W.; Watanabe, A.; Jae, J.; Tsang, Y.F.; Kim, Y.M. Co-feeding effect of waste plastic films on the catalytic pyrolysis of Quercus variabilis over microporous HZSM-5 and HY catalysts. Chem. Eng. J. 2019, 378, 122151. [Google Scholar] [CrossRef]
- Wang, X.; Ma, D.; Jin, Q.; Deng, S.; Stančin, H.; Tan, H.; Mikulčić, H. Synergistic effects of biomass and polyurethane co-pyrolysis on the yield, reactivity, and heating value of biochar at high temperatures. Fuel Process. Technol. 2019, 194, 106127. [Google Scholar] [CrossRef]
- Xue, Y.; Wang, C.; Hu, Z.; Zhou, Y.; Xiao, Y.; Wang, T. Pyrolysis of sewage sludge by electromagnetic induction: Biochar properties and application in adsorption removal of Pb(II), Cd(II) from aqueous solution. Waste Manag. 2019, 89, 48–56. [Google Scholar] [CrossRef]
- Frišták, V.; Pipíška, M.; Soja, G. Pyrolysis treatment of sewage sludge: A promising way to produce phosphorus fertilizer. J. Clean. Prod. 2018, 172, 1772–1778. [Google Scholar] [CrossRef]
- Sobek, S.; Werle, S. Kinetic modelling of waste wood devolatilization during pyrolysis based on thermogravimetric data and solar pyrolysis reactor performance. Fuel 2020, 261, 116459. [Google Scholar] [CrossRef]
- Mishra, R.K.; Mohanty, K. Pyrolysis of three waste biomass: Effect of biomass bed thickness and distance between successive beds on pyrolytic products yield and properties. Renew. Energy 2019, 141, 549–558. [Google Scholar] [CrossRef]
- Mohseni-Bandpei, A.; Majlesi, M.; Rafiee, M.; Nojavan, S.; Nowrouz, P.; Zolfagharpour, H. Polycyclic aromatic hydrocarbons (PAHs) formation during the fast pyrolysis of hazardous health-care waste. Chemosphere 2019, 227, 277–288. [Google Scholar] [CrossRef]
- Kadlimatti, H.M.; Raj Mohan, B.; Saidutta, M.B. Bio-oil from microwave assisted pyrolysis of food waste-optimization using response surface methodology. Biomass Bioenergy 2019, 123, 25–33. [Google Scholar] [CrossRef]
- Elkhalifa, S.; Al-Ansari, T.; Mackey, H.R.; McKay, G. Food waste to biochars through pyrolysis: A review. Resour. Conserv. Recycl. 2019, 144, 310–320. [Google Scholar] [CrossRef]
- Fernandez, A.; Román, C.; Mazza, G.; Rodriguez, R. Determination of effective moisture diffusivity and thermodynamic properties variation of regional wastes under different atmospheres. Case Stud. Therm. Eng. 2018, 12, 248–257. [Google Scholar] [CrossRef]
- Alves, J.L.F.; Da Silva, J.C.G.; da Silva Filho, V.F.; Alves, R.F.; Ahmad, M.S.; Ahmad, M.S.; de Araujo Galdino, W.V.; De Sena, R.F. Bioenergy potential of red macroalgae Gelidium floridanum by pyrolysis: Evaluation of kinetic triplet and thermodynamics parameters. Bioresour. Technol. 2019, 291, 121892. [Google Scholar] [CrossRef]
- Tahir, M.H.; Zhao, Z.; Ren, J.; Rasool, T.; Naqvi, S.R. Thermo-kinetics and gaseous product analysis of banana peel pyrolysis for its bioenergy potential. Biomass Bioenergy 2019, 122, 193–201. [Google Scholar] [CrossRef]
- Gözke, G. Kinetic and thermodynamic analyses based on thermogravimetric pyrolysis of watermelon seed by isoconversional and master plots methods. Renew. Energy 2022, 201, 916–927. [Google Scholar] [CrossRef]
- White, J.E.; Catallo, W.J.; Legendre, B.L. Biomass pyrolysis kinetics: A comparative critical review with relevant agricultural residue case studies. J. Anal. Appl. Pyrolysis 2011, 91, 1–33. [Google Scholar] [CrossRef]
- Gašparovič, L.; Labovský, J.; Markoš, J.; Jelemenský, L. Calculation of Kinetic Parameters of the Thermal Decomposition of Wood by Distributed Activation Energy Model (DAEM). Chem. Biochem. Eng. Q 2012, 26, 45–53. [Google Scholar]
- Caballero, J.A.; Conesa, J.A. Mathematical considerations for nonisothermal kinetics in thermal decomposition. J. Anal. Appl. Pyrolysis 2005, 73, 85–100. [Google Scholar] [CrossRef]
- Chandrasekaran, A.; Ramachandran, S.; Subbiah, S. Determination of kinetic parameters in the pyrolysis operation and thermal behavior of Prosopis juliflora using thermogravimetric analysis. Bioresour. Technol. 2017, 233, 413–422. [Google Scholar] [CrossRef] [PubMed]
- Badshah, S.L.; Shah, Z.; Francisco Alves, J.L.; Gomes da Silva, J.C.; Iqbal, A. Pyrolysis of the freshwater macroalgae Spirogyra crassa: Evaluating its bioenergy potential using kinetic triplet and thermodynamic parameters. Renew. Energy 2021, 179, 1169–1178. [Google Scholar] [CrossRef]
- Patidar, K.; Singathia, A.; Vashishtha, M.; Kumar Sangal, V.; Upadhyaya, S. Investigation of kinetic and thermodynamic parameters approaches to non-isothermal pyrolysis of mustard stalk using model-free and master plots methods. Mater. Sci. Energy Technol. 2022, 5, 6–14. [Google Scholar] [CrossRef]
- Kumar Mishra, R.; Mohanty, K. Kinetic analysis and pyrolysis behavior of low-value waste lignocellulosic biomass for its bioenergy potential using thermogravimetric analyzer. Mater. Sci. Energy Technol. 2021, 4, 136–147. [Google Scholar] [CrossRef]
- Yan, J.; Yang, Q.; Zhang, L.; Lei, Z.; Li, Z.; Wang, Z.; Ren, S.; Kang, S.; Shui, H. Investigation of kinetic and thermodynamic parameters of coal pyrolysis with model-free fitting methods. Carbon Resour. Convers. 2020, 3, 173–181. [Google Scholar] [CrossRef]
- Clement, S.; Lovell, R.T. Comparison of processing yield and nutrient composition of cultured Nile tilapia (Oreochromis niloticus) and channel catfish (Ictalurus punctatus). Aquaculture 1994, 119, 299–310. [Google Scholar] [CrossRef]
- Iffah Farhah Mohd Yusof, N.; Aqilah Shamsuddin, N.; Aini Zakaria, H.; Farizan Munajat, N. Exploring the potential of fish waste (Sardinella fimbriata) through pyrolysis: A study of kinetics and thermodynamics using isoconversional methods. Mater. Sci. Energy Technol. 2023, 6, 460–471. [Google Scholar] [CrossRef]
- Reza, M.S.; Azad, A.K.; Bakar, M.S.A.; Karim, M.R.; Sharifpur, M.; Taweekun, J. Evaluation of Thermochemical Characteristics and Pyrolysis of Fish Processing Waste for Renewable Energy Feedstock. Sustainability 2022, 14, 1203. [Google Scholar] [CrossRef]
- Fadhil, A.B.; Ahmed, A.I.; Salih, H.A. Production of liquid fuels and activated carbons from fish waste. Fuel 2017, 187, 435–445. [Google Scholar] [CrossRef]
- Kraiem, T.; Ben Hassen-Trabelsi, A.; Naoui, S.; Belayouni, H.; Jeguirim, M. Characterization of the liquid products obtained from Tunisian waste fish fats using the pyrolysis process. Fuel Process. Technol. 2015, 138, 404–412. [Google Scholar] [CrossRef]
- Ahmed, G.; Annapureddy, P.K.R.; Kishore, N. Study on non-isothermal pyrolysis of Azadirachta Indica for kinetic triplets and thermodynamics evaluation. Bioresour. Technol. Rep. 2024, 25, 101794. [Google Scholar] [CrossRef]
- Li, Y.; Wang, Y.; Chai, M.; Li, C.; Yellezuome, D.; Liu, R. Pyrolysis kinetics and thermodynamic parameters of bamboo residues and its three main components using thermogravimetric analysis. Biomass Bioenergy 2023, 170, 106705. [Google Scholar] [CrossRef]
- Wang, K.; Shan, T.; Li, B.; Zheng, Y.; Xu, H.; Wang, C.; Tian, X. Study on pyrolysis characteristics, kinetics and thermodynamics of waste tires catalytic pyrolysis with low-cost catalysts. Fuel 2024, 356, 129644. [Google Scholar] [CrossRef]
- Wang, Y.; Yang, S.; Bao, G.; Wang, H. Investigation on prospective bioenergy from pyrolysis of macadamia nut shell waste using multicomponent Fraser-Suzuki kinetic model, kinetic triplet and thermodynamic parameters. J. Energy Inst. 2024, 114, 101611. [Google Scholar] [CrossRef]
- Jo, J.H.; Kim, S.S.; Shim, J.W.; Lee, Y.E.; Yoo, Y.S. Pyrolysis Characteristics and Kinetics of Food Wastes. Energies 2017, 10, 1191. [Google Scholar] [CrossRef]
- Norisham, S.F.; Munajat, N.F. Torrefaction of fish waste (Sardinella fimbriata) in a fixed bed reactor: Yields and biochar characterization. IOP. Conf. Ser. Earth Environ. Sci. 2021, 765, 012022. [Google Scholar] [CrossRef]
- Ming, X.; Xu, F.; Jiang, Y.; Zong, P.; Wang, B.; Li, J.; Qiao, Y.; Tian, Y. Thermal degradation of food waste by TG-FTIR and Py-GC/MS: Pyrolysis behaviors, products, kinetic and thermodynamic analysis. J. Clean. Prod. 2020, 244, 118713. [Google Scholar] [CrossRef]
- Nyambura, S.M.; Jufei, W.; Hua, L.; Xuebin, F.; Xingjia, P.; Bohong, L.; Ahmad, R.; Jialiang, X.; Bertrand, G.V.; Ndiithi, J.; et al. Microwave co-pyrolysis of kitchen food waste and rice straw for waste reduction and sustainable biohydrogen production: Thermo-kinetic analysis and evolved gas analysis. Sustain. Energy Technol. Assess. 2022, 52, 102072. [Google Scholar] [CrossRef]
- Zhao, J.; Wang, Z.; Li, J.; Yan, B.; Chen, G. Pyrolysis of food waste and food waste solid digestate: A comparative investigation. Bioresour. Technol. 2022, 354, 127191. [Google Scholar] [CrossRef]
- Ben Abdallah, A.; Ben Hassen Trabelsi, A.; Navarro, M.V.; Veses, A.; García, T.; Mihoubi, D. Pyrolysis of tea and coffee wastes: Effect of physicochemical properties on kinetic and thermodynamic characteristics. J. Therm. Anal. Calorim. 2023, 148, 2501–2515. [Google Scholar] [CrossRef] [PubMed]
- Embaye, T.M.; Ahmed, M.B.; Deng, N.; Cui, W.; Bukhsh, K.; Zhang, L.; Zhu, L.; Wang, X. Co-pyrolysis behavior of municipal solid waste and food waste residue: A thermogravimetric study to discern synergistic effect. Process Saf. Environ. Prot. 2024, 189, 1274–1284. [Google Scholar] [CrossRef]
- Alves, J.L.F.; da Silva, J.C.G.; Mumbach, G.D.; Arias, S.; Pacheco, J.G.A.; Di Domenico, M.; Marangoni, C. Valorization of royal palm tree agroindustrial waste via pyrolysis with a focus on physicochemical properties, kinetic triplet, thermodynamic parameters, and volatile products. Biomass Bioenergy 2023, 177, 106937. [Google Scholar] [CrossRef]
- Gupta, S.; Gupta, G.K.; Mondal, M.K. Thermal degradation characteristics, kinetics, thermodynamic, and reaction mechanism analysis of pistachio shell pyrolysis for its bioenergy potentia. Biomass Convers. Biorefinery 2022, 12, 4847–4861. [Google Scholar] [CrossRef]
- Mumbach, G.D.; Alves, J.L.F.; da Silva, J.C.G.; Di Domenico, M.; Marangoni, C.; Machado, R.A.F.; Bolzan, A. Investigation on prospective bioenergy from pyrolysis of butia seed waste using TGA-FTIR: Assessment of kinetic triplet, thermodynamic parameters and evolved volatiles. Renew. Energy 2022, 191, 238–250. [Google Scholar] [CrossRef]
- Rasam, S.; Moshfegh Haghighi, A.; Azizi, K.; Soria-Verdugo, A.; Keshavarz Moraveji, M. Thermal behavior, thermodynamics and kinetics of co-pyrolysis of binary and ternary mixtures of biomass through thermogravimetric analysis. Fuel 2020, 280, 118665. [Google Scholar] [CrossRef]
- Açıkalın, K.; Gözke, G. Thermogravimetric pyrolysis of onion skins: Determination of kinetic and thermodynamic parameters for devolatilization stages using the combinations of isoconversional and master plot methods. Bioresour. Technol. 2021, 342, 125936. [Google Scholar] [CrossRef]
- Vyazovkin, S.; Burnham, A.K.; Criado, J.M.; Pérez-Maqueda, L.A.; Popescu, C.; Sbirrazzuoli, N. ICTAC Kinetics Committee recommendations for performing kinetic computations on thermal analysis data. Thermochim. Acta 2011, 520, 1–19. [Google Scholar] [CrossRef]
- da Silva, J.C.G.; de Albuquerque, J.G.; de Araujo Galdino, W.V.; de Sena, R.F.; Andersen, S.L.F. Single-step and multi-step thermokinetic study—Deconvolution method as a simple pathway for describe properly the biomass pyrolysis for energy conversion. Energy Convers. Manag. 2020, 209, 112653. [Google Scholar] [CrossRef]
- da Silva, J.C.G.; Alves, J.L.F.; de Araujo Galdino, W.V.; Andersen, S.L.F.; de Sena, R.F. Pyrolysis kinetic evaluation by single-step for waste wood from reforestation. Waste Manag. 2018, 72, 265–273. [Google Scholar] [CrossRef]
- Badshah, S.L.; Shah, Z.; Alves, J.L.F.; da Silva, J.C.G.; Noreen, N.; Iqbal, A. Kinetic and thermodynamics study of the pyrolytic process of the freshwater macroalga, Chara vulgaris. J. Appl. Phycol. 2021, 33, 2511–2521. [Google Scholar] [CrossRef]
- Friedman, H.L. Kinetics of thermal degradation of char-forming plastics from thermogravimetry. Application to a phenolic plastic. J. Polym. Sci. Part C Polym. Symp. 1964, 6, 183–195. [Google Scholar] [CrossRef]
- Handawy, M.K.M.; Im, I.T.; Abdelmotalib, H.M. Thermal degradation kinetics and reaction mechanisms of HDPE and PS plastic wastes using a micro combustion calorimeter. J. Mech. Sci. Technol. 2024, 38, 7007–7018. [Google Scholar] [CrossRef]
- Kissinger, H.E. Reaction Kinetics in Differential Thermal Analysis. Anal. Chem. 1957, 29, 1702–1706. [Google Scholar] [CrossRef]
- Akahira, T. Trans Joint convention of four electrical institutes. Res. Rep. Chiba Inst. Technol. 1971, 16, 22–31. [Google Scholar] [CrossRef]
- Hu, Y.; Wang, Z.; Cheng, X.; Ma, C. Non-isothermal TGA study on the combustion reaction kinetics and mechanism of low-rank coal char. RSC Adv. 2018, 8, 22909–22916. [Google Scholar] [CrossRef] [PubMed]
- Starink, M.J. The determination of activation energy from linear heating rate experiments: A comparison of the accuracy of isoconversion methods. Thermochim. Acta 2003, 404, 163–176. [Google Scholar] [CrossRef]
- Starink, M.J. A new method for the derivation of activation energies from experiments performed at constant heating rate. Thermochim. Acta 1996, 288, 97–104. [Google Scholar] [CrossRef]
- Flynn, J.H.; Wall, L.A. A quick, direct method for the determination of activation energy from thermogravimetric data. J. Polym. Sci. B 1966, 4, 323–328. [Google Scholar] [CrossRef]
- Takeo, O. A new method of analyzing thermogravimetric Data. Bull. Chem. Soc. Jpn. 1965, 38, 1881–1886. [Google Scholar] [CrossRef]
- Criado, J.M.; Málek, J.; Ortega, A. Applicability of the master plots in kinetic analysis of non-isothermal data. Thermochim. Acta 1989, 147, 377–385. [Google Scholar] [CrossRef]
- Šesták, J.; Berggren, G. Study of the kinetics of the mechanism of solid-state reactions at increasing temperatures. Thermochim. Acta 1971, 3, 1–12. [Google Scholar] [CrossRef]
- Vasudev, V.; Ku, X.; Lin, J. Pyrolysis of algal biomass: Determination of the kinetic triplet and thermodynamic analysis. Bioresour. Technol. 2020, 317, 124007. [Google Scholar] [CrossRef]
- Snegirev, A.Y. Generalized approach to model pyrolysis of flammable materials. Thermochim. Acta 2014, 590, 242–250. [Google Scholar] [CrossRef]
- Snegirev, A.; Talalov, V.; Stepanov, V.; Harris, J. Formal kinetics of polymer pyrolysis for modeling of ignition and burning in fire tests. In Proceedings of the 13th International Conference Interflam, Nr Windsor, UK, 24–26 June 2013; pp. 755–768. [Google Scholar]
- Snegirev, A.Y.; Talalov, V.A.; Stepanov, V.V.; Korobeinichev, O.P.; Gerasimov, I.E.; Shmakov, A.G. Autocatalysis in thermal decomposition of polymers. Polym. Degrad. Stab. 2017, 137, 151–161. [Google Scholar] [CrossRef]
- Agrawal, A.; Chakraborty, S. A kinetic study of pyrolysis and combustion of microalgae Chlorella vulgaris using thermo-gravimetric analysis. Bioresour. Technol. 2013, 128, 72–80. [Google Scholar] [CrossRef]
- Coker, A.K. Industrial and Laboratory Reactors—Chemical Reaction Hazards and Process Integration of Reactors, Ludwig’s Applied Process Design for Chemical and Petrochemical Plants; Gulf Professional Publishing: Oxford, UK, 2015; pp. 1095–1208. [Google Scholar] [CrossRef]
- Sbirrazzuoli, N. Determination of pre-exponential factors and of the mathematical functions f(α) or G(α) that describe the reaction mechanism in a model-free way. Thermochim. Acta 2013, 564, 59–69. [Google Scholar] [CrossRef]
- Kumar, M.; Shukla, S.K.; Upadhyay, S.N.; Mishra, P.K. Analysis of thermal degradation of banana (Musa balbisiana) trunk biomass waste using iso-conversional models. Bioresour. Technol. 2020, 310, 123393. [Google Scholar] [CrossRef]
- Sahoo, A.; Kumar, S.; Kumar, J.; Bhaskar, T. A detailed assessment of pyrolysis kinetics of invasive lignocellulosic biomasses (Prosopis juliflora and Lantana camara) by thermogravimetric analysis. Bioresour. Technol. 2021, 319, 124060. [Google Scholar] [CrossRef]
- Al-Rumaihi, A.; Parthasarathy, P.; Fernandez, A.; Al-Ansari, T.; Mackey, H.R.; Rodriguez, R.; Mazza, G.; McKay, G. Thermal degradation characteristics and kinetic study of camel manure pyrolysis. J. Environ. Chem. Eng. 2021, 9, 106071. [Google Scholar] [CrossRef]
- Ahmad, M.S.; Mehmood, M.A.; Al Ayed, O.S.; Ye, G.; Luo, H.; Ibrahim, M.; Rashid, U.; Arbi Nehdi, I.; Qadir, G. Kinetic analyses and pyrolytic behavior of Para grass (Urochloa mutica) for its bioenergy potential. Bioresour. Technol. 2017, 224, 708–713. [Google Scholar] [CrossRef]
- Mohammed, H.I.; Garba, K.; Ahmed, S.I.; Abubakar, L.G. Thermodynamics and kinetics of Doum (Hyphaene thebaica) shell using thermogravimetric analysis: A study on pyrolysis pathway to produce bioenergy. Renew. Energy 2022, 200, 1275–1285. [Google Scholar] [CrossRef]
- Florentino-Madiedo, L.; Vega, M.F.; Díaz-Faes, E.; Barriocanal, C. Evaluation of synergy during co-pyrolysis of torrefied sawdust, coal and paraffin. A kinetic and thermodynamic study. Fuel 2021, 292, 120305. [Google Scholar] [CrossRef]
- Chen, F.; Zhang, F.; Yang, S.; Liu, H.; Wang, H.; Hu, J. Investigation of pyrolysis kinetics, thermodynamics, product characteristics and reaction mechanism of rubber seed oil. Energy Convers. Manag. 2021, 244, 114535. [Google Scholar] [CrossRef]
- Varma, A.K.; Lal, N.; Rathore, A.K.; Katiyar, R.; Thakur, L.S.; Shankar, R.; Mondal, P. Thermal, kinetic and thermodynamic study for co-pyrolysis of pine needles and styrofoam using thermogravimetric analysis. Energy 2021, 218, 119404. [Google Scholar] [CrossRef]
- Müsellim, E.; Tahir, M.H.; Ahmad, M.S.; Ceylan, S. Thermokinetic and TG/DSC-FTIR study of pea waste biomass pyrolysis. Appl. Therm. Eng. 2018, 137, 54–61. [Google Scholar] [CrossRef]
- Kumar, M.; Mishra, P.K.; Upadhyay, S.N. Thermal degradation of rice husk: Effect of pre-treatment on kinetic and thermodynamic parameters. Fuel 2020, 268, 117164. [Google Scholar] [CrossRef]
- Xu, X.; Chen, R.; Pan, R.; Zhang, D. Pyrolysis Kinetics, Thermodynamics, and Volatiles of Representative Pine Wood with Thermogravimetry–Fourier Transform Infrared Analysis. Energy Fuels 2020, 34, 1859–1869. [Google Scholar] [CrossRef]
- Tahir, M.H.; Çakman, G.; Goldfarb, J.L.; Topcu, Y.; Naqvi, S.R.; Ceylan, S. Demonstrating the suitability of canola residue biomass to biofuel conversion via pyrolysis through reaction kinetics, thermodynamics and evolved gas analyses. Bioresour. Technol. 2019, 279, 67–73. [Google Scholar] [CrossRef]



| Feedstock | Methods Used | Heating Rate, β °C/min | Kinetic Triplt Parameters | Ref. |
|---|---|---|---|---|
| Azadirachta indica biomass |
| β = 10, 20, 30 and 40 °C/min |
| [44] |
| Macroalgae Spirogyra crassa |
|
|
| [35] |
| Bamboo residues and three main components (cellulose, hemicellulose, and lignin) |
|
|
| [45] |
| Waste tires with spent FCC catalyst, red mud, and fly ash |
|
|
| [46] |
| Macadamia nutshell waste (MNSW) |
| β = 10, 15, 20 and 25 °C/min |
| [47] |
| Waste Food | ||||
| Food waste (cereals, meat, vegetables, and mixed waste) | TGA, DTG, Friedman method | β = 5, 10, 15, and 20 °C/min |
| [48] |
| Raw Fish waste (Sardinella fimbriata) | Fixed-bed torrefaction reactor | - | - | [49] |
| Raw Fish processing waste (Neotrygon kuhlii) | TGA, DTG, FTIR, SEM/EDX, Fixed Bed Reactor | β = 25 °C/min | Non | [41] |
| Fish waste (Sardinella fimbriata) |
| β = 10, 20, and 30 °C/min |
| [40] |
| Waste food (pork and rice) |
| β = 30, 60, and 90 °C/min |
| [50] |
| Kitchen Food Waste and Rice Straw |
| β = 10, 20, and 30 °C/min |
| [51] |
| Food waste and waste solid digestate food |
| β = 5, 10, 15, 20, and 25 °C/min |
| [52] |
| Tea and coffee wastes |
| β = 10, 25, 50 and 100 °C/min |
| [53] |
| Municipal solid waste and food waste |
|
|
| [54] |
| Fried tilapia fish waste (FTFW) |
|
|
| Current study |
| Method | Governing Equation | Plotting Method | Slope | Equation No. |
|---|---|---|---|---|
| Friedman [64] | Plotting y-axis against x-axis | (10) | ||
| KAS [66,67] | Plotting y-axis against x-axis | (11) | ||
| Starink [68,69,70] | Plotting y-axis against x-axis | (12) | ||
| FWO [71,72] | Plotting y-axis against x-axis | (13) |
| Heating Rate β °C/min | Peak | Peak Temperature °C | Peak Mass Loss % | DTG %/min |
|---|---|---|---|---|
| 10 | 1st peak | 143.9 | 96.1 | 0.6615 |
| 2nd peak | 387.3 | 54.68 | 3.912 | |
| 15 | 1st peak | 147.5 | 96.72 | 1.21485 |
| 2nd peak | 398.92 | 51.27 | 6.267 | |
| 20 | 1st peak | 183.1 | 96.29 | 1.1356 |
| 2nd peak | 407.57 | 62.22 | 7.658 |
| Feedstock | Method | Average Ea Range (kJ/mol) | Ref. |
|---|---|---|---|
| Fried fish tilapia waste | KAS, Starink, FWO | (96.7–109.7) | Present study |
| Sardinella fimbriata fish waste | KAS, Starink, FWO | (83.75–123.75) | [40] |
| Petroleum sludge | KAS, Starink, FWO | 41.31–133.89 | [85] |
| Doum shell | KAS, Starink, FWO | 118.15–142.81 | [86] |
| α | Model | Coefficients | Stage |
|---|---|---|---|
| 0.1–0.5 | m = 1, n = 2.1, P = 2 | First stage | |
| 0.5–0.9 | n = 1.23 m = 1.4 = 0.05 | Second stage |
| α | Friedman | KAS | Starink | FWO | ||||
|---|---|---|---|---|---|---|---|---|
| Ea [kJ/mol] | A [min−1] | Eα [kJ/mol] | A [min−1] | Ea [kJ/mol] | A [min−1] | Ea [kJ/mol] | A [min−1] | |
| 0.1 | 43.23 | 1.29 × 10+04 | 21.95 | 6.09 × 10+01 | 24.06 | 1.04 × 10+02 | 31.61 | 6.93 × 10+02 |
| 0.15 | 105.83 | 6.40 × 10+09 | 46.82 | 1.03 × 10+04 | 50.95 | 2.63 × 10+04 | 58.72 | 1.52 × 10+05 |
| 0.2 | 92.06 | 1.38 × 10+08 | 71.16 | 1.55 × 10+6 | 77.26 | 5.75 × 10+06 | 84.74 | 2.87 × 10+07 |
| 0.25 | 106.63 | 1.62 × 10+09 | 88.39 | 3.6 × 10+07 | 95.88 | 1.74 × 10+08 | 103.14 | 7.85 × 10+08 |
| 0.3 | 109.93 | 1.99 × 10+09 | 95.43 | 1.06 × 10+08 | 103.49 | 5.41 × 10+08 | 110.86 | 2.40 × 10+09 |
| 0.35 | 94.06 | 5.89 × 10+07 | 95.36 | 7.62 × 10+7 | 101.61 | 3.77 × 10+08 | 110.95 | 1.67 × 10+09 |
| 0.4 | 108.96 | 8.04 × 10+08 | 94.78 | 5.09 × 10+07 | 97.09 | 7.99 × 10+07 | 110.53 | 1.09 × 10+09 |
| 0.45 | 83.18 | 3.96 × 10+06 | 94.35 | 3.35 × 10+7 | 95.53 | 4.20 × 10+07 | 110.27 | 7.05 × 10+08 |
| 0.5 | 87.07 | 6.54 × 10+06 | 94.82 | 2.80 × 10+07 | 96.01 | 3.51 × 10+07 | 110.95 | 5.83 × 10+08 |
| 0.55 | 105.54 | 1.61 × 10+08 | 96.71 | 3.13 × 10+07 | 99.08 | 4.86 × 10+07 | 113.12 | 6.54 × 10+08 |
| 0.6 | 124.51 | 4.05 × 10+09 | 99.77 | 4.43 × 10+07 | 102.22 | 6.93 × 10+07 | 116.49 | 9.38 × 10+08 |
| 0.65 | 141.60 | 6.91 × 10+10 | 103.64 | 7.46 × 10+07 | 106.16 | 1.17 × 10+08 | 120.71 | 1.61 × 10+09 |
| 0.7 | 119.62 | 1.06 × 10+09 | 107.80 | 1.29 × 10+08 | 110.41 | 2.06 × 10+08 | 125.24 | 2.87 × 10+09 |
| 0.75 | 162.26 | 1.44 × 10+12 | 110.69 | 1.70 × 10+08 | 113.37 | 2.73 × 10+08 | 128.45 | 3.83 × 10+09 |
| 0.8 | 129.63 | 3.05 × 10+09 | 114.60 | 2.28 × 10+08 | 120.82 | 6.66 × 10+08 | 132.76 | 5.23 × 10+09 |
| 0.85 | 190.41 | 3.87 × 10+13 | 128.80 | 1.183 × 10+09 | 131.86 | 1.98 × 10+09 | 148.00 | 3.02 × 10+10 |
| 0.9 | 208.20 | 2.63 × 10+14 | 179.30 | 2.380 × 10+12 | 181.23 | 3.26 × 10+12 | 148.00 | 1.46 × 10+10 |
| Feedstock | Method | ∆H (kJ/mol) | ∆G (kJ/mol) | ∆S (J/mol·K) | Ref. |
|---|---|---|---|---|---|
| FTFW | Friedman | 113.45 | 192.71 | −130 | Current study |
| KAS | 91.78 | 171.04 | −130 | ||
| Starink | 95.58 | 174.83 | −126 | ||
| FWO | 104.73 | 183.99 | −126 | ||
| Sardinella fimbriata fish wastes | FWO | 109.53 | 185.5 | −150 | [40] |
| KAS | 95.38 | 185.5 | |||
| Pine needles and styrofoam | FWO | 104.24 | 131.24 | −0.04 | [89] |
| Pistachio shell | KAS | 160.87 | 182.15 | −33.99 | [56] |
| Friedman | 185.16 | 181.42 | 3.83 | ||
| Butia seed waste | KAS | 133.98 | [57] | ||
| Pea factory waste (PW) | Mean value | 207.62 | 174.5 | [90] | |
| Rice husk | KAS | 214.60 | 175.5 | 63.1 | [91] |
| Pine wood | Mean value | 198.39 | [92] | ||
| Canola residue | Mean value | 131.7 | 154.7 | [93] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Handawy, M.K.M.; Im, I.-T.; Lee, G.W.; Abdelmotalib, H.M. Kinetic and Thermodynamic Analysis of Fried Tilapia Fish Waste Pyrolysis for Biofuel Production. Recycling 2025, 10, 61. https://doi.org/10.3390/recycling10020061
Handawy MKM, Im I-T, Lee GW, Abdelmotalib HM. Kinetic and Thermodynamic Analysis of Fried Tilapia Fish Waste Pyrolysis for Biofuel Production. Recycling. 2025; 10(2):61. https://doi.org/10.3390/recycling10020061
Chicago/Turabian StyleHandawy, Mohamed Koraiem M., Ik-Tae Im, Gyo Woo Lee, and Hamada Mohamed Abdelmotalib. 2025. "Kinetic and Thermodynamic Analysis of Fried Tilapia Fish Waste Pyrolysis for Biofuel Production" Recycling 10, no. 2: 61. https://doi.org/10.3390/recycling10020061
APA StyleHandawy, M. K. M., Im, I.-T., Lee, G. W., & Abdelmotalib, H. M. (2025). Kinetic and Thermodynamic Analysis of Fried Tilapia Fish Waste Pyrolysis for Biofuel Production. Recycling, 10(2), 61. https://doi.org/10.3390/recycling10020061






