A Multi-Shot Approach for Spatial Resolution Improvement of Multispectral Images from an MSFA Sensor
Abstract
:1. Introduction
- Setting up a dataset for our experiments, consisting in transforming images from a database of 31 into 8 bands to simulate our 8-band MSFA moxel. These images will then be mosaicked with our MSFA filter to simulate a snapshot from our camera;
- Development of a new composition method with a multi-shot approach to reduce the number of null pixels in sparse images while maintaining the same number of spectral bands;
- Performed visual and analytical comparisons using validation metrics to evaluate our experiments, demonstrating the improvement in spatial resolution of the final image obtained after demosaicing.
2. Related Works on Improving the Spatial Resolution of MSFA Images
3. Materials and Methods
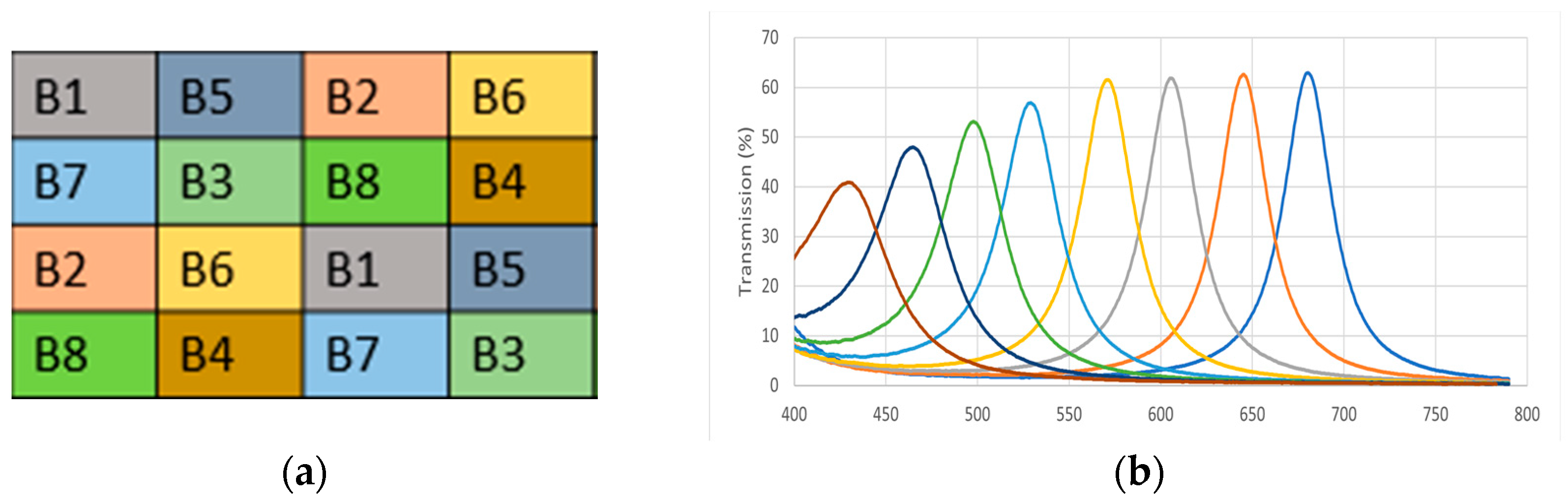
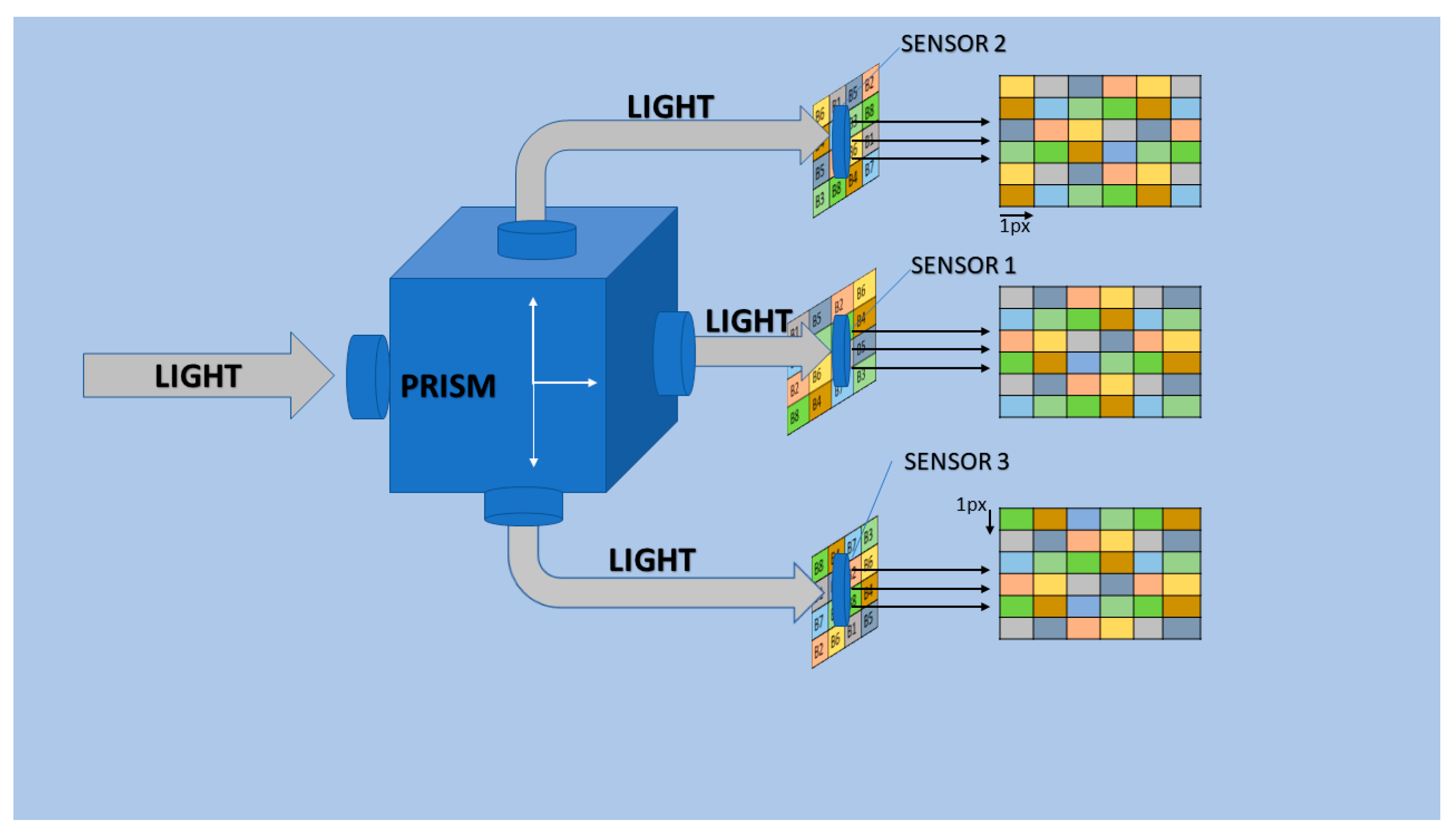
3.1. The MSFA Moxel
- Dominant bands: the probability of the appearance of certain bands in the MSFA moxel is higher than others;
- Nondominant bands: all bands in the MSFA moxel have the same probability of appearance.
3.2. Dataset
- Determination of the desired number of bands for the resulting multispectral image, in our study, eight bands.
- Definition of Gaussian filter full width at half maximum (FWHM) in nanometers; in our study, this width is 30 nm.
- Calculating the standard deviation of the Gaussian filter corresponding to the defined FWHM is necessary because the shape of the Gaussian is determined by its standard deviation.
- Calculation of the central wavelength of each Gaussian filter. we use a distance of 3 times the standard deviation of the start wavelength. Then, we move at a calculated interval between filters and end at a distance of 3 times the standard deviation of the end wavelength. Subsequently, we round the values to the nearest integer and sample at the desired spectral interval.
- Creation of Gaussian filters using a Gaussian function. Each filter is calculated based on the similarity between the spectral wavelength and the central wavelength of the filter. The greater the similarity, the higher the filter weight. Filters are normalized to ensure that their sum equals 1.
- The recovery of original image data from 31 bands is followed by filtering using the created Gaussian filters.
- Multiplication of Gaussian filters to the weighted data to perform the 8-band multispectral transformation, selecting the appropriate spectral bands.
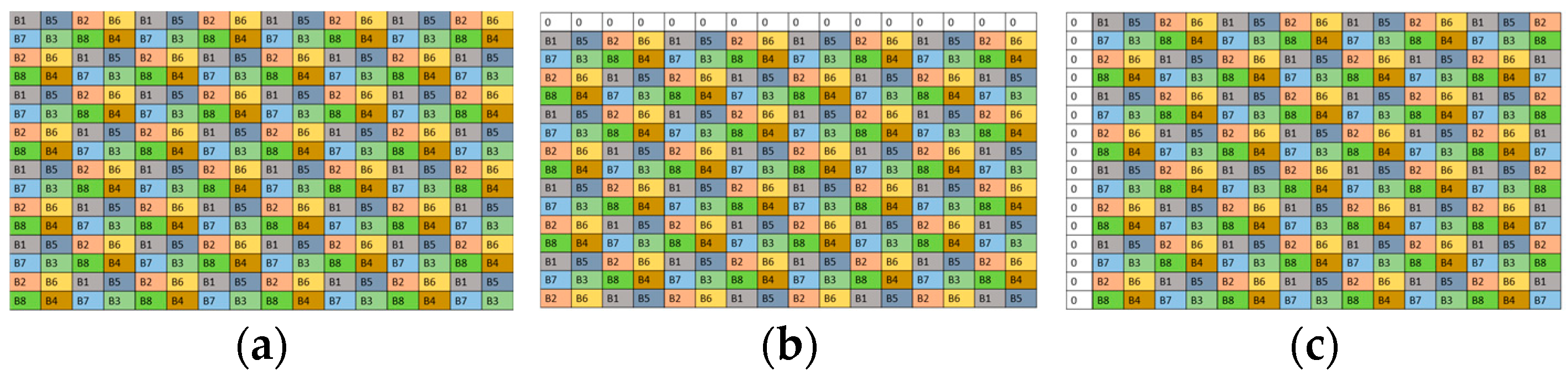
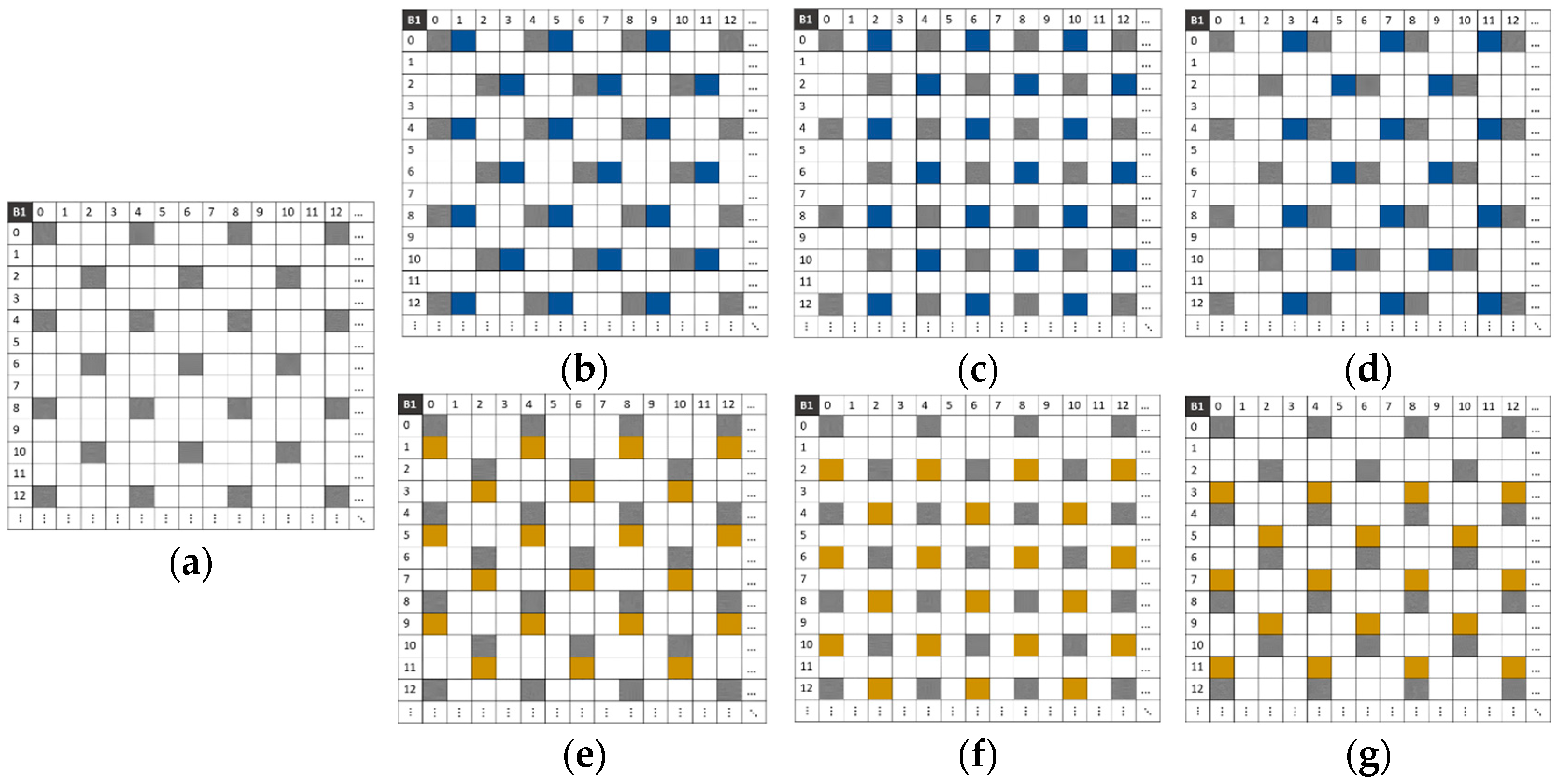
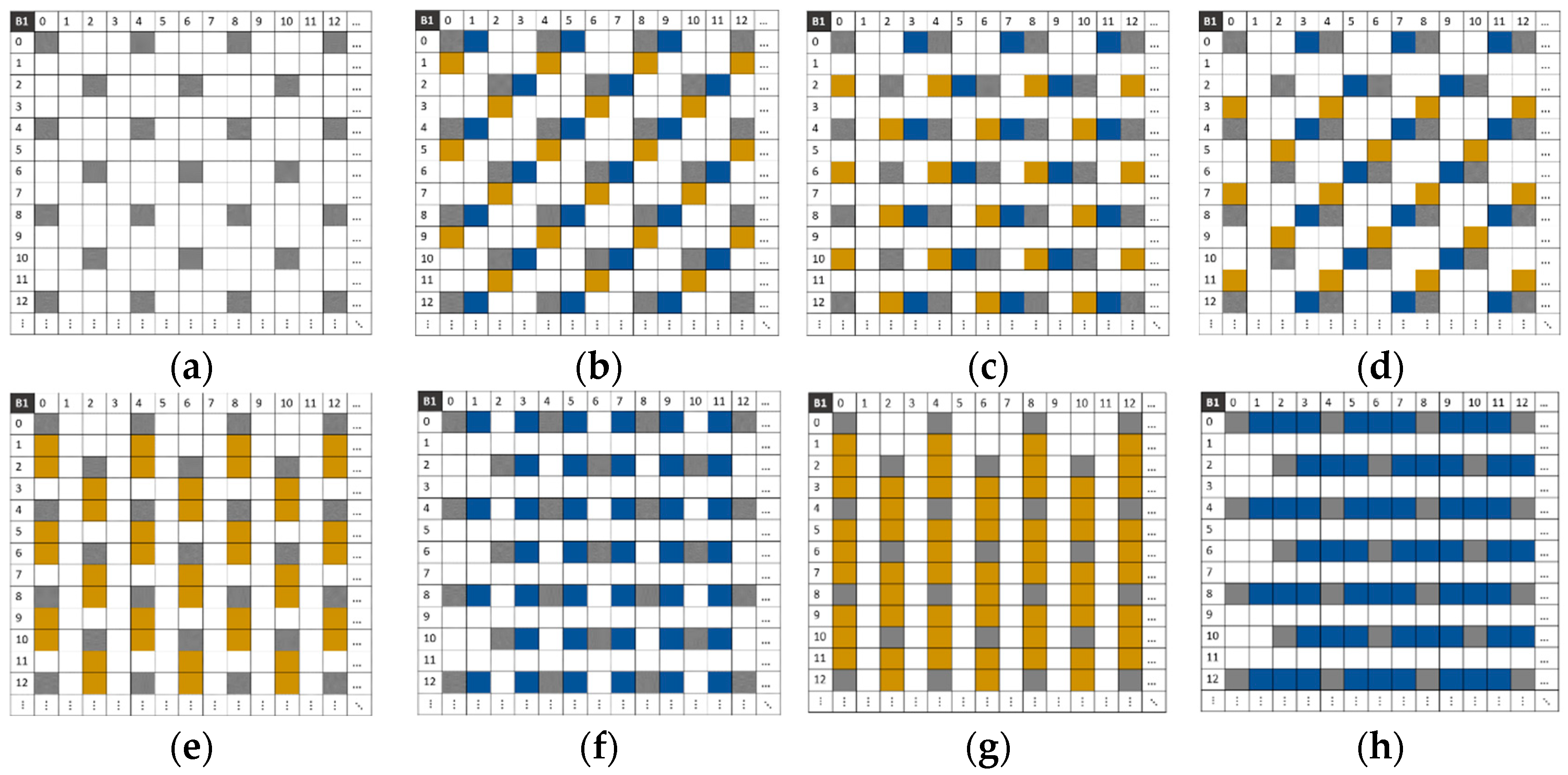
3.3. Mosaicking Process to Obtain Sparse Images
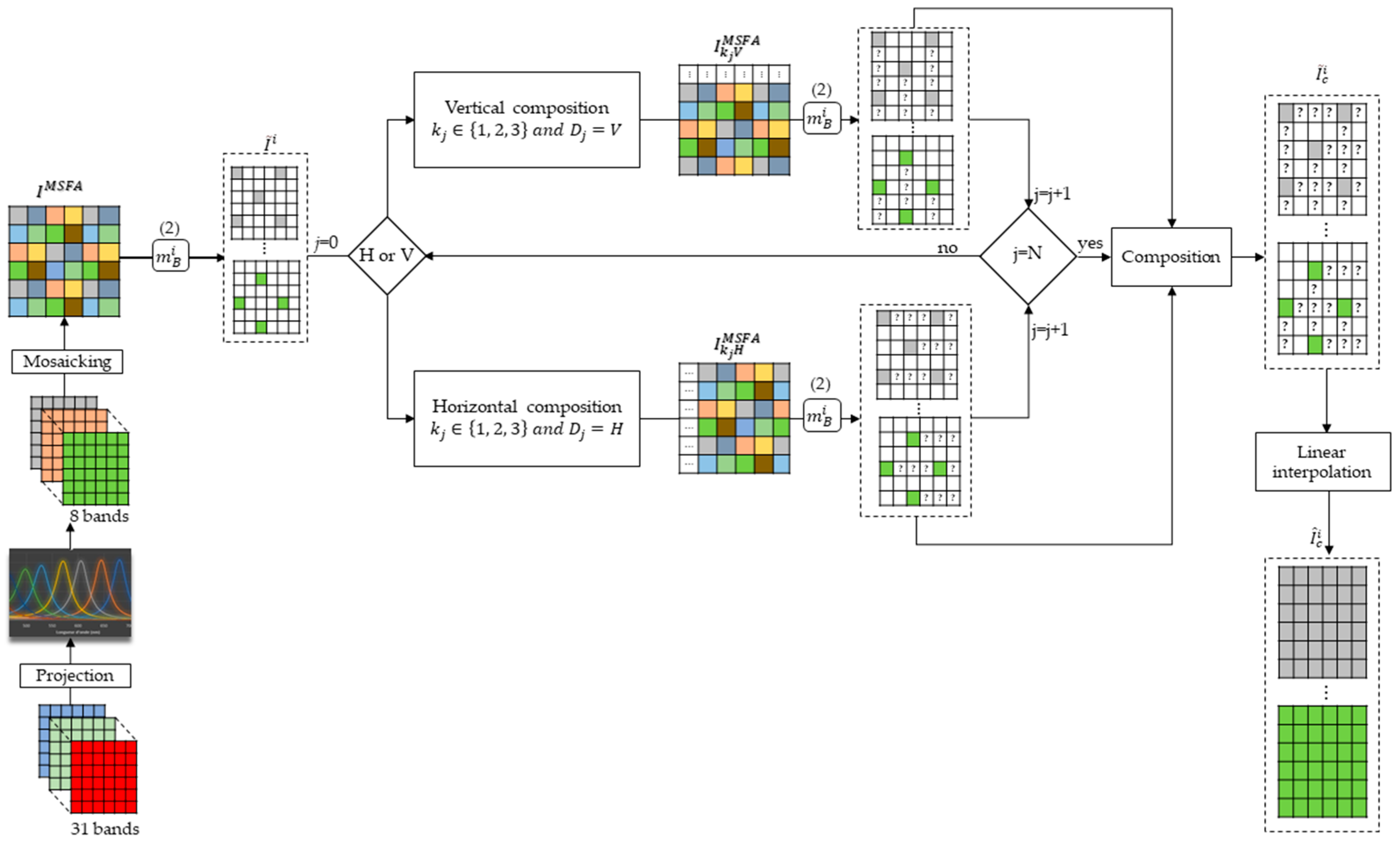
3.4. Conceptualization of the Method
3.5. Sparse Image Composition
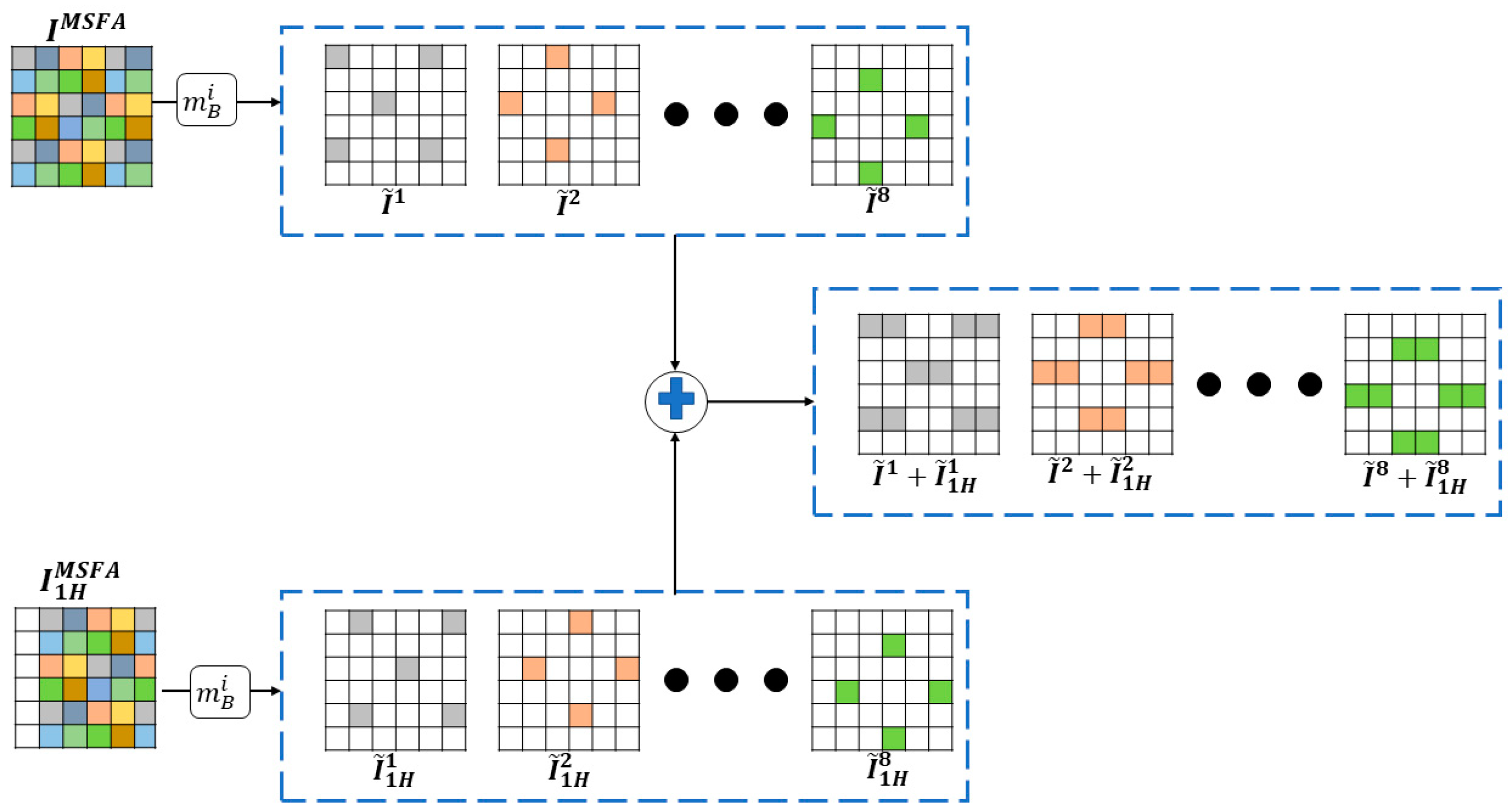
3.5.1. Case of the Composition of Two Sparse Images
- The camera takes a first snapshot from which we obtain a mosaic ;
- The camera moves k pixel(s) on the D axis and takes a second snapshot, from which a second mosaic is obtained;
- The separation into sparse image is performed on the mosaics and with Formula (2), resulting in sparse images and ;
- The addition of the two sparse images is performed, such that .
3.5.2. Cases of Sparse Images Greater Than Two
- The camera takes a first snapshot from which a mosaic is obtained.
- The separation into sparse images is performed on the mosaics using Formula (2), resulting in the sparse images .
- The initialization step sets the values of to and j to 1.
- As long as j ≤ N:
- The camera moves along the Dj axis by kj pixels from its position (0, 0) and takes a snapshot, and a new mosaic is obtained.
- The new mosaic is decomposed using Formula (2), resulting in sparse images .
- The above sparse image is added to the previous sparse image , and the value of j is incremented.
- In the end, we get composite sparse images .
3.6. Bilinear Interpolation
| Algorithm 1: Bilinear interpolation. |
| Input: sparse_image, method |
| Output: InterpIMG |
| BEGIN |
| Width = sparse_image.width |
| Height = sparse_image.height |
| XI = value grid going from 1 to height + 1 |
| YI = value grid going from 1 to width + 1 |
| Ind = coordinates of data to interpolate |
| Z = values of non-null indices |
| InterpIMG = grid_interpolation(Ind,Z,(XI, YI), fill_value = 2.2 × 10−16) |
| END |
| Algorithm 2: grid_interpolation. |
| Input: points, values, grid, method, fill_value |
| // points: The coordinates of the data to interpolate |
| // values: The corresponding values at the data points |
| // grid: The grid on which to interpolate the data |
| // fill_value: the value to use for points outside the input grid |
| Output: InterpIMG |
| BEGIN |
| For each point (x, y) in grid: |
| If (x, y) is outside of the input points: |
| Assign fill_value to InterpIMG(x, y) |
| Else: |
| Find the k (2 ≤ k ≤ 4) nearest data points within a rectangular grid, with 2 along each axis |
| Calculate the weights for interpolation based on distance |
| Interpolate the value at (x, y) using the input values in points and interpolation weights |
| Assign the new value to InterpIMG(x, y) |
| End If |
| End For |
| End If |
| END |
3.7. The General Architecture of Our Method
4. Experiments and Results
4.1. Metric
- PSNR (Peak Signal to Noise Ratio) [29]: PSNR is a widely used metric to assess the quality of a reconstructed or compressed image compared to the original image. This metric measures the ratio between the maximum power of the signal (which is called the peak signal) and the power of the noise that degrades the quality of the image representation (also known as the corrupting noise). Higher PSNR values indicate better image quality because they represent a higher ratio of signal power to noise power.where n is the number of spectral bands in the MSFA moxel.
- SAM (Spectral Angle Metric) [30] calculates the angle between two spectral vectors in a high-dimensional space. Each spectral vector represents the spectral reflectance or irradiance of a pixel over several spectral bands.The smaller the angle between two spectral vectors, the more similar the spectra are considered to be.
- SSIM (Structural Similarity Index Measure) [31]: SSIM is a method used to measure the similarity between two images. This technique compares the structural information, luminance, and contrast of the two images, taking into account the characteristics of the human visual system. Compared to simpler metrics such as Mean Square Error (MSE) or PSNR, SSIM provides a more comprehensive assessment of image similarity by considering perceptual factors. The SSIM value ranges from 0 to 1, where
- ∘
- 1 indicates perfect similarity between images.
- ∘
- 0 indicates no similarity between images.
We use the structural_similarity function of the python skimage.metrics module to compute this metric. - RMSE (Root Mean Square Error) [32]: RMSE is a commonly used metric to evaluate the accuracy of predictions by measuring the average size of the errors between the predicted and actual values in a given set of predictions. The metric is expressed in the same unit as the target value. For example, if the target value is to predict a certain value, and we obtain an RMSE of 10, this indicates that the predicted value varies on average by ±10 from the actual value. The formula for calculating the RMSE is as follows:
4.2. Quantitative Evaluation
- ‘a’ corresponds to a snapshot without displacement
- ‘b’ corresponds to a snapshot after a displacement of 1 pixel on the H-axis
- ‘c’ corresponds to a snapshot after a displacement of 1 pixel on the V-axis
- ‘d’ corresponds to a snapshot after a displacement of 2 pixels on the H-axis
- ‘e’ corresponds to a snapshot after a displacement of 2 pixels on the V-axis
- ‘f’ corresponds to a snapshot after a displacement of 3 pixels on the H-axis
- ‘g’ corresponds to a snapshot after a displacement of 3 pixels on the V-axis
4.3. Qualitative Assessment
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chambino, L.L.; Silva, J.S.; Bernardino, A. Multispectral Facial Recognition: A Review. IEEE Access 2020, 8, 207871–207883. [Google Scholar] [CrossRef]
- Zhang, K.; Zhang, F.; Wan, W.; Yu, H.; Sun, J.; Del Ser, J.; Elyan, E.; Hussain, A. Panchromatic and Multispectral Image Fusion for Remote Sensing and Earth Observation: Concepts, Taxonomy, Literature Review, Evaluation Methodologies and Challenges Ahead. Inf. Fusion 2023, 93, 227–242. [Google Scholar] [CrossRef]
- Ma, F.; Yuan, M.; Kozak, I. Multispectral Imaging: Review of Current Applications. Surv. Ophthalmol. 2023, 68, 889–904. [Google Scholar] [CrossRef] [PubMed]
- Mohammadi, V.; Gouton, P.; Rossé, M.; Katakpe, K.K. Design and Development of Large-Band Dual-MSFA Sensor Camera for Precision Agriculture. Sensors 2023, 24, 64. [Google Scholar] [CrossRef] [PubMed]
- Gebhart, S.C.; Thompson, R.C.; Mahadevan-Jansen, A. Liquid-Crystal Tunable Filter Spectral Imaging for Brain Tumor Demarcation. Appl. Opt. 2007, 46, 1896. [Google Scholar] [CrossRef] [PubMed]
- Harris, S.E.; Wallace, R.W. Acousto-Optic Tunable Filter. J. Opt. Soc. Am. 1969, 59, 744. [Google Scholar] [CrossRef]
- Lapray, P.-J.; Wang, X.; Thomas, J.-B.; Gouton, P. Multispectral Filter Arrays: Recent Advances and Practical Implementation. Sensors 2014, 14, 21626–21659. [Google Scholar] [CrossRef] [PubMed]
- Monno, Y.; Kitao, T.; Tanaka, M.; Okutomi, M. Optimal Spectral Sensitivity Functions for a Single-Camera One-Shot Multispectral Imaging System. In Proceedings of the 2012 19th IEEE International Conference on Image Processing, Orlando, FL, USA, 30 September–3 October 2012; IEEE: Orlando, FL, USA, 2012; pp. 2137–2140. [Google Scholar]
- Rathi, V.; Goyal, P. Generic Multispectral Demosaicking Using Spectral Correlation between Spectral Bands and Pseudo-Panchromatic Image. Signal Process. Image Commun. 2023, 110, 116893. [Google Scholar] [CrossRef]
- Shrestha, R.; Hardeberg, J.Y.; Khan, R. Spatial Arrangement of Color Filter Array for Multispectral Image Acquisition; Widenhorn, R., Nguyen, V., Eds.; San Francisco Airport: San Francisco, CA, USA, 2011; p. 787503. [Google Scholar]
- Monno, Y.; Kikuchi, S.; Tanaka, M.; Okutomi, M. A Practical One-Shot Multispectral Imaging System Using a Single Image Sensor. IEEE Trans. Image Process. 2015, 24, 3048–3059. [Google Scholar] [CrossRef]
- Mohammadi, V.; Sodjinou, S.G.; Katakpe, K.K.; Rossé, M.; Gouton, P. Development of a Multi-Spectral Camera for Computer Vision Applications. In Proceedings of the International Conference on Computer Graphics, Visualization and Computer Vision (WSCG 2022), Pilsen, Czech Republic, 17–20 May 2022. [Google Scholar]
- Thomas, J.-B.; Lapray, P.-J.; Gouton, P.; Clerc, C. Spectral Characterization of a Prototype SFA Camera for Joint Visible and NIR Acquisition. Sensors 2016, 16, 993. [Google Scholar] [CrossRef]
- Monno, Y.; Tanaka, M.; Okutomi, M. Multispectral Demosaicking Using Guided Filter; Battiato, S., Rodricks, B.G., Sampat, N., Imai, F.H., Xiao, F., Eds.; SPIE: Burlingame, CA, USA, 2012; p. 82990O. [Google Scholar]
- Wang, Z.; Zhang, G.; Hu, B. Generic Demosaicking Method for Multispectral Filter Arrays Based on Adaptive Frequency Domain Filtering. In Proceedings of the 2021 4th International Conference on Sensors, Signal and Image Processing, Nanjing, China, 15–17 October 2021; ACM: New York, NY, USA, 2021; pp. 66–71. [Google Scholar]
- Rathi, V.; Goyal, P. Generic Multispectral Demosaicking Based on Directional Interpolation. IEEE Access 2022, 10, 64715–64728. [Google Scholar] [CrossRef]
- Zhang, X.; Dai, Y.; Zhang, G.; Zhang, X.; Hu, B. A Snapshot Multi-Spectral Demosaicing Method for Multi-Spectral Filter Array Images Based on Channel Attention Network. Sensors 2024, 24, 943. [Google Scholar] [CrossRef] [PubMed]
- Monno, Y.; Teranaka, H.; Yoshizaki, K.; Tanaka, M.; Okutomi, M. Single-Sensor RGB-NIR Imaging: High-Quality System Design and Prototype Implementation. IEEE Sens. J. 2019, 19, 497–507. [Google Scholar] [CrossRef]
- Mihoubi, S.; Losson, O.; Mathon, B.; Macaire, L. Multispectral Demosaicing Using Pseudo-Panchromatic Image. IEEE Trans. Comput. Imaging 2017, 3, 982–995. [Google Scholar] [CrossRef]
- Mizutani, J.; Ogawa, S.; Shinoda, K.; Hasegawa, M.; Kato, S. Multispectral Demosaicking Algorithm Based on Inter-Channel Correlation. In Proceedings of the 2014 IEEE Visual Communications and Image Processing Conference, Valletta, Malta, 7–10 December 2014; pp. 474–477. [Google Scholar]
- Brauers, J.; Aach, T. A Color Filter Array Based Multispectral Camera. In Proceedings of the Workshop Farbbildverarbeitung, Ilmenau, Germany, 5–6 October 2006. [Google Scholar]
- Jeong, K.; Kim, S.; Kang, M.G. Multispectral Demosaicing Based on Iterative-Linear-Regression Model for Estimating Pseudo-Panchromatic Image. Sensors 2024, 24, 760. [Google Scholar] [CrossRef] [PubMed]
- Miao, L.; Qi, H.; Ramanath, R.; Snyder, W.E. Binary Tree-Based Generic Demosaicking Algorithm for Multispectral Filter Arrays. IEEE Trans. Image Process. 2006, 15, 3550–3558. [Google Scholar] [CrossRef] [PubMed]
- Rathi, V.; Goyal, P. Convolution Filter Based Efficient Multispectral Image Demosaicking for Compact MSFAs. In Proceedings of the 16th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications, SCITEPRESS—Science and Technology Publications, Virtual Event, 8–10 February 2021; pp. 112–121. [Google Scholar]
- Liu, S.; Zhang, Y.; Chen, J.; Lim, K.P.; Rahardja, S. A Deep Joint Network for Multispectral Demosaicking Based on Pseudo-Panchromatic Images. IEEE J. Sel. Top. Signal Process. 2022, 16, 622–635. [Google Scholar] [CrossRef]
- Zhao, B.; Zheng, J.; Dong, Y.; Shen, N.; Yang, J.; Cao, Y.; Cao, Y. PPI Edge Infused Spatial–Spectral Adaptive Residual Network for Multispectral Filter Array Image Demosaicing. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5405214. [Google Scholar] [CrossRef]
- Miao, L.; Qi, H. The Design and Evaluation of a Generic Method for Generating Mosaicked Multispectral Filter Arrays. IEEE Trans. Image Process. 2006, 15, 2780–2791. [Google Scholar] [CrossRef]
- Thomas, J.-B.; Lapray, P.-J.; Gouton, P. HDR Imaging Pipeline for Spectral Filter Array Cameras. In Image Analysis; Sharma, P., Bianchi, F.M., Eds.; Lecture Notes in Computer Science; Springer International Publishing: Cham, Switzerland, 2017; Volume 10270, pp. 401–412. ISBN 978-3-319-59128-5. [Google Scholar]
- Huynh-Thu, Q.; Ghanbari, M. Scope of Validity of PSNR in Image/Video Quality Assessment. Electron. Lett. 2008, 44, 800. [Google Scholar] [CrossRef]
- Kruse, F.A.; Lefkoff, A.B.; Boardman, J.W.; Heidebrecht, K.B.; Shapiro, A.T.; Barloon, P.J.; Goetz, A.F.H. The spectral image processing system (SIPS)—interactive visualization and analysis of imaging spectrometer data. Remote Sens. Environ. 1993, 44, 145–163. [Google Scholar] [CrossRef]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image Quality Assessment: From Error Visibility to Structural Similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef] [PubMed]
- Hodson, T.O. Root-Mean-Square Error (RMSE) or Mean Absolute Error (MAE): When to Use Them or Not. Geosci. Model Dev. 2022, 15, 5481–5487. [Google Scholar] [CrossRef]
- Ding, K.; Wang, M.; Chen, M.; Wang, X.; Ni, K.; Zhou, Q.; Bai, B. Snapshot Spectral Imaging: From Spatial-Spectral Mapping to Metasurface-Based Imaging. Nanophotonics 2024, 13, 1303–1330. [Google Scholar] [CrossRef]








| Snapshots | 1 | 2 | 3 | 4 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Displacements | a | ab | ac | ad | ae | af | ag | abc | acf | abg | afg | abd | acg | abdf | aceg |
| Butterfly | 25.46 | 26.07 | 25.94 | 25.56 | 25.55 | 26.07 | 25.94 | 26.53 | 26.44 | 26.47 | 26.53 | 26.47 | 26.44 | 26.06 | 25.89 |
| Butterfly2 | 24.19 | 24.49 | 24.66 | 24.35 | 24.35 | 24.49 | 24.66 | 24.90 | 24.62 | 24.70 | 24.90 | 24.71 | 24.71 | 24.44 | 24.59 |
| Butterfly3 | 28.31 | 28.56 | 28.91 | 28.39 | 28.39 | 28.56 | 28.90 | 29.10 | 28.95 | 29.03 | 29.10 | 29.01 | 28.99 | 28.51 | 28.83 |
| Butterfly4 | 27.86 | 28.13 | 28.49 | 27.94 | 27.93 | 28.13 | 28.49 | 28.70 | 28.59 | 28.62 | 28.70 | 28.60 | 28.53 | 28.08 | 28.34 |
| Butterfly5 | 28.38 | 29.06 | 28.56 | 28.46 | 28.46 | 29.07 | 28.56 | 29.17 | 29.09 | 29.09 | 29.17 | 29.06 | 29.01 | 29.01 | 28.44 |
| Butterfly6 | 25.84 | 26.36 | 26.20 | 25.97 | 25.96 | 26.36 | 26.20 | 26.66 | 26.54 | 26.54 | 26.65 | 26.54 | 26.53 | 26.32 | 26.14 |
| Butterfly7 | 27.54 | 27.88 | 28.20 | 27.64 | 27.63 | 27.88 | 28.20 | 28.51 | 28.34 | 28.43 | 28.51 | 28.43 | 28.40 | 27.85 | 28.15 |
| Butterfly8 | 27.97 | 28.08 | 28.64 | 28.04 | 28.04 | 28.09 | 28.64 | 28.69 | 28.40 | 28.56 | 28.68 | 28.51 | 28.48 | 28.00 | 28.49 |
| Colorchart | 27.32 | 27.68 | 27.90 | 27.40 | 27.40 | 27.68 | 27.90 | 28.20 | 28.20 | 28.20 | 28.20 | 28.18 | 28.14 | 27.66 | 27.83 |
| CD | 33.87 | 34.12 | 34.20 | 34.01 | 34.02 | 34.12 | 34.20 | 34.39 | 34.31 | 34.29 | 34.38 | 34.31 | 34.32 | 34.13 | 34.19 |
| Cloth2 | 27.48 | 28.12 | 27.73 | 27.69 | 27.68 | 28.11 | 27.73 | 28.37 | 28.13 | 28.15 | 28.35 | 28.19 | 28.24 | 28.11 | 27.75 |
| Cloth3 | 29.86 | 30.15 | 30.11 | 30.09 | 30.08 | 30.15 | 30.12 | 30.27 | 30.02 | 30.05 | 30.27 | 29.87 | 30.05 | 29.89 | 30.05 |
| Cloth6 | 29.19 | 29.86 | 29.43 | 29.35 | 29.34 | 29.86 | 29.43 | 30.01 | 29.82 | 29.84 | 29.99 | 29.77 | 29.80 | 29.71 | 29.35 |
| Flower | 29.17 | 29.53 | 29.61 | 29.28 | 29.28 | 29.53 | 29.61 | 29.89 | 29.69 | 29.80 | 29.89 | 29.76 | 29.77 | 29.46 | 29.54 |
| Flower2 | 28.15 | 28.83 | 28.55 | 28.23 | 28.23 | 28.84 | 28.55 | 29.23 | 29.13 | 29.14 | 29.23 | 29.13 | 29.12 | 28.80 | 28.50 |
| Flower3 | 30.91 | 31.31 | 31.22 | 31.03 | 31.03 | 31.30 | 31.22 | 31.55 | 31.41 | 31.45 | 31.54 | 31.45 | 31.45 | 31.27 | 31.18 |
| Party | 25.97 | 26.42 | 26.17 | 26.10 | 26.09 | 26.41 | 26.16 | 26.47 | 26.38 | 26.39 | 26.45 | 26.24 | 26.32 | 26.22 | 26.07 |
| Tape | 26.35 | 26.59 | 27.17 | 26.56 | 26.56 | 26.59 | 27.17 | 27.34 | 27.15 | 27.17 | 27.33 | 27.13 | 27.24 | 26.49 | 27.24 |
| Tape2 | 25.25 | 25.68 | 25.84 | 25.55 | 25.55 | 25.68 | 25.84 | 26.15 | 25.88 | 25.99 | 26.13 | 26.11 | 26.07 | 25.75 | 25.88 |
| Tshirts2 | 23.42 | 23.80 | 23.72 | 23.59 | 23.59 | 23.81 | 23.73 | 23.99 | 23.71 | 23.74 | 23.98 | 23.53 | 23.71 | 23.47 | 23.64 |
| Average | 27.62 | 28.04 | 28.06 | 27.76 | 27.76 | 28.04 | 28.06 | 28.41 | 28.24 | 28.28 | 28.40 | 28.25 | 28.27 | 27.96 | 28.00 |
| Snapshots | 1 | 2 | 3 | 4 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Displacements | a | ab | ac | ad | ae | af | ag | abc | acf | abg | afg | abd | acg | abdf | aceg |
| Butterfly | 1.98 | 1.55 | 1.61 | 1.50 | 1.50 | 1.55 | 1.61 | 1.42 | 1.48 | 1.46 | 1.42 | 1.14 | 1.01 | 1.23 | 1.10 |
| Butterfly2 | 4.29 | 3.61 | 3.63 | 3.27 | 3.27 | 3.60 | 3.63 | 3.29 | 3.43 | 3.42 | 3.29 | 2.57 | 2.58 | 2.66 | 2.68 |
| Butterfly3 | 4.87 | 4.37 | 4.38 | 4.27 | 4.27 | 4.37 | 4.38 | 4.23 | 4.34 | 4.32 | 4.22 | 3.98 | 3.98 | 4.03 | 4.05 |
| Butterfly4 | 3.76 | 3.36 | 3.41 | 3.33 | 3.33 | 3.36 | 3.41 | 3.26 | 3.37 | 3.36 | 3.25 | 3.12 | 3.08 | 3.15 | 3.14 |
| Butterfly5 | 3.23 | 2.70 | 2.71 | 2.56 | 2.56 | 2.70 | 2.72 | 2.49 | 2.61 | 2.60 | 2.50 | 2.10 | 2.08 | 2.18 | 2.17 |
| Butterfly6 | 2.70 | 2.33 | 2.35 | 2.27 | 2.27 | 2.32 | 2.35 | 2.18 | 2.27 | 2.25 | 2.18 | 1.99 | 1.96 | 2.06 | 2.03 |
| Butterfly7 | 3.96 | 3.36 | 3.39 | 3.31 | 3.30 | 3.36 | 3.39 | 3.30 | 3.41 | 3.39 | 3.29 | 3.15 | 3.08 | 3.19 | 3.11 |
| Butterfly8 | 3.53 | 3.25 | 3.13 | 2.79 | 2.79 | 3.26 | 3.12 | 2.85 | 3.03 | 3.01 | 2.85 | 2.10 | 2.46 | 2.16 | 2.57 |
| Colorchart | 5.16 | 4.67 | 4.30 | 4.16 | 4.17 | 4.67 | 4.30 | 4.18 | 4.26 | 4.25 | 4.18 | 2.96 | 3.65 | 3.04 | 3.76 |
| CD | 3.65 | 3.40 | 3.09 | 3.06 | 3.06 | 3.40 | 3.09 | 2.99 | 3.12 | 3.10 | 2.99 | 2.24 | 2.75 | 2.32 | 2.85 |
| Cloth2 | 3.73 | 3.10 | 3.24 | 2.99 | 2.99 | 3.10 | 3.24 | 2.99 | 3.04 | 3.03 | 2.99 | 2.60 | 2.50 | 2.66 | 2.58 |
| Cloth3 | 4.40 | 3.57 | 3.59 | 3.31 | 3.30 | 3.57 | 3.59 | 3.39 | 3.40 | 3.39 | 3.39 | 2.57 | 2.51 | 2.64 | 2.60 |
| Cloth6 | 4.86 | 4.00 | 3.98 | 3.67 | 3.68 | 4.00 | 3.98 | 3.70 | 3.88 | 3.86 | 3.71 | 2.86 | 2.92 | 2.93 | 3.01 |
| Flower | 3.21 | 2.81 | 2.85 | 2.77 | 2.77 | 2.81 | 2.84 | 2.69 | 2.76 | 2.75 | 2.69 | 2.50 | 2.53 | 2.54 | 2.63 |
| Flower2 | 3.25 | 2.85 | 2.88 | 2.79 | 2.79 | 2.85 | 2.88 | 2.73 | 2.82 | 2.80 | 2.72 | 2.53 | 2.53 | 2.57 | 2.61 |
| Flower3 | 3.74 | 3.27 | 3.37 | 3.26 | 3.26 | 3.27 | 3.37 | 3.17 | 3.26 | 3.25 | 3.16 | 3.01 | 2.99 | 3.05 | 3.10 |
| Party | 4.25 | 3.58 | 3.34 | 3.12 | 3.13 | 3.58 | 3.34 | 3.10 | 3.28 | 3.27 | 3.10 | 1.95 | 2.44 | 2.03 | 2.55 |
| Tape | 2.26 | 1.97 | 1.99 | 1.96 | 1.96 | 1.97 | 1.99 | 1.82 | 1.92 | 1.90 | 1.83 | 1.70 | 1.70 | 1.78 | 1.78 |
| Tape2 | 5.07 | 4.40 | 4.44 | 4.30 | 4.30 | 4.40 | 4.44 | 4.26 | 4.41 | 4.39 | 4.25 | 4.00 | 3.97 | 4.05 | 4.03 |
| Tshirts2 | 5.43 | 4.50 | 4.36 | 3.99 | 3.99 | 4.50 | 4.37 | 4.05 | 4.16 | 4.14 | 4.05 | 2.76 | 3.08 | 2.84 | 3.17 |
| Average | 3.87 | 3.33 | 3.30 | 3.13 | 3.13 | 3.33 | 3.30 | 3.11 | 3.21 | 3.20 | 3.10 | 2.59 | 2.69 | 2.65 | 2.78 |
| Snapshots | 1 | 2 | 3 | 4 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Displacements | a | ab | ac | ad | ae | af | ag | abc | acf | abg | afg | abd | acg | abdf | aceg |
| Butterfly | 0.692 | 0.717 | 0.719 | 0.725 | 0.725 | 0.717 | 0.719 | 0.729 | 0.710 | 0.711 | 0.729 | 0.722 | 0.722 | 0.723 | 0.723 |
| Butterfly2 | 0.659 | 0.686 | 0.686 | 0.695 | 0.695 | 0.686 | 0.686 | 0.700 | 0.677 | 0.677 | 0.699 | 0.688 | 0.692 | 0.690 | 0.695 |
| Butterfly3 | 0.674 | 0.692 | 0.691 | 0.694 | 0.694 | 0.692 | 0.691 | 0.696 | 0.680 | 0.680 | 0.697 | 0.683 | 0.682 | 0.686 | 0.684 |
| Butterfly4 | 0.677 | 0.697 | 0.697 | 0.701 | 0.701 | 0.697 | 0.698 | 0.704 | 0.685 | 0.686 | 0.705 | 0.690 | 0.688 | 0.693 | 0.690 |
| Butterfly5 | 0.682 | 0.710 | 0.710 | 0.718 | 0.718 | 0.709 | 0.710 | 0.723 | 0.703 | 0.703 | 0.723 | 0.717 | 0.719 | 0.717 | 0.720 |
| Butterfly6 | 0.686 | 0.707 | 0.707 | 0.711 | 0.711 | 0.706 | 0.707 | 0.715 | 0.694 | 0.694 | 0.715 | 0.699 | 0.699 | 0.702 | 0.702 |
| Butterfly7 | 0.638 | 0.660 | 0.658 | 0.664 | 0.663 | 0.660 | 0.658 | 0.667 | 0.647 | 0.647 | 0.668 | 0.653 | 0.653 | 0.655 | 0.656 |
| Butterfly8 | 0.636 | 0.658 | 0.659 | 0.662 | 0.662 | 0.658 | 0.659 | 0.663 | 0.651 | 0.650 | 0.663 | 0.656 | 0.653 | 0.659 | 0.654 |
| Colorchart | 0.628 | 0.656 | 0.649 | 0.658 | 0.659 | 0.655 | 0.649 | 0.660 | 0.646 | 0.646 | 0.660 | 0.651 | 0.655 | 0.653 | 0.658 |
| CD | 0.547 | 0.597 | 0.607 | 0.623 | 0.622 | 0.597 | 0.607 | 0.631 | 0.598 | 0.600 | 0.629 | 0.634 | 0.639 | 0.632 | 0.638 |
| Cloth2 | 0.567 | 0.606 | 0.606 | 0.619 | 0.619 | 0.606 | 0.606 | 0.624 | 0.598 | 0.598 | 0.623 | 0.619 | 0.618 | 0.621 | 0.618 |
| Cloth3 | 0.620 | 0.650 | 0.648 | 0.657 | 0.657 | 0.649 | 0.648 | 0.661 | 0.639 | 0.639 | 0.660 | 0.651 | 0.650 | 0.654 | 0.653 |
| Cloth6 | 0.671 | 0.694 | 0.694 | 0.699 | 0.699 | 0.694 | 0.694 | 0.702 | 0.687 | 0.687 | 0.702 | 0.694 | 0.694 | 0.696 | 0.696 |
| Flower | 0.671 | 0.701 | 0.704 | 0.712 | 0.712 | 0.701 | 0.704 | 0.717 | 0.697 | 0.698 | 0.716 | 0.716 | 0.714 | 0.717 | 0.715 |
| Flower2 | 0.759 | 0.773 | 0.775 | 0.777 | 0.777 | 0.773 | 0.775 | 0.779 | 0.768 | 0.769 | 0.779 | 0.772 | 0.772 | 0.773 | 0.773 |
| Flower3 | 0.732 | 0.752 | 0.753 | 0.757 | 0.757 | 0.752 | 0.752 | 0.760 | 0.746 | 0.746 | 0.760 | 0.753 | 0.753 | 0.755 | 0.754 |
| Party | 0.733 | 0.751 | 0.750 | 0.754 | 0.754 | 0.751 | 0.750 | 0.757 | 0.744 | 0.744 | 0.757 | 0.749 | 0.748 | 0.751 | 0.749 |
| Tape | 0.662 | 0.679 | 0.680 | 0.681 | 0.681 | 0.679 | 0.680 | 0.683 | 0.667 | 0.667 | 0.683 | 0.667 | 0.666 | 0.670 | 0.669 |
| Tape2 | 0.612 | 0.637 | 0.636 | 0.644 | 0.644 | 0.637 | 0.636 | 0.649 | 0.620 | 0.620 | 0.650 | 0.627 | 0.635 | 0.629 | 0.639 |
| Tshirts2 | 0.613 | 0.660 | 0.658 | 0.675 | 0.675 | 0.660 | 0.658 | 0.681 | 0.654 | 0.653 | 0.680 | 0.682 | 0.680 | 0.682 | 0.680 |
| Average | 0.658 | 0.684 | 0.684 | 0.691 | 0.691 | 0.684 | 0.684 | 0.695 | 0.676 | 0.676 | 0.695 | 0.686 | 0.687 | 0.688 | 0.688 |
| Snapshots | 1 | 2 | 3 | 4 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Displacements | a | ab | ac | ad | ae | af | ag | abc | acf | abg | afg | abd | acg | abdf | aceg |
| Butterfly | 5.54 | 5.13 | 5.16 | 5.25 | 5.25 | 5.13 | 5.17 | 4.91 | 5.03 | 5.01 | 4.92 | 4.89 | 4.88 | 5.03 | 5.06 |
| Butterfly2 | 8.23 | 7.74 | 7.68 | 7.64 | 7.65 | 7.73 | 7.68 | 7.40 | 7.71 | 7.67 | 7.40 | 7.34 | 7.33 | 7.46 | 7.39 |
| Butterfly3 | 3.61 | 3.41 | 3.37 | 3.44 | 3.44 | 3.41 | 3.37 | 3.27 | 3.34 | 3.32 | 3.27 | 3.25 | 3.25 | 3.36 | 3.31 |
| Butterfly4 | 3.61 | 3.39 | 3.34 | 3.42 | 3.42 | 3.39 | 3.34 | 3.24 | 3.31 | 3.29 | 3.23 | 3.23 | 3.23 | 3.34 | 3.29 |
| Butterfly5 | 3.46 | 3.21 | 3.30 | 3.30 | 3.30 | 3.21 | 3.30 | 3.16 | 3.21 | 3.21 | 3.16 | 3.15 | 3.15 | 3.17 | 3.26 |
| Butterfly6 | 5.84 | 5.44 | 5.48 | 5.50 | 5.50 | 5.45 | 5.48 | 5.25 | 5.39 | 5.38 | 5.26 | 5.21 | 5.22 | 5.30 | 5.35 |
| Butterfly7 | 3.71 | 3.48 | 3.45 | 3.54 | 3.54 | 3.48 | 3.45 | 3.31 | 3.40 | 3.38 | 3.31 | 3.31 | 3.30 | 3.44 | 3.38 |
| Butterfly8 | 4.27 | 4.05 | 3.95 | 4.03 | 4.03 | 4.05 | 3.95 | 3.87 | 3.98 | 3.95 | 3.87 | 3.85 | 3.84 | 3.98 | 3.85 |
| Colorchart | 3.26 | 3.04 | 3.04 | 3.11 | 3.11 | 3.04 | 3.04 | 2.95 | 2.97 | 2.97 | 2.95 | 2.94 | 2.93 | 3.04 | 3.01 |
| CD | 2.31 | 2.21 | 2.23 | 2.23 | 2.23 | 2.21 | 2.23 | 2.17 | 2.21 | 2.21 | 2.17 | 2.18 | 2.17 | 2.20 | 2.20 |
| Cloth2 | 6.08 | 5.79 | 5.82 | 5.66 | 5.66 | 5.79 | 5.82 | 5.51 | 5.79 | 5.78 | 5.51 | 5.46 | 5.51 | 5.48 | 5.63 |
| Cloth3 | 5.15 | 4.96 | 4.93 | 4.93 | 4.93 | 4.96 | 4.93 | 4.85 | 5.02 | 5.00 | 4.86 | 5.00 | 4.91 | 5.00 | 4.88 |
| Cloth6 | 5.68 | 5.35 | 5.41 | 5.38 | 5.39 | 5.35 | 5.41 | 5.25 | 5.41 | 5.40 | 5.25 | 5.32 | 5.31 | 5.33 | 5.36 |
| Flower | 4.86 | 4.61 | 4.60 | 4.62 | 4.62 | 4.61 | 4.60 | 4.49 | 4.59 | 4.57 | 4.49 | 4.47 | 4.47 | 4.52 | 4.53 |
| Flower2 | 5.05 | 4.73 | 4.78 | 4.80 | 4.80 | 4.73 | 4.79 | 4.60 | 4.71 | 4.70 | 4.61 | 4.60 | 4.60 | 4.64 | 4.71 |
| Flower3 | 3.81 | 3.60 | 3.62 | 3.61 | 3.61 | 3.60 | 3.62 | 3.52 | 3.60 | 3.59 | 3.52 | 3.50 | 3.50 | 3.52 | 3.55 |
| Party | 5.86 | 5.51 | 5.61 | 5.59 | 5.59 | 5.51 | 5.61 | 5.45 | 5.51 | 5.51 | 5.46 | 5.45 | 5.45 | 5.46 | 5.56 |
| Tape | 5.82 | 5.52 | 5.44 | 5.44 | 5.44 | 5.51 | 5.44 | 5.25 | 5.45 | 5.44 | 5.26 | 5.30 | 5.22 | 5.43 | 5.21 |
| Tape2 | 7.93 | 7.34 | 7.32 | 7.26 | 7.27 | 7.34 | 7.32 | 7.01 | 7.30 | 7.27 | 7.02 | 6.92 | 6.93 | 7.04 | 7.01 |
| Tshirts2 | 8.36 | 7.77 | 7.75 | 7.69 | 7.7 | 7.77 | 7.75 | 7.44 | 7.73 | 7.7 | 7.45 | 7.35 | 7.36 | 7.47 | 7.44 |
| Average | 4.95 | 4.66 | 4.66 | 4.67 | 4.67 | 4.66 | 4.66 | 4.50 | 4.63 | 4.61 | 4.50 | 4.49 | 4.49 | 4.56 | 4.55 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yao, J.Y.A.; Ayikpa, K.J.; Gouton, P.; Kone, T. A Multi-Shot Approach for Spatial Resolution Improvement of Multispectral Images from an MSFA Sensor. J. Imaging 2024, 10, 140. https://doi.org/10.3390/jimaging10060140
Yao JYA, Ayikpa KJ, Gouton P, Kone T. A Multi-Shot Approach for Spatial Resolution Improvement of Multispectral Images from an MSFA Sensor. Journal of Imaging. 2024; 10(6):140. https://doi.org/10.3390/jimaging10060140
Chicago/Turabian StyleYao, Jean Yves Aristide, Kacoutchy Jean Ayikpa, Pierre Gouton, and Tiemoman Kone. 2024. "A Multi-Shot Approach for Spatial Resolution Improvement of Multispectral Images from an MSFA Sensor" Journal of Imaging 10, no. 6: 140. https://doi.org/10.3390/jimaging10060140
APA StyleYao, J. Y. A., Ayikpa, K. J., Gouton, P., & Kone, T. (2024). A Multi-Shot Approach for Spatial Resolution Improvement of Multispectral Images from an MSFA Sensor. Journal of Imaging, 10(6), 140. https://doi.org/10.3390/jimaging10060140








